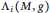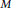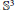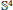Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Saparbayeva, B. T.
2016.
On the Schrödinger operator connected with a family of Hamiltonian-minimal Lagrangian surfaces in ℂP 2.
Siberian Mathematical Journal,
Vol. 57,
Issue. 6,
p.
1077.
Karpukhin, Mikhail A.
2016.
Upper Bounds for the First Eigenvalue of the Laplacian on Non-Orientable Surfaces.
International Mathematics Research Notices,
Vol. 2016,
Issue. 20,
p.
6200.
Nadirashvili, Nikolai S.
and
Penskoi, Alexei V.
2018.
An isoperimetric inequality for the second non-zero eigenvalue of the Laplacian on the projective plane.
Geometric and Functional Analysis,
Vol. 28,
Issue. 5,
p.
1368.
Cianci, Donato
Karpukhin, Mikhail
and
Medvedev, Vladimir
2019.
On branched minimal immersions of surfaces by first eigenfunctions.
Annals of Global Analysis and Geometry,
Vol. 56,
Issue. 4,
p.
667.
Penskoi, Alexei Viktorovich
2019.
Изопериметрические неравенства для высших собственных значений оператора Лапласа-Бельтрами на поверхностях.
Труды Математического института имени В. А. Стеклова,
Vol. 305,
Issue. ,
p.
291.
Penskoi, Alexei V.
2019.
Isoperimetric Inequalities for Higher Eigenvalues of the Laplace—Beltrami Operator on Surfaces.
Proceedings of the Steklov Institute of Mathematics,
Vol. 305,
Issue. 1,
p.
270.
Morozov, Egor
2024.
Index of Bipolar Surfaces to Otsuki Tori.
Mathematical Physics, Analysis and Geometry,
Vol. 27,
Issue. 4,