Hostname: page-component-7dd5485656-frp75 Total loading time: 0 Render date: 2025-10-31T23:15:06.574Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniqueness of 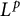$L^p$ subsolutions to the heat equation on Finsler measure spaces

Part of: Global differential geometry Partial differential equations on manifolds; differential operators

Published online by Cambridge University Press:  05 June 2023

Qiaoling Xia Open the ORCID record for Qiaoling Xia [Opens in a new window]
Qiaoling Xia*
Affiliation:
Department of Mathematics, School of Sciences, Hangzhou Dianzi University, Hangzhou, Zhejiang Province 310018, P.R. China
*
e-mail: xiaqiaoling@hdu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 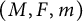$(M, F, m)$ be a forward complete Finsler measure space. In this paper, we prove that any nonnegative global subsolution in 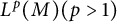$L^p(M)(p>1)$ to the heat equation on 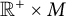$\mathbb R^+\times M$ is uniquely determined by the initial data. Moreover, we give an 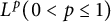$L^p(0<p\leq 1)$ Liouville-type theorem for nonnegative subsolutions u to the heat equation on $\mathbb R\times M$ by establishing the local 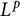$L^p$ mean value inequality for u on M with Ric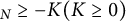$_N\geq -K(K\geq 0)$.

Keywords

Finsler measure spaceweighted Ricci curvatureheat equationmean value inequality

MSC classification

Primary: 53C60: Finsler spaces and generalizations (areal metrics)
Secondary: 58J35: Heat and other parabolic equation methods 53C23: Global geometric and topological methods (à la Gromov); differential geometric analysis on metric spaces

Information

Type
Article
Information
Canadian Mathematical Bulletin , Volume 67 , Issue 1 , March 2024 , pp. 166 - 175
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This paper is supported by the NNSFC (Grant No. 12071423) and the Scientific Research Foundation of HDU (Grant No. KYS075621060).

References

Kristály, A. and Rudas, I. J., Elliptic problems on the ball endowed with Funk-type metrics . Nonlinear Anal. 119(2015), 199–208.CrossRefGoogle Scholar
Li, P., Uniqueness of ${L}^1$ solutions for the Laplace equation and the heat equation on Riemannian manifold . J. Diff. Geom. 20(1984), 447–457.Google Scholar
Ohta Finsler, S., Interpolation inequalities . Calc. Var. PDE 36(2009), 211–249.CrossRefGoogle Scholar
Ohta, S. and Sturm, K.-T., Heat flow on Finsler manifolds . Comm. Pure Appl. Math. 62(2009), 1386–1433.CrossRefGoogle Scholar
Ohta, S. and Sturm, K.-T., Bochner–Weitzenböck formula and Li–Yau estimates on Finsler manifolds . Adv. Math. 252(2014), 429–448.CrossRefGoogle Scholar
Schoen, R. and Yau, S.-T., Lectures on differential geometry, International Press, Cambridge, MA, 1994.Google Scholar
Shen, Z., Lectures on Finsler geometry, World Scientific Publishing Co., Singapore, 2001.CrossRefGoogle Scholar
Wu, B., Comparison theorems in Finsler geometry with weighted curvature bounds and related results . J. Korean Math. Soc. 52(2015), no. 3, 603–624.CrossRefGoogle Scholar
Xia, C., Local gradient estimate for harmonic functions on Finsler manifolds . Calc. Var. PDE 51(2014), 849–865.CrossRefGoogle Scholar
Xia, Q., Local and global gradient estimates for Finsler $p$ -harmonic functions . Commu. Anal. Geom. 30(2022), no. 2, 451–500.CrossRefGoogle Scholar
Xia, Q., Li–Yau’s estimates on Finsler manifolds . J. Geom. Anal. 33(2023), no. 49, 1–33.Google Scholar
Xia, Q., Generalized Li-Yau's inequalities on Finsler manifolds. Preprint.Google Scholar
Xia, Q., Some ${L}^p$ -Liouville theorems on Finsler manifolds . Diff. Geom. Appl. 87(2023), 101987.CrossRefGoogle Scholar
Zhang, F. and Xia, Q., Some Liouville-type theorems for harmonic functions on Finsler manifolds . J. Math. Anal. Appl. 417(2014), 979–995.CrossRefGoogle Scholar