Hostname: page-component-7dd5485656-npwhs Total loading time: 0 Render date: 2025-10-31T00:22:29.618Z Has data issue: false hasContentIssue false
  • English
  • Français

Vanishing Fourier Transforms and Generalized Differences in 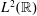$L^{2}(\mathbb{R})$

Part of: Harmonic analysis in one variable

Published online by Cambridge University Press:  16 October 2018

Rodney Nillsen
Rodney Nillsen*
Affiliation:
Department of Mathematics and Applied Statistics, University of Wollongong, Wollongong, NSW 2522, Australia Email: nillsen@uow.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \mathbb{R}$ and 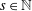$s\in \mathbb{N}$ be given. Let 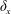$\unicode[STIX]{x1D6FF}_{x}$ denote the Dirac measure at 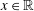$x\in \mathbb{R}$, and let $\ast$ denote convolution. If 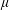$\unicode[STIX]{x1D707}$ is a measure, 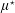$\unicode[STIX]{x1D707}^{\star }$ is the measure that assigns to each Borel set 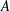$A$ the value 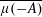$\overline{\unicode[STIX]{x1D707}(-A)}$. If 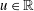$u\in \mathbb{R}$, we put 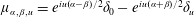$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},u}=e^{iu(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})/2}\unicode[STIX]{x1D6FF}_{0}-e^{iu(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})/2}\unicode[STIX]{x1D6FF}_{u}$. Then we call a function 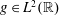$g\in L^{2}(\mathbb{R})$ a generalized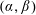$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$-difference of order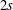$2s$ if for some 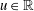$u\in \mathbb{R}$ and 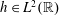$h\in L^{2}(\mathbb{R})$ we have $g=[\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},u}+\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},u}^{\star }]^{s}\ast h$. We denote by 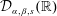${\mathcal{D}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},s}(\mathbb{R})$ the vector space of all functions 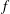$f$ in 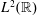$L^{2}(\mathbb{R})$ such that 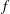$f$ is a finite sum of generalized 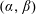$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$-differences of order 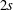$2s$. It is shown that every function in 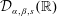${\mathcal{D}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},s}(\mathbb{R})$ is a sum of 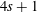$4s+1$ generalized $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$-differences of order 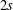$2s$. Letting 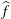$\widehat{f}$ denote the Fourier transform of a function 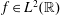$f\in L^{2}(\mathbb{R})$, it is shown that 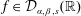$f\in {\mathcal{D}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},s}(\mathbb{R})$ if and only if 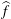$\widehat{f}$  “vanishes” near $\unicode[STIX]{x1D6FC}$ and 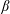$\unicode[STIX]{x1D6FD}$ at a rate comparable with 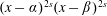$(x-\unicode[STIX]{x1D6FC})^{2s}(x-\unicode[STIX]{x1D6FD})^{2s}$. In fact, ${\mathcal{D}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},s}(\mathbb{R})$ is a Hilbert space where the inner product of functions 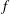$f$ and 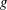$g$ is 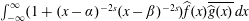$\int _{-\infty }^{\infty }(1+(x-\unicode[STIX]{x1D6FC})^{-2s}(x-\unicode[STIX]{x1D6FD})^{-2s})\widehat{f}(x)\overline{\widehat{g}(x)}\,dx$. Letting 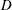$D$ denote differentiation, and letting 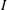$I$ denote the identity operator, the operator 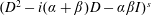$(D^{2}-i(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})D-\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}I)^{s}$ is bounded with multiplier 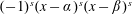$(-1)^{s}(x-\unicode[STIX]{x1D6FC})^{s}(x-\unicode[STIX]{x1D6FD})^{s}$, and the Sobolev subspace of 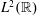$L^{2}(\mathbb{R})$ of order 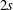$2s$ can be given a norm equivalent to the usual one so that 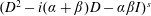$(D^{2}-i(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})D-\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}I)^{s}$ becomes an isometry onto the Hilbert space 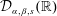${\mathcal{D}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},s}(\mathbb{R})$. So a space ${\mathcal{D}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},s}(\mathbb{R})$ may be regarded as a type of Sobolev space having a negative index.

Keywords

Fourier transformgeneralized differenceHilbert spacemultiplier

MSC classification

Primary: 42A38: Fourier and Fourier-Stieltjes transforms and other transforms of Fourier type 42A45: Multipliers

Information

Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 2 , June 2019 , pp. 393 - 404
Copyright
© Canadian Mathematical Society 2018 

References

Bourgain, J., Translation invariant forms on L p (G), 1 < p < ∞ . Ann. Inst. Fourier (Grenoble) 36(1986), 97–104.Google Scholar
Johnson, B. E., A proof of the translation invariant form conjecture for L 2(G) . Bull. Sci. Math. 107(1983), 301–310.Google Scholar
Meisters, G., Some discontinuous translation-invariant linear forms . J. Funct. Anal. 12(1973), 199–210.Google Scholar
Meisters, G., Some problems and results on translation-invariant linear forms . In: Lecture Notes in Math., 975, eds. Bachar, J. M. and Bade, W. G., et al. Springer, New York, 1983, pp. 423–444.Google Scholar
Meisters, G. and  Schmidt, W., Translation invariant linear forms on L 2(G) for compact abelian groups G . J. Funct. Anal. 11(1972), 407–424.Google Scholar
Nillsen, R., Banach spaces of functions and distributions characterized by singular integrals involving the Fourier transform . J. Funct. Anal. 110(1992), 73–95.Google Scholar
Nillsen, R., Difference spaces and Invariant Linear Forms. Lecture Notes in Math., 1586, Springer, Berlin–Heidelberg–New York, 1994.Google Scholar
Nillsen, R., Vanishing Fourier coefficients and the expression of functions in L 2(T) as sums of generalized differences . J. Math. Anal. Appl. 455(2017), 1425–1443.Google Scholar
Ross, K. A., A trip from classical to abstract Fourier analysis . Notices Amer. Math. Soc. 61(2014), 1032–1038.Google Scholar
Stromberg, K. R., An Introduction to Classical Real Analysis. Wadsworth, Belmont, 1981.Google Scholar