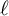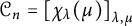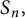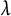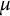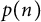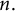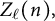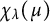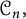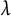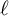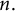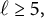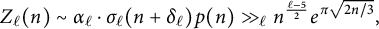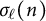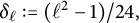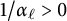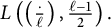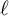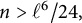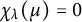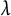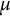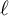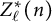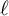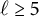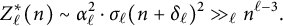1 Introduction and statement of results
Let
$\mathcal {C}_n =\left [\chi _{\lambda }(\mu )\right ]_{\lambda ,\mu }$
be the usual character table (see, for example, [Reference James and Kerber6, Reference Sagan13, Reference Stanley14]) for the symmetric group
$S_n,$
where the indices
$\lambda $
and
$\mu $
both vary over the
$p(n)$
many integer partitions of n. Confirming conjectures of Miller [Reference Miller9], Peluse and Soundararajan [Reference Peluse11, Reference Peluse and Soundararajan12] recently proved that if
$\ell $
is prime, then almost all of the
$p(n)^2$
entries in
$\mathcal {C}_n,$
as
$n\rightarrow +\infty ,$
are multiples of
$\ell .$
We note that Miller conjectured that the same conclusion holds for arbitrary prime powers, a claim which remains open.
In recent papers [Reference Miller8, Reference Miller9], Miller raised the problem of determining the limiting behavior of
$Z(n),$
the number of zero entries in
$\mathcal {C}_n.$
Despite the remarkable theorem of Peluse and Soundararajan, little is known. Moreover, due to the rapid growth of
$p(n),$
it is computationally infeasible to compute many values of
$Z(n).$
Consequently, there are no conjectures that are supported with substantial numerics. For example, is there a limiting proportion for the zeros in
$\mathcal {C}_n$
? Such a proportion would be given by the limit
$$ \begin{align*}\lim_{n\rightarrow +\infty} \frac{Z(n)}{p(n)^2}. \end{align*} $$
Limited numerics suggest that such a limit might exist, and might be
$\approx 0.36$
(see Table 3 of [Reference Miller9]). However, this is a dubious guess at best. What is more, the simpler problem of determining whether
$\liminf _{n\rightarrow +\infty }Z(n)/p(n)^2>0$
also seems to be out of reach. In view of these difficulties, McKay [Reference He5] posed a less ambitious problem; he asked for lower bounds arising from
$\ell $
-cores that illustrate the rapid growth of
$Z(n).$
Here, we answer this question, and for primes
$\ell \geq 5,$
we obtain asymptotic formulas for
$$ \begin{align} Z_{\ell}(n):=\#\left \{ (\lambda, \mu) \ : \ \chi_{\lambda}(\mu)=0 \ \ {\mathrm{with}\ \lambda\ \mathrm{an}\ \ell\mathrm{-core}}\right\}. \end{align} $$
To this end, suppose that
$\lambda =(\lambda _1, \lambda _2,\dots , \lambda _s)$
is a partition of
$n.$
As is typical in the representation theory of symmetric groups, we make use of
$\ell $
-core partitions, which are defined using Young diagrams of partitions, the left-justified arrays of cells where the row lengths are the parts. The hook for the cell in position
$(k,j)$
is the set of cells below or to the right of that cell, including the cell itself, and so its hook length
$h_{\lambda }(k,j):=(\lambda _k-k)+(\lambda ^{\prime }_j-j)+1.$
Here,
$\lambda ^{\prime }_j$
is the number of boxes in the jth column of the diagram. We say that
$\lambda $
is an
$\ell $
-core partition if none of its hook lengths are multiples of
$\ell .$
If
$c_{\ell }(n)$
denotes the number of
$\ell $
-core partitions of n, then we have (see, for example, [Reference Garvan, Kim and Stanton2, Reference Klyachko7]) the generating function
$$ \begin{align*}\sum_{n=0}^{\infty} c_{\ell}(n)q^n=\prod_{n=1}^{\infty} \frac{(1-q^{\ell n})^{\ell}}{(1-q^n)}. \end{align*} $$
Example The Young diagram of the partition
$\lambda :=(5,4,1),$
where each cell is labeled with its hook length, is given in Figure 1.
Figure 1 Hook lengths for
$\lambda =(5,4,1)$
.
By inspection, we see that
$\lambda $
is an
$\ell $
-core for every prime
$\ell>7.$
To state the asymptotics formulas, we let
$L\left (\left ( \frac {\cdot }{\ell } \right ),s\right )$
be the Dirichlet L-function for the Legendre symbol
$\left ( \frac {\cdot }{\ell } \right ),$
and let
$$ \begin{align} \alpha_{\ell}:= \frac{(2\pi)^{\frac{\ell-1}{2}}}{\left(\frac{\ell-3}{2}\right)! \cdot \ell^{\frac{\ell}{2}}\cdot L\left(\left( \frac{\cdot}{\ell} \right)\!,\frac{\ell-1}{2}\right)}. \end{align} $$
By the functional equations of these Dirichlet L-functions and the theory of generalized Bernoulli numbers, we have that
$1/\alpha _{\ell }$
is always a positive integer (see page 339 of [Reference Granville and Ono3]). For example, we have
$1/\alpha _5=1, 1/\alpha _7=8, 1/\alpha _{11}=1,275,$
and
$1/\alpha _{13}=33,463.$
In addition, we require the integers
$\delta _{\ell }:=(\ell ^2-1)/24,$
and the twisted Legendre symbol divisor functions
$$ \begin{align} \sigma_{\ell}(n):=\sum_{1\leq d\mid n} \left( \frac{n/d}{\ell} \right)d^{\frac{\ell-3}{2}}. \end{align} $$
In terms of these quantities and functions, we obtain the following asymptotics for
$Z_{\ell }(n).$
Theorem 1.1 If
$\ell \geq 5$
is prime, then, as
$n\rightarrow +\infty $
, we have
$$ \begin{align*}Z_{\ell}(n)\sim \alpha_{\ell} \cdot \sigma_{\ell}(n+\delta_{\ell}) p(n)\gg_{\ell} n^{\frac{\ell-5}{2}} e^{\pi \sqrt{2n/3}}. \end{align*} $$
Remark Apart from a density zero subset, we have that
$Z_\ell (n)=0$
when
$\ell \in \{2, 3\}$
(see [Reference Granville and Ono3]).
As a corollary, we find that
$Z(n)/p(n)$
grows faster than any power of
$n.$
Corollary 1.2 If
$d>0,$
then
$$ \begin{align*}\lim_{n\rightarrow +\infty}\frac{Z(n)}{p(n)\cdot n^d}=+\infty. \end{align*} $$
Remark We note that Corollary 1.2 is weaker than
$$ \begin{align*}Z(n)/p(n)^2 \gg 1/\log n, \end{align*} $$
which can be found in the discussion after Lemma 2.3 of Peluse’s paper [Reference Peluse11].
We turn to the problem of describing the zero entries in
$\mathcal {C}_n$
where both indices
$\lambda $
and
$\mu $
are
$\ell $
-core partitions. For prime
$\ell $
and large
$n,$
the entries in
$\mathcal {C}_n$
indexed by
$\ell $
-core pairs
$(\lambda , \mu )$
always have
$\chi _{\lambda }(\mu )=0.$
Theorem 1.3 Suppose that
$\ell $
is prime, and let
$N_{\ell }:=(\ell ^6- 2\ell ^5 + 2\ell ^4 -3\ell ^2 + 2\ell )/24.$
If
$n>N_{\ell }$
and
$\lambda , \mu \vdash n$
are
$\ell $
-core partitions, then
$\chi _{\lambda }(\mu )=0.$
If
$Z^*_{\ell }(n)$
denotes the number of vanishing entries
$\chi _{\lambda }(\mu )=0$
indexed by
$\ell $
-core partitions
$\lambda , \mu \vdash n,$
then we have the following corollary.
Corollary 1.4 For primes
$\ell ,$
the following are true.
(1) Apart from a density zero subset, we have that
$Z^*_\ell (n)=0$
when
$\ell \in \{2, 3\}.$
(2) If
$\ell \geq 5$
, then, as
$n\rightarrow +\infty $
, we have
$$ \begin{align*}Z^*_{\ell}(n)\sim \alpha_{\ell}^2 \cdot \sigma_{\ell}(n+\delta_{\ell})^2 \gg_{\ell} n^{\ell-3}. \end{align*} $$
To obtain these results, we use the well-known vanishing result that follows from the Murnaghan–Nakayama rule and says that
$\chi _\lambda (\mu )=0$
whenever
$\mu $
has a part that is not the length of any hook in
$\lambda $
. Therefore, our goal is reduced to counting pairs of partitions
$(\lambda , \mu )$
of large
$n,$
where
$\mu $
has a part that is a multiple of
$\ell ,$
and where
$\lambda $
is an
$\ell $
-core. Theorem 1.1 is obtained by estimating these counts using asymptotics and lower bounds for various partition functions due to Hardy and Ramanujan, Hagis, and Granville and the second author.
Theorem 1.3 concerns the cases where
$(\lambda , \mu )$
are both
$\ell $
-cores, and is a consequence of the fact (see Theorem 3.1) that every large
$\ell $
-core has a part that is a multiple of
$\ell .$
This fact is proved using the “abacus theory” of
$\ell $
-cores, and is a generalization of Section 3 of [Reference Ono and Sze10] by Sze and the second author in the case of four-core partitions. Corollary 1.4 then follows from the asymptotics for
$c_{\ell }(n)$
due to Granville and the second author.
This paper is organized as follows. Section 2 recalls the well-known vanishing result and bounds, as well as the asymptotics and estimates for the relevant partition functions. Section 3 gives the abacus theory of
$\ell $
-cores and the statement and proof of Theorem 3.1. In Section 4, we employ these results to prove Theorems 1.1 and 1.3 and Corollaries 1.2 and 1.4.
2 Nuts and bolts
In this section, we recall essential facts that we require for the proofs of our results. We first state a criterion that guarantees the vanishing of character values, and then we give estimates for the relevant partition functions.
2.1 Criterion for the vanishing of
$\chi _{\lambda }(\mu )$
Here, we recall a standard partition theoretic criterion that guarantees the vanishing of a character value
$\chi _{\lambda }(\mu )$
. Suppose that
$\lambda =(\lambda _1,\dots , \lambda _s)$
and
$\mu =(\mu _1, \dots , \mu _t)$
are partitions of size n, and let
$\{h_{\lambda }(i,j)\}$
be the multiset of hook lengths for
$\lambda .$
Thanks to the Murnaghan–Nakayama formula (see, for example, Theorem 2.4.7 of [Reference James and Kerber6]), we have that
$\chi _{\lambda }(\mu )=0$
when
$\{ \mu _i\}$
is not a subset of
$\{h_{\lambda }(i,j)\}$
.
Given a prime
$\ell ,$
this immediately gives natural families of vanishing character table entries indexed by pairs of partitions
$(\lambda , \mu )$
of n, where
$\mu $
has a part that is a multiple of
$\ell ,$
and
$\lambda $
is an
$\ell $
-core partition. To make use of this observation, we recall that a partition
$\mu $
is A-regular if none of its parts
$\mu _i$
are multiples of
$A.$
If
$p_{A}(n)$
denotes the number of A-regular partitions of n, then one easily confirms the generating function
$$ \begin{align*}\sum_{n=0}^{\infty} p_{A}(n)q^n=\prod_{n=1}^{\infty} \frac{(1-q^{An})}{(1-q^n)}= \prod_{n=1}^{\infty}\left (1+q^n+q^{2n}+\dots+q^{(A-1)n}\right)\!, \end{align*} $$
which shows that
$p_{A}(n)$
is also the number of partitions of n where the parts appear at most
$A-1$
times. In terms of
$p(n), p_{\ell }(n)$
, and
$c_{\ell }(n)$
, we have the following lower bounds for
$Z(n).$
Lemma 2.1 If
$\ell $
is prime, then the following are true.
(1) If
$\mu \vdash n$
is not an
$\ell $
-regular partition and
$\lambda \vdash n$
is an
$\ell $
-core partition, then
$\chi _{\lambda }(\mu )=0.$
(2) If n is a positive integer, then we have
$$ \begin{align*}Z_{\ell}(n)\geq \left(p(n)-p_{\ell}(n)\right)\cdot c_{\ell}(n). \end{align*} $$
Proof (1) By hypothesis,
$\mu $
is not
$\ell $
-regular, meaning that it has a part that is a multiple of
$\ell .$
As
$\lambda $
is an
$\ell $
-core, none of its hook lengths are multiples of
$\ell .$
Therefore,
$\chi _{\lambda }(\mu )=0$
by Murnaghan–Nakayama.
(2) The number of partitions of n that are not
$\ell $
-regular is
$p(n)-p_{\ell }(n).$
Therefore, (1) gives the conclusion that
$$ \begin{align*}Z_{\ell}(n) {\color{black}\ \geq \ } (p(n)-p_{\ell}(n))c_{\ell}(n). \\[-34pt] \end{align*} $$
2.2 Estimates for some partition functions
Here, we recall asymptotics and lower bounds for the partition functions we require to prove Theorem 1.1 and Corollary 1.4. First, we have the celebrated Hardy–Ramanujan asymptotic for
$p(n).$
Theorem 2.2 As
$n\rightarrow +\infty $
, we have
$$ \begin{align*}p(n)\sim \dfrac{1}{4n\sqrt{3}}\cdot \exp(\pi \sqrt{2n/3}). \end{align*} $$
Hagis obtained asymptotics for
$p_A(n),$
the number of A-regular partitions of
$n.$
Letting
$t=A-1$
in Corollary 4.2 of [Reference Hagis4], we have the following asymptotic formula.
Theorem 2.3 If
$A\geq 2,$
then we have
$$ \begin{align*}p_A(n)=C_A (24n-1+A)^{-\frac{3}{4}}\exp\left(C\sqrt{\frac{A-1}{A}\left(n+\frac{A-1}{24}\right)}\right) \left(1+O(n^{-\frac{1}{2}})\right)\!, \end{align*} $$
where
$C:=\pi \sqrt {2/3}$
and
$C_A:=\sqrt {12}A^{-\frac {3}{4}}(A-1)^{\frac {1}{4}}.$
Finally, we recall facts about
$c_t(n),$
the number of t-core partitions of n that were obtained by Granville and the second author in [Reference Granville and Ono3]. In terms of
$\alpha _{\ell }$
defined in (1.2), and the twisted Legendre symbol divisor functions
$\sigma _{\ell }(n)$
defined in (1.3), we have the following theorem.
Theorem 2.4 The following are true.
(1) We have that
$$ \begin{align*}c_2(n)=\begin{cases} 1, \ \ \ \ \ \ &{\text{if}}\ \,n\ \mathrm{is\ a\ triangular\ number,}\\ 0, \ \ \ \ \ \ &\text{otherwise}. \end{cases} \end{align*} $$
(2) If n is a nonnegative integer, then
$$ \begin{align*}c_3(n)=\sum_{d\mid (3n+1)} \left( \frac{d}{3} \right)\!. \end{align*} $$
In particular,
$c_3(n)=0$
for almost all n.
(3) If
$t\geq 4$
and n is a nonnegative integer, then
$c_t(n)>0.$
(4) If n is a nonnegative integer, then
$c_5(n)=\sigma _5(n+1).$
(5) If
$\ell \geq 7$
is prime, then, as
$n\rightarrow +\infty $
, we have
$$ \begin{align*}c_{\ell}(n)\sim \alpha_{\ell}\cdot \sigma_{\ell}(n+\delta_{\ell}). \end{align*} $$
(6) If
$\ell \geq 11$
is prime and n is sufficiently large, then we have
$$ \begin{align*}c_{\ell}(n)> \frac{2\alpha_{\ell}}{5} \cdot n^{\frac{\ell-3}{2}}. \end{align*} $$
Proof Claim (1) is a straightforward observation. Claims (2), (4), and (5) are proved on pages 339 and 340 of [Reference Granville and Ono3]. Claim (3) is Theorem 1 of [Reference Granville and Ono3], whereas (6) is Theorem 4 of [Reference Granville and Ono3].
3 Abaci and large
$\ell $
-core partitions
Throughout this section, suppose that
$\ell $
is prime. The main result here is the following theorem, which shows that every sufficiently large
$\ell $
-core partition has a part that is a multiple of
$\ell .$
Theorem 3.1 Suppose that
$\ell $
is prime, and let
$N_{\ell }:=(\ell ^6- 2\ell ^5 + 2\ell ^4 -3\ell ^2 + 2\ell )/24 .$
If
$n>N_{\ell },$
then every
$\ell $
-core partition of size n has a part that is a multiple of
$\ell .$
Remark We note that
$N_{\ell }<\ell ^6/24$
is not optimal. Indeed, if we let
$N^{\max }_{\ell }$
be the largest n admitting an
$\ell $
-regular
$\ell $
-core partition, then it turns out that
$N_3^{\max }=10$
and
$N_3=16.$
3.1 Abaci theory
We make use of the theory of abaci for partitions (see, for example, [Reference Erdmann and Michler1, Reference James and Kerber6]). In particular, let
$\lambda = \lambda _1 \geq \lambda _2 \geq \cdots \geq \lambda _s> 0$
be a partition of n. For each
$1 \leq i \leq s,$
define the ith structure number
$B_i := \lambda _i -i+s$
, so that
$B_i = h_\lambda (i,1),$
the hook length of cell
$(i,1)$
.
Using these structure numbers, we represent the partition
$\lambda $
as an
$\ell $
-abacus
$\mathfrak {A}_{\lambda },$
consisting of beads placed on rods numbered
$0, 1,\dots , \ell -1.$
For each
$B_i$
, there is a unique pair of integers (
$r_i,c_i)$
for which
$B_i = \ell (r_i - 1) + c_i$
and
$0 \leq c_i \leq \ell -1$
. The abacus
$\mathfrak {A}_{\lambda }$
then consists of s beads, where for each i, one places a bead in position
$(r_i,c_i)$
.
Lemma 3.2 [Reference James and Kerber6, Lemma 2.7.13]
Assuming the notation above,
$\lambda $
is an
$\ell $
-core if and only if all of the beads in
$\mathfrak {A}_{\lambda }$
lie at the top of their respective rods without gaps.
In view of this lemma, we may represent an abacus of an
$\ell $
-core partition by
$\ell $
-tuples of nonnegative integers, say
$(b_0, \dots , b_{\ell -1}),$
where
$b_i$
denotes the number of beads in column i. However, such representations are not unique as they generally allow for parts of size zero. We have the following elementary lemma.
Lemma 3.3 [Reference Ono and Sze10, Lemma 1]
The following abaci both represent the same
$\ell $
-core partition:
$$ \begin{align*}(b_0,b_1,\dots,b_{\ell-1}) \quad \text{and} \quad (b_{\ell-1} +1,b_0,b_1,\dots,b_{\ell-2}).\end{align*} $$
By repeatedly applying this lemma, we may canonically define the unique abacus representation for an
$\ell $
-core to be the one with zero beads in the first column. Thus, when we talk about the abacus representation of an
$\ell $
-core
$\lambda $
, we will always mean the abacus of the form
$\mathfrak {A}_{\lambda } = (0, b_1, \ldots , b_{\ell -1}).$
Footnote
1
Using these abaci, we offer the following lemma that will allow us to rule out the existence of partitions that are simultaneously
$\ell $
-core and
$\ell $
-regular for all but finitely many n.
Lemma 3.4 Suppose that
$\mathfrak {A}_{\lambda } = (0, b_1, \dots , b_{\ell -1})$
is the abacus corresponding to an
$\ell $
-core
$\lambda ,$
and suppose that there is an integer
$k\geq 0$
such that, for each
$1\leq i\leq \ell -1$
, we have either
$b_i\leq k$
or
$b_i\geq k+\ell .$
If there is at least one j for which
$b_j\geq k+\ell ,$
then
$\lambda $
is not an
$\ell $
-regular partition.
Remark Let
$\mathfrak {A}_{\lambda } = (0, b_1, \ldots , b_{\ell -1})$
be the abacus of an
$\ell $
-core
$\lambda .$
If
$\min (b_1, \ldots , b_{\ell -1}) \geq \ell ,$
then the proof of the lemma will show that
$\lambda $
has a part of exact size
$\ell $
. These are the cases where one can choose
$k=0$
in the lemma.
Proof By our hypothesis, we may fix j for which
$b_j \geq k + \ell $
. Let
$\delta $
denote the total number of columns with length at least
$k+\ell $
. Note that if
$B_{i}$
and
$B_{i'}$
are structure numbers corresponding to consecutive beads in column j between rows
$k+1$
and
${k+\ell}$
, then
$|i-i'| = \delta $
. Furthermore, we have
$|B_i - B_{i'}| = \ell $
. Generalizing the observation that
$B_{i-1}-B_i = \lambda _{i-1}-\lambda _i + 1$
, we have
$$\begin{align*}|\lambda_{i} - \lambda_{i'}| = |B_{i} - B_{i'}| -\delta = \ell - \delta. \end{align*}$$
In particular, the difference between parts corresponding to consecutive beads in column j between rows
$k+1$
and
$k+\ell $
is fixed and coprime to
$\ell .$
As a consequence, these parts form a modulus
$\ell -\delta $
arithmetic progression consisting of
$\ell $
values. Thus, the parts cover all residue classes modulo
$\ell $
, and so includes a part that is a multiple of
$\ell $
.
Example Let
$\ell =3$
, and consider the three-core abacus
$(0, 4,1)$
as shown below.
$$ \begin{align*}\begin{array}{c|ccc} 1& \cdot & \circ & \circ \\ 2& \cdot & \circ & \cdot \\ 3& \cdot & \circ & \cdot \\ 4& \cdot & \circ & \cdot \\ \end{array}\end{align*} $$
We illustrate Lemma 3.4 with
$k=1.$
Since
$b_1=3+1=4$
and
$b_2 =1$
, the lemma asserts that
$\lambda $
has a part that is a multiple of 3. The structure numbers are found to be
$B_1 = 10$
,
$B_2 = 7$
,
$B_3=4$
,
$B_4=2$
, and
$B_1=1$
, and we compute that
$\lambda _1 = 10+1-5 = 6$
,
$\lambda _2 = 4$
,
$\lambda _3 = 2$
, and
$\lambda _4 = \lambda _5 =1$
. In particular,
$\lambda _1$
is a multiple of 3.
Finally, consider the abacus with the bead in row 4 removed. One easily checks that the corresponding partition is
$3$
-regular, demonstrating that the condition on the size of the gap in column lengths cannot be relaxed.
With two more observations, we will be able to construct an abacus which gives an upper bound for the size of an
$\ell $
-regular
$\ell $
-core partition.
First, suppose that
$\lambda $
and
$\lambda '$
are
$\ell $
-cores with
$\mathfrak {A}_\lambda =(0, b_1, \dots , b_{\ell -1})$
and
$\mathfrak {A}_{\lambda '} =(0, b_1', \dots , b_{\ell -1}')$
. Then we say
$\mathfrak {A}_\lambda \leq \mathfrak {A}_{\lambda '}$
if
$b_i \leq b_i'$
for all
$1 \leq i \leq \ell -1$
. This relation endows the set of
$\ell $
-core abaci with the structure of a directed partially ordered set. It is not hard to show that
$\mathfrak {A}_\lambda \leq \mathfrak {A}_{\lambda '}$
implies
$|\lambda | \leq |\lambda '|$
.
For the purpose of obtaining
$N_{\ell },$
the following lemma allows us to restrict our attention to those abaci where the
$b_i$
are weakly increasing.
Lemma 3.5 Suppose that
$\lambda =(\lambda _1,\dots ,\lambda _s)$
is an
$\ell $
-core partition of n with abacus
$\mathfrak {A}_{\lambda }=(0, b_1, \dots , b_{\ell -1}).$
If there exist
$1 \leq i < j \leq \ell -1$
for which
$b_j < b_i,$
then the abacus
$\mathfrak {A}'$
obtained by swapping
$b_i$
and
$b_j$
represents an
$\ell $
-core partition
$\lambda '$
with
$\lambda ' \vdash n'>n$
.
Proof We may write
$$ \begin{align*} n = \sum_{k=1}^s \lambda_k = \sum_{k=1}^s (B_k + k -s) = \sum_{k=1}^s B_k + \sum_{k=1}^s (k-s), \end{align*} $$
and likewise
$n' = \sum _{k=1}^s B^{\prime }_k + \sum _{k=1}^s (k-s)$
, where s remains the same because we have not changed the total number of beads. Since the second sum is the same in both expressions, it suffices to prove that
$\sum _{i=1}^s B_k < \sum _{i=1}^s B^{\prime }_k.$
Computing columnwise, we have
$$ \begin{align*} \sum_{k=1}^s B_k &= \sum_{m=1}^{b_i}\left(3(m-1)+i\right) + \sum_{m=1}^{b_j}\left(3(m-1)+j\right) + \underset{k \neq i,j}{\sum_{k=1}^{\ell-1}}\sum_{m=1}^{b_k} \left(3(m-1)+k\right) \\ & \quad < \sum_{m=1}^{b_i}\left(3(m-1)+j\right) + \sum_{m=1}^{b_j}\left(3(m-1)+i\right) + \underset{k \neq i,j}{\sum_{k=1}^{\ell-1}}\sum_{m=1}^{b_k} \left(3(m-1)+k\right) \\ &=\sum_{k=1}^s B_k', \end{align*} $$
as desired, where the inequality holds since
$i<j$
and
$b_i> b_j$
.
3.2 Proof of Theorem 3.1
We aim to find an upper bound on n such that
$\lambda \vdash n$
can be an
$\ell $
-regular
$\ell $
-core partition. To do this, we will construct a partition
$\Lambda $
such that
$\lambda $
being an
$\ell $
-regular
$\ell $
-core implies
$|\lambda | \leq |\Lambda |$
. By Lemma 3.5, it suffices to restrict our attention to those
$\ell $
-cores whose abaci have weakly increasing column lengths. Suppose that
$\lambda $
is a weakly increasing
$\ell $
-regular
$\ell $
-core with abacus
$\mathfrak {A}_\lambda = (0, b_1, \dots , b_{\ell -1})$
. By Lemma 3.4, we must have
$\min (b_1, \dots , b_{\ell -1}) = b_1 \leq \ell -1$
. By the same logic, we must have
$b_i \leq i(\ell -1)$
, for all
$1\leq i \leq \ell -1$
.
Then, if
$\Lambda $
is the partition with abacus
$\mathfrak {A}_{\Lambda } = (0, \ell -1, 2(\ell -1), \dots , (\ell -1)^2)$
, we immediately have
$\mathfrak {A}_\lambda \leq \mathfrak {A}_\Lambda $
, which implies that
$|\lambda | \leq |\Lambda |$
. Then
$N_\ell := |\Lambda |$
gives an upper bound on n. By direct calculation, we find that
$$\begin{align*}|\Lambda| = \sum_{i=1}^s (B_i +i-s)= \sum_{i=1}^{\ell-1} \sum_{j=1}^{i(\ell-1)} \left( \ell(j-1)+i \right) + \sum_{i=1}^{s} (i-s) = \frac{\ell^6- 2\ell^5 + 2\ell^4 -3\ell^2 + 2\ell}{24}, \end{align*}$$
where
$s = \ell (\ell -1)^2/2$
, giving the desired conclusion.
4 Proofs of our results
We are now in a position to prove Theorems 1.1 and 1.3 and Corollaries 1.2 and 1.4.
Proof of Theorem 1.1
We note that Theorems 2.2 and 2.3 imply that
$$ \begin{align*}\lim_{n\rightarrow +\infty}\frac{p(n)-p_{\ell}(n)}{p(n)}=1. \end{align*} $$
The claim now follows by combining Lemma 2.1(2) and Theorems 2.2 and 2.4(4–6).
Proof of Corollary 1.2
This claim follows from Theorem 1.1 by choosing primes
$\ell \rightarrow +\infty .$
Proof of Theorem 1.3
By Theorem 3.1, every
$\ell $
-core partition of size
$n>N_{\ell }$
has a part that is a multiple of
$\ell .$
Since every hook length of an
$\ell $
-core is not a multiple of
$\ell $
, it follows from Murnaghan–Nakayama that whenever
$\lambda , \mu \vdash n$
are
$\ell $
-cores with
$n>N_{\ell },$
we have
$\chi _{\lambda }(\mu )=0.$
Acknowledgment
The authors thank Sarah Peluse and Richard Stanley as well as the referee for helpful comments that improved this paper.
Open access
