Article contents
Monochromatic paths and cycles in 2-edge-coloured graphs with large minimum degree
Published online by Cambridge University Press: 14 June 2021
Abstract
A graph G arrows a graph H if in every 2-edge-colouring of G there exists a monochromatic copy of H. Schelp had the idea that if the complete graph 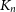 $K_n$ arrows a small graph H, then every ‘dense’ subgraph of
$K_n$ arrows a small graph H, then every ‘dense’ subgraph of 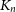 $K_n$ also arrows H, and he outlined some problems in this direction. Our main result is in this spirit. We prove that for every sufficiently large n, if
$K_n$ also arrows H, and he outlined some problems in this direction. Our main result is in this spirit. We prove that for every sufficiently large n, if 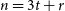 $n = 3t+r$ where
$n = 3t+r$ where 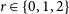 $r \in \{0,1,2\}$ and G is an n-vertex graph with
$r \in \{0,1,2\}$ and G is an n-vertex graph with 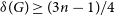 $\delta(G) \ge (3n-1)/4$, then for every 2-edge-colouring of G, either there are cycles of every length
$\delta(G) \ge (3n-1)/4$, then for every 2-edge-colouring of G, either there are cycles of every length 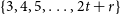 $\{3, 4, 5, \dots, 2t+r\}$ of the same colour, or there are cycles of every even length
$\{3, 4, 5, \dots, 2t+r\}$ of the same colour, or there are cycles of every even length 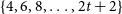 $\{4, 6, 8, \dots, 2t+2\}$ of the samecolour.
$\{4, 6, 8, \dots, 2t+2\}$ of the samecolour.
Our result is tight in the sense that no longer cycles (of length 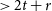 $>2t+r$) can be guaranteed and the minimum degree condition cannot be reduced. It also implies the conjecture of Schelp that for every sufficiently large n, every
$>2t+r$) can be guaranteed and the minimum degree condition cannot be reduced. It also implies the conjecture of Schelp that for every sufficiently large n, every 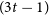 $(3t-1)$-vertex graph G with minimum degree larger than
$(3t-1)$-vertex graph G with minimum degree larger than 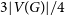 $3|V(G)|/4$ arrows the path
$3|V(G)|/4$ arrows the path 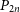 $P_{2n}$ with 2n vertices. Moreover, it implies for sufficiently large n the conjecture by Benevides, Łuczak, Scott, Skokan and White that for
$P_{2n}$ with 2n vertices. Moreover, it implies for sufficiently large n the conjecture by Benevides, Łuczak, Scott, Skokan and White that for 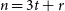 $n=3t+r$ where
$n=3t+r$ where 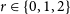 $r \in \{0,1,2\}$ and every n-vertex graph G with
$r \in \{0,1,2\}$ and every n-vertex graph G with 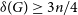 $\delta(G) \ge 3n/4$, in each 2-edge-colouring of G there exists a monochromatic cycle of length at least
$\delta(G) \ge 3n/4$, in each 2-edge-colouring of G there exists a monochromatic cycle of length at least 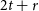 $2t+r$.
$2t+r$.
MSC classification
Information
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
Footnotes
Research of this author is partially supported by NSF Grant DMS-1764123, Arnold O. Beckman Research Award (UIUC) Campus Research Board 18132 and the Langan Scholar Fund (UIUC).
Research of this author is supported in part by NSF grant DMS-1600592, Arnold O. Beckman Research Award (UIUC) RB20003 and by grants 18-01-00353 and 19-01-00682 of the Russian Foundation for Basic Research.
The work was partially done while M. Lavrov was a postdoc at Department of Mathematics, University of Illinois at Urbanaâ–Champaign.
The work was partially done while X. Liu was a PhD student at Department of Mathematics, University of Illinois at Urbana–Champaign. Research of this author was supported by the Waldemar J., Barbara G., and Juliette Alexandra Trjitzinsky Fellowship.
Dedicated to the memory of Richard H. Schelp
References
- 5
- Cited by


