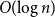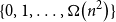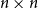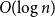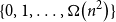1. Introduction
Given a graph
![]() $G$
we write
$G$
we write
![]() $\mbox{hom}(G)$
to denote the homogeneous number of
$\mbox{hom}(G)$
to denote the homogeneous number of
![]() $G$
, given by
$G$
, given by
In its simplest form, Ramsey’s theorem [Reference Ramsey30], [Reference Erdős, Szckeres, Gessel and Rota15] states that any
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
satisfies
$G$
satisfies
![]() $\operatorname{hom}(G) = \Omega (\!\log n)$
and a classical result of Erdős [Reference Erdős14] shows that this behaviour is essentially optimal; there are
$\operatorname{hom}(G) = \Omega (\!\log n)$
and a classical result of Erdős [Reference Erdős14] shows that this behaviour is essentially optimal; there are
![]() $n$
-vertex Ramsey graphs
$n$
-vertex Ramsey graphs
![]() $G_0$
with
$G_0$
with
![]() $\operatorname{hom}(G_0) = O (\!\log n)$
. However, the existence of such Ramsey graphs has only been demonstrated indirectly via probabilistic methods and finding explicit constructions of graphs exhibiting such behaviour remains a tantalising open problem (a
$\operatorname{hom}(G_0) = O (\!\log n)$
. However, the existence of such Ramsey graphs has only been demonstrated indirectly via probabilistic methods and finding explicit constructions of graphs exhibiting such behaviour remains a tantalising open problem (a
![]() $ \$ $
1000 Erdős problem [Reference Chung and Graham11]).
$ \$ $
1000 Erdős problem [Reference Chung and Graham11]).
Despite the challenges in constructing Ramsey graphs, and perhaps influenced by them, there has been much success in understanding the intrinsic properties possessed by these graphs. For example, Ramsey graphs have been shown to (roughly) exhibit similar behaviour to the Erdős-Renyi random graph w.h.p. with respect to edge density [Reference Erdős and Szemerédi16], non-isomorphic induced subgraphs [Reference Shelah31], universality of small induced subgraphs [Reference Prömel and Rödl29], and the possible edge sizes and degrees appearing in induced subgraphs [Reference Kwan and Sudakov23], [Reference Kwan and Sudakov22], [Reference Jenssen, Long, Keevash and Yepremyan19].
A challenging remaining problem in this context is the Erdős–McKay conjecture [Reference Erdős17]. Informally, the conjecture asks whether every Ramsey graph must contain (essentially) the entire interval of possible induced subgraph sizes. More precisely the conjecture asks whether every
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
with
$G$
with
![]() $\operatorname{hom}(G) \leq C \log n$
satisfies
$\operatorname{hom}(G) \leq C \log n$
satisfies
![]() $\left\{0,\ldots, \Omega _C\!\left(n^2\right)\right\} \subset \{e(G[U])\,:\, U \subset V(G)\}$
. The best known bound for the conjecture is due to Alon, Krivelevich and Sudakov [Reference Alon, Krivelevich and Sudakov1] who proved that such graphs necessarily contain induced subgraphs of each size in
$\left\{0,\ldots, \Omega _C\!\left(n^2\right)\right\} \subset \{e(G[U])\,:\, U \subset V(G)\}$
. The best known bound for the conjecture is due to Alon, Krivelevich and Sudakov [Reference Alon, Krivelevich and Sudakov1] who proved that such graphs necessarily contain induced subgraphs of each size in
![]() $\left\{0, \ldots, n^{\Omega _C(1)}\right\}$
. The conjecture was also proved for random graphs (in a strong form) by Calkin, Frieze and McKay in [Reference Calkin, Frieze and McKay10]. More recently, Kwan and Sudakov [Reference Kwan and Sudakov23] gave further support proving that such graphs necessarily contain induced subgraphs of
$\left\{0, \ldots, n^{\Omega _C(1)}\right\}$
. The conjecture was also proved for random graphs (in a strong form) by Calkin, Frieze and McKay in [Reference Calkin, Frieze and McKay10]. More recently, Kwan and Sudakov [Reference Kwan and Sudakov23] gave further support proving that such graphs necessarily contain induced subgraphs of
![]() $\Omega _C\big(n^2\big)$
different sizes, which improved an earlier almost quadratic bound of Narayanan, Sahasrabuhde and Tomon [Reference Narayanan, Sahasrabudhe and Tomon25].
$\Omega _C\big(n^2\big)$
different sizes, which improved an earlier almost quadratic bound of Narayanan, Sahasrabuhde and Tomon [Reference Narayanan, Sahasrabudhe and Tomon25].
Our aim here is to study the natural analogue of this conjecture for bipartite graphs. Recall that the bipartite analogue of Ramsey’s theorem states that any balanced bipartite graph
![]() $G = (V_1, V_2, E)$
with
$G = (V_1, V_2, E)$
with
![]() $|V_1| = |V_2| = n$
contains either
$|V_1| = |V_2| = n$
contains either
![]() $K_{t,t}$
or
$K_{t,t}$
or
![]() $\overline{K_{t,t}}$
as an induced subgraph with
$\overline{K_{t,t}}$
as an induced subgraph with
![]() $t = \Omega (\!\log n)$
. This type of behaviour is again known to be the best possible in general, though explicit constructions of ‘bipartite Ramsey graphs’ are also unknown. In fact, these are more challenging in a sense as such constructions would lead to constructions in the usual Ramsey setting (see e.g. [Reference Barak, Rao, Shaltiel and Wigderson7]). In part, this has contributed to significant interest in Ramsey results in the bipartite setting, e.g. see [Reference Conlon13], [Reference Collins, Riasanovsky, Wallace and Radziszowski12], [Reference Axenovich, Sereni, Snyder and Weber4] [Reference Axenovich, Tompkins and Weber5], [Reference Bucić, Letzter and Sudakov8], [Reference Souza32].
$t = \Omega (\!\log n)$
. This type of behaviour is again known to be the best possible in general, though explicit constructions of ‘bipartite Ramsey graphs’ are also unknown. In fact, these are more challenging in a sense as such constructions would lead to constructions in the usual Ramsey setting (see e.g. [Reference Barak, Rao, Shaltiel and Wigderson7]). In part, this has contributed to significant interest in Ramsey results in the bipartite setting, e.g. see [Reference Conlon13], [Reference Collins, Riasanovsky, Wallace and Radziszowski12], [Reference Axenovich, Sereni, Snyder and Weber4] [Reference Axenovich, Tompkins and Weber5], [Reference Bucić, Letzter and Sudakov8], [Reference Souza32].
Given the context above, and the difficulties in the Erdős–McKay conjecture, it is natural to ask what can be said about the edge sizes of induced subgraphs in balanced
![]() $n$
-vertex bipartite Ramsey graphs? A general result of Narayanan, Sahasrabuhde and Tomon [Reference Narayanan, Sahasrabudhe and Tomon27] gives some information here. These authors also studied a generalisation of the Erdős ‘multiplication table problem’ and showed that any bipartite graph with
$n$
-vertex bipartite Ramsey graphs? A general result of Narayanan, Sahasrabuhde and Tomon [Reference Narayanan, Sahasrabudhe and Tomon27] gives some information here. These authors also studied a generalisation of the Erdős ‘multiplication table problem’ and showed that any bipartite graph with
![]() $m$
edges has induced subgraphs of
$m$
edges has induced subgraphs of
![]() $\widetilde{\Omega }(m)$
distinct sizes. Recently, Baksys and Chen [Reference Baksys and Chen6] raised the bipartite Ramsey question and proved an analogue of Kwan and Sudakov’s theorem: any balanced bipartite Ramsey graph on vertex classes of order
$\widetilde{\Omega }(m)$
distinct sizes. Recently, Baksys and Chen [Reference Baksys and Chen6] raised the bipartite Ramsey question and proved an analogue of Kwan and Sudakov’s theorem: any balanced bipartite Ramsey graph on vertex classes of order
![]() $n$
has induced subgraphs of
$n$
has induced subgraphs of
![]() $\Omega \big(n^2\big)$
different edge sizes.
$\Omega \big(n^2\big)$
different edge sizes.
Our main theorem extends this line of research, proving an analogue of the Erdős–McKay conjecture in the bipartite setting. Before stating it, we give a more precise definition of the Ramsey property for bipartite graphs, in a slightly more general setting.
Definition 1.1.
Given
![]() $C\gt 0$
, a graph
$C\gt 0$
, a graph
![]() $G = (V_1, V_2, E)$
is called
$G = (V_1, V_2, E)$
is called
![]() $C$
-bipartite-Ramsey if for any
$C$
-bipartite-Ramsey if for any
![]() $t_1\geq C\log _2|V_1|$
and
$t_1\geq C\log _2|V_1|$
and
![]() $t_2\geq C\log _2|V_2|$
there is no induced copy of
$t_2\geq C\log _2|V_2|$
there is no induced copy of
![]() $K_{t_1,t_2}$
or
$K_{t_1,t_2}$
or
![]() $\overline{K_{t_1,t_2}}$
in
$\overline{K_{t_1,t_2}}$
in
![]() $G$
.
$G$
.
We will often simply say that
![]() $G$
is a
$G$
is a
![]() $C$
-Ramsey graph when it is clear that
$C$
-Ramsey graph when it is clear that
![]() $G$
is bipartite.
$G$
is bipartite.
We can now state our main result, which gives an analogue of the Erdős–McKay conjecture in the bipartite Ramsey setting.
Theorem 1.2.
Given
![]() $C\gt 0$
there is
$C\gt 0$
there is
![]() $\alpha \gt 0$
such that the following holds. Suppose that
$\alpha \gt 0$
such that the following holds. Suppose that
![]() $G = (V_1, V_2,E)$
is a
$G = (V_1, V_2,E)$
is a
![]() $C$
-bipartite-Ramsey graph. Then
$C$
-bipartite-Ramsey graph. Then
![]() $\{0,\ldots, \alpha |V_1||V_2|\} \subset \{e(G[U])\,:\, U \subset V(G)\}$
.
$\{0,\ldots, \alpha |V_1||V_2|\} \subset \{e(G[U])\,:\, U \subset V(G)\}$
.
Our proof of Theorem 1.2 follows a similar line of approach to [Reference Narayanan, Sahasrabudhe and Tomon25], [Reference Kwan and Sudakov23] and [Reference Baksys and Chen6], in which we first show that one can get close to the desired edge sizes and then refine this to show that certain perturbations are typically available to allow one to adjust to the exact size. Anti-concentration estimates are a key tool in ensuring that the desired perturbations are ‘sufficiently rich’ here. We prove such bounds using diversity of vertices and diversity for pairs of vertices, introduced by Bukh and Sudakov [Reference Bukh and Sudakov9] and Kwan and Sudakov [Reference Kwan and Sudakov23], respectively, though a different notion of pair diversity was key here in obtaining the required behaviour. We were also able to keep track of the perturbation structure using certain sumset techniques.
Update: After this paper was submitted, Kwan, Sah, Sauermann and Sawhney [Reference Kwan, Sah, Sauermann and Sawhney21] uploaded a remarkable paper, which has completely resolved the Erdős
![]() $-$
McKay conjecture. The proof is a tour de force, combining a wide range of techniques, and it is significantly different from our approach here.
$-$
McKay conjecture. The proof is a tour de force, combining a wide range of techniques, and it is significantly different from our approach here.
Notation. Given disjoint sets
![]() $V_1$
and
$V_1$
and
![]() $V_2$
we write
$V_2$
we write
![]() $G = (V_1, V_2,E)$
to represent a bipartite graph
$G = (V_1, V_2,E)$
to represent a bipartite graph
![]() $G$
with vertex set
$G$
with vertex set
![]() $V(G)=V_1\sqcup V_2$
and edge set
$V(G)=V_1\sqcup V_2$
and edge set
![]() $E(G)=E\subset V_1\times V_2$
. The edge density of
$E(G)=E\subset V_1\times V_2$
. The edge density of
![]() $G$
is given by
$G$
is given by
![]() $e(G)\large{/}|V_1||V_2|$
. Given
$e(G)\large{/}|V_1||V_2|$
. Given
![]() $U_i \subset V_i$
for
$U_i \subset V_i$
for
![]() $i = 1,2$
we write
$i = 1,2$
we write
![]() $G[U_1, U_2]$
to denote the induced subgraph
$G[U_1, U_2]$
to denote the induced subgraph
![]() $G[U_1, U_2] = (U_1, U_2, E \cap (U_1 \times U_2))$
.
$G[U_1, U_2] = (U_1, U_2, E \cap (U_1 \times U_2))$
.
Given a graph
![]() $G$
and
$G$
and
![]() $u,v\in V(G)$
, we write
$u,v\in V(G)$
, we write
![]() $u\sim v$
if
$u\sim v$
if
![]() $u$
and
$u$
and
![]() $v$
are adjacent vertices in
$v$
are adjacent vertices in
![]() $G$
. The neighbourhood of
$G$
. The neighbourhood of
![]() $u$
is given by
$u$
is given by
![]() $N_G(u) = \{v\in V(G)\,:\, u\sim v\}$
and given
$N_G(u) = \{v\in V(G)\,:\, u\sim v\}$
and given
![]() $S \subset V(G)$
we let
$S \subset V(G)$
we let
![]() $N^S_G(u) \,:\!=\, N_G(u) \cap S$
; we will omit the subscript
$N^S_G(u) \,:\!=\, N_G(u) \cap S$
; we will omit the subscript
![]() $G$
when the graph is clear from the context. We write
$G$
when the graph is clear from the context. We write
![]() $d^S_G(u) = \big|N^S_G(u)\big|$
.
$d^S_G(u) = \big|N^S_G(u)\big|$
.
Given vertices
![]() $u,v\in V(G)$
we write
$u,v\in V(G)$
we write
![]() $\text{div}_G(u,v)$
for the symmetric difference
$\text{div}_G(u,v)$
for the symmetric difference
![]() $N(u)\triangle N(v)$
. The biased diversity of
$N(u)\triangle N(v)$
. The biased diversity of
![]() $u$
and
$u$
and
![]() $v$
, denoted by
$v$
, denoted by
![]() $\text{divb}_G(u,v)$
, is going to be the largest of the two sets
$\text{divb}_G(u,v)$
, is going to be the largest of the two sets
![]() $N(u)\setminus N(v)$
and
$N(u)\setminus N(v)$
and
![]() $N(v)\setminus N(u)$
. If these have the same size, then we arbitrarily pick one of the sets to be
$N(v)\setminus N(u)$
. If these have the same size, then we arbitrarily pick one of the sets to be
![]() $\text{divb}_G(u,v)$
. Clearly
$\text{divb}_G(u,v)$
. Clearly
![]() $|\text{divb}_G(u,v)|\geq |\text{div}_G(u,v)|/2$
.
$|\text{divb}_G(u,v)|\geq |\text{div}_G(u,v)|/2$
.
We will also be interested in ordered pairs of vertices
![]() $\boldsymbol{{p}}= (u,v) \in \binom{V(G)}{2}$
. Naturally, given such a pair
$\boldsymbol{{p}}= (u,v) \in \binom{V(G)}{2}$
. Naturally, given such a pair
![]() $\boldsymbol{{p}}$
we can define
$\boldsymbol{{p}}$
we can define
![]() $\text{div}_G(\boldsymbol{{p}})\,:\!=\,\text{div}_G(u,v)$
. We will also make the convention throughout that all pairs are ordered so that
$\text{div}_G(\boldsymbol{{p}})\,:\!=\,\text{div}_G(u,v)$
. We will also make the convention throughout that all pairs are ordered so that
![]() $\text{divb}_G(\boldsymbol{{p}})=N(u) \setminus N(v)$
, which implies
$\text{divb}_G(\boldsymbol{{p}})=N(u) \setminus N(v)$
, which implies
![]() $d(u) \geq d(v)$
. Moreover, for later diversity purposes, we will need to study
$d(u) \geq d(v)$
. Moreover, for later diversity purposes, we will need to study
![]() $\operatorname{deg-diff}^{S}({\bf p})\,:\!=\,d_G^S(u)-d_G^S(v)$
.
$\operatorname{deg-diff}^{S}({\bf p})\,:\!=\,d_G^S(u)-d_G^S(v)$
.
Given integers
![]() $m \leq n$
we will write
$m \leq n$
we will write
![]() $[m,n]$
to denote the interval
$[m,n]$
to denote the interval
![]() $\{m, m+1, \ldots, n\}$
and given
$\{m, m+1, \ldots, n\}$
and given
![]() $n \in{\mathbb N}$
we write
$n \in{\mathbb N}$
we write
![]() $[n]$
for the interval
$[n]$
for the interval
![]() $\{1,\ldots, n\}$
. All logarithms in the paper will be base
$\{1,\ldots, n\}$
. All logarithms in the paper will be base
![]() $2$
unless otherwise stated. Floor and ceiling signs are omitted throughout for clarity of presentation.
$2$
unless otherwise stated. Floor and ceiling signs are omitted throughout for clarity of presentation.
2. Collected tools
Before beginning in earnest on the proof of the theorem, we make two simple observations on the relation between vertex classes and the size of a
![]() $C$
-bipartite-Ramsey graph
$C$
-bipartite-Ramsey graph
![]() $G = (V_1, V_2, E)$
, which are useful for future reference.
$G = (V_1, V_2, E)$
, which are useful for future reference.
Given any
 $\alpha \in (0,1)$
and
$\alpha \in (0,1)$
and
 $U_i \subset V_i$
with
$U_i \subset V_i$
with
 $|U_i| \geq |V_i|^{\alpha }$
for
$|U_i| \geq |V_i|^{\alpha }$
for
 $i = 1,2$
, the induced graph
$i = 1,2$
, the induced graph
 $G[U_1, U_2]$
is
$G[U_1, U_2]$
is
 $(C \alpha ^{-1})$
-Ramsey.
$(C \alpha ^{-1})$
-Ramsey.Suppose that
 $|V_1| \geq |V_2|$
and let
$|V_1| \geq |V_2|$
and let
 $W \subset V_2$
of size
$W \subset V_2$
of size
 $|W| = 2C \log |V_2|$
. By the pigeonhole principle there is a set
$|W| = 2C \log |V_2|$
. By the pigeonhole principle there is a set
 $U \subset V_1$
with
$U \subset V_1$
with
 $|U| \geq |V_1|2^{-|W|}$
such that for all
$|U| \geq |V_1|2^{-|W|}$
such that for all
 $u\in U$
one has
$u\in U$
one has
 $N_G^W(u) = W^{\prime}$
. It follows that
$N_G^W(u) = W^{\prime}$
. It follows that
 $G$
contains an induced
$G$
contains an induced
 $K_{t_1, t_2}$
or
$K_{t_1, t_2}$
or
 $\overline{K_{t_1,t_2}}$
where
$\overline{K_{t_1,t_2}}$
where
 $t_1 = |V_1|2^{-|W|}$
and
$t_1 = |V_1|2^{-|W|}$
and
 $t_2 = C \log |V_2|$
. As
$t_2 = C \log |V_2|$
. As
 $G$
is
$G$
is
 $C$
-Ramsey it follows that
$C$
-Ramsey it follows that
 $t_1 \leq C \log |V_1|$
, which in particular gives
$t_1 \leq C \log |V_1|$
, which in particular gives
 $|V_1| \leq |V_2|^{O_C(1)}$
. Thus the vertex classes of
$|V_1| \leq |V_2|^{O_C(1)}$
. Thus the vertex classes of
 $C$
-bipartite-Ramsey graphs are necessarily polynomially related.
$C$
-bipartite-Ramsey graphs are necessarily polynomially related.
2.1 Density control
We start by proving a density result for bipartite Ramsey graphs, which is the analogue of the Erdős-Szemerédi theorem [Reference Erdős and Szemerédi16] for Ramsey graphs in general. The proof uses a well-known argument due to Kovari
![]() $-$
Sós
$-$
Sós
![]() $-$
Turán [Reference Kovari, Sós and Turán20].
$-$
Turán [Reference Kovari, Sós and Turán20].
Lemma 2.1.
Given
![]() $C\gt 1$
there is
$C\gt 1$
there is
![]() $n_C\in \mathbb{N}$
such that the following holds. Suppose that
$n_C\in \mathbb{N}$
such that the following holds. Suppose that
![]() $G = (V_1, V_2,E)$
is a
$G = (V_1, V_2,E)$
is a
![]() $C$
-bipartite-Ramsey graph with
$C$
-bipartite-Ramsey graph with
![]() $|V_1|,|V_2|\geq n_C$
. Then
$|V_1|,|V_2|\geq n_C$
. Then
![]() $G$
has edge density between
$G$
has edge density between
![]() $(16C)^{-1}$
and
$(16C)^{-1}$
and
![]() $1-(16C)^{-1}$
.
$1-(16C)^{-1}$
.
Proof. To see this let
![]() $\varepsilon =(16C)^{-1}, t_1=C\log |V_1|$
,
$\varepsilon =(16C)^{-1}, t_1=C\log |V_1|$
,
![]() $t_2=C\log |V_2|$
and assume that
$t_2=C\log |V_2|$
and assume that
![]() $t_1\leq t_2$
. It is enough to show that our graph cannot have density larger than
$t_1\leq t_2$
. It is enough to show that our graph cannot have density larger than
![]() $1-\varepsilon$
, as the other statement follows by looking at the (bipartite) complement
$1-\varepsilon$
, as the other statement follows by looking at the (bipartite) complement
![]() $\overline{G}$
.
$\overline{G}$
.
For the sake of contradiction, suppose the density
![]() $d(G) \gt 1-\varepsilon$
, and let us count in two ways the number
$d(G) \gt 1-\varepsilon$
, and let us count in two ways the number
![]() $M$
of stars
$M$
of stars
![]() $K_{t_1,1}$
which are formed by taking a single vertex in
$K_{t_1,1}$
which are formed by taking a single vertex in
![]() $V_2$
and
$V_2$
and
![]() $t_1$
of its neighbours. On one hand, each vertex
$t_1$
of its neighbours. On one hand, each vertex
![]() $v\in V_2$
contributes
$v\in V_2$
contributes
![]() $\binom{d(v)}{t_1}$
stars, giving us:
$\binom{d(v)}{t_1}$
stars, giving us:
Here we have used Jensen’s inequality for the map
![]() $x\to \binom{x}{t_1}$
in the second inequality, and that
$x\to \binom{x}{t_1}$
in the second inequality, and that
![]() $t_1 \leq \varepsilon |V_1|$
for the final step, as
$t_1 \leq \varepsilon |V_1|$
for the final step, as
![]() $|V_1| \geq n_C$
.
$|V_1| \geq n_C$
.
On the other hand, if
![]() $G$
is
$G$
is
![]() $K_{t_1,t_2}$
-free then for each subset
$K_{t_1,t_2}$
-free then for each subset
![]() $S\subset V_1$
of
$S\subset V_1$
of
![]() $t_1$
vertices there are at most
$t_1$
vertices there are at most
![]() $t_2-1$
vertices in
$t_2-1$
vertices in
![]() $V_2$
that can form a star with
$V_2$
that can form a star with
![]() $S$
, and so
$S$
, and so
![]() $M\leq (t_2-1)\binom{|V_1|}{t_1}$
. Combined with (1) this gives
$M\leq (t_2-1)\binom{|V_1|}{t_1}$
. Combined with (1) this gives
![]() $|V_2| \leq (t_2-1) (1-2\varepsilon )^{-t_1} \leq |V_2|^{1/2} e^{4\varepsilon t_1}$
, using that
$|V_2| \leq (t_2-1) (1-2\varepsilon )^{-t_1} \leq |V_2|^{1/2} e^{4\varepsilon t_1}$
, using that
![]() $|V_2| \geq n_C$
and that
$|V_2| \geq n_C$
and that
![]() $1 - x \geq e^{-2x}$
for
$1 - x \geq e^{-2x}$
for
![]() $x \in [0, 1/2]$
. It follows that
$x \in [0, 1/2]$
. It follows that
![]() $|V_2| \leq e^{8\varepsilon t_2} = |V_1|^{8C\varepsilon } = |V_2|^{1/2}$
, a contradiction.
$|V_2| \leq e^{8\varepsilon t_2} = |V_1|^{8C\varepsilon } = |V_2|^{1/2}$
, a contradiction.
Corollary 2.2.
For any
![]() $C\gt 1$
there exists
$C\gt 1$
there exists
![]() $n_C\in \mathbb{N}$
such that the following holds true. Any
$n_C\in \mathbb{N}$
such that the following holds true. Any
![]() $C$
-bipartite-Ramsey graph
$C$
-bipartite-Ramsey graph
![]() $G = (V_1,V_2,E)$
with
$G = (V_1,V_2,E)$
with
![]() $|V_1|,|V_2|\geq n_C$
contains at least
$|V_1|,|V_2|\geq n_C$
contains at least
![]() $2|V_1|/3$
vertices in
$2|V_1|/3$
vertices in
![]() $V_1$
which all have degrees between
$V_1$
which all have degrees between
![]() $(32C)^{-1}|V_2|$
and
$(32C)^{-1}|V_2|$
and
![]() $(1-(32C)^{-1})|V_2|$
.
$(1-(32C)^{-1})|V_2|$
.
Proof. Suppose for the sake of contradiction that the conclusion is not true. Let
![]() $\varepsilon \,:\!=\,1/32C$
and suppose at most
$\varepsilon \,:\!=\,1/32C$
and suppose at most
![]() $2|V_1|/3$
vertices
$2|V_1|/3$
vertices
![]() $v\in V_1$
have degrees between
$v\in V_1$
have degrees between
![]() $\varepsilon |V_2|$
and
$\varepsilon |V_2|$
and
![]() $(1-\varepsilon )|V_2|$
. Then, by the pigeonhole principle, without loss of generality we can assume that there is a set
$(1-\varepsilon )|V_2|$
. Then, by the pigeonhole principle, without loss of generality we can assume that there is a set
![]() $U_1 \subset V_1$
with
$U_1 \subset V_1$
with
![]() $|U_1| \geq |V_1|/6$
such that all vertices in
$|U_1| \geq |V_1|/6$
such that all vertices in
![]() $U_1$
have degree less than
$U_1$
have degree less than
![]() $\varepsilon |V_2|$
. But then the edge density of the induced bipartite graph
$\varepsilon |V_2|$
. But then the edge density of the induced bipartite graph
![]() $G[U_1,V_2]$
is less than
$G[U_1,V_2]$
is less than
![]() $\varepsilon$
. On the other hand, it is easy to see that if
$\varepsilon$
. On the other hand, it is easy to see that if
![]() $G$
is
$G$
is
![]() $C$
-bipartite-Ramsey, since
$C$
-bipartite-Ramsey, since
![]() $6|U_1| \geq |V_1| \geq n_C$
, the graph
$6|U_1| \geq |V_1| \geq n_C$
, the graph
![]() $G[U_1,V_2]$
is
$G[U_1,V_2]$
is
![]() $2C$
-bipartite-Ramsey. This is a contradiction by Lemma 2.1.
$2C$
-bipartite-Ramsey. This is a contradiction by Lemma 2.1.
In particular, we can repeatedly make use of Corollary 2.2 inside a bipartite graph to obtain the following result, which will be useful later.
Lemma 2.3.
Given
![]() $C\gt 1$
and a natural number
$C\gt 1$
and a natural number
![]() $L$
there is
$L$
there is
![]() $n_0\in \mathbb{N}$
such that the following holds. Suppose that
$n_0\in \mathbb{N}$
such that the following holds. Suppose that
![]() $G = (V_1, V_2, E)$
is a
$G = (V_1, V_2, E)$
is a
![]() $C$
-bipartite-Ramsey graph with
$C$
-bipartite-Ramsey graph with
![]() $|V_i|\geq n_0$
. Then, taking
$|V_i|\geq n_0$
. Then, taking
![]() $\varepsilon _i\,:\!=\,(64C)^{-i}$
for all
$\varepsilon _i\,:\!=\,(64C)^{-i}$
for all
![]() $i\in [L]$
, one can find vertices
$i\in [L]$
, one can find vertices
![]() $U\,:\!=\,\{u_1,u_2,\ldots,u_L\}\subset V_1$
such that
$U\,:\!=\,\{u_1,u_2,\ldots,u_L\}\subset V_1$
such that
![]() $ \Big|N(u_i)\setminus \underset{j\lt i}{\bigcup }N(u_j) \Big|\geq \varepsilon _i|V_2|$
and
$ \Big|N(u_i)\setminus \underset{j\lt i}{\bigcup }N(u_j) \Big|\geq \varepsilon _i|V_2|$
and
![]() $ \Big|V_2\setminus \underset{j\leq i}{\bigcup } N(u_j) \Big|\geq \varepsilon _i|V_2|$
for all
$ \Big|V_2\setminus \underset{j\leq i}{\bigcup } N(u_j) \Big|\geq \varepsilon _i|V_2|$
for all
![]() $i\in [L]$
.
$i\in [L]$
.
Proof. By Corollary 2.2 we can pick
![]() $u_1\in V_1$
such that
$u_1\in V_1$
such that
![]() $d(u_1)\in [\varepsilon _1|V_2|,(1-\varepsilon _1)|V_2|]$
. Our requirement is clearly satisfied for
$d(u_1)\in [\varepsilon _1|V_2|,(1-\varepsilon _1)|V_2|]$
. Our requirement is clearly satisfied for
![]() $i=1$
. Now let us assume that we have found
$i=1$
. Now let us assume that we have found
![]() $u_1,u_2,\ldots,u_i$
with
$u_1,u_2,\ldots,u_i$
with
![]() $i \lt L$
that satisfy our requirements and let us look for a vertex
$i \lt L$
that satisfy our requirements and let us look for a vertex
![]() $u_{i+1}$
.
$u_{i+1}$
.
Let
![]() $S_i\,:\!=\,V_1\setminus \{u_1,u_2,\ldots,u_i\}$
and
$S_i\,:\!=\,V_1\setminus \{u_1,u_2,\ldots,u_i\}$
and
![]() $T_i\,:\!=\,V_2\setminus \underset{j\leq i}{\cup } N(u_j)$
. Note that
$T_i\,:\!=\,V_2\setminus \underset{j\leq i}{\cup } N(u_j)$
. Note that
![]() $|S_i| \geq |V_1| - L \geq |V_1|^{1/2}$
and that
$|S_i| \geq |V_1| - L \geq |V_1|^{1/2}$
and that
![]() $|T_i| \geq (64C)^{-L}|V_2| \geq |V_2|^{1/2}$
since
$|T_i| \geq (64C)^{-L}|V_2| \geq |V_2|^{1/2}$
since
![]() $|V_1|, |V_2| \geq n_0$
. Therefore, the subgraph
$|V_1|, |V_2| \geq n_0$
. Therefore, the subgraph
![]() $G[S_i,T_i]$
is
$G[S_i,T_i]$
is
![]() $(2C)$
-bipartite-Ramsey. Thus, by Corollary 2.2, it follows that we can find a vertex
$(2C)$
-bipartite-Ramsey. Thus, by Corollary 2.2, it follows that we can find a vertex
![]() $u_{i+1}\in S_1$
such that
$u_{i+1}\in S_1$
such that
![]() $d^{T_i}_G(u_{i+1})\in [\varepsilon _1|T_i|,(1-\varepsilon _1)|T_i|]$
. But this is precisely the vertex we were looking for, as then we have
$d^{T_i}_G(u_{i+1})\in [\varepsilon _1|T_i|,(1-\varepsilon _1)|T_i|]$
. But this is precisely the vertex we were looking for, as then we have
![]() $\Big|N(u_{i+1})\setminus \underset{j\leq i}{\cup }N(u_j)\Big|\geq d^{T_i}_G(u_{i+1})\geq \varepsilon _1|T_i|\geq \varepsilon _{i+1}|V_2|$
and we also get that
$\Big|N(u_{i+1})\setminus \underset{j\leq i}{\cup }N(u_j)\Big|\geq d^{T_i}_G(u_{i+1})\geq \varepsilon _1|T_i|\geq \varepsilon _{i+1}|V_2|$
and we also get that
![]() $\Big|V_2\setminus \underset{j\leq i+1}{\cup } N(u_j)\Big|\geq \Big|T_i\setminus N^{T_i}_{G}(u_{i+1})\Big|\geq \varepsilon _1|T_i| \geq \varepsilon _{i+1}|V_2|$
.
$\Big|V_2\setminus \underset{j\leq i+1}{\cup } N(u_j)\Big|\geq \Big|T_i\setminus N^{T_i}_{G}(u_{i+1})\Big|\geq \varepsilon _1|T_i| \geq \varepsilon _{i+1}|V_2|$
.
By repeating this step
![]() $L$
times we reach our conclusion.
$L$
times we reach our conclusion.
2.2 Richness and diversity
We will use the notion of richness, which was introduced by Kwan and Sudakov [Reference Kwan and Sudakov23].
Definition 2.4.
Given
![]() $\delta,\varepsilon \gt 0$
, a bipartite graph
$\delta,\varepsilon \gt 0$
, a bipartite graph
![]() $G = (V_1, V_2,E)$
is
$G = (V_1, V_2,E)$
is
![]() $(\delta,\varepsilon )$
-bipartite-rich if for each
$(\delta,\varepsilon )$
-bipartite-rich if for each
![]() $i\in \{1,2\}$
the following holds: for every set
$i\in \{1,2\}$
the following holds: for every set
![]() $W \subset V_i$
with
$W \subset V_i$
with
![]() $|W| \geq \delta |V_i|$
there are at most
$|W| \geq \delta |V_i|$
there are at most
![]() $|V_{3-i}|^{1/5}$
vertices
$|V_{3-i}|^{1/5}$
vertices
![]() $v \in V_{3-i}$
such that
$v \in V_{3-i}$
such that
![]() $|N(v) \cap W| \leq \varepsilon |V_{3-i}|$
or
$|N(v) \cap W| \leq \varepsilon |V_{3-i}|$
or
![]() $|\overline{N}(v) \cap W| \lt \varepsilon |V_{3-i}|$
.
$|\overline{N}(v) \cap W| \lt \varepsilon |V_{3-i}|$
.
By adapting a result of Kwan and Sudakov (Lemma 4 in [Reference Kwan and Sudakov23]) to the bipartite context, we show that the Ramsey setting guarantees richness. Perhaps the most striking difference here is that in a general Ramsey setting one needs to move to a subgraph to find richness, whereas in the bipartite setting Ramsey graphs already possess it.
Lemma 2.5.
Given
![]() $C,\delta \gt 0$
there is
$C,\delta \gt 0$
there is
![]() $\varepsilon \gt 0$
and
$\varepsilon \gt 0$
and
![]() $n_0\in \mathbb{N}$
such that the following holds true. Every
$n_0\in \mathbb{N}$
such that the following holds true. Every
![]() $C$
-bipartite-Ramsey graph
$C$
-bipartite-Ramsey graph
![]() $G = (V_1, V_2,E)$
with
$G = (V_1, V_2,E)$
with
![]() $|V_1|, |V_2|\geq n_0$
is
$|V_1|, |V_2|\geq n_0$
is
![]() $(\delta,\varepsilon )$
-bipartite-rich.
$(\delta,\varepsilon )$
-bipartite-rich.
Proof. It is enough to prove that the bipartite-richness condition holds when
![]() $i = 1$
. So set
$i = 1$
. So set
![]() $\varepsilon \,:\!=\,(200C)^{-1}$
and suppose there is a set
$\varepsilon \,:\!=\,(200C)^{-1}$
and suppose there is a set
![]() $U_1\subset V_1$
with
$U_1\subset V_1$
with
![]() $|U_1|\geq \delta |V_1|$
which contradicts the bipartite-richness condition – more precisely that there is a set
$|U_1|\geq \delta |V_1|$
which contradicts the bipartite-richness condition – more precisely that there is a set
![]() $W_2\subset V_2$
with
$W_2\subset V_2$
with
![]() $|W_2|\geq |V_2|^{1/5}$
such that
$|W_2|\geq |V_2|^{1/5}$
such that
![]() $|N(v)\cap U_1|\lt \varepsilon |U_1|$
or
$|N(v)\cap U_1|\lt \varepsilon |U_1|$
or
![]() $|\overline{N(v)}\cap U_1|\lt \varepsilon |U_1|$
for all
$|\overline{N(v)}\cap U_1|\lt \varepsilon |U_1|$
for all
![]() $v\in W_2$
. Without loss of generality, we can assume that there is a subset
$v\in W_2$
. Without loss of generality, we can assume that there is a subset
![]() $U_2\subset W_2$
of size
$U_2\subset W_2$
of size
![]() $|V_2|^{1/5}/2$
such that
$|V_2|^{1/5}/2$
such that
![]() $|N(v)\cap U_1|\lt \varepsilon |U_1|$
for all
$|N(v)\cap U_1|\lt \varepsilon |U_1|$
for all
![]() $v\in W_2$
. But this means that the edge density of
$v\in W_2$
. But this means that the edge density of
![]() $G[U_1,U_2]$
is less than
$G[U_1,U_2]$
is less than
![]() $\varepsilon$
.
$\varepsilon$
.
On the other hand, as
![]() $|U_i| \geq |V_i|^{1/5}/2 \geq |V_i|^{1/6}$
as
$|U_i| \geq |V_i|^{1/5}/2 \geq |V_i|^{1/6}$
as
![]() $|V_i| \geq n_C$
, and since
$|V_i| \geq n_C$
, and since
![]() $G = G[V_1,V_2]$
is
$G = G[V_1,V_2]$
is
![]() $C$
-Ramsey, it follows
$C$
-Ramsey, it follows
![]() $G[U_1, U_2]$
is
$G[U_1, U_2]$
is
![]() $6C$
-Ramsey. But by Lemma 2.1 such a graph must have edge density at least
$6C$
-Ramsey. But by Lemma 2.1 such a graph must have edge density at least
![]() $(196C)^{-1}\gt \varepsilon,$
which is a contradiction, thus proving our result.
$(196C)^{-1}\gt \varepsilon,$
which is a contradiction, thus proving our result.
Next, we discuss the notion of diversity, which was introduced by Bukh and Sudakov [Reference Bukh and Sudakov9] (in the non-bipartite setting).
Definition 2.6.
A bipartite graph
![]() $G = (V_1, V_2,E)$
is said to be
$G = (V_1, V_2,E)$
is said to be
![]() $c$
-bipartite-diverse if for each
$c$
-bipartite-diverse if for each
![]() $i\in \{1,2\}$
the following holds: every vertex
$i\in \{1,2\}$
the following holds: every vertex
![]() $v\in V_i$
has
$v\in V_i$
has
![]() $|\text{div}_G(v,w)|\leq c|V_{3-i}|$
for at most
$|\text{div}_G(v,w)|\leq c|V_{3-i}|$
for at most
![]() $|V_i|^{1/5}$
vertices
$|V_i|^{1/5}$
vertices
![]() $w \in V_i$
.
$w \in V_i$
.
We also introduce a useful diversity notion for pairs. We note that diversity for pairs was also considered by Kwan and Sudakov in [Reference Kwan and Sudakov23], who considered multisets of neighbourhoods, but we require a different notion suitable for our later applications.
Definition 2.7.
A bipartite graph
![]() $G = (V_1, V_2,E)$
is said to be
$G = (V_1, V_2,E)$
is said to be
![]() $(c,\alpha )$
-pair-diverse if for each
$(c,\alpha )$
-pair-diverse if for each
![]() $i\in \{1,2\}$
the following holds true for both
$i\in \{1,2\}$
the following holds true for both
![]() $i = 1,2$
. For each ordered pair
$i = 1,2$
. For each ordered pair
![]() $\boldsymbol{{p}}\in \binom{V_i}{2}$
with
$\boldsymbol{{p}}\in \binom{V_i}{2}$
with
![]() $|\text{div}(\boldsymbol{{p}})|\geq \alpha |V_{3-i}|$
there are at most
$|\text{div}(\boldsymbol{{p}})|\geq \alpha |V_{3-i}|$
there are at most
![]() $|V_i|^{1/5}$
pairwise vertex disjoint pairs
$|V_i|^{1/5}$
pairwise vertex disjoint pairs
![]() $\boldsymbol{{p}}^\prime =(x,y) \in \binom{V_i}{2}$
such that
$\boldsymbol{{p}}^\prime =(x,y) \in \binom{V_i}{2}$
such that
![]() $|\text{divb}_G(\boldsymbol{{p}})\setminus N(x)|\leq c|V_{3-i}|$
or
$|\text{divb}_G(\boldsymbol{{p}})\setminus N(x)|\leq c|V_{3-i}|$
or
![]() $|\text{divb}_G(\boldsymbol{{p}})\setminus N(y)|\leq c|V_{3-i}|$
.
$|\text{divb}_G(\boldsymbol{{p}})\setminus N(y)|\leq c|V_{3-i}|$
.
Lemma 2.8.
Let
![]() $G = (V_1, V_2,E)$
be a
$G = (V_1, V_2,E)$
be a
![]() $(\delta,\varepsilon )$
-bipartite-rich graph with
$(\delta,\varepsilon )$
-bipartite-rich graph with
![]() $\delta \leq 1/2$
. Then:
$\delta \leq 1/2$
. Then:
-
(i)
 $G$
is
$G$
is
 $\varepsilon/2$
-diverse;
$\varepsilon/2$
-diverse;
-
(ii)
 $G$
is
$G$
is
 $(\alpha \varepsilon/2,\alpha )$
-pair-diverse for all
$(\alpha \varepsilon/2,\alpha )$
-pair-diverse for all
 $\alpha \geq 2\delta$
.
$\alpha \geq 2\delta$
.
Proof. It is enough to show that each property holds when taking
![]() $i = 1$
.
$i = 1$
.
(i) For each
![]() $v\in V_1$
either
$v\in V_1$
either
![]() $|N(v)| \geq |V_2|/2$
or
$|N(v)| \geq |V_2|/2$
or
![]() $|\overline{N(v)}|\geq |V_2|/2$
. In the former case, all but at most
$|\overline{N(v)}|\geq |V_2|/2$
. In the former case, all but at most
![]() $|V_1|^{1/5}$
vertices
$|V_1|^{1/5}$
vertices
![]() $w\in V_1$
we have
$w\in V_1$
we have
![]() $|N(v)\cap \overline{N(w)}|\geq \varepsilon |N(v)|\geq \varepsilon/2\cdot |V_2|$
, and in the latter, for all but at most
$|N(v)\cap \overline{N(w)}|\geq \varepsilon |N(v)|\geq \varepsilon/2\cdot |V_2|$
, and in the latter, for all but at most
![]() $|V_1|^{1/5}$
vertices
$|V_1|^{1/5}$
vertices
![]() $w\in V_1$
we have
$w\in V_1$
we have
![]() $|\overline{N(v)}\cap{N(w)}|\geq \varepsilon |\overline{N(v)}|\geq \varepsilon/2\cdot |V_2|$
. In either case, there are at most
$|\overline{N(v)}\cap{N(w)}|\geq \varepsilon |\overline{N(v)}|\geq \varepsilon/2\cdot |V_2|$
. In either case, there are at most
![]() $|V_1|^{1/5}$
vertices
$|V_1|^{1/5}$
vertices
![]() $w\in V_1$
with
$w\in V_1$
with
![]() $|\text{div}_G(v,w)| \lt \varepsilon/2\cdot |V_2|$
, as desired.
$|\text{div}_G(v,w)| \lt \varepsilon/2\cdot |V_2|$
, as desired.
(ii) Suppose now there is an ordered pair
![]() $\boldsymbol{{p}}\,:\!=\,\{x,y\}\in \binom{V_1}{2}$
and a collection
$\boldsymbol{{p}}\,:\!=\,\{x,y\}\in \binom{V_1}{2}$
and a collection
![]() $Y$
of
$Y$
of
![]() $|V_1|^{1/5}$
vertex disjoint pairs
$|V_1|^{1/5}$
vertex disjoint pairs
![]() $\boldsymbol{{p}}_i\,:\!=\,(x_i,y_i) \in \binom{V_1}{2}$
such that
$\boldsymbol{{p}}_i\,:\!=\,(x_i,y_i) \in \binom{V_1}{2}$
such that
![]() $|\text{divb}(\boldsymbol{{p}})\setminus N(x_i)|\leq \alpha \varepsilon/2\cdot |V_2|$
for each
$|\text{divb}(\boldsymbol{{p}})\setminus N(x_i)|\leq \alpha \varepsilon/2\cdot |V_2|$
for each
![]() $i$
. Note that if
$i$
. Note that if
![]() $|\text{div}(\boldsymbol{{p}})|\geq \alpha |V_2|$
then
$|\text{div}(\boldsymbol{{p}})|\geq \alpha |V_2|$
then
![]() $|\text{divb}(\boldsymbol{{p}})|\geq \alpha/2\cdot |V_2|$
, as
$|\text{divb}(\boldsymbol{{p}})|\geq \alpha/2\cdot |V_2|$
, as
![]() $\text{divb}(\boldsymbol{{p}})$
is simply the largest of the two sets
$\text{divb}(\boldsymbol{{p}})$
is simply the largest of the two sets
![]() $N(x)\setminus N(y)$
and
$N(x)\setminus N(y)$
and
![]() $N(y)\setminus N(x)$
, whose union is
$N(y)\setminus N(x)$
, whose union is
![]() $\text{div}(\boldsymbol{{p}})$
. But in this case there are
$\text{div}(\boldsymbol{{p}})$
. But in this case there are
![]() $|V_1|^{1/5}$
distinct vertices
$|V_1|^{1/5}$
distinct vertices
![]() $z_i \in \{x_i, y_i\}$
such that
$z_i \in \{x_i, y_i\}$
such that
![]() $|\text{divb}(\boldsymbol{{p}})\cap \overline{N(z_i)}|\leq \alpha \varepsilon/2\cdot |V_2|\leq \varepsilon |\text{divb}(\boldsymbol{{p}})|$
, which contradicts the richness of the set
$|\text{divb}(\boldsymbol{{p}})\cap \overline{N(z_i)}|\leq \alpha \varepsilon/2\cdot |V_2|\leq \varepsilon |\text{divb}(\boldsymbol{{p}})|$
, which contradicts the richness of the set
![]() $\text{divb}(\boldsymbol{{p}})$
.
$\text{divb}(\boldsymbol{{p}})$
.
2.3 Probabilistic tools
Throughout the proof, we will use Markov’s inequality, Chebyshev’s inequality, the Chernoff bound and Turán’s theorem. Statements and proofs of all of these can be found, for example, in [Reference Alon and Spencer3]. We will also need a probabilistic variation of the Erdős–Littlewood–Offord theorem, a proof of which can be found, for instance in [Reference Jenssen, Long, Keevash and Yepremyan19], or more generally as a consequence of the Doeblin-Kolmogorov-Levy-Rogozin theorem.
Theorem 2.9.
Fix some non-zero parameters
![]() $a_1,a_2,\ldots,a_n\in \mathbb{R}$
and
$a_1,a_2,\ldots,a_n\in \mathbb{R}$
and
![]() $\alpha \in (0,0.5]$
, then let
$\alpha \in (0,0.5]$
, then let
![]() $p_1,p_2,\ldots,p_n\in [\alpha,1-\alpha ]$
. Suppose that
$p_1,p_2,\ldots,p_n\in [\alpha,1-\alpha ]$
. Suppose that
![]() $X_1,X_2,\ldots, X_n$
are independent Bernoulli random variables with
$X_1,X_2,\ldots, X_n$
are independent Bernoulli random variables with
![]() $X_i\sim Be(p_i)$
. Then the following holds:
$X_i\sim Be(p_i)$
. Then the following holds:
The following natural proposition will be useful in our proof of Theorem 1.2.
Proposition 2.10.
Given an integer
![]() $d\geq 2$
, there is an integer
$d\geq 2$
, there is an integer
![]() $n_0\,:\!=\,n_0(d)$
such that if
$n_0\,:\!=\,n_0(d)$
such that if
![]() $X$
is a uniformly chosen subset of
$X$
is a uniformly chosen subset of
![]() $[n]$
, where
$[n]$
, where
![]() $n\geq n_0$
, then for any integer
$n\geq n_0$
, then for any integer
![]() $k$
with
$k$
with
![]() $0\leq k\lt d$
one has:
$0\leq k\lt d$
one has:
Comparable statements already exist in the literature (see for example Lemma 2.3 in [Reference Ferber, Hardiman and Krivelevich18] for a more quantitative behaviour), but to keep the paper contained we outline a simple proof, showing that it can be easily deduced from a standard result about stochastic processes. The next few paragraphs represent a brief introduction to this topic and, for more details, the reader can refer to [Reference Norris28].
A Markov chain is a sequence
![]() $\boldsymbol{{X}}\,:\!=\,(X_n)_{n\geq 0}$
of random variables taking values in some common ground set
$\boldsymbol{{X}}\,:\!=\,(X_n)_{n\geq 0}$
of random variables taking values in some common ground set
![]() $I$
such that, for all
$I$
such that, for all
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $i_0,i_1,\ldots,i_{n}\in I$
, one has:
$i_0,i_1,\ldots,i_{n}\in I$
, one has:
A Markov chain is called homogeneous if, in addition,
![]() $p_{i,j}\,:\!=\,\mathbb P(X_n=j|X_{n-1}=i)$
depends only on the states
$p_{i,j}\,:\!=\,\mathbb P(X_n=j|X_{n-1}=i)$
depends only on the states
![]() $i$
and
$i$
and
![]() $j$
, not on the time
$j$
, not on the time
![]() $n$
. These quantities are known as the transition probabilities of the chain. We are only interested in homogeneous chains, and we can observe that in order to describe such a chain it is enough to have the initial distribution
$n$
. These quantities are known as the transition probabilities of the chain. We are only interested in homogeneous chains, and we can observe that in order to describe such a chain it is enough to have the initial distribution
![]() $\lambda$
of
$\lambda$
of
![]() $X_0$
, given by
$X_0$
, given by
![]() $\lambda _i\,:\!=\,\mathbb P(X_0=i)$
, and the transition matrix
$\lambda _i\,:\!=\,\mathbb P(X_0=i)$
, and the transition matrix
![]() $P\,:\!=\,(p_{i,j})_{i,j\in I}$
. Moreover, if we write
$P\,:\!=\,(p_{i,j})_{i,j\in I}$
. Moreover, if we write
![]() $p_{i,j}^{(n)}$
for
$p_{i,j}^{(n)}$
for
![]() $\mathbb P\!\left(X_{k+n}=j|X_k=i\right)$
, then it is easy to see that
$\mathbb P\!\left(X_{k+n}=j|X_k=i\right)$
, then it is easy to see that
![]() $p_{i,j}^{(n)}=(P^n)_{i,j}$
.
$p_{i,j}^{(n)}=(P^n)_{i,j}$
.
A Markov chain
![]() $\boldsymbol{{X}}$
on the set
$\boldsymbol{{X}}$
on the set
![]() $I$
with transition matrix
$I$
with transition matrix
![]() $P\,:\!=\,(p_{i,j})_{i,j\in I}$
is called irreducible if for all
$P\,:\!=\,(p_{i,j})_{i,j\in I}$
is called irreducible if for all
![]() $i,j\in I$
there is
$i,j\in I$
there is
![]() $n\geq 0$
such that
$n\geq 0$
such that
![]() $p_{i,j}^{(n)}\gt 0$
. The period of a state
$p_{i,j}^{(n)}\gt 0$
. The period of a state
![]() $i\in I$
is defined to be the greatest common divisor of the set
$i\in I$
is defined to be the greatest common divisor of the set
![]() $\left\{n\geq 1\,:\,p_{i,i}^{(n)}\gt 0\right\}$
. The Markov chain
$\left\{n\geq 1\,:\,p_{i,i}^{(n)}\gt 0\right\}$
. The Markov chain
![]() $\boldsymbol{{X}}$
is called aperiodic if all its states have period
$\boldsymbol{{X}}$
is called aperiodic if all its states have period
![]() $1$
.
$1$
.
We say
![]() $\pi = (\pi _i)_{j\in I}$
is a stationary distribution for a Markov chain
$\pi = (\pi _i)_{j\in I}$
is a stationary distribution for a Markov chain
![]() $\boldsymbol{{X}}$
if starting the chain from
$\boldsymbol{{X}}$
if starting the chain from
![]() $X_0$
with distribution
$X_0$
with distribution
![]() $\pi$
implies that
$\pi$
implies that
![]() $X_n$
has distribution
$X_n$
has distribution
![]() $\pi$
for all
$\pi$
for all
![]() $n\geq 1$
. As the distribution of
$n\geq 1$
. As the distribution of
![]() $X_n$
is given by
$X_n$
is given by
![]() $\pi P^n$
, where
$\pi P^n$
, where
![]() $P$
is the transition matrix, we deduce that
$P$
is the transition matrix, we deduce that
![]() $\pi$
is a stationary distribution if and only if
$\pi$
is a stationary distribution if and only if
![]() $\pi P=\pi$
.
$\pi P=\pi$
.
Theorem 2.11.
Suppose
![]() $\boldsymbol{{X}}$
is an irreducible and aperiodic Markov chain on a ground set
$\boldsymbol{{X}}$
is an irreducible and aperiodic Markov chain on a ground set
![]() $I$
with transition matrix
$I$
with transition matrix
![]() $P$
, stationary distribution
$P$
, stationary distribution
![]() $\pi$
and any initial distribution. Then, for all
$\pi$
and any initial distribution. Then, for all
![]() $j\in I$
, one has
$j\in I$
, one has
![]() $\mathbb P(X_n=j)\to \pi _j$
as
$\mathbb P(X_n=j)\to \pi _j$
as
![]() $n\to \infty$
.
$n\to \infty$
.
Proof of Proposition 2.10. We can view choosing
![]() $X$
as going through each number from
$X$
as going through each number from
![]() $1$
to
$1$
to
![]() $n$
and independently tossing a fair coin for each to decide whether it is an element of
$n$
and independently tossing a fair coin for each to decide whether it is an element of
![]() $X$
or not. Thus
$X$
or not. Thus
![]() $|X|\ (\text{mod }d)$
can be viewed as a Markov chain on
$|X|\ (\text{mod }d)$
can be viewed as a Markov chain on
![]() $\{0,1,2,\ldots,d-1\}$
starting at
$\{0,1,2,\ldots,d-1\}$
starting at
![]() $0$
and with transition probabilities
$0$
and with transition probabilities
![]() $p_{i,i}=p_{i,i-1}=0.5$
for each
$p_{i,i}=p_{i,i-1}=0.5$
for each
![]() $0\leq i\lt d$
, where indices ar taken modulo
$0\leq i\lt d$
, where indices ar taken modulo
![]() $d$
. This chain is aperiodic as
$d$
. This chain is aperiodic as
![]() $p_{i,i}^{(1)}=0.5$
, and it is also irreducible as we can reach state
$p_{i,i}^{(1)}=0.5$
, and it is also irreducible as we can reach state
![]() $i$
from state
$i$
from state
![]() $j$
in
$j$
in
![]() $i-j(\text{mod }d)$
steps with positive probability. It is easy to see that the stationary distribution
$i-j(\text{mod }d)$
steps with positive probability. It is easy to see that the stationary distribution
![]() $\pi$
is given by
$\pi$
is given by
![]() $\pi _i=1/d$
. The conclusion now follows from Theorem 2.11.
$\pi _i=1/d$
. The conclusion now follows from Theorem 2.11.
2.4 Progressions in sumsets
Given sets
![]() $A_1,\ldots, A_K \subset{\mathbb Z}$
, the sumset of
$A_1,\ldots, A_K \subset{\mathbb Z}$
, the sumset of
![]() $A_1,\ldots, A_K$
is the set
$A_1,\ldots, A_K$
is the set
![]() $A_1 + \ldots + A_K$
given by
$A_1 + \ldots + A_K$
given by
Much research has focused on the topic of estimating the size or understanding the structure of sumsets under certain assumptions on the sets (see for example [Reference Szemerédi and Vu33] or Chapter 2 of [Reference Tao and Vu34]). For our purposes, the following elementary estimate will suffice.
Lemma 2.12.
Given
![]() $\delta, B\gt 0$
there are
$\delta, B\gt 0$
there are
![]() $C, d_0 \geq 1$
such that the following holds. Suppose that
$C, d_0 \geq 1$
such that the following holds. Suppose that
![]() $A_1,\ldots, A_K \subset [{-}M,M]$
with
$A_1,\ldots, A_K \subset [{-}M,M]$
with
![]() $K \geq CM$
and that
$K \geq CM$
and that
![]() $|A_i| \geq \delta M \geq 2$
for all
$|A_i| \geq \delta M \geq 2$
for all
![]() $i\in [K]$
. Then there is
$i\in [K]$
. Then there is
![]() $a\in{\mathbb Z}$
and
$a\in{\mathbb Z}$
and
![]() $d \in{\mathbb N}$
with
$d \in{\mathbb N}$
with
![]() $1 \leq d \leq d_0$
such that:
$1 \leq d \leq d_0$
such that:
Proof. We will prove the statement under the assumption that
![]() $A_i \subset [0,M]$
for all
$A_i \subset [0,M]$
for all
![]() $i\in [K]$
. Note that the general case follows immediately by taking translations of the sets, i.e. replacing
$i\in [K]$
. Note that the general case follows immediately by taking translations of the sets, i.e. replacing
![]() $A_i$
with
$A_i$
with
![]() $A^{\prime}_i = A_i-c_i$
for
$A^{\prime}_i = A_i-c_i$
for
![]() $c_i = \min \{a\,:\, a\in A_i\}$
. Indeed if (2) holds for
$c_i = \min \{a\,:\, a\in A_i\}$
. Indeed if (2) holds for
![]() $A^{\prime}_1,\ldots, A^{\prime}_K$
(which may now lie in
$A^{\prime}_1,\ldots, A^{\prime}_K$
(which may now lie in
![]() $[0,2M]$
instead of
$[0,2M]$
instead of
![]() $[{-}M,M]$
) then (2) also holds for
$[{-}M,M]$
) then (2) also holds for
![]() $A_1,\ldots, A_K$
(possibly with a different value of
$A_1,\ldots, A_K$
(possibly with a different value of
![]() $a$
). The same argument also allows us to assume that
$a$
). The same argument also allows us to assume that
![]() $0 \in A_i$
for all
$0 \in A_i$
for all
![]() $i \in [K]$
.
$i \in [K]$
.
Next, we double count pairs
![]() $(m,j)\in [M]\times [K]$
for which
$(m,j)\in [M]\times [K]$
for which
![]() $m$
is among the largest
$m$
is among the largest
![]() $\delta M/2$
elements in
$\delta M/2$
elements in
![]() $A_j$
. Counting by each set
$A_j$
. Counting by each set
![]() $A_j$
, we deduce that there are
$A_j$
, we deduce that there are
![]() $\delta KM/2$
such pairs. Therefore, there is
$\delta KM/2$
such pairs. Therefore, there is
![]() $M^\prime \in [M]$
which appears in at least
$M^\prime \in [M]$
which appears in at least
![]() $\delta K/2$
of these pairs. Let
$\delta K/2$
of these pairs. Let
![]() $J\,:\!=\,\{j\in [K]\,:\,M^\prime \in A_j\}$
, so that
$J\,:\!=\,\{j\in [K]\,:\,M^\prime \in A_j\}$
, so that
![]() $|J|\geq \delta K/2$
, and note that
$|J|\geq \delta K/2$
, and note that
![]() $|A_j\cap [0,M^\prime ]|\geq \delta M/2$
as
$|A_j\cap [0,M^\prime ]|\geq \delta M/2$
as
![]() $M^\prime$
is one of the largest
$M^\prime$
is one of the largest
![]() $\delta M/2$
elements in
$\delta M/2$
elements in
![]() $A_j$
. Recalling that also
$A_j$
. Recalling that also
![]() $0\in A_j$
, by restricting all the sets to
$0\in A_j$
, by restricting all the sets to
![]() $[0,M^{\prime}]$
, then eventually reordering them and slightly adjusting the parameter
$[0,M^{\prime}]$
, then eventually reordering them and slightly adjusting the parameter
![]() $C$
, we can now assume that
$C$
, we can now assume that
![]() $A_i\subset [0,M]$
for all
$A_i\subset [0,M]$
for all
![]() $i\in [K]$
, but with
$i\in [K]$
, but with
![]() $\{0,M\} \subset A_i$
as well.
$\{0,M\} \subset A_i$
as well.
Given a set
![]() $S \subset{\mathbb Z}$
, we will let
$S \subset{\mathbb Z}$
, we will let
![]() $\overline{S} \,:\!=\, \{a \in [0,M-1]\,:\, a \equiv s \mod M \mbox{ for some } s \in S\}$
. For each
$\overline{S} \,:\!=\, \{a \in [0,M-1]\,:\, a \equiv s \mod M \mbox{ for some } s \in S\}$
. For each
![]() $i\in [K]$
let
$i\in [K]$
let
![]() $S_i \,:\!=\, \overline{A_1 + \cdots + A_i}$
. By reordering the sets
$S_i \,:\!=\, \overline{A_1 + \cdots + A_i}$
. By reordering the sets
![]() $A_1,\ldots, A_K$
, we may assume that
$A_1,\ldots, A_K$
, we may assume that
![]() $|S_{i+1}| \gt |S_{i}|$
for
$|S_{i+1}| \gt |S_{i}|$
for
![]() $i \leq K^{\prime}$
and that
$i \leq K^{\prime}$
and that
![]() $S_i = S_{K^{\prime}}$
for all
$S_i = S_{K^{\prime}}$
for all
![]() $i \geq K^{\prime}$
. Observe that
$i \geq K^{\prime}$
. Observe that
![]() $S_{K^{\prime}}\subset [0,M-1]$
and that
$S_{K^{\prime}}\subset [0,M-1]$
and that
![]() $|S_{K^{\prime}}| \geq |S_1| + (K^{\prime}-1) \geq K^{\prime}+ 1$
, therefore
$|S_{K^{\prime}}| \geq |S_1| + (K^{\prime}-1) \geq K^{\prime}+ 1$
, therefore
![]() $K^{\prime} \lt M$
.
$K^{\prime} \lt M$
.
Now, as
![]() $0 \in A_i$
for all
$0 \in A_i$
for all
![]() $i\in [K]$
, we have
$i\in [K]$
, we have
![]() $0 \in S_{K^{\prime}} \subset \overline{S_{K^{\prime}} + A_{K^{\prime}+1}} = S_{K^{\prime}+1}$
. As
$0 \in S_{K^{\prime}} \subset \overline{S_{K^{\prime}} + A_{K^{\prime}+1}} = S_{K^{\prime}+1}$
. As
![]() $|S_{K^{\prime}+1}| = |S_{K^{\prime}}|$
, it follows that the set
$|S_{K^{\prime}+1}| = |S_{K^{\prime}}|$
, it follows that the set
![]() $S_{K^{\prime}}$
contains the subgroup of
$S_{K^{\prime}}$
contains the subgroup of
![]() ${\mathbb Z}_M$
generated by
${\mathbb Z}_M$
generated by
![]() $A_{K^{\prime}+1}$
. However, recalling that
$A_{K^{\prime}+1}$
. However, recalling that
![]() $|S_{K^{\prime}}| = |S_{K^{\prime}+1}| \geq |A_{K^{\prime}+1}| \geq \delta M$
, we obtain that there is some
$|S_{K^{\prime}}| = |S_{K^{\prime}+1}| \geq |A_{K^{\prime}+1}| \geq \delta M$
, we obtain that there is some
![]() $d \leq d_0(\delta )$
with
$d \leq d_0(\delta )$
with
![]() $d|M$
such that
$d|M$
such that
![]() $\{id \,:\, 0\leq i \leq M/d\} \subset S_{K^{\prime}} \subset S_M$
.
$\{id \,:\, 0\leq i \leq M/d\} \subset S_{K^{\prime}} \subset S_M$
.
To proceed with the last step, recall that
![]() $\{0,M\} \in A_i$
for all
$\{0,M\} \in A_i$
for all
![]() $i\in [K]$
. Using this, it is easy to see that as
$i\in [K]$
. Using this, it is easy to see that as
![]() $\{id \,:\, 0\leq i \leq M/d\} \subset S_{K^{\prime}} \subset S_M$
, we have
$\{id \,:\, 0\leq i \leq M/d\} \subset S_{K^{\prime}} \subset S_M$
, we have
![]() $\{M^2 + id\,:\, 0 \leq i \leq M/d\} \subset A_1 + \cdots + A_{2M}$
. More generally, as
$\{M^2 + id\,:\, 0 \leq i \leq M/d\} \subset A_1 + \cdots + A_{2M}$
. More generally, as
![]() $d | M$
, we have:
$d | M$
, we have:
and so (2) holds by taking
![]() $a = M^2$
and
$a = M^2$
and
![]() $K \geq CM \geq (B + 2)M$
. This completes the proof.
$K \geq CM \geq (B + 2)M$
. This completes the proof.
3. Proof of Theorem 1.2
3.1 Pair-stars and pair-matchings
We start this section by defining two constructions which will be of central importance in our attempt to find induced subgraphs of many sizes. Let
![]() $G = (V_1, V_2,E)$
be a bipartite graph.
$G = (V_1, V_2,E)$
be a bipartite graph.
An
![]() $\varepsilon$
-pair-star of size
$\varepsilon$
-pair-star of size
![]() $k$
rooted at
$k$
rooted at
![]() $x_0$
associated to
$x_0$
associated to
![]() $V_1$
is a set
$V_1$
is a set
![]() ${\mathcal{P}}_S = \{x_0, x_1,x_2,\ldots,x_k\} \subset V_1$
which satisfies the following properties:
${\mathcal{P}}_S = \{x_0, x_1,x_2,\ldots,x_k\} \subset V_1$
which satisfies the following properties:
-
(i)
 $|d_G(x_j)-d_G(x_0)|\leq{|V_2|}^{0.5}$
for all
$|d_G(x_j)-d_G(x_0)|\leq{|V_2|}^{0.5}$
for all
 $j\in [k]$
;
$j\in [k]$
; -
(ii)
 $|\text{div}(x_i,x_j)|\geq \varepsilon |V_2|$
for all
$|\text{div}(x_i,x_j)|\geq \varepsilon |V_2|$
for all
 $i\neq j$
in
$i\neq j$
in
 $[0,k]$
.
$[0,k]$
.
We define the head of
![]() ${\mathcal{P}}_S$
to be the set
${\mathcal{P}}_S$
to be the set
![]() $H({\mathcal{P}}_S) = \{x_0\}$
.
$H({\mathcal{P}}_S) = \{x_0\}$
.
An
![]() $\varepsilon$
-pair-matching of size
$\varepsilon$
-pair-matching of size
![]() $k$
associated to
$k$
associated to
![]() $V_1$
is a collection
$V_1$
is a collection
![]() ${\mathcal{P}}_M = \{\boldsymbol{{p}}_1,\boldsymbol{{p}}_2,\ldots,\boldsymbol{{p}}_k\}$
of vertex disjoint ordered pairs of vertices in
${\mathcal{P}}_M = \{\boldsymbol{{p}}_1,\boldsymbol{{p}}_2,\ldots,\boldsymbol{{p}}_k\}$
of vertex disjoint ordered pairs of vertices in
![]() $V_1$
which satisfy the following properties:
$V_1$
which satisfy the following properties:
-
(i)
 ${\bf p}_i = (x_i, y_i)$
for all
${\bf p}_i = (x_i, y_i)$
for all
 $i\in [k]$
and the pairs
$i\in [k]$
and the pairs
 ${\bf p}_1, \ldots,{\bf p}_k$
are vertex disjoint;
${\bf p}_1, \ldots,{\bf p}_k$
are vertex disjoint; -
(ii)
 $\operatorname{deg-diff}^{}({\boldsymbol{{p}}_i})\leq |V_2|^{0.5}$
for all
$\operatorname{deg-diff}^{}({\boldsymbol{{p}}_i})\leq |V_2|^{0.5}$
for all
 $i\in [k]$
;
$i\in [k]$
; -
(iii)
 $|\text{divb}(\boldsymbol{{p}}_i)\setminus N(x_j)|\geq \varepsilon |V_2|$
and
$|\text{divb}(\boldsymbol{{p}}_i)\setminus N(x_j)|\geq \varepsilon |V_2|$
and
 $|\text{divb}(\boldsymbol{{p}}_i)\setminus N(y_j)|\geq \varepsilon |V_2|$
for all
$|\text{divb}(\boldsymbol{{p}}_i)\setminus N(y_j)|\geq \varepsilon |V_2|$
for all
 $i \neq j$
in
$i \neq j$
in
 $[k]$
.
$[k]$
.
We define the head of
![]() ${\mathcal{P}}_M$
to be
${\mathcal{P}}_M$
to be
![]() $H({\mathcal{P}}_M) = \{x_i\,:\, i \in [k]\}$
.
$H({\mathcal{P}}_M) = \{x_i\,:\, i \in [k]\}$
.
By swapping
![]() $V_1$
and
$V_1$
and
![]() $V_2$
above, we can define pair-stars and pair-matchings associated to
$V_2$
above, we can define pair-stars and pair-matchings associated to
![]() $V_2$
. Our result in this subsection gives large pair-stars or large pair-matchings in
$V_2$
. Our result in this subsection gives large pair-stars or large pair-matchings in
![]() $C$
-Ramsey graphs.
$C$
-Ramsey graphs.
Lemma 3.1.
Given
![]() $C\gt 1$
there is
$C\gt 1$
there is
![]() $\varepsilon \gt 0$
and
$\varepsilon \gt 0$
and
![]() $n_C\in \mathbb{N}$
such that the following holds. Suppose that
$n_C\in \mathbb{N}$
such that the following holds. Suppose that
![]() $G = (V_1, V_2,E)$
is a
$G = (V_1, V_2,E)$
is a
![]() $C$
-bipartite-Ramsey graph with
$C$
-bipartite-Ramsey graph with
![]() $|V_1|\geq |V_2|/2 \geq n_C$
. Then either:
$|V_1|\geq |V_2|/2 \geq n_C$
. Then either:
 $V_1$
contains an
$V_1$
contains an
 $\varepsilon$
-pair-star of size
$\varepsilon$
-pair-star of size
 $|V_1|^{0.5}$
, or
$|V_1|^{0.5}$
, or
 $V_1$
contains an
$V_1$
contains an
 $\varepsilon$
-pair-matching of size
$\varepsilon$
-pair-matching of size
 $|V_1|^{0.5}$
.
$|V_1|^{0.5}$
.
Proof. Let us start by dividing the interval
![]() $[0,|V_2|]$
into
$[0,|V_2|]$
into
![]() $\ell \,:\!=\,{|V_2|}^{1/2}$
disjoint intervals
$\ell \,:\!=\,{|V_2|}^{1/2}$
disjoint intervals
![]() $I_1,I_2,\ldots I_l$
of length
$I_1,I_2,\ldots I_l$
of length
![]() ${|V_2|}^{1/2}$
and let, for each interval
${|V_2|}^{1/2}$
and let, for each interval
![]() $I_j$
,
$I_j$
,
![]() $n_j$
denote the number of vertices in
$n_j$
denote the number of vertices in
![]() $V_1$
whose degree lie in
$V_1$
whose degree lie in
![]() $I_j$
. Now any vertices
$I_j$
. Now any vertices
![]() $x, y \in I_j$
with
$x, y \in I_j$
with
![]() $d(x) \geq d(y)$
give an ordered pair
$d(x) \geq d(y)$
give an ordered pair
![]() $\boldsymbol{{p}} = (x,y)$
with
$\boldsymbol{{p}} = (x,y)$
with
![]() $\operatorname{deg-diff}^{}({{\bf p}}) \leq{|V_2|}^{1/2}$
. Obviously
$\operatorname{deg-diff}^{}({{\bf p}}) \leq{|V_2|}^{1/2}$
. Obviously
![]() $n_1+n_2+\ldots + n_{\ell }=|V_1|$
, so by Jensen’s inequality the collection
$n_1+n_2+\ldots + n_{\ell }=|V_1|$
, so by Jensen’s inequality the collection
![]() $\mathcal{S}$
of such ordered pairs
$\mathcal{S}$
of such ordered pairs
![]() $\boldsymbol{{p}} = (x,y) \in \binom{V_1}{2}$
has size:
$\boldsymbol{{p}} = (x,y) \in \binom{V_1}{2}$
has size:
 \begin{align*} |{\mathcal{S}}| \geq \sum _{j=1}^{\ell }\binom{n_j}{2}\geq \ell \cdot \binom{|V_1|/\ell }{2} \geq \frac{|V_1||\big (|V_1|/\ell -1\big )}{2} \geq \frac{|V_1|^{1.5}}{4}, \end{align*}
\begin{align*} |{\mathcal{S}}| \geq \sum _{j=1}^{\ell }\binom{n_j}{2}\geq \ell \cdot \binom{|V_1|/\ell }{2} \geq \frac{|V_1||\big (|V_1|/\ell -1\big )}{2} \geq \frac{|V_1|^{1.5}}{4}, \end{align*}
using
![]() $\ell = |V_2|^{0.5} \leq (2|V_1| )^{0.5}$
and
$\ell = |V_2|^{0.5} \leq (2|V_1| )^{0.5}$
and
![]() $|V_1| \geq n_C$
. By Lemmas 2.8 and 2.5, we deduce that our graph
$|V_1| \geq n_C$
. By Lemmas 2.8 and 2.5, we deduce that our graph
![]() $G$
is
$G$
is
![]() $\varepsilon _0$
-diverse, where
$\varepsilon _0$
-diverse, where
![]() $\varepsilon _0\,:\!=\,(400C)^{-1}$
. Therefore, at most
$\varepsilon _0\,:\!=\,(400C)^{-1}$
. Therefore, at most
![]() $|V_1|^{1.2}=o(|\mathcal{S}|)$
pairs from
$|V_1|^{1.2}=o(|\mathcal{S}|)$
pairs from
![]() $\mathcal{S}$
fail to be
$\mathcal{S}$
fail to be
![]() ${\varepsilon }_0$
-diverse. By removing such pairs, we obtain a collection
${\varepsilon }_0$
-diverse. By removing such pairs, we obtain a collection
![]() $\mathcal{S}_0$
of size at least
$\mathcal{S}_0$
of size at least
![]() $|V_1|^{1.5}/8$
such that
$|V_1|^{1.5}/8$
such that
![]() $\operatorname{deg-diff}\!({\bf p}) \leq |V_2|^{1/2}$
and
$\operatorname{deg-diff}\!({\bf p}) \leq |V_2|^{1/2}$
and
![]() $|\text{div}(\boldsymbol{{p}})|\geq \varepsilon _0|V_2|$
for all
$|\text{div}(\boldsymbol{{p}})|\geq \varepsilon _0|V_2|$
for all
![]() $\boldsymbol{{p}}\in \mathcal{S}_0$
.
$\boldsymbol{{p}}\in \mathcal{S}_0$
.
Next, we view the elements of
![]() $\mathcal{S}_0$
as the (unordered) edges of a graph
$\mathcal{S}_0$
as the (unordered) edges of a graph
![]() $H$
on
$H$
on
![]() $V(G)$
. We claim that either
$V(G)$
. We claim that either
![]() $H$
has a matching of size
$H$
has a matching of size
![]() $m\,:\!=\, |V_1|^{0.75}/4$
or a set of
$m\,:\!=\, |V_1|^{0.75}/4$
or a set of
![]() $m+1$
edges that have a common vertex. To see why this is true, suppose that neither of these two events hold and let
$m+1$
edges that have a common vertex. To see why this is true, suppose that neither of these two events hold and let
![]() $M$
be a largest matching in
$M$
be a largest matching in
![]() $H$
. Then
$H$
. Then
![]() $|M|\lt m$
and so all the edges in
$|M|\lt m$
and so all the edges in
![]() $e(H)\setminus M$
must be adjacent to an edge of
$e(H)\setminus M$
must be adjacent to an edge of
![]() $M$
. But because of the other condition, each edge of
$M$
. But because of the other condition, each edge of
![]() $M$
has at most
$M$
has at most
![]() $2m$
other edges adjacent to it. Thus,
$2m$
other edges adjacent to it. Thus,
![]() $e(H)\lt 2m^2 \leq |\mathcal{S}_0|$
, which is a contradiction.
$e(H)\lt 2m^2 \leq |\mathcal{S}_0|$
, which is a contradiction.
Let us now observe that this set of edges will create our pair-star or pair-matching. Indeed, assume first that we have obtained
![]() $m+1$
edges
$m+1$
edges
![]() $x_0x_1,x_0x_2,\ldots,x_0x_{m+1}$
in
$x_0x_1,x_0x_2,\ldots,x_0x_{m+1}$
in
![]() $\mathcal{S}_0$
. Again, by diversity, each vertex
$\mathcal{S}_0$
. Again, by diversity, each vertex
![]() $x_j$
has at most
$x_j$
has at most
![]() $|V_1|^{0.2}$
other vertices
$|V_1|^{0.2}$
other vertices
![]() $x_i$
such that
$x_i$
such that
![]() $|\text{div}(x_j,x_i)|\lt \varepsilon _0|V_2|$
. Thus, by Turán theorem there is a set
$|\text{div}(x_j,x_i)|\lt \varepsilon _0|V_2|$
. Thus, by Turán theorem there is a set
![]() $I\subset [0, m+1]$
, with
$I\subset [0, m+1]$
, with
![]() $0 \in I$
, of size at least
$0 \in I$
, of size at least
![]() $(m+1)/(1+|V_1|^{0.2}) \geq |V_1|^{0.5}$
such that
$(m+1)/(1+|V_1|^{0.2}) \geq |V_1|^{0.5}$
such that
![]() $|\text{div}(x_j,x_i)|\geq \varepsilon _0|V_2|$
for all
$|\text{div}(x_j,x_i)|\geq \varepsilon _0|V_2|$
for all
![]() $i\neq j$
in
$i\neq j$
in
![]() $I$
. Taking
$I$
. Taking
![]() $x_0$
as the root gives our pair-star.
$x_0$
as the root gives our pair-star.
In the other case, assume that we have obtained
![]() $m$
disjoint ordered pairs
$m$
disjoint ordered pairs
![]() ${\bf p}_1,\ldots,{\bf p}_m$
in
${\bf p}_1,\ldots,{\bf p}_m$
in
![]() ${\mathcal{S}}_0$
, with
${\mathcal{S}}_0$
, with
![]() ${\bf p}_i = (x_i, y_i)$
. Then, by Lemmas 2.5 and 2.8 our graph
${\bf p}_i = (x_i, y_i)$
. Then, by Lemmas 2.5 and 2.8 our graph
![]() $G$
is
$G$
is
![]() $((\varepsilon _0/2)^2, \varepsilon _0/2)$
-pair-diverse, so for each pair
$((\varepsilon _0/2)^2, \varepsilon _0/2)$
-pair-diverse, so for each pair
![]() $(x_j,y_j)$
there are at most
$(x_j,y_j)$
there are at most
![]() $|V_1|^{0.2}$
other pairwise disjoint edges
$|V_1|^{0.2}$
other pairwise disjoint edges
![]() $x_iy_i$
such that
$x_iy_i$
such that
![]() $|\text{divb}(x_j,y_j)\setminus N(x_i)|\lt (\varepsilon _0/2)^2 |V_2|$
or
$|\text{divb}(x_j,y_j)\setminus N(x_i)|\lt (\varepsilon _0/2)^2 |V_2|$
or
![]() $|\text{divb}(x_j,y_j)\setminus N(y_i)|\lt (\varepsilon _0/2)^2 |V_2|$
. Setting
$|\text{divb}(x_j,y_j)\setminus N(y_i)|\lt (\varepsilon _0/2)^2 |V_2|$
. Setting
![]() $\varepsilon = (\varepsilon _0/2)^2$
, by Turán, there is a set
$\varepsilon = (\varepsilon _0/2)^2$
, by Turán, there is a set
![]() $I\subset [m]$
of size at least
$I\subset [m]$
of size at least
![]() $m (1+|V_1|^{0.2} )^{-1} \geq |V_1|^{0.5}$
such that
$m (1+|V_1|^{0.2} )^{-1} \geq |V_1|^{0.5}$
such that
![]() $|\text{divb}({\bf p}_j)\setminus N(x_i)|\geq \varepsilon |V_2|$
and
$|\text{divb}({\bf p}_j)\setminus N(x_i)|\geq \varepsilon |V_2|$
and
![]() $|\text{divb}({\bf p}_j)\setminus N(y_i)|\geq \varepsilon |V_2|$
for all
$|\text{divb}({\bf p}_j)\setminus N(y_i)|\geq \varepsilon |V_2|$
for all
![]() $i\neq j$
in
$i\neq j$
in
![]() $I$
. This represents our pair-matching.
$I$
. This represents our pair-matching.
3.2 Degree control from pair-stars and pair-matchings
Our next aim is to show that when picking a subset
![]() $W \subset V_2$
uniformly at random, there is a very good chance that pair-stars and pair-matchings associated to
$W \subset V_2$
uniformly at random, there is a very good chance that pair-stars and pair-matchings associated to
![]() $V_1$
produce well distributed degree sets in
$V_1$
produce well distributed degree sets in
![]() $W$
. The following lemma will be useful in this context.
$W$
. The following lemma will be useful in this context.
Lemma 3.2.
Let
![]() $G = (V_1, V_2, E)$
be a bipartite graph and suppose the subset
$G = (V_1, V_2, E)$
be a bipartite graph and suppose the subset
![]() $W \subset V_2$
is selected uniformly at random. Then:
$W \subset V_2$
is selected uniformly at random. Then:
-
(i) if
 $x, y \in V_1$
with
$x, y \in V_1$
with
 $|{\text{div}}(x,y)|\geq \delta |V_2|$
then
$|{\text{div}}(x,y)|\geq \delta |V_2|$
then
 $\mathbb P (d^{W}(x)=d^{W}(y) ) =O_{\delta } (|V_2|^{-0.5} ).$
$\mathbb P (d^{W}(x)=d^{W}(y) ) =O_{\delta } (|V_2|^{-0.5} ).$
-
(ii) if
 $\boldsymbol{{p}}_1=(x_1,y_1)\in \binom{V_1}{2}$
and
$\boldsymbol{{p}}_1=(x_1,y_1)\in \binom{V_1}{2}$
and
 $\boldsymbol{{p}}_2=(x_2,y_2)\in \binom{V_1}{2}$
with
$\boldsymbol{{p}}_2=(x_2,y_2)\in \binom{V_1}{2}$
with
 $|{\text{divb}}(\boldsymbol{{p}}_1)\setminus N(x_2)|\geq \delta |V_2|$
and
$|{\text{divb}}(\boldsymbol{{p}}_1)\setminus N(x_2)|\geq \delta |V_2|$
and
 $|{\text{divb}}(\boldsymbol{{p}}_1)\setminus N(y_2)|\geq \delta |V_2|$
then
$|{\text{divb}}(\boldsymbol{{p}}_1)\setminus N(y_2)|\geq \delta |V_2|$
then
 $ \mathbb P ( \operatorname{deg-diff}^{ }({{\bf p}_1}){W}=\operatorname{deg-diff}^{ }({{\bf p}_2}){W} )=O_\delta (|V_2|^{-0.5} ).$
$ \mathbb P ( \operatorname{deg-diff}^{ }({{\bf p}_1}){W}=\operatorname{deg-diff}^{ }({{\bf p}_2}){W} )=O_\delta (|V_2|^{-0.5} ).$
Proof. (i) We will use a classical randomness exposure argument. Suppose we reveal the random set
![]() $W$
on
$W$
on
![]() $V_2\setminus \text{div}(x,y)$
. Then, given such a choice, the difference
$V_2\setminus \text{div}(x,y)$
. Then, given such a choice, the difference
![]() $d^{W}(x)-d^{W}(y)$
becomes
$d^{W}(x)-d^{W}(y)$
becomes
![]() $d^{U}(x)-d^{U}(y)+\text{constant}$
, where
$d^{U}(x)-d^{U}(y)+\text{constant}$
, where
![]() $U \,:\!=\,W \cap \text{div}(x,y)$
. Now,
$U \,:\!=\,W \cap \text{div}(x,y)$
. Now,
![]() $d^{U}(x)-d^{U}(y)\,:\!=\,\sum _{v\in \text{div}(x,y)}\theta _vX_v$
, where for each
$d^{U}(x)-d^{U}(y)\,:\!=\,\sum _{v\in \text{div}(x,y)}\theta _vX_v$
, where for each
![]() $v\in \text{div}(x,y)$
we have
$v\in \text{div}(x,y)$
we have
![]() $\theta _v\in \{-1,1\}$
and
$\theta _v\in \{-1,1\}$
and
![]() $X_v\sim \text{Bern}(0.5)$
. Since
$X_v\sim \text{Bern}(0.5)$
. Since
![]() $|\text{div}(x,y)|\geq \delta |V_2|$
, by Theorem 2.9, the random variable
$|\text{div}(x,y)|\geq \delta |V_2|$
, by Theorem 2.9, the random variable
![]() $d^{W^{\prime}}(x)-d^{W^{\prime}}(y)$
hits any particular value with probability
$d^{W^{\prime}}(x)-d^{W^{\prime}}(y)$
hits any particular value with probability
![]() $O_\delta (|V_2|^{-1/2} )$
. The conclusion follows from the law of total probability.
$O_\delta (|V_2|^{-1/2} )$
. The conclusion follows from the law of total probability.
(ii) The argument here is similar, but a little more involved. By the choice of the ordering we have
![]() $\mbox{divb}({\bf p}_1) = N(x_1) \setminus N(y_1)$
. Note that the condition in the lemma now gives that the set
$\mbox{divb}({\bf p}_1) = N(x_1) \setminus N(y_1)$
. Note that the condition in the lemma now gives that the set
![]() $T = \mbox{divb}({\bf p}_1) \setminus N(x_2) = N(x_1) \setminus ( N(x_2) \cup N(y_1) )$
satisfies
$T = \mbox{divb}({\bf p}_1) \setminus N(x_2) = N(x_1) \setminus ( N(x_2) \cup N(y_1) )$
satisfies
![]() $|T| \geq \delta |V_2|$
. Letting
$|T| \geq \delta |V_2|$
. Letting
![]() $X$
denote the random variable
$X$
denote the random variable
![]() $X = \operatorname{deg-diff}^{W}\!({{\bf p}_1}) - \operatorname{deg-diff}^{W}\!({{\bf p}_2})$
we have:
$X = \operatorname{deg-diff}^{W}\!({{\bf p}_1}) - \operatorname{deg-diff}^{W}\!({{\bf p}_2})$
we have:
Now note that if we expose the random set
![]() $W \cap (V_2 \setminus T)$
, then the random variable
$W \cap (V_2 \setminus T)$
, then the random variable
![]() $X$
reduces to
$X$
reduces to
![]() $d^{W \cap T}(x_1)+d^{W \cap T}(y_2)-C$
, where
$d^{W \cap T}(x_1)+d^{W \cap T}(y_2)-C$
, where
![]() $C$
is some constant depending only on
$C$
is some constant depending only on
![]() $W\cap (V_2 \cap T)$
– crucially, here we use that
$W\cap (V_2 \cap T)$
– crucially, here we use that
![]() $y_1$
and
$y_1$
and
![]() $x_2$
have no neighbour in
$x_2$
have no neighbour in
![]() $T$
. But
$T$
. But
![]() $d^{W \cap T}(x_1)+d^{W \cap T}(y_2)=\sum _{v\in T}\theta _vX_v$
where
$d^{W \cap T}(x_1)+d^{W \cap T}(y_2)=\sum _{v\in T}\theta _vX_v$
where
![]() $\theta _v\in \{1,2\}$
is a constant for each
$\theta _v\in \{1,2\}$
is a constant for each
![]() $v\in T$
and
$v\in T$
and
![]() $X_v\sim \text{Bern}(0.5)$
so that
$X_v\sim \text{Bern}(0.5)$
so that
![]() $\{X_v\}_{v\in T}$
are independent. By Theorem 2.9, since
$\{X_v\}_{v\in T}$
are independent. By Theorem 2.9, since
![]() $|T|\geq \delta |V_2|$
, the random variable
$|T|\geq \delta |V_2|$
, the random variable
![]() $d^{W \cap T}(x_1)+d^{W\cap T}(y_2)$
takes any particular value with probability at most
$d^{W \cap T}(x_1)+d^{W\cap T}(y_2)$
takes any particular value with probability at most
![]() $O_\delta (|V_2|^{-0.5} )$
. The conclusion again follows from the law of total probability.
$O_\delta (|V_2|^{-0.5} )$
. The conclusion again follows from the law of total probability.
Let
![]() $G = (V_1, V_2, E)$
be a bipartite graph and select a vertex set
$G = (V_1, V_2, E)$
be a bipartite graph and select a vertex set
![]() $W \subset V_2$
. Given an
$W \subset V_2$
. Given an
![]() $\varepsilon$
-pair star
$\varepsilon$
-pair star
![]() ${\mathcal{P}} = \{x_0,x_1,\ldots, x_k\}$
rooted at
${\mathcal{P}} = \{x_0,x_1,\ldots, x_k\}$
rooted at
![]() $x_0$
and associated to
$x_0$
and associated to
![]() $V_1$
, we write:
$V_1$
, we write:
The following lemma provides a useful estimate on the size of
![]() $A_{\mathcal{P}}^W$
.
$A_{\mathcal{P}}^W$
.
Lemma 3.3.
Given
![]() $\varepsilon \gt 0$
there is
$\varepsilon \gt 0$
there is
![]() $\delta \gt 0$
such that the following holds. Let
$\delta \gt 0$
such that the following holds. Let
![]() $G = (V_1, V_2, E)$
be a bipartite graph with
$G = (V_1, V_2, E)$
be a bipartite graph with
![]() $|V_1|\geq |V_2|/2$
and let
$|V_1|\geq |V_2|/2$
and let
![]() ${\mathcal{P}} = \{x_0,\ldots, x_{|V_2|^{0.5}}\}$
be a
${\mathcal{P}} = \{x_0,\ldots, x_{|V_2|^{0.5}}\}$
be a
![]() $\varepsilon$
-pair-star of size
$\varepsilon$
-pair-star of size
![]() ${|V_2|}^{0.5}$
rooted at
${|V_2|}^{0.5}$
rooted at
![]() $x_0$
and associated to
$x_0$
and associated to
![]() $V_1$
. Suppose that a set
$V_1$
. Suppose that a set
![]() $W \subset B$
is selected uniformly at random, then
$W \subset B$
is selected uniformly at random, then
![]() ${\mathbb{P}}\! \left(|A_{\mathcal{P}}^W| \geq \delta |V_2|^{0.5} \right) \geq 3/4$
.
${\mathbb{P}}\! \left(|A_{\mathcal{P}}^W| \geq \delta |V_2|^{0.5} \right) \geq 3/4$
.
Proof. To begin, pick
![]() $j\in [|V_2|^{0.5}]$
and set
$j\in [|V_2|^{0.5}]$
and set
![]() $D_j \,:\!=\, d^W(x_j) - d^W(x_0)$
. By Chebyshev’s inequality, we have
$D_j \,:\!=\, d^W(x_j) - d^W(x_0)$
. By Chebyshev’s inequality, we have
![]() $ |D_j-\mathbb E[D_j] |\leq 2{|V_2|}^{0.5}$
with probability at least
$ |D_j-\mathbb E[D_j] |\leq 2{|V_2|}^{0.5}$
with probability at least
![]() $15/16$
. As
$15/16$
. As
![]() $ |\mathbb E[D_j] |\leq |V_2|^{1/2}/2$
, it follows by triangle inequality that
$ |\mathbb E[D_j] |\leq |V_2|^{1/2}/2$
, it follows by triangle inequality that
![]() $\mathbb P (|d^{W}(x_0)-d^{W}(x_j)|\leq 3|V_2|^{0.5} )\geq 15/16$
.
$\mathbb P (|d^{W}(x_0)-d^{W}(x_j)|\leq 3|V_2|^{0.5} )\geq 15/16$
.
Next, call a vertex
![]() $x_j$
with
$x_j$
with
![]() $j\in [|V_2|^{0.5}]$
bad if
$j\in [|V_2|^{0.5}]$
bad if
![]() $|d^{W}(x_0)-d^{W}(x_j)|\leq 3|V_2|^{0.5}$
and good otherwise. Note
$|d^{W}(x_0)-d^{W}(x_j)|\leq 3|V_2|^{0.5}$
and good otherwise. Note
![]() $\mathbb P(x_j\text{ is bad})\leq 1/16$
and so
$\mathbb P(x_j\text{ is bad})\leq 1/16$
and so
![]() $\mathbb E [ |\{j\in [|V_1|^{0.5}]\,:\,x_j\text{ is bad}\} | ]\leq |V_2|^{0.5}/16$
. If
$\mathbb E [ |\{j\in [|V_1|^{0.5}]\,:\,x_j\text{ is bad}\} | ]\leq |V_2|^{0.5}/16$
. If
![]() $U$
denotes the set of good vertices, then it follows by Markov that
$U$
denotes the set of good vertices, then it follows by Markov that
![]() $\mathbb P (|U|\geq |V_2|^{0.5}/2 )\geq 7/8$
.
$\mathbb P (|U|\geq |V_2|^{0.5}/2 )\geq 7/8$
.
Now we build a graph
![]() $H$
on
$H$
on
![]() $\{x_1,\ldots, x_{|V_2|^{1/2}}\}$
where we join two vertices by an edge in
$\{x_1,\ldots, x_{|V_2|^{1/2}}\}$
where we join two vertices by an edge in
![]() $H$
if their degrees in
$H$
if their degrees in
![]() $W$
are equal. By Lemma 3.2 (i) there is an edge in
$W$
are equal. By Lemma 3.2 (i) there is an edge in
![]() $H$
between two vertices
$H$
between two vertices
![]() $x_i$
and
$x_i$
and
![]() $x_j$
with probability
$x_j$
with probability
![]() $O_{\varepsilon } (|V_2|^{-1/2} )$
. Therefore,
$O_{\varepsilon } (|V_2|^{-1/2} )$
. Therefore,
![]() $\mathbb E[e(H)]=O_{\varepsilon } ((|V_2|^{0.5})^2\cdot |V_2|^{-0.5} )$
and by Markov we easily deduce that, with probability at least
$\mathbb E[e(H)]=O_{\varepsilon } ((|V_2|^{0.5})^2\cdot |V_2|^{-0.5} )$
and by Markov we easily deduce that, with probability at least
![]() $7/8$
, one has
$7/8$
, one has
![]() $e(H)=O_{\varepsilon } (|V_2|^{0.5} )$
.
$e(H)=O_{\varepsilon } (|V_2|^{0.5} )$
.
Combining our estimates, by applying the union bound we find that
![]() $|U| \geq |V_2|^{0.5}/2$
and that
$|U| \geq |V_2|^{0.5}/2$
and that
![]() $e(H[U]) \leq e(H)=O_{\varepsilon } (|V_2|^{0.5} )$
with probability at least
$e(H[U]) \leq e(H)=O_{\varepsilon } (|V_2|^{0.5} )$
with probability at least
![]() $3/4$
. But then the average degree of
$3/4$
. But then the average degree of
![]() $H$
is of order
$H$
is of order
![]() $O_{\varepsilon } (1 )$
, hence by Turán
$O_{\varepsilon } (1 )$
, hence by Turán
![]() $H$
contains an independent set of size
$H$
contains an independent set of size
![]() $\Omega _{\varepsilon } ({|V_2|^{0.5}} )$
. This set though gives us precisely the vertices with pairwise distinct degrees that we sought.
$\Omega _{\varepsilon } ({|V_2|^{0.5}} )$
. This set though gives us precisely the vertices with pairwise distinct degrees that we sought.
Let
![]() $G = (V_1, V_2, E)$
be a bipartite graph, and set
$G = (V_1, V_2, E)$
be a bipartite graph, and set
![]() $W \subset V_2$
. Given an
$W \subset V_2$
. Given an
![]() $\varepsilon$
-pair-matching
$\varepsilon$
-pair-matching
![]() ${\mathcal{P}} = \{{\bf p}_1,\ldots,{\bf p}_k\}$
associated to
${\mathcal{P}} = \{{\bf p}_1,\ldots,{\bf p}_k\}$
associated to
![]() $V_1$
, we write:
$V_1$
, we write:
The following lemma gives the analogous estimate for
![]() $A_{\mathcal{P}}^W$
when
$A_{\mathcal{P}}^W$
when
![]() ${\mathcal{P}}$
is an pair-matching and can be proven in exactly the same way as in Lemma 3.3, replacing Lemma 3.2 (i) in the proof with Lemma 3.2 (ii) instead.
${\mathcal{P}}$
is an pair-matching and can be proven in exactly the same way as in Lemma 3.3, replacing Lemma 3.2 (i) in the proof with Lemma 3.2 (ii) instead.
Lemma 3.4.
Given
![]() $\varepsilon \gt 0$
there is
$\varepsilon \gt 0$
there is
![]() $\delta \gt 0$
such that the following holds. Let
$\delta \gt 0$
such that the following holds. Let
![]() $G = (V_1, V_2, E)$
be a bipartite graph with
$G = (V_1, V_2, E)$
be a bipartite graph with
![]() $|V_1|\geq |V_2|/2$
and let
$|V_1|\geq |V_2|/2$
and let
![]() ${\mathcal{P}}$
be a
${\mathcal{P}}$
be a
![]() $\varepsilon$
-pair-matching in
$\varepsilon$
-pair-matching in
![]() $V_1$
of size
$V_1$
of size
![]() $|V_2|^{0.5}$
. Suppose that a set
$|V_2|^{0.5}$
. Suppose that a set
![]() $W \subset B$
is selected uniformly at random, then
$W \subset B$
is selected uniformly at random, then
![]() ${\mathbb{P}} (|A_{\mathcal{P}}^W| \geq \delta |V_2|^{0.5} ) \geq 3/4$
.
${\mathbb{P}} (|A_{\mathcal{P}}^W| \geq \delta |V_2|^{0.5} ) \geq 3/4$
.
3.3 Breaking modular obstructions
Lemma 3.5.
Given a natural number
![]() $d \gt 1$
and
$d \gt 1$
and
![]() $\varepsilon \gt 0$
there are
$\varepsilon \gt 0$
there are
![]() $L, D \gt 0$
such that the following holds. Suppose that
$L, D \gt 0$
such that the following holds. Suppose that
![]() $G = (V_1, V_2, E)$
is a bipartite graph and that
$G = (V_1, V_2, E)$
is a bipartite graph and that
![]() $\{u_1,\ldots, u_L\} \subset V_1$
such that
$\{u_1,\ldots, u_L\} \subset V_1$
such that
![]() $S_i = N_G(u_i) \setminus \cup _{j \lt i} N_G(u_j)$
satisfies
$S_i = N_G(u_i) \setminus \cup _{j \lt i} N_G(u_j)$
satisfies
![]() $|S_i| \geq D$
for all
$|S_i| \geq D$
for all
![]() $i\in [L]$
. Then, if a subset
$i\in [L]$
. Then, if a subset
![]() $W$
is chosen uniformly at random from
$W$
is chosen uniformly at random from
![]() $V_2$
, with probability at least
$V_2$
, with probability at least
![]() $1 - \varepsilon$
for every pair
$1 - \varepsilon$
for every pair
![]() $(k,m)$
with
$(k,m)$
with
![]() $0 \leq k \leq m$
and
$0 \leq k \leq m$
and
![]() $2 \leq m \leq d$
there is
$2 \leq m \leq d$
there is
![]() $i\in [L]$
such that
$i\in [L]$
such that
![]() $d_G^{W}(u_i) \equiv k \mod m$
.
$d_G^{W}(u_i) \equiv k \mod m$
.
Proof. Suppose that
![]() $W \subset V_2$
is selected as in the lemma. To begin, we fix a pair
$W \subset V_2$
is selected as in the lemma. To begin, we fix a pair
![]() $(k,m)$
so that
$(k,m)$
so that
![]() $0 \leq k \leq m$
and
$0 \leq k \leq m$
and
![]() $2 \leq m\leq d$
. For
$2 \leq m\leq d$
. For
![]() $i \in [L]$
let
$i \in [L]$
let
![]() $E_i$
denote the event
$E_i$
denote the event
![]() $E_i \,:\!=\, \left\{d^W_G(u_i) \not \equiv k \mod m\right\}$
. Our first aim is to upper bound
$E_i \,:\!=\, \left\{d^W_G(u_i) \not \equiv k \mod m\right\}$
. Our first aim is to upper bound
![]() ${\mathbb{P}} \left( \cap _{i\in [L]} E_i \right)$
. To do this, we can observe that:
${\mathbb{P}} \left( \cap _{i\in [L]} E_i \right)$
. To do this, we can observe that:
 \begin{align*} \mathbb P\big (\cap _{i=1}^L E_i\big )=\prod _{i=1}^L \mathbb P\!\left (E_i|\cap _{j\lt i}E_j\right ). \end{align*}
\begin{align*} \mathbb P\big (\cap _{i=1}^L E_i\big )=\prod _{i=1}^L \mathbb P\!\left (E_i|\cap _{j\lt i}E_j\right ). \end{align*}
Now the event
![]() $\cap _{j\lt i}E_i$
is entirely determined by the choice of
$\cap _{j\lt i}E_i$
is entirely determined by the choice of
![]() $W^{\prime} = W \cap (V_2 \setminus S_i)$
. Thus, to upper bound
$W^{\prime} = W \cap (V_2 \setminus S_i)$
. Thus, to upper bound
![]() $\mathbb P \!\left(E_i|\cap _{j\lt i}E_j \right)$
, it suffices to upper bound
$\mathbb P \!\left(E_i|\cap _{j\lt i}E_j \right)$
, it suffices to upper bound
![]() $\mathbb P\! \left(E_i|W^{\prime} = W_0 \right)$
for each choice of
$\mathbb P\! \left(E_i|W^{\prime} = W_0 \right)$
for each choice of
![]() $W_0$
. However, given such a choice of
$W_0$
. However, given such a choice of
![]() $W_0$
, the conditional probability
$W_0$
, the conditional probability
![]() $\mathbb P\! \left(E_i|W^{\prime}=W_0 \right)$
becomes
$\mathbb P\! \left(E_i|W^{\prime}=W_0 \right)$
becomes
![]() $\mathbb P\! \left(d^{W\cap S_i}_G(u_i)\not \equiv k_i\ (\text{mod }m) \right)$
for some
$\mathbb P\! \left(d^{W\cap S_i}_G(u_i)\not \equiv k_i\ (\text{mod }m) \right)$
for some
![]() $0\leq k_i\lt m$
. Besides this, from our hypothesis we know that
$0\leq k_i\lt m$
. Besides this, from our hypothesis we know that
![]() $W \cap S_i \sim \mbox{Bin}(|S_i|,0.5)$
and
$W \cap S_i \sim \mbox{Bin}(|S_i|,0.5)$
and
![]() $|S_i| \geq D$
, so by Proposition 2.10 this gives
$|S_i| \geq D$
, so by Proposition 2.10 this gives
![]() $\mathbb P\! \left(E_i|\cap _{j\lt i}E_j \right) \leq \max _{W_0}{\mathbb{P}}\left(E_i| W^{\prime} = W_0\right) \leq d(d+1)^{-1}$
. Combining all these, we obtain:
$\mathbb P\! \left(E_i|\cap _{j\lt i}E_j \right) \leq \max _{W_0}{\mathbb{P}}\left(E_i| W^{\prime} = W_0\right) \leq d(d+1)^{-1}$
. Combining all these, we obtain:
 \begin{align*} \mathbb P\big (\cap _{i=1}^L E_i\big ) \leq \prod _{i=1}^L \mathbb P\!\left (E_i|\cap _{j\lt i}E_j\right ) \leq \Big ( 1 - \frac{1}{d+1} \Big ) ^{L}\leq \exp \!\left ({-}L(d+1)^{-1}\right ). \end{align*}
\begin{align*} \mathbb P\big (\cap _{i=1}^L E_i\big ) \leq \prod _{i=1}^L \mathbb P\!\left (E_i|\cap _{j\lt i}E_j\right ) \leq \Big ( 1 - \frac{1}{d+1} \Big ) ^{L}\leq \exp \!\left ({-}L(d+1)^{-1}\right ). \end{align*}
To finish the proof, let
![]() $F_{(k,m)}$
denote the event that
$F_{(k,m)}$
denote the event that
![]() $\{d_G^W(u_i) \not \equiv k \mod m \mbox{ for all } i\in [L]\}$
. We have shown that
$\{d_G^W(u_i) \not \equiv k \mod m \mbox{ for all } i\in [L]\}$
. We have shown that
![]() ${\mathbb{P}}(F_{(k,m)}) \leq \exp\!\left( -L(d+1)^{-1} \right)$
. It follows that the probability that some congruence is not obtained is
${\mathbb{P}}(F_{(k,m)}) \leq \exp\!\left( -L(d+1)^{-1} \right)$
. It follows that the probability that some congruence is not obtained is
![]() ${\mathbb{P}}\! \left( \cup _{(k,m)} F_{k,m} \right) \leq \sum _{(k,m)}{\mathbb{P}}\!\left(F_{k,m}\right) \leq d^2 \exp\!\left({-}L(d+1)^{-1} \right) \leq \varepsilon$
, provided that
${\mathbb{P}}\! \left( \cup _{(k,m)} F_{k,m} \right) \leq \sum _{(k,m)}{\mathbb{P}}\!\left(F_{k,m}\right) \leq d^2 \exp\!\left({-}L(d+1)^{-1} \right) \leq \varepsilon$
, provided that
![]() $L$
(and
$L$
(and
![]() $D$
from above) are sufficiently large.
$D$
from above) are sufficiently large.
3.4 Completing the proof of Theorem 1.2
The following lemma is the final key step in our proof.
Lemma 3.6.
Given
![]() $C\gt 1$
, there are constants
$C\gt 1$
, there are constants
![]() $a_C \gt 0$
and
$a_C \gt 0$
and
![]() $n_C\in \mathbb{N}$
such that the following holds. Every
$n_C\in \mathbb{N}$
such that the following holds. Every
![]() $C$
-bipartite-Ramsey graph
$C$
-bipartite-Ramsey graph
![]() $G = (V_1, V_2, E)$
with
$G = (V_1, V_2, E)$
with
![]() $|V_1|,|V_2|\geq n_C$
has:
$|V_1|,|V_2|\geq n_C$
has:
Proof. We start by fixing parameters
![]() $1\geq C^{-1} \gg \varepsilon \gg \delta \gg d_0^{-1} \gg L^{-1} \gg C_0^{-1} \gg c \gg n_C^{-1} \gt 0$
. Without loss of generality, we may assume that
$1\geq C^{-1} \gg \varepsilon \gg \delta \gg d_0^{-1} \gg L^{-1} \gg C_0^{-1} \gg c \gg n_C^{-1} \gt 0$
. Without loss of generality, we may assume that
![]() $|V_1| \geq |V_2|$
. We also fix an arbitrary set
$|V_1| \geq |V_2|$
. We also fix an arbitrary set
![]() $V^{\prime}_2 \subset V_2$
with
$V^{\prime}_2 \subset V_2$
with
![]() $|V^{\prime}_2| = c|V_2|$
and a partition
$|V^{\prime}_2| = c|V_2|$
and a partition
![]() $V_1 = U_1 \cup U_2 \cup U_3$
, where
$V_1 = U_1 \cup U_2 \cup U_3$
, where
![]() $|U_i| \geq |V_1|/4$
for
$|U_i| \geq |V_1|/4$
for
![]() $i\in [3]$
.
$i\in [3]$
.
To begin, we claim that there are
![]() ${\mathcal{P}}_1,\ldots,{\mathcal{P}}_K$
with
${\mathcal{P}}_1,\ldots,{\mathcal{P}}_K$
with
![]() $K \,:\!=\, C_0|V_2|^{0.5}$
such that each
$K \,:\!=\, C_0|V_2|^{0.5}$
such that each
![]() ${\mathcal{P}}_i$
is either an
${\mathcal{P}}_i$
is either an
![]() $\varepsilon$
-pair-star or a
$\varepsilon$
-pair-star or a
![]() $\varepsilon$
-pair-matching in
$\varepsilon$
-pair-matching in
![]() $G\left[U_1, V^{\prime}_2\right]$
of size
$G\left[U_1, V^{\prime}_2\right]$
of size
![]() $|V^{\prime}_2|^{0.5}$
and so that the
$|V^{\prime}_2|^{0.5}$
and so that the
![]() ${\mathcal{P}}_i$
’s are all vertex disjoint. To see this, suppose that we have found
${\mathcal{P}}_i$
’s are all vertex disjoint. To see this, suppose that we have found
![]() ${\mathcal{P}}_1,\ldots,{\mathcal{P}}_i$
and now seek
${\mathcal{P}}_1,\ldots,{\mathcal{P}}_i$
and now seek
![]() ${\mathcal{P}}_{i+1}$
. Let
${\mathcal{P}}_{i+1}$
. Let
![]() $U^{\prime}_1$
denote the subset of
$U^{\prime}_1$
denote the subset of
![]() $U_1$
with the vertices of
$U_1$
with the vertices of
![]() $\cup _{j\leq i}{\mathcal{P}}_j$
removed and apply Lemma 3.1 to
$\cup _{j\leq i}{\mathcal{P}}_j$
removed and apply Lemma 3.1 to
![]() $G\!\left[U^{\prime}_1, V^{\prime}_2\right]$
, noting that as
$G\!\left[U^{\prime}_1, V^{\prime}_2\right]$
, noting that as
![]() $|U^{\prime}_1| \geq |U_1| - 2 K |V^{\prime}_2|^{0.5} \geq |U_1| - 2(C_0|V_2|^{0.5}) (c|V_1|)^{0.5} \geq |U_1|/2 \geq |V_1|/8$
, making
$|U^{\prime}_1| \geq |U_1| - 2 K |V^{\prime}_2|^{0.5} \geq |U_1| - 2(C_0|V_2|^{0.5}) (c|V_1|)^{0.5} \geq |U_1|/2 \geq |V_1|/8$
, making
![]() $G\!\left[U^{\prime}_1, V^{\prime}_2\right]$
a
$G\!\left[U^{\prime}_1, V^{\prime}_2\right]$
a
![]() $2C$
-Ramsey graph. By Lemma 3.1, we can find a
$2C$
-Ramsey graph. By Lemma 3.1, we can find a
![]() $\varepsilon$
-star-pair or a
$\varepsilon$
-star-pair or a
![]() $\varepsilon$
-pair-matching
$\varepsilon$
-pair-matching
![]() ${\mathcal{P}}_{i+1}$
of size
${\mathcal{P}}_{i+1}$
of size
![]() $|U^{\prime}_1|^{0.5} \geq |V^{\prime}_2|^{0.5}$
, which gives the desired set (perhaps after removing some of its elements). Thus such a collection
$|U^{\prime}_1|^{0.5} \geq |V^{\prime}_2|^{0.5}$
, which gives the desired set (perhaps after removing some of its elements). Thus such a collection
![]() ${\mathcal{P}}_1,\ldots,{\mathcal{P}}_K$
exists.
${\mathcal{P}}_1,\ldots,{\mathcal{P}}_K$
exists.
Our next step is to apply Lemma 2.3 to
![]() $G\!\left[U_2, V^{\prime}_2\right]$
, which is again
$G\!\left[U_2, V^{\prime}_2\right]$
, which is again
![]() $2C$
-Ramsey, to find a set
$2C$
-Ramsey, to find a set
![]() $S_2 = \{s_1,\ldots, s_L\} \subset U_2$
such that
$S_2 = \{s_1,\ldots, s_L\} \subset U_2$
such that
![]() $\big|N(s_i) \setminus ( \cup _{j\lt i}N(s_j) )\big| \geq |V_2|^{0.5}$
for all
$\big|N(s_i) \setminus ( \cup _{j\lt i}N(s_j) )\big| \geq |V_2|^{0.5}$
for all
![]() $i\in [L]$
. It is possible to do this since
$i\in [L]$
. It is possible to do this since
![]() $C^{-1} \gg L^{-1} \gg n_C^{-1}$
.
$C^{-1} \gg L^{-1} \gg n_C^{-1}$
.
The final step of preparation is to select a set
![]() $W \subset V^{\prime}_2$
uniformly at random. For each
$W \subset V^{\prime}_2$
uniformly at random. For each
![]() $i\in [K]$
let
$i\in [K]$
let
![]() $A_i \,:\!=\, A_{{\mathcal{P}}_i}^W$
. Now consider the following events:
$A_i \,:\!=\, A_{{\mathcal{P}}_i}^W$
. Now consider the following events:
Let
 ${\mathcal{E}}_1$
denote the event that, for at least
${\mathcal{E}}_1$
denote the event that, for at least
 $K/2$
values
$K/2$
values
 $i\in [K]$
, we have
$i\in [K]$
, we have
 $|A_i| \geq \delta |V^{\prime}_2|^{1/2}$
. By Lemmas 3.3 and 3.4, and using that
$|A_i| \geq \delta |V^{\prime}_2|^{1/2}$
. By Lemmas 3.3 and 3.4, and using that
 $\varepsilon \gg \delta$
, we see that for any
$\varepsilon \gg \delta$
, we see that for any
 $A_i$
we have
$A_i$
we have
 $|A_i| \geq \delta |W|^{1/2}$
with probability at least
$|A_i| \geq \delta |W|^{1/2}$
with probability at least
 $3/4$
, so a simple application of Markov gives
$3/4$
, so a simple application of Markov gives
 ${\mathbb{P}}({\mathcal{E}}_1) \geq 1/2$
;
${\mathbb{P}}({\mathcal{E}}_1) \geq 1/2$
;Secondly, let
 ${\mathcal{E}}_2$
denote the event that, for every
${\mathcal{E}}_2$
denote the event that, for every
 $0 \leq k \leq m$
and
$0 \leq k \leq m$
and
 $2 \leq m \leq d_0$
, there exists
$2 \leq m \leq d_0$
, there exists
 $s \in S_2$
with
$s \in S_2$
with
 $d^W_G(s) \equiv k \mod m$
. By the choice of
$d^W_G(s) \equiv k \mod m$
. By the choice of
 $S_2$
, Lemma 3.5 gives
$S_2$
, Lemma 3.5 gives
 ${\mathbb{P}}({\mathcal{E}}_2) \geq 7/8$
;
${\mathbb{P}}({\mathcal{E}}_2) \geq 7/8$
;Lastly, let
 ${\mathcal{E}}_3$
denote the event that
${\mathcal{E}}_3$
denote the event that
 $|W| \geq |V^{\prime}_2|/4$
. By Chebyshev’s inequality
$|W| \geq |V^{\prime}_2|/4$
. By Chebyshev’s inequality
 ${\mathbb{P}}({\mathcal{E}}_3) \geq 7/8$
.
${\mathbb{P}}({\mathcal{E}}_3) \geq 7/8$
.
It follows from the union bound that
![]() ${\mathbb{P}}({\mathcal{E}}_1 \cap{\mathcal{E}}_2 \cap{\mathcal{E}}_3) \geq 1/2$
. Fix a choice of
${\mathbb{P}}({\mathcal{E}}_1 \cap{\mathcal{E}}_2 \cap{\mathcal{E}}_3) \geq 1/2$
. Fix a choice of
![]() $W \subset V^{\prime}_2 \subset V_2$
for which all three events occur. By reordering, we get that
$W \subset V^{\prime}_2 \subset V_2$
for which all three events occur. By reordering, we get that
![]() $|A_i| \geq \delta |V^{\prime}_2|^{1/2} \geq \delta |W|^{1/2}$
for
$|A_i| \geq \delta |V^{\prime}_2|^{1/2} \geq \delta |W|^{1/2}$
for
![]() $i\in [K/2]$
.
$i\in [K/2]$
.
We are now ready to complete the proof. Take
![]() $V_1^{\mbox{init}}$
to be the union of the heads of
$V_1^{\mbox{init}}$
to be the union of the heads of
![]() ${\mathcal{P}}_i$
, i.e.
${\mathcal{P}}_i$
, i.e.
![]() $V_1^{\mbox{init}} \,:\!=\, \cup _{i \leq L/2} H({\mathcal{P}}_i)$
, and
$V_1^{\mbox{init}} \,:\!=\, \cup _{i \leq L/2} H({\mathcal{P}}_i)$
, and
![]() $e_0 \,:\!=\, e(G[V_1^{\mbox{init}}, W])$
. Take
$e_0 \,:\!=\, e(G[V_1^{\mbox{init}}, W])$
. Take
![]() $a \in A_i$
and note the following:
$a \in A_i$
and note the following:
-
(i) If
 ${\mathcal{P}}_i = \{x_0,\ldots, x_{|V^{\prime}_2|^{0.5}}\}$
is a pair-star rooted at
${\mathcal{P}}_i = \{x_0,\ldots, x_{|V^{\prime}_2|^{0.5}}\}$
is a pair-star rooted at
 $x_0$
, then by definition
$x_0$
, then by definition
 $d^W(x_j) - d^W(x_0) = a$
for some
$d^W(x_j) - d^W(x_0) = a$
for some
 $j\in \left[\big|V^{\prime}_2\big|^{1/2}\right]$
. Removing
$j\in \left[\big|V^{\prime}_2\big|^{1/2}\right]$
. Removing
 $x_0$
from
$x_0$
from
 $V_1^{\mbox{init}}$
and adding
$V_1^{\mbox{init}}$
and adding
 $x_j$
changes the number of edges in the resulting graph by exactly
$x_j$
changes the number of edges in the resulting graph by exactly
 $a$
.
$a$
. -
(ii) Similarly, if
 ${\mathcal{P}}_i$
is a pair-matching, then there is
${\mathcal{P}}_i$
is a pair-matching, then there is
 ${\bf p} = (x,y) \in{\mathcal{P}}_i$
such that
${\bf p} = (x,y) \in{\mathcal{P}}_i$
such that
 $\operatorname{deg-diff}^{W}\!({{\bf p}}) = a$
. Removing
$\operatorname{deg-diff}^{W}\!({{\bf p}}) = a$
. Removing
 $x$
from
$x$
from
 $V_1^{\mbox{init}}$
and adding
$V_1^{\mbox{init}}$
and adding
 $y$
to it changes the number of edges by exactly
$y$
to it changes the number of edges by exactly
 $a$
.
$a$
. -
(iii) The edits from different
 ${\mathcal{P}}_i$
’s can be performed independently of one another, resulting in the same changes to the edge size given in (i) and (ii).
${\mathcal{P}}_i$
’s can be performed independently of one another, resulting in the same changes to the edge size given in (i) and (ii).
From observations (i)
![]() $-$
(iii) we can immediately deduce that:
$-$
(iii) we can immediately deduce that:
By definition of
![]() $A_i\,:\!=\,A_{{\mathcal{P}}_i}^W$
, we have
$A_i\,:\!=\,A_{{\mathcal{P}}_i}^W$
, we have
![]() $A_i \subset \left[{-}3|V^{\prime}_2|^{1/2}, 3|V^{\prime}_2|^{1/2}\right] \subset \left[{-}6|W|^{1/2}, 6|W|^{1/2}\right]$
and
$A_i \subset \left[{-}3|V^{\prime}_2|^{1/2}, 3|V^{\prime}_2|^{1/2}\right] \subset \left[{-}6|W|^{1/2}, 6|W|^{1/2}\right]$
and
![]() $|A_i| \geq \delta |W|^{1/2}$
. By taking
$|A_i| \geq \delta |W|^{1/2}$
. By taking
![]() $M = 6|W|^{1/2}$
and
$M = 6|W|^{1/2}$
and
![]() $B = 1$
in Lemma 2.12, as
$B = 1$
in Lemma 2.12, as
![]() $\delta,1 \gg C_0^{-1}, d_0^{-1}$
, it follows that there is
$\delta,1 \gg C_0^{-1}, d_0^{-1}$
, it follows that there is
![]() $a \in{\mathbb Z}$
and
$a \in{\mathbb Z}$
and
![]() $1 \leq d \leq d_0$
such that (2) holds, which gives:
$1 \leq d \leq d_0$
such that (2) holds, which gives:
Furthermore, as
![]() $d \leq d_0$
, by the choice of
$d \leq d_0$
, by the choice of
![]() $S_2$
there are
$S_2$
there are
![]() $s_{i_0}, s_{i_1},\ldots, s_{i_{d-1}} \in S_2$
with
$s_{i_0}, s_{i_1},\ldots, s_{i_{d-1}} \in S_2$
with
![]() $d^W(s_j) \equiv j \mod d$
for each
$d^W(s_j) \equiv j \mod d$
for each
![]() $j\in [0,d-1]$
. Combined with (3), setting
$j\in [0,d-1]$
. Combined with (3), setting
![]() $e_1 = e_0 + a + |W|$
, this gives:
$e_1 = e_0 + a + |W|$
, this gives:
To finish the proof, note that
![]() $|U_3| \geq |V_1|/4 \geq |V_1|^{1/2}$
and
$|U_3| \geq |V_1|/4 \geq |V_1|^{1/2}$
and
![]() $|W| \geq |V^{\prime}_2|/4 \geq |V_2|^{1/2}$
. As
$|W| \geq |V^{\prime}_2|/4 \geq |V_2|^{1/2}$
. As
![]() $G$
is
$G$
is
![]() $C$
-Ramsey, we get that
$C$
-Ramsey, we get that
![]() $G[U_3, W]$
is
$G[U_3, W]$
is
![]() $(2C)$
-Ramsey. It follows from Corollary 2.2 that at least
$(2C)$
-Ramsey. It follows from Corollary 2.2 that at least
![]() $2|U_3|/3$
vertices in
$2|U_3|/3$
vertices in
![]() $U_3$
have degrees between
$U_3$
have degrees between
![]() $(64C)^{-1}|W|$
and
$(64C)^{-1}|W|$
and
![]() $(1-(64C)^{-1})|W|$
in
$(1-(64C)^{-1})|W|$
in
![]() $G[U_3, W]$
. In particular,
$G[U_3, W]$
. In particular,
![]() $\{e(G[U^{\prime},W]) \,:\, U^{\prime} \subset U_3\}$
contains an element from each interval
$\{e(G[U^{\prime},W]) \,:\, U^{\prime} \subset U_3\}$
contains an element from each interval
![]() $[|W|i, |W|(i+1)]$
with
$[|W|i, |W|(i+1)]$
with
![]() $i\in [0,(96C)^{-1}|U_3|]$
. However,
$i\in [0,(96C)^{-1}|U_3|]$
. However,
![]() $e(G[U \cup \{s\} \cup U^{\prime}, W]) = e(G[U \cup \{s\}, W]) + e(G[ U^{\prime}, W])$
for any
$e(G[U \cup \{s\} \cup U^{\prime}, W]) = e(G[U \cup \{s\}, W]) + e(G[ U^{\prime}, W])$
for any
![]() $U \subset U_1, s \in S_2$
and
$U \subset U_1, s \in S_2$
and
![]() $U^{\prime} \subset U_3$
. Therefore, we deduce from (4) that:
$U^{\prime} \subset U_3$
. Therefore, we deduce from (4) that:
We can finally claim that the lemma holds with
![]() $a_C \,:\!=\, c/4000C$
. To see this, note that:
$a_C \,:\!=\, c/4000C$
. To see this, note that:
where we have used that
![]() $|W| \leq c|V_2|$
, that
$|W| \leq c|V_2|$
, that
![]() $c \ll C_0^{-1}, C^{-1}$
, and that
$c \ll C_0^{-1}, C^{-1}$
, and that
![]() $|V_2| \leq |V_1|$
.
$|V_2| \leq |V_1|$
.
Since
![]() $a_C|V_1||V_2| = (c/4000C)|V_1||V_2| \leq (200C)^{-1}|U_3||W|$
, it is quite easy to observe that
$a_C|V_1||V_2| = (c/4000C)|V_1||V_2| \leq (200C)^{-1}|U_3||W|$
, it is quite easy to observe that
![]() $[a_C|V_1||V_2|, 2a_C|V_1||V_2|] \subset \{e(G[U])\,:\, U \subset V(G)\}$
, as required. This completes the proof.
$[a_C|V_1||V_2|, 2a_C|V_1||V_2|] \subset \{e(G[U])\,:\, U \subset V(G)\}$
, as required. This completes the proof.
With Lemma 3.6 in hand, it is now easy to complete the proof of Theorem 1.2.
Proof of Theorem 1.2. By making
![]() $\alpha$
small enough we may assume, without losing generality, that
$\alpha$
small enough we may assume, without losing generality, that
![]() $|V_1|\geq |V_2|$
and that
$|V_1|\geq |V_2|$
and that
![]() $|V_2|$
is large enough so that our estimates below hold. We can also assume that
$|V_2|$
is large enough so that our estimates below hold. We can also assume that
![]() $C\gt 1$
since the Ramsey condition still holds when we increase
$C\gt 1$
since the Ramsey condition still holds when we increase
![]() $C$
.
$C$
.
First note that as
![]() $G = (V_1, V_2, E)$
is
$G = (V_1, V_2, E)$
is
![]() $C$
-Ramsey, there is a vertex
$C$
-Ramsey, there is a vertex
![]() $v \in V_2$
with degree at least
$v \in V_2$
with degree at least
![]() $(32C)^{-1}|V_1|$
in
$(32C)^{-1}|V_1|$
in
![]() $V_1$
, by Corollary 2.2. But then the induced subgraphs of the form
$V_1$
, by Corollary 2.2. But then the induced subgraphs of the form
![]() $G[W, \{v\}]$
, where
$G[W, \{v\}]$
, where
![]() $W \subset V_1$
, give all edge sizes in
$W \subset V_1$
, give all edge sizes in
![]() $[0,(32C)^{-1}|V_1|]$
(and so in particular the analogue of the Alon
$[0,(32C)^{-1}|V_1|]$
(and so in particular the analogue of the Alon
![]() $-$
Krivelevich
$-$
Krivelevich
![]() $-$
Sudakov theorem from [Reference Alon, Krivelevich and Sudakov1] is easier in the bipartite Ramsey context).
$-$
Sudakov theorem from [Reference Alon, Krivelevich and Sudakov1] is easier in the bipartite Ramsey context).
On the other hand, observe that by fixing any
![]() $W_1 \subset V_1$
and
$W_1 \subset V_1$
and
![]() $W_2 \subset V_2$
with
$W_2 \subset V_2$
with
![]() $|W_i| \geq |V_i|^{1/3}$
for
$|W_i| \geq |V_i|^{1/3}$
for
![]() $i \in \{1,2\}$
, the graph
$i \in \{1,2\}$
, the graph
![]() $H = G[W_1, W_2]$
is
$H = G[W_1, W_2]$
is
![]() $(3C)$
-Ramsey, as
$(3C)$
-Ramsey, as
![]() $G$
is
$G$
is
![]() $C$
-Ramsey. It follows by applying Lemma 3.6 to
$C$
-Ramsey. It follows by applying Lemma 3.6 to
![]() $H$
that there are induced subgraphs of each size in
$H$
that there are induced subgraphs of each size in
![]() $[a_{3C}|W_1||W_2|, 2a_{3C}|W_1||W_2|]$
. It follows, taking
$[a_{3C}|W_1||W_2|, 2a_{3C}|W_1||W_2|]$
. It follows, taking
![]() $M = \{(m_1, m_2)\,:\, |V_i|^{1/3} \leq m_i \leq |V_i| \mbox{ for } i \in \{1,2\}\}$
, that
$M = \{(m_1, m_2)\,:\, |V_i|^{1/3} \leq m_i \leq |V_i| \mbox{ for } i \in \{1,2\}\}$
, that
![]() $G$
contains a subgraph of each size in
$G$
contains a subgraph of each size in
![]() $\cup _{(m_1,m_2) \in M} [a_{3C}m_1m_2, 2a_{3C}m_1m_2]$
. It can be easily seen that these sets together cover the interval
$\cup _{(m_1,m_2) \in M} [a_{3C}m_1m_2, 2a_{3C}m_1m_2]$
. It can be easily seen that these sets together cover the interval
![]() $[a_C(|V_1||V_2|)^{1/3}, 2a_C |V_1||V_2|]$
.
$[a_C(|V_1||V_2|)^{1/3}, 2a_C |V_1||V_2|]$
.
Finally, note that the intervals
![]() $[0,(32C)^{-1}|V_1|]$
and
$[0,(32C)^{-1}|V_1|]$
and
![]() $[a_{3C}(|V_1||V_2|)^{1/3}, 2a_{3C} |V_1||V_2|]$
together cover
$[a_{3C}(|V_1||V_2|)^{1/3}, 2a_{3C} |V_1||V_2|]$
together cover
![]() $[0, 2a_{3C} |V_1||V_2|]$
, since
$[0, 2a_{3C} |V_1||V_2|]$
, since
![]() $|V_1| \geq |V_2|$
and
$|V_1| \geq |V_2|$
and
![]() $|V_2|$
is large enough, thus completing the proof of the theorem.
$|V_2|$
is large enough, thus completing the proof of the theorem.
4. Concluding remarks
In this paper, we have proven a bipartite analogue of the Erdős–McKay conjecture, showing that any
![]() $C$
-bipartite-Ramsey graph
$C$
-bipartite-Ramsey graph
![]() $G = (V_1, V_2, E)$
must contain induced subgraphs of all sizes in
$G = (V_1, V_2, E)$
must contain induced subgraphs of all sizes in
![]() $[0, \Omega _C(|V_1||V_2|)]$
. Of course the Erdős–McKay conjecture itself remains an outstanding problem, and we hope that some of our ideas will be useful in future approaches here.
$[0, \Omega _C(|V_1||V_2|)]$
. Of course the Erdős–McKay conjecture itself remains an outstanding problem, and we hope that some of our ideas will be useful in future approaches here.
Another interesting direction is to understand the effect of weakening the Ramsey hypothesis in Theorem 1.2, as considered already in a number of other settings (see e.g. [Reference Alon and Bollobás2], [Reference Narayanan and Tomon26], [Reference Long and Ploscaru24]). That is, what are we able to say about the edge sizes of induced subgraphs of a bipartite graph
![]() $G = (V_1, V_2, E)$
, which do not contain induced copies of
$G = (V_1, V_2, E)$
, which do not contain induced copies of
![]() $K_{t_1,t_2}$
or
$K_{t_1,t_2}$
or
![]() $\overline{K_{t_1, t_2}}$
, where
$\overline{K_{t_1, t_2}}$
, where
![]() $t_1$
and
$t_1$
and
![]() $t_2$
are now general parameters?
$t_2$
are now general parameters?
Lastly, we note that Narayanan, Sahasrabudhe and Tomon in [Reference Narayanan, Sahasrabudhe and Tomon27] showed that any bipartite graph with
![]() $m$
edges must have induced subgraphs of
$m$
edges must have induced subgraphs of
![]() $\Omega (m/ \log ^{12}\!(m))$
different sizes. An obvious upper bound here for the number of such sizes is
$\Omega (m/ \log ^{12}\!(m))$
different sizes. An obvious upper bound here for the number of such sizes is
![]() $m$
, though if
$m$
, though if
![]() $m$
is a perfect square
$m$
is a perfect square
![]() $m = k^2$
then the complete bipartite graphs
$m = k^2$
then the complete bipartite graphs
![]() $K_{k,k}$
allows only
$K_{k,k}$
allows only
![]() $m/ (\!\log m)^{0.086\ldots + o(1)}$
edge sizes. The authors of [Reference Narayanan, Sahasrabudhe and Tomon27] conjecture that when
$m/ (\!\log m)^{0.086\ldots + o(1)}$
edge sizes. The authors of [Reference Narayanan, Sahasrabudhe and Tomon27] conjecture that when
![]() $m = k^2$
the graph
$m = k^2$
the graph
![]() $K_{k,k}$
is extremal here. It would be interesting to understand whether our approach, perhaps combined with stability arguments, could be applied to improve knowledge here.
$K_{k,k}$
is extremal here. It would be interesting to understand whether our approach, perhaps combined with stability arguments, could be applied to improve knowledge here.