Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kravstov, Dmitry
Krokhmal, Nikolay
and
Shabanov, Dmitry
2019.
Panchromatic 3-colorings of random hypergraphs.
European Journal of Combinatorics,
Vol. 78,
Issue. ,
p.
28.
Демидович, Ю А
and
Demidovich, Yu A
2020.
Двухцветные раскраски гиперграфов с большим обхватом.
Математические заметки,
Vol. 108,
Issue. 2,
p.
200.
Demidovich, Yurii Aleksandrovich
2020.
Новая нижняя оценка наименьшего числа ребер простого однородного гиперграфа без свойства $B_k$.
Дискретная математика,
Vol. 32,
Issue. 4,
p.
10.
Shabanov, Dmitry Aleksandrovich
and
Shaikheeva, Taliya Maratovna
2020.
О предписанном хроматическом числе
полных многодольных гиперграфов и
кратных покрытиях независимыми множествами.
Математические заметки,
Vol. 107,
Issue. 3,
p.
454.
Raigorodskii, A. M.
and
Cherkashin, D. D.
2020.
Extremal problems in hypergraph colourings.
Russian Mathematical Surveys,
Vol. 75,
Issue. 1,
p.
89.
Akhmejanova, Margarita
and
Shabanov, Dmitry
2020.
Coloring hypergraphs with bounded cardinalities of edge intersections.
Discrete Mathematics,
Vol. 343,
Issue. 4,
p.
111692.
Akhmejanova, Margarita B.
and
Shabanov, Dmitry A.
2020.
Equitable colorings of hypergraphs with few edges.
Discrete Applied Mathematics,
Vol. 276,
Issue. ,
p.
2.
Shabanov, D. A.
and
Shaikheeva, T. M.
2020.
The List-Chromatic Number of Complete Multipartite Hypergraphs and Multiple Covers by Independent Sets.
Mathematical Notes,
Vol. 107,
Issue. 3-4,
p.
499.
Raigorodskii, Andrei Mikhailovich
and
Cherkashin, Danila Dmitrievich
2020.
Экстремальные задачи в раскрасках гиперграфов.
Успехи математических наук,
Vol. 75,
Issue. 1(451),
p.
95.
Demidovich, Yu. A.
2020.
2-Colorings of Hypergraphs with Large Girth.
Mathematical Notes,
Vol. 108,
Issue. 1-2,
p.
188.
Khuzieva, A. E.
2022.
Random Constructions of Hypergraphs with Large Girth and Without Panchromatic Colorings.
Journal of Mathematical Sciences,
Vol. 262,
Issue. 4,
p.
581.
Demidovich, Yury A.
2022.
New lower bound for the minimal number of edges of simple uniform hypergraph without the property Bk
.
Discrete Mathematics and Applications,
Vol. 32,
Issue. 3,
p.
155.
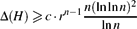 $$\Delta(H)\geqslant c\cdot r^{n-1}\ffrac{n(\ln\ln n)^2}{\ln n}$$
$$\Delta(H)\geqslant c\cdot r^{n-1}\ffrac{n(\ln\ln n)^2}{\ln n}$$ 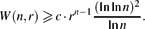 $$W(n,r)\geqslant c\cdot r^{n-1}\ffrac{(\ln\ln n)^2}{\ln n}.$$
$$W(n,r)\geqslant c\cdot r^{n-1}\ffrac{(\ln\ln n)^2}{\ln n}.$$ 
