Article contents
Counting Intersecting and Pairs of Cross-Intersecting Families
Published online by Cambridge University Press: 16 October 2017
Abstract
A family of subsets of {1,. . .,n} is called intersecting if any two of its sets intersect. A classical result in extremal combinatorics due to Erdős, Ko and Rado determines the maximum size of an intersecting family of k-subsets of {1,. . .,n}. In this paper we study the following problem: How many intersecting families of k-subsets of {1,. . .,n} are there? Improving a result of Balogh, Das, Delcourt, Liu and Sharifzadeh, we determine this quantity asymptotically for n ≥ 2k+2+2 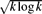 $\sqrt{k\log k}$ and k → ∞. Moreover, under the same assumptions we also determine asymptotically the number of non-trivial intersecting families, that is, intersecting families for which the intersection of all sets is empty. We obtain analogous results for pairs of cross-intersecting families.
$\sqrt{k\log k}$ and k → ∞. Moreover, under the same assumptions we also determine asymptotically the number of non-trivial intersecting families, that is, intersecting families for which the intersection of all sets is empty. We obtain analogous results for pairs of cross-intersecting families.
MSC classification
Information
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2017
References
- 9
- Cited by

