Hostname: page-component-76fb5796d-vvkck Total loading time: 0 Render date: 2024-04-27T04:21:33.989Z Has data issue: false hasContentIssue false
  • English
  • Français

Estimating parameters associated with monotone properties

Part of: Algorithms - Computer Science Theory of computing Discrete mathematics in relation to computer science Graph theory

Published online by Cambridge University Press:  24 March 2020

Carlos Hoppen ,
Yoshiharu Kohayakawa ,
Richard Lang ,
Hanno Lefmann  and
Henrique Stagni
Carlos Hoppen
Affiliation:
Instituto de Matemática, UFRGS, Avenida Bento Gonçalves, 9500, 91501-970Porto Alegre, RS, Brazil
Yoshiharu Kohayakawa
Affiliation:
Instituto de Matemática e Estatística, Universidade de São Paulo, Rua do Matão 1010, 05508-090São Paulo, Brazil
Richard Lang
Affiliation:
Combinatorics and Optimization, University of Waterloo, N2L 3G1WaterlooON, Canada
Hanno Lefmann
Affiliation:
Fakultät für Informatik, Technische Universität Chemnitz, Straße der Nationen 62, 09111Chemnitz, Germany
Henrique Stagni*
Affiliation:
Instituto de Matemática e Estatística, Universidade de São Paulo, Rua do Matão 1010, 05508-090São Paulo, Brazil
*
*Corresponding author. Email: stagni@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

There has been substantial interest in estimating the value of a graph parameter, i.e. of a real-valued function defined on the set of finite graphs, by querying a randomly sampled substructure whose size is independent of the size of the input. Graph parameters that may be successfully estimated in this way are said to be testable or estimable, and the sample complexity qz = qz(ε) of an estimable parameter z is the size of a random sample of a graph G required to ensure that the value of z(G) may be estimated within an error of ε with probability at least 2/3. In this paper, for any fixed monotone graph property 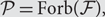$\mathcal{P}= \text{Forb}\!(\mathcal{F}),$ we study the sample complexity of estimating a bounded graph parameter z that, for an input graph G, counts the number of spanning subgraphs of G that satisfy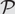$\mathcal{P}$. To improve upon previous upper bounds on the sample complexity, we show that the vertex set of any graph that satisfies a monotone property 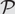$\mathcal{P}$ may be partitioned equitably into a constant number of classes in such a way that the cluster graph induced by the partition is not far from satisfying a natural weighted graph generalization of 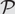$\mathcal{P}$. Properties for which this holds are said to be recoverable, and the study of recoverable properties may be of independent interest.

MSC classification

Primary: 68W20: Randomized algorithms
Secondary: 68W25: Approximation algorithms 68Q25: Analysis of algorithms and problem complexity 68R10: Graph theory (including graph drawing) 05C35: Extremal problems 05C85: Graph algorithms
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 29 , Issue 4 , July 2020 , pp. 616 - 632
Check for updates
Copyright
© Cambridge University Press 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alon, N. (2002) Testing subgraphs in large graphs. Random Struct. Alg. 21 359–370.Google Scholar
Alon, N., Duke, R. A., Lefmann, H., Rödl, V. and Yuster, R. (1994) The algorithmic aspects of the regularity lemma. J. Algorithms 16 80–109.Google Scholar
Alon, N., Fischer, E., Krivelevich, M. and Szegedy, M. (2000) Efficient testing of large graphs. Combinatorica 20 451–476.CrossRefGoogle Scholar
Alon, N., Fischer, E., Newman, I. and Shapira, A. (2009) A combinatorial characterization of the testable graph properties: It’s all about regularity. SIAM J. Comput. 39 143–167.CrossRefGoogle Scholar
Alon, N. and Shapira, A. (2008) A characterization of the (natural) graph properties testable with one-sided error. SIAM J. Comput. 37 1703–1727.CrossRefGoogle Scholar
Alon, N. and Shapira, A. (2008) Every monotone graph property is testable. SIAM J. Comput. 38 505–522.CrossRefGoogle Scholar
Alon, N., Shapira, A. and Sudakov, B. (2009) Additive approximation for edge-deletion problems. Ann. of Math. 170 371–411.CrossRefGoogle Scholar
Balogh, J., Bollobás, B. and Simonovits, M. (2004) The number of graphs without forbidden subgraphs. J. Combin. Theory Ser. B 91 1–24.CrossRefGoogle Scholar
Balogh, J. and Samotij, W. (2011) The number of K s,t-free graphs. J. Lond. Math. Soc. (2) 83 368–388.CrossRefGoogle Scholar
Bollobás, B. (1998) Hereditary properties of graphs: Asymptotic enumeration, global structure, and colouring. Documenta Math. Extra Vol. ICM III 333–342.Google Scholar
Borgs, C., Chayes, J. T., Lovász, L., Sós, V. T. and Vesztergombi, K. (2008) Convergent sequences of dense graphs I: Subgraph frequencies, metric properties and testing. Adv. Math. 219 1801–1851.Google Scholar
Conlon, D. and Fox, J. (2012) Bounds for graph regularity and removal lemmas. Geom. Funct. Anal. 22 1191–1256.Google Scholar
Conlon, D. and Fox, J. (2013) Graph removal lemmas. In Surveys in Combinatorics 2013, Vol. 409 of London Mathematical Society Lecture Note Series, Cambridge University Press, pp. 1–49.CrossRefGoogle Scholar
Duke, R. A., Lefmann, H. and Rödl, V. (1995) A fast approximation algorithm for computing the frequencies of subgraphs in a given graph. SIAM J. Comput. 24 598–620.Google Scholar
Erdős, P., Frankl, P. and Rödl, V. (1986) The asymptotic number of graphs not containing a fixed subgraph and a problem for hypergraphs having no exponent. Graphs Combin. 2 113–121.Google Scholar
Erdős, P., Kleitman, D. J. and Rothschild, B. L. (1976) Asymptotic enumeration of Kn-free graphs. In Colloquio Internazionale sulle Teorie Combinatorie (Rome, 1973), Vol. II, Accademia Nazionale dei Lincei, Rome, pp. 19–27.Google Scholar
Erdős, P. and Simonovits, M. (1983) Supersaturated graphs and hypergraphs. Combinatorica 3 181–192.Google Scholar
Fischer, E. and Newman, I. (2007) Testing versus estimation of graph properties. SIAM J. Comput. 37 482–501.Google Scholar
Fox, J. (2011) A new proof of the graph removal lemma. Ann. of Math. (2) 174 561–579.CrossRefGoogle Scholar
Fox, J., Lovász, L. M. and Zhao, Y. (2017) On regularity lemmas and their algorithmic applications. Combin. Probab. Comput. 26 481–505.Google Scholar
Frieze, A. and Kannan, R. (1999) Quick approximation to matrices and applications. Combinatorica 19 175–220.CrossRefGoogle Scholar
Füredi, Z. (1995) Extremal hypergraphs and combinatorial geometry. In Proceedings of the International Congress of Mathematicians 1994, Birkhäuser, pp. 1343–1352.CrossRefGoogle Scholar
Gishboliner, L. and Shapira, A. (2017) Removal lemmas with polynomial bounds. In STOC’17: Proceedings of the 49th Annual ACM SIGACT Symposium on Theory of Computing, ACM, pp. 510–522.CrossRefGoogle Scholar
Goldreich, O. (2010) Property Testing: Current Research and Surveys, Vol. 6390 of Lecture Notes in Computer Science, Springer.Google Scholar
Goldreich, O., Goldwasser, S. and Ron, D. (1998) Property testing and its connection to learning and approximation. J. Assoc. Comput. Mach. 45 653–750.CrossRefGoogle Scholar
Goldreich, O. and Trevisan, L. (2003) Three theorems regarding testing graph properties. Random Struct. Alg. 23 23–57.CrossRefGoogle Scholar
Gowers, W. T. (1997) Lower bounds of tower type for Szemerédi’s uniformity lemma. Geom. Funct. Anal. 7 322–337.CrossRefGoogle Scholar
Hoppen, C., Kohayakawa, Y., Lang, R., Lefmann, H. and Stagni, H. (2016) Estimating parameters associated with monotone properties. In Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques (APPROX/RANDOM 2016) (Jansen, K., Mathieu, C., Rolim, J. D. P. and Umans, C., eds), Vol. 60 of Leibniz International Proceedings in Informatics (LIPIcs), Schloss Dagstuhl–Leibniz-Zentrum für Informatik, pp. 35:1–35:13.Google Scholar
Jukna, S. (2001) Extremal Combinatorics: With Applications in Computer Science, second edition (2011), Texts in Theoretical Computer Science, Springer.Google Scholar
Komlós, J. and Simonovits, M. (1996) Szemerédi’s regularity lemma and its applications in graph theory. In Combinatorics: Paul Erdős is Eighty (Keszthely 1993), Vol. 2 of Bolyai Society Mathematical Studies, János Bolyai Mathematical Society, pp. 295–352.Google Scholar
Lovász, L. and Szegedy, B. (2007) Szemerédi’s lemma for the analyst. Geom. Funct. Anal. 17 252–270.CrossRefGoogle Scholar
Moshkovitz, G. and Shapira, A. (2019) A sparse regular approximation lemma. Trans. Amer. Math. Soc. 371 6779–6814.CrossRefGoogle Scholar
Parnas, M., Ron, D. and Rubinfeld, R. (2006) Tolerant property testing and distance approximation. J. Comput. System Sci. 72 1012–1042.CrossRefGoogle Scholar
Prömel, H. J. and Steger, A. (1992) The asymptotic number of graphs not containing a fixed color-critical subgraph. Combinatorica 12 463–473.CrossRefGoogle Scholar
Prömel, H. J. and Steger, A. (1996) Counting H-free graphs. Discrete Math. 154 311–315.CrossRefGoogle Scholar
Ruzsa, I. Z. and Szemerédi, E. (1978) Triple systems with no six points carrying three triangles. In Combinatorics (Proc. Fifth Hungarian Colloq., Keszthely, 1976), Vol. 18 of Colloquia Mathematica Societatis János Bolyai, North-Holland, pp. 939–945.Google Scholar
Szemerédi, E. (1976) Regular partitions of graphs. Colloq. Internat. CNRS 260 399–401.Google Scholar
Tao, T. (2006) A variant of the hypergraph removal lemma. J. Combin. Theory Ser. A 113 1257–1280.CrossRefGoogle Scholar