Hostname: page-component-89b8bd64d-4ws75 Total loading time: 0 Render date: 2026-05-06T22:36:24.386Z Has data issue: false hasContentIssue false
  • English
  • Français

Hypergraphs with uniform Turán density equal to 8/27

Part of: Graph theory Extremal combinatorics

Published online by Cambridge University Press:  17 December 2025

Frederik Garbe Open the ORCID record for Frederik Garbe [Opens in a new window] ,
Daniel Il’kovič ,
Daniel Kráľ Open the ORCID record for Daniel Kráľ [Opens in a new window] ,
Filip Kučerák  and
Ander Lamaison Open the ORCID record for Ander Lamaison [Opens in a new window]
Frederik Garbe*
Affiliation:
Czech Academy of Sciences, Institute of Computer Science, Prague, Czech Republic Faculty of Informatics, Masaryk University, Brno, Czech Republic
Daniel Il’kovič
Affiliation:
Faculty of Informatics, Masaryk University, Brno, Czech Republic Institute of Mathematics, Leipzig University, Leipzig, Germany Mathematics Institute and DIMAP, University of Warwick, Coventry, UK
Daniel Kráľ
Affiliation:
Faculty of Informatics, Masaryk University, Brno, Czech Republic Institute of Mathematics, Leipzig University, Leipzig, Germany Max Planck Institute for Mathematics in the Sciences, Leipzig, Germany
Filip Kučerák
Affiliation:
Faculty of Informatics, Masaryk University, Brno, Czech Republic Max Planck Institute for Mathematics in the Sciences, Leipzig, Germany
Ander Lamaison
Affiliation:
Faculty of Informatics, Masaryk University, Brno, Czech Republic Extremal Combinatorics and Probability Group (ECOPRO), Institute for Basic Science (IBS), Daejeon, South Korea
*
Corresponding author: Frederik Garbe; Email: garbe@cs.cas.cz
Get access Rights & Permissions [Opens in a new window]

Abstract

In the 1980s, Erdős and Sós initiated the study of Turán problems with a uniformity condition on the distribution of edges: the uniform Turán density of a hypergraph 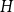$H$ is the infimum over all 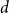$d$ for which any sufficiently large hypergraph with the property that all its linear-size subhypergraphs have density at least 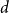$d$ contains 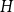$H$. In particular, they asked to determine the uniform Turán densities of 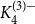$K_4^{(3)-}$ and 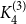$K_4^{(3)}$. After more than 30 years, the former was solved in [Israel J. Math. 211 (2016), 349 – 366] and [J. Eur. Math. Soc. 20 (2018), 1139 – 1159], while the latter still remains open. Till today, there are known constructions of 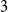$3$-uniform hypergraphs with uniform Turán density equal to 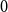$0$, 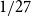$1/27$, 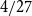$4/27$, and 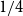$1/4$ only. We extend this list by a fifth value: we prove an easy to verify sufficient condition for the uniform Turán density to be equal to 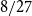$8/27$ and identify hypergraphs satisfying this condition.

Keywords

hypergraphsuniform Turán density

MSC classification

Primary: 05C65: Hypergraphs
Secondary: 05D99: None of the above, but in this section

Information

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 35 , Issue 2 , March 2026 , pp. 280 - 289
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bucić, M., Cooper, J. W., Král’, D., Mohr, S. and Correia, D. M. (2023) Uniform Turán density of cycles. Trans. Am. Math. Soc. 376 4765–4809.CrossRefGoogle Scholar
Chen, A.Y. and Schülke, B. (2025) Beyond the broken tetrahedron. Comb. Probab. Comput. 1–12.Google Scholar
Chung, F. and Lu, L. (1999) An upper bound for the Turán number $t_3(n,4)$ . J. Comb. Theory A 87 381–389.CrossRefGoogle Scholar
Cooper, J. W. (2018) Uniform Turán density, MSc Thesis, University of Warwick.Google Scholar
Erdős, P. (1981) On the combinatorial problems which I would most like to see solved. Combinatorica 1 25–42.CrossRefGoogle Scholar
Erdős, P. (1990) Problems and results on graphs and hypergraphs: similarities and differences. In Mathematics of Ramsey theory, Vol. 5 (Nešetřil, J. and Rödl, V., eds), Algorithms and Combinatorics, Springer, pp. 223–233.CrossRefGoogle Scholar
Erdős, P. and Simonovits, M. (1966) A limit theorem in graph theory. Stud. Sci. Math. Hung. 1 51–57.Google Scholar
Erdős, P., and Sós, V. T. (1982) On Ramsey—Turán type theorems for hypergraphs. Combinatorica 2 289–295.CrossRefGoogle Scholar
Erdős, P. and Stone, A. H. (1946) On the structure of linear graphs. Bull. Am. Math. Soc. 52 1087–1091.CrossRefGoogle Scholar
Frankl, P. and Füredi, Z. (1984) An exact result for 3-graphs. Discrete Math. 50 323–328.CrossRefGoogle Scholar
Garbe, F., Král’, D. and Lamaison, A. (2024) Hypergraphs with minimum positive uniform Turán density. Isr. J. Math. 259 701–726.CrossRefGoogle Scholar
Glebov, R., Král’, D. and Volec, J. (2016) A problem of Erdős and Sós on 3-graphs. Isr. J. Math. 211 349–366.CrossRefGoogle Scholar
Keevash, P. (2011) Hypergraph Turán problems. In Surveys in Combinatorics 2011, (Chapman, R., eds), London Mathematical Society Lecture Note Series, Cambridge University Press, pp. 83–140.CrossRefGoogle Scholar
Lamaison, A. (2024) Palettes determine uniform Turán density, preprint arXiv: 2408.09643.Google Scholar
Li, H., Lin, H., Wang, G.-H. and Zhou, W.-L. (2025) Hypergraphs with a quarter uniform Turán density. J. Oper. Res. Soc. China.CrossRefGoogle Scholar
Mantel, W. (1907) Problem 28. Wiskundige Opgaven 10 60–61.Google Scholar
Razborov, A. A. (2007) Flag algebras. J. Symb. Log. 72 1239–1282.CrossRefGoogle Scholar
Razborov, A. A. (2010) On 3-hypergraphs with forbidden 4-vertex configurations. SIAM J. Discrete Math. 24 946–963.CrossRefGoogle Scholar
Reiher, C. (2020) Extremal problems in uniformly dense hypergraphs. Eur. J. Combin. 88 103117.CrossRefGoogle Scholar
Reiher, C., Rödl, V. and Schacht, M. (2016) Embedding tetrahedra into quasirandom hypergraphs. J. Comb. Theory B 121 229–247.CrossRefGoogle Scholar
Reiher, C., Rödl, V. and Schacht, M. (2018) Hypergraphs with vanishing Turán density in uniformly dense hypergraphs. J. London Math. Soc. 97 77–97.CrossRefGoogle Scholar
Reiher, C., Rödl, V. and Schacht, M. (2018) On a generalisation of Mantel’s Theorem to uniformly dense hypergraphs. Int. Math. Res. Notices 16 4899–4941.CrossRefGoogle Scholar
Reiher, C., Rödl, V. and Schacht, M. (2018) On a Turán problem in weakly quasirandom 3-uniform hypergraphs. J. Eur. Math. Soc. 20 1139–1159.CrossRefGoogle Scholar
Reiher, C., Rödl, V. and Schacht, M. (2018) Some remarks on π. In Connections in Discrete Mathematics: A Celebration of the Work of Ron Graham, (Butler, S., Cooper, J. and Hurlbert, G., eds), pp. 214–239.CrossRefGoogle Scholar
Rödl, V. (1986) On universality of graphs with uniformly distributed edges. Discrete Math. 59 125–134.CrossRefGoogle Scholar
Sidorenko, A. (1995) What we know and what we do not know about Turán numbers. Graph. Combin. 11 179–199.CrossRefGoogle Scholar
Turán, P. (1941) On an extremal problem in graph theory. Matematikai és Fizikai Lapok 48 436–452.Google Scholar