Hostname: page-component-6766d58669-bkrcr Total loading time: 0 Render date: 2026-05-23T17:29:12.745Z Has data issue: false hasContentIssue false
  • English
  • Français

Turán-Ramsey Theorems and Kp-Independence Numbers

Published online by Cambridge University Press:  12 September 2008

P. Erdős ,
A. Hajnal ,
M. Simonovits ,
V. T. Sós  and
E. Szemerédi
P. Erdős
Affiliation:
Mathematical Institute of the Hungarian Academy of Sciences, Budapest.
A. Hajnal
Affiliation:
Mathematical Institute of the Hungarian Academy of Sciences, Budapest.
M. Simonovits
Affiliation:
Mathematical Institute of the Hungarian Academy of Sciences, Budapest.
V. T. Sós
Affiliation:
Mathematical Institute of the Hungarian Academy of Sciences, Budapest.
E. Szemerédi
Affiliation:
Mathematical Institute of the Hungarian Academy of Sciences, Budapest.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let the Kp-independence number αp (G) of a graph G be the maximum order of an induced subgraph in G that contains no Kp. (So K2-independence number is just the maximum size of an independent set.) For given integers r, p, m > 0 and graphs L1,…,Lr, we define the corresponding Turán-Ramsey function RTp(n, L1,…,Lr, m) to be the maximum number of edges in a graph Gn of order n such that αp(Gn) ≤ m and there is an edge-colouring of G with r colours such that the jth colour class contains no copy of Lj, for j = 1,…, r. In this continuation of [11] and [12], we will investigate the problem where, instead of α(Gn) = o(n), we assume (for some fixed p > 2) the stronger condition that αp(Gn) = o(n). The first part of the paper contains multicoloured Turán-Ramsey theorems for graphs Gn of order n with small Kp-independence number αp(Gn). Some structure theorems are given for the case αp(Gn) = o(n), showing that there are graphs with fairly simple structure that are within o(n2) of the extremal size; the structure is described in terms of the edge densities between certain sets of vertices.

The second part of the paper is devoted to the case r = 1, i.e., to the problem of determining the asymptotic value of

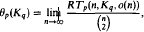
for p < q. Several results are proved, and some other problems and conjectures are stated.

Information

Type
Research Article
Information
Combinatorics, Probability and Computing , Volume 3 , Issue 3 , September 1994 , pp. 297 - 325
Copyright
Copyright © Cambridge University Press 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

[1]Bollobás, B. (1989) An extension of the isoperimetric inequality on the sphere. Elemente der Math. 44 121–124.Google Scholar
[2]Bollobás, B. (1978) Extremal graph theory, Academic Press, London.Google Scholar
[3]Bollobás, B. and Erdős, P. (1976) On a Ramsey-Turán type problem. Journal of Combinatorial Theory B 21 166–168.Google Scholar
[4]Brown, W. G., Erdős, P. and Simonovits, M. (1973) Extremal problems for directed graphs. Journal of Combinatorial Theory B 15 (1) 77–93.CrossRefGoogle Scholar
[5]Brown, W. G., Erdős, P. and Simonovits, M. (1978) On multigraph extremal problems. In: J., Bermond et al. (ed.) Problèmes Combinatoires et Thèorie des Graphes, (Proc. Conf. Orsay 1976), CNRS Paris63–66.Google Scholar
[6]Brown, W. G., Erdős, P. and Simonovits, M. (1985) Inverse extremal digraph problems. Finite and Infinite Sets, Eger (Hungary) 1981. Colloq. Math. Soc. J. Bolyai 37, Akad. Kiadó, Budapest119–156.Google Scholar
[7]Brown, W. G., Erdős, P. and Simonovits, M. (1985) Algorithmic Solution of Extremal Digraph Problems. Transactions of the American Math Soc. 292/2421–449.CrossRefGoogle Scholar
[8]Erdős, P. (1968) On some new inequalities concerning extremal properties of graphs. In: Erdős, P. and Katona, G. (ed. ) Theory of Graphs (Proc. Coll. Tihany, Hungary, 1966), Acad. Press N.Y.77–81.Google Scholar
[9]Erdős, P. (1961) Graph Theory and Probability, II. Canad. Journal of Math. 13 346–352.CrossRefGoogle Scholar
[10]Erdős, P. and Hajnal, A. (1966) On chromatic number of graphs and set-systems. Ada Math. Acad. Sci. Hung. 17 61–99.CrossRefGoogle Scholar
[11]Erdős, P., Hajnal, A., Sós, V. T. and Szemerédi, E. (1983) More results on Ramsey-Turán type problems. Combinatorica 3 (1) 69–82.CrossRefGoogle Scholar
[12]Erdős, P., Hajnal, A., Simonovits, M, Sós, V. T. and Szemerédi, E. (1993) Turán-Ramsey theorems and simple asymptotically extremal structures. Combinatorica 13 31–56.CrossRefGoogle Scholar
[13]Erdős, P., Meir, A., Sós, V. T. and Turán, P. (1972) On some applications of graph theory I. Discrete Math. 2 (3) 207–228.CrossRefGoogle Scholar
[14]Erdős, P., Meir, A., Só's, V. T. and Turán, P. (1971) On some applications of graph theory II. Studies in Pure Mathematics (presented to R. Rado), Academic Press, London89–99.Google Scholar
[15]Erdős, P., Meir, A., Sós, V. T. and Turán, P. (1972) On some applications of graph theory III. Canadian Math. Bulletin 15 27–32.Google Scholar
[16]Erdős, P. and Rogers, C. A. (1962) The construction of certain graphs. Canadian Journal of Math 702–707. (Reprinted in Art of Counting, MIT PRESS.)Google Scholar
[17]Erdős, P. and Simonovits, M. (1966) A limit theorem in graph theory. Studia Sci. Math. Hungar. 1 51–57.Google Scholar
[18]Erdős, P. and Só, V. T. (1969) Some remarks on Ramsey's and Turin's theorems. In: Erdős, P. et al. (eds.) Combin. Theory and Appl. Mathem. Coll. Soc. J. Bolyai 4, Balatonfüred395–404.Google Scholar
[19]Erdős, P. and Stone, A. H. (1946) On the structure of linear graphs. Bull. Amer. Math. Soc. 52 1089–1091.CrossRefGoogle Scholar
[20]Frankl, P. and Rödl, V. (1988) Some Ramsey-Turán type results for hypergraphs. Combinatorica 8 (4) 323–332.CrossRefGoogle Scholar
[21]Graham, R. L., Rothschild, B. L. and Spencer, J. (1980) Ramsey Theory, Wiley Interscience, Ser. in Discrete Math.Google Scholar
[22]Katona, G. (1985) Probabilistic inequalities from extremal graph results (a survey). Annals of Discrete Math. 28 159–170.Google Scholar
[23]Ramsey, F. P. (1930) On a problem of formal logic. Proc. London Math. Soc, 2nd Series 30 264–286.CrossRefGoogle Scholar
[24]Shamir, E. (1988) Generalized stability and chromatic numbers of random graphs (preprint, under publication).Google Scholar
[25]Sidorenko, A. F. (1980) Klasszi gipergrafov i verojatnosztynije nyeravensztva, Dokladi 254/3,Google Scholar
[26]Sidorenko, A. F. (1983) (Translation) Extremal estimates of probability measures and their combinatorial nature. Math. USSR - Izv 20 N3 503–533 MR 84d: 60031. (Original: Izvest. Acad. Nauk SSSR. ser. matem. 46 N3 535–568.)CrossRefGoogle Scholar
[27]Sidorenko, A. F. (1989) Asymptotic solution for a new class of forbidden r-graphs. Combinatorica 9 (2) 207–215.CrossRefGoogle Scholar
[28]Simonovits, M. (1968) A method for solving extremal problems in graph theory. In: Erdős, P. and Katona, G. (ed.) Theory of Graphs (Proc. Coll. Tihany, Hungary, 1966), Acad. Press N. Y. 279–319.Google Scholar
[29]Simonovits, M. (1983) Extremal Graph Theory. In: Beineke, and Wilson, (ed.) Selected Topics in Graph Theory, Academic Press, London, New York, San Francisco161–200.Google Scholar
[30]Sós, V. T. (1969) On extremal problems in graph theory. Proc. Calgary International Conf. on Combinatorial Structures and their Application407–410.Google Scholar
[31]Szemerédi, E. (1972) On graphs containing no complete subgraphs with 4 vertices (in Hungarian). Mat. Lapok 23 111–116.Google Scholar
[32]Szemerédi, E. (1978) On regular partitions of graphs. In: Bermond, J. et al. . (ed.) Problèmes Combinatoires et Théorie des Graphes, (Proc. Conf. Orsay 1976), CNRS Paris 399–401.Google Scholar
[33]Turán, P. (1941) On an extremal problem in graph theory (in Hungarian). Matematikai Lapok 48 436–452.Google Scholar
[34]Turán, P. (1954) On the theory of graphs. Colloq. Math. 3 19–30.CrossRefGoogle Scholar
[35]Turán, P. (1969) Applications of graph theory to geometry and potential theory. In: Proc. Calgary International Conf. on Combinatorial Structures and their Application423–434.Google Scholar
[36]Turán, P. (1972) Constructive theory of functions. Proc. Internat. Conference in Varna, Bulgaria, 1970, Izdat. Bolgar Akad. Nauk, Sofia.Google Scholar
[37]Turán, P. (1970) A general inequality of potential theory. Proc. Naval Research Laboratory, Washington137–141.Google Scholar
[38]Turán, P. (1989) Collected papers of Paul Turán Vol 1–3, Akadé;miai Kiadò, Budapest.Google Scholar
[39]Zykov, A. A. (1949) On some properties of linear complexes. Mat Sbornik 24 163–188. (Amer. Math. Soc. Translations 79 (1952)).Google Scholar