Hostname: page-component-5b777bbd6c-ks5gx Total loading time: 0 Render date: 2025-06-20T16:55:18.989Z Has data issue: false hasContentIssue false
  • English
  • Français

Four-fold Massey products in Galois cohomology

Part of: Operations and obstructions Homological methods (field theory)

Published online by Cambridge University Press:  17 August 2018

Pierre Guillot ,
Ján Mináč  and
Adam Topaz
Pierre Guillot
Affiliation:
Université de Strasbourg & CNRS, Institut de Recherche Mathématique Avancée, UMR 7501, F-67000 Strasbourg, France email guillot@math.unistra.fr
Ján Mináč
Affiliation:
Department of Mathematics, Western University, London, Ontario, N6A 5B7, Canada email minac@uwo.ca
Adam Topaz
Affiliation:
Mathematical Institute, University of Oxford, Andrew Wiles Building, Radcliffe Observatory Quarter, Woodstock Road, Oxford OX2 6GG, UK email topaz@maths.ox.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

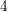In this paper, we develop a new necessary and sufficient condition for the vanishing of $4$-Massey products of elements in the modulo-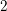$2$ Galois cohomology of a field. This new description allows us to define a splitting variety for 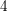$4$-Massey products, which is shown in the appendix to satisfy a local-to-global principle over number fields. As a consequence, we prove that, for a number field, all such 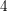$4$-Massey products vanish whenever they are defined. This provides new explicit restrictions on the structure of absolute Galois groups of number fields.

Keywords

Massey productsGalois cohomologysplitting varietygroup cohomology

MSC classification

Primary: 55S30: Massey products 12G05: Galois cohomology
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 9 , September 2018 , pp. 1921 - 1959
Copyright
© The Authors 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Arason, J. K., Cohomologische Invarianten quadratischer Formen , J. Algebra 36 (1975), 448–491.Google Scholar
Colliot-Thélène, J.-L., L’arithmétique des variétés rationnelles , Ann. Fac. Sci. Toulouse Math. (6) 1 (1992), 295–336.Google Scholar
Colliot-Thélène, J.-L. and Sansuc, J.-J., The rationality problem for fields of invariants under linear algebraic groups (with special regards to the Brauer group) , in Algebraic groups and homogeneous spaces, Tata Institute of Fundamental Research Studies in Mathematics (Tata Institute of Fundamental Research, Mumbai, 2007), 113–186.Google Scholar
Colliot-Thélène, J.-L. and Swinnerton-Dyer, P., Hasse principle and weak approximation for pencils of Severi–Brauer and similar varieties , J. Reine Angew. Math. 453 (1994), 49–112.Google Scholar
Deligne, P., Griffiths, P., Morgan, J. and Sullivan, D., Real homotopy theory of Kähler manifolds , Invent. Math. 29 (1975), 245–274.Google Scholar
Dwyer, W. G., Homology, Massey products and maps between groups , J. Pure Appl. Algebra 6 (1975), 177–190.Google Scholar
Efrat, I., The Zassenhaus filtration, Massey products, and representations of profinite groups , Adv. Math. 263 (2014), 389–411.Google Scholar
Efrat, I. and Matzri, E., Vanishing of Massey products and Brauer groups , Canad. Math. Bull. 58 (2015), 730–740.Google Scholar
Efrat, I. and Matzri, E., Triple Massey products and absolute Galois groups , J. Eur. Math. Soc. (JEMS) 19 (2017), 3629–3640.Google Scholar
Efrat, I. and Mináč, J., On the descending central sequence of absolute Galois groups , Amer. J. Math. 133 (2011), 1503–1532.Google Scholar
Elman, R. and Lam, T. Y., Quadratic forms under algebraic extensions , Math. Ann. 219 (1976), 21–42.Google Scholar
Fenn, R. A., Techniques of geometric topology, London Mathematical Society Lecture Note Series, vol. 57 (Cambridge University Press, Cambridge, 1983).Google Scholar
Gao, W., Leep, D. B., Mináč, J. and Smith, T. L., Galois groups over nonrigid fields , in Valuation theory and its applications, Vol. II, Saskatoon, SK, 1999, Fields Institute Communications, vol. 33 (American Mathematical Society, Providence, RI, 2003), 61–77.Google Scholar
Graber, T., Harris, J. and Starr, J., Families of rationally connected varieties , J. Amer. Math. Soc. 16 (2003), 57–67.Google Scholar
Grothendieck, A., Le groupe de Brauer, I, II, III , in Dix exposés sur la cohomologie des schémas (North-Holland, Amsterdam, 1968), 46–188.Google Scholar
Haesemeyer, C. and Weibel, C., Norm varieties and the chain lemma (after Markus Rost) , in Algebraic topology, Abel Symposia, vol. 4 (Springer, Berlin, 2009), 95–130.Google Scholar
Harpaz, Y. and Wittenberg, O., On the fibration method for zero-cycles and rational points , Ann. of Math. (2) 183 (2016), 229–295.Google Scholar
Hopkins, M. J. and Wickelgren, K. G., Splitting varieties for triple Massey products , J. Pure Appl. Algebra 219 (2015), 1304–1319.Google Scholar
Isaksen, D. C., When is a fourfold Massey product defined? Proc. Amer. Math. Soc. 143 (2015), 2235–2239.Google Scholar
Massey, W. S., Some higher order cohomology operations , in Symposium internacional de topología algebraica International symposium on algebraic topology (Universidad Nacional Autónoma de México and UNESCO, Mexico City, 1958), 145–154.Google Scholar
Matzri, E., Triple Massey products in Galois cohomology, Preprint (2014), arXiv:1411.4146.Google Scholar
Milne, J. S., Étale cohomology, Princeton Mathematical Series, vol. 33 (Princeton University Press, Princeton, NJ, 1980).Google Scholar
Mináč, J. and Spira., M., Witt rings and Galois groups , Ann. of Math. (2) 144 (1996), 35–60.Google Scholar
Mináč, J. and Tân, N. D., The kernel unipotent conjecture and the vanishing of Massey products for odd rigid fields , Adv. Math. 273 (2015), 242–270.Google Scholar
Mináč, J. and Tân, N. D., Triple Massey products over global fields , Doc. Math. 20 (2015), 1467–1480.Google Scholar
Mináč, J. and Tân, N. D., Triple Massey products vanish over all fields , J. Lond. Math. Soc. (2) 94 (2016), 909–932.Google Scholar
Mináč, J. and Tân, N. D., Construction of unipotent Galois extensions and Massey products , Adv. Math. 304 (2017), 1021–1054.Google Scholar
Mináč, J. and Tân, N. D., Counting Galois U4(F p )-extensions using Massey products , J. Number Theory 176 (2017), 76–112.Google Scholar
Mináč, J. and Tân, N. D., Triple Massey products and Galois theory , J. Eur. Math. Soc. (JEMS) 19 (2017), 255–284.Google Scholar
Morgan, J. W., The algebraic topology of smooth algebraic varieties , Publ. Math. Inst. Hautes Études Sci. (1978), 137–204.Google Scholar
Morgan, J. W., Correction to: ‘The algebraic topology of smooth algebraic varieties’ [Inst. Hautes Études Sci. Publ. Math. No. 48 (1978), 137–204; MR0516917 (80e:55020)] , Publ. Math. Inst. Hautes Études Sci. (1986), 185.Google Scholar
Morishita, M., On certain analogies between knots and primes , J. Reine Angew. Math. 550 (2002), 141–167.Google Scholar
Morishita, M., Milnor invariants and Massey products for prime numbers , Compos. Math. 140 (2004), 69–83.Google Scholar
Neukirch, J., Algebraic number theory, Grundlehren der mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 322 (Springer, Berlin, 1999).Google Scholar
Neukirch, J., Schmidt, A. and Wingberg, K., Cohomology of number fields, Grundlehren der mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 323, second edition (Springer, Berlin, 2008).Google Scholar
Rost, M., Chain lemma for splitting fields of symbols, Preprint (1998).Google Scholar
Saltman, D. J., The Brauer group and the center of generic matrices , J. Algebra 97 (1985), 53–67.Google Scholar
Sharifi, R. T., Massey products and ideal class groups , J. Reine Angew. Math. 603 (2007), 1–33.Google Scholar
Skorobogatov, A. N., Descent on fibrations over the projective line , Amer. J. Math. 118 (1996), 905–923.Google Scholar
Sullivan, D., Infinitesimal computations in topology , Publ. Math. Inst. Hautes Études Sci. 47 (1977), 269–331.Google Scholar
Suslin, A. and Joukhovitski, S., Norm varieties , J. Pure Appl. Algebra 206 (2006), 245–276.Google Scholar
Tate, J., Relations between K 2 and Galois cohomology , Invent. Math. 36 (1976), 257–274.Google Scholar
Voevodsky, V., On motivic cohomology with Z/l-coefficients , Ann. of Math. (2) 174 (2011), 401–438.Google Scholar
Vogel, D., On the Galois group of 2-extensions with restricted ramification , J. Reine Angew. Math. 581 (2005), 117–150.Google Scholar
Weibel, C., The norm residue isomorphism theorem , J. Topol. 2 (2009), 346–372.Google Scholar
Wickelgren, K., Lower central series obstructions to homotopy sections of curves over number fields, PhD thesis, Stanford University (2009).Google Scholar
Wickelgren, K., n-nilpotent obstructions to 𝜋1 sections of ℙ1 -{0, 1, ∞} and Massey products , in Galois–Teichmüller theory and arithmetic geometry, Advanced Studies in Pure Mathematics, vol. 63 (Mathematical Society of Japan, Tokyo, 2012), 579–600.Google Scholar
Wickelgren, K., On 3-nilpotent obstructions to 𝜋1 sections for ℙℚ 1 -{0, 1, ∞} , in The arithmetic of fundamental groups—PIA 2010, Contributions in Mathematical and Computational Sciences, vol. 2 (Springer, Heidelberg, 2012), 281–328.Google Scholar