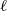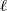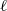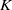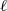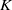Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Iijima, Yu
2017.
Difference between l-adic Galois representations and pro-l outer Galois representations associated to hyperbolic curves.
manuscripta mathematica,
Vol. 153,
Issue. 1-2,
p.
129.
Virdol, Cristian
2017.
Cyclicity and Titchmarsh divisor problem for Drinfeld modules.
Kyoto Journal of Mathematics,
Vol. 57,
Issue. 3,
Böckle, Gebhard
Gajda, Wojciech
and
Petersen, Sebastian
2018.
Independence of ℓ\ell-adic representations of geometric Galois groups.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2018,
Issue. 736,
p.
69.
Cadoret, Anna
and
Tamagawa, Akio
2019.
On the Geometric Image of $\mathbb{F}_{\ell}$-Linear Representations of étale Fundamental Groups.
International Mathematics Research Notices,
Vol. 2019,
Issue. 9,
p.
2735.
JARDEN, MOSHE
and
PETERSEN, SEBASTIAN
2019.
TORSION OF ABELIAN VARIETIES OVER LARGE ALGEBRAIC EXTENSIONS OF.
Nagoya Mathematical Journal,
Vol. 234,
Issue. ,
p.
46.
Illusie, Luc
2022.
Constructibilité générique et uniformité en
ℓ.
Tunisian Journal of Mathematics,
Vol. 4,
Issue. 1,
p.
159.