Hostname: page-component-7dd5485656-gs9qr Total loading time: 0 Render date: 2025-10-28T12:23:41.822Z Has data issue: false hasContentIssue false
  • English
  • Français

A local-global question in automorphic forms

Part of: Lie groups Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  26 April 2013

U. K. Anandavardhanan  and
Dipendra Prasad
U. K. Anandavardhanan
Affiliation:
Department of Mathematics, Indian Institute of Technology Bombay, Mumbai - 400 076, India email anand@math.iitb.ac.in
Dipendra Prasad
Affiliation:
Tata Institute of Fundamental Research, Homi Bhabha Road, Mumbai - 400 005, India email dprasad@math.tifr.res.in
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we consider the 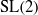$\mathrm{SL} (2)$ analogue of two well-known theorems about period integrals of automorphic forms on 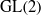$\mathrm{GL} (2)$: one due to Harder–Langlands–Rapoport about non-vanishing of period integrals on 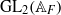${\mathrm{GL} }_{2} ({ \mathbb{A} }_{F} )$ of cuspidal automorphic representations on 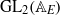${\mathrm{GL} }_{2} ({ \mathbb{A} }_{E} )$ where 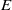$E$ is a quadratic extension of a number field 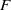$F$, and the other due to Waldspurger involving toric periods of automorphic forms on 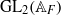${\mathrm{GL} }_{2} ({ \mathbb{A} }_{F} )$. In both these cases, now involving 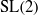$\mathrm{SL} (2)$, we analyze period integrals on global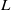$L$-packets; we prove that under certain conditions, a global automorphic 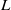$L$-packet which at each place of a number field has a distinguished representation, contains globally distinguished representations, and further, an automorphic representation which is locally distinguished is globally distinguished.

Keywords

period integralslocally distinguished representationsglobally distinguished representationsbase changeAsai liftAsai L-functioncentral L-valuesepsilon factorsfibers of functorial liftssimultaneous non-vanishing of L-functions

MSC classification

Secondary: 11F70: Representation-theoretic methods; automorphic representations over local and global fields 22E55: Representations of Lie and linear algebraic groups over global fields and adèle rings

Information

Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 6 , June 2013 , pp. 959 - 995
Copyright
© The Author(s) 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Anandavardhanan, U. K., Kable, A. C. and Tandon, R., Distinguished representations and poles of twisted tensor $L$-functions, Proc. Amer. Math. Soc. 132 (2004), 2875–2883; MR 2063106 (2005g:11080).Google Scholar
Anandavardhanan, U. K. and Prasad, D., Distinguished representations for $\mathrm{SL} (2)$, Math. Res. Lett. 10 (2003), 867–878; MR 2025061 (2004j:22018).Google Scholar
Anandavardhanan, U. K. and Prasad, D., On the $\mathrm{SL} (2)$ period integral, Amer. J. Math. 128 (2006), 1429–1453; MR 2275907 (2008b:22014).Google Scholar
Blasius, D., On multiplicities for $\mathrm{SL} (n)$, Israel J. Math. 88 (1994), 237–251; MR 1303497 (95i:11049).Google Scholar
Flicker, Y. Z., Twisted tensors and Euler products, Bull. Soc. Math. France 116 (1988), 295–313; MR 984899 (89m:11049).Google Scholar
Flicker, Y. Z., On distinguished representations, J. Reine Angew. Math. 418 (1991), 139–172; MR 1111204 (92i:22019).Google Scholar
Flicker, Y. Z. and Hakim, J. L., Quaternionic distinguished representations, Amer. J. Math. 116 (1994), 683–736; MR 1277452 (95i:22028).Google Scholar
Friedberg, S. and Hoffstein, J., Nonvanishing theorems for automorphic $L$-functions on $\mathrm{GL} (2)$, Ann. of Math. (2) 142 (1995), 385–423; MR 1343325 (96e:11072).Google Scholar
Fröhlich, A. and Queyrut, J., On the functional equation of the Artin $L$-function for characters of real representations, Invent. Math. 20 (1973), 125–138; MR 0321888 (48 #253).Google Scholar
Gan, W. T., Gross, B. H. and Prasad, D., Symplectic local root numbers, central critical l-values, and restriction problems in the representation theory of classical groups, Astérisque 346 (2012), 1–109.Google Scholar
Gross, B. H. and Prasad, D., On the decomposition of a representation of ${\mathrm{SO} }_{n} $ when restricted to ${\mathrm{SO} }_{n- 1} $, Canad. J. Math. 44 (1992), 974–1002; MR 1186476 (93j:22031).Google Scholar
Hakim, J., Distinguished $p$-adic representations, Duke Math. J. 62 (1991), 1–22; MR 1104321 (92c:22037).Google Scholar
Harder, G., Langlands, R. P. and Rapoport, M., Algebraische Zyklen auf Hilbert–Blumenthal–Flächen, J. Reine Angew. Math. 366 (1986), 53–120; MR 833013 (87k:11066).Google Scholar
Jacquet, H., On the nonvanishing of some $L$-functions, Proc. Indian Acad. Sci. Math. Sci. 97 (1987), 117–155; MR 983610 (90e:11079).Google Scholar
Jacquet, H. and Lai, K. F., A relative trace formula, Compositio Math. 54 (1985), 243–310; MR 783512 (86j:11059).Google Scholar
Kable, A. C., Asai $L$-functions and Jacquet’s conjecture, Amer. J. Math. 126 (2004), 789–820; MR 2075482 (2005g:11083).CrossRefGoogle Scholar
Krishnamurthy, M., The Asai transfer to ${\mathrm{GL} }_{4} $ via the Langlands–Shahidi method, Int. Math. Res. Not. 41 (2003), 2221–2254; MR 2000968 (2004i:11050).Google Scholar
Krishnamurthy, M., Determination of cusp forms on $GL(2)$ by coefficients restricted to quadratic subfields, J. Number Theory 132 (2012), 1359–1384; with an appendix by Dipendra Prasad and Dinakar Remakrishnan; MR 2899809.Google Scholar
Larsen, M., On the conjugacy of element-conjugate homomorphisms, Israel J. Math. 88 (1994), 253–277; MR 1303498 (95k:20073).Google Scholar
Labesse, J.-P. and Langlands, R. P., $L$-indistinguishability for $\mathrm{SL} (2)$, Canad. J. Math. 31 (1979), 726–785; MR 540902 (81b:22017).Google Scholar
Murty, V. K. and Prasad, D., Tate cycles on a product of two Hilbert modular surfaces, J. Number Theory 80 (2000), 25–43; MR 1735646 (2000m:14028).Google Scholar
Prasad, D., Invariant forms for representations of ${\mathrm{GL} }_{2} $ over a local field, Amer. J. Math. 114 (1992), 1317–1363; MR 1198305 (93m:22011).Google Scholar
Prasad, D., On an extension of a theorem of Tunnell, Compositio Math. 94 (1994), 19–28; MR 1302309 (95k:22023).Google Scholar
Prasad, D., A relative local langlands conjecture.Google Scholar
Ramakrishnan, D., Modularity of the Rankin–Selberg $L$-series, and multiplicity one for $\mathrm{SL} (2)$, Ann. of Math. (2) 152 (2000), 45–111; MR 1792292 (2001g:11077).Google Scholar
Saito, H., On Tunnell’s formula for characters of $\mathrm{GL} (2)$, Compositio Math. 85 (1993), 99–108; MR 1199206 (93m:22021).Google Scholar
Sakellaridis, Y. and Venkatesh, A., Periods and harmonic analysis on spherical varieties.Google Scholar
Serre, J.-P., Galois cohomology, Springer Monographs in Mathematics, English edition (Springer, Berlin, 2002), translated from the French by Patrick Ion and revised by the author; MR 1867431 (2002i:12004.Google Scholar
Tunnell, J. B., Local $\epsilon $-factors and characters of $\mathrm{GL} (2)$, Amer. J. Math. 105 (1983), 1277–1307; MR 721997 (86a:22018).Google Scholar
Waldspurger, J.-L., Sur les valeurs de certaines fonctions $L$ automorphes en leur centre de symétrie, Compositio Math. 54 (1985), 173–242; MR 783511 (87g:11061b).Google Scholar
Waldspurger, J.-L., Correspondances de Shimura et quaternions, Forum Math. 3 (1991), 219–307; MR 1103429 (92g:11054).Google Scholar