Hostname: page-component-7dd5485656-zklqj Total loading time: 0 Render date: 2025-10-27T09:11:04.445Z Has data issue: false hasContentIssue false
  • English
  • Français

Measure equivalence rigidity via s-malleable deformations

Part of: Ergodic theory Selfadjoint operator algebras

Published online by Cambridge University Press:  14 August 2023

Daniel Drimbe
Daniel Drimbe*
Affiliation:
Department of Mathematics, KU Leuven, Celestijnenlaan 200b, B-3001 Leuven, Belgium daniel.drimbe@kuleuven.be
Get access Rights & Permissions [Opens in a new window]

Abstract

We single out a large class of groups 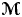${\rm {\boldsymbol {\mathscr {M}}}}$ for which the following unique prime factorization result holds: if 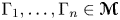$\Gamma _1,\ldots,\Gamma _n\in {\rm {\boldsymbol {\mathscr {M}}}}$ and $\Gamma _1\times \cdots \times \Gamma _n$ is measure equivalent to a product $\Lambda _1\times \cdots \times \Lambda _m$ of infinite icc groups, then 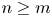$n \ge m$, and if $n = m$, then, after permutation of the indices, 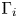$\Gamma _i$ is measure equivalent to 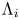$\Lambda _i$, for all 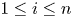$1\leq i\leq n$. This provides an analogue of Monod and Shalom's theorem [Orbit equivalence rigidity and bounded cohomology, Ann. of Math. 164 (2006), 825–878] for groups that belong to 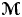${\rm {\boldsymbol {\mathscr {M}}}}$. Class 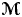${\rm {\boldsymbol {\mathscr {M}}}}$ is constructed using groups whose von Neumann algebras admit an s-malleable deformation in the sense of Sorin Popa and it contains all icc non-amenable groups 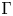$\Gamma$ for which either (i) 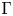$\Gamma$ is an arbitrary wreath product group with amenable base or (ii) 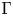$\Gamma$ admits an unbounded 1-cocycle into its left regular representation. Consequently, we derive several orbit equivalence rigidity results for actions of product groups that belong to 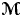${\rm {\boldsymbol {\mathscr {M}}}}$. Finally, for groups 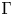$\Gamma$ satisfying condition (ii), we show that all embeddings of group von Neumann algebras of non-amenable inner amenable groups into 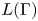$L(\Gamma )$ are ‘rigid’. In particular, we provide an alternative solution to a question of Popa that was recently answered by Ding, Kunnawalkam Elayavalli, and Peterson [Properly Proximal von Neumann Algebras, Preprint (2022), arXiv:2204.00517].

Keywords

measure equivalenceorbit equivalencePopa's deformation/rigidity theoryprime II1 factors

MSC classification

Primary: 37A20: Orbit equivalence, cocycles, ergodic equivalence relations 46L10: General theory of von Neumann algebras 46L36: Classification of factors

Information

Type
Research Article
Information
Compositio Mathematica , Volume 159 , Issue 10 , October 2023 , pp. 2023 - 2050
Check for updates
Copyright
© 2023 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The author holds the postdoctoral fellowship fundamental research 12T5221N of the Research Foundation Flanders.

References

Anantharaman, C. and Popa, S., An introduction to II $_1$ factors, book in preparation, available on Sorin Popa's website: https://www.math.ucla.edu/~popa/Books/IIunV15.pdf.Google Scholar
Bannon, J., Marrakchi, A., Ozawa, N., Full factors and co-amenable inclusions, Comm. Math. Phys. 378 (2020), 1107–1121.10.1007/s00220-020-03816-yCrossRefGoogle Scholar
Bekka, B., de la Harpe, P. and Valette, A., Kazhdan's property (T), New Mathematical Monographs, vol. 11 (Cambridge University Press, Cambridge, 2008).CrossRefGoogle Scholar
Berbec, M. and Vaes, S., W$^*$-superrigidity for group von Neumann algebras of left–right wreath products, Proc. Lond. Math. Soc. (3) 108 (2014), 1116–1152.CrossRefGoogle Scholar
Boutonnet, R., Ioana, A. and Peterson, J., Properly proximal groups and their von Neumann algebras, Ann. Sci. Éc. Norm. Supér. (4) 54 (2021), 445–482.CrossRefGoogle Scholar
Brown, N. and Ozawa, N., C*-algebras and finite-dimensional approximations, Grad. Stud. Math., vol. 88 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Chifan, I. and Das, S., Primeness results for II $_1$ factors associated with fibered product groups, Preprint (2019).Google Scholar
Chifan, I., de Santiago, R. and Sinclair, T., W$^*$-rigidity for the von Neumann algebras of products of hyperbolic groups, Geom. Funct. Anal. 26 (2016), 136–159.CrossRefGoogle Scholar
Chifan, I., de Santiago, R. and Sucpikarnon, W., Tensor product decompositions of II$_1$ factors arising from extensions of amalgamated free product groups, Commun. Math. Phys. 364 (2018), 1163–1194.10.1007/s00220-018-3175-zCrossRefGoogle Scholar
Chifan, I., Diaz-Arias, A. and Drimbe, D., $W^*$ and $C^*$-superrigidity results for coinduced groups, Preprint (2021), arXiv:2107.05976.Google Scholar
Chifan, I., Drimbe, D. and Ioana, A., Tensor product indecomposability results for existentially closed factors, Preprint (2022), arXiv:2208.00259.Google Scholar
Chifan, I. and Ioana, A., Ergodic subequivalence relations induced by a Bernoulli action, Geom. Funct. Anal. 20 (2010), 53–67.CrossRefGoogle Scholar
Chifan, I. and Ioana, A., Amalgamated free product rigidity for group von Neumann algebras, Adv. Math. 329 (2018), 819–850.CrossRefGoogle Scholar
Chifan, I., Popa, S. and Sizemore, O., OE and W$^*$-rigidity results for actions by wreath product groups, J. Funct. Anal. 263 (2012), 3422–3448.CrossRefGoogle Scholar
Chifan, I. and Sinclair, T., On the structural theory of II$_1$ factors of negatively curved groups, Ann. Sci. Éc. Norm. Supér. (4) 46 (2013), 1–33.10.24033/asens.2183CrossRefGoogle Scholar
Connes, A., Classification of injective factors, Ann. Math. 104 (1976), 73–115.10.2307/1971057CrossRefGoogle Scholar
Connes, A., Feldman, J. and Weiss, B., An amenable equivalence relations is generated by a single transformation, Ergodic Theory Dynam. Systems 1 (1981), 431–450.CrossRefGoogle Scholar
de Santiago, R., Hayes, B., Hoff, D. and Sinclair, T., Maximal rigid subalgebras of deformations and L$^2$-cohomology, Anal. PDE, to appear. Preprint (2020).Google Scholar
Ding, C., Kunnawalkam Elayavalli, S. and Peterson, J., Properly Proximal von Neumann Algebras, Preprint (2022), arXiv:2204.00517.Google Scholar
Drimbe, D., Prime II$_1$ factors arising from actions of product groups, J. Funct. Anal. 278 (2020), 108366.CrossRefGoogle Scholar
Drimbe, D., Orbit equivalence rigidity for product actions, Comm. Math. Phys. 379 (2020), 41–59.CrossRefGoogle Scholar
Drimbe, D., Product rigidity in von Neumann and C$^*$-algebras via s-malleable deformations, Comm. Math. Phys. 388 (2021), 329–349.CrossRefGoogle Scholar
Drimbe, D., Hoff, D. and Ioana, A., Prime II$_1$ factors arising from irreducible lattices in product of rank one simple Lie groups, J. Reine Angew. Math., to appear. Preprint (2016), arXiv:1611.02209.Google Scholar
Drimbe, D., Ioana, A. and Peterson, J., Cocycle superrigidity for profinite actions of irreducible lattices, Groups Geom. Dyn., to appear. Preprint (2019).Google Scholar
Dye, H., On groups of measure preserving transformation. I, Amer. J. Math. 81 (1959), 119–159.CrossRefGoogle Scholar
Effros, E. G., Property $\Gamma$ and inner amenability, Proc. Amer. Math. Soc. 47 (1975), 483–486.Google Scholar
Furman, A., Orbit equivalence rigidity, Ann. of Math. (2) 150 (1999), 1083–1108.10.2307/121063CrossRefGoogle Scholar
Furman, A., A survey of measured group theory, in Geometry, Rigidity, and Group Actions (The University of Chicago Press, Chicago and London, 2011), 296–374.Google Scholar
Gaboriau, D., Co$\hat u$t des relations d’équivalence et de groupes, Invent. Math. 139 (2000), 41–98.CrossRefGoogle Scholar
Gaboriau, D., Invariants $\ell ^2$ de relations d'equivalence et de groupes, Publ. Math. Inst. Hautes Études Sci. 95 (2002), 93–150.CrossRefGoogle Scholar
Gaboriau, D., Orbit equivalence and measured group theory, in Proceedings of the ICM (Hyderabad, India, 2010), vol. III (Hindustan Book Agency, 2010), 1501–1527.Google Scholar
Ge, L., Applications of free entropy to finite von Neumann algebras. II, Ann. of Math. (2) 147 (1998), 143–157.10.2307/120985CrossRefGoogle Scholar
Gromov, M., Asymptotic invariants of infinite groups, in Geometric group theory, Vol. 2, London Mathematical Society Lecture Note Series, vol. 182 (Cambridge University Press, Cambridge, 1993), 1–295.Google Scholar
Horbez, C. and Huang, J., Measure equivalence rigidity among the Higman groups, Preprint (2022), arXiv:2206.00884.Google Scholar
Horbez, C., Huang, J. and Ioana, A., Orbit equivalence rigidity of irreducible actions of right-angled Artin groups, Compos. Math., to appear. Preprint (2021), arXiv:2110.04141.Google Scholar
Houdayer, C. and Ueda, Y., Rigidity of free product von Neumann algebras, Compos. Math. 152 (2016), 2461–2492.CrossRefGoogle Scholar
Ioana, A., Rigidity results for wreath product of II$_1$ factors, J. Funct. Anal. 252 (2007), 763–791.10.1016/j.jfa.2007.04.005CrossRefGoogle Scholar
Ioana, A., W$^*$ -superrigidity for Bernoulli actions of property (T) groups, J. Amer. Math. Soc. 24 (2011), 1175–1226.CrossRefGoogle Scholar
Ioana, A., Uniqueness of the group measure space decomposition for Popa's $\mathcal {H}\mathcal {T}$ factors, Geom. Funct. Anal. 22 (2012), 699–732.CrossRefGoogle Scholar
Ioana, A., Classification and rigidity for von Neumann algebras, in European Congress of Mathematics, Kraków, 2–7 July, 2012 (EMS Press, 2014), 601–625.CrossRefGoogle Scholar
Ioana, A., Cartan subalgebras of amalgamated free product II$_1$ factors. With an appendix by Adrian Ioana and Stefaan Vaes, Ann. Sci. Éc. Norm. Supér. (4) 48 (2015), 71–130.10.24033/asens.2239CrossRefGoogle Scholar
Ioana, A., Rigidity for von Neumann algebras, in Proceedings of the International Congress of Mathematicians—Rio de Janeiro 2018, Invited lectures, vol. III (World Scientific, Hackensack, NJ, 2018), 1639–1672.CrossRefGoogle Scholar
Ioana, A., Peterson, J. and Popa, S., Amalgamated free products of weakly rigid factors and calculation of their symmetry groups, Acta Math. 200 (2008), 85–153.10.1007/s11511-008-0024-5CrossRefGoogle Scholar
Ioana, A., Popa, S. and Vaes, S., A class of superrigid group von Neumann algebras, Ann. of Math. (2) 178 (2013), 231–286.CrossRefGoogle Scholar
Ioana, A. and Spaas, P., A class of II$_1$ factors with a unique McDuff decomposition, Math. Ann. 375 (2019), 177–212.CrossRefGoogle Scholar
Ishan, I., Peterson, J. and Ruth, L., Von Neumann equivalence and properly proximal groups, Preprint (2019), arXiv:1910.08682.Google Scholar
Isono, Y. and Marrakchi, A., Tensor product decompositions and rigidity of full factors, Ann. Sci. Éc. Norm. Supér. (4), to appear. Preprint (2019).Google Scholar
Kida, Y., Orbit equivalence rigidity for ergodic actions of the mapping class group, Geom. Dedicata 131 (2008), 99–109.CrossRefGoogle Scholar
Kida, Y., Measure equivalence rigidity of the mapping class group, Ann. of Math. (2) 171 (2010), 1851–1901.CrossRefGoogle Scholar
Krogager, A. and Vaes, S., A class of II$_1$ factors with exactly two crossed product decompositions, Math. Pures Appl., to appear. Preprint (2015), arXiv:1512.06677J.Google Scholar
Monod, N. and Shalom, Y., Orbit equivalence rigidity and bounded cohomology, Ann. of Math. 164 (2006), 825–878.10.4007/annals.2006.164.825CrossRefGoogle Scholar
Murray, F. J. and von Neumann, J., Rings of operators. IV, Ann. Math. 44 (1943), 716–808.10.2307/1969107CrossRefGoogle Scholar
Ornstein, D. and Weiss, B., Ergodic theory of amenable group actions. I. The Rohlin lemma, Bull. Amer. Math. Soc. (N.S.) 2 (1980), 161–164.CrossRefGoogle Scholar
Ozawa, N., Solid von Neumann algebras, Acta Math. 192 (2004), 111–117.CrossRefGoogle Scholar
Ozawa, N., A Kurosh-type theorem for type II$_1$ factors, Int. Math. Res. Not. IMRN 2006 (2006), 097560.Google Scholar
Ozawa, N. and Popa, S., On a class of II$_1$ factors with at most one Cartan subalgebra, Ann. of Math. (2) 172 (2010), 713–749.CrossRefGoogle Scholar
Peterson, J., L$^2$-rigidity in von Neumann algebras, Invent. Math. 175 (2009), 417–433.CrossRefGoogle Scholar
Peterson, J. and Thom, A., Group cocycles and the ring of affiliated operators, Invent. Math. 185 (2011), 561–592; MR 2827095 (2012j:22004).CrossRefGoogle Scholar
Popa, S., Orthogonal pairs of $*$-subalgebras in finite von Neumann algebras, J. Operator Theory 9 (1983), 253–268.Google Scholar
Popa, S., On a class of type II$_1$ factors with Betti numbers invariants, Ann. of Math. 163 (2006), 809–899.10.4007/annals.2006.163.809CrossRefGoogle Scholar
Popa, S., Strong rigidity of II$_1$ factors arising from malleable actions of w-rigid groups. I, Invent. Math. 165 (2006), 369–408.CrossRefGoogle Scholar
Popa, S., Strong rigidity of II$_11$ factors arising from malleable actions of w-rigid groups. II, Invent. Math. 165 (2006), 409–452.CrossRefGoogle Scholar
Popa, S., Deformation and rigidity for group actions and von Neumann algebras, in Proceedings of the ICM (Madrid, 2006), vol. I (European Mathematical Society Publishining House, 2007), 445–477.10.4171/022-1/18CrossRefGoogle Scholar
Popa, S., On Ozawa's property for free group factors, Int. Math. Res. Not. IMRN 2007 (2007), Art. ID rnm036.Google Scholar
Popa, S., On the superrigidity of malleable actions with spectral gap, J. Amer. Math. Soc. 21 (2008), 981–1000.CrossRefGoogle Scholar
Popa, S., UCLA lecture notes, Functional analysis seminar, January 8, 2021.Google Scholar
Popa, S. and Vaes, S., Group measure space decomposition of II$_1$ factors and W$^*$-superrigidity, Invent. Math. 182 (2010), 371–417.CrossRefGoogle Scholar
Popa, S. and Vaes, S., Unique Cartan decomposition for II$_1$ factors arising from arbitrary actions of free groups, Acta Math. 212 (2014), 141–198.10.1007/s11511-014-0110-9CrossRefGoogle Scholar
Sako, H., Measure equivalence rigidity and bi-exactness of groups, J. Funct. Anal. 257 (2009), 3167–3202.CrossRefGoogle Scholar
Shalom, Y., Measurable group theory, in European Congress of Mathematics (European Mathematical Society Publishing House, 2005), 391–423.Google Scholar
Sizemore, O. and Winchester, A., Unique prime decomposition results for factors coming from wreath product groups, Pacific J. Math. 265 (2013), 221–232.10.2140/pjm.2013.265.221CrossRefGoogle Scholar
Tucker-Drob, R. D., Invariant means and the structure of inner amenable groups, Duke Math. J. 169 (2014), 2571–2628.Google Scholar
Vaes, S., Rigidity results for Bernoulli actions and their von Neumann algebras (after Sorin Popa), Séminaire Bourbaki, exposé 961, Astérisque 311 (2007), 237–294.Google Scholar
Vaes, S., Explicit computations of all finite index bimodules for a family of II$_1$ factors, Ann. Sci. Éc. Norm. Supér. (4) 41 (2008), 743–788.CrossRefGoogle Scholar
Vaes, S., Rigidity for von Neumann algebras and their invariants, in Proceedings of the ICM (Hyderabad, India, 2010), vol. III (Hindustan Book Agency, 2010), 1624–1650.Google Scholar
Vaes, S., An inner amenable group whose von Neumann algebra does not have property Gamma, Acta Math. 208 (2012), 389–394.CrossRefGoogle Scholar
Vaes, S., One-cohomology and the uniqueness of the group measure space decomposition of a II$_1$ factor, Math. Ann. 355 (2013), 661–696.CrossRefGoogle Scholar
Zimmer, R., Ergodic theory and semisimple groups, Monographs in Mathematics, vol. 81 (Basel, Birkḧauser, 1984).CrossRefGoogle Scholar