Hostname: page-component-89b8bd64d-j4x9h Total loading time: 0 Render date: 2026-05-06T20:39:51.388Z Has data issue: false hasContentIssue false
  • English
  • Français

Modular forms of half-integral weight on exceptional groups

Part of: Discontinuous groups and automorphic forms Linear algebraic groups and related topics

Published online by Cambridge University Press:  22 February 2024

Spencer Leslie  and
Aaron Pollack Open the ORCID record for Aaron Pollack [Opens in a new window]
Spencer Leslie
Affiliation:
Department of Mathematics, Boston College, Chestnut Hill, MA 02467, USA spencer.leslie@bc.edu
Aaron Pollack
Affiliation:
Department of Mathematics, The University of California San Diego, La Jolla, CA 92093, USA apollack@ucsd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We define a notion of modular forms of half-integral weight on the quaternionic exceptional groups. We prove that they have a well-behaved notion of Fourier coefficients, which are complex numbers defined up to multiplication by 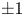${\pm }1$. We analyze the minimal modular form 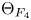$\Theta _{F_4}$ on the double cover of 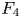$F_4$, following Loke–Savin and Ginzburg. Using 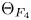$\Theta _{F_4}$, we define a modular form of weight 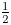$\tfrac {1}{2}$ on (the double cover of) 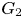$G_2$. We prove that the Fourier coefficients of this modular form on 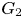$G_2$ see the 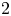$2$-torsion in the narrow class groups of totally real cubic fields.

Keywords

automorphic minimal representationquaternionic modular formshalf-integral weight modular formscovering groups

MSC classification

Primary: 11F03: Modular and automorphic functions 11F30: Fourier coefficients of automorphic forms
Secondary: 20G41: Exceptional groups

Information

Type
Research Article
Information
Compositio Mathematica , Volume 160 , Issue 3 , March 2024 , pp. 657 - 707
Check for updates
Copyright
© 2024 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

SL has been supported by an AMS-Simons Travel Award and by NSF grant DMS-1902865. AP has been supported by the Simons Foundation via Collaboration Grant number 585147, by the NSF via grant numbers 2101888 and 2144021, and by an AMS Centennial Research Fellowship.

References

Adams, J., Barbasch, D., Paul, A., Trapa, P. and Vogan, D. A. Jr., Unitary Shimura correspondences for split real groups, J. Amer. Math. Soc. 20 (2007), 701–751; MR 2291917.Google Scholar
Bernstein, I. N. and Zelevinsky, A. V., Induced representations of reductive $p$-adic groups. I, Ann. Sci. Éc. Norm. Supér. (4) 10 (1977), 441–472; MR 579172.CrossRefGoogle Scholar
Brylinski, J.-L. and Deligne, P., Central extensions of reductive groups by ${\boldsymbol K}_2$, Publ. Math. Inst. Hautes Études Sci. 94 (2001), 5–85; MR 1896177.CrossRefGoogle Scholar
Bump, D., Friedberg, S. and Ginzburg, D., Small representations for odd orthogonal groups, Int. Math. Res. Not. IMRN 2003 (2003), 1363–1393; MR 1968295.Google Scholar
Casselman, W., Introduction to the theory of admissible representations of $p$-adic reductive groups, Preprint (1995), https://personal.math.ubc.ca/~cass/research/pdf/p-adic-book.pdf.Google Scholar
Chinta, G., Friedberg, S. and Hoffstein, J., Double Dirichlet series and theta functions, in Contributions in analytic and algebraic number theory, Springer Proceedings in Mathematics, vol. 9 (Springer, New York, 2012), 149–170; MR 3060459.CrossRefGoogle Scholar
Cohen, H., Sums involving the values at negative integers of $L$-functions of quadratic characters, Math. Ann. 217 (1975), 271–285; MR 382192.CrossRefGoogle Scholar
Dalal, R., Counting discrete, level- $1$, quaternionic automorphic representations on $G_2$, J. Inst. Math. Jussieu (2023), doi: 10.1017/S1474748023000476.CrossRefGoogle Scholar
Deligne, P., Extensions centrales de groupes algébriques simplement connexes et cohomologie galoisienne, Publ. Math. Inst. Hautes Études Sci. 84 (1996), 35–89; MR 1441006.Google Scholar
Deligne, P. and Gross, B. H., On the exceptional series, and its descendants, C. R. Math. Acad. Sci. Paris 335 (2002), 877–881; MR 1952563.CrossRefGoogle Scholar
Friedberg, S. and Ginzburg, D., Descent and theta functions for metaplectic groups, J. Eur. Math. Soc. (JEMS) 20 (2018), 1913–1957; MR 3854895.CrossRefGoogle Scholar
Gan, W. T., An automorphic theta module for quaternionic exceptional groups, Canad. J. Math. 52 (2000), 737–756; MR 1767400.CrossRefGoogle Scholar
Gan, W. T. and Gao, F., The Langlands–Weissman program for Brylinski–Deligne extensions, in L-groups and the Langlands program for covering groups, Astérisque, vol. 398 (Société Mathématique de France, 2018), 187–275; MR 3802419.Google Scholar
Gan, W. T., Gross, B. and Savin, G., Fourier coefficients of modular forms on $G_2$, Duke Math. J. 115 (2002), 105–169; MR 1932327.CrossRefGoogle Scholar
Gan, W. T. and Savin, G., On minimal representations definitions and properties, Represent. Theory 9 (2005), 46–93; MR 2123125.Google Scholar
Gao, F., Distinguished theta representations for certain covering groups, Pacific J. Math. 290 (2017), 333–379.Google Scholar
Gelbart, S. S., Weil's representation and the spectrum of the metaplectic group, Lecture Notes in Mathematics, vol. 530 (Springer, Berlin–New York, 1976); MR 0424695.CrossRefGoogle Scholar
Gelbart, S. and Piatetski-Shapiro, I. I., Distinguished representations and modular forms of half-integral weight, Invent. Math. 59 (1980), 145–188; MR 577359.CrossRefGoogle Scholar
Ginzburg, D., Towards a classification of global integral constructions and functorial liftings using the small representations method, Adv. Math. 254 (2014), 157–186; MR 3161096.CrossRefGoogle Scholar
Ginzburg, D., On certain global constructions of automorphic forms related to a small representation of $F_4$, J. Number Theory 200 (2019), 1–95; MR 3944431.CrossRefGoogle Scholar
Gross, B. H., Some remarks on signs in functional equations, Ramanujan J. 7 (2003), 91–93; MR 2035794.CrossRefGoogle Scholar
Gross, B. H. and Wallach, N. R., A distinguished family of unitary representations for the exceptional groups of real rank =4, in Lie theory and geometry, Progress in Mathematics, vol. 123 (Birkhäuser, Boston, MA, 1994), 289–304; MR 1327538.CrossRefGoogle Scholar
Gross, B. H. and Wallach, N. R., On quaternionic discrete series representations, and their continuations, J. Reine Angew. Math. 481 (1996), 73–123; MR 1421947.Google Scholar
Huang, J.-S., Pandžić, P. and Savin, G., New dual pair correspondences, Duke Math. J. 82 (1996), 447–471; MR 1387237.CrossRefGoogle Scholar
Karasiewicz, E., A Hecke algebra on the double cover of a Chevalley group over $\Bbb {Q}_2$, Algebra Number Theory 15 (2021), 1729–1753; MR 4333663.CrossRefGoogle Scholar
Kazhdan, D. A. and Patterson, S. J., Metaplectic forms, Publ. Math. Inst. Hautes Études Sci. 59 (1984), 35–142; MR 743816.CrossRefGoogle Scholar
Leslie, S., A generalized theta lifting, CAP representations, and Arthur parameters, Trans. Amer. Math. Soc. 372 (2019), 5069–5121; MR 4009400.CrossRefGoogle Scholar
The LMFDB Collaboration, The L-functions and modular forms database, 2020, http://www.lmfdb.org [accessed 31 July 2020].Google Scholar
Loke, H. Y. and Savin, G., Modular forms on non-linear double covers of algebraic groups, Trans. Amer. Math. Soc. 362 (2010), 4901–4920; MR 2645055.CrossRefGoogle Scholar
Matsumoto, H., Sur les sous-groupes arithmétiques des groupes semi-simples déployés, Ann. Sci. École Norm. Supér. (4) 2 (1969), 1–62; MR 240214.CrossRefGoogle Scholar
Merkurćev, A. S. and Suslin, A. A., $K$-cohomology of Severi-Brauer varieties and the norm residue homomorphism, Izv. Akad. Nauk SSSR Ser. Mat. 46 (1982), 1011–1046, 1135–1136; MR 675529.Google Scholar
Milne, J. S., Algebraic groups: the theory of group schemes of finite type over a field, Cambridge Studies in Advanced Mathematics, vol. 170 (Cambridge University Press, Cambridge, 2017); MR 3729270.CrossRefGoogle Scholar
Patterson, S. J., Whittaker models of generalized theta series1, in Seminar on number theory, Paris 1982–83 (Paris, 1982/1983), Progress in Mathematics, vol. 51 (Birkhäuser, Boston, MA, 1984), 199–232; MR 791596.Google Scholar
Pollack, A., Lifting laws and arithmetic invariant theory, Camb. J. Math. 6 (2018), 347–449; MR 3870360.CrossRefGoogle Scholar
Pollack, A., The Fourier expansion of modular forms on quaternionic exceptional groups, Duke Math. J. 169 (2020), 1209–1280; MR 4094735.CrossRefGoogle Scholar
Pollack, A., A quaternionic Saito–Kurokawa lift and cusp forms on $G_2$, Algebra Number Theory 15 (2021), 1213–1244; MR 4283102.CrossRefGoogle Scholar
Pollack, A., The minimal modular form on quaternionic $E_8$, J. Inst. Math. Jussieu 21 (2022), 603–636; MR 4386823.CrossRefGoogle Scholar
Pollack, A., Modular forms on exceptional groups, Arizona Winter School notes (2022), https://swc-math.github.io/aws/2022/index.html.Google Scholar
Pollack, A., Modular forms on indefinite orthogonal groups of rank three, J. Number Theory 238 (2022), 611–675, with appendix ‘Next to minimal representation’ by Gordan Savin; MR 4430112.CrossRefGoogle Scholar
Sage Developers, Sagemath, the Sage Mathematics Software System (2022), https://www.sagemath.org.Google Scholar
Stein, M. R., Surjective stability in dimension $0$ for $K_{2}$ and related functors, Trans. Amer. Math. Soc. 178 (1973), 165–191; MR 327925.Google Scholar
Steinberg, R., Lectures on Chevalley groups, University Lecture Series, vol. 66 (American Mathematical Society, Providence, RI, 2016); Notes prepared by John Faulkner and Robert Wilson, Revised and corrected edition of the 1968 original [MR 0466335], with a foreword by Robert R. Snapp; MR 3616493.CrossRefGoogle Scholar
Swaminathan, A., Average $2$-torsion in class groups of rings associated to binary $n$-ic forms, Preprint (2021).Google Scholar
Tate, J., Relations between $K_{2}$ and Galois cohomology, Invent. Math. 36 (1976), 257–274; MR 429837.Google Scholar
Thańg, N. Q., Number of connected components of groups of real points of adjoint groups, Comm. Algebra 28 (2000), 1097–1110; MR 1742643.Google Scholar
Wallach, N. R., Generalized Whittaker vectors for holomorphic and quaternionic representations, Comment. Math. Helv. 78 (2003), 266–307; MR 1988198.CrossRefGoogle Scholar
Weissman, M. H., $D_4$ modular forms, Amer. J. Math. 128 (2006), 849–898; MR 2251588.CrossRefGoogle Scholar
Weissman, M. H., Covers of tori over local and global fields, Amer. J. Math. 138 (2016), 1533–1573; MR 3595494.CrossRefGoogle Scholar
Weissman, M. H., L-groups and parameters for covering groups, in L-groups and the Langlands program for covering groups, Astérisque, vol. 398 (Société Mathématique de France, 2018), 33–186; MR 3802418.Google Scholar
Zagier, D., Nombres de classes et formes modulaires de poids $3/2$, C. R. Acad. Sci. Paris Sér. A-B 281 (1975), A883–A886; MR 429750.Google Scholar