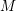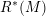Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Randal-Williams, Oscar
2018.
Some phenomena in tautological rings of manifolds.
Selecta Mathematica,
Vol. 24,
Issue. 4,
p.
3835.
Hebestreit, Fabian
Land, Markus
Lück, Wolfgang
and
Randal-Williams, Oscar
2021.
A vanishing theorem for tautological classes of aspherical manifolds.
Geometry & Topology,
Vol. 25,
Issue. 1,
p.
47.
Krannich, Manuel
2021.
On characteristic classes of exotic manifold bundles.
Mathematische Annalen,
Vol. 379,
Issue. 1-2,
p.
1.
RANDAL-WILLIAMS, OSCAR
2022.
TAUTOLOGICAL RINGS AND STABILISATION.
Glasgow Mathematical Journal,
Vol. 64,
Issue. 1,
p.
231.
Berglund, Alexander
2022.
Characteristic classes for families of bundles.
Selecta Mathematica,
Vol. 28,
Issue. 3,
Baraglia, David
2023.
Tautological classes of definite
4–manifolds.
Geometry & Topology,
Vol. 27,
Issue. 2,
p.
641.
Prigge, Nils
2025.
Tautological rings of fake quaternionic spaces.
Selecta Mathematica,
Vol. 31,
Issue. 1,