Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
Hostname: page-component-544b6db54f-n9d2k Total loading time: 0.263 Render date: 2021-10-22T08:13:41.786Z Has data issue: true Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "metricsAbstractViews": false, "figures": true, "newCiteModal": false, "newCitedByModal": true, "newEcommerce": true, "newUsageEvents": true }
  • English
Compositio Mathematica Compositio Mathematica

Article contents

Amalgamated free product type III factors with at most one Cartan subalgebra

Part of: Selfadjoint operator algebras Ergodic theory

Published online by Cambridge University Press:  13 December 2013

Rémi Boutonnet ,
Cyril Houdayer  and
Sven Raum
Rémi Boutonnet*
Affiliation:
ENS Lyon, UMPA UMR 5669, 69364 Lyon cedex 7, France
Cyril Houdayer
Affiliation:
CNRS–ENS Lyon, UMPA UMR 5669, 69364 Lyon cedex 7, France email cyril.houdayer@ens-lyon.fr
Sven Raum
Affiliation:
ENS Lyon, UMPA UMR 5669, 69364 Lyon cedex 7, France email sven.raum@ens-lyon.fr
*
remi.boutonnet@ens-lyon.fr
Rights & Permissions[Opens in a new window]

Abstract

HTML view is not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

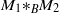We investigate Cartan subalgebras in nontracial amalgamated free product von Neumann algebras ${\mathop{M{}_{1} \ast }\nolimits}_{B} {M}_{2} $ over an amenable von Neumann subalgebra 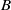$B$. First, we settle the problem of the absence of Cartan subalgebra in arbitrary free product von Neumann algebras. Namely, we show that any nonamenable free product von Neumann algebra 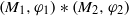$({M}_{1} , {\varphi }_{1} )\ast ({M}_{2} , {\varphi }_{2} )$ with respect to faithful normal states has no Cartan subalgebra. This generalizes the tracial case that was established by A. Ioana [Cartan subalgebras of amalgamated free product 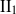${\mathrm{II} }_{1} $factors, arXiv:1207.0054]. Next, we prove that any countable nonsingular ergodic equivalence relation 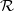$ \mathcal{R} $ defined on a standard measure space and which splits as the free product 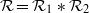$ \mathcal{R} = { \mathcal{R} }_{1} \ast { \mathcal{R} }_{2} $ of recurrent subequivalence relations gives rise to a nonamenable factor 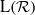$\mathrm{L} ( \mathcal{R} )$ with a unique Cartan subalgebra, up to unitary conjugacy. Finally, we prove unique Cartan decomposition for a class of group measure space factors 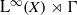${\mathrm{L} }^{\infty } (X)\rtimes \Gamma $ arising from nonsingular free ergodic actions 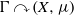$\Gamma \curvearrowright (X, \mu )$ on standard measure spaces of amalgamated groups 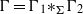$\Gamma = {\mathop{\Gamma {}_{1} \ast }\nolimits}_{\Sigma } {\Gamma }_{2} $ over a finite subgroup 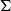$\Sigma $.

Keywords

amalgamated free productsCartan subalgebrasdeformation/rigidity theorynoncommutative flow of weightsnonsingular equivalence relations

MSC classification

Secondary: 46L10: General theory of von Neumann algebras 46L54: Free probability and free operator algebras 37A40: Nonsingular (and infinite-measure preserving) transformations
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 1 , January 2014 , pp. 143 - 174
Copyright
© The Author(s) 2013 

References

Adams, S., Indecomposability of equivalence relations generated by word hyperbolic groups, Topology 33 (1994), 785–798.CrossRefGoogle Scholar
Alvarez, A., Théorème de Kurosh pour les relations d’équivalence boréliennes, Ann. Inst. Fourier (Grenoble) 60 (2010), 1161–1200.CrossRefGoogle Scholar
Anantharaman-Delaroche, C., Amenable correspondences and approximation properties for von Neumann algebras, Pacific J. Math. 171 (1995), 309–341.CrossRefGoogle Scholar
Brown, N. P. and Ozawa, N., ${C}^{\ast } $-algebras and finite-dimensional approximations, in Graduate Studies in Mathematics, Vol. 88 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Chifan, I. and Houdayer, C., Bass–Serre rigidity results in von Neumann algebras, Duke Math. J. 153 (2010), 23–54.CrossRefGoogle Scholar
Chifan, I. and Sinclair, T., On the structural theory of ${\mathrm{II} }_{1} $ factors of negatively curved groups, Ann. Sci. Éc. Norm. Supér. (4) 46 (2013), 1–33.CrossRefGoogle Scholar
Chifan, I., Sinclair, T. and Udrea, B., On the structural theory of ${\mathrm{II} }_{1} $ factors of negatively curved groups, II. Actions by product groups, Adv. Math. 245 (2013), 208–236.CrossRefGoogle Scholar
Connes, A., Une classification des facteurs de type $\mathrm{III} $, Ann. Sci. Éc. Norm. Supér. (4) 6 (1973), 133–252.CrossRefGoogle Scholar
Connes, A., Classification of injective factors, Ann. of Math. 104 (1976), 73–115.CrossRefGoogle Scholar
Connes, A., Noncommutative geometry (Academic Press, San Diego, CA, 1994).Google Scholar
Connes, A., Feldman, J. and Weiss, B., An amenable equivalence relation is generated by a single transformation, Ergodic Theory Dynam. Systems 1 (1981), 431–450.CrossRefGoogle Scholar
Connes, A. and Jones, V. F. R., A ${\mathrm{II} }_{1} $ factor with two non-conjugate Cartan subalgebras, Bull. Amer. Math. Soc. 6 (1982), 211–212.CrossRefGoogle Scholar
Connes, A. and Takesaki, M., The flow of weights on factors of type III, Tohoku Math. J. 29 (1977), 473–575.CrossRefGoogle Scholar
Dykema, K., Free products of hyperfinite von Neumann algebras and free dimension, Duke Math. J. 69 (1993), 97–119.CrossRefGoogle Scholar
Falcone, A. J. and Takesaki, M., Non-commutative flow of weights on a von Neumann algebra, J. Funct. Anal. 182 (2001), 170–206.CrossRefGoogle Scholar
Feldman, J. and Moore, C. C., Ergodic equivalence relations, cohomology, and von Neumann algebras. $\mathrm{I} $ and $\mathrm{II} $, Trans. Amer. Math. Soc. 234 (1977), 289–324; 325–359.CrossRefGoogle Scholar
Gaboriau, D., Coût des relations d’équivalence et des groupes, Invent. Math. 139 (2000), 41–98.CrossRefGoogle Scholar
Houdayer, C., Strongly solid group factors which are not interpolated free group factors, Math. Ann. 346 (2010), 969–989.CrossRefGoogle Scholar
Houdayer, C. and Ricard, É., Approximation properties and absence of Cartan subalgebra for free Araki–Woods factors, Adv. Math. 228 (2011), 764–802.CrossRefGoogle Scholar
Houdayer, C and Vaes, S., Type $\mathrm{III} $ factors with unique Cartan decomposition, J. Math. Pures Appl. (9) 100 (2013), 564–590.CrossRefGoogle Scholar
Ioana, A., Cartan subalgebras of amalgamated free product ${\mathrm{II} }_{1} $factors, arXiv:1207.0054.Google Scholar
Ioana, A., Classification and rigidity for von Neumann algebras, in Proceedings of the 6th European Congress of Mathematics (Krakow, 2012) (European Mathematical Society, Zürich), to appear, arXiv:1212.0453.Google Scholar
Ioana, A., Peterson, J. and Popa, S., Amalgamated free products of $w$-rigid factors and calculation of their symmetry groups, Acta Math. 200 (2008), 85–153.CrossRefGoogle Scholar
Jung, K., Strongly $1$-bounded von Neumann algebras, Geom. Funct. Anal. 17 (2007), 1180–1200.CrossRefGoogle Scholar
Kesten, H., Full Banach mean values on countable groups, Math. Scand. 7 (1959), 146–156.CrossRefGoogle Scholar
Krieger, W., On ergodic flows and the isomorphism of factors, Math. Ann. 223 (1976), 19–70.CrossRefGoogle Scholar
Maharam, D., Incompressible transformations, Fund. Math. 56 (1964), 35–50.CrossRefGoogle Scholar
Ozawa, N. and Popa, S., On a class of  ${\mathrm{II} }_{1} $ factors with at most one Cartan subalgebra, Ann. of Math. (2) 172 (2010), 713–749.CrossRefGoogle Scholar
Ozawa, N. and Popa, S., On a class of  ${\mathrm{II} }_{1} $ factors with at most one Cartan subalgebra $\mathrm{II} $, Amer. J. Math. 132 (2010), 841–866.CrossRefGoogle Scholar
Popa, S., On a class of type ${\mathrm{II} }_{1} $ factors with Betti numbers invariants, Ann. of Math. (2) 163 (2006), 809–899.CrossRefGoogle Scholar
Popa, S., Strong rigidity of ${\mathrm{II} }_{1} $ factors arising from malleable actions of w-rigid groups $\mathrm{I} $, $\mathrm{II} $, Invent. Math. 165 (2006), 369–408; 409–451.CrossRefGoogle Scholar
Popa, S., Deformation and rigidity for group actions and von Neumann algebras, in Proceedings of the International Congress of Mathematicians (Madrid, 2006), Vol. I (European Mathematical Society, Zürich, 2007), 445–477.CrossRefGoogle Scholar
Popa, S., On the superrigidity of malleable actions with spectral gap, J. Amer. Math. Soc. 21 (2008), 981–1000.CrossRefGoogle Scholar
Popa, S. and Vaes, S., Unique Cartan decomposition for ${\mathrm{II} }_{1} $factors arising from arbitrary actions of free groups, Acta Math., to appear, arXiv:1111.6951.Google Scholar
Popa, S. and Vaes, S., Unique Cartan decomposition for ${\mathrm{II} }_{1} $factors arising from arbitrary actions of hyperbolic groups, J. Reine Angew. Math., to appear, arXiv:1201.2824.Google Scholar
Shlyakhtenko, D., Prime type $\mathrm{III} $ factors, Proc. Natl. Acad. Sci. USA 97 (2000), 12439–12441.CrossRefGoogle ScholarPubMed
Speelman, A. and Vaes, S., A class of  ${\mathrm{II} }_{1} $ factors with many non conjugate Cartan subalgebras, Adv. Math. 231 (2012), 2224–2251.CrossRefGoogle Scholar
Takesaki, M., Theory of operator algebras. $\mathrm{I} $, in Encyclopaedia of mathematical sciences, Vol. 124, Operator Algebras and Non-commutative Geometry, vol. 5 (Springer, Berlin, 2002).Google Scholar
Takesaki, M., Theory of operator algebras. $\mathrm{II} $, in Encyclopaedia of mathematical sciences, Vol. 125, Operator Algebras and Non-commutative Geometry, vol. 6 (Springer, Berlin, 2003).Google Scholar
Ueda, Y., Amalgamated free products over Cartan subalgebra, Pacific J. Math. 191 (1999), 359–392.CrossRefGoogle Scholar
Ueda, Y., Factoriality, type classification and fullness for free product von Neumann algebras, Adv. Math. 228 (2011), 2647–2671.CrossRefGoogle Scholar
Ueda, Y., Some analysis on amalgamated free products of von Neumann algebras in non-tracial setting, J. Lond. Math. Soc. 88 (2013), 25–48.CrossRefGoogle Scholar
Vaes, S., Rigidity results for Bernoulli actions and their von Neumann algebras (after S. Popa), Séminaire Bourbaki, exposé 961. Astérisque 311 (2007), 237–294.Google Scholar
Vaes, S., Explicit computations of all finite index bimodules for a family of  ${\mathrm{II} }_{1} $ factors, Ann. Sci. Éc. Norm. Supér. (4) 41 (2008), 743–788.CrossRefGoogle Scholar
Vaes, S., Rigidity for von Neumann algebras and their invariants, in Proceedings of the International Congress of Mathematicians (Hyderabad, 2010), Vol. III (Hindustan Book Agency, New Delhi, 2010), 1624–1650.Google Scholar
Vaes, S., One-cohomology and the uniqueness of the group measure space decomposition of a ${\mathrm{II} }_{1} $ factor, Math. Ann. 355 (2013), 661–696.CrossRefGoogle Scholar
Voiculescu, D.-V., Symmetries of some reduced free product ${C}^{\ast } $-algebras., in Operator algebras and their connections with topology and ergodic theory, Lecture Notes in Mathematics, vol. 1132 (Springer, Heidelberg, 1985), 556–588.CrossRefGoogle Scholar
Voiculescu, D.-V., Dykema, K. J. and Nica, A., Free random variables, CRM Monograph Series 1 (American Mathematical Society, Providence, RI, 1992).CrossRefGoogle Scholar
Voiculescu, D.-V., The analogues of entropy and of Fisher’s information measure in free probability theory. $\mathrm{III} $. The absence of Cartan subalgebras, Geom. Funct. Anal. 6 (1996), 172–199.CrossRefGoogle Scholar
You have Access
14
Cited by

Send article to Kindle

To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about sending to your Kindle.

Note you can select to send to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be sent to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Amalgamated free product type III factors with at most one Cartan subalgebra
Available formats
×

Send article to Dropbox

To send this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Dropbox.

Amalgamated free product type III factors with at most one Cartan subalgebra
Available formats
×

Send article to Google Drive

To send this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Google Drive.

Amalgamated free product type III factors with at most one Cartan subalgebra
Available formats
×
×

Reply to: Submit a response

Please enter your response.

Your details

Please enter a valid email address.

Conflicting interests

Do you have any conflicting interests? *