Hostname: page-component-89b8bd64d-46n74 Total loading time: 0 Render date: 2026-05-06T14:57:27.637Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounding Lagrangian widths via geodesic paths

Part of: Symplectic geometry, contact geometry

Published online by Cambridge University Press:  17 September 2014

Matthew Strom Borman  and
Mark McLean
Matthew Strom Borman
Affiliation:
Department of Mathematics, Stanford University, Stanford, CA 94305, USA email borman@math.uchicago.edu
Mark McLean
Affiliation:
Institute of Mathematics, University of Aberdeen, Aberdeen AB24 3FX, UK email mmclean@abdn.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

The width of a Lagrangian is the largest capacity of a ball that can be symplectically embedded into the ambient manifold such that the ball intersects the Lagrangian exactly along the real part of the ball. Due to Dimitroglou Rizell, finite width is an obstruction to a Lagrangian admitting an exact Lagrangian cap in the sense of Eliashberg–Murphy. In this paper we introduce a new method for bounding the width of a Lagrangian 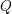$Q$ by considering the Lagrangian Floer cohomology of an auxiliary Lagrangian 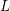$L$ with respect to a Hamiltonian whose chords correspond to geodesic paths in 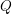$Q$. This is formalized as a wrapped version of the Floer–Hofer–Wysocki capacity and we establish an associated energy–capacity inequality with the help of a closed–open map. For any orientable Lagrangian 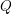$Q$ admitting a metric of non-positive sectional curvature in a Liouville manifold, we show the width of 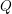$Q$ is bounded above by four times its displacement energy.

Keywords

symplectic manifoldLagrangian manifoldLagrangian widthLagrangian packingsymplectic capacitysymplectic cohomologywrapped Floer cohomologygeodesic flow

MSC classification

Primary: 53D12: Lagrangian submanifolds; Maslov index 53D25: Geodesic flows 53D40: Floer homology and cohomology, symplectic aspects

Information

Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 12 , December 2014 , pp. 2143 - 2183
Copyright
© The Author(s) 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abbondandolo, A. and Schwarz, M., Note on Floer homology and loop space homology, in Morse theoretic methods in nonlinear analysis and in symplectic topology, NATO Science Series II Mathematics, Physics and Chemistry, vol. 217 (Springer, Dordrecht, 2006), 75–108.Google Scholar
Abbondandolo, A. and Schwarz, M., On the Floer homology of cotangent bundles, Comm. Pure Appl. Math. 59 (2006), 254–316.Google Scholar
Abbondandolo, A. and Schwarz, M., Floer homology of cotangent bundles and the loop product, Geom. Topol. 14 (2010), 1569–1722.Google Scholar
Abouzaid, M., On the wrapped Fukaya category and based loops, J. Symplectic Geom. 10 (2012), 27–79.Google Scholar
Abouzaid, M. and Seidel, P., An open string analogue of Viterbo functoriality, Geom. Topol. 14 (2010), 627–718.CrossRefGoogle Scholar
Albers, P., On the extrinsic topology of Lagrangian submanifolds, Int. Math. Res. Not. IMRN 2005 (2005), 2341–2371.Google Scholar
Albers, P., A Lagrangian Piunikhin–Salamon–Schwarz morphism and two comparison homomorphisms in Floer homology, Int. Math. Res. Not. IMRN, Art. ID rnm 134, 56pp (2008).Google Scholar
Albers, P., Erratum for “On the extrinsic topology of Lagrangian submanifolds”, Int. Math. Res. Not. IMRN 2010 (2010), 1363–1369.Google Scholar
Alexander, H., Continuing 1-dimensional analytic sets, Math. Ann. 191 (1971), 143–144.Google Scholar
Audin, M., Lalonde, F. and Polterovich, L., Symplectic rigidity: Lagrangian submanifolds, in Holomorphic curves in symplectic geometry, Progress in Mathematics, vol. 117 (Birkhäuser, Basel, 1994), 271–321.CrossRefGoogle Scholar
Barraud, J.-F. and Cornea, O., Homotopic dynamics in symplectic topology, in Morse theoretic methods in nonlinear analysis and in symplectic topology, NATO Science Series II: Mathematics, Physics and Chemistry, vol. 217 (Springer, Dordrecht, 2006), 109–148.CrossRefGoogle Scholar
Barraud, J.-F. and Cornea, O., Lagrangian intersections and the Serre spectral sequence, Ann. of Math. (2) 166 (2007), 657–722.Google Scholar
Biran, P., A stability property of symplectic packing, Invent. Math. 136 (1999), 123–155.Google Scholar
Biran, P., From symplectic packing to algebraic geometry and back, in European Congress of Mathematics, Vol. II (Barcelona, 2000), Progress in Mathematics, vol. 202 (Birkhäuser, Basel, 2001), 507–524.Google Scholar
Biran, P. and Cornea, O., Rigidity and uniruling for Lagrangian submanifolds, Geom. Topol. 13 (2009), 2881–2989.Google Scholar
Biran, P., Polterovich, L. and Salamon, D., Propagation in Hamiltonian dynamics and relative symplectic homology, Duke Math. J. 119 (2003), 65–118.Google Scholar
Buhovsky, L., A maximal relative symplectic packing construction, J. Symplectic Geom. 8 (2010), 67–72.Google Scholar
Buse, O. and Hind, R., Symplectic embeddings of ellipsoids in dimension greater than four, Geom. Topol. 15 (2011), 2091–2110.Google Scholar
Cieliebak, K., Floer, A., Hofer, H. and Wysocki, K., Applications of symplectic homology. II. Stability of the action spectrum, Math. Z. 223 (1996), 27–45.Google Scholar
Cieliebak, K. and Latschev, J., The role of string topology in symplectic field theory, in New perspectives and challenges in symplectic field theory, CRM Proceedings Lecture Notes, vol. 49 (American Mathematical Society, Providence, RI, 2009), 113–146.Google Scholar
Chantraine, B., Some non-collarable slices of Lagrangian surfaces, Bull. Lond. Math. Soc. 44 (2012), 981–987.Google Scholar
Charette, F., A geometric refinement of a theorem of Chekanov, J. Symplectic Geom. 10 (2012), 475–491.Google Scholar
Charette, F., Uniruling for orientable Lagrangian surfaces, Preprint (2014), arXiv:1401:1953.Google Scholar
Cornea, O. and Lalonde, F., Cluster homology, Preprint (2005), arXiv:math.SG/0508345v1.Google Scholar
Cornea, O. and Lalonde, F., Cluster homology: an overview of the construction and results, Electron. Res. Announc. Amer. Math. Soc. 12 (2006), 1–12 (electronic).Google Scholar
Damian, M., Floer homology on the universal cover, Audin’s conjecture and other constraints on Lagrangian submanifolds, Comment. Math. Helv. 87 (2012), 433–462.CrossRefGoogle Scholar
Rizell, G. D., Exact Lagrangian caps and non-uniruled Lagrangian submanifolds, Preprint (2013), arXiv:1306.4667.Google Scholar
Dragnev, D. L., Symplectic rigidity, symplectic fixed points, and global perturbations of Hamiltonian systems, Comm. Pure Appl. Math. 61 (2008), 346–370.CrossRefGoogle Scholar
Duistermaat, J. J., On the Morse index in variational calculus, Adv. Math. 21 (1976), 173–195.Google Scholar
Ekholm, T., Eliashberg, Y., Murphy, E. and Smith, I., Constructing exact Lagrangian immersions with few double points, Geom. Funct. Anal. 23 (2013), 1772–1803.Google Scholar
Eliashberg, Y., New invariants of open symplectic and contact manifolds, J. Amer. Math. Soc. 4 (1991), 513–520.Google Scholar
Eliashberg, Y. and Murphy, E., Lagrangian caps, Geom. Funct. Anal. 23 (2013), 1483–1514.Google Scholar
Evans, J. D. and Kędra, J., Remarks on monotone Lagrangians in $\mathbb{C}^{n}$, Preprint (2011),arXiv:1110.0927.Google Scholar
Fefferman, C. and Phong, D. H., Symplectic geometry and positivity of pseudodifferential operators, Proc. Natl Acad. Sci. USA 79 (1982), 710–713.Google Scholar
Fish, J. W., Target-local Gromov compactness, Geom. Topol. 2 (2011), 765–826.CrossRefGoogle Scholar
Floer, A., Morse theory for Lagrangian intersections, J. Differential Geom. 28 (1988), 513–547.Google Scholar
Floer, A., The unregularized gradient flow of the symplectic action, Comm. Pure Appl. Math. 41 (1988), 775–813.Google Scholar
Floer, A., Symplectic fixed points and holomorphic spheres, Comm. Math. Phys. 120 (1989), 575–611.Google Scholar
Floer, A., Witten’s complex and infinite-dimensional Morse theory, J. Differential Geom. 30 (1989), 207–221.Google Scholar
Floer, A. and Hofer, H., Symplectic homology. I. Open sets in Cn, Math. Z. 215 (1994), 37–88.Google Scholar
Floer, A., Hofer, H. and Salamon, D., Transversality in elliptic Morse theory for the symplectic action, Duke Math. J. 80 (1995), 251–292.Google Scholar
Floer, A., Hofer, H. and Wysocki, K., Applications of symplectic homology. I, Math. Z. 217 (1994), 577–606.Google Scholar
Fukaya, K., Application of Floer homology of Langrangian submanifolds to symplectic topology, in Morse theoretic methods in nonlinear analysis and in symplectic topology, NATO Science Series II: Mathematics, Physics and Chemistry, vol. 217 (Springer, Dordrecht, 2006), 231–276.Google Scholar
Ginzburg, V. L., Coisotropic intersections, Duke Math. J. 140 (2007), 111–163.Google Scholar
Ginzburg, V. L., The Conley conjecture, Ann. of Math. (2) 172 (2010), 1127–1180.CrossRefGoogle Scholar
Ginzburg, V. L., On Maslov class rigidity for coisotropic submanifolds, Pacific J. Math. 250 (2011), 139–161.Google Scholar
Grauert, H. and Remmert, R., Coherent analytic sheaves, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 265 (Springer-Verlag, Berlin, 1984).Google Scholar
Gromov, M. L., A topological technique for the construction of solutions of differential equations and inequalities, Actes du Congrès International des Mathématiciens (Nice, 1970), Tome 2 (Gauthier-Villars, Paris, 1971), 221–225.Google Scholar
Gromov, M., Pseudoholomorphic curves in symplectic manifolds, Invent. Math. 82 (1985), 307–347.Google Scholar
Guth, L., Metaphors in systolic geometry, in Proceedings of the international congress of mathematicians. Vol. II (Hindustan Book Agency, New Delhi, 2010), 745–768.Google Scholar
Hermann, D., Holomorphic curves and Hamiltonian systems in an open set with restricted contact-type boundary, Duke Math. J. 103 (2000), 335–374.Google Scholar
Hermann, D., Inner and outer Hamiltonian capacities, Bull. Soc. Math. France 132 (2004), 509–541.CrossRefGoogle Scholar
Hind, R. and Kerman, E., New obstructions to symplectic embeddings, Invent. Math. 196 (2014), 383–452.Google Scholar
Hofer, H., On the topological properties of symplectic maps, Proc. Roy. Soc. Edinburgh Sect. A 115 (1990), 25–38.Google Scholar
Hofer, H. and Zehnder, E., Symplectic invariants and Hamiltonian dynamics, Birkhäuser Advanced Texts: Basler Lehrbücher (Birkhäuser, Basel, 1994).Google Scholar
Humilière, V., Leclercq, R. and Seyfaddini, S., Coisotropic rigidity and $C^{0}$-symplectic geometry, Preprint (2013), arXiv:1305.1287v1.Google Scholar
Hutchings, M., Embedded contact homology and its applications, in Proceedings of the international congress of mathematicians. Vol. II (Hindustan Book Agency, New Delhi, 2010), 1022–1041.Google Scholar
Irie, K., Symplectic homology of disc cotangent bundles of domains in Euclidean space, Preprint (2012), arXiv:1211.2184.Google Scholar
Kerman, E., Action selectors and Maslov class rigidity, Int. Math. Res. Not. IMRN 23 (2009), 4395–4427.Google Scholar
Kerman, E. and Şirikçi, N. I., Maslov class rigidity for Lagrangian submanifolds via Hofer’s geometry, Comment. Math. Helv. 85 (2010), 907–949.Google Scholar
Leclercq, R., Spectral invariants in Lagrangian Floer theory, J. Mod. Dyn. 2 (2008), 249–286.CrossRefGoogle Scholar
Lees, J. A., On the classification of Lagrange immersions, Duke Math. J. 43 (1976), 217–224.CrossRefGoogle Scholar
Lisi, S. and Rieser, A., Coisotropic Hofer–Zehnder capacities and non-squeezing for relative embeddings, Preprint (2013), arXiv:1312.7334.Google Scholar
McDuff, D. and Polterovich, L., Symplectic packings and algebraic geometry, Invent. Math. 115 (1994), 405–434. With appendix by Y. Karshon.Google Scholar
McDuff, D. and Schlenk, F., The embedding capacity of 4-dimensional symplectic ellipsoids, Ann. of Math. (2) 175 (2012), 1191–1282.Google Scholar
Milnor, J., Morse theory: based on lecture notes by M. Spivak and R. Wells, Annals of Mathematics Studies, vol. 51 (Princeton University Press, Princeton, NJ, 1963).Google Scholar
Murphy, E., Loose Legendrian embeddings in high dimensional contact manifolds, Preprint (2012), arXiv:1201.2245.Google Scholar
Oh, Y.-G., Floer cohomology of Lagrangian intersections and pseudo-holomorphic disks. I, Comm. Pure Appl. Math. 46 (1993), 949–993.Google Scholar
Oh, Y.-G., Addendum to: “Floer cohomology of Lagrangian intersections and pseudo-holomorphic disks. I”, Comm. Pure Appl. Math. 48 (1995), 1299–1302.Google Scholar
Paternain, G. P., Polterovich, L. and Siburg, K. F., Boundary rigidity for Lagrangian submanifolds, non-removable intersections, and Aubry–Mather theory, Mosc. Math. J. 3 (2003), 593–619; 745. Dedicated to Vladimir I. Arnold on the occasion of his 65th birthday.Google Scholar
Polterovich, L., The geometry of the group of symplectic diffeomorphisms, Lectures in Mathematics ETH Zürich (Birkhäuser, Basel, 2001).CrossRefGoogle Scholar
Rieser, A., Lagrangian blow-ups, blow-downs, and applications to real packing, Preprint (2010), arXiv:1012.1034v2.Google Scholar
Robbin, J. and Salamon, D., The Maslov index for paths, Topology 32 (1993), 827–844.CrossRefGoogle Scholar
Robbin, J. and Salamon, D., The spectral flow and the Maslov index, Bull. Lond. Math. Soc. 27 (1995), 1–33.Google Scholar
Salamon, D. A. and Weber, J., Floer homology and the heat flow, Geom. Funct. Anal. 16 (2006), 1050–1138.Google Scholar
Salamon, D. and Zehnder, E., Morse theory for periodic solutions of Hamiltonian systems and the Maslov index, Comm. Pure Appl. Math. 45 (1992), 1303–1360.Google Scholar
Schlenk, F., Embedding problems in symplectic geometry, de Gruyter Expositions in Mathematics, vol. 40 (Walter de Gruyter, Berlin, 2005).Google Scholar
Schlenk, F., Packing symplectic manifolds by hand, J. Symplectic Geom. 3 (2005), 313–340.Google Scholar
Sikorav, J.-C., Rigidité symplectique dans le cotangent de T n, Duke Math. J. 59 (1989), 759–763.Google Scholar
Sikorav, J.-C., Quelques propriétés des plongements Lagrangiens, in Mém. Soc. Math. France (N.S.) (1991), 151–167. Analyse globale et physique mathématique (Lyon, 1989).Google Scholar
Sikorav, J.-C., Some properties of holomorphic curves in almost complex manifolds, in Holomorphic curves in symplectic geometry, Progress in Mathematics, vol. 117 (Birkhäuser, Basel, 1994), 165–189.Google Scholar
Traynor, L., Symplectic packing constructions, J. Differential Geom. 42 (1995), 411–429.Google Scholar
Viterbo, C., A new obstruction to embedding Lagrangian tori, Invent. Math. 100 (1990), 301–320.Google Scholar
Viterbo, C., Plongements lagrangiens et capacités symplectiques de tores dans R2n, C. R. Acad. Sci. Paris Sér. I Math. 311 (1990), 487–490.Google Scholar
Viterbo, C., Functors and computations in Floer homology with applications. I, Geom. Funct. Anal. 9 (1999), 985–1033.Google Scholar
Weinstein, A., Symplectic manifolds and their Lagrangian submanifolds, Adv. Math. 6 (1971), 329–356.Google Scholar
Zehmisch, K., The codisc radius capacity, Electron. Res. Announc. Amer. Math. Soc. 20 (2013), 77–96 (electronic).Google Scholar