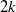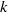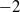Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tarasca, Nicola
2015.
Double Total Ramifications for Curves of Genus 2.
International Mathematics Research Notices,
Vol. 2015,
Issue. 19,
p.
9569.
Schaffler, Luca
2015.
On the cone of effective 2-cycles on.
European Journal of Mathematics,
Vol. 1,
Issue. 4,
p.
669.
Chen, Dawei
and
Tarasca, Nicola
2016.
Loci of curves with subcanonical points in low genus.
Mathematische Zeitschrift,
Vol. 284,
Issue. 3-4,
p.
683.
Chan, Melody
López Martín, Alberto
Pflueger, Nathan
and
Teixidor i Bigas, Montserrat
2017.
Genera of Brill-Noether curves and staircase paths in Young tableaux.
Transactions of the American Mathematical Society,
Vol. 370,
Issue. 5,
p.
3405.
Chan, Melody
and
Pflueger, Nathan
2020.
Euler characteristics of Brill-Noether varieties.
Transactions of the American Mathematical Society,
Vol. 374,
Issue. 3,
p.
1513.
Kennedy-Hunt, Patrick
Nabijou, Navid
Shafi, Qaasim
and
Zheng, Wanlong
2024.
Divisors and curves on logarithmic mapping spaces.
Selecta Mathematica,
Vol. 30,
Issue. 4,
Teixidor i Bigas, Montserrat
2025.
Brill-Noether loci.
manuscripta mathematica,
Vol. 176,
Issue. 1,
Esteves, Eduardo
Santos, Renan
and
Vital, Eduardo
2026.
Quiver representations arising from degenerations of linear series, I.
Communications in Algebra,
Vol. 54,
Issue. 2,
p.
525.