Article contents
Characterization of products of theta divisors
Published online by Cambridge University Press: 30 June 2014
Abstract
We study products of irreducible theta divisors from two points of view. On the one hand, we characterize them as normal subvarieties of abelian varieties such that a desingularization has holomorphic Euler characteristic 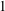 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}1$. On the other hand, we identify them up to birational equivalence among all varieties of maximal Albanese dimension. We also describe the structure of varieties
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}1$. On the other hand, we identify them up to birational equivalence among all varieties of maximal Albanese dimension. We also describe the structure of varieties 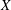 $X$ of maximal Albanese dimension, with holomorphic Euler characteristic
$X$ of maximal Albanese dimension, with holomorphic Euler characteristic 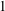 $1$ and irregularity
$1$ and irregularity 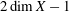 $2\dim X-1$.
$2\dim X-1$.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2014
References
- 6
- Cited by

