Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Klurman, Oleksiy
and
Mangerel, Alexander P.
2018.
Rigidity theorems for multiplicative functions.
Mathematische Annalen,
Vol. 372,
Issue. 1-2,
p.
651.
TERÄVÄINEN, JONI
2018.
ON BINARY CORRELATIONS OF MULTIPLICATIVE FUNCTIONS.
Forum of Mathematics, Sigma,
Vol. 6,
Issue. ,
Kátai, Imre
and
Phong, Bui Minh
2019.
On the pairs of completely multiplicative functions satisfying some relation.
Acta Scientiarum Mathematicarum,
Vol. 85,
Issue. 1-2,
p.
139.
Tao, Terence
and
Teräväinen, Joni
2019.
The structure of logarithmically averaged correlations of multiplicative functions, with applications to the Chowla and Elliott conjectures.
Duke Mathematical Journal,
Vol. 168,
Issue. 11,
Ng, Nathan
and
Thom, Mark
2019.
Bounds and conjectures for additive divisor sums.
Functiones et Approximatio Commentarii Mathematici,
Vol. 60,
Issue. 1,
Maynard, James
2019.
The twin prime conjecture.
Japanese Journal of Mathematics,
Vol. 14,
Issue. 2,
p.
175.
Matomäki, Kaisa
Radziwiłł, Maksym
and
Tao, Terence
2020.
Fourier uniformity of bounded multiplicative functions in short intervals on average.
Inventiones mathematicae,
Vol. 220,
Issue. 1,
p.
1.
Klurman, Oleksiy
and
Kurlberg, Pär
2020.
A note on multiplicative automatic sequences, II.
Bulletin of the London Mathematical Society,
Vol. 52,
Issue. 1,
p.
185.
Aymone, Marco
2020.
A note on multiplicative functions resembling the Möbius function.
Journal of Number Theory,
Vol. 212,
Issue. ,
p.
113.
Klurman, Oleksiy
and
Mangerel, Alexander P.
2020.
On the orbits of multiplicative pairs.
Algebra & Number Theory,
Vol. 14,
Issue. 1,
p.
155.
Matthiesen, Lilian
2020.
Linear correlations of multiplicative functions.
Proceedings of the London Mathematical Society,
Vol. 121,
Issue. 2,
p.
372.
Gomilko, Alexander
Lemańczyk, Mariusz
and
de la Rue, Thierry
2021.
On Furstenberg systems of aperiodic multiplicative functions of Matomäki, Radziwiłł, and Tao.
Journal of Modern Dynamics,
Vol. 17,
Issue. 0,
p.
529.
Lelas, Nikola
2021.
Extremal behaviour of ± 1-valued completely multiplicative functions in function fields.
Glasnik Matematicki,
Vol. 56,
Issue. 1,
p.
79.
de la Bretèche, Régis
and
Granville, Andrew
2022.
Exponential sums with multiplicative coefficients and applications.
Transactions of the American Mathematical Society,
Vol. 375,
Issue. 10,
p.
6875.
Mangerel, Alexander P.
2022.
Additive functions in short intervals, gaps and a conjecture of Erdős.
The Ramanujan Journal,
Vol. 59,
Issue. 4,
p.
1023.
Aymone, Marco
2022.
The Erdős discrepancy problem over the squarefree and cubefree integers.
Mathematika,
Vol. 68,
Issue. 1,
p.
51.
Ramaré, Olivier
2022.
Excursions in Multiplicative Number Theory.
p.
187.
Aymone, Marco
2022.
Complex Valued Multiplicative Functions with Bounded Partial Sums.
Bulletin of the Brazilian Mathematical Society, New Series,
Vol. 53,
Issue. 4,
p.
1317.
Klurman, Oleksiy
Mangerel, Alexander P.
and
Teräväinen, Joni
2023.
Correlations of multiplicative functions in function fields.
Mathematika,
Vol. 69,
Issue. 1,
p.
155.
Jiang, Yujiao
and
Lü, Guangshi
2024.
Correlations of Multiplicative Functions with Coefficients of Automorphic L-Functions.
International Mathematics Research Notices,
Vol. 2024,
Issue. 2,
p.
1733.
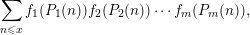 $$\begin{eqnarray}\mathop{\sum }_{n\leqslant x}f_{1}(P_{1}(n))f_{2}(P_{2}(n))\cdots f_{m}(P_{m}(n)),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n\leqslant x}f_{1}(P_{1}(n))f_{2}(P_{2}(n))\cdots f_{m}(P_{m}(n)),\end{eqnarray}$$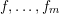 $f,\ldots ,f_{m}$ are bounded ‘pretentious’ multiplicative functions, under certain natural hypotheses. We then deduce several desirable consequences. First, we characterize all multiplicative functions
$f,\ldots ,f_{m}$ are bounded ‘pretentious’ multiplicative functions, under certain natural hypotheses. We then deduce several desirable consequences. First, we characterize all multiplicative functions 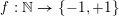 $f:\mathbb{N}\rightarrow \{-1,+1\}$ with bounded partial sums. This answers a question of Erdős from
$f:\mathbb{N}\rightarrow \{-1,+1\}$ with bounded partial sums. This answers a question of Erdős from 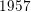 $1957$ in the form conjectured by Tao. Second, we show that if the average of the first divided difference of the multiplicative function is zero, then either
$1957$ in the form conjectured by Tao. Second, we show that if the average of the first divided difference of the multiplicative function is zero, then either 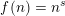 $f(n)=n^{s}$ for
$f(n)=n^{s}$ for 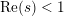 $\operatorname{Re}(s)<1$ or
$\operatorname{Re}(s)<1$ or 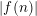 $|f(n)|$ is small on average. This settles an old conjecture of Kátai. Third, we apply our theorem to count the number of representations of
$|f(n)|$ is small on average. This settles an old conjecture of Kátai. Third, we apply our theorem to count the number of representations of 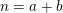 $n=a+b$ , where
$n=a+b$ , where 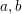 $a,b$ belong to some multiplicative subsets of
$a,b$ belong to some multiplicative subsets of 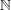 $\mathbb{N}$ . This gives a new ‘circle method-free’ proof of a result of Brüdern.
$\mathbb{N}$ . This gives a new ‘circle method-free’ proof of a result of Brüdern.
