Hostname: page-component-7dd5485656-2pp2p Total loading time: 0 Render date: 2025-10-30T18:19:00.883Z Has data issue: false hasContentIssue false
  • English
  • Français

Cycle classes in overconvergent rigid cohomology and a semistable Lefschetz 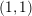$(1,1)$ theorem

Part of: Arithmetic algebraic geometry Cycles and subschemes (Co)homology theory

Published online by Cambridge University Press:  02 May 2019

Christopher Lazda  and
Ambrus Pál
Christopher Lazda
Affiliation:
Korteweg-de Vries Institute, Universiteit van Amsterdam, P.O. Box 94248, 1090 GE Amsterdam, The Netherlands email c.d.lazda@uva.nl
Ambrus Pál
Affiliation:
Department of Mathematics, Imperial College London, Huxley Building, 180 Queen’s Gate, London SW7 2AZ, UK email a.pal@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we prove a semistable version of the variational Tate conjecture for divisors in crystalline cohomology, showing that for 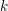$k$ a perfect field of characteristic 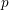$p$, a rational (logarithmic) line bundle on the special fibre of a semistable scheme over 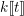$k\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$ lifts to the total space if and only if its first Chern class does. The proof is elementary, using standard properties of the logarithmic de Rham–Witt complex. As a corollary, we deduce similar algebraicity lifting results for cohomology classes on varieties over global function fields. Finally, we give a counter-example to show that the variational Tate conjecture for divisors cannot hold with 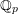$\mathbb{Q}_{p}$-coefficients.

Keywords

Picard groupscrystalline cohomologysemistable reductionTate conjecture

MSC classification

Primary: 14C22: Picard groups
Secondary: 14F30: $p$-adic cohomology, crystalline cohomology 11G25: Varieties over finite and local fields

Information

Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 5 , May 2019 , pp. 1025 - 1045
Copyright
© The Authors 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Berthelot, P., Breen, L. and Messing, W., Théorie de Dieudonné Cristalline II, Lecture Notes in Mathematics, vol. 930 (Springer, Berlin, 1982), doi:10.1007/BFb0093025.Google Scholar
Berthelot, P. and Ogus, A., F-isocrystals and de Rham cohomology. I , Invent. Math. 72 (1983), 159–199, doi:10.1007/BF01389319.Google Scholar
Caro, D., Hard Lefschetz theorem in p-adic cohomology , Rend. Semin. Mat. Univ. Padova 136 (2016), 225–255, doi:10.4171/RSMUP/136-15.Google Scholar
Caro, D. and Vauclair, D., Logarithmic $p$ -bases and arithmetical differential modules, Preprint (2015), arXiv:1511.07797.Google Scholar
de Jong, A. J., Crystalline Dieudonné module theory via formal and rigid geometry , Publ. Math. Inst. Hautes Études Sci. 82 (1995), 5–96, http://www.numdam.org/item?id=PMIHES_1995_82_5_0.Google Scholar
de Jong, A. J., Homomorphisms of Barsotti–Tate groups and crystals in positive charateristic , Invent. Math. 134 (1998), 301–333, doi:10.1007/s002220050266.Google Scholar
Hyodo, O. and Kato, K., Semi-stable reduction and crystalline cohomology with logarithmic poles , Astérisque (1994), 221–268; Périodes $p$ -adiques (Bures-sur-Yvette, 1988).Google Scholar
Illusie, L., Complexe de de Rham–Witt et cohomologie cristalline , Ann. Sci. École Norm. Supér. (4) 12 (1979), 501–661, http://www.numdam.org/item?id=ASENS_1979_4_12_4_501_0.Google Scholar
Kato, K., Logarithmic structures of Fontaine–Illusie , inAlgebraic analysis geometry number theory, 191–224. (Johns Hopkins University Press, 1989).Google Scholar
Kato, K., The explicit reciprocity law and the cohomology of Fontaine–Messing , Bull. Soc. Math. France 119 (1991), 397–441, http://www.numdam.org/item?id=BSMF_1991_119_4_397_0.10.24033/bsmf.2173Google Scholar
Kedlaya, K. S., Descent theorems for overconvergent $F$ -crystals, PhD thesis, Massachusetts Institute of Technology (2000).Google Scholar
Kedlaya, K. S., Full faithfulness for overconvergent F-isocrystals , in Geometric aspects of Dwork theory, Vols I, II (Walter de Gruyter, Berlin, 2004), 819–835.Google Scholar
Kedlaya, K. S., Semistable reduction for overconvergent F-isocrystals I: Unipotence and logarithmic extensions , Compositio Math. 143 (2007), 1164–1212, doi:10.1112/S0010437X07002886.Google Scholar
Lazda, C. and Pál, A., Rigid cohomology over Laurent series fields, Algebra and Applications, vol. 21 (Springer, Cham, 2016).Google Scholar
Langer, A. and Zink, T., De Rham–Witt cohomology for a proper and smooth morphism , J. Inst. Math. Jussieu 3 (2004), 231–314, doi:10.1017/S1474748004000088.Google Scholar
Langer, A. and Zink, T., Gauß–Manin connection via Witt-differentials , Nagoya Math. J. 179 (2005), 1–16, http://projecteuclid.org/euclid.nmj/112851845.Google Scholar
Matsuue, H., On relative and overconvergent de Rham–Witt cohomology for log schemes , Math. Z. 286 (2017), 19–87, doi:10.1007/s00209-016-1755-1.Google Scholar
Messing, W., The crystals associated to Barsotti–Tate groups: with applications to abelian schemes , Lecture Notes in Mathematics, vol. 264 (Springer, Berlin, 1972).Google Scholar
Morrow, M., A variational Tate conjecture in crystalline cohomology, J. Eur. Math. Soc. (JEMS), to appear. Preprint (2014), arXiv:1408.6783.Google Scholar
Morrow, M., $K$ -theory and logarithmic Hodge–Witt sheaves of formal schemes in characteristic  $p$ , Ann. Sci. Éc. Norm. Supér., to appear. Preprint (2015), arXiv:1512.04703.Google Scholar
Matsuda, S. and Trihan, F., Image directe supérieure et unipotence , J. Reine Angew. Math. 469 (2004), 47–54, doi:10.1515/crll.2004.028.Google Scholar
Pál, A., The $p$ -adic monodromy group of abelian varieties over global function fields in charcateristic $p$ , Preprint (2015), arXiv:1512.03587.Google Scholar
Petrequin, D., Classes de Chern et classes de cycles en cohomologie rigide , Bull. Soc. Math. France 131 (2003), 59–121, http://eudml.org/doc/272359.Google Scholar
Popescu, D., General Néron desingularization and approximation , Nagoya Math. J. 104 (1986), 85–115, http://projecteuclid.org/euclid.nmj/1118780554.Google Scholar
Silverman, J. H., The arithmetic of elliptic curves, Graduate Texts in Mathematics, vol. 106 (Springer, New York, 1986).Google Scholar
Tsuzuki, N., Slope filtration of quasi-unipotent overconvergent F-isocrystals , Ann. Inst. Fourier, Grenoble 48 (1998), 379–412, http://www.numdam.org/item?id=AIF_1998_48_2_379_0.Google Scholar
Yamashita, G., The p-adic Lefschetz (1, 1) theorem in the semistable case, and the Picard number jumping locus , Math. Res. Lett. 18 (2011), 107–124, doi:10.4310/MRL.2011.v18.n1.a8.Google Scholar