Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-24T20:16:49.919Z Has data issue: false hasContentIssue false
  • English
  • Français

Group schemes and local densities of quadratic lattices in residue characteristic 2

Part of: Linear algebraic groups and related topics Algebraic groups Forms and linear algebraic groups

Published online by Cambridge University Press:  05 December 2014

Sungmun Cho
Sungmun Cho*
Affiliation:
Department of Mathematics, Purdue University, West Lafayette, IN 47907, USA email sungmuncho12@gmail.com Current address: Department of Mathematics, University of Toronto, Toronto, ON M5S 2E4, Canada
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The celebrated Smith–Minkowski–Siegel mass formula expresses the mass of a quadratic lattice 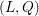$(L,Q)$ as a product of local factors, called the local densities of 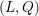$(L,Q)$. This mass formula is an essential tool for the classification of integral quadratic lattices. In this paper, we will describe the local density formula explicitly by observing the existence of a smooth affine group scheme 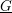$\underline{G}$ over 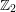$\mathbb{Z}_{2}$ with generic fiber 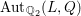$\text{Aut}_{\mathbb{Q}_{2}}(L,Q)$, which satisfies 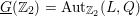$\underline{G}(\mathbb{Z}_{2})=\text{Aut}_{\mathbb{Z}_{2}}(L,Q)$. Our method works for any unramified finite extension of 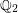$\mathbb{Q}_{2}$. Therefore, we give a long awaited proof for the local density formula of Conway and Sloane and discover its generalization to unramified finite extensions of 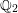$\mathbb{Q}_{2}$. As an example, we give the mass formula for the integral quadratic form 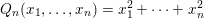$Q_{n}(x_{1},\dots ,x_{n})=x_{1}^{2}+\cdots +x_{n}^{2}$ associated to a number field 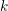$k$ which is totally real and such that the ideal 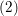$(2)$ is unramified over 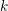$k$.

Keywords

local densitiesmass formulagroup schemessmooth integral models

MSC classification

Primary: 11E41: Class numbers of quadratic and Hermitian forms 11E95: $p$-adic theory 14L15: Group schemes 20G25: Linear algebraic groups over local fields and their integers
Secondary: 11E12: Quadratic forms over global rings and fields 11E57: Classical groups
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 5 , May 2015 , pp. 793 - 827
Copyright
© The Author 2014 

References

Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron models, Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 21 (Springer, Berlin, 1990).CrossRefGoogle Scholar
Conway, J. H. and Sloane, J. A., Low-dimensional lattices, IV: the mass formula, Proc. R. Soc. Lond. Ser. A 419 (1988), 259–286.Google Scholar
Gan, W. T. and Yu, J.-K., Group schemes and local densities, Duke Math. J. 105 (2000), 497–524.CrossRefGoogle Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, New York, 1977).CrossRefGoogle Scholar
Kitaoka, Y., Arithmetic of quadratic forms, Cambridge Tracts in Mathematics, vol. 106 (Cambridge University Press, Cambridge, 1993).CrossRefGoogle Scholar
Knus, M.-A., Merkurjev, A., Rost, M. and Tignol, J.-P., The book of involutions, Colloquium Publications, vol. 44 (American Mathematical Society, Providence, RI, 1998).CrossRefGoogle Scholar
Neukirch, J., Algebraic number theory, Grundlehren der mathematischen Wissenschaften, vol. 322 (Springer, Berlin, 1999).CrossRefGoogle Scholar
O’Meara, O. T., Quadratic forms over local fields, Amer. J. Math. 77 (1955), 87–116.CrossRefGoogle Scholar
O’Meara, O. T., Introduction to quadratic forms, Classics in Mathematics (Springer, Berlin, 2000), reprint of 1973 edition.Google Scholar
Pall, G., The weight of a genus of positive n-ary quadratic forms, Proceedings of Symposia in Pure Mathematics, vol. 8 (American Mathematical Society, Providence, RI, 1965), 95–105.Google Scholar
Sato, F. and Hironaka, Y., Local densities of representations of quadratic forms over p-adic integers (the non-dyadic case), J. Number Theory 83 (2000), 106–136.CrossRefGoogle Scholar
Watson, G. L., The 2-adic density of a quadratic form, Mathematika 23 (1976), 94–106.CrossRefGoogle Scholar