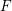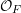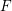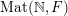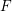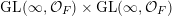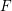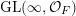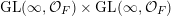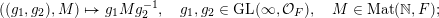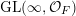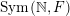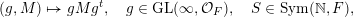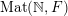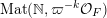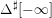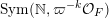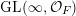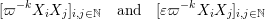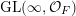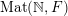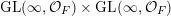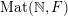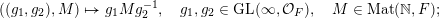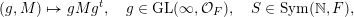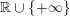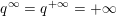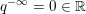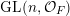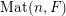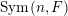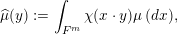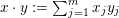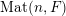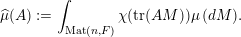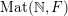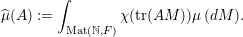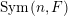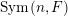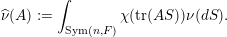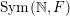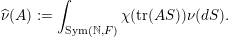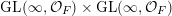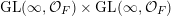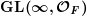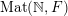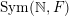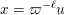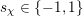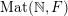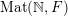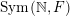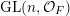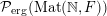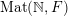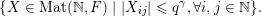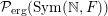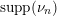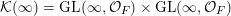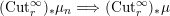1 Introduction
Given a group action on a topological space, it is natural to try to describe the corresponding space of ergodic invariant probability measures. For some very classical actions, such as, for example, that of the shift on the space of infinite binary sequences, the space of ergodic measures is huge and does not seem to admit a reasonable description. On the other hand, for a number of natural actions of infinite-dimensional groups, a complete classification is possible. For example, De Finetti’s Theorem (1937) claims that for the action of the infinite symmetric group on the space of infinite binary sequences, all ergodic probability measures are Bernoulli, and Schoenberg’s Theorem (1951) claims that for the action of the infinite orthogonal group on the space of infinite
![]() $\mathbb{R}$
-valued sequences, all ergodic probability measures are Gaussian. In both these examples, the space of ergodic probability measures is one dimensional. Pickrell [Reference PickrellPic87, Reference PickrellPic90, Reference PickrellPic91] and, by a different method, Olshanski and Vershik [Reference Olshanski and VershikOV96], classified all ergodic unitarily invariant measures on the space of infinite Hermitian matrices. In this case, an ergodic measure is determined by infinitely many parameters.
$\mathbb{R}$
-valued sequences, all ergodic probability measures are Gaussian. In both these examples, the space of ergodic probability measures is one dimensional. Pickrell [Reference PickrellPic87, Reference PickrellPic90, Reference PickrellPic91] and, by a different method, Olshanski and Vershik [Reference Olshanski and VershikOV96], classified all ergodic unitarily invariant measures on the space of infinite Hermitian matrices. In this case, an ergodic measure is determined by infinitely many parameters.
In this paper, we study classification of ergodic measures for actions related to the following inductive limit group
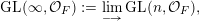 $$\begin{eqnarray}\displaystyle \operatorname{GL}(\infty ,{\mathcal{O}}_{F}):=\lim _{\longrightarrow }\operatorname{GL}(n,{\mathcal{O}}_{F}), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{GL}(\infty ,{\mathcal{O}}_{F}):=\lim _{\longrightarrow }\operatorname{GL}(n,{\mathcal{O}}_{F}), & & \displaystyle\end{eqnarray}$$
where
![]() ${\mathcal{O}}_{F}$
is the ring of integers in a non-discrete locally compact non-Archimedean field
${\mathcal{O}}_{F}$
is the ring of integers in a non-discrete locally compact non-Archimedean field
![]() $F$
and
$F$
and
 $\operatorname{GL}(n,{\mathcal{O}}_{F})$
is the compact group of invertible
$\operatorname{GL}(n,{\mathcal{O}}_{F})$
is the compact group of invertible
![]() $n\times n$
matrices over
$n\times n$
matrices over
![]() ${\mathcal{O}}_{F}$
. Denote by
${\mathcal{O}}_{F}$
. Denote by
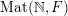 $\operatorname{Mat}(\mathbb{N},F)$
(respectively
$\operatorname{Mat}(\mathbb{N},F)$
(respectively
 $\operatorname{Sym}(\mathbb{N},F)$
) the space of infinite matrices (respectively infinite symmetric matrices) over
$\operatorname{Sym}(\mathbb{N},F)$
) the space of infinite matrices (respectively infinite symmetric matrices) over
![]() $F$
. Our main results are:
$F$
. Our main results are:
-
(i) the classification of the ergodic probability measures for the group action of
 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
on
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
on
 $\operatorname{Mat}(\mathbb{N},F)$
defined by
$\operatorname{Mat}(\mathbb{N},F)$
defined by  $$\begin{eqnarray}\displaystyle ((g_{1},g_{2}),M)\mapsto g_{1}Mg_{2}^{-1},\quad g_{1},g_{2}\in \operatorname{GL}(\infty ,{\mathcal{O}}_{F}),\quad M\in \operatorname{Mat}(\mathbb{N},F); & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle ((g_{1},g_{2}),M)\mapsto g_{1}Mg_{2}^{-1},\quad g_{1},g_{2}\in \operatorname{GL}(\infty ,{\mathcal{O}}_{F}),\quad M\in \operatorname{Mat}(\mathbb{N},F); & & \displaystyle \nonumber\end{eqnarray}$$
-
(ii) the classification of the ergodic probability measures for the group action of
 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
on
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
on
 $\operatorname{Sym}(\mathbb{N},F)$
defined by where
$\operatorname{Sym}(\mathbb{N},F)$
defined by where $$\begin{eqnarray}\displaystyle (g,M)\mapsto gMg^{t},\quad g\in \operatorname{GL}(\infty ,{\mathcal{O}}_{F}),\quad S\in \operatorname{Sym}(\mathbb{N},F), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (g,M)\mapsto gMg^{t},\quad g\in \operatorname{GL}(\infty ,{\mathcal{O}}_{F}),\quad S\in \operatorname{Sym}(\mathbb{N},F), & & \displaystyle \nonumber\end{eqnarray}$$
 $g^{t}$
is the transposition of
$g^{t}$
is the transposition of
 $g$
.
$g$
.
We proceed to the precise formulation. Let
![]() $F$
be a non-discrete locally compact non-Archimedean field (for example, the field of
$F$
be a non-discrete locally compact non-Archimedean field (for example, the field of
![]() $p$
-adic numbers). Let
$p$
-adic numbers). Let
![]() $|\cdot |$
be the absolute value on
$|\cdot |$
be the absolute value on
![]() $F$
. The ring
$F$
. The ring
![]() ${\mathcal{O}}_{F}$
of integers in
${\mathcal{O}}_{F}$
of integers in
![]() $F$
is given by
$F$
is given by
 $\{x\in F:|x|\leqslant 1\}$
. The unique maximal and principal ideal of
$\{x\in F:|x|\leqslant 1\}$
. The unique maximal and principal ideal of
![]() ${\mathcal{O}}_{F}$
is given by
${\mathcal{O}}_{F}$
is given by
 $\{x\in F:|x|<1\}$
. Throughout the paper, we fix any generator
$\{x\in F:|x|<1\}$
. Throughout the paper, we fix any generator
![]() $\unicode[STIX]{x1D71B}$
of
$\unicode[STIX]{x1D71B}$
of
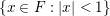 $\{x\in F:|x|<1\}$
, that is,
$\{x\in F:|x|<1\}$
, that is,
 $\{x\in F:|x|<1\}=\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
. The quotient
$\{x\in F:|x|<1\}=\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
. The quotient
 ${\mathcal{O}}_{F}/\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
is a finite field with
${\mathcal{O}}_{F}/\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
is a finite field with
![]() $q$
elements.
$q$
elements.
Define the inductively compact group
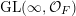 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
by (1). Set
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
by (1). Set
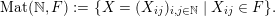 $$\begin{eqnarray}\displaystyle \operatorname{Mat}(\mathbb{N},F):=\{X=(X_{ij})_{i,j\in \mathbb{N}}\mid X_{ij}\in F\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Mat}(\mathbb{N},F):=\{X=(X_{ij})_{i,j\in \mathbb{N}}\mid X_{ij}\in F\}. & & \displaystyle \nonumber\end{eqnarray}$$
Let
 $\operatorname{Mat}(\infty ,F)$
denote the subspace of
$\operatorname{Mat}(\infty ,F)$
denote the subspace of
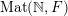 $\operatorname{Mat}(\mathbb{N},F)$
consisting of matrices whose all but a finite number of coefficients are zero. Define also
$\operatorname{Mat}(\mathbb{N},F)$
consisting of matrices whose all but a finite number of coefficients are zero. Define also
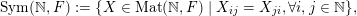 $$\begin{eqnarray}\displaystyle \operatorname{Sym}(\mathbb{N},F):=\{X\in \operatorname{Mat}(\mathbb{N},F)\mid X_{ij}=X_{ji},\forall i,j\in \mathbb{N}\}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Sym}(\mathbb{N},F):=\{X\in \operatorname{Mat}(\mathbb{N},F)\mid X_{ij}=X_{ji},\forall i,j\in \mathbb{N}\}, & & \displaystyle \nonumber\end{eqnarray}$$
and let
 $\operatorname{Sym}(\infty ,F):=\operatorname{Sym}(\mathbb{N},F)\cap \operatorname{Mat}(\infty ,F)$
.
$\operatorname{Sym}(\infty ,F):=\operatorname{Sym}(\mathbb{N},F)\cap \operatorname{Mat}(\infty ,F)$
.
Throughout the paper, by the usual identification
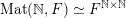 $\operatorname{Mat}(\mathbb{N},F)\simeq F^{\mathbb{N}\times \mathbb{N}}$
, we equip
$\operatorname{Mat}(\mathbb{N},F)\simeq F^{\mathbb{N}\times \mathbb{N}}$
, we equip
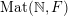 $\operatorname{Mat}(\mathbb{N},F)$
with the Tychonoff’s product topology. The set
$\operatorname{Mat}(\mathbb{N},F)$
with the Tychonoff’s product topology. The set
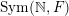 $\operatorname{Sym}(\mathbb{N},F)$
is equipped with the induced topology by the natural embedding
$\operatorname{Sym}(\mathbb{N},F)$
is equipped with the induced topology by the natural embedding
 $\operatorname{Sym}(\mathbb{N},F)\subset \operatorname{Mat}(\mathbb{N},F)$
.
$\operatorname{Sym}(\mathbb{N},F)\subset \operatorname{Mat}(\mathbb{N},F)$
.
1.1 Classification of ergodic measures on
 $\operatorname{Mat}(\mathbb{N},F)$
$\operatorname{Mat}(\mathbb{N},F)$
Let
![]() $\unicode[STIX]{x1D6E5}$
be the set of non-increasing sequences in
$\unicode[STIX]{x1D6E5}$
be the set of non-increasing sequences in
 $\mathbb{Z}\cup \{-\infty \}$
, that is,
$\mathbb{Z}\cup \{-\infty \}$
, that is,
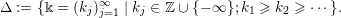 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}:=\{\Bbbk =(k_{j})_{j=1}^{\infty }\mid k_{j}\in \mathbb{Z}\cup \{-\infty \};k_{1}\geqslant k_{2}\geqslant \cdots \,\}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}:=\{\Bbbk =(k_{j})_{j=1}^{\infty }\mid k_{j}\in \mathbb{Z}\cup \{-\infty \};k_{1}\geqslant k_{2}\geqslant \cdots \,\}. & & \displaystyle\end{eqnarray}$$
By the inclusion
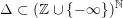 $\unicode[STIX]{x1D6E5}\subset (\mathbb{Z}\cup \{-\infty \})^{\mathbb{N}}$
, we equip
$\unicode[STIX]{x1D6E5}\subset (\mathbb{Z}\cup \{-\infty \})^{\mathbb{N}}$
, we equip
![]() $\unicode[STIX]{x1D6E5}$
with the induced topology of the Tychonoff’s product topology on
$\unicode[STIX]{x1D6E5}$
with the induced topology of the Tychonoff’s product topology on
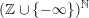 $(\mathbb{Z}\cup \{-\infty \})^{\mathbb{N}}$
.
$(\mathbb{Z}\cup \{-\infty \})^{\mathbb{N}}$
.
To each sequence
![]() $\Bbbk \in \unicode[STIX]{x1D6E5}$
, we now assign an ergodic
$\Bbbk \in \unicode[STIX]{x1D6E5}$
, we now assign an ergodic
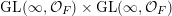 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measure on
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measure on
 $\operatorname{Mat}(\mathbb{N},F)$
. Let
$\operatorname{Mat}(\mathbb{N},F)$
. Let
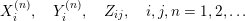 $$\begin{eqnarray}\displaystyle X_{i}^{(n)},\quad Y_{i}^{(n)},\quad Z_{ij},\quad i,j,n=1,2,\ldots & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X_{i}^{(n)},\quad Y_{i}^{(n)},\quad Z_{ij},\quad i,j,n=1,2,\ldots & & \displaystyle \nonumber\end{eqnarray}$$
be independent random variables, each sampled with respect to the normalized Haar measure on the compact additive group
![]() ${\mathcal{O}}_{F}$
. In what follows, we use the convention
${\mathcal{O}}_{F}$
. In what follows, we use the convention
 $\unicode[STIX]{x1D71B}^{\infty }=0$
.
$\unicode[STIX]{x1D71B}^{\infty }=0$
.
Definition 1.1. Given an element
![]() $\Bbbk \in \unicode[STIX]{x1D6E5}$
, let
$\Bbbk \in \unicode[STIX]{x1D6E5}$
, let
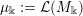 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}_{\Bbbk }:={\mathcal{L}}(M_{\Bbbk }) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}_{\Bbbk }:={\mathcal{L}}(M_{\Bbbk }) & & \displaystyle \nonumber\end{eqnarray}$$
be the probability distribution of the infinite random matrix
![]() $M_{\Bbbk }$
defined as follows. Write
$M_{\Bbbk }$
defined as follows. Write
 $k:=\lim _{n\rightarrow \infty }k_{n}\in \mathbb{Z}\cup \{-\infty \}$
and set
$k:=\lim _{n\rightarrow \infty }k_{n}\in \mathbb{Z}\cup \{-\infty \}$
and set
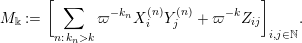 $$\begin{eqnarray}\displaystyle M_{\Bbbk }:=\biggl[\mathop{\sum }_{n:\,k_{n}>k}\unicode[STIX]{x1D71B}^{-k_{n}}X_{i}^{(n)}Y_{j}^{(n)}+\unicode[STIX]{x1D71B}^{-k}Z_{ij}\biggr]_{i,j\in \mathbb{N}}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{\Bbbk }:=\biggl[\mathop{\sum }_{n:\,k_{n}>k}\unicode[STIX]{x1D71B}^{-k_{n}}X_{i}^{(n)}Y_{j}^{(n)}+\unicode[STIX]{x1D71B}^{-k}Z_{ij}\biggr]_{i,j\in \mathbb{N}}. & & \displaystyle \nonumber\end{eqnarray}$$
Remark 1.2. For the constant sequence
 $\Bbbk =(-\infty ,\ldots ,-\infty ,\ldots )\in \unicode[STIX]{x1D6E5}$
, using the convention
$\Bbbk =(-\infty ,\ldots ,-\infty ,\ldots )\in \unicode[STIX]{x1D6E5}$
, using the convention
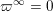 $\unicode[STIX]{x1D71B}^{\infty }=0$
, the corresponding matrix
$\unicode[STIX]{x1D71B}^{\infty }=0$
, the corresponding matrix
![]() $M_{\Bbbk }$
defined in Definition 1.1 is the zero matrix
$M_{\Bbbk }$
defined in Definition 1.1 is the zero matrix
 $O\in \operatorname{Mat}(\mathbb{N},F)$
and hence the measure
$O\in \operatorname{Mat}(\mathbb{N},F)$
and hence the measure
![]() $\unicode[STIX]{x1D707}_{\Bbbk }$
is the Dirac measure at the point
$\unicode[STIX]{x1D707}_{\Bbbk }$
is the Dirac measure at the point
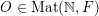 $O\in \operatorname{Mat}(\mathbb{N},F)$
.
$O\in \operatorname{Mat}(\mathbb{N},F)$
.
Let
 ${\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
be the space of ergodic
${\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
be the space of ergodic
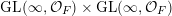 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measures on
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measures on
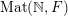 $\operatorname{Mat}(\mathbb{N},F)$
, endowed with the induced weak topology. The classification of
$\operatorname{Mat}(\mathbb{N},F)$
, endowed with the induced weak topology. The classification of
 ${\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
is given by the following.
${\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
is given by the following.
Theorem 1.3. The map
![]() $\Bbbk \mapsto \unicode[STIX]{x1D707}_{\Bbbk }$
is a homeomorphism between
$\Bbbk \mapsto \unicode[STIX]{x1D707}_{\Bbbk }$
is a homeomorphism between
![]() $\unicode[STIX]{x1D6E5}$
and
$\unicode[STIX]{x1D6E5}$
and
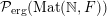 ${\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
.
${\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
.
Remark 1.4. By Theorem 1.3, the space
 ${\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
is weakly closed in the space of all Borel measures on
${\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
is weakly closed in the space of all Borel measures on
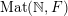 $\operatorname{Mat}(\mathbb{N},F)$
and is
$\operatorname{Mat}(\mathbb{N},F)$
and is
![]() $\unicode[STIX]{x1D70E}$
-compact; moreover, any measure
$\unicode[STIX]{x1D70E}$
-compact; moreover, any measure
 $\unicode[STIX]{x1D707}_{\Bbbk }\in {\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
is compactly supported.
$\unicode[STIX]{x1D707}_{\Bbbk }\in {\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
is compactly supported.
Let us explain Theorem 1.3 in more detail. We have the following elementary ergodic measures.
-
– (Haar type measures) For any
 $k\in \mathbb{Z}$
, the normalized Haar measure on
$k\in \mathbb{Z}$
, the normalized Haar measure on
 $\operatorname{Mat}(\mathbb{N},\unicode[STIX]{x1D71B}^{-k}{\mathcal{O}}_{F})$
is
$\operatorname{Mat}(\mathbb{N},\unicode[STIX]{x1D71B}^{-k}{\mathcal{O}}_{F})$
is
 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-ergodic.
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-ergodic. -
– (Non-symmetric Wishart type measures) Let
 $X_{1},Y_{1},X_{2},Y_{2},\ldots$
be independent and uniformly distributed on
$X_{1},Y_{1},X_{2},Y_{2},\ldots$
be independent and uniformly distributed on
 ${\mathcal{O}}_{F}$
. For any
${\mathcal{O}}_{F}$
. For any
 $k\in \mathbb{Z}$
, the probability distribution of the random matrix is
$k\in \mathbb{Z}$
, the probability distribution of the random matrix is $$\begin{eqnarray}\displaystyle [\unicode[STIX]{x1D71B}^{-k}X_{i}Y_{j}]_{i,j\in \mathbb{N}} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle [\unicode[STIX]{x1D71B}^{-k}X_{i}Y_{j}]_{i,j\in \mathbb{N}} & & \displaystyle \nonumber\end{eqnarray}$$
 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-ergodic.
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-ergodic.
Theorem 1.3 implies that any ergodic
 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measure on
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measure on
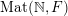 $\operatorname{Mat}(\mathbb{N},F)$
can be obtained as a possibly infinite convolution of the above two types of elementary ones.
$\operatorname{Mat}(\mathbb{N},F)$
can be obtained as a possibly infinite convolution of the above two types of elementary ones.
1.2 Classification of ergodic measures on
 $\operatorname{Sym}(\mathbb{N},F)$
$\operatorname{Sym}(\mathbb{N},F)$
In what follows, when dealing with the ergodic measures on
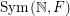 $\operatorname{Sym}(\mathbb{N},F)$
, we always assume that the field
$\operatorname{Sym}(\mathbb{N},F)$
, we always assume that the field
![]() $F$
is non-dyadic, that is, the cardinality of the field of residue class
$F$
is non-dyadic, that is, the cardinality of the field of residue class
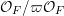 ${\mathcal{O}}_{F}/\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
is not a power of 2.
${\mathcal{O}}_{F}/\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
is not a power of 2.
The group of units of
![]() ${\mathcal{O}}_{F}$
is given by
${\mathcal{O}}_{F}$
is given by
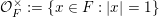 ${\mathcal{O}}_{F}^{\times }:=\{x\in F:|x|=1\}$
. Denote by
${\mathcal{O}}_{F}^{\times }:=\{x\in F:|x|=1\}$
. Denote by
![]() $({\mathcal{O}}_{F}^{\times })^{2}$
the subgroup of
$({\mathcal{O}}_{F}^{\times })^{2}$
the subgroup of
![]() ${\mathcal{O}}_{F}^{\times }$
defined by
${\mathcal{O}}_{F}^{\times }$
defined by
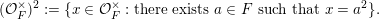 $$\begin{eqnarray}\displaystyle ({\mathcal{O}}_{F}^{\times })^{2}:=\{x\in {\mathcal{O}}_{F}^{\times }:\text{there exists }a\in F\text{ such that }x=a^{2}\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle ({\mathcal{O}}_{F}^{\times })^{2}:=\{x\in {\mathcal{O}}_{F}^{\times }:\text{there exists }a\in F\text{ such that }x=a^{2}\}. & & \displaystyle \nonumber\end{eqnarray}$$
If
![]() $F$
is non-dyadic, then the quotient
$F$
is non-dyadic, then the quotient
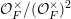 ${\mathcal{O}}_{F}^{\times }/({\mathcal{O}}_{F}^{\times })^{2}$
has two elements. Throughout the paper, we fix a non-square unit
${\mathcal{O}}_{F}^{\times }/({\mathcal{O}}_{F}^{\times })^{2}$
has two elements. Throughout the paper, we fix a non-square unit
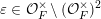 $\unicode[STIX]{x1D700}\in {\mathcal{O}}_{F}^{\times }\,\setminus \,({\mathcal{O}}_{F}^{\times })^{2}$
.
$\unicode[STIX]{x1D700}\in {\mathcal{O}}_{F}^{\times }\,\setminus \,({\mathcal{O}}_{F}^{\times })^{2}$
.
We now explicitly describe the parametrization of ergodic
 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measures on
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measures on
 $\operatorname{Sym}(\mathbb{N},F)$
.
$\operatorname{Sym}(\mathbb{N},F)$
.
Recall the definition (2) of the set
![]() $\unicode[STIX]{x1D6E5}$
of non-increasing sequences in
$\unicode[STIX]{x1D6E5}$
of non-increasing sequences in
 $\mathbb{Z}\cup \{-\infty \}$
. A sequence
$\mathbb{Z}\cup \{-\infty \}$
. A sequence
 $(k_{j})_{j\in \mathbb{N}}\in \unicode[STIX]{x1D6E5}$
is called finite if
$(k_{j})_{j\in \mathbb{N}}\in \unicode[STIX]{x1D6E5}$
is called finite if
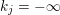 $k_{j}=-\infty$
for all sufficiently large
$k_{j}=-\infty$
for all sufficiently large
![]() $j$
. In this case, either
$j$
. In this case, either
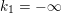 $k_{1}=-\infty$
, and then we identity the sequence with an empty sequence, or
$k_{1}=-\infty$
, and then we identity the sequence with an empty sequence, or
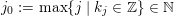 $j_{0}:=\max \{j\mid k_{j}\in \mathbb{Z}\}\in \mathbb{N}$
, and then we identify
$j_{0}:=\max \{j\mid k_{j}\in \mathbb{Z}\}\in \mathbb{N}$
, and then we identify
![]() $(k_{j})_{j\in \mathbb{N}}$
with
$(k_{j})_{j\in \mathbb{N}}$
with
![]() $(k_{j})_{j=1}^{j_{0}}$
and
$(k_{j})_{j=1}^{j_{0}}$
and
![]() $j_{0}$
is called the length of the sequence. Conversely, for any finite non-increasing sequence
$j_{0}$
is called the length of the sequence. Conversely, for any finite non-increasing sequence
![]() $(k_{j})_{j=1}^{n}$
in
$(k_{j})_{j=1}^{n}$
in
![]() $\mathbb{Z}$
, we identify it with the element in
$\mathbb{Z}$
, we identify it with the element in
![]() $\unicode[STIX]{x1D6E5}$
by adding infinitely many
$\unicode[STIX]{x1D6E5}$
by adding infinitely many
![]() $-\infty$
at the end of
$-\infty$
at the end of
![]() $(k_{j})_{j=1}^{n}$
.
$(k_{j})_{j=1}^{n}$
.
For any
![]() $k\in \mathbb{Z}$
, let
$k\in \mathbb{Z}$
, let
![]() $\mathbb{Z}_{{>}k}$
denote the set of integers strictly larger than
$\mathbb{Z}_{{>}k}$
denote the set of integers strictly larger than
![]() $k$
. We introduce the following four subsets of
$k$
. We introduce the following four subsets of
![]() $\unicode[STIX]{x1D6E5}$
:
$\unicode[STIX]{x1D6E5}$
:
-
–
 $\unicode[STIX]{x1D6E5}[k]$
, the set of non-increasing sequences of finite length in
$\unicode[STIX]{x1D6E5}[k]$
, the set of non-increasing sequences of finite length in
 $\mathbb{Z}_{{>}k}$
;
$\mathbb{Z}_{{>}k}$
; -
–
 $\unicode[STIX]{x1D6E5}^{\sharp }[k]$
, the set of strictly decreasing sequences in
$\unicode[STIX]{x1D6E5}^{\sharp }[k]$
, the set of strictly decreasing sequences in
 $\mathbb{Z}_{{>}k}$
(which are automatically of finite length);
$\mathbb{Z}_{{>}k}$
(which are automatically of finite length); -
–
 $\unicode[STIX]{x1D6E5}[-\infty ]$
, the set of non-increasing sequences in
$\unicode[STIX]{x1D6E5}[-\infty ]$
, the set of non-increasing sequences in
 $\mathbb{Z}$
of finite length or of infinite length tending to
$\mathbb{Z}$
of finite length or of infinite length tending to
 $-\infty$
;
$-\infty$
; -
–
 $\unicode[STIX]{x1D6E5}^{\sharp }[-\infty ]$
, the set of strictly decreasing sequences of finite or infinite length in
$\unicode[STIX]{x1D6E5}^{\sharp }[-\infty ]$
, the set of strictly decreasing sequences of finite or infinite length in
 $\mathbb{Z}$
.
$\mathbb{Z}$
.
Note that for any
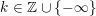 $k\in \mathbb{Z}\cup \{-\infty \}$
, the following relations hold:
$k\in \mathbb{Z}\cup \{-\infty \}$
, the following relations hold:
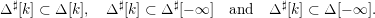 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}^{\sharp }[k]\subset \unicode[STIX]{x1D6E5}[k],\quad \unicode[STIX]{x1D6E5}^{\sharp }[k]\subset \unicode[STIX]{x1D6E5}^{\sharp }[-\infty ]\quad \text{and}\quad \unicode[STIX]{x1D6E5}^{\sharp }[k]\subset \unicode[STIX]{x1D6E5}[-\infty ]. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}^{\sharp }[k]\subset \unicode[STIX]{x1D6E5}[k],\quad \unicode[STIX]{x1D6E5}^{\sharp }[k]\subset \unicode[STIX]{x1D6E5}^{\sharp }[-\infty ]\quad \text{and}\quad \unicode[STIX]{x1D6E5}^{\sharp }[k]\subset \unicode[STIX]{x1D6E5}[-\infty ]. & & \displaystyle \nonumber\end{eqnarray}$$
We introduce the parameter space
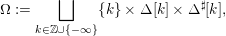 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FA}:=\bigsqcup _{k\in \mathbb{Z}\cup \{-\infty \}}\{k\}\times \unicode[STIX]{x1D6E5}[k]\times \unicode[STIX]{x1D6E5}^{\sharp }[k], & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FA}:=\bigsqcup _{k\in \mathbb{Z}\cup \{-\infty \}}\{k\}\times \unicode[STIX]{x1D6E5}[k]\times \unicode[STIX]{x1D6E5}^{\sharp }[k], & & \displaystyle\end{eqnarray}$$
where
![]() $\{k\}$
is the singleton with a single element
$\{k\}$
is the singleton with a single element
![]() $k$
. The space
$k$
. The space
![]() $\unicode[STIX]{x1D6FA}$
is equipped with the topology induced by the inclusion:
$\unicode[STIX]{x1D6FA}$
is equipped with the topology induced by the inclusion:
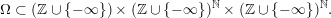 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FA}\subset (\mathbb{Z}\cup \{-\infty \})\times (\mathbb{Z}\cup \{-\infty \})^{\mathbb{N}}\times (\mathbb{Z}\cup \{-\infty \})^{\mathbb{N}}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FA}\subset (\mathbb{Z}\cup \{-\infty \})\times (\mathbb{Z}\cup \{-\infty \})^{\mathbb{N}}\times (\mathbb{Z}\cup \{-\infty \})^{\mathbb{N}}. & & \displaystyle \nonumber\end{eqnarray}$$
To each element
![]() $h\in \unicode[STIX]{x1D6FA}$
, we assign an ergodic
$h\in \unicode[STIX]{x1D6FA}$
, we assign an ergodic
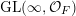 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measure on
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measure on
 $\operatorname{Sym}(\mathbb{N},F)$
as follows. Let
$\operatorname{Sym}(\mathbb{N},F)$
as follows. Let
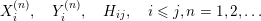 $$\begin{eqnarray}\displaystyle X_{i}^{(n)},\quad Y_{i}^{(n)},\quad H_{ij},\quad i\leqslant j,n=1,2,\ldots & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X_{i}^{(n)},\quad Y_{i}^{(n)},\quad H_{ij},\quad i\leqslant j,n=1,2,\ldots & & \displaystyle \nonumber\end{eqnarray}$$
be independent random variables uniformly distributed on
![]() ${\mathcal{O}}_{F}$
. In particular, define
${\mathcal{O}}_{F}$
. In particular, define
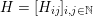 $$\begin{eqnarray}\displaystyle H=[H_{ij}]_{i,j\in \mathbb{N}} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H=[H_{ij}]_{i,j\in \mathbb{N}} & & \displaystyle\end{eqnarray}$$
by setting
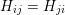 $H_{ij}=H_{ji}$
if
$H_{ij}=H_{ji}$
if
![]() $i>j$
, then
$i>j$
, then
![]() $H$
is an infinite symmetric random matrix sampled uniformly from
$H$
is an infinite symmetric random matrix sampled uniformly from
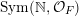 $\operatorname{Sym}(\mathbb{N},{\mathcal{O}}_{F})$
.
$\operatorname{Sym}(\mathbb{N},{\mathcal{O}}_{F})$
.
Definition 1.5. For any
![]() $h\in \unicode[STIX]{x1D6FA}$
given by
$h\in \unicode[STIX]{x1D6FA}$
given by
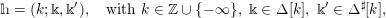 $$\begin{eqnarray}\displaystyle h=(k;\Bbbk ,\Bbbk ^{\prime }),\quad \text{with }k\in \mathbb{Z}\cup \{-\infty \},~\Bbbk \in \unicode[STIX]{x1D6E5}[k],~\Bbbk ^{\prime }\in \unicode[STIX]{x1D6E5}^{\sharp }[k], & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h=(k;\Bbbk ,\Bbbk ^{\prime }),\quad \text{with }k\in \mathbb{Z}\cup \{-\infty \},~\Bbbk \in \unicode[STIX]{x1D6E5}[k],~\Bbbk ^{\prime }\in \unicode[STIX]{x1D6E5}^{\sharp }[k], & & \displaystyle \nonumber\end{eqnarray}$$
we define
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D708}_{h}:={\mathcal{L}}(S_{h}), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D708}_{h}:={\mathcal{L}}(S_{h}), & & \displaystyle \nonumber\end{eqnarray}$$
as the probability distribution of the infinite symmetric random matrix
![]() $S_{h}$
defined as follows. First let
$S_{h}$
defined as follows. First let
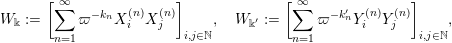 $$\begin{eqnarray}\displaystyle W_{\Bbbk }:=\mathop{\biggl[\mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D71B}^{-k_{n}}X_{i}^{(n)}X_{j}^{(n)}\biggr]}\nolimits_{i,j\in \mathbb{N}},\quad W_{\Bbbk ^{\prime }}:=\mathop{\biggl[\mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D71B}^{-k_{n}^{\prime }}Y_{i}^{(n)}Y_{j}^{(n)}\biggr]}\nolimits_{i,j\in \mathbb{N}}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle W_{\Bbbk }:=\mathop{\biggl[\mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D71B}^{-k_{n}}X_{i}^{(n)}X_{j}^{(n)}\biggr]}\nolimits_{i,j\in \mathbb{N}},\quad W_{\Bbbk ^{\prime }}:=\mathop{\biggl[\mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D71B}^{-k_{n}^{\prime }}Y_{i}^{(n)}Y_{j}^{(n)}\biggr]}\nolimits_{i,j\in \mathbb{N}}, & & \displaystyle \nonumber\end{eqnarray}$$
and then set
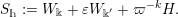 $$\begin{eqnarray}\displaystyle S_{h}:=W_{\Bbbk }+\unicode[STIX]{x1D700}W_{\Bbbk ^{\prime }}+\unicode[STIX]{x1D71B}^{-k}H. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S_{h}:=W_{\Bbbk }+\unicode[STIX]{x1D700}W_{\Bbbk ^{\prime }}+\unicode[STIX]{x1D71B}^{-k}H. & & \displaystyle \nonumber\end{eqnarray}$$
Remark 1.6. For the element
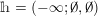 $h=(-\infty ;\emptyset ,\emptyset )$
, where
$h=(-\infty ;\emptyset ,\emptyset )$
, where
![]() $\emptyset$
means the empty sequence in
$\emptyset$
means the empty sequence in
![]() $\mathbb{Z}$
, the corresponding matrix
$\mathbb{Z}$
, the corresponding matrix
![]() $S_{h}$
defined in Definition 1.5 is the zero matrix
$S_{h}$
defined in Definition 1.5 is the zero matrix
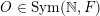 $O\in \operatorname{Sym}(\mathbb{N},F)$
and hence the measure
$O\in \operatorname{Sym}(\mathbb{N},F)$
and hence the measure
![]() $\unicode[STIX]{x1D708}_{h}$
is the Dirac measure at the point
$\unicode[STIX]{x1D708}_{h}$
is the Dirac measure at the point
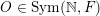 $O\in \operatorname{Sym}(\mathbb{N},F)$
.
$O\in \operatorname{Sym}(\mathbb{N},F)$
.
Remark 1.7. The strictly decreasing assumption on the sequences
 $\Bbbk ^{\prime }\in \unicode[STIX]{x1D6E5}^{\sharp }[k]$
is imposed for the uniqueness of parametrization. The reason is the following:
$\Bbbk ^{\prime }\in \unicode[STIX]{x1D6E5}^{\sharp }[k]$
is imposed for the uniqueness of parametrization. The reason is the following:
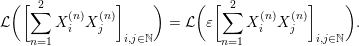 $$\begin{eqnarray}\displaystyle {\mathcal{L}}\biggl(\mathop{\biggl[\mathop{\sum }_{n=1}^{2}X_{i}^{(n)}X_{j}^{(n)}\biggr]}\nolimits_{i,j\in \mathbb{N}}\biggr)={\mathcal{L}}\biggl(\unicode[STIX]{x1D700}\mathop{\biggl[\mathop{\sum }_{n=1}^{2}X_{i}^{(n)}X_{j}^{(n)}\biggr]}\nolimits_{i,j\in \mathbb{N}}\biggr). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{L}}\biggl(\mathop{\biggl[\mathop{\sum }_{n=1}^{2}X_{i}^{(n)}X_{j}^{(n)}\biggr]}\nolimits_{i,j\in \mathbb{N}}\biggr)={\mathcal{L}}\biggl(\unicode[STIX]{x1D700}\mathop{\biggl[\mathop{\sum }_{n=1}^{2}X_{i}^{(n)}X_{j}^{(n)}\biggr]}\nolimits_{i,j\in \mathbb{N}}\biggr). & & \displaystyle\end{eqnarray}$$
For the detail, see Remark 4.8 and the proof of Proposition 5.3 below.
Let
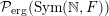 ${\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))$
be the space of ergodic
${\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))$
be the space of ergodic
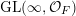 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measures on
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measures on
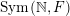 $\operatorname{Sym}(\mathbb{N},F)$
, endowed with the induced weak topology. The classification of
$\operatorname{Sym}(\mathbb{N},F)$
, endowed with the induced weak topology. The classification of
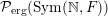 ${\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))$
is given by the following.
${\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))$
is given by the following.
Theorem 1.8. Assume that
![]() $F$
is non-dyadic. Then the map
$F$
is non-dyadic. Then the map
![]() $h\mapsto \unicode[STIX]{x1D708}_{h}$
is a homeomorphism between
$h\mapsto \unicode[STIX]{x1D708}_{h}$
is a homeomorphism between
![]() $\unicode[STIX]{x1D6FA}$
and
$\unicode[STIX]{x1D6FA}$
and
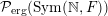 ${\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))$
.
${\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))$
.
Remark 1.9. By Theorem 1.8, the space
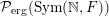 ${\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))$
is weakly closed in the space of all Borel measures on
${\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))$
is weakly closed in the space of all Borel measures on
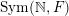 $\operatorname{Sym}(\mathbb{N},F)$
and is
$\operatorname{Sym}(\mathbb{N},F)$
and is
![]() $\unicode[STIX]{x1D70E}$
-compact. Moreover, any measure
$\unicode[STIX]{x1D70E}$
-compact. Moreover, any measure
 $\unicode[STIX]{x1D708}_{h}\in {\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))$
is compactly supported.
$\unicode[STIX]{x1D708}_{h}\in {\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))$
is compactly supported.
Theorem 1.8 can be explained as follows. We have the following elementary ergodic measures.
-
– (Haar type measures) For any
 $k\in \mathbb{Z}$
, the normalized Haar measure on
$k\in \mathbb{Z}$
, the normalized Haar measure on
 $\operatorname{Sym}(\mathbb{N},\unicode[STIX]{x1D71B}^{-k}{\mathcal{O}}_{F})$
is
$\operatorname{Sym}(\mathbb{N},\unicode[STIX]{x1D71B}^{-k}{\mathcal{O}}_{F})$
is
 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-ergodic.
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-ergodic. -
– (Symmetric Wishart type measures) Let
 $X_{1},X_{2},\ldots$
be independent copies of
$X_{1},X_{2},\ldots$
be independent copies of
 $F$
-valued random variables, all of which are uniformly distributed on
$F$
-valued random variables, all of which are uniformly distributed on
 ${\mathcal{O}}_{F}$
. For any
${\mathcal{O}}_{F}$
. For any
 $k\in \mathbb{Z}$
, the distributions of the infinite rank-one random matrices are
$k\in \mathbb{Z}$
, the distributions of the infinite rank-one random matrices are $$\begin{eqnarray}[\unicode[STIX]{x1D71B}^{-k}X_{i}X_{j}]_{i,j\in \mathbb{N}}\quad \text{and}\quad [\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-k}X_{i}X_{j}]_{i,j\in \mathbb{N}}\end{eqnarray}$$
$$\begin{eqnarray}[\unicode[STIX]{x1D71B}^{-k}X_{i}X_{j}]_{i,j\in \mathbb{N}}\quad \text{and}\quad [\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-k}X_{i}X_{j}]_{i,j\in \mathbb{N}}\end{eqnarray}$$
 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-ergodic.
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-ergodic.
Theorem 1.8 implies that any ergodic
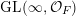 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measure on
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measure on
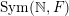 $\operatorname{Sym}(\mathbb{N},F)$
can be obtained as a possibly infinite convolution of the above two types of elementary ones.
$\operatorname{Sym}(\mathbb{N},F)$
can be obtained as a possibly infinite convolution of the above two types of elementary ones.
1.3 Characteristic functions of ergodic measures
Let
![]() $\unicode[STIX]{x1D712}\in \widehat{F}$
be a fixed character of
$\unicode[STIX]{x1D712}\in \widehat{F}$
be a fixed character of
![]() $F$
such that
$F$
such that
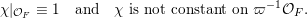 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}|_{{\mathcal{O}}_{F}}\equiv 1\quad \text{and}\quad \unicode[STIX]{x1D712}\text{ is not constant on }\unicode[STIX]{x1D71B}^{-1}{\mathcal{O}}_{F}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}|_{{\mathcal{O}}_{F}}\equiv 1\quad \text{and}\quad \unicode[STIX]{x1D712}\text{ is not constant on }\unicode[STIX]{x1D71B}^{-1}{\mathcal{O}}_{F}. & & \displaystyle\end{eqnarray}$$
Given a Borel probability measure
![]() $\unicode[STIX]{x1D707}$
on
$\unicode[STIX]{x1D707}$
on
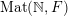 $\operatorname{Mat}(\mathbb{N},F)$
, its characteristic function, or Fourier transform,
$\operatorname{Mat}(\mathbb{N},F)$
, its characteristic function, or Fourier transform,
![]() $\widehat{\unicode[STIX]{x1D707}}$
is defined on
$\widehat{\unicode[STIX]{x1D707}}$
is defined on
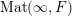 $\operatorname{Mat}(\infty ,F)$
by the formula
$\operatorname{Mat}(\infty ,F)$
by the formula
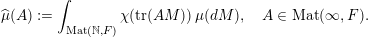 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}}(A):=\int _{\operatorname{Mat}(\mathbb{N},F)}\unicode[STIX]{x1D712}(\operatorname{tr}(AM))\,\unicode[STIX]{x1D707}(dM),\quad A\in \operatorname{Mat}(\infty ,F). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}}(A):=\int _{\operatorname{Mat}(\mathbb{N},F)}\unicode[STIX]{x1D712}(\operatorname{tr}(AM))\,\unicode[STIX]{x1D707}(dM),\quad A\in \operatorname{Mat}(\infty ,F). & & \displaystyle \nonumber\end{eqnarray}$$
Similarly, given a Borel probability measure
![]() $\unicode[STIX]{x1D708}$
on
$\unicode[STIX]{x1D708}$
on
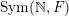 $\operatorname{Sym}(\mathbb{N},F)$
, its characteristic function
$\operatorname{Sym}(\mathbb{N},F)$
, its characteristic function
![]() $\widehat{\unicode[STIX]{x1D708}}$
is defined on
$\widehat{\unicode[STIX]{x1D708}}$
is defined on
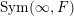 $\operatorname{Sym}(\infty ,F)$
by the formula
$\operatorname{Sym}(\infty ,F)$
by the formula
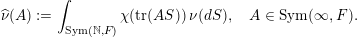 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(A):=\int _{\operatorname{Sym}(\mathbb{N},F)}\unicode[STIX]{x1D712}(\operatorname{tr}(AS))\,\unicode[STIX]{x1D708}(dS),\quad A\in \operatorname{Sym}(\infty ,F). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(A):=\int _{\operatorname{Sym}(\mathbb{N},F)}\unicode[STIX]{x1D712}(\operatorname{tr}(AS))\,\unicode[STIX]{x1D708}(dS),\quad A\in \operatorname{Sym}(\infty ,F). & & \displaystyle \nonumber\end{eqnarray}$$
Let
 $\operatorname{Mat}(n,F)$
be the space of
$\operatorname{Mat}(n,F)$
be the space of
![]() $n\times n$
matrices with entries in
$n\times n$
matrices with entries in
![]() $F$
. Every
$F$
. Every
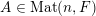 $A\in \operatorname{Mat}(n,F)$
can be written (see Lemma 2.4 below) in the form
$A\in \operatorname{Mat}(n,F)$
can be written (see Lemma 2.4 below) in the form
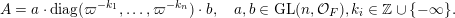 $$\begin{eqnarray}\displaystyle A=a\cdot \operatorname{diag}(\unicode[STIX]{x1D71B}^{-k_{1}},\ldots ,\unicode[STIX]{x1D71B}^{-k_{n}})\cdot b,\quad a,b\in \operatorname{GL}(n,{\mathcal{O}}_{F}),k_{i}\in \mathbb{Z}\cup \{-\infty \}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A=a\cdot \operatorname{diag}(\unicode[STIX]{x1D71B}^{-k_{1}},\ldots ,\unicode[STIX]{x1D71B}^{-k_{n}})\cdot b,\quad a,b\in \operatorname{GL}(n,{\mathcal{O}}_{F}),k_{i}\in \mathbb{Z}\cup \{-\infty \}. & & \displaystyle \nonumber\end{eqnarray}$$
These numbers
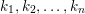 $k_{1},k_{2},\ldots ,k_{n}$
, taken with multiplicities, are uniquely determined by
$k_{1},k_{2},\ldots ,k_{n}$
, taken with multiplicities, are uniquely determined by
![]() $A$
and are called the singular numbers of
$A$
and are called the singular numbers of
![]() $A$
. The collection of the singular numbers of the matrix
$A$
. The collection of the singular numbers of the matrix
![]() $A$
is denoted by
$A$
is denoted by
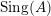 $\text{Sing}(A)$
.
$\text{Sing}(A)$
.
After the computation of characteristic functions for the probability measures in the list of measures defined in Definition 1.1 (see Proposition 4.1 below), Theorem 1.3 can be reformulated in the following form.
Theorem 1.10. The characteristic functions of ergodic
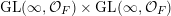 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measures on
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measures on
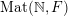 $\operatorname{Mat}(\mathbb{N},F)$
are exactly of the form
$\operatorname{Mat}(\mathbb{N},F)$
are exactly of the form
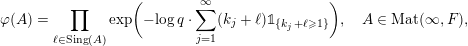 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}(A)=\mathop{\prod }_{\ell \in \text{Sing}(A)}\exp \biggl(-\text{log}\,q\cdot \mathop{\sum }_{j=1}^{\infty }(k_{j}+\ell )\unicode[STIX]{x1D7D9}_{\{k_{j}+\ell \geqslant 1\}}\biggr),\quad A\in \operatorname{Mat}(\infty ,F), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}(A)=\mathop{\prod }_{\ell \in \text{Sing}(A)}\exp \biggl(-\text{log}\,q\cdot \mathop{\sum }_{j=1}^{\infty }(k_{j}+\ell )\unicode[STIX]{x1D7D9}_{\{k_{j}+\ell \geqslant 1\}}\biggr),\quad A\in \operatorname{Mat}(\infty ,F), & & \displaystyle \nonumber\end{eqnarray}$$
where
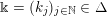 $\Bbbk =(k_{j})_{j\in \mathbb{N}}\in \unicode[STIX]{x1D6E5}$
is the parameter sequence.
$\Bbbk =(k_{j})_{j\in \mathbb{N}}\in \unicode[STIX]{x1D6E5}$
is the parameter sequence.
For formulating a similar statement in the symmetric case, we need to introduce a function
 $\unicode[STIX]{x1D703}:F\rightarrow \mathbb{C}$
by
$\unicode[STIX]{x1D703}:F\rightarrow \mathbb{C}$
by
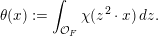 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(x):=\int _{{\mathcal{O}}_{F}}\unicode[STIX]{x1D712}(z^{2}\cdot x)\,dz. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(x):=\int _{{\mathcal{O}}_{F}}\unicode[STIX]{x1D712}(z^{2}\cdot x)\,dz. & & \displaystyle\end{eqnarray}$$
Properties of the function
![]() $\unicode[STIX]{x1D703}$
are summarized in Proposition 4.5 below.
$\unicode[STIX]{x1D703}$
are summarized in Proposition 4.5 below.
Let
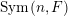 $\operatorname{Sym}(n,F)$
be the space of
$\operatorname{Sym}(n,F)$
be the space of
![]() $n\times n$
symmetric matrices with entries in
$n\times n$
symmetric matrices with entries in
![]() $F$
. Note that if the field
$F$
. Note that if the field
![]() $F$
is non-dyadic, then any
$F$
is non-dyadic, then any
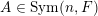 $A\in \operatorname{Sym}(n,F)$
can be written (see Lemma 2.7 below) in the form
$A\in \operatorname{Sym}(n,F)$
can be written (see Lemma 2.7 below) in the form
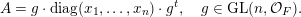 $$\begin{eqnarray}\displaystyle A=g\cdot \operatorname{diag}(x_{1},\ldots ,x_{n})\cdot g^{t},\quad g\in \operatorname{GL}(n,{\mathcal{O}}_{F}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A=g\cdot \operatorname{diag}(x_{1},\ldots ,x_{n})\cdot g^{t},\quad g\in \operatorname{GL}(n,{\mathcal{O}}_{F}). & & \displaystyle \nonumber\end{eqnarray}$$
After the computation of characteristic functions for the probability measures in the list of measures defined in Definition 1.5 (see Proposition 4.4), Theorem 1.8 can be reformulated in the following form.
Theorem 1.11. Assume that
![]() $F$
is non-dyadic. Then the characteristic functions of the ergodic
$F$
is non-dyadic. Then the characteristic functions of the ergodic
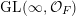 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measures on
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measures on
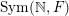 $\operatorname{Sym}(\mathbb{N},F)$
are exactly given by
$\operatorname{Sym}(\mathbb{N},F)$
are exactly given by
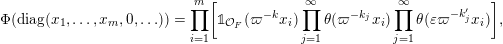 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}(\operatorname{diag}(x_{1},\ldots ,x_{m},0,\ldots ))=\mathop{\prod }_{i=1}^{m}\biggl[\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(\unicode[STIX]{x1D71B}^{-k}x_{i})\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-k_{j}}x_{i})\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-k_{j}^{\prime }}x_{i})\biggr], & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}(\operatorname{diag}(x_{1},\ldots ,x_{m},0,\ldots ))=\mathop{\prod }_{i=1}^{m}\biggl[\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(\unicode[STIX]{x1D71B}^{-k}x_{i})\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-k_{j}}x_{i})\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-k_{j}^{\prime }}x_{i})\biggr], & & \displaystyle \nonumber\end{eqnarray}$$
where
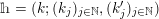 $h=(k;(k_{j})_{j\in \mathbb{N}},(k_{j}^{\prime })_{j\in \mathbb{N}})$
is a parameter in
$h=(k;(k_{j})_{j\in \mathbb{N}},(k_{j}^{\prime })_{j\in \mathbb{N}})$
is a parameter in
![]() $\unicode[STIX]{x1D6FA}$
introduced in (3).
$\unicode[STIX]{x1D6FA}$
introduced in (3).
1.4 Spherical representations
Our classification theorems, Theorems 1.3 and 1.8, can equivalently be formulated as a classification of spherical representations of analogues, in our context, of the infinite dimensional Cartan motion groups
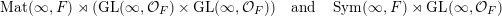 $$\begin{eqnarray}\displaystyle \operatorname{Mat}(\infty ,F)\rtimes (\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F}))\quad \text{and}\quad \operatorname{Sym}(\infty ,F)\rtimes \operatorname{GL}(\infty ,{\mathcal{O}}_{F}) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Mat}(\infty ,F)\rtimes (\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F}))\quad \text{and}\quad \operatorname{Sym}(\infty ,F)\rtimes \operatorname{GL}(\infty ,{\mathcal{O}}_{F}) & & \displaystyle \nonumber\end{eqnarray}$$
respectively. We explain this in more detail for
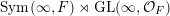 $\operatorname{Sym}(\infty ,F)\rtimes \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
.
$\operatorname{Sym}(\infty ,F)\rtimes \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
.
Recall that
 $\operatorname{Sym}(n,F)\rtimes \operatorname{GL}(n,{\mathcal{O}}_{F})$
is the semi-direct product of the additive group
$\operatorname{Sym}(n,F)\rtimes \operatorname{GL}(n,{\mathcal{O}}_{F})$
is the semi-direct product of the additive group
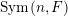 $\operatorname{Sym}(n,F)$
and the general linear group
$\operatorname{Sym}(n,F)$
and the general linear group
 $\operatorname{GL}(n,{\mathcal{O}}_{F})$
. Elements of
$\operatorname{GL}(n,{\mathcal{O}}_{F})$
. Elements of
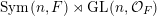 $\operatorname{Sym}(n,F)\rtimes \operatorname{GL}(n,{\mathcal{O}}_{F})$
are pairs
$\operatorname{Sym}(n,F)\rtimes \operatorname{GL}(n,{\mathcal{O}}_{F})$
are pairs
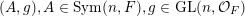 $(A,g),A\in \operatorname{Sym}(n,F),g\in \operatorname{GL}(n,{\mathcal{O}}_{F})$
and the rule of multiplication is given by
$(A,g),A\in \operatorname{Sym}(n,F),g\in \operatorname{GL}(n,{\mathcal{O}}_{F})$
and the rule of multiplication is given by
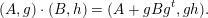 $$\begin{eqnarray}(A,g)\cdot (B,h)=(A+gBg^{t},gh).\end{eqnarray}$$
$$\begin{eqnarray}(A,g)\cdot (B,h)=(A+gBg^{t},gh).\end{eqnarray}$$
The group
 $\operatorname{Sym}(\infty ,F)\rtimes \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
is defined in a similar way and is of course the inductive limit of the sequence
$\operatorname{Sym}(\infty ,F)\rtimes \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
is defined in a similar way and is of course the inductive limit of the sequence
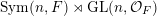 $\operatorname{Sym}(n,F)\rtimes \operatorname{GL}(n,{\mathcal{O}}_{F})$
. The groups
$\operatorname{Sym}(n,F)\rtimes \operatorname{GL}(n,{\mathcal{O}}_{F})$
. The groups
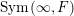 $\operatorname{Sym}(\infty ,F)$
and
$\operatorname{Sym}(\infty ,F)$
and
 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
are canonically identified with subgroups of
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
are canonically identified with subgroups of
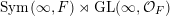 $\operatorname{Sym}(\infty ,F)\rtimes \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
by the following embeddings
$\operatorname{Sym}(\infty ,F)\rtimes \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
by the following embeddings
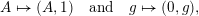 $$\begin{eqnarray}A\mapsto (A,1)\quad \text{and}\quad g\mapsto (0,g),\end{eqnarray}$$
$$\begin{eqnarray}A\mapsto (A,1)\quad \text{and}\quad g\mapsto (0,g),\end{eqnarray}$$
where
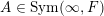 $A\in \operatorname{Sym}(\infty ,F)$
and
$A\in \operatorname{Sym}(\infty ,F)$
and
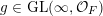 $g\in \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
.
$g\in \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
.
A unitary representation
![]() $\unicode[STIX]{x1D70C}$
of
$\unicode[STIX]{x1D70C}$
of
 $\operatorname{Sym}(\infty ,F)\rtimes \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
in a Hilbert space
$\operatorname{Sym}(\infty ,F)\rtimes \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
in a Hilbert space
![]() $H(\unicode[STIX]{x1D70C})$
is called spherical if it is irreducible and the subspace
$H(\unicode[STIX]{x1D70C})$
is called spherical if it is irreducible and the subspace
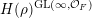 $H(\unicode[STIX]{x1D70C})^{\operatorname{GL}(\infty ,{\mathcal{O}}_{F})}$
of
$H(\unicode[STIX]{x1D70C})^{\operatorname{GL}(\infty ,{\mathcal{O}}_{F})}$
of
 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant vectors in
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant vectors in
![]() $H(\unicode[STIX]{x1D70C})$
is non-trivial; in which case, by irreducibility, the subspace
$H(\unicode[STIX]{x1D70C})$
is non-trivial; in which case, by irreducibility, the subspace
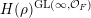 $H(\unicode[STIX]{x1D70C})^{\operatorname{GL}(\infty ,{\mathcal{O}}_{F})}$
has dimension one. A vector
$H(\unicode[STIX]{x1D70C})^{\operatorname{GL}(\infty ,{\mathcal{O}}_{F})}$
has dimension one. A vector
 $h\in H(\unicode[STIX]{x1D70C})^{\operatorname{GL}(\infty ,{\mathcal{O}}_{F})}$
of norm 1 is called a spherical vector of
$h\in H(\unicode[STIX]{x1D70C})^{\operatorname{GL}(\infty ,{\mathcal{O}}_{F})}$
of norm 1 is called a spherical vector of
![]() $\unicode[STIX]{x1D70C}$
and the function
$\unicode[STIX]{x1D70C}$
and the function
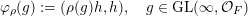 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}(g):=(\unicode[STIX]{x1D70C}(g)h,h),\quad g\in \operatorname{GL}(\infty ,{\mathcal{O}}_{F})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}(g):=(\unicode[STIX]{x1D70C}(g)h,h),\quad g\in \operatorname{GL}(\infty ,{\mathcal{O}}_{F})\end{eqnarray}$$
is called the spherical function of
![]() $\unicode[STIX]{x1D70C}$
. The spherical function
$\unicode[STIX]{x1D70C}$
. The spherical function
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}$
is an invariant of the spherical representation
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}$
is an invariant of the spherical representation
![]() $\unicode[STIX]{x1D70C}$
and it uniquely determines
$\unicode[STIX]{x1D70C}$
and it uniquely determines
![]() $\unicode[STIX]{x1D70C}$
. As a bi-invariant function with respect to the subgroup
$\unicode[STIX]{x1D70C}$
. As a bi-invariant function with respect to the subgroup
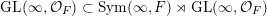 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\subset \operatorname{Sym}(\infty ,F)\rtimes \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
, the function
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\subset \operatorname{Sym}(\infty ,F)\rtimes \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
, the function
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}$
is uniquely determined by its restriction
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}$
is uniquely determined by its restriction
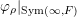 $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}|_{\operatorname{Sym}(\infty ,F)}$
.
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}|_{\operatorname{Sym}(\infty ,F)}$
.
Given an ergodic
 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measure
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measure
![]() $\unicode[STIX]{x1D708}$
on
$\unicode[STIX]{x1D708}$
on
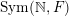 $\operatorname{Sym}(\mathbb{N},F)$
, one may define a spherical representation
$\operatorname{Sym}(\mathbb{N},F)$
, one may define a spherical representation
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D708}}$
in the Hilbert space
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D708}}$
in the Hilbert space
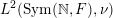 $L^{2}(\operatorname{Sym}(\mathbb{N},F),\unicode[STIX]{x1D708})$
as follows:
$L^{2}(\operatorname{Sym}(\mathbb{N},F),\unicode[STIX]{x1D708})$
as follows:
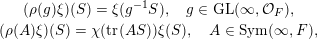 $$\begin{eqnarray}\displaystyle & (\unicode[STIX]{x1D70C}(g)\unicode[STIX]{x1D709})(S)=\unicode[STIX]{x1D709}(g^{-1}S),\quad g\in \operatorname{GL}(\infty ,{\mathcal{O}}_{F}), & \displaystyle \nonumber\\ \displaystyle & (\unicode[STIX]{x1D70C}(A)\unicode[STIX]{x1D709})(S)=\unicode[STIX]{x1D712}(\operatorname{tr}(AS))\unicode[STIX]{x1D709}(S),\quad A\in \operatorname{Sym}(\infty ,F), & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & (\unicode[STIX]{x1D70C}(g)\unicode[STIX]{x1D709})(S)=\unicode[STIX]{x1D709}(g^{-1}S),\quad g\in \operatorname{GL}(\infty ,{\mathcal{O}}_{F}), & \displaystyle \nonumber\\ \displaystyle & (\unicode[STIX]{x1D70C}(A)\unicode[STIX]{x1D709})(S)=\unicode[STIX]{x1D712}(\operatorname{tr}(AS))\unicode[STIX]{x1D709}(S),\quad A\in \operatorname{Sym}(\infty ,F), & \displaystyle \nonumber\end{eqnarray}$$
where
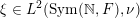 $\unicode[STIX]{x1D709}\in L^{2}(\operatorname{Sym}(\mathbb{N},F),\unicode[STIX]{x1D708})$
and
$\unicode[STIX]{x1D709}\in L^{2}(\operatorname{Sym}(\mathbb{N},F),\unicode[STIX]{x1D708})$
and
 $S\in \operatorname{Sym}(\mathbb{N},F)$
. The spherical vector can be chosen as the constant function
$S\in \operatorname{Sym}(\mathbb{N},F)$
. The spherical vector can be chosen as the constant function
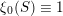 $\unicode[STIX]{x1D709}_{0}(S)\equiv 1$
.
$\unicode[STIX]{x1D709}_{0}(S)\equiv 1$
.
Proposition 1.12. The map
![]() $\unicode[STIX]{x1D708}\mapsto \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D708}}$
defines a bijection between the set of ergodic
$\unicode[STIX]{x1D708}\mapsto \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D708}}$
defines a bijection between the set of ergodic
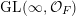 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measures on
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measures on
 $\operatorname{Sym}(\mathbb{N},F)$
and the set of spherical representations of the group
$\operatorname{Sym}(\mathbb{N},F)$
and the set of spherical representations of the group
 $\operatorname{Sym}(\infty ,F)\rtimes \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
.
$\operatorname{Sym}(\infty ,F)\rtimes \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
.
The proof of Proposition 1.12 is the same as that of Olshanski and Vershik [Reference Olshanski and VershikOV96, Proposition 1.5].
1.5 An outline of the argument
Our argument relies on the Vershik–Kerov ergodic method in the spirit of Olshanski and Vershik [Reference Olshanski and VershikOV96]. The implementation of individual steps is, however, quite different. In the case of measures on
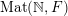 $\operatorname{Mat}(\mathbb{N},F)$
and the case of measures on
$\operatorname{Mat}(\mathbb{N},F)$
and the case of measures on
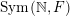 $\operatorname{Sym}(\mathbb{N},F)$
, the main steps are:
$\operatorname{Sym}(\mathbb{N},F)$
, the main steps are:
-
– explicit construction of ergodic measures, see Definitions 1.1 and 1.5;
-
– the asymptotic formulae for the analogues of Harish-Chandra–Izykson–Zuber orbital integrals, see Theorem 7.1, Theorem 7.4 in the case of measures on
 $\operatorname{Mat}(\mathbb{N},F)$
and Theorem 7.5, Theorem 7.6 in the case of measures on
$\operatorname{Mat}(\mathbb{N},F)$
and Theorem 7.5, Theorem 7.6 in the case of measures on
 $\operatorname{Sym}(\mathbb{N},F)$
;
$\operatorname{Sym}(\mathbb{N},F)$
;
-
– proof of completeness of the lists of ergodic measures, see Theorems 8.8 and 8.14 respectively.
We now explain our method in greater detail in the case of measures on
 $\operatorname{Sym}(\mathbb{N},F)$
.
$\operatorname{Sym}(\mathbb{N},F)$
.
(1) The Vershik–Kerov method: approximation of ergodic measures by orbital measures. While we follow the general scheme of Vershik and Kerov, a number of details are different.
Given
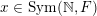 $x\in \operatorname{Sym}(\mathbb{N},F)$
and
$x\in \operatorname{Sym}(\mathbb{N},F)$
and
![]() $n\in \mathbb{N}$
, let
$n\in \mathbb{N}$
, let
 $m_{\operatorname{GL}(n,{\mathcal{O}}_{F})}(x)$
denote the unique
$m_{\operatorname{GL}(n,{\mathcal{O}}_{F})}(x)$
denote the unique
 $\operatorname{GL}(n,{\mathcal{O}}_{F})$
-invariant probability measure on
$\operatorname{GL}(n,{\mathcal{O}}_{F})$
-invariant probability measure on
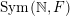 $\operatorname{Sym}(\mathbb{N},F)$
supported on the orbit
$\operatorname{Sym}(\mathbb{N},F)$
supported on the orbit
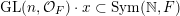 $\operatorname{GL}(n,{\mathcal{O}}_{F})\cdot x\subset \operatorname{Sym}(\mathbb{N},F)$
. Let
$\operatorname{GL}(n,{\mathcal{O}}_{F})\cdot x\subset \operatorname{Sym}(\mathbb{N},F)$
. Let
 $\mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))$
be the class of probability measures
$\mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))$
be the class of probability measures
![]() $\unicode[STIX]{x1D708}$
on
$\unicode[STIX]{x1D708}$
on
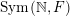 $\operatorname{Sym}(\mathbb{N},F)$
verifying the condition: there exists a sequence of positive integers
$\operatorname{Sym}(\mathbb{N},F)$
verifying the condition: there exists a sequence of positive integers
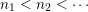 $n_{1}<n_{2}<\cdots \,$
and a sequence
$n_{1}<n_{2}<\cdots \,$
and a sequence
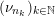 $(\unicode[STIX]{x1D708}_{n_{k}})_{k\in \mathbb{N}}$
of probability measures with
$(\unicode[STIX]{x1D708}_{n_{k}})_{k\in \mathbb{N}}$
of probability measures with
![]() $\unicode[STIX]{x1D708}_{n_{k}}$
being a
$\unicode[STIX]{x1D708}_{n_{k}}$
being a
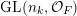 $\operatorname{GL}(n_{k},{\mathcal{O}}_{F})$
-orbital measure supported on
$\operatorname{GL}(n_{k},{\mathcal{O}}_{F})$
-orbital measure supported on
 $\operatorname{Sym}(n_{k},F)\subset \operatorname{Sym}(\mathbb{N},F)$
, such that
$\operatorname{Sym}(n_{k},F)\subset \operatorname{Sym}(\mathbb{N},F)$
, such that
![]() $\unicode[STIX]{x1D708}_{n_{k}}$
converges weakly to
$\unicode[STIX]{x1D708}_{n_{k}}$
converges weakly to
![]() $\unicode[STIX]{x1D708}$
.
$\unicode[STIX]{x1D708}$
.
As a variant of Vershik’s Theorem (see Theorem 6.3 below), we obtain the following inclusion:
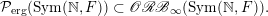 $$\begin{eqnarray}\displaystyle {\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))\subset \mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F)). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))\subset \mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F)). & & \displaystyle \nonumber\end{eqnarray}$$
Note that, a priori, we do not know whether the inverse inclusion holds.
(2) Main ingredients: Classification of
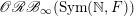 $\mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))$
.
$\mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))$
.
(i) Computation of orbital integrals. To describe
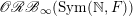 $\mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))$
, we need to understand the asymptotic behaviour of the characteristic functions of orbital measures of the compact groups
$\mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))$
, we need to understand the asymptotic behaviour of the characteristic functions of orbital measures of the compact groups
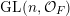 $\operatorname{GL}(n,{\mathcal{O}}_{F})$
. Recalling the assumption on the character
$\operatorname{GL}(n,{\mathcal{O}}_{F})$
. Recalling the assumption on the character
![]() $\unicode[STIX]{x1D712}\in \widehat{F}$
in (6), we obtain an asymptotic formula for the following orbital integral:
$\unicode[STIX]{x1D712}\in \widehat{F}$
in (6), we obtain an asymptotic formula for the following orbital integral:
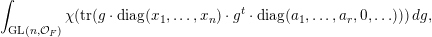 $$\begin{eqnarray}\displaystyle \int _{\operatorname{GL}(n,{\mathcal{O}}_{F})}\unicode[STIX]{x1D712}(\operatorname{tr}(g\cdot \operatorname{diag}(x_{1},\ldots ,x_{n})\cdot g^{t}\cdot \operatorname{diag}(a_{1},\ldots ,a_{r},0,\ldots )))\,dg, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{\operatorname{GL}(n,{\mathcal{O}}_{F})}\unicode[STIX]{x1D712}(\operatorname{tr}(g\cdot \operatorname{diag}(x_{1},\ldots ,x_{n})\cdot g^{t}\cdot \operatorname{diag}(a_{1},\ldots ,a_{r},0,\ldots )))\,dg, & & \displaystyle\end{eqnarray}$$
where
![]() $dg$
is the normalized Haar measure of
$dg$
is the normalized Haar measure of
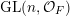 $\operatorname{GL}(n,{\mathcal{O}}_{F})$
. The formula we obtain for the integral (8) is uniformly asymptotically multiplicative, that is, the orbital integral (8) has the same asymptotic behaviour, uniformly on the choices of
$\operatorname{GL}(n,{\mathcal{O}}_{F})$
. The formula we obtain for the integral (8) is uniformly asymptotically multiplicative, that is, the orbital integral (8) has the same asymptotic behaviour, uniformly on the choices of
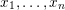 $x_{1},\ldots ,x_{n}$
, as the following product of much simpler orbital integrals:
$x_{1},\ldots ,x_{n}$
, as the following product of much simpler orbital integrals:
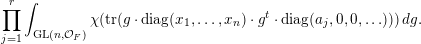 $$\begin{eqnarray}\displaystyle \mathop{\prod }_{j=1}^{r}\int _{\operatorname{GL}(n,{\mathcal{O}}_{F})}\unicode[STIX]{x1D712}(\operatorname{tr}(g\cdot \operatorname{diag}(x_{1},\ldots ,x_{n})\cdot g^{t}\cdot \operatorname{diag}(a_{j},0,0,\ldots )))\,dg. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\prod }_{j=1}^{r}\int _{\operatorname{GL}(n,{\mathcal{O}}_{F})}\unicode[STIX]{x1D712}(\operatorname{tr}(g\cdot \operatorname{diag}(x_{1},\ldots ,x_{n})\cdot g^{t}\cdot \operatorname{diag}(a_{j},0,0,\ldots )))\,dg. & & \displaystyle \nonumber\end{eqnarray}$$
See Theorem 7.6 for the details.
Explicit computation of the above orbital integral requires some Fourier analysis on the field
![]() $F$
and quite a few combinatorial arguments in which we compute the cardinality of various sets of matrices over the finite field
$F$
and quite a few combinatorial arguments in which we compute the cardinality of various sets of matrices over the finite field
![]() $\mathbf{F}_{q}$
.
$\mathbf{F}_{q}$
.
(ii) Multiplicativity of characteristic functions for limits of orbital measures. An immediate consequence of the uniform asymptotic multiplicativity for the orbital integral (8) is that for any
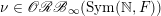 $\unicode[STIX]{x1D708}\in \mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))$
, its characteristic function
$\unicode[STIX]{x1D708}\in \mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))$
, its characteristic function
![]() $\widehat{\unicode[STIX]{x1D708}}$
possesses an exact multiplicativity property, that is, for any
$\widehat{\unicode[STIX]{x1D708}}$
possesses an exact multiplicativity property, that is, for any
![]() $r\in \mathbb{N}$
and any
$r\in \mathbb{N}$
and any
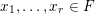 $x_{1},\ldots ,x_{r}\in F$
,
$x_{1},\ldots ,x_{r}\in F$
,
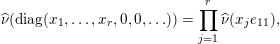 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(\operatorname{diag}(x_{1},\ldots ,x_{r},0,0,\ldots ))=\mathop{\prod }_{j=1}^{r}\widehat{\unicode[STIX]{x1D708}}(x_{j}e_{11}), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(\operatorname{diag}(x_{1},\ldots ,x_{r},0,0,\ldots ))=\mathop{\prod }_{j=1}^{r}\widehat{\unicode[STIX]{x1D708}}(x_{j}e_{11}), & & \displaystyle\end{eqnarray}$$
where
![]() $e_{11}$
is the elementary matrix whose
$e_{11}$
is the elementary matrix whose
![]() $(1,1)$
-coefficient is
$(1,1)$
-coefficient is
![]() $1$
. This multiplicativity result implies in particular that the classification of the class
$1$
. This multiplicativity result implies in particular that the classification of the class
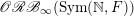 $\mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))$
is reduced to the classification of the class of functions on
$\mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))$
is reduced to the classification of the class of functions on
![]() $F$
defined by
$F$
defined by
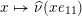 $x\mapsto \widehat{\unicode[STIX]{x1D708}}(xe_{11})$
.
$x\mapsto \widehat{\unicode[STIX]{x1D708}}(xe_{11})$
.
(3) Ergodicity: Proof of the inclusion:
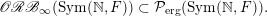 $$\begin{eqnarray}\displaystyle \mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))\subset {\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F)). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))\subset {\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F)). & & \displaystyle \nonumber\end{eqnarray}$$
Our direct proof of ergodicity for all measures in
 $\mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))$
uses an argument of Okounkov and Olshanski [Reference Okounkov and OlshanskiOO98]: ergodicity for measures in
$\mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))$
uses an argument of Okounkov and Olshanski [Reference Okounkov and OlshanskiOO98]: ergodicity for measures in
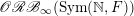 $\mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))$
is derived from the De Finetti Theorem, see Theorem 3.10 below for the details. This approach of proving ergodicity can be also applied to different situations, such as that of Olshanski and Vershik in [Reference Olshanski and VershikOV96].
$\mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))$
is derived from the De Finetti Theorem, see Theorem 3.10 below for the details. This approach of proving ergodicity can be also applied to different situations, such as that of Olshanski and Vershik in [Reference Olshanski and VershikOV96].
(4) Proof of the equality
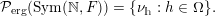 $$\begin{eqnarray}\displaystyle {\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))=\{\unicode[STIX]{x1D708}_{h}:h\in \unicode[STIX]{x1D6FA}\}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))=\{\unicode[STIX]{x1D708}_{h}:h\in \unicode[STIX]{x1D6FA}\}. & & \displaystyle\end{eqnarray}$$
By comparing the characteristic functions
![]() $\widehat{\unicode[STIX]{x1D708}_{h}}$
for all the measures
$\widehat{\unicode[STIX]{x1D708}_{h}}$
for all the measures
![]() $\unicode[STIX]{x1D708}_{h}$
with
$\unicode[STIX]{x1D708}_{h}$
with
![]() $h\in \unicode[STIX]{x1D6FA}$
and that of measures in
$h\in \unicode[STIX]{x1D6FA}$
and that of measures in
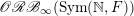 $\mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))$
, we obtain the equality
$\mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))$
, we obtain the equality
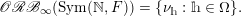 $$\begin{eqnarray}\displaystyle \mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))=\{\unicode[STIX]{x1D708}_{h}:h\in \unicode[STIX]{x1D6FA}\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))=\{\unicode[STIX]{x1D708}_{h}:h\in \unicode[STIX]{x1D6FA}\}. & & \displaystyle \nonumber\end{eqnarray}$$
Combining this equality with the results obtained in the previous steps, we finally get the desired equality (10).
1.6 Organization of the paper
The exposition, which we tried to make essentially self-contained, is organized as follows.
In § 2, we recall the definition of ergodic measures and the necessary definitions related to non-discrete locally compact non-Archimedean fields, linear groups over them and Fourier transforms in this setting.
In § 3, we prove that all the measures on
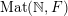 $\operatorname{Mat}(\mathbb{N},F)$
from the family
$\operatorname{Mat}(\mathbb{N},F)$
from the family
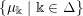 $\{\unicode[STIX]{x1D707}_{\Bbbk }\mid \Bbbk \in \unicode[STIX]{x1D6E5}\}$
introduced in Definition 1.1 are
$\{\unicode[STIX]{x1D707}_{\Bbbk }\mid \Bbbk \in \unicode[STIX]{x1D6E5}\}$
introduced in Definition 1.1 are
 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant and ergodic and that all the measures on
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant and ergodic and that all the measures on
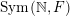 $\operatorname{Sym}(\mathbb{N},F)$
from the family
$\operatorname{Sym}(\mathbb{N},F)$
from the family
 $\{\unicode[STIX]{x1D708}_{h}\mid h\in \unicode[STIX]{x1D6FA}\}$
introduced in Definition 1.5 are
$\{\unicode[STIX]{x1D708}_{h}\mid h\in \unicode[STIX]{x1D6FA}\}$
introduced in Definition 1.5 are
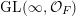 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant and ergodic.
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant and ergodic.
In § 4, we give explicit formulae for characteristic functions of measures from the two families
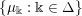 $\{\unicode[STIX]{x1D707}_{\Bbbk }:\Bbbk \in \unicode[STIX]{x1D6E5}\}$
and
$\{\unicode[STIX]{x1D707}_{\Bbbk }:\Bbbk \in \unicode[STIX]{x1D6E5}\}$
and
 $\{\unicode[STIX]{x1D708}_{h}:h\in \unicode[STIX]{x1D6FA}\}$
.
$\{\unicode[STIX]{x1D708}_{h}:h\in \unicode[STIX]{x1D6FA}\}$
.
In § 5, we prove that the parametrization maps
![]() $\Bbbk \mapsto \unicode[STIX]{x1D707}_{\Bbbk }$
from
$\Bbbk \mapsto \unicode[STIX]{x1D707}_{\Bbbk }$
from
![]() $\unicode[STIX]{x1D6E5}$
to
$\unicode[STIX]{x1D6E5}$
to
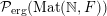 ${\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
and
${\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
and
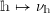 $h\mapsto \unicode[STIX]{x1D708}_{h}$
from
$h\mapsto \unicode[STIX]{x1D708}_{h}$
from
![]() $\unicode[STIX]{x1D6FA}$
to
$\unicode[STIX]{x1D6FA}$
to
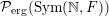 ${\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))$
are injective.
${\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))$
are injective.
In § 6, we introduce orbital measures and recall the Vershik–Kerov ergodic method for dealing with ergodic measures for inductively compact groups.
In § 7, we obtain the asymptotic formula for orbital integrals of the type (8).
In § 8, we complete the classifications by proving that the parametrization maps
![]() $\Bbbk \mapsto \unicode[STIX]{x1D707}_{\Bbbk }$
and
$\Bbbk \mapsto \unicode[STIX]{x1D707}_{\Bbbk }$
and
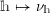 $h\mapsto \unicode[STIX]{x1D708}_{h}$
are surjective.
$h\mapsto \unicode[STIX]{x1D708}_{h}$
are surjective.
In § 9, we show that the parametrization maps
![]() $\Bbbk \mapsto \unicode[STIX]{x1D707}_{\Bbbk }$
and
$\Bbbk \mapsto \unicode[STIX]{x1D707}_{\Bbbk }$
and
 $h\mapsto \unicode[STIX]{x1D708}_{h}$
are homeomorphisms between corresponding topological spaces.
$h\mapsto \unicode[STIX]{x1D708}_{h}$
are homeomorphisms between corresponding topological spaces.
Proofs of some routine technical lemmata are given in Appendix A.
2 Preliminaries
2.1 Ergodic measures
2.1.1 Ergodicity
Let
![]() ${\mathcal{X}}$
be a Polish space, that is, it is homeomorphic to a complete metric space that has a countable dense subset. Denote by
${\mathcal{X}}$
be a Polish space, that is, it is homeomorphic to a complete metric space that has a countable dense subset. Denote by
![]() ${\mathcal{P}}({\mathcal{X}})$
the set of Borel probability measures on
${\mathcal{P}}({\mathcal{X}})$
the set of Borel probability measures on
![]() ${\mathcal{X}}$
. Denote by
${\mathcal{X}}$
. Denote by
![]() $C_{b}({\mathcal{X}})$
the space of bounded continuous complex-valued functions on
$C_{b}({\mathcal{X}})$
the space of bounded continuous complex-valued functions on
![]() ${\mathcal{X}}$
. Recall that a sequence
${\mathcal{X}}$
. Recall that a sequence
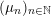 $(\unicode[STIX]{x1D707}_{n})_{n\in \mathbb{N}}$
in
$(\unicode[STIX]{x1D707}_{n})_{n\in \mathbb{N}}$
in
![]() ${\mathcal{P}}({\mathcal{X}})$
is said to converge weakly to
${\mathcal{P}}({\mathcal{X}})$
is said to converge weakly to
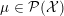 $\unicode[STIX]{x1D707}\in {\mathcal{P}}({\mathcal{X}})$
and is denoted by
$\unicode[STIX]{x1D707}\in {\mathcal{P}}({\mathcal{X}})$
and is denoted by
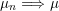 $\unicode[STIX]{x1D707}_{n}\Longrightarrow \unicode[STIX]{x1D707}$
if for any
$\unicode[STIX]{x1D707}_{n}\Longrightarrow \unicode[STIX]{x1D707}$
if for any
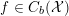 $f\in C_{b}({\mathcal{X}})$
, we have
$f\in C_{b}({\mathcal{X}})$
, we have
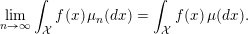 $$\begin{eqnarray}\displaystyle \lim _{n\rightarrow \infty }\int _{{\mathcal{X}}}f(x)\,\unicode[STIX]{x1D707}_{n}(dx)=\int _{{\mathcal{X}}}f(x)\,\unicode[STIX]{x1D707}(dx). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{n\rightarrow \infty }\int _{{\mathcal{X}}}f(x)\,\unicode[STIX]{x1D707}_{n}(dx)=\int _{{\mathcal{X}}}f(x)\,\unicode[STIX]{x1D707}(dx). & & \displaystyle \nonumber\end{eqnarray}$$
Given a group action of a group
![]() $G$
on
$G$
on
![]() ${\mathcal{X}}$
, we denote by
${\mathcal{X}}$
, we denote by
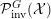 ${\mathcal{P}}_{\text{inv}}^{G}({\mathcal{X}})$
the set of
${\mathcal{P}}_{\text{inv}}^{G}({\mathcal{X}})$
the set of
![]() $G$
-invariant Borel probability measures on
$G$
-invariant Borel probability measures on
![]() ${\mathcal{X}}$
. By definition, a
${\mathcal{X}}$
. By definition, a
![]() $G$
-invariant Borel probability measure
$G$
-invariant Borel probability measure
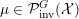 $\unicode[STIX]{x1D707}\in {\mathcal{P}}_{\text{inv}}^{G}({\mathcal{X}})$
is ergodic, if for any
$\unicode[STIX]{x1D707}\in {\mathcal{P}}_{\text{inv}}^{G}({\mathcal{X}})$
is ergodic, if for any
![]() $G$
-invariant Borel subset
$G$
-invariant Borel subset
![]() ${\mathcal{A}}\subset {\mathcal{X}}$
, either
${\mathcal{A}}\subset {\mathcal{X}}$
, either
 $\unicode[STIX]{x1D707}({\mathcal{A}})=0$
or
$\unicode[STIX]{x1D707}({\mathcal{A}})=0$
or
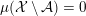 $\unicode[STIX]{x1D707}({\mathcal{X}}\,\setminus \,{\mathcal{A}})=0$
. The totality of ergodic
$\unicode[STIX]{x1D707}({\mathcal{X}}\,\setminus \,{\mathcal{A}})=0$
. The totality of ergodic
![]() $G$
-invariant probability measures on
$G$
-invariant probability measures on
![]() ${\mathcal{X}}$
is denoted by
${\mathcal{X}}$
is denoted by
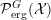 ${\mathcal{P}}_{\text{erg}}^{G}({\mathcal{X}})$
. If the group action is clear from the context, we denote
${\mathcal{P}}_{\text{erg}}^{G}({\mathcal{X}})$
. If the group action is clear from the context, we denote
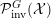 ${\mathcal{P}}_{\text{inv}}^{G}({\mathcal{X}})$
and
${\mathcal{P}}_{\text{inv}}^{G}({\mathcal{X}})$
and
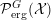 ${\mathcal{P}}_{\text{erg}}^{G}({\mathcal{X}})$
simply by
${\mathcal{P}}_{\text{erg}}^{G}({\mathcal{X}})$
simply by
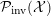 ${\mathcal{P}}_{\text{inv}}({\mathcal{X}})$
and
${\mathcal{P}}_{\text{inv}}({\mathcal{X}})$
and
 ${\mathcal{P}}_{\text{erg}}({\mathcal{X}})$
respectively.
${\mathcal{P}}_{\text{erg}}({\mathcal{X}})$
respectively.
2.1.2 Indecomposability and ergodicity
Using the notation as before, a measure
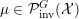 $\unicode[STIX]{x1D707}\in {\mathcal{P}}_{\text{inv}}^{G}({\mathcal{X}})$
is called indecomposable in
$\unicode[STIX]{x1D707}\in {\mathcal{P}}_{\text{inv}}^{G}({\mathcal{X}})$
is called indecomposable in
 ${\mathcal{P}}_{\text{inv}}^{G}({\mathcal{X}})$
if the equality
${\mathcal{P}}_{\text{inv}}^{G}({\mathcal{X}})$
if the equality
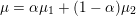 $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D707}_{1}+(1-\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D707}_{2}$
with
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D707}_{1}+(1-\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D707}_{2}$
with
 $\unicode[STIX]{x1D6FC}\in (0,1)$
,
$\unicode[STIX]{x1D6FC}\in (0,1)$
,
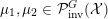 $\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}\in {\mathcal{P}}_{\text{inv}}^{G}({\mathcal{X}})$
, implies
$\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}\in {\mathcal{P}}_{\text{inv}}^{G}({\mathcal{X}})$
, implies
 $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{1}=\unicode[STIX]{x1D707}_{2}$
. Recall that a Borel subset
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{1}=\unicode[STIX]{x1D707}_{2}$
. Recall that a Borel subset
![]() ${\mathcal{A}}\subset {\mathcal{X}}$
is called almost
${\mathcal{A}}\subset {\mathcal{X}}$
is called almost
![]() $G$
-invariant with respect to a measure
$G$
-invariant with respect to a measure
 $\unicode[STIX]{x1D707}\in {\mathcal{P}}_{\text{inv}}^{G}({\mathcal{X}})$
if for every
$\unicode[STIX]{x1D707}\in {\mathcal{P}}_{\text{inv}}^{G}({\mathcal{X}})$
if for every
![]() $g\in G$
, we have
$g\in G$
, we have
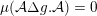 $\unicode[STIX]{x1D707}({\mathcal{A}}\unicode[STIX]{x1D6E5}g.{\mathcal{A}})=0$
, where
$\unicode[STIX]{x1D707}({\mathcal{A}}\unicode[STIX]{x1D6E5}g.{\mathcal{A}})=0$
, where
 $g.{\mathcal{A}}=\{g.x:x\in {\mathcal{A}}\}$
and
$g.{\mathcal{A}}=\{g.x:x\in {\mathcal{A}}\}$
and
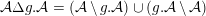 ${\mathcal{A}}\unicode[STIX]{x1D6E5}g.{\mathcal{A}}=({\mathcal{A}}\,\setminus \,g.{\mathcal{A}})\cup (g.{\mathcal{A}}\,\setminus \,{\mathcal{A}})$
.
${\mathcal{A}}\unicode[STIX]{x1D6E5}g.{\mathcal{A}}=({\mathcal{A}}\,\setminus \,g.{\mathcal{A}})\cup (g.{\mathcal{A}}\,\setminus \,{\mathcal{A}})$
.
A Borel probability measure
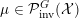 $\unicode[STIX]{x1D707}\in {\mathcal{P}}_{\text{inv}}^{G}({\mathcal{X}})$
is indecomposable in
$\unicode[STIX]{x1D707}\in {\mathcal{P}}_{\text{inv}}^{G}({\mathcal{X}})$
is indecomposable in
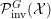 ${\mathcal{P}}_{\text{inv}}^{G}({\mathcal{X}})$
if and only if any Borel subset
${\mathcal{P}}_{\text{inv}}^{G}({\mathcal{X}})$
if and only if any Borel subset
![]() ${\mathcal{A}}\subset {\mathcal{X}}$
which is almost
${\mathcal{A}}\subset {\mathcal{X}}$
which is almost
![]() $G$
-invariant with respect to the measure
$G$
-invariant with respect to the measure
![]() $\unicode[STIX]{x1D707}$
satisfies either
$\unicode[STIX]{x1D707}$
satisfies either
 $\unicode[STIX]{x1D707}({\mathcal{A}})=0$
or
$\unicode[STIX]{x1D707}({\mathcal{A}})=0$
or
 $\unicode[STIX]{x1D707}({\mathcal{X}}\,\setminus \,{\mathcal{A}})=0$
(see [Reference BogolyubovBog69, Reference FominFom50] and [Reference BufetovBuf14, Proposition 1]).
$\unicode[STIX]{x1D707}({\mathcal{X}}\,\setminus \,{\mathcal{A}})=0$
(see [Reference BogolyubovBog69, Reference FominFom50] and [Reference BufetovBuf14, Proposition 1]).
Indecomposable Borel probability measures in
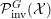 ${\mathcal{P}}_{\text{inv}}^{G}({\mathcal{X}})$
are a fortiori ergodic. For actions of general groups, ergodic probability measures may fail to be indecomposable, see [Reference BufetovBuf14, § 5] for a counterexample of Kolmogorov. Nevertheless, it is proved in [Reference BufetovBuf14, Proposition 2] that for action of inductively compact groups, and thus including the actions in our main Theorems 1.3 and 1.8, etc, the notions of indecomposability and ergodicity coincide.
${\mathcal{P}}_{\text{inv}}^{G}({\mathcal{X}})$
are a fortiori ergodic. For actions of general groups, ergodic probability measures may fail to be indecomposable, see [Reference BufetovBuf14, § 5] for a counterexample of Kolmogorov. Nevertheless, it is proved in [Reference BufetovBuf14, Proposition 2] that for action of inductively compact groups, and thus including the actions in our main Theorems 1.3 and 1.8, etc, the notions of indecomposability and ergodicity coincide.
Note that for the action of countable groups, the notions of indecomposability and ergodicity coincide. Indeed, if
![]() $G$
is a countable group and
$G$
is a countable group and
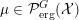 $\unicode[STIX]{x1D707}\in {\mathcal{P}}_{\text{erg}}^{G}({\mathcal{X}})$
, then for any
$\unicode[STIX]{x1D707}\in {\mathcal{P}}_{\text{erg}}^{G}({\mathcal{X}})$
, then for any
![]() $G$
-almost invariant Borel subset
$G$
-almost invariant Borel subset
![]() ${\mathcal{A}}\subset {\mathcal{X}}$
with respect to the measure
${\mathcal{A}}\subset {\mathcal{X}}$
with respect to the measure
![]() $\unicode[STIX]{x1D707}$
, the Borel subset
$\unicode[STIX]{x1D707}$
, the Borel subset
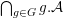 $\bigcap _{g\in G}g.{\mathcal{A}}$
is
$\bigcap _{g\in G}g.{\mathcal{A}}$
is
![]() $G$
-invariant and hence, by the ergodicity of
$G$
-invariant and hence, by the ergodicity of
![]() $\unicode[STIX]{x1D707}$
, we have
$\unicode[STIX]{x1D707}$
, we have
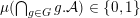 $\unicode[STIX]{x1D707}(\bigcap _{g\in G}g.{\mathcal{A}})\in \{0,1\}$
. Since
$\unicode[STIX]{x1D707}(\bigcap _{g\in G}g.{\mathcal{A}})\in \{0,1\}$
. Since
![]() ${\mathcal{A}}$
is
${\mathcal{A}}$
is
![]() $G$
-almost invariant with respect to
$G$
-almost invariant with respect to
![]() $\unicode[STIX]{x1D707}$
and since
$\unicode[STIX]{x1D707}$
and since
![]() $G$
is countable, we also have
$G$
is countable, we also have
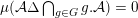 $\unicode[STIX]{x1D707}({\mathcal{A}}\unicode[STIX]{x1D6E5}\bigcap _{g\in G}g.{\mathcal{A}})=0$
. Therefore,
$\unicode[STIX]{x1D707}({\mathcal{A}}\unicode[STIX]{x1D6E5}\bigcap _{g\in G}g.{\mathcal{A}})=0$
. Therefore,
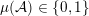 $\unicode[STIX]{x1D707}({\mathcal{A}})\in \{0,1\}$
. This proves that
$\unicode[STIX]{x1D707}({\mathcal{A}})\in \{0,1\}$
. This proves that
![]() $\unicode[STIX]{x1D707}$
is indecomposable.
$\unicode[STIX]{x1D707}$
is indecomposable.
2.2 Fields and integers
Let
![]() $F$
be a non-discrete locally compact non-Archimedean field. The classification of local fields (see, e.g., Ramakrishnan and Valenza’s book [Reference Ramakrishnan and ValenzaRV99, Theorem 4-12]) implies that
$F$
be a non-discrete locally compact non-Archimedean field. The classification of local fields (see, e.g., Ramakrishnan and Valenza’s book [Reference Ramakrishnan and ValenzaRV99, Theorem 4-12]) implies that
![]() $F$
is isomorphic to one of the following fields:
$F$
is isomorphic to one of the following fields:
-
– a finite extension of the field
 $\mathbb{Q}_{p}$
of
$\mathbb{Q}_{p}$
of
 $p$
-adic numbers for some prime
$p$
-adic numbers for some prime
 $p$
;
$p$
; -
– the field of formal Laurent series over a finite field.
Let
![]() $|\cdot |$
be the absolute value on
$|\cdot |$
be the absolute value on
![]() $F$
and denote by
$F$
and denote by
![]() $d(\cdot ,\cdot )$
the ultrametric on
$d(\cdot ,\cdot )$
the ultrametric on
![]() $F$
defined by
$F$
defined by
 $d(x,y)=|x-y|$
. The ring of integers in
$d(x,y)=|x-y|$
. The ring of integers in
![]() $F$
is given by
$F$
is given by
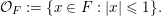 $$\begin{eqnarray}\displaystyle {\mathcal{O}}_{F}:=\{x\in F:|x|\leqslant 1\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{O}}_{F}:=\{x\in F:|x|\leqslant 1\}. & & \displaystyle \nonumber\end{eqnarray}$$
The subset
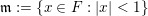 $\mathfrak{m}:=\{x\in F:|x|<1\}$
is the unique maximal ideal of
$\mathfrak{m}:=\{x\in F:|x|<1\}$
is the unique maximal ideal of
![]() ${\mathcal{O}}_{F}$
. The ideal
${\mathcal{O}}_{F}$
. The ideal
![]() $\mathfrak{m}$
is principal. Any generator of
$\mathfrak{m}$
is principal. Any generator of
![]() $\mathfrak{m}$
is called a uniformizer of
$\mathfrak{m}$
is called a uniformizer of
![]() $F$
. Throughout the paper, we fix any uniformizer
$F$
. Throughout the paper, we fix any uniformizer
![]() $\unicode[STIX]{x1D71B}$
of
$\unicode[STIX]{x1D71B}$
of
![]() $F$
, that is,
$F$
, that is,
 $\mathfrak{m}=\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
. The field
$\mathfrak{m}=\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
. The field
 ${\mathcal{O}}_{F}/\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
is finite with
${\mathcal{O}}_{F}/\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
is finite with
![]() $q=p^{f}$
elements for a prime number
$q=p^{f}$
elements for a prime number
![]() $p$
and a positive integer
$p$
and a positive integer
![]() $f\in \mathbb{N}$
. If
$f\in \mathbb{N}$
. If
![]() $q=2^{f}$
, then we say that
$q=2^{f}$
, then we say that
![]() $F$
is dyadic, otherwise, we say that
$F$
is dyadic, otherwise, we say that
![]() $F$
is non-dyadic.
$F$
is non-dyadic.
We write
 $\mathbf{F}_{q}:={\mathcal{O}}_{F}/\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
. The quotient map is denoted by
$\mathbf{F}_{q}:={\mathcal{O}}_{F}/\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
. The quotient map is denoted by
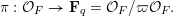 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}:{\mathcal{O}}_{F}\rightarrow \mathbf{F}_{q}={\mathcal{O}}_{F}/\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}:{\mathcal{O}}_{F}\rightarrow \mathbf{F}_{q}={\mathcal{O}}_{F}/\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}. & & \displaystyle \nonumber\end{eqnarray}$$
Fix a complete set of representatives
 ${\mathcal{C}}_{q}\subset {\mathcal{O}}_{F}$
of cosets of
${\mathcal{C}}_{q}\subset {\mathcal{O}}_{F}$
of cosets of
![]() $\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
in
$\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
in
![]() ${\mathcal{O}}_{F}$
and assume that
${\mathcal{O}}_{F}$
and assume that
![]() $0\in {\mathcal{C}}_{q}$
. The restriction of the quotient map
$0\in {\mathcal{C}}_{q}$
. The restriction of the quotient map
![]() $\unicode[STIX]{x1D70B}$
on the finite set
$\unicode[STIX]{x1D70B}$
on the finite set
![]() ${\mathcal{C}}_{q}$
is a bijection:
${\mathcal{C}}_{q}$
is a bijection:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}:{\mathcal{C}}_{q}\xrightarrow[{}]{\text{bijection}}\mathbf{F}_{q}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}:{\mathcal{C}}_{q}\xrightarrow[{}]{\text{bijection}}\mathbf{F}_{q}. & & \displaystyle\end{eqnarray}$$
Any element of
![]() $F$
is uniquely expanded as a convergent series in
$F$
is uniquely expanded as a convergent series in
![]() $F$
:
$F$
:
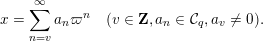 $$\begin{eqnarray}\displaystyle x=\mathop{\sum }_{n=v}^{\infty }a_{n}\unicode[STIX]{x1D71B}^{n}\quad (v\in \mathbf{Z},a_{n}\in {\mathcal{C}}_{q},a_{v}\neq 0). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle x=\mathop{\sum }_{n=v}^{\infty }a_{n}\unicode[STIX]{x1D71B}^{n}\quad (v\in \mathbf{Z},a_{n}\in {\mathcal{C}}_{q},a_{v}\neq 0). & & \displaystyle\end{eqnarray}$$
If
![]() $x\in F$
is given by the series (12), then we define the
$x\in F$
is given by the series (12), then we define the
![]() $F$
-valuation of
$F$
-valuation of
![]() $x$
by
$x$
by
 $\text{ord}_{F}(x):=v$
. By convention, we set
$\text{ord}_{F}(x):=v$
. By convention, we set
 $\text{ord}_{F}(0)=\infty$
. The absolute value and the
$\text{ord}_{F}(0)=\infty$
. The absolute value and the
![]() $F$
-valuation of any element
$F$
-valuation of any element
![]() $x\in F$
are related by the formula
$x\in F$
are related by the formula
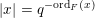 $|x|=q^{-\text{ord}_{F}(x)}$
.
$|x|=q^{-\text{ord}_{F}(x)}$
.
2.3 Group actions
Let
 $\operatorname{GL}(n,F)$
and
$\operatorname{GL}(n,F)$
and
 $\operatorname{GL}(n,{\mathcal{O}}_{F})$
denote the groups of invertible
$\operatorname{GL}(n,{\mathcal{O}}_{F})$
denote the groups of invertible
![]() $n\times n$
matrices over
$n\times n$
matrices over
![]() $F$
and
$F$
and
![]() ${\mathcal{O}}_{F}$
respectively. The group
${\mathcal{O}}_{F}$
respectively. The group
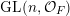 $\operatorname{GL}(n,{\mathcal{O}}_{F})$
is embedded naturally into
$\operatorname{GL}(n,{\mathcal{O}}_{F})$
is embedded naturally into
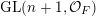 $\operatorname{GL}(n+1,{\mathcal{O}}_{F})$
by
$\operatorname{GL}(n+1,{\mathcal{O}}_{F})$
by
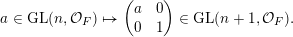 $$\begin{eqnarray}\displaystyle a\in \operatorname{GL}(n,{\mathcal{O}}_{F})\mapsto \left(\begin{array}{@{}cc@{}}a & 0\\ 0 & 1\end{array}\right)\in \operatorname{GL}(n+1,{\mathcal{O}}_{F}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a\in \operatorname{GL}(n,{\mathcal{O}}_{F})\mapsto \left(\begin{array}{@{}cc@{}}a & 0\\ 0 & 1\end{array}\right)\in \operatorname{GL}(n+1,{\mathcal{O}}_{F}). & & \displaystyle\end{eqnarray}$$
Define an inductive limit group
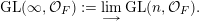 $$\begin{eqnarray}\displaystyle \operatorname{GL}(\infty ,{\mathcal{O}}_{F}):=\lim _{\longrightarrow }\operatorname{GL}(n,{\mathcal{O}}_{F}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{GL}(\infty ,{\mathcal{O}}_{F}):=\lim _{\longrightarrow }\operatorname{GL}(n,{\mathcal{O}}_{F}). & & \displaystyle \nonumber\end{eqnarray}$$
Equivalently,
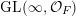 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
is the group of infinite invertible matrices
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
is the group of infinite invertible matrices
 $g=(g_{ij})_{i,j\in \mathbb{N}}$
over
$g=(g_{ij})_{i,j\in \mathbb{N}}$
over
![]() ${\mathcal{O}}_{F}$
such that
${\mathcal{O}}_{F}$
such that
 $g_{ij}=\unicode[STIX]{x1D6FF}_{ij}$
if
$g_{ij}=\unicode[STIX]{x1D6FF}_{ij}$
if
![]() $i+j$
is large enough.
$i+j$
is large enough.
Let
 $\operatorname{Mat}(n,F)$
and
$\operatorname{Mat}(n,F)$
and
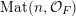 $\operatorname{Mat}(n,{\mathcal{O}}_{F})$
denote the spaces of all
$\operatorname{Mat}(n,{\mathcal{O}}_{F})$
denote the spaces of all
![]() $n\times n$
matrices over
$n\times n$
matrices over
![]() $F$
and
$F$
and
![]() ${\mathcal{O}}_{F}$
respectively. Define
${\mathcal{O}}_{F}$
respectively. Define
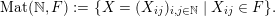 $$\begin{eqnarray}\operatorname{Mat}(\mathbb{N},F):=\{X=(X_{ij})_{i,j\in \mathbb{N}}\mid X_{ij}\in F\}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Mat}(\mathbb{N},F):=\{X=(X_{ij})_{i,j\in \mathbb{N}}\mid X_{ij}\in F\}.\end{eqnarray}$$
Let
 $\operatorname{Mat}(\infty ,F)$
denote the subspace of
$\operatorname{Mat}(\infty ,F)$
denote the subspace of
 $\operatorname{Mat}(\mathbb{N},F)$
consisting of matrices whose all but a finite number of coefficients are zeros. Define also
$\operatorname{Mat}(\mathbb{N},F)$
consisting of matrices whose all but a finite number of coefficients are zeros. Define also
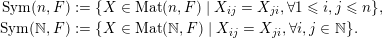 $$\begin{eqnarray}\displaystyle \operatorname{Sym}(n,F) & := & \displaystyle \{X\in \operatorname{Mat}(n,F)\mid X_{ij}=X_{ji},\forall 1\leqslant i,j\leqslant n\},\nonumber\\ \displaystyle \operatorname{Sym}(\mathbb{N},F) & := & \displaystyle \{X\in \operatorname{Mat}(\mathbb{N},F)\mid X_{ij}=X_{ji},\forall i,j\in \mathbb{N}\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Sym}(n,F) & := & \displaystyle \{X\in \operatorname{Mat}(n,F)\mid X_{ij}=X_{ji},\forall 1\leqslant i,j\leqslant n\},\nonumber\\ \displaystyle \operatorname{Sym}(\mathbb{N},F) & := & \displaystyle \{X\in \operatorname{Mat}(\mathbb{N},F)\mid X_{ij}=X_{ji},\forall i,j\in \mathbb{N}\}.\nonumber\end{eqnarray}$$
Set
 $\operatorname{Sym}(\infty ,F):=\operatorname{Sym}(\mathbb{N},F)\cap \operatorname{Mat}(\infty ,F)$
.
$\operatorname{Sym}(\infty ,F):=\operatorname{Sym}(\mathbb{N},F)\cap \operatorname{Mat}(\infty ,F)$
.
Two natural group actions under consideration in this paper are:
-
– the group action of
 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
on
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
on
 $\operatorname{Mat}(\mathbb{N},F)$
defined by
$\operatorname{Mat}(\mathbb{N},F)$
defined by  $$\begin{eqnarray}\displaystyle ((g_{1},g_{2}),M)\mapsto g_{1}Mg_{2}^{-1},\quad g_{1},g_{2}\in \operatorname{GL}(\infty ,{\mathcal{O}}_{F}),\quad M\in \operatorname{Mat}(\mathbb{N},F); & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle ((g_{1},g_{2}),M)\mapsto g_{1}Mg_{2}^{-1},\quad g_{1},g_{2}\in \operatorname{GL}(\infty ,{\mathcal{O}}_{F}),\quad M\in \operatorname{Mat}(\mathbb{N},F); & & \displaystyle \nonumber\end{eqnarray}$$
-
– the group action of
 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
on
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
on
 $\operatorname{Sym}(\mathbb{N},F)$
defined by where
$\operatorname{Sym}(\mathbb{N},F)$
defined by where $$\begin{eqnarray}\displaystyle (g,M)\mapsto gMg^{t},\quad g\in \operatorname{GL}(\infty ,{\mathcal{O}}_{F}),\quad S\in \operatorname{Sym}(\mathbb{N},F), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (g,M)\mapsto gMg^{t},\quad g\in \operatorname{GL}(\infty ,{\mathcal{O}}_{F}),\quad S\in \operatorname{Sym}(\mathbb{N},F), & & \displaystyle \nonumber\end{eqnarray}$$
 $g^{t}$
is the transposition of
$g^{t}$
is the transposition of
 $g$
.
$g$
.
2.4 Conventions
Given a finite set
![]() $B$
, we denote by
$B$
, we denote by
![]() $\#B$
its cardinality.
$\#B$
its cardinality.
Let
 $(\unicode[STIX]{x1D6F4},{\mathcal{B}},m)$
be a measurable space equipped with a positive measure
$(\unicode[STIX]{x1D6F4},{\mathcal{B}},m)$
be a measurable space equipped with a positive measure
![]() $m$
and let
$m$
and let
![]() $f$
be a real or complex valued integrable function defined on
$f$
be a real or complex valued integrable function defined on
![]() $\unicode[STIX]{x1D6F4}$
. If
$\unicode[STIX]{x1D6F4}$
. If
![]() $A\subset \unicode[STIX]{x1D6F4}$
is measurable and
$A\subset \unicode[STIX]{x1D6F4}$
is measurable and
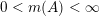 $0<m(A)<\infty$
, then we write
$0<m(A)<\infty$
, then we write
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x2A0D}_{A}f(x)\,dm(x):=\frac{1}{m(A)}\int _{A}f(x)\,dm(x). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x2A0D}_{A}f(x)\,dm(x):=\frac{1}{m(A)}\int _{A}f(x)\,dm(x). & & \displaystyle\end{eqnarray}$$
For any random variable
![]() $Y$
, we denote its distribution by
$Y$
, we denote its distribution by
![]() ${\mathcal{L}}(Y)$
.
${\mathcal{L}}(Y)$
.
We establish conventions concerning the empty set
![]() $\emptyset$
. Let
$\emptyset$
. Let
![]() $(r_{i})_{i\in I}$
be a family of real numbers (or complex numbers for the last two formulae). We set
$(r_{i})_{i\in I}$
be a family of real numbers (or complex numbers for the last two formulae). We set
 $$\begin{eqnarray}\inf _{i\in \emptyset }r_{i}=+\infty ,\quad \sup _{i\in \emptyset }r_{i}=-\infty ,\quad \mathop{\sum }_{i\in \emptyset }r_{i}=0,\quad \mathop{\prod }_{i\in \emptyset }r_{i}=1.\end{eqnarray}$$
$$\begin{eqnarray}\inf _{i\in \emptyset }r_{i}=+\infty ,\quad \sup _{i\in \emptyset }r_{i}=-\infty ,\quad \mathop{\sum }_{i\in \emptyset }r_{i}=0,\quad \mathop{\prod }_{i\in \emptyset }r_{i}=1.\end{eqnarray}$$
The following conventions will also be used.
-
– As elements in
 $F$
,
$F$
,
 $\unicode[STIX]{x1D71B}^{\infty }=\unicode[STIX]{x1D71B}^{+\infty }=0\in F$
.
$\unicode[STIX]{x1D71B}^{\infty }=\unicode[STIX]{x1D71B}^{+\infty }=0\in F$
. -
– As elements in
 $\mathbb{R}\cup \{+\infty \}$
,
$\mathbb{R}\cup \{+\infty \}$
,
 $q^{\infty }=q^{+\infty }=+\infty$
and
$q^{\infty }=q^{+\infty }=+\infty$
and
 $q^{-\infty }=0\in \mathbb{R}$
.
$q^{-\infty }=0\in \mathbb{R}$
.
2.5 Haar measure on
 $\operatorname{GL}(n,{\mathcal{O}}_{F})$
$\operatorname{GL}(n,{\mathcal{O}}_{F})$
For any
![]() $n\in \mathbb{N}$
, denote by
$n\in \mathbb{N}$
, denote by
![]() $d\text{vol}_{n}$
the Haar measure on
$d\text{vol}_{n}$
the Haar measure on
![]() $F^{n}$
normalized by the condition
$F^{n}$
normalized by the condition
 $\operatorname{vol}_{n}({\mathcal{O}}_{F}^{n})=1$
. If there is no confusion, we will use the simplified notation
$\operatorname{vol}_{n}({\mathcal{O}}_{F}^{n})=1$
. If there is no confusion, we will use the simplified notation
![]() $\operatorname{vol}(\cdot )$
for
$\operatorname{vol}(\cdot )$
for
![]() $\operatorname{vol}_{n}(\cdot )$
.
$\operatorname{vol}_{n}(\cdot )$
.
Remark 2.1. The Haar measure
![]() $\operatorname{vol}_{n}$
on
$\operatorname{vol}_{n}$
on
![]() $F^{n}$
is preserved by any linear map represented by a matrix from the group
$F^{n}$
is preserved by any linear map represented by a matrix from the group
 $\operatorname{GL}(n,{\mathcal{O}}_{F})$
.
$\operatorname{GL}(n,{\mathcal{O}}_{F})$
.
For any
![]() $n$
, we fix a Haar measure
$n$
, we fix a Haar measure
![]() $\operatorname{vol}(\cdot )$
on
$\operatorname{vol}(\cdot )$
on
 $\operatorname{Mat}(n,F)$
normalized by
$\operatorname{Mat}(n,F)$
normalized by
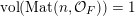 $\operatorname{vol}(\operatorname{Mat}(n,{\mathcal{O}}_{F}))=1$
. Up to a multiplicative constant, the Haar measure on the locally compact group
$\operatorname{vol}(\operatorname{Mat}(n,{\mathcal{O}}_{F}))=1$
. Up to a multiplicative constant, the Haar measure on the locally compact group
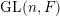 $\operatorname{GL}(n,F)$
is uniquely given (see, e.g., Neretin [Reference NeretinNer13]) by
$\operatorname{GL}(n,F)$
is uniquely given (see, e.g., Neretin [Reference NeretinNer13]) by
 $$\begin{eqnarray}\displaystyle |\text{det}(M)|^{-n}\cdot \operatorname{vol}(dM). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\text{det}(M)|^{-n}\cdot \operatorname{vol}(dM). & & \displaystyle\end{eqnarray}$$
Let
 $\operatorname{GL}(n,\mathbf{F}_{q})$
be the group of invertible
$\operatorname{GL}(n,\mathbf{F}_{q})$
be the group of invertible
![]() $n\times n$
matrices over
$n\times n$
matrices over
![]() $\mathbf{F}_{q}$
. Set
$\mathbf{F}_{q}$
. Set
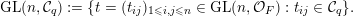 $$\begin{eqnarray}\displaystyle \operatorname{GL}(n,{\mathcal{C}}_{q}):=\{t=(t_{ij})_{1\leqslant i,j\leqslant n}\in \operatorname{GL}(n,{\mathcal{O}}_{F}):t_{ij}\in {\mathcal{C}}_{q}\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{GL}(n,{\mathcal{C}}_{q}):=\{t=(t_{ij})_{1\leqslant i,j\leqslant n}\in \operatorname{GL}(n,{\mathcal{O}}_{F}):t_{ij}\in {\mathcal{C}}_{q}\}. & & \displaystyle \nonumber\end{eqnarray}$$
Proposition 2.2. A standard partition of
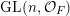 $\operatorname{GL}(n,{\mathcal{O}}_{F})$
is given by
$\operatorname{GL}(n,{\mathcal{O}}_{F})$
is given by
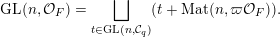 $$\begin{eqnarray}\displaystyle \operatorname{GL}(n,{\mathcal{O}}_{F})=\bigsqcup _{t\in \operatorname{GL}(n,{\mathcal{C}}_{q})}(t+\operatorname{Mat}(n,\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{GL}(n,{\mathcal{O}}_{F})=\bigsqcup _{t\in \operatorname{GL}(n,{\mathcal{C}}_{q})}(t+\operatorname{Mat}(n,\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})). & & \displaystyle\end{eqnarray}$$
In particular, we have
 $$\begin{eqnarray}\displaystyle \operatorname{vol}(\operatorname{GL}(n,{\mathcal{O}}_{F}))=\mathop{\prod }_{j=1}^{n}(1-q^{-j}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{vol}(\operatorname{GL}(n,{\mathcal{O}}_{F}))=\mathop{\prod }_{j=1}^{n}(1-q^{-j}). & & \displaystyle\end{eqnarray}$$
Proof. By definition,
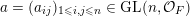 $a=(a_{ij})_{1\leqslant i,j\leqslant n}\in \operatorname{GL}(n,{\mathcal{O}}_{F})$
implies that
$a=(a_{ij})_{1\leqslant i,j\leqslant n}\in \operatorname{GL}(n,{\mathcal{O}}_{F})$
implies that
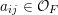 $a_{ij}\in {\mathcal{O}}_{F}$
and
$a_{ij}\in {\mathcal{O}}_{F}$
and
 $|\text{det}(a)|=1$
. Now take any
$|\text{det}(a)|=1$
. Now take any
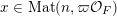 $x\in \operatorname{Mat}(n,\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})$
. First, we have
$x\in \operatorname{Mat}(n,\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})$
. First, we have
 $a+x\in \operatorname{Mat}(n,{\mathcal{O}}_{F})$
. Second, write
$a+x\in \operatorname{Mat}(n,{\mathcal{O}}_{F})$
. Second, write
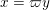 $x=\unicode[STIX]{x1D71B}y$
with
$x=\unicode[STIX]{x1D71B}y$
with
 $y\in \operatorname{Mat}(n,{\mathcal{O}}_{F})$
. By definition, there exists
$y\in \operatorname{Mat}(n,{\mathcal{O}}_{F})$
. By definition, there exists
![]() $z\in {\mathcal{O}}_{F}$
, such that
$z\in {\mathcal{O}}_{F}$
, such that
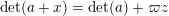 $\det (a+x)=\det (a)+\unicode[STIX]{x1D71B}z$
. Since
$\det (a+x)=\det (a)+\unicode[STIX]{x1D71B}z$
. Since
 $|\unicode[STIX]{x1D71B}z|\leqslant q^{-1}$
, by ultrametricity, we obtain
$|\unicode[STIX]{x1D71B}z|\leqslant q^{-1}$
, by ultrametricity, we obtain
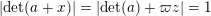 $|\text{det}(a+x)|=|\text{det}(a)+\unicode[STIX]{x1D71B}z|=1$
, whence
$|\text{det}(a+x)|=|\text{det}(a)+\unicode[STIX]{x1D71B}z|=1$
, whence
 $a+x\in \operatorname{GL}(n,{\mathcal{O}}_{F})$
and the set on the right-hand side of (16) is contained in
$a+x\in \operatorname{GL}(n,{\mathcal{O}}_{F})$
and the set on the right-hand side of (16) is contained in
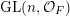 $\operatorname{GL}(n,{\mathcal{O}}_{F})$
. Conversely, since
$\operatorname{GL}(n,{\mathcal{O}}_{F})$
. Conversely, since
![]() ${\mathcal{C}}_{q}$
is a complete set of representatives of the cosets of
${\mathcal{C}}_{q}$
is a complete set of representatives of the cosets of
![]() $\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
in
$\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
in
![]() ${\mathcal{O}}_{F}$
, for any
${\mathcal{O}}_{F}$
, for any
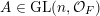 $A\in \operatorname{GL}(n,{\mathcal{O}}_{F})$
, there exists a unique
$A\in \operatorname{GL}(n,{\mathcal{O}}_{F})$
, there exists a unique
 $t\in \operatorname{GL}(n,{\mathcal{C}}_{q})$
, such that
$t\in \operatorname{GL}(n,{\mathcal{C}}_{q})$
, such that
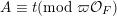 $A\equiv t(\operatorname{mod}\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})$
. This completes the proof of (16).
$A\equiv t(\operatorname{mod}\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})$
. This completes the proof of (16).
Recalling that
 $$\begin{eqnarray}\displaystyle \#\text{GL}(n,{\mathcal{C}}_{q})=\#\text{GL}(n,\mathbf{F}_{q})=\mathop{\prod }_{j=0}^{n-1}(q^{n}-q^{j}), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \#\text{GL}(n,{\mathcal{C}}_{q})=\#\text{GL}(n,\mathbf{F}_{q})=\mathop{\prod }_{j=0}^{n-1}(q^{n}-q^{j}), & & \displaystyle \nonumber\end{eqnarray}$$
we arrive at (17). ◻
By Proposition 2.2,
 $\operatorname{GL}(n,{\mathcal{O}}_{F})$
is an open subgroup of
$\operatorname{GL}(n,{\mathcal{O}}_{F})$
is an open subgroup of
 $\operatorname{GL}(n,F)$
. It follows that the restriction on
$\operatorname{GL}(n,F)$
. It follows that the restriction on
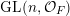 $\operatorname{GL}(n,{\mathcal{O}}_{F})$
of the Haar measure (15) on
$\operatorname{GL}(n,{\mathcal{O}}_{F})$
of the Haar measure (15) on
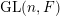 $\operatorname{GL}(n,F)$
is a Haar measure on
$\operatorname{GL}(n,F)$
is a Haar measure on
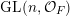 $\operatorname{GL}(n,{\mathcal{O}}_{F})$
. Consequently, the normalized Haar measure on
$\operatorname{GL}(n,{\mathcal{O}}_{F})$
. Consequently, the normalized Haar measure on
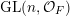 $\operatorname{GL}(n,{\mathcal{O}}_{F})$
is given by
$\operatorname{GL}(n,{\mathcal{O}}_{F})$
is given by
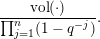 $$\begin{eqnarray}\displaystyle \frac{\operatorname{vol}(\cdot )}{\mathop{\prod }_{j=1}^{n}(1-q^{-j})}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\operatorname{vol}(\cdot )}{\mathop{\prod }_{j=1}^{n}(1-q^{-j})}. & & \displaystyle\end{eqnarray}$$
Let
![]() $T(n)$
be sampled uniformly from the finite set
$T(n)$
be sampled uniformly from the finite set
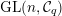 $\operatorname{GL}(n,{\mathcal{C}}_{q})$
; let
$\operatorname{GL}(n,{\mathcal{C}}_{q})$
; let
![]() $V(n)$
be sampled with respect to the normalized Haar measure on
$V(n)$
be sampled with respect to the normalized Haar measure on
 $\operatorname{Mat}(n,\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})$
and independent of
$\operatorname{Mat}(n,\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})$
and independent of
![]() $T(n)$
.
$T(n)$
.
Proposition 2.3. The random matrix
 $T(n)+V(n)$
is a Haar random matrix on
$T(n)+V(n)$
is a Haar random matrix on
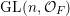 $\operatorname{GL}(n,{\mathcal{O}}_{F})$
; that is, the distribution law
$\operatorname{GL}(n,{\mathcal{O}}_{F})$
; that is, the distribution law
 ${\mathcal{L}}(T(n)+V(n))$
coincides with the normalized Haar measure on
${\mathcal{L}}(T(n)+V(n))$
coincides with the normalized Haar measure on
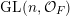 $\operatorname{GL}(n,{\mathcal{O}}_{F})$
.
$\operatorname{GL}(n,{\mathcal{O}}_{F})$
.
2.6 Diagonalization in
 $\operatorname{Mat}(n,F)$
$\operatorname{Mat}(n,F)$
Lemma 2.4 (See, e.g., Neretin [Reference NeretinNer13, § 1.3]).
Every matrix
 $A\in \operatorname{Mat}(n,F)$
can be written in the form
$A\in \operatorname{Mat}(n,F)$
can be written in the form
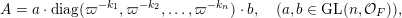 $$\begin{eqnarray}\displaystyle A=a\cdot \operatorname{diag}(\unicode[STIX]{x1D71B}^{-k_{1}},\unicode[STIX]{x1D71B}^{-k_{2}},\ldots ,\unicode[STIX]{x1D71B}^{-k_{n}})\cdot b,\quad (a,b\in \operatorname{GL}(n,{\mathcal{O}}_{F})), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A=a\cdot \operatorname{diag}(\unicode[STIX]{x1D71B}^{-k_{1}},\unicode[STIX]{x1D71B}^{-k_{2}},\ldots ,\unicode[STIX]{x1D71B}^{-k_{n}})\cdot b,\quad (a,b\in \operatorname{GL}(n,{\mathcal{O}}_{F})), & & \displaystyle\end{eqnarray}$$
where
 $k_{1}\geqslant k_{2}\geqslant \cdots \geqslant k_{n}\geqslant -\infty$
and
$k_{1}\geqslant k_{2}\geqslant \cdots \geqslant k_{n}\geqslant -\infty$
and
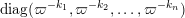 $\operatorname{diag}(\unicode[STIX]{x1D71B}^{-k_{1}},\unicode[STIX]{x1D71B}^{-k_{2}},\ldots ,\unicode[STIX]{x1D71B}^{-k_{n}})$
is the diagonal matrix with diagonal coefficients
$\operatorname{diag}(\unicode[STIX]{x1D71B}^{-k_{1}},\unicode[STIX]{x1D71B}^{-k_{2}},\ldots ,\unicode[STIX]{x1D71B}^{-k_{n}})$
is the diagonal matrix with diagonal coefficients
 $\unicode[STIX]{x1D71B}^{-k_{1}},\unicode[STIX]{x1D71B}^{-k_{2}},\ldots ,\unicode[STIX]{x1D71B}^{-k_{n}}$
. Moreover, the
$\unicode[STIX]{x1D71B}^{-k_{1}},\unicode[STIX]{x1D71B}^{-k_{2}},\ldots ,\unicode[STIX]{x1D71B}^{-k_{n}}$
. Moreover, the
![]() $n$
-tuple
$n$
-tuple
 $(k_{1},k_{2},\ldots ,k_{n})$
is uniquely determined by the matrix
$(k_{1},k_{2},\ldots ,k_{n})$
is uniquely determined by the matrix
![]() $A$
.
$A$
.
2.7 Square-units in
 $F$
$F$
The group of units of the ring
![]() ${\mathcal{O}}_{F}$
is given by
${\mathcal{O}}_{F}$
is given by
 ${\mathcal{O}}_{F}^{\times }:=\{x\in F:|x|=1\}$
. Let
${\mathcal{O}}_{F}^{\times }:=\{x\in F:|x|=1\}$
. Let
![]() $({\mathcal{O}}_{F}^{\times })^{2}$
be the subgroup of
$({\mathcal{O}}_{F}^{\times })^{2}$
be the subgroup of
![]() ${\mathcal{O}}_{F}^{\times }$
defined by
${\mathcal{O}}_{F}^{\times }$
defined by
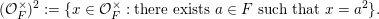 $$\begin{eqnarray}\displaystyle ({\mathcal{O}}_{F}^{\times })^{2}:=\{x\in {\mathcal{O}}_{F}^{\times }:\text{there exists }a\in F\text{ such that }x=a^{2}\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle ({\mathcal{O}}_{F}^{\times })^{2}:=\{x\in {\mathcal{O}}_{F}^{\times }:\text{there exists }a\in F\text{ such that }x=a^{2}\}. & & \displaystyle \nonumber\end{eqnarray}$$
Let
![]() ${\mathcal{C}}_{q}^{\times }$
denote the set
${\mathcal{C}}_{q}^{\times }$
denote the set
 ${\mathcal{C}}_{q}\,\setminus \,\{0\}$
and define
${\mathcal{C}}_{q}\,\setminus \,\{0\}$
and define
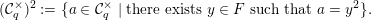 $$\begin{eqnarray}\displaystyle ({\mathcal{C}}_{q}^{\times })^{2}:=\{a\in {\mathcal{C}}_{q}^{\times }\mid \text{there exists }y\in F\text{ such that }a=y^{2}\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle ({\mathcal{C}}_{q}^{\times })^{2}:=\{a\in {\mathcal{C}}_{q}^{\times }\mid \text{there exists }y\in F\text{ such that }a=y^{2}\}. & & \displaystyle \nonumber\end{eqnarray}$$
Write
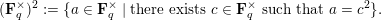 $$\begin{eqnarray}\displaystyle (\mathbf{F}_{q}^{\times })^{2}:=\{a\in \mathbf{F}_{q}^{\times }\mid \text{there exists }c\in \mathbf{F}_{q}^{\times }\text{such that }a=c^{2}\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\mathbf{F}_{q}^{\times })^{2}:=\{a\in \mathbf{F}_{q}^{\times }\mid \text{there exists }c\in \mathbf{F}_{q}^{\times }\text{such that }a=c^{2}\}. & & \displaystyle \nonumber\end{eqnarray}$$
Lemma 2.5. Assume that
![]() $F$
is non-dyadic. Then
$F$
is non-dyadic. Then
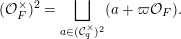 $$\begin{eqnarray}\displaystyle ({\mathcal{O}}_{F}^{\times })^{2}=\bigsqcup _{a\in ({\mathcal{C}}_{q}^{\times })^{2}}(a+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle ({\mathcal{O}}_{F}^{\times })^{2}=\bigsqcup _{a\in ({\mathcal{C}}_{q}^{\times })^{2}}(a+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}). & & \displaystyle\end{eqnarray}$$
Consequently, the map
![]() $\unicode[STIX]{x1D70B}$
in (11) induces a bijection:
$\unicode[STIX]{x1D70B}$
in (11) induces a bijection:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}:({\mathcal{C}}_{q}^{\times })^{2}\xrightarrow[{}]{\mathit{bijection}}(\mathbf{F}_{q}^{\times })^{2}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}:({\mathcal{C}}_{q}^{\times })^{2}\xrightarrow[{}]{\mathit{bijection}}(\mathbf{F}_{q}^{\times })^{2}. & & \displaystyle\end{eqnarray}$$
Proof. Since
![]() $F$
is non-dyadic, we have
$F$
is non-dyadic, we have
![]() $|2|=1$
. For any
$|2|=1$
. For any
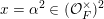 $x=\unicode[STIX]{x1D6FC}^{2}\in ({\mathcal{O}}_{F}^{\times })^{2}$
, since
$x=\unicode[STIX]{x1D6FC}^{2}\in ({\mathcal{O}}_{F}^{\times })^{2}$
, since
![]() ${\mathcal{C}}_{q}$
is a complete set of representatives for
${\mathcal{C}}_{q}$
is a complete set of representatives for
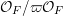 ${\mathcal{O}}_{F}/\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
, there exists
${\mathcal{O}}_{F}/\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
, there exists
![]() $a\in {\mathcal{C}}_{q}^{\times }$
, such that
$a\in {\mathcal{C}}_{q}^{\times }$
, such that
 $x\equiv a(\operatorname{mod}\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})$
, that is,
$x\equiv a(\operatorname{mod}\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})$
, that is,
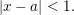 $$\begin{eqnarray}\displaystyle |x-a|<1. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |x-a|<1. & & \displaystyle\end{eqnarray}$$
Take any
![]() $b\in {\mathcal{O}}_{F}^{\times }$
such that
$b\in {\mathcal{O}}_{F}^{\times }$
such that
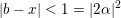 $|b-x|<1=|2\unicode[STIX]{x1D6FC}|^{2}$
. Then the polynomial
$|b-x|<1=|2\unicode[STIX]{x1D6FC}|^{2}$
. Then the polynomial
 $P_{b}(X)=X^{2}-b\in {\mathcal{O}}_{F}[X]$
satisfies
$P_{b}(X)=X^{2}-b\in {\mathcal{O}}_{F}[X]$
satisfies
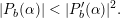 $$\begin{eqnarray}\displaystyle |P_{b}(\unicode[STIX]{x1D6FC})|<|P_{b}^{\prime }(\unicode[STIX]{x1D6FC})|^{2}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |P_{b}(\unicode[STIX]{x1D6FC})|<|P_{b}^{\prime }(\unicode[STIX]{x1D6FC})|^{2}. & & \displaystyle\end{eqnarray}$$
By Hensel’s lemma (see Cassels [Reference CasselsCas86, pp. 49–51]), the inequality (23) implies that there exists
![]() $\unicode[STIX]{x1D6FD}\in F$
such that
$\unicode[STIX]{x1D6FD}\in F$
such that
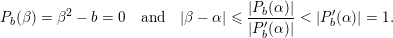 $$\begin{eqnarray}\displaystyle P_{b}(\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D6FD}^{2}-b=0\quad \text{and}\quad |\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FC}|\leqslant \frac{|P_{b}(\unicode[STIX]{x1D6FC})|}{|P_{b}^{\prime }(\unicode[STIX]{x1D6FC})|}<|P_{b}^{\prime }(\unicode[STIX]{x1D6FC})|=1. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{b}(\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D6FD}^{2}-b=0\quad \text{and}\quad |\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FC}|\leqslant \frac{|P_{b}(\unicode[STIX]{x1D6FC})|}{|P_{b}^{\prime }(\unicode[STIX]{x1D6FC})|}<|P_{b}^{\prime }(\unicode[STIX]{x1D6FC})|=1. & & \displaystyle\end{eqnarray}$$
In particular, we have
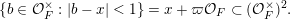 $$\begin{eqnarray}\displaystyle \{b\in {\mathcal{O}}_{F}^{\times }:|b-x|<1\}=x+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}\subset ({\mathcal{O}}_{F}^{\times })^{2}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \{b\in {\mathcal{O}}_{F}^{\times }:|b-x|<1\}=x+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}\subset ({\mathcal{O}}_{F}^{\times })^{2}. & & \displaystyle\end{eqnarray}$$
Combining (22) and (25), we get
 $a\in ({\mathcal{O}}_{F}^{\times })^{2}$
. Hence
$a\in ({\mathcal{O}}_{F}^{\times })^{2}$
. Hence
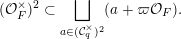 $$\begin{eqnarray}\displaystyle ({\mathcal{O}}_{F}^{\times })^{2}\subset \bigsqcup _{a\in ({\mathcal{C}}_{q}^{\times })^{2}}(a+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle ({\mathcal{O}}_{F}^{\times })^{2}\subset \bigsqcup _{a\in ({\mathcal{C}}_{q}^{\times })^{2}}(a+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}). & & \displaystyle \nonumber\end{eqnarray}$$
Conversely, since
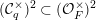 $({\mathcal{C}}_{q}^{\times })^{2}\subset ({\mathcal{O}}_{F}^{\times })^{2}$
, for any
$({\mathcal{C}}_{q}^{\times })^{2}\subset ({\mathcal{O}}_{F}^{\times })^{2}$
, for any
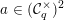 $a\in ({\mathcal{C}}_{q}^{\times })^{2}$
, replacing
$a\in ({\mathcal{C}}_{q}^{\times })^{2}$
, replacing
![]() $x$
by
$x$
by
![]() $a$
in the above argument, the inclusion (25) implies
$a$
in the above argument, the inclusion (25) implies
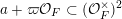 $a+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}\subset ({\mathcal{O}}_{F}^{\times })^{2}$
. Hence
$a+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}\subset ({\mathcal{O}}_{F}^{\times })^{2}$
. Hence
 $$\begin{eqnarray}\displaystyle \text{}\bigsqcup _{a\in ({\mathcal{C}}_{q}^{\times })^{2}}(a+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})\subset ({\mathcal{O}}_{F}^{\times })^{2}.\Box & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{}\bigsqcup _{a\in ({\mathcal{C}}_{q}^{\times })^{2}}(a+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})\subset ({\mathcal{O}}_{F}^{\times })^{2}.\Box & & \displaystyle \nonumber\end{eqnarray}$$
Remark 2.6. Recall that if
![]() $F$
is non-dyadic, then the quotient group
$F$
is non-dyadic, then the quotient group
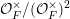 ${\mathcal{O}}_{F}^{\times }/({\mathcal{O}}_{F}^{\times })^{2}$
has two elements.
${\mathcal{O}}_{F}^{\times }/({\mathcal{O}}_{F}^{\times })^{2}$
has two elements.
2.8 Diagonalization in
 $\operatorname{Sym}(n,F)$
$\operatorname{Sym}(n,F)$
In what follows, we fix a non-square unit
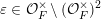 $\unicode[STIX]{x1D700}\in {\mathcal{O}}_{F}^{\times }\,\setminus \,({\mathcal{O}}_{F}^{\times })^{2}$
. By Remark 2.6, the following set
$\unicode[STIX]{x1D700}\in {\mathcal{O}}_{F}^{\times }\,\setminus \,({\mathcal{O}}_{F}^{\times })^{2}$
. By Remark 2.6, the following set
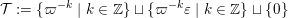 $$\begin{eqnarray}\displaystyle {\mathcal{T}}:=\{\unicode[STIX]{x1D71B}^{-k}\mid k\in \mathbb{Z}\}\sqcup \{\unicode[STIX]{x1D71B}^{-k}\unicode[STIX]{x1D700}\mid k\in \mathbb{Z}\}\sqcup \{0\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{T}}:=\{\unicode[STIX]{x1D71B}^{-k}\mid k\in \mathbb{Z}\}\sqcup \{\unicode[STIX]{x1D71B}^{-k}\unicode[STIX]{x1D700}\mid k\in \mathbb{Z}\}\sqcup \{0\} & & \displaystyle\end{eqnarray}$$
is a complete set of representatives for the quotient
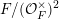 $F/({\mathcal{O}}_{F}^{\times })^{2}$
.
$F/({\mathcal{O}}_{F}^{\times })^{2}$
.
Lemma 2.7. Assume that
![]() $F$
is non-dyadic. Then any symmetric matrix
$F$
is non-dyadic. Then any symmetric matrix
 $A\in \operatorname{Sym}(n,F)$
can be written in the form
$A\in \operatorname{Sym}(n,F)$
can be written in the form
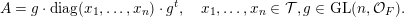 $$\begin{eqnarray}\displaystyle A=g\cdot \operatorname{diag}(x_{1},\ldots ,x_{n})\cdot g^{t},\quad x_{1},\ldots ,x_{n}\in {\mathcal{T}},g\in \operatorname{GL}(n,{\mathcal{O}}_{F}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A=g\cdot \operatorname{diag}(x_{1},\ldots ,x_{n})\cdot g^{t},\quad x_{1},\ldots ,x_{n}\in {\mathcal{T}},g\in \operatorname{GL}(n,{\mathcal{O}}_{F}). & & \displaystyle \nonumber\end{eqnarray}$$
Proof. Since
![]() ${\mathcal{T}}$
is a complete set of representatives for the quotient
${\mathcal{T}}$
is a complete set of representatives for the quotient
 $F/({\mathcal{O}}_{F}^{\times })^{2}$
, it suffices to show that any symmetric matrix
$F/({\mathcal{O}}_{F}^{\times })^{2}$
, it suffices to show that any symmetric matrix
 $A\in \operatorname{Sym}(n,F)$
is diagonalizable. Assume that
$A\in \operatorname{Sym}(n,F)$
is diagonalizable. Assume that
![]() $A$
is not a zero matrix. We claim that, up to passing
$A$
is not a zero matrix. We claim that, up to passing
![]() $A$
to
$A$
to
![]() $gAg^{t}$
for some
$gAg^{t}$
for some
 $g\in \operatorname{GL}(n,{\mathcal{O}}_{F})$
, we may assume that the
$g\in \operatorname{GL}(n,{\mathcal{O}}_{F})$
, we may assume that the
![]() $(1,1)$
-coefficient of
$(1,1)$
-coefficient of
![]() $A$
has maximal absolute value.
$A$
has maximal absolute value.
Case 1: Assume first that there exists
 $1\leqslant i_{0}\leqslant n$
, such that
$1\leqslant i_{0}\leqslant n$
, such that
 $|A_{i_{0}i_{0}}|=\max _{1\leqslant i,j\leqslant n}|A_{ij}|$
. If
$|A_{i_{0}i_{0}}|=\max _{1\leqslant i,j\leqslant n}|A_{ij}|$
. If
![]() $i_{0}=1$
, then there is nothing to prove. Otherwise, take
$i_{0}=1$
, then there is nothing to prove. Otherwise, take
 $g=M_{(1i_{0})}$
, where
$g=M_{(1i_{0})}$
, where
![]() $M_{(1i_{0})}$
is the permutation matrix associated with the transposition
$M_{(1i_{0})}$
is the permutation matrix associated with the transposition
![]() $(1i_{0})$
. Then the matrix
$(1i_{0})$
. Then the matrix
![]() $gAg^{t}$
has
$gAg^{t}$
has
![]() $A_{i_{0}i_{0}}$
as its
$A_{i_{0}i_{0}}$
as its
![]() $(1,1)$
-coefficient.
$(1,1)$
-coefficient.
Case 2: Now assume that there exists
![]() $i_{0}<j_{0}$
such that
$i_{0}<j_{0}$
such that
 $$\begin{eqnarray}\displaystyle |A_{i_{0}j_{0}}|=\max _{1\leqslant i,j\leqslant n}|A_{ij}|>\max _{1\leqslant i\leqslant n}|A_{ii}|. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |A_{i_{0}j_{0}}|=\max _{1\leqslant i,j\leqslant n}|A_{ij}|>\max _{1\leqslant i\leqslant n}|A_{ii}|. & & \displaystyle\end{eqnarray}$$
Let us do operations on the submatrix indexed by
 $\{i_{0},j_{0}\}\times \{i_{0},j_{0}\}$
as follows:
$\{i_{0},j_{0}\}\times \{i_{0},j_{0}\}$
as follows:
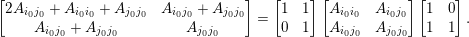 $$\begin{eqnarray}\displaystyle \left[\begin{array}{@{}cc@{}}2A_{i_{0}j_{0}}+A_{i_{0}i_{0}}+A_{j_{0}j_{0}} & A_{i_{0}j_{0}}+A_{j_{0}j_{0}}\\ A_{i_{0}j_{0}}+A_{j_{0}j_{0}} & A_{j_{0}j_{0}}\end{array}\right]=\left[\begin{array}{@{}cc@{}}1 & 1\\ 0 & 1\end{array}\right]\left[\begin{array}{@{}cc@{}}A_{i_{0}i_{0}} & A_{i_{0}j_{0}}\\ A_{i_{0}j_{0}} & A_{j_{0}j_{0}}\end{array}\right]\left[\begin{array}{@{}cc@{}}1 & 0\\ 1 & 1\end{array}\right]. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left[\begin{array}{@{}cc@{}}2A_{i_{0}j_{0}}+A_{i_{0}i_{0}}+A_{j_{0}j_{0}} & A_{i_{0}j_{0}}+A_{j_{0}j_{0}}\\ A_{i_{0}j_{0}}+A_{j_{0}j_{0}} & A_{j_{0}j_{0}}\end{array}\right]=\left[\begin{array}{@{}cc@{}}1 & 1\\ 0 & 1\end{array}\right]\left[\begin{array}{@{}cc@{}}A_{i_{0}i_{0}} & A_{i_{0}j_{0}}\\ A_{i_{0}j_{0}} & A_{j_{0}j_{0}}\end{array}\right]\left[\begin{array}{@{}cc@{}}1 & 0\\ 1 & 1\end{array}\right]. & & \displaystyle \nonumber\end{eqnarray}$$
Since
![]() $F$
is non-dyadic and non-Archimedean, (27) implies
$F$
is non-dyadic and non-Archimedean, (27) implies
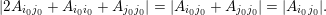 $$\begin{eqnarray}\displaystyle |2A_{i_{0}j_{0}}+A_{i_{0}i_{0}}+A_{j_{0}j_{0}}|=|A_{i_{0}j_{0}}+A_{j_{0}j_{0}}|=|A_{i_{0}j_{0}}|. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |2A_{i_{0}j_{0}}+A_{i_{0}i_{0}}+A_{j_{0}j_{0}}|=|A_{i_{0}j_{0}}+A_{j_{0}j_{0}}|=|A_{i_{0}j_{0}}|. & & \displaystyle \nonumber\end{eqnarray}$$
This shows that we can reduce the second case to the first case where a diagonal coefficient has maximal absolute value.
Now assume that
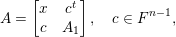 $$\begin{eqnarray}\displaystyle A=\left[\begin{array}{@{}cc@{}}x & c^{t}\\ c & A_{1}\end{array}\right],\quad c\in F^{n-1}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A=\left[\begin{array}{@{}cc@{}}x & c^{t}\\ c & A_{1}\end{array}\right],\quad c\in F^{n-1}, & & \displaystyle \nonumber\end{eqnarray}$$
such that
![]() $x$
attains the maximal absolute value of all coefficients of
$x$
attains the maximal absolute value of all coefficients of
![]() $A$
. Then
$A$
. Then
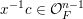 $x^{-1}c\in {\mathcal{O}}_{F}^{n-1}$
and we have
$x^{-1}c\in {\mathcal{O}}_{F}^{n-1}$
and we have
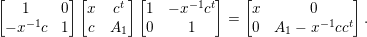 $$\begin{eqnarray}\displaystyle \left[\begin{array}{@{}cc@{}}1 & 0\\ -x^{-1}c & 1\end{array}\right]\left[\begin{array}{@{}cc@{}}x & c^{t}\\ c & A_{1}\end{array}\right]\left[\begin{array}{@{}cc@{}}1 & -x^{-1}c^{t}\\ 0 & 1\end{array}\right]=\left[\begin{array}{@{}cc@{}}x & 0\\ 0 & A_{1}-x^{-1}cc^{t}\end{array}\right]. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left[\begin{array}{@{}cc@{}}1 & 0\\ -x^{-1}c & 1\end{array}\right]\left[\begin{array}{@{}cc@{}}x & c^{t}\\ c & A_{1}\end{array}\right]\left[\begin{array}{@{}cc@{}}1 & -x^{-1}c^{t}\\ 0 & 1\end{array}\right]=\left[\begin{array}{@{}cc@{}}x & 0\\ 0 & A_{1}-x^{-1}cc^{t}\end{array}\right]. & & \displaystyle \nonumber\end{eqnarray}$$
By continuing the above procedure on the submatrix
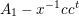 $A_{1}-x^{-1}cc^{t}$
, we prove finally that
$A_{1}-x^{-1}cc^{t}$
, we prove finally that
![]() $A$
is diagonalizable.◻
$A$
is diagonalizable.◻
Remark 2.8. The assumption that
![]() $F$
is non-dyadic is necessary in Lemma 2.7. Indeed, if
$F$
is non-dyadic is necessary in Lemma 2.7. Indeed, if
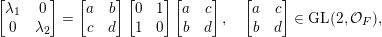 $$\begin{eqnarray}\displaystyle \left[\begin{array}{@{}cc@{}}\unicode[STIX]{x1D706}_{1} & 0\\ 0 & \unicode[STIX]{x1D706}_{2}\end{array}\right]=\left[\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right]\left[\begin{array}{@{}cc@{}}0 & 1\\ 1 & 0\end{array}\right]\left[\begin{array}{@{}cc@{}}a & c\\ b & d\end{array}\right],\quad \left[\begin{array}{@{}cc@{}}a & c\\ b & d\end{array}\right]\in \operatorname{GL}(2,{\mathcal{O}}_{F}), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left[\begin{array}{@{}cc@{}}\unicode[STIX]{x1D706}_{1} & 0\\ 0 & \unicode[STIX]{x1D706}_{2}\end{array}\right]=\left[\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right]\left[\begin{array}{@{}cc@{}}0 & 1\\ 1 & 0\end{array}\right]\left[\begin{array}{@{}cc@{}}a & c\\ b & d\end{array}\right],\quad \left[\begin{array}{@{}cc@{}}a & c\\ b & d\end{array}\right]\in \operatorname{GL}(2,{\mathcal{O}}_{F}), & & \displaystyle \nonumber\end{eqnarray}$$
then
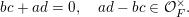 $$\begin{eqnarray}\displaystyle bc+ad=0,\quad ad-bc\in {\mathcal{O}}_{F}^{\times }. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle bc+ad=0,\quad ad-bc\in {\mathcal{O}}_{F}^{\times }. & & \displaystyle \nonumber\end{eqnarray}$$
It follows that
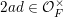 $2ad\in {\mathcal{O}}_{F}^{\times }$
and hence
$2ad\in {\mathcal{O}}_{F}^{\times }$
and hence
![]() $2\in {\mathcal{O}}_{F}^{\times }$
. This implies that
$2\in {\mathcal{O}}_{F}^{\times }$
. This implies that
![]() $F$
is non-dyadic.
$F$
is non-dyadic.
2.9 Characteristic functions
Denote by
![]() $\widehat{F}$
the Pontryagin dual of the additive group
$\widehat{F}$
the Pontryagin dual of the additive group
![]() $F$
. Elements in
$F$
. Elements in
![]() $\widehat{F}$
are called characters of
$\widehat{F}$
are called characters of
![]() $F$
. Throughout the paper, we fix a non-trivial character
$F$
. Throughout the paper, we fix a non-trivial character
![]() $\unicode[STIX]{x1D712}\in \widehat{F}$
such that
$\unicode[STIX]{x1D712}\in \widehat{F}$
such that
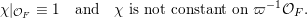 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}|_{{\mathcal{O}}_{F}}\equiv 1\quad \text{and}\quad \unicode[STIX]{x1D712}\text{ is not constant on }\unicode[STIX]{x1D71B}^{-1}{\mathcal{O}}_{F}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}|_{{\mathcal{O}}_{F}}\equiv 1\quad \text{and}\quad \unicode[STIX]{x1D712}\text{ is not constant on }\unicode[STIX]{x1D71B}^{-1}{\mathcal{O}}_{F}. & & \displaystyle\end{eqnarray}$$
For any
![]() $y\in F$
, define a character
$y\in F$
, define a character
![]() $\unicode[STIX]{x1D712}_{y}\in \widehat{F}$
by
$\unicode[STIX]{x1D712}_{y}\in \widehat{F}$
by
 $\unicode[STIX]{x1D712}_{y}(x)=\unicode[STIX]{x1D712}(yx)$
. The map
$\unicode[STIX]{x1D712}_{y}(x)=\unicode[STIX]{x1D712}(yx)$
. The map
![]() $y\mapsto \unicode[STIX]{x1D712}_{y}$
from
$y\mapsto \unicode[STIX]{x1D712}_{y}$
from
![]() $F$
to
$F$
to
![]() $\widehat{F}$
defines a group isomorphism.
$\widehat{F}$
defines a group isomorphism.
We write explicitly characteristic functions of probability measures in the following situations.
-
(i) If
 $\unicode[STIX]{x1D707}$
is a Borel probability measure on
$\unicode[STIX]{x1D707}$
is a Borel probability measure on
 $F^{m}$
, then
$F^{m}$
, then
 $\widehat{\unicode[STIX]{x1D707}}$
is defined on
$\widehat{\unicode[STIX]{x1D707}}$
is defined on
 $F^{m}$
by where
$F^{m}$
by where $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}}(y):=\int _{F^{m}}\unicode[STIX]{x1D712}(x\cdot y)\unicode[STIX]{x1D707}\,(dx), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}}(y):=\int _{F^{m}}\unicode[STIX]{x1D712}(x\cdot y)\unicode[STIX]{x1D707}\,(dx), & & \displaystyle \nonumber\end{eqnarray}$$
 $x\cdot y:=\sum _{j=1}^{m}x_{j}y_{j}$
.
$x\cdot y:=\sum _{j=1}^{m}x_{j}y_{j}$
.
-
(ii) If
 $\unicode[STIX]{x1D707}$
is a Borel probability measure on
$\unicode[STIX]{x1D707}$
is a Borel probability measure on
 $\operatorname{Mat}(n,F)$
, then
$\operatorname{Mat}(n,F)$
, then
 $\widehat{\unicode[STIX]{x1D707}}$
is defined on
$\widehat{\unicode[STIX]{x1D707}}$
is defined on
 $\operatorname{Mat}(n,F)$
by
$\operatorname{Mat}(n,F)$
by  $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}}(A):=\int _{\operatorname{Mat}(n,F)}\unicode[STIX]{x1D712}(\operatorname{tr}(AM))\unicode[STIX]{x1D707}\,(dM). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}}(A):=\int _{\operatorname{Mat}(n,F)}\unicode[STIX]{x1D712}(\operatorname{tr}(AM))\unicode[STIX]{x1D707}\,(dM). & & \displaystyle \nonumber\end{eqnarray}$$
-
(iii) If
 $\unicode[STIX]{x1D707}$
is a Borel probability measure on
$\unicode[STIX]{x1D707}$
is a Borel probability measure on
 $\operatorname{Mat}(\mathbb{N},F)$
, then
$\operatorname{Mat}(\mathbb{N},F)$
, then
 $\widehat{\unicode[STIX]{x1D707}}$
is defined on
$\widehat{\unicode[STIX]{x1D707}}$
is defined on
 $\operatorname{Mat}(\infty ,F)$
by (29)
$\operatorname{Mat}(\infty ,F)$
by (29) $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}}(A):=\int _{\operatorname{Mat}(\mathbb{N},F)}\unicode[STIX]{x1D712}(\operatorname{tr}(AM))\unicode[STIX]{x1D707}\,(dM). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}}(A):=\int _{\operatorname{Mat}(\mathbb{N},F)}\unicode[STIX]{x1D712}(\operatorname{tr}(AM))\unicode[STIX]{x1D707}\,(dM). & & \displaystyle\end{eqnarray}$$
-
(iv) If
 $\unicode[STIX]{x1D708}$
is a Borel probability measure on
$\unicode[STIX]{x1D708}$
is a Borel probability measure on
 $\operatorname{Sym}(n,F)$
, then
$\operatorname{Sym}(n,F)$
, then
 $\widehat{\unicode[STIX]{x1D708}}$
is defined on
$\widehat{\unicode[STIX]{x1D708}}$
is defined on
 $\operatorname{Sym}(n,F)$
by
$\operatorname{Sym}(n,F)$
by  $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(A):=\int _{\operatorname{Sym}(n,F)}\unicode[STIX]{x1D712}(\operatorname{tr}(AS))\unicode[STIX]{x1D708}(dS). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(A):=\int _{\operatorname{Sym}(n,F)}\unicode[STIX]{x1D712}(\operatorname{tr}(AS))\unicode[STIX]{x1D708}(dS). & & \displaystyle \nonumber\end{eqnarray}$$
-
(v) If
 $\unicode[STIX]{x1D708}$
is a Borel probability measure on
$\unicode[STIX]{x1D708}$
is a Borel probability measure on
 $\operatorname{Sym}(\mathbb{N},F)$
, then
$\operatorname{Sym}(\mathbb{N},F)$
, then
 $\widehat{\unicode[STIX]{x1D708}}$
is defined on
$\widehat{\unicode[STIX]{x1D708}}$
is defined on
 $\operatorname{Sym}(\infty ,F)$
by
$\operatorname{Sym}(\infty ,F)$
by  $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(A):=\int _{\operatorname{Sym}(\mathbb{N},F)}\unicode[STIX]{x1D712}(\operatorname{tr}(AS))\unicode[STIX]{x1D708}(dS). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(A):=\int _{\operatorname{Sym}(\mathbb{N},F)}\unicode[STIX]{x1D712}(\operatorname{tr}(AS))\unicode[STIX]{x1D708}(dS). & & \displaystyle \nonumber\end{eqnarray}$$
Since the corresponding groups are locally compact, Theorem 31.5 in Hewitt and Ross [Reference Hewitt and RossHR70, p. 212] implies that in cases (i), (ii) and (iv), the characteristic function
![]() $\widehat{\unicode[STIX]{x1D707}}$
determines
$\widehat{\unicode[STIX]{x1D707}}$
determines
![]() $\unicode[STIX]{x1D707}$
uniquely. The same statement holds for cases (iii) and (v). Indeed, although the additive groups
$\unicode[STIX]{x1D707}$
uniquely. The same statement holds for cases (iii) and (v). Indeed, although the additive groups
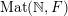 $\operatorname{Mat}(\mathbb{N},F)$
and
$\operatorname{Mat}(\mathbb{N},F)$
and
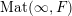 $\operatorname{Mat}(\infty ,F)$
are not locally compact and we can not apply the result on locally compact groups directly, we may use the fact that any Borel probability measure
$\operatorname{Mat}(\infty ,F)$
are not locally compact and we can not apply the result on locally compact groups directly, we may use the fact that any Borel probability measure
![]() $\unicode[STIX]{x1D707}$
on
$\unicode[STIX]{x1D707}$
on
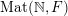 $\operatorname{Mat}(\mathbb{N},F)$
is uniquely determined by its finite dimensional projections
$\operatorname{Mat}(\mathbb{N},F)$
is uniquely determined by its finite dimensional projections
 $(\operatorname{Cut}_{n}^{\infty })_{\ast }(\unicode[STIX]{x1D707})$
and (29) contains all information for
$(\operatorname{Cut}_{n}^{\infty })_{\ast }(\unicode[STIX]{x1D707})$
and (29) contains all information for
 $\widehat{(\operatorname{Cut}_{n}^{\infty })_{\ast }(\unicode[STIX]{x1D707})}$
,
$\widehat{(\operatorname{Cut}_{n}^{\infty })_{\ast }(\unicode[STIX]{x1D707})}$
,
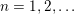 $n=1,2,\ldots \,$
. Case (v) is treated similarly.
$n=1,2,\ldots \,$
. Case (v) is treated similarly.
Remark 2.9. If
![]() $\unicode[STIX]{x1D707}$
is a probability measure on
$\unicode[STIX]{x1D707}$
is a probability measure on
 $\operatorname{Mat}(n,F)$
which is invariant under the action of the group
$\operatorname{Mat}(n,F)$
which is invariant under the action of the group
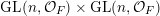 $\operatorname{GL}(n,{\mathcal{O}}_{F})\times \operatorname{GL}(n,{\mathcal{O}}_{F})$
, then for any
$\operatorname{GL}(n,{\mathcal{O}}_{F})\times \operatorname{GL}(n,{\mathcal{O}}_{F})$
, then for any
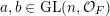 $a,b\in \operatorname{GL}(n,{\mathcal{O}}_{F})$
, we have
$a,b\in \operatorname{GL}(n,{\mathcal{O}}_{F})$
, we have
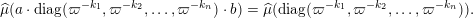 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}}(a\cdot \operatorname{diag}(\unicode[STIX]{x1D71B}^{-k_{1}},\unicode[STIX]{x1D71B}^{-k_{2}},\ldots ,\unicode[STIX]{x1D71B}^{-k_{n}})\cdot b)=\widehat{\unicode[STIX]{x1D707}}(\operatorname{diag}(\unicode[STIX]{x1D71B}^{-k_{1}},\unicode[STIX]{x1D71B}^{-k_{2}},\ldots ,\unicode[STIX]{x1D71B}^{-k_{n}})). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}}(a\cdot \operatorname{diag}(\unicode[STIX]{x1D71B}^{-k_{1}},\unicode[STIX]{x1D71B}^{-k_{2}},\ldots ,\unicode[STIX]{x1D71B}^{-k_{n}})\cdot b)=\widehat{\unicode[STIX]{x1D707}}(\operatorname{diag}(\unicode[STIX]{x1D71B}^{-k_{1}},\unicode[STIX]{x1D71B}^{-k_{2}},\ldots ,\unicode[STIX]{x1D71B}^{-k_{n}})). & & \displaystyle\end{eqnarray}$$
Similarly, if
![]() $\unicode[STIX]{x1D708}$
is a
$\unicode[STIX]{x1D708}$
is a
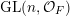 $\operatorname{GL}(n,{\mathcal{O}}_{F})$
-invariant probability measure on
$\operatorname{GL}(n,{\mathcal{O}}_{F})$
-invariant probability measure on
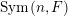 $\operatorname{Sym}(n,F)$
, then for any
$\operatorname{Sym}(n,F)$
, then for any
 $g\in \operatorname{GL}(n,{\mathcal{O}}_{F})$
, we have
$g\in \operatorname{GL}(n,{\mathcal{O}}_{F})$
, we have
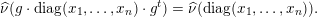 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(g\cdot \operatorname{diag}(x_{1},\ldots ,x_{n})\cdot g^{t})=\widehat{\unicode[STIX]{x1D708}}(\operatorname{diag}(x_{1},\ldots ,x_{n})). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(g\cdot \operatorname{diag}(x_{1},\ldots ,x_{n})\cdot g^{t})=\widehat{\unicode[STIX]{x1D708}}(\operatorname{diag}(x_{1},\ldots ,x_{n})). & & \displaystyle\end{eqnarray}$$
Similar statements hold for
 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measures on
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measures on
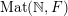 $\operatorname{Mat}(\mathbb{N},F)$
and for
$\operatorname{Mat}(\mathbb{N},F)$
and for
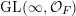 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measures on
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant probability measures on
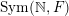 $\operatorname{Sym}(\mathbb{N},F)$
.
$\operatorname{Sym}(\mathbb{N},F)$
.
Let
![]() $m\in \mathbb{N}$
. Given any Borel probability measures
$m\in \mathbb{N}$
. Given any Borel probability measures
 $\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{m}$
on
$\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{m}$
on
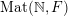 $\operatorname{Mat}(\mathbb{N},F)$
(respectively
$\operatorname{Mat}(\mathbb{N},F)$
(respectively
 $\operatorname{Sym}(\mathbb{N},F)$
), their convolution
$\operatorname{Sym}(\mathbb{N},F)$
), their convolution
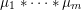 $\unicode[STIX]{x1D707}_{1}\ast \cdots \ast \unicode[STIX]{x1D707}_{m}$
is defined as follows: let
$\unicode[STIX]{x1D707}_{1}\ast \cdots \ast \unicode[STIX]{x1D707}_{m}$
is defined as follows: let
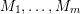 $M_{1},\ldots ,M_{m}$
be independent random matrices such that
$M_{1},\ldots ,M_{m}$
be independent random matrices such that
 ${\mathcal{L}}(M_{i})=\unicode[STIX]{x1D707}_{i},i=1,\ldots ,m$
and set
${\mathcal{L}}(M_{i})=\unicode[STIX]{x1D707}_{i},i=1,\ldots ,m$
and set
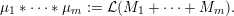 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}_{1}\ast \cdots \ast \unicode[STIX]{x1D707}_{m}:={\mathcal{L}}(M_{1}+\cdots +M_{m}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}_{1}\ast \cdots \ast \unicode[STIX]{x1D707}_{m}:={\mathcal{L}}(M_{1}+\cdots +M_{m}). & & \displaystyle \nonumber\end{eqnarray}$$
The characteristic function of
 $\unicode[STIX]{x1D707}_{1}\ast \cdots \ast \unicode[STIX]{x1D707}_{m}$
is given by the formula
$\unicode[STIX]{x1D707}_{1}\ast \cdots \ast \unicode[STIX]{x1D707}_{m}$
is given by the formula
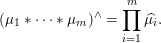 $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D707}_{1}\ast \cdots \ast \unicode[STIX]{x1D707}_{m})^{\wedge }=\mathop{\prod }_{i=1}^{m}\widehat{\unicode[STIX]{x1D707}_{i}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D707}_{1}\ast \cdots \ast \unicode[STIX]{x1D707}_{m})^{\wedge }=\mathop{\prod }_{i=1}^{m}\widehat{\unicode[STIX]{x1D707}_{i}}. & & \displaystyle\end{eqnarray}$$
3 Invariance and ergodicity
In this section, we prove that all the measures on
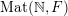 $\operatorname{Mat}(\mathbb{N},F)$
from the family
$\operatorname{Mat}(\mathbb{N},F)$
from the family
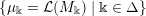 $\{\unicode[STIX]{x1D707}_{\Bbbk }={\mathcal{L}}(M_{\Bbbk })\mid \Bbbk \in \unicode[STIX]{x1D6E5}\}$
introduced in Definition 1.1 are
$\{\unicode[STIX]{x1D707}_{\Bbbk }={\mathcal{L}}(M_{\Bbbk })\mid \Bbbk \in \unicode[STIX]{x1D6E5}\}$
introduced in Definition 1.1 are
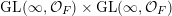 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant and ergodic and that all the measures on
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant and ergodic and that all the measures on
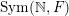 $\operatorname{Sym}(\mathbb{N},F)$
from the family
$\operatorname{Sym}(\mathbb{N},F)$
from the family
 $\{\unicode[STIX]{x1D708}_{h}={\mathcal{L}}(S_{h})\mid h\in \unicode[STIX]{x1D6FA}\}$
introduced in Definition 1.5 are
$\{\unicode[STIX]{x1D708}_{h}={\mathcal{L}}(S_{h})\mid h\in \unicode[STIX]{x1D6FA}\}$
introduced in Definition 1.5 are
 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant and ergodic.
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant and ergodic.
3.1
 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariance for probability measures
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariance for probability measures
 $\unicode[STIX]{x1D707}_{\Bbbk }$
$\unicode[STIX]{x1D707}_{\Bbbk }$
Proposition 3.1. For any
![]() $\Bbbk \in \unicode[STIX]{x1D6E5}$
, the probability measure
$\Bbbk \in \unicode[STIX]{x1D6E5}$
, the probability measure
![]() $\unicode[STIX]{x1D707}_{\Bbbk }$
on
$\unicode[STIX]{x1D707}_{\Bbbk }$
on
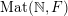 $\operatorname{Mat}(\mathbb{N},F)$
is
$\operatorname{Mat}(\mathbb{N},F)$
is
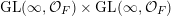 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant.
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant.
Recall that the normalized integral
![]() $\unicode[STIX]{x2A0D}$
is introduced in (14).
$\unicode[STIX]{x2A0D}$
is introduced in (14).
Remark 3.2. For any
![]() $n\geqslant 1$
, we have
$n\geqslant 1$
, we have
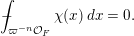 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x2A0D}_{\unicode[STIX]{x1D71B}^{-n}{\mathcal{O}}_{F}}\unicode[STIX]{x1D712}(x)\,dx=0. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x2A0D}_{\unicode[STIX]{x1D71B}^{-n}{\mathcal{O}}_{F}}\unicode[STIX]{x1D712}(x)\,dx=0. & & \displaystyle\end{eqnarray}$$
Indeed, for any fixed
![]() $n\geqslant 1$
, the character
$n\geqslant 1$
, the character
![]() $\unicode[STIX]{x1D712}$
defines a non-trivial character
$\unicode[STIX]{x1D712}$
defines a non-trivial character
![]() $\widetilde{\unicode[STIX]{x1D712}}$
of the finite group
$\widetilde{\unicode[STIX]{x1D712}}$
of the finite group
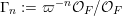 $\unicode[STIX]{x1D6E4}_{n}:=\unicode[STIX]{x1D71B}^{-n}{\mathcal{O}}_{F}/{\mathcal{O}}_{F}$
by
$\unicode[STIX]{x1D6E4}_{n}:=\unicode[STIX]{x1D71B}^{-n}{\mathcal{O}}_{F}/{\mathcal{O}}_{F}$
by
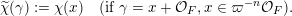 $$\begin{eqnarray}\displaystyle \widetilde{\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D6FE}):=\unicode[STIX]{x1D712}(x)\quad (\text{if }\unicode[STIX]{x1D6FE}=x+{\mathcal{O}}_{F},x\in \unicode[STIX]{x1D71B}^{-n}{\mathcal{O}}_{F}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D6FE}):=\unicode[STIX]{x1D712}(x)\quad (\text{if }\unicode[STIX]{x1D6FE}=x+{\mathcal{O}}_{F},x\in \unicode[STIX]{x1D71B}^{-n}{\mathcal{O}}_{F}). & & \displaystyle \nonumber\end{eqnarray}$$
By orthogonality of the character
![]() $\widetilde{\unicode[STIX]{x1D712}}$
and the trivial character, we have
$\widetilde{\unicode[STIX]{x1D712}}$
and the trivial character, we have
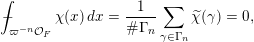 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x2A0D}_{\unicode[STIX]{x1D71B}^{-n}{\mathcal{O}}_{F}}\unicode[STIX]{x1D712}(x)\,dx=\frac{1}{\#\unicode[STIX]{x1D6E4}_{n}}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{n}}\widetilde{\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D6FE})=0, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x2A0D}_{\unicode[STIX]{x1D71B}^{-n}{\mathcal{O}}_{F}}\unicode[STIX]{x1D712}(x)\,dx=\frac{1}{\#\unicode[STIX]{x1D6E4}_{n}}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{n}}\widetilde{\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D6FE})=0, & & \displaystyle \nonumber\end{eqnarray}$$
and (33) is proved.
Lemma 3.3. For any
![]() $y\in F$
and any
$y\in F$
and any
![]() $l\in \mathbb{Z}$
, we have
$l\in \mathbb{Z}$
, we have
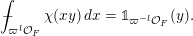 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x2A0D}_{\unicode[STIX]{x1D71B}^{l}{\mathcal{O}}_{F}}\unicode[STIX]{x1D712}(xy)\,dx=\unicode[STIX]{x1D7D9}_{\unicode[STIX]{x1D71B}^{-l}{\mathcal{O}}_{F}}(y). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x2A0D}_{\unicode[STIX]{x1D71B}^{l}{\mathcal{O}}_{F}}\unicode[STIX]{x1D712}(xy)\,dx=\unicode[STIX]{x1D7D9}_{\unicode[STIX]{x1D71B}^{-l}{\mathcal{O}}_{F}}(y). & & \displaystyle\end{eqnarray}$$
Proof. First assume that
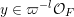 $y\in \unicode[STIX]{x1D71B}^{-l}{\mathcal{O}}_{F}$
. Then for any
$y\in \unicode[STIX]{x1D71B}^{-l}{\mathcal{O}}_{F}$
. Then for any
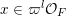 $x\in \unicode[STIX]{x1D71B}^{l}{\mathcal{O}}_{F}$
, we have
$x\in \unicode[STIX]{x1D71B}^{l}{\mathcal{O}}_{F}$
, we have
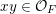 $xy\in {\mathcal{O}}_{F}$
. Consequently, by (28), we have
$xy\in {\mathcal{O}}_{F}$
. Consequently, by (28), we have
 $\unicode[STIX]{x2A0D}_{\unicode[STIX]{x1D71B}^{l}{\mathcal{O}}_{F}}\unicode[STIX]{x1D712}(xy)\,dx=1.$
Now assume that
$\unicode[STIX]{x2A0D}_{\unicode[STIX]{x1D71B}^{l}{\mathcal{O}}_{F}}\unicode[STIX]{x1D712}(xy)\,dx=1.$
Now assume that
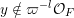 $y\notin \unicode[STIX]{x1D71B}^{-l}{\mathcal{O}}_{F}$
. Since the Haar measure
$y\notin \unicode[STIX]{x1D71B}^{-l}{\mathcal{O}}_{F}$
. Since the Haar measure
![]() $d\text{vol}$
on
$d\text{vol}$
on
![]() $F$
is invariant under the multiplication action by any element
$F$
is invariant under the multiplication action by any element
![]() $u\in {\mathcal{O}}_{F}^{\times }$
, without loss of generality, we may assume that
$u\in {\mathcal{O}}_{F}^{\times }$
, without loss of generality, we may assume that
![]() $y=\unicode[STIX]{x1D71B}^{k}$
with
$y=\unicode[STIX]{x1D71B}^{k}$
with
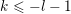 $k\leqslant -l-1$
. By (33), we have
$k\leqslant -l-1$
. By (33), we have
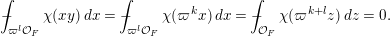 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x2A0D}_{\unicode[STIX]{x1D71B}^{l}{\mathcal{O}}_{F}}\unicode[STIX]{x1D712}(xy)\,dx=\unicode[STIX]{x2A0D}_{\unicode[STIX]{x1D71B}^{l}{\mathcal{O}}_{F}}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{k}x)\,dx=\unicode[STIX]{x2A0D}_{{\mathcal{O}}_{F}}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{k+l}z)\,dz=0. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x2A0D}_{\unicode[STIX]{x1D71B}^{l}{\mathcal{O}}_{F}}\unicode[STIX]{x1D712}(xy)\,dx=\unicode[STIX]{x2A0D}_{\unicode[STIX]{x1D71B}^{l}{\mathcal{O}}_{F}}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{k}x)\,dx=\unicode[STIX]{x2A0D}_{{\mathcal{O}}_{F}}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{k+l}z)\,dz=0. & & \displaystyle \nonumber\end{eqnarray}$$
This completes the proof of (34). ◻
Lemma 3.4. For any
![]() $m\in \mathbb{N}$
, the distribution of the random vector
$m\in \mathbb{N}$
, the distribution of the random vector
 $(X_{i}^{(1)})_{i=1}^{m}$
is
$(X_{i}^{(1)})_{i=1}^{m}$
is
 $\operatorname{GL}(m,{\mathcal{O}}_{F})$
-invariant.
$\operatorname{GL}(m,{\mathcal{O}}_{F})$
-invariant.
Proof. Write
 $X=(X_{i}^{(1)})_{i=1}^{m}$
. It suffices to prove that for any
$X=(X_{i}^{(1)})_{i=1}^{m}$
. It suffices to prove that for any
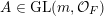 $A\in \operatorname{GL}(m,{\mathcal{O}}_{F})$
and any
$A\in \operatorname{GL}(m,{\mathcal{O}}_{F})$
and any
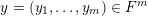 $y=(y_{1},\ldots ,y_{m})\in F^{m}$
, we have
$y=(y_{1},\ldots ,y_{m})\in F^{m}$
, we have
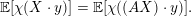 $$\begin{eqnarray}\displaystyle \mathbb{E}[\unicode[STIX]{x1D712}(X\cdot y)]=\mathbb{E}[\unicode[STIX]{x1D712}((AX)\cdot y)]. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{E}[\unicode[STIX]{x1D712}(X\cdot y)]=\mathbb{E}[\unicode[STIX]{x1D712}((AX)\cdot y)]. & & \displaystyle\end{eqnarray}$$
By the independence between
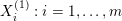 $X_{i}^{(1)}:i=1,\ldots ,m$
and Lemma 3.3, we have
$X_{i}^{(1)}:i=1,\ldots ,m$
and Lemma 3.3, we have
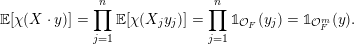 $$\begin{eqnarray}\displaystyle \mathbb{E}[\unicode[STIX]{x1D712}(X\cdot y)]=\mathop{\prod }_{j=1}^{n}\mathbb{E}[\unicode[STIX]{x1D712}(X_{j}y_{j})]=\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(y_{j})=\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}^{m}}(y). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{E}[\unicode[STIX]{x1D712}(X\cdot y)]=\mathop{\prod }_{j=1}^{n}\mathbb{E}[\unicode[STIX]{x1D712}(X_{j}y_{j})]=\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(y_{j})=\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}^{m}}(y). & & \displaystyle \nonumber\end{eqnarray}$$
Similarly,
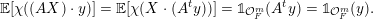 $$\begin{eqnarray}\displaystyle \mathbb{E}[\unicode[STIX]{x1D712}((AX)\cdot y)]=\mathbb{E}[\unicode[STIX]{x1D712}(X\cdot (A^{t}y))]=\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}^{m}}(A^{t}y)=\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}^{m}}(y). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{E}[\unicode[STIX]{x1D712}((AX)\cdot y)]=\mathbb{E}[\unicode[STIX]{x1D712}(X\cdot (A^{t}y))]=\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}^{m}}(A^{t}y)=\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}^{m}}(y). & & \displaystyle \nonumber\end{eqnarray}$$
Proof of Proposition 3.1.
It suffices to prove that the following probability measures
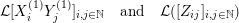 $$\begin{eqnarray}\displaystyle {\mathcal{L}}[X_{i}^{(1)}Y_{j}^{(1)}]_{i,j\in \mathbb{N}}\quad \text{and}\quad {\mathcal{L}}([Z_{ij}]_{i,j\in \mathbb{N}}) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{L}}[X_{i}^{(1)}Y_{j}^{(1)}]_{i,j\in \mathbb{N}}\quad \text{and}\quad {\mathcal{L}}([Z_{ij}]_{i,j\in \mathbb{N}}) & & \displaystyle \nonumber\end{eqnarray}$$
are
 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant. The invariance of both measures follows immediately from Lemma 3.4.◻
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant. The invariance of both measures follows immediately from Lemma 3.4.◻
3.2
 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-ergodicity for probability measures
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-ergodicity for probability measures
 $\unicode[STIX]{x1D707}_{\Bbbk }$
$\unicode[STIX]{x1D707}_{\Bbbk }$
Theorem 3.5. For any
![]() $\Bbbk \in \unicode[STIX]{x1D6E5}$
, the probability measure
$\Bbbk \in \unicode[STIX]{x1D6E5}$
, the probability measure
![]() $\unicode[STIX]{x1D707}_{\Bbbk }$
on
$\unicode[STIX]{x1D707}_{\Bbbk }$
on
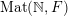 $\operatorname{Mat}(\mathbb{N},F)$
is
$\operatorname{Mat}(\mathbb{N},F)$
is
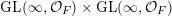 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-ergodic.
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-ergodic.
The map
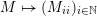 $M\mapsto (M_{ii})_{i\in \mathbb{N}}$
from
$M\mapsto (M_{ii})_{i\in \mathbb{N}}$
from
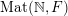 $\operatorname{Mat}(\mathbb{N},F)$
to
$\operatorname{Mat}(\mathbb{N},F)$
to
![]() $F^{\mathbb{N}}$
induces an affine map
$F^{\mathbb{N}}$
induces an affine map
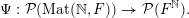 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F9}:{\mathcal{P}}(\operatorname{Mat}(\mathbb{N},F))\rightarrow {\mathcal{P}}(F^{\mathbb{N}}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F9}:{\mathcal{P}}(\operatorname{Mat}(\mathbb{N},F))\rightarrow {\mathcal{P}}(F^{\mathbb{N}}). & & \displaystyle \nonumber\end{eqnarray}$$
Let
![]() $S(n)$
denote the group of permutations of the set
$S(n)$
denote the group of permutations of the set
 $\{1,2,\ldots ,n\}$
and set
$\{1,2,\ldots ,n\}$
and set
 $S(\infty ):=\bigcup _{n\in \mathbb{N}}S(n)$
. The group
$S(\infty ):=\bigcup _{n\in \mathbb{N}}S(n)$
. The group
![]() $S(\infty )$
acts naturally on
$S(\infty )$
acts naturally on
![]() $F^{\mathbb{N}}$
by permutations of coordinates.
$F^{\mathbb{N}}$
by permutations of coordinates.
Lemma 3.6. For any
 $\unicode[STIX]{x1D707}\in {\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F))$
, we have
$\unicode[STIX]{x1D707}\in {\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F))$
, we have
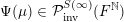 $\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707})\in {\mathcal{P}}_{\text{inv}}^{S(\infty )}(F^{\mathbb{N}})$
. Moreover, the restriction map
$\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707})\in {\mathcal{P}}_{\text{inv}}^{S(\infty )}(F^{\mathbb{N}})$
. Moreover, the restriction map
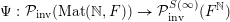 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F9}:{\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F))\rightarrow {\mathcal{P}}_{\text{inv}}^{S(\infty )}(F^{\mathbb{N}}) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F9}:{\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F))\rightarrow {\mathcal{P}}_{\text{inv}}^{S(\infty )}(F^{\mathbb{N}}) & & \displaystyle\end{eqnarray}$$
is an affine embedding.
Proof. Let
 $\unicode[STIX]{x1D707}\in {\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F))$
. For any
$\unicode[STIX]{x1D707}\in {\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F))$
. For any
 $\unicode[STIX]{x1D70E}\in S(\infty )$
, the associated permutation matrix
$\unicode[STIX]{x1D70E}\in S(\infty )$
, the associated permutation matrix
![]() $M_{\unicode[STIX]{x1D70E}}$
, defined by
$M_{\unicode[STIX]{x1D70E}}$
, defined by
 $$\begin{eqnarray}\displaystyle M_{\unicode[STIX]{x1D70E}}(i,j):=1_{\unicode[STIX]{x1D70E}(i)=j}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{\unicode[STIX]{x1D70E}}(i,j):=1_{\unicode[STIX]{x1D70E}(i)=j}, & & \displaystyle \nonumber\end{eqnarray}$$
is an element in
 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
. By the invariance of
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
. By the invariance of
![]() $\unicode[STIX]{x1D707}$
under the multiplication by all permutation matrices
$\unicode[STIX]{x1D707}$
under the multiplication by all permutation matrices
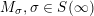 $M_{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D70E}\in S(\infty )$
on left and on right, it is easy to see that
$M_{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D70E}\in S(\infty )$
on left and on right, it is easy to see that
 $\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707})\in {\mathcal{P}}_{\text{inv}}^{S(\infty )}(F^{\mathbb{N}})$
.
$\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707})\in {\mathcal{P}}_{\text{inv}}^{S(\infty )}(F^{\mathbb{N}})$
.
Now we show that the map (36) is injective. By the definition of pushforward map, the Fourier transform of
![]() $\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707})$
is given as follows: for any
$\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707})$
is given as follows: for any
 $x_{1},\ldots ,x_{r}\in F$
,
$x_{1},\ldots ,x_{r}\in F$
,
 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707})}((x_{1},\ldots ,x_{r},0,0,\ldots ))=\widehat{\unicode[STIX]{x1D707}}(\operatorname{diag}(x_{1},\ldots ,x_{r},0,0,\ldots )). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707})}((x_{1},\ldots ,x_{r},0,0,\ldots ))=\widehat{\unicode[STIX]{x1D707}}(\operatorname{diag}(x_{1},\ldots ,x_{r},0,0,\ldots )). & & \displaystyle\end{eqnarray}$$
By Remark 2.9,
![]() $\widehat{\unicode[STIX]{x1D707}}$
is determined by
$\widehat{\unicode[STIX]{x1D707}}$
is determined by
 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}}(\operatorname{diag}(x_{1},\ldots ,x_{r},0,0,\ldots )),\quad x_{1},\ldots ,x_{r}\in F. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}}(\operatorname{diag}(x_{1},\ldots ,x_{r},0,0,\ldots )),\quad x_{1},\ldots ,x_{r}\in F. & & \displaystyle \nonumber\end{eqnarray}$$
Now, the equality (37) implies that
![]() $\widehat{\unicode[STIX]{x1D707}}$
and hence
$\widehat{\unicode[STIX]{x1D707}}$
and hence
![]() $\unicode[STIX]{x1D707}$
itself is determined uniquely by
$\unicode[STIX]{x1D707}$
itself is determined uniquely by
![]() $\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707})$
. The injectivity of the map (36) is proved.◻
$\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707})$
. The injectivity of the map (36) is proved.◻
In what follows, for any convex set
![]() $C$
, we denote by
$C$
, we denote by
![]() $\text{Ext}(C)$
the set of extreme points of
$\text{Ext}(C)$
the set of extreme points of
![]() $C$
.
$C$
.
Remark 3.7. Recall here the definition of indecomposability in § 2.1.2. Since
![]() $S(\infty )$
is countable, we have
$S(\infty )$
is countable, we have
 $$\begin{eqnarray}\displaystyle \text{Ext}({\mathcal{P}}_{\text{inv}}^{S(\infty )}({\mathcal{X}}^{\mathbb{N}}))={\mathcal{P}}_{\text{erg}}^{S(\infty )}({\mathcal{X}}^{\mathbb{N}}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Ext}({\mathcal{P}}_{\text{inv}}^{S(\infty )}({\mathcal{X}}^{\mathbb{N}}))={\mathcal{P}}_{\text{erg}}^{S(\infty )}({\mathcal{X}}^{\mathbb{N}}). & & \displaystyle \nonumber\end{eqnarray}$$
Proof of Theorem 3.5.
By construction, for any
![]() $\Bbbk \in \unicode[STIX]{x1D6E5}$
, the measure
$\Bbbk \in \unicode[STIX]{x1D6E5}$
, the measure
![]() $\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707}_{\Bbbk })$
is Bernoulli. Indeed, the definition
$\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707}_{\Bbbk })$
is Bernoulli. Indeed, the definition
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{\Bbbk }={\mathcal{L}}\biggl(\biggl[\mathop{\sum }_{n:k_{n}>k}\unicode[STIX]{x1D71B}^{-k_{n}}X_{i}^{(n)}Y_{j}^{(n)}+\unicode[STIX]{x1D71B}^{-k}Z_{ij}\biggr]_{i,j\in \mathbb{N}}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{\Bbbk }={\mathcal{L}}\biggl(\biggl[\mathop{\sum }_{n:k_{n}>k}\unicode[STIX]{x1D71B}^{-k_{n}}X_{i}^{(n)}Y_{j}^{(n)}+\unicode[STIX]{x1D71B}^{-k}Z_{ij}\biggr]_{i,j\in \mathbb{N}}\biggr)\end{eqnarray}$$
implies that the diagonal marginal measure
![]() $\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707}_{\Bbbk })$
is
$\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707}_{\Bbbk })$
is
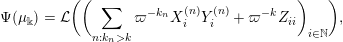 $$\begin{eqnarray}\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707}_{\Bbbk })={\mathcal{L}}\biggl(\biggl(\mathop{\sum }_{n:k_{n}>k}\unicode[STIX]{x1D71B}^{-k_{n}}X_{i}^{(n)}Y_{i}^{(n)}+\unicode[STIX]{x1D71B}^{-k}Z_{ii}\biggr)_{i\in \mathbb{N}}\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707}_{\Bbbk })={\mathcal{L}}\biggl(\biggl(\mathop{\sum }_{n:k_{n}>k}\unicode[STIX]{x1D71B}^{-k_{n}}X_{i}^{(n)}Y_{i}^{(n)}+\unicode[STIX]{x1D71B}^{-k}Z_{ii}\biggr)_{i\in \mathbb{N}}\biggr),\end{eqnarray}$$
and our original assumption, that all
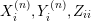 $X_{i}^{(n)},Y_{i}^{(n)},Z_{ii}$
are independent sampled with respect to the normalized Haar measure on the compact additive group
$X_{i}^{(n)},Y_{i}^{(n)},Z_{ii}$
are independent sampled with respect to the normalized Haar measure on the compact additive group
![]() ${\mathcal{O}}_{F}$
, implies that the measure
${\mathcal{O}}_{F}$
, implies that the measure
![]() $\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707}_{\Bbbk })$
is Bernoulli. Consequently, by the De Finetti Theorem,
$\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707}_{\Bbbk })$
is Bernoulli. Consequently, by the De Finetti Theorem,
![]() $\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707}_{\Bbbk })$
is
$\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707}_{\Bbbk })$
is
![]() $S(\infty )$
-ergodic. Therefore, by Remark 3.7,
$S(\infty )$
-ergodic. Therefore, by Remark 3.7,
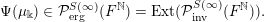 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707}_{\Bbbk })\in {\mathcal{P}}_{\text{erg}}^{S(\infty )}(F^{\mathbb{N}})=\text{Ext}({\mathcal{P}}_{\text{inv}}^{S(\infty )}(F^{\mathbb{N}})). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707}_{\Bbbk })\in {\mathcal{P}}_{\text{erg}}^{S(\infty )}(F^{\mathbb{N}})=\text{Ext}({\mathcal{P}}_{\text{inv}}^{S(\infty )}(F^{\mathbb{N}})). & & \displaystyle \nonumber\end{eqnarray}$$
It is clear that for any convex subset
![]() $C$
of
$C$
of
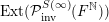 $\text{Ext}({\mathcal{P}}_{\text{inv}}^{S(\infty )}(F^{\mathbb{N}}))$
, we have
$\text{Ext}({\mathcal{P}}_{\text{inv}}^{S(\infty )}(F^{\mathbb{N}}))$
, we have
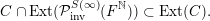 $$\begin{eqnarray}C\cap \text{Ext}({\mathcal{P}}_{\text{inv}}^{S(\infty )}(F^{\mathbb{N}}))\subset \text{Ext}(C).\end{eqnarray}$$
$$\begin{eqnarray}C\cap \text{Ext}({\mathcal{P}}_{\text{inv}}^{S(\infty )}(F^{\mathbb{N}}))\subset \text{Ext}(C).\end{eqnarray}$$
Taking
 $C=\unicode[STIX]{x1D6F9}({\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F)))$
, we see that
$C=\unicode[STIX]{x1D6F9}({\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F)))$
, we see that
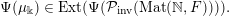 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707}_{\Bbbk })\in \text{Ext}(\unicode[STIX]{x1D6F9}({\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F)))). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707}_{\Bbbk })\in \text{Ext}(\unicode[STIX]{x1D6F9}({\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F)))). & & \displaystyle\end{eqnarray}$$
By Lemma 3.6,
![]() $\unicode[STIX]{x1D6F9}$
is an affine embedding. Hence
$\unicode[STIX]{x1D6F9}$
is an affine embedding. Hence
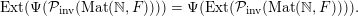 $$\begin{eqnarray}\displaystyle \text{Ext}(\unicode[STIX]{x1D6F9}({\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F))))=\unicode[STIX]{x1D6F9}(\text{Ext}({\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F)))). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Ext}(\unicode[STIX]{x1D6F9}({\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F))))=\unicode[STIX]{x1D6F9}(\text{Ext}({\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F)))). & & \displaystyle \nonumber\end{eqnarray}$$
The relation (38) implies
 $\unicode[STIX]{x1D707}_{\Bbbk }\in \text{Ext}({\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F)))$
. Since indecomposability implies ergodicity, we get the desired relation
$\unicode[STIX]{x1D707}_{\Bbbk }\in \text{Ext}({\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F)))$
. Since indecomposability implies ergodicity, we get the desired relation
 $\unicode[STIX]{x1D707}_{\Bbbk }\in {\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
. ◻
$\unicode[STIX]{x1D707}_{\Bbbk }\in {\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
. ◻
3.3
 $\mathbf{GL}\boldsymbol{(}\boldsymbol{\infty }\boldsymbol{,}\,\boldsymbol{{\mathcal{O}}}_{\boldsymbol{F}}\boldsymbol{ )}$
-invariance for probability measures
$\mathbf{GL}\boldsymbol{(}\boldsymbol{\infty }\boldsymbol{,}\,\boldsymbol{{\mathcal{O}}}_{\boldsymbol{F}}\boldsymbol{ )}$
-invariance for probability measures
 $\boldsymbol{\unicode[STIX]{x1D708}}_{h}$
$\boldsymbol{\unicode[STIX]{x1D708}}_{h}$
Proposition 3.8. For any
![]() $h\in \unicode[STIX]{x1D6FA}$
, the probability measure
$h\in \unicode[STIX]{x1D6FA}$
, the probability measure
![]() $\unicode[STIX]{x1D708}_{h}$
on
$\unicode[STIX]{x1D708}_{h}$
on
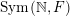 $\operatorname{Sym}(\mathbb{N},F)$
is
$\operatorname{Sym}(\mathbb{N},F)$
is
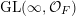 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant.
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant.
Lemma 3.9. The normalized Haar measure on
 $\operatorname{Sym}(n,{\mathcal{O}}_{F})$
is invariant under the natural action of the group
$\operatorname{Sym}(n,{\mathcal{O}}_{F})$
is invariant under the natural action of the group
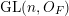 $\operatorname{GL}(n,O_{F})$
.
$\operatorname{GL}(n,O_{F})$
.
Proof. For any
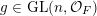 $g\in \operatorname{GL}(n,{\mathcal{O}}_{F})$
, the linear map
$g\in \operatorname{GL}(n,{\mathcal{O}}_{F})$
, the linear map
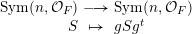 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}rcl@{}}\operatorname{Sym}(n,{\mathcal{O}}_{F})\ & \longrightarrow \ & \operatorname{Sym}(n,{\mathcal{O}}_{F})\\ S\ & \mapsto \ & gSg^{t}\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}rcl@{}}\operatorname{Sym}(n,{\mathcal{O}}_{F})\ & \longrightarrow \ & \operatorname{Sym}(n,{\mathcal{O}}_{F})\\ S\ & \mapsto \ & gSg^{t}\end{array}\right. & & \displaystyle\end{eqnarray}$$
is invertible. Clearly, if we use the group identification
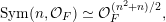 $$\begin{eqnarray}\operatorname{Sym}(n,{\mathcal{O}}_{F})\simeq {\mathcal{O}}_{F}^{(n^{2}+n)/2},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Sym}(n,{\mathcal{O}}_{F})\simeq {\mathcal{O}}_{F}^{(n^{2}+n)/2},\end{eqnarray}$$
then the linear map (39) is represented by an invertible matrix from
 $\operatorname{GL}((n^{2}+n)/2,{\mathcal{O}}_{F})$
. Hence by Remark 2.1, it preserves the normalized Haar measure.◻
$\operatorname{GL}((n^{2}+n)/2,{\mathcal{O}}_{F})$
. Hence by Remark 2.1, it preserves the normalized Haar measure.◻
Proof of Proposition 3.8.
It suffices to prove the
 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariance of the following probability measures on
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariance of the following probability measures on
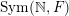 $\operatorname{Sym}(\mathbb{N},F)$
:
$\operatorname{Sym}(\mathbb{N},F)$
:
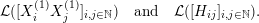 $$\begin{eqnarray}\displaystyle {\mathcal{L}}([X_{i}^{(1)}X_{j}^{(1)}]_{i,j\in \mathbb{N}})\quad \text{and}\quad {\mathcal{L}}([H_{ij}]_{i,j\in \mathbb{N}}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{L}}([X_{i}^{(1)}X_{j}^{(1)}]_{i,j\in \mathbb{N}})\quad \text{and}\quad {\mathcal{L}}([H_{ij}]_{i,j\in \mathbb{N}}). & & \displaystyle \nonumber\end{eqnarray}$$
The
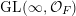 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariance of
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariance of
 ${\mathcal{L}}([X_{i}^{(1)}X_{j}^{(1)}]_{i,j\in \mathbb{N}})$
follows immediately from Lemma 3.4, while the
${\mathcal{L}}([X_{i}^{(1)}X_{j}^{(1)}]_{i,j\in \mathbb{N}})$
follows immediately from Lemma 3.4, while the
 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariance of
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariance of
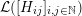 ${\mathcal{L}}([H_{ij}]_{i,j\in \mathbb{N}})$
follows from Lemma 3.9.◻
${\mathcal{L}}([H_{ij}]_{i,j\in \mathbb{N}})$
follows from Lemma 3.9.◻
3.4
 $\mathbf{GL}\boldsymbol{(}\boldsymbol{\infty }\boldsymbol{,}\,\boldsymbol{{\mathcal{O}}}_{\boldsymbol{F}}\boldsymbol{ )}$
-ergodicity for probability measures
$\mathbf{GL}\boldsymbol{(}\boldsymbol{\infty }\boldsymbol{,}\,\boldsymbol{{\mathcal{O}}}_{\boldsymbol{F}}\boldsymbol{ )}$
-ergodicity for probability measures
 $\boldsymbol{\unicode[STIX]{x1D708}}_{h}$
$\boldsymbol{\unicode[STIX]{x1D708}}_{h}$
Theorem 3.10. For any
![]() $h\in \unicode[STIX]{x1D6FA}$
, the probability measure
$h\in \unicode[STIX]{x1D6FA}$
, the probability measure
![]() $\unicode[STIX]{x1D708}_{h}$
on
$\unicode[STIX]{x1D708}_{h}$
on
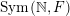 $\operatorname{Sym}(\mathbb{N},F)$
is
$\operatorname{Sym}(\mathbb{N},F)$
is
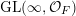 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-ergodic.
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-ergodic.
The map
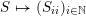 $S\mapsto (S_{ii})_{i\in \mathbb{N}}$
from
$S\mapsto (S_{ii})_{i\in \mathbb{N}}$
from
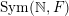 $\operatorname{Sym}(\mathbb{N},F)$
to
$\operatorname{Sym}(\mathbb{N},F)$
to
![]() $F^{\mathbb{N}}$
induces an affine map
$F^{\mathbb{N}}$
induces an affine map
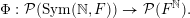 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}:{\mathcal{P}}(\operatorname{Sym}(\mathbb{N},F))\rightarrow {\mathcal{P}}(F^{\mathbb{N}}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}:{\mathcal{P}}(\operatorname{Sym}(\mathbb{N},F))\rightarrow {\mathcal{P}}(F^{\mathbb{N}}). & & \displaystyle \nonumber\end{eqnarray}$$
Lemma 3.11. For any
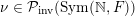 $\unicode[STIX]{x1D708}\in {\mathcal{P}}_{\text{inv}}(\operatorname{Sym}(\mathbb{N},F))$
, we have
$\unicode[STIX]{x1D708}\in {\mathcal{P}}_{\text{inv}}(\operatorname{Sym}(\mathbb{N},F))$
, we have
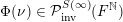 $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D708})\in {\mathcal{P}}_{\text{inv}}^{S(\infty )}(F^{\mathbb{N}})$
. Moreover, the restriction map
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D708})\in {\mathcal{P}}_{\text{inv}}^{S(\infty )}(F^{\mathbb{N}})$
. Moreover, the restriction map
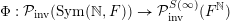 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}:{\mathcal{P}}_{\text{inv}}(\operatorname{Sym}(\mathbb{N},F))\rightarrow {\mathcal{P}}_{\text{inv}}^{S(\infty )}(F^{\mathbb{N}}) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}:{\mathcal{P}}_{\text{inv}}(\operatorname{Sym}(\mathbb{N},F))\rightarrow {\mathcal{P}}_{\text{inv}}^{S(\infty )}(F^{\mathbb{N}}) & & \displaystyle \nonumber\end{eqnarray}$$
is an affine embedding.
Proof. The proof is similar to that of Lemma 3.6. ◻
4 Explicit computation of characteristic functions
In this section, we give explicit formulae for characteristic functions of measures from the two families
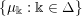 $\{\unicode[STIX]{x1D707}_{\Bbbk }:\Bbbk \in \unicode[STIX]{x1D6E5}\}$
and
$\{\unicode[STIX]{x1D707}_{\Bbbk }:\Bbbk \in \unicode[STIX]{x1D6E5}\}$
and
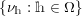 $\{\unicode[STIX]{x1D708}_{h}:h\in \unicode[STIX]{x1D6FA}\}$
.
$\{\unicode[STIX]{x1D708}_{h}:h\in \unicode[STIX]{x1D6FA}\}$
.
4.1 Measures on
 $\operatorname{Mat}(\mathbb{N},F)$
$\operatorname{Mat}(\mathbb{N},F)$
By the elementary observation (30), for studying the characteristic functions of
![]() $\unicode[STIX]{x1D707}_{\Bbbk }$
, it suffices to compute
$\unicode[STIX]{x1D707}_{\Bbbk }$
, it suffices to compute
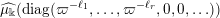 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}_{\Bbbk }}(\operatorname{diag}(\unicode[STIX]{x1D71B}^{-\ell _{1}},\ldots ,\unicode[STIX]{x1D71B}^{-\ell _{r}},0,0,\ldots )) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}_{\Bbbk }}(\operatorname{diag}(\unicode[STIX]{x1D71B}^{-\ell _{1}},\ldots ,\unicode[STIX]{x1D71B}^{-\ell _{r}},0,0,\ldots )) & & \displaystyle \nonumber\end{eqnarray}$$
for any
![]() $r\in \mathbb{N}$
and any
$r\in \mathbb{N}$
and any
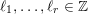 $\ell _{1},\ldots ,\ell _{r}\in \mathbb{Z}$
.
$\ell _{1},\ldots ,\ell _{r}\in \mathbb{Z}$
.
Proposition 4.1. For any
 $\Bbbk =(k_{n})_{n\in \mathbb{N}}\in \unicode[STIX]{x1D6E5}$
and any
$\Bbbk =(k_{n})_{n\in \mathbb{N}}\in \unicode[STIX]{x1D6E5}$
and any
![]() $\ell \in \mathbb{Z}$
, we have
$\ell \in \mathbb{Z}$
, we have
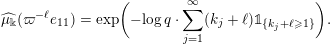 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}_{\Bbbk }}(\unicode[STIX]{x1D71B}^{-\ell }e_{11})=\exp \biggl(-\text{log}\,q\cdot \mathop{\sum }_{j=1}^{\infty }(k_{j}+\ell )\unicode[STIX]{x1D7D9}_{\{k_{j}+\ell \geqslant 1\}}\biggr). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}_{\Bbbk }}(\unicode[STIX]{x1D71B}^{-\ell }e_{11})=\exp \biggl(-\text{log}\,q\cdot \mathop{\sum }_{j=1}^{\infty }(k_{j}+\ell )\unicode[STIX]{x1D7D9}_{\{k_{j}+\ell \geqslant 1\}}\biggr). & & \displaystyle\end{eqnarray}$$
More generally, for any
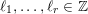 $\ell _{1},\ldots ,\ell _{r}\in \mathbb{Z}$
, we have
$\ell _{1},\ldots ,\ell _{r}\in \mathbb{Z}$
, we have
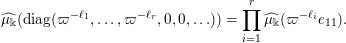 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}_{\Bbbk }}(\operatorname{diag}(\unicode[STIX]{x1D71B}^{-\ell _{1}},\ldots ,\unicode[STIX]{x1D71B}^{-\ell _{r}},0,0,\ldots ))=\mathop{\prod }_{i=1}^{r}\widehat{\unicode[STIX]{x1D707}_{\Bbbk }}(\unicode[STIX]{x1D71B}^{-\ell _{i}}e_{11}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}_{\Bbbk }}(\operatorname{diag}(\unicode[STIX]{x1D71B}^{-\ell _{1}},\ldots ,\unicode[STIX]{x1D71B}^{-\ell _{r}},0,0,\ldots ))=\mathop{\prod }_{i=1}^{r}\widehat{\unicode[STIX]{x1D707}_{\Bbbk }}(\unicode[STIX]{x1D71B}^{-\ell _{i}}e_{11}). & & \displaystyle\end{eqnarray}$$
Introduce a function
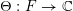 $\unicode[STIX]{x1D6E9}:F\rightarrow \mathbb{C}$
by
$\unicode[STIX]{x1D6E9}:F\rightarrow \mathbb{C}$
by
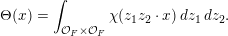 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}(x)=\int _{{\mathcal{O}}_{F}\times {\mathcal{O}}_{F}}\unicode[STIX]{x1D712}(z_{1}z_{2}\cdot x)\,dz_{1}\,dz_{2}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}(x)=\int _{{\mathcal{O}}_{F}\times {\mathcal{O}}_{F}}\unicode[STIX]{x1D712}(z_{1}z_{2}\cdot x)\,dz_{1}\,dz_{2}. & & \displaystyle\end{eqnarray}$$
Lemma 4.2. The function
![]() $\unicode[STIX]{x1D6E9}$
is given by
$\unicode[STIX]{x1D6E9}$
is given by
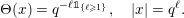 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}(x)=q^{-\ell \unicode[STIX]{x1D7D9}_{\{\ell \geqslant 1\}}},\quad |x|=q^{\ell }. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}(x)=q^{-\ell \unicode[STIX]{x1D7D9}_{\{\ell \geqslant 1\}}},\quad |x|=q^{\ell }. & & \displaystyle \nonumber\end{eqnarray}$$
Proof. Let
![]() $|x|=q^{\ell }$
. Then there exists
$|x|=q^{\ell }$
. Then there exists
![]() $u\in {\mathcal{O}}_{F}^{\times }$
, such that
$u\in {\mathcal{O}}_{F}^{\times }$
, such that
 $x=\unicode[STIX]{x1D71B}^{-\ell }u$
. By rotation invariance,
$x=\unicode[STIX]{x1D71B}^{-\ell }u$
. By rotation invariance,
 $\unicode[STIX]{x1D6E9}(x)=\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D71B}^{-\ell })$
. Now by Lemma 3.3,
$\unicode[STIX]{x1D6E9}(x)=\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D71B}^{-\ell })$
. Now by Lemma 3.3,
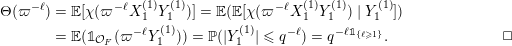 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D71B}^{-\ell }) & = & \displaystyle \mathbb{E}[\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{-\ell }X_{1}^{(1)}Y_{1}^{(1)})]=\mathbb{E}(\mathbb{E}[\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{-\ell }X_{1}^{(1)}Y_{1}^{(1)})\mid Y_{1}^{(1)}])\nonumber\\ \displaystyle & = & \displaystyle \mathbb{E}(\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(\unicode[STIX]{x1D71B}^{-\ell }Y_{1}^{(1)}))=\mathbb{P}(|Y_{1}^{(1)}|\leqslant q^{-\ell })=q^{-\ell \unicode[STIX]{x1D7D9}_{\{\ell \geqslant 1\}}}.\Box \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D71B}^{-\ell }) & = & \displaystyle \mathbb{E}[\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{-\ell }X_{1}^{(1)}Y_{1}^{(1)})]=\mathbb{E}(\mathbb{E}[\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{-\ell }X_{1}^{(1)}Y_{1}^{(1)})\mid Y_{1}^{(1)}])\nonumber\\ \displaystyle & = & \displaystyle \mathbb{E}(\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(\unicode[STIX]{x1D71B}^{-\ell }Y_{1}^{(1)}))=\mathbb{P}(|Y_{1}^{(1)}|\leqslant q^{-\ell })=q^{-\ell \unicode[STIX]{x1D7D9}_{\{\ell \geqslant 1\}}}.\Box \nonumber\end{eqnarray}$$
Remark 4.3. In the formulae below, for graphical convenience, we write
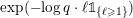 $\exp (-\text{log}\,q\cdot \ell \unicode[STIX]{x1D7D9}_{\{\ell \geqslant 1\}})$
instead of
$\exp (-\text{log}\,q\cdot \ell \unicode[STIX]{x1D7D9}_{\{\ell \geqslant 1\}})$
instead of
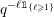 $q^{-\ell \unicode[STIX]{x1D7D9}_{\{\ell \geqslant 1\}}}$
.
$q^{-\ell \unicode[STIX]{x1D7D9}_{\{\ell \geqslant 1\}}}$
.
Proof of Proposition 4.1.
The identity (41) follows from the independence between all diagonal coefficient of
![]() $M_{\Bbbk }$
. So we only need to prove the identity (40).
$M_{\Bbbk }$
. So we only need to prove the identity (40).
First assume that
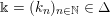 $\Bbbk =(k_{n})_{n\in \mathbb{N}}\in \unicode[STIX]{x1D6E5}$
is such that
$\Bbbk =(k_{n})_{n\in \mathbb{N}}\in \unicode[STIX]{x1D6E5}$
is such that
 $\lim _{n\rightarrow \infty }k_{n}=-\infty$
. By the independence between all
$\lim _{n\rightarrow \infty }k_{n}=-\infty$
. By the independence between all
![]() $X_{1}^{(n)}$
and
$X_{1}^{(n)}$
and
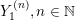 $Y_{1}^{(n)},n\in \mathbb{N}$
, we have
$Y_{1}^{(n)},n\in \mathbb{N}$
, we have
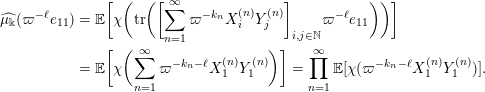 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}_{\Bbbk }}(\unicode[STIX]{x1D71B}^{-\ell }e_{11}) & = & \displaystyle \mathbb{E}\biggl[\unicode[STIX]{x1D712}\biggl(\operatorname{tr}\hspace{-0.8pt}\biggl(\mathop{\biggl[\mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D71B}^{-k_{n}}X_{i}^{(n)}Y_{j}^{(n)}\biggr]}\nolimits_{i,j\in \mathbb{N}}\unicode[STIX]{x1D71B}^{-\ell }e_{11}\biggr)\biggr)\biggr]\nonumber\\ \displaystyle & = & \displaystyle \mathbb{E}\biggl[\unicode[STIX]{x1D712}\biggl(\mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D71B}^{-k_{n}-\ell }X_{1}^{(n)}Y_{1}^{(n)}\biggr)\biggr]=\mathop{\prod }_{n=1}^{\infty }\mathbb{E}[\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{-k_{n}-\ell }X_{1}^{(n)}Y_{1}^{(n)})].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}_{\Bbbk }}(\unicode[STIX]{x1D71B}^{-\ell }e_{11}) & = & \displaystyle \mathbb{E}\biggl[\unicode[STIX]{x1D712}\biggl(\operatorname{tr}\hspace{-0.8pt}\biggl(\mathop{\biggl[\mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D71B}^{-k_{n}}X_{i}^{(n)}Y_{j}^{(n)}\biggr]}\nolimits_{i,j\in \mathbb{N}}\unicode[STIX]{x1D71B}^{-\ell }e_{11}\biggr)\biggr)\biggr]\nonumber\\ \displaystyle & = & \displaystyle \mathbb{E}\biggl[\unicode[STIX]{x1D712}\biggl(\mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D71B}^{-k_{n}-\ell }X_{1}^{(n)}Y_{1}^{(n)}\biggr)\biggr]=\mathop{\prod }_{n=1}^{\infty }\mathbb{E}[\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{-k_{n}-\ell }X_{1}^{(n)}Y_{1}^{(n)})].\nonumber\end{eqnarray}$$
By Lemma 4.2, we get
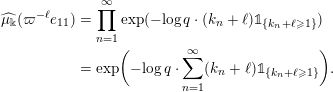 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}_{\Bbbk }}(\unicode[STIX]{x1D71B}^{-\ell }e_{11}) & = & \displaystyle \mathop{\prod }_{n=1}^{\infty }\exp (-\text{log}\,q\cdot (k_{n}+\ell )\unicode[STIX]{x1D7D9}_{\{k_{n}+\ell \geqslant 1\}})\nonumber\\ \displaystyle & = & \displaystyle \exp \biggl(-\text{log}\,q\cdot \mathop{\sum }_{n=1}^{\infty }(k_{n}+\ell )\unicode[STIX]{x1D7D9}_{\{k_{n}+\ell \geqslant 1\}}\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}_{\Bbbk }}(\unicode[STIX]{x1D71B}^{-\ell }e_{11}) & = & \displaystyle \mathop{\prod }_{n=1}^{\infty }\exp (-\text{log}\,q\cdot (k_{n}+\ell )\unicode[STIX]{x1D7D9}_{\{k_{n}+\ell \geqslant 1\}})\nonumber\\ \displaystyle & = & \displaystyle \exp \biggl(-\text{log}\,q\cdot \mathop{\sum }_{n=1}^{\infty }(k_{n}+\ell )\unicode[STIX]{x1D7D9}_{\{k_{n}+\ell \geqslant 1\}}\biggr).\nonumber\end{eqnarray}$$
Now assume that there exists
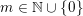 $m\in \mathbb{N}\cup \{0\}$
and
$m\in \mathbb{N}\cup \{0\}$
and
![]() $k\in \mathbb{Z}$
, such that
$k\in \mathbb{Z}$
, such that
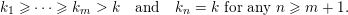 $$\begin{eqnarray}\displaystyle k_{1}\geqslant \cdots \geqslant k_{m}>k\quad \text{and}\quad k_{n}=k\text{ for any }n\geqslant m+1. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle k_{1}\geqslant \cdots \geqslant k_{m}>k\quad \text{and}\quad k_{n}=k\text{ for any }n\geqslant m+1. & & \displaystyle \nonumber\end{eqnarray}$$
By previous computation and the formula (32) for the characteristic functions of convolutions of probability measures, we only need to consider the case when
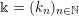 $\Bbbk =(k_{n})_{n\in \mathbb{N}}$
is such that
$\Bbbk =(k_{n})_{n\in \mathbb{N}}$
is such that
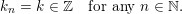 $$\begin{eqnarray}\displaystyle k_{n}=k\in \mathbb{Z}\quad \text{for any }n\in \mathbb{N}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle k_{n}=k\in \mathbb{Z}\quad \text{for any }n\in \mathbb{N}. & & \displaystyle \nonumber\end{eqnarray}$$
In this case,
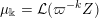 $\unicode[STIX]{x1D707}_{\Bbbk }={\mathcal{L}}(\unicode[STIX]{x1D71B}^{-k}Z)$
with
$\unicode[STIX]{x1D707}_{\Bbbk }={\mathcal{L}}(\unicode[STIX]{x1D71B}^{-k}Z)$
with
![]() $Z$
an infinite random matrix sampled uniformly from
$Z$
an infinite random matrix sampled uniformly from
 $\operatorname{Mat}(\mathbb{N},{\mathcal{O}}_{F})$
. Hence by Lemma 3.3, we obtain
$\operatorname{Mat}(\mathbb{N},{\mathcal{O}}_{F})$
. Hence by Lemma 3.3, we obtain
 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}_{\Bbbk }}(\unicode[STIX]{x1D71B}^{-\ell }e_{11})=\mathbb{E}[\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{-\ell -k}Z_{11})]=\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(\unicode[STIX]{x1D71B}^{-\ell -k})=\unicode[STIX]{x1D7D9}_{\{k+\ell \leqslant 0\}}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}_{\Bbbk }}(\unicode[STIX]{x1D71B}^{-\ell }e_{11})=\mathbb{E}[\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{-\ell -k}Z_{11})]=\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(\unicode[STIX]{x1D71B}^{-\ell -k})=\unicode[STIX]{x1D7D9}_{\{k+\ell \leqslant 0\}}. & & \displaystyle \nonumber\end{eqnarray}$$
But if
![]() $k_{n}=k$
for any
$k_{n}=k$
for any
![]() $n\in \mathbb{N}$
, we have
$n\in \mathbb{N}$
, we have
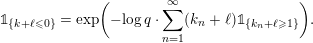 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D7D9}_{\{k+\ell \leqslant 0\}}=\exp \biggl(-\text{log}\,q\cdot \mathop{\sum }_{n=1}^{\infty }(k_{n}+\ell )\unicode[STIX]{x1D7D9}_{\{k_{n}+\ell \geqslant 1\}}\biggr). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D7D9}_{\{k+\ell \leqslant 0\}}=\exp \biggl(-\text{log}\,q\cdot \mathop{\sum }_{n=1}^{\infty }(k_{n}+\ell )\unicode[STIX]{x1D7D9}_{\{k_{n}+\ell \geqslant 1\}}\biggr). & & \displaystyle\end{eqnarray}$$
This proves the identity (40) in the second case and we complete the proof of Proposition 4.1. ◻
4.2 Measures on
 $\operatorname{Sym}(\mathbb{N},F)$
$\operatorname{Sym}(\mathbb{N},F)$
By the elementary observation (31), for studying the characteristic function of
![]() $\unicode[STIX]{x1D708}_{h}$
, it suffices to compute
$\unicode[STIX]{x1D708}_{h}$
, it suffices to compute
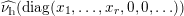 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}_{h}}(\operatorname{diag}(x_{1},\ldots ,x_{r},0,0,\ldots )) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}_{h}}(\operatorname{diag}(x_{1},\ldots ,x_{r},0,0,\ldots )) & & \displaystyle \nonumber\end{eqnarray}$$
for any
![]() $r\in \mathbb{N}$
and any
$r\in \mathbb{N}$
and any
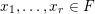 $x_{1},\ldots ,x_{r}\in F$
.
$x_{1},\ldots ,x_{r}\in F$
.
Recall the definition (7) for the function
![]() $\unicode[STIX]{x1D703}$
:
$\unicode[STIX]{x1D703}$
:
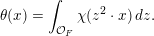 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(x)=\int _{{\mathcal{O}}_{F}}\unicode[STIX]{x1D712}(z^{2}\cdot x)\,dz. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(x)=\int _{{\mathcal{O}}_{F}}\unicode[STIX]{x1D712}(z^{2}\cdot x)\,dz. & & \displaystyle \nonumber\end{eqnarray}$$
Proposition 4.4. Let
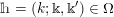 $h=(k;\Bbbk ,\Bbbk ^{\prime })\in \unicode[STIX]{x1D6FA}$
. Then for any
$h=(k;\Bbbk ,\Bbbk ^{\prime })\in \unicode[STIX]{x1D6FA}$
. Then for any
![]() $x\in F$
, we have
$x\in F$
, we have
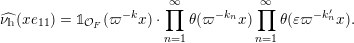 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}_{h}}(xe_{11})=\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(\unicode[STIX]{x1D71B}^{-k}x)\cdot \mathop{\prod }_{n=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-k_{n}}x)\mathop{\prod }_{n=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-k_{n}^{\prime }}x). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}_{h}}(xe_{11})=\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(\unicode[STIX]{x1D71B}^{-k}x)\cdot \mathop{\prod }_{n=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-k_{n}}x)\mathop{\prod }_{n=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-k_{n}^{\prime }}x). & & \displaystyle\end{eqnarray}$$
More generally, for any
![]() $r\in \mathbb{N}$
and any
$r\in \mathbb{N}$
and any
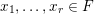 $x_{1},\ldots ,x_{r}\in F$
, we have
$x_{1},\ldots ,x_{r}\in F$
, we have
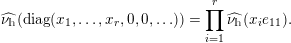 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}_{h}}(\operatorname{diag}(x_{1},\ldots ,x_{r},0,0,\ldots ))=\mathop{\prod }_{i=1}^{r}\widehat{\unicode[STIX]{x1D708}_{h}}(x_{i}e_{11}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}_{h}}(\operatorname{diag}(x_{1},\ldots ,x_{r},0,0,\ldots ))=\mathop{\prod }_{i=1}^{r}\widehat{\unicode[STIX]{x1D708}_{h}}(x_{i}e_{11}). & & \displaystyle\end{eqnarray}$$
Define a function
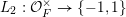 $L_{2}:{\mathcal{O}}_{F}^{\times }\rightarrow \{-1,1\}$
by setting
$L_{2}:{\mathcal{O}}_{F}^{\times }\rightarrow \{-1,1\}$
by setting
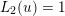 $L_{2}(u)=1$
if
$L_{2}(u)=1$
if
![]() $u$
is a square element in
$u$
is a square element in
![]() ${\mathcal{O}}_{F}^{\times }$
and setting
${\mathcal{O}}_{F}^{\times }$
and setting
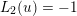 $L_{2}(u)=-1$
if
$L_{2}(u)=-1$
if
![]() $u$
is a non-square element in
$u$
is a non-square element in
![]() ${\mathcal{O}}_{F}^{\times }$
. Write
${\mathcal{O}}_{F}^{\times }$
. Write
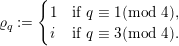 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D71A}_{q}:=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }q\equiv 1(\operatorname{mod}4),\\ i\quad & \text{if }q\equiv 3(\operatorname{mod}4).\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D71A}_{q}:=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }q\equiv 1(\operatorname{mod}4),\\ i\quad & \text{if }q\equiv 3(\operatorname{mod}4).\end{array}\right. & & \displaystyle\end{eqnarray}$$
Recall that for any
![]() $x\in F$
, we have
$x\in F$
, we have
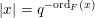 $|x|=q^{-\text{ord}_{F}(x)}$
.
$|x|=q^{-\text{ord}_{F}(x)}$
.
Proposition 4.5. The function
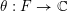 $\unicode[STIX]{x1D703}:F\rightarrow \mathbb{C}$
is continuous and satisfies the following properties.
$\unicode[STIX]{x1D703}:F\rightarrow \mathbb{C}$
is continuous and satisfies the following properties.
-
(i) If
 $|x|\leqslant 1$
, then
$|x|\leqslant 1$
, then
 $\unicode[STIX]{x1D703}(x)=1$
.
$\unicode[STIX]{x1D703}(x)=1$
. -
(ii) If
 $|x|>1$
and
$|x|>1$
and
 $\text{ord}_{F}(x)\equiv 0(\operatorname{mod}2)$
, then
$\text{ord}_{F}(x)\equiv 0(\operatorname{mod}2)$
, then
 $\unicode[STIX]{x1D703}(x)=|x|^{-1/2}$
.
$\unicode[STIX]{x1D703}(x)=|x|^{-1/2}$
. -
(iii) If
 $|x|>1$
and
$|x|>1$
and
 $\text{ord}_{F}(x)\equiv 1(\operatorname{mod}2)$
, then by writing
$\text{ord}_{F}(x)\equiv 1(\operatorname{mod}2)$
, then by writing
 $x=\unicode[STIX]{x1D71B}^{-\ell }u$
with
$x=\unicode[STIX]{x1D71B}^{-\ell }u$
with
 $\ell \in \mathbb{N}$
and
$\ell \in \mathbb{N}$
and
 $u\in {\mathcal{O}}_{F}^{\times }$
, we have (47)where
$u\in {\mathcal{O}}_{F}^{\times }$
, we have (47)where $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(x)=s_{\unicode[STIX]{x1D712}}\unicode[STIX]{x1D71A}_{q}\cdot \frac{L_{2}(u)}{|x|^{1/2}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(x)=s_{\unicode[STIX]{x1D712}}\unicode[STIX]{x1D71A}_{q}\cdot \frac{L_{2}(u)}{|x|^{1/2}}, & & \displaystyle\end{eqnarray}$$
 $s_{\unicode[STIX]{x1D712}}\in \{-1,1\}$
depends on the choice of
$s_{\unicode[STIX]{x1D712}}\in \{-1,1\}$
depends on the choice of
 $\unicode[STIX]{x1D712}$
.
$\unicode[STIX]{x1D712}$
.
In particular,
![]() $\unicode[STIX]{x1D703}$
satisfies the following property:
$\unicode[STIX]{x1D703}$
satisfies the following property:
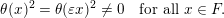 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(x)^{2}=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}x)^{2}\neq 0\quad \text{for all }x\in F. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(x)^{2}=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}x)^{2}\neq 0\quad \text{for all }x\in F. & & \displaystyle\end{eqnarray}$$
Moreover, if
 $x=\unicode[STIX]{x1D71B}^{-\ell }u$
with
$x=\unicode[STIX]{x1D71B}^{-\ell }u$
with
 $\ell \in \mathbb{Z}\cup \{-\infty \}$
and
$\ell \in \mathbb{Z}\cup \{-\infty \}$
and
![]() $u\in {\mathcal{O}}_{F}^{\times }$
$u\in {\mathcal{O}}_{F}^{\times }$
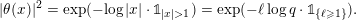 $$\begin{eqnarray}\displaystyle |\unicode[STIX]{x1D703}(x)|^{2}=\exp (-\text{log}\,|x|\cdot \unicode[STIX]{x1D7D9}_{|x|>1})=\exp (-\ell \log q\cdot \unicode[STIX]{x1D7D9}_{\{\ell \geqslant 1\}}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\unicode[STIX]{x1D703}(x)|^{2}=\exp (-\text{log}\,|x|\cdot \unicode[STIX]{x1D7D9}_{|x|>1})=\exp (-\ell \log q\cdot \unicode[STIX]{x1D7D9}_{\{\ell \geqslant 1\}}). & & \displaystyle\end{eqnarray}$$
Let us postpone the proof of Proposition 4.5 to § 10.
Remark 4.6. Proposition 4.5 is related to the calculations of the Gaussian integrals in Neretin [Reference NeretinNer11, § 11.1] and Vladimirov et al. [Reference Vladimirov, Volovich and ZelenovVVZ94, ch. V] in the particular case when the field
![]() $F$
is the field
$F$
is the field
![]() $\mathbb{Q}_{p}$
of
$\mathbb{Q}_{p}$
of
![]() $p$
-adic numbers.
$p$
-adic numbers.
Lemma 4.7. Fix an element
![]() $a\in F$
. Then for any
$a\in F$
. Then for any
 $\Bbbk =(k_{j})_{j\in \mathbb{N}}\in \unicode[STIX]{x1D6E5}$
, the infinite product
$\Bbbk =(k_{j})_{j\in \mathbb{N}}\in \unicode[STIX]{x1D6E5}$
, the infinite product
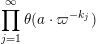 $$\begin{eqnarray}\displaystyle \mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}}) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}}) & & \displaystyle\end{eqnarray}$$
converges. Moreover, if
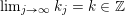 $\lim _{j\rightarrow \infty }k_{j}=k\in \mathbb{Z}$
, then
$\lim _{j\rightarrow \infty }k_{j}=k\in \mathbb{Z}$
, then
 $$\begin{eqnarray}\displaystyle \mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}})=\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(a\cdot \unicode[STIX]{x1D71B}^{-k})\cdot \mathop{\prod }_{j\in \{n\mid k_{n}>k\}}\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}})=\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(a\cdot \unicode[STIX]{x1D71B}^{-k})\cdot \mathop{\prod }_{j\in \{n\mid k_{n}>k\}}\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}}). & & \displaystyle\end{eqnarray}$$
Proof. Let
 $\Bbbk =(k_{j})_{j\in \mathbb{N}}\in \unicode[STIX]{x1D6E5}$
. Since
$\Bbbk =(k_{j})_{j\in \mathbb{N}}\in \unicode[STIX]{x1D6E5}$
. Since
![]() $\Bbbk$
is a non-increasing sequence, we have
$\Bbbk$
is a non-increasing sequence, we have
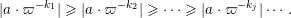 $$\begin{eqnarray}\displaystyle |a\cdot \unicode[STIX]{x1D71B}^{-k_{1}}|\geqslant |a\cdot \unicode[STIX]{x1D71B}^{-k_{2}}|\geqslant \cdots \geqslant |a\cdot \unicode[STIX]{x1D71B}^{-k_{j}}|\cdots \,. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |a\cdot \unicode[STIX]{x1D71B}^{-k_{1}}|\geqslant |a\cdot \unicode[STIX]{x1D71B}^{-k_{2}}|\geqslant \cdots \geqslant |a\cdot \unicode[STIX]{x1D71B}^{-k_{j}}|\cdots \,. & & \displaystyle \nonumber\end{eqnarray}$$
Then either there exists
![]() $j_{0}\in \mathbb{N}$
, such that
$j_{0}\in \mathbb{N}$
, such that
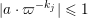 $|a\cdot \unicode[STIX]{x1D71B}^{-k_{j}}|\leqslant 1$
for all
$|a\cdot \unicode[STIX]{x1D71B}^{-k_{j}}|\leqslant 1$
for all
![]() $j\geqslant j_{0}$
or
$j\geqslant j_{0}$
or
 $|a\cdot \unicode[STIX]{x1D71B}^{-k_{j}}|>1$
for all
$|a\cdot \unicode[STIX]{x1D71B}^{-k_{j}}|>1$
for all
![]() $j\in \mathbb{N}$
. Consequently, the infinite product (50) either is a finite product or equals
$j\in \mathbb{N}$
. Consequently, the infinite product (50) either is a finite product or equals
![]() $0$
. The identity (51) follows immediately form (49).◻
$0$
. The identity (51) follows immediately form (49).◻
Proof of Proposition 4.4.
The identity (45) follows from the independence between all diagonal coefficient of
![]() $S_{h}$
. So we only need to prove the identity (44).
$S_{h}$
. So we only need to prove the identity (44).
Case 1:
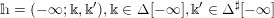 $h=(-\infty ;\Bbbk ,\Bbbk ^{\prime }),\Bbbk \in \unicode[STIX]{x1D6E5}[-\infty ],\Bbbk ^{\prime }\in \unicode[STIX]{x1D6E5}^{\sharp }[-\infty ]$
.
$h=(-\infty ;\Bbbk ,\Bbbk ^{\prime }),\Bbbk \in \unicode[STIX]{x1D6E5}[-\infty ],\Bbbk ^{\prime }\in \unicode[STIX]{x1D6E5}^{\sharp }[-\infty ]$
.
In this case, we have
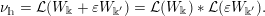 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D708}_{h}={\mathcal{L}}(W_{\Bbbk }+\unicode[STIX]{x1D700}W_{\Bbbk ^{\prime }})={\mathcal{L}}(W_{\Bbbk })\ast {\mathcal{L}}(\unicode[STIX]{x1D700}W_{\Bbbk ^{\prime }}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D708}_{h}={\mathcal{L}}(W_{\Bbbk }+\unicode[STIX]{x1D700}W_{\Bbbk ^{\prime }})={\mathcal{L}}(W_{\Bbbk })\ast {\mathcal{L}}(\unicode[STIX]{x1D700}W_{\Bbbk ^{\prime }}). & & \displaystyle \nonumber\end{eqnarray}$$
Thus for proving (45), it suffices to prove it for the probability measures
![]() ${\mathcal{L}}(W_{\Bbbk })$
and
${\mathcal{L}}(W_{\Bbbk })$
and
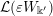 ${\mathcal{L}}(\unicode[STIX]{x1D700}W_{\Bbbk ^{\prime }})$
. For instance, we have
${\mathcal{L}}(\unicode[STIX]{x1D700}W_{\Bbbk ^{\prime }})$
. For instance, we have
 $$\begin{eqnarray}\displaystyle \widehat{{\mathcal{L}}(W_{\Bbbk })}(xe_{11}) & = & \displaystyle \mathbb{E}\biggl[\unicode[STIX]{x1D712}\biggl(\operatorname{tr}\hspace{-0.8pt}\biggl(\mathop{\biggl[\mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D71B}^{-k_{n}}X_{i}^{(n)}X_{j}^{(n)}\biggr]}\nolimits_{i,j\in \mathbb{N}}xe_{11}\biggr)\biggr)\biggr]\nonumber\\ \displaystyle & = & \displaystyle \mathbb{E}\biggl[\unicode[STIX]{x1D712}\biggl(\mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D71B}^{-k_{n}}(X_{1}^{(n)})^{2}x\biggr)\biggr]=\mathbb{E}\biggl[\mathop{\prod }_{n=1}^{\infty }\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{-k_{n}}(X_{1}^{(n)})^{2}x)\biggr].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{{\mathcal{L}}(W_{\Bbbk })}(xe_{11}) & = & \displaystyle \mathbb{E}\biggl[\unicode[STIX]{x1D712}\biggl(\operatorname{tr}\hspace{-0.8pt}\biggl(\mathop{\biggl[\mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D71B}^{-k_{n}}X_{i}^{(n)}X_{j}^{(n)}\biggr]}\nolimits_{i,j\in \mathbb{N}}xe_{11}\biggr)\biggr)\biggr]\nonumber\\ \displaystyle & = & \displaystyle \mathbb{E}\biggl[\unicode[STIX]{x1D712}\biggl(\mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D71B}^{-k_{n}}(X_{1}^{(n)})^{2}x\biggr)\biggr]=\mathbb{E}\biggl[\mathop{\prod }_{n=1}^{\infty }\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{-k_{n}}(X_{1}^{(n)})^{2}x)\biggr].\nonumber\end{eqnarray}$$
Then by dominated convergence theorem and the independence between all
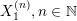 $X_{1}^{(n)},n\in \mathbb{N}$
, we get
$X_{1}^{(n)},n\in \mathbb{N}$
, we get
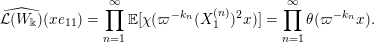 $$\begin{eqnarray}\displaystyle \widehat{{\mathcal{L}}(W_{\Bbbk })}(xe_{11})=\mathop{\prod }_{n=1}^{\infty }\mathbb{E}[\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{-k_{n}}(X_{1}^{(n)})^{2}x)]=\mathop{\prod }_{n=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-k_{n}}x). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{{\mathcal{L}}(W_{\Bbbk })}(xe_{11})=\mathop{\prod }_{n=1}^{\infty }\mathbb{E}[\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{-k_{n}}(X_{1}^{(n)})^{2}x)]=\mathop{\prod }_{n=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-k_{n}}x). & & \displaystyle \nonumber\end{eqnarray}$$
Similar computation works for
 ${\mathcal{L}}(\unicode[STIX]{x1D700}W_{\Bbbk ^{\prime }})$
.
${\mathcal{L}}(\unicode[STIX]{x1D700}W_{\Bbbk ^{\prime }})$
.
Case 2: There exists
![]() $k\in \mathbb{Z}$
and
$k\in \mathbb{Z}$
and
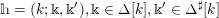 $h=(k;\Bbbk ,\Bbbk ^{\prime }),\Bbbk \in \unicode[STIX]{x1D6E5}[k],\Bbbk ^{\prime }\in \unicode[STIX]{x1D6E5}^{\sharp }[k]$
.
$h=(k;\Bbbk ,\Bbbk ^{\prime }),\Bbbk \in \unicode[STIX]{x1D6E5}[k],\Bbbk ^{\prime }\in \unicode[STIX]{x1D6E5}^{\sharp }[k]$
.
In this case, we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D708}_{h} & ={\mathcal{L}}(W_{\Bbbk }+\unicode[STIX]{x1D700}W_{\Bbbk ^{\prime }}+\unicode[STIX]{x1D71B}^{-k}H)={\mathcal{L}}(W_{\Bbbk })\ast {\mathcal{L}}(\unicode[STIX]{x1D700}W_{\Bbbk ^{\prime }})\ast {\mathcal{L}}(\unicode[STIX]{x1D71B}^{-k}H). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D708}_{h} & ={\mathcal{L}}(W_{\Bbbk }+\unicode[STIX]{x1D700}W_{\Bbbk ^{\prime }}+\unicode[STIX]{x1D71B}^{-k}H)={\mathcal{L}}(W_{\Bbbk })\ast {\mathcal{L}}(\unicode[STIX]{x1D700}W_{\Bbbk ^{\prime }})\ast {\mathcal{L}}(\unicode[STIX]{x1D71B}^{-k}H). & \displaystyle \nonumber\end{eqnarray}$$
By (32), for proving (45), it suffices to prove it for the probability measures
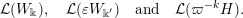 $$\begin{eqnarray}\displaystyle {\mathcal{L}}(W_{\Bbbk }),\quad {\mathcal{L}}(\unicode[STIX]{x1D700}W_{\Bbbk ^{\prime }})\quad \text{and}\quad {\mathcal{L}}(\unicode[STIX]{x1D71B}^{-k}H). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{L}}(W_{\Bbbk }),\quad {\mathcal{L}}(\unicode[STIX]{x1D700}W_{\Bbbk ^{\prime }})\quad \text{and}\quad {\mathcal{L}}(\unicode[STIX]{x1D71B}^{-k}H). & & \displaystyle \nonumber\end{eqnarray}$$
By the computation in Case 1, we only need to verify (45) for
 ${\mathcal{L}}(\unicode[STIX]{x1D71B}^{-k}H)$
. A simple computation yields the desired identity
${\mathcal{L}}(\unicode[STIX]{x1D71B}^{-k}H)$
. A simple computation yields the desired identity
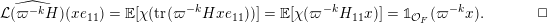 $$\begin{eqnarray}\displaystyle \widehat{{\mathcal{L}}(\unicode[STIX]{x1D71B}^{-k}H)}(xe_{11})=\mathbb{E}[\unicode[STIX]{x1D712}(\operatorname{tr}(\unicode[STIX]{x1D71B}^{-k}Hxe_{11}))]=\mathbb{E}[\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{-k}H_{11}x)]=\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(\unicode[STIX]{x1D71B}^{-k}x).\Box & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{{\mathcal{L}}(\unicode[STIX]{x1D71B}^{-k}H)}(xe_{11})=\mathbb{E}[\unicode[STIX]{x1D712}(\operatorname{tr}(\unicode[STIX]{x1D71B}^{-k}Hxe_{11}))]=\mathbb{E}[\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{-k}H_{11}x)]=\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(\unicode[STIX]{x1D71B}^{-k}x).\Box & & \displaystyle \nonumber\end{eqnarray}$$
Remark 4.8. Let us prove the identity (5) mentioned in Remark 1.7. Write
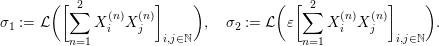 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}_{1}:={\mathcal{L}}\biggl(\mathop{\biggl[\mathop{\sum }_{n=1}^{2}X_{i}^{(n)}X_{j}^{(n)}\biggr]}\nolimits_{i,j\in \mathbb{N}}\biggr),\quad \unicode[STIX]{x1D70E}_{2}:={\mathcal{L}}\biggl(\unicode[STIX]{x1D700}\mathop{\biggl[\mathop{\sum }_{n=1}^{2}X_{i}^{(n)}X_{j}^{(n)}\biggr]}\nolimits_{i,j\in \mathbb{N}}\biggr). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}_{1}:={\mathcal{L}}\biggl(\mathop{\biggl[\mathop{\sum }_{n=1}^{2}X_{i}^{(n)}X_{j}^{(n)}\biggr]}\nolimits_{i,j\in \mathbb{N}}\biggr),\quad \unicode[STIX]{x1D70E}_{2}:={\mathcal{L}}\biggl(\unicode[STIX]{x1D700}\mathop{\biggl[\mathop{\sum }_{n=1}^{2}X_{i}^{(n)}X_{j}^{(n)}\biggr]}\nolimits_{i,j\in \mathbb{N}}\biggr). & & \displaystyle \nonumber\end{eqnarray}$$
Note that
![]() $\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}$
are both
$\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}$
are both
 $\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant. Since for any
$\operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
-invariant. Since for any
![]() $x\in F$
, we have
$x\in F$
, we have
 $\unicode[STIX]{x1D703}(x)^{2}=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}x)^{2}$
. Consequently
$\unicode[STIX]{x1D703}(x)^{2}=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}x)^{2}$
. Consequently
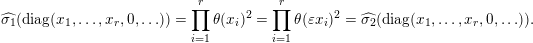 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D70E}_{1}}(\operatorname{diag}(x_{1},\ldots ,x_{r},0,\ldots ))=\mathop{\prod }_{i=1}^{r}\unicode[STIX]{x1D703}(x_{i})^{2}=\mathop{\prod }_{i=1}^{r}\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}x_{i})^{2}=\widehat{\unicode[STIX]{x1D70E}_{2}}(\operatorname{diag}(x_{1},\ldots ,x_{r},0,\ldots )). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D70E}_{1}}(\operatorname{diag}(x_{1},\ldots ,x_{r},0,\ldots ))=\mathop{\prod }_{i=1}^{r}\unicode[STIX]{x1D703}(x_{i})^{2}=\mathop{\prod }_{i=1}^{r}\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}x_{i})^{2}=\widehat{\unicode[STIX]{x1D70E}_{2}}(\operatorname{diag}(x_{1},\ldots ,x_{r},0,\ldots )). & & \displaystyle \nonumber\end{eqnarray}$$
It follows that
 $\unicode[STIX]{x1D70E}_{1}=\unicode[STIX]{x1D70E}_{2}$
.
$\unicode[STIX]{x1D70E}_{1}=\unicode[STIX]{x1D70E}_{2}$
.
5 Uniqueness of parametrization
In this section, we will prove two uniqueness results, Propositions 5.1 and 5.3.
5.1 Measures on
 $\operatorname{Mat}(\mathbb{N},F)$
$\operatorname{Mat}(\mathbb{N},F)$
Proposition 5.1. Let
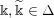 $\Bbbk ,\widetilde{\Bbbk }\in \unicode[STIX]{x1D6E5}$
. Then
$\Bbbk ,\widetilde{\Bbbk }\in \unicode[STIX]{x1D6E5}$
. Then
 $\unicode[STIX]{x1D707}_{\Bbbk }=\unicode[STIX]{x1D707}_{\widetilde{\Bbbk }}$
if and only if
$\unicode[STIX]{x1D707}_{\Bbbk }=\unicode[STIX]{x1D707}_{\widetilde{\Bbbk }}$
if and only if
![]() $\Bbbk =\widetilde{\Bbbk }$
.
$\Bbbk =\widetilde{\Bbbk }$
.
Lemma 5.2. The map
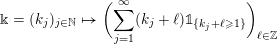 $$\begin{eqnarray}\displaystyle \Bbbk =(k_{j})_{j\in \mathbb{N}}\mapsto \mathop{\biggl(\mathop{\sum }_{j=1}^{\infty }(k_{j}+\ell )\unicode[STIX]{x1D7D9}_{\{k_{j}+\ell \geqslant 1\}}\biggr)}\nolimits_{\ell \in \mathbb{Z}} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Bbbk =(k_{j})_{j\in \mathbb{N}}\mapsto \mathop{\biggl(\mathop{\sum }_{j=1}^{\infty }(k_{j}+\ell )\unicode[STIX]{x1D7D9}_{\{k_{j}+\ell \geqslant 1\}}\biggr)}\nolimits_{\ell \in \mathbb{Z}} & & \displaystyle \nonumber\end{eqnarray}$$
from
![]() $\unicode[STIX]{x1D6E5}$
to
$\unicode[STIX]{x1D6E5}$
to
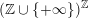 $(\mathbb{Z}\cup \{+\infty \})^{\mathbb{Z}}$
is injective.
$(\mathbb{Z}\cup \{+\infty \})^{\mathbb{Z}}$
is injective.
Proof. We need to show that if
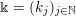 $\Bbbk =(k_{j})_{j\in \mathbb{N}}$
and
$\Bbbk =(k_{j})_{j\in \mathbb{N}}$
and
 $\widetilde{\Bbbk }=(\widetilde{k}_{j})_{j\in \mathbb{N}}$
are two distinct elements in
$\widetilde{\Bbbk }=(\widetilde{k}_{j})_{j\in \mathbb{N}}$
are two distinct elements in
![]() $\unicode[STIX]{x1D6E5}$
, then there exists
$\unicode[STIX]{x1D6E5}$
, then there exists
![]() $\ell \in \mathbb{Z}$
, such that
$\ell \in \mathbb{Z}$
, such that
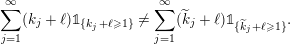 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{j=1}^{\infty }(k_{j}+\ell )\unicode[STIX]{x1D7D9}_{\{k_{j}+\ell \geqslant 1\}}\neq \mathop{\sum }_{j=1}^{\infty }(\widetilde{k}_{j}+\ell )\unicode[STIX]{x1D7D9}_{\{\widetilde{k}_{j}+\ell \geqslant 1\}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{j=1}^{\infty }(k_{j}+\ell )\unicode[STIX]{x1D7D9}_{\{k_{j}+\ell \geqslant 1\}}\neq \mathop{\sum }_{j=1}^{\infty }(\widetilde{k}_{j}+\ell )\unicode[STIX]{x1D7D9}_{\{\widetilde{k}_{j}+\ell \geqslant 1\}}. & & \displaystyle\end{eqnarray}$$
By assumption, there exists
![]() $j_{0}\in \mathbb{N}$
, such that
$j_{0}\in \mathbb{N}$
, such that
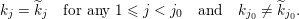 $$\begin{eqnarray}\displaystyle k_{j}=\widetilde{k}_{j}\quad \text{for any }1\leqslant j<j_{0}\quad \text{and}\quad k_{j_{0}}\neq \widetilde{k}_{j_{0}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle k_{j}=\widetilde{k}_{j}\quad \text{for any }1\leqslant j<j_{0}\quad \text{and}\quad k_{j_{0}}\neq \widetilde{k}_{j_{0}}. & & \displaystyle\end{eqnarray}$$
By symmetry, let us assume that
 $k_{j_{0}}>\widetilde{k}_{j_{0}}$
. Under this assumption (whether
$k_{j_{0}}>\widetilde{k}_{j_{0}}$
. Under this assumption (whether
![]() $\widetilde{k}_{j_{0}}$
equals to
$\widetilde{k}_{j_{0}}$
equals to
![]() $-\infty$
or not), we will have
$-\infty$
or not), we will have
![]() $k_{j_{0}}\in \mathbb{Z}$
. Now by taking
$k_{j_{0}}\in \mathbb{Z}$
. Now by taking
 $\ell =1-k_{j_{0}}\in \mathbb{Z}$
, we have
$\ell =1-k_{j_{0}}\in \mathbb{Z}$
, we have
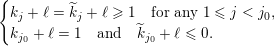 $$\begin{eqnarray}\displaystyle \left\{\begin{array}{@{}l@{}}k_{j}+\ell =\widetilde{k}_{j}+\ell \geqslant 1\quad \text{for any }1\leqslant j<j_{0},\quad \\ k_{j_{0}}+\ell =1\quad \text{and}\quad \widetilde{k}_{j_{0}}+\ell \leqslant 0.\quad \end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left\{\begin{array}{@{}l@{}}k_{j}+\ell =\widetilde{k}_{j}+\ell \geqslant 1\quad \text{for any }1\leqslant j<j_{0},\quad \\ k_{j_{0}}+\ell =1\quad \text{and}\quad \widetilde{k}_{j_{0}}+\ell \leqslant 0.\quad \end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
Consequently,
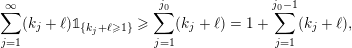 $$\begin{eqnarray}\mathop{\sum }_{j=1}^{\infty }(k_{j}+\ell )\unicode[STIX]{x1D7D9}_{\{k_{j}+\ell \geqslant 1\}}\geqslant \mathop{\sum }_{j=1}^{j_{0}}(k_{j}+\ell )=1+\mathop{\sum }_{j=1}^{j_{0}-1}(k_{j}+\ell ),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{j=1}^{\infty }(k_{j}+\ell )\unicode[STIX]{x1D7D9}_{\{k_{j}+\ell \geqslant 1\}}\geqslant \mathop{\sum }_{j=1}^{j_{0}}(k_{j}+\ell )=1+\mathop{\sum }_{j=1}^{j_{0}-1}(k_{j}+\ell ),\end{eqnarray}$$
while
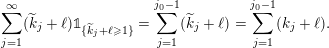 $$\begin{eqnarray}\mathop{\sum }_{j=1}^{\infty }(\widetilde{k}_{j}+\ell )\unicode[STIX]{x1D7D9}_{\{\widetilde{k}_{j}+\ell \geqslant 1\}}=\mathop{\sum }_{j=1}^{j_{0}-1}(\widetilde{k}_{j}+\ell )=\mathop{\sum }_{j=1}^{j_{0}-1}(k_{j}+\ell ).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{j=1}^{\infty }(\widetilde{k}_{j}+\ell )\unicode[STIX]{x1D7D9}_{\{\widetilde{k}_{j}+\ell \geqslant 1\}}=\mathop{\sum }_{j=1}^{j_{0}-1}(\widetilde{k}_{j}+\ell )=\mathop{\sum }_{j=1}^{j_{0}-1}(k_{j}+\ell ).\end{eqnarray}$$
Thus we prove that the inequality (52) holds for
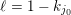 $\ell =1-k_{j_{0}}$
.◻
$\ell =1-k_{j_{0}}$
.◻
5.2 Measures on
 $\operatorname{Sym}(\mathbb{N},F)$
$\operatorname{Sym}(\mathbb{N},F)$
Proposition 5.3. Let
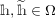 $h,\widetilde{h}\in \unicode[STIX]{x1D6FA}$
. Then
$h,\widetilde{h}\in \unicode[STIX]{x1D6FA}$
. Then
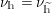 $\unicode[STIX]{x1D708}_{h}=\unicode[STIX]{x1D708}_{\widetilde{h}}$
if and only if
$\unicode[STIX]{x1D708}_{h}=\unicode[STIX]{x1D708}_{\widetilde{h}}$
if and only if
![]() $h=\widetilde{h}$
.
$h=\widetilde{h}$
.
Remark 5.4. Any element
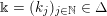 $\Bbbk =(k_{j})_{j\in \mathbb{N}}\in \unicode[STIX]{x1D6E5}$
is uniquely determined by the bi-infinite sequence in
$\Bbbk =(k_{j})_{j\in \mathbb{N}}\in \unicode[STIX]{x1D6E5}$
is uniquely determined by the bi-infinite sequence in
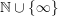 $\mathbb{N}\cup \{\infty \}$
:
$\mathbb{N}\cup \{\infty \}$
:
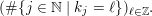 $$\begin{eqnarray}\displaystyle (\#\{j\in \mathbb{N}\mid k_{j}=\ell \})_{\ell \in \mathbb{Z}}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\#\{j\in \mathbb{N}\mid k_{j}=\ell \})_{\ell \in \mathbb{Z}}. & & \displaystyle \nonumber\end{eqnarray}$$
Proof of Proposition 5.3.
Let
 $h=(k;\Bbbk ,\Bbbk ^{\prime })$
and
$h=(k;\Bbbk ,\Bbbk ^{\prime })$
and
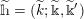 $\widetilde{h}=(\widetilde{k};\widetilde{\Bbbk },\widetilde{\Bbbk }^{\prime })$
be two elements in
$\widetilde{h}=(\widetilde{k};\widetilde{\Bbbk },\widetilde{\Bbbk }^{\prime })$
be two elements in
![]() $\unicode[STIX]{x1D6FA}$
such that
$\unicode[STIX]{x1D6FA}$
such that
 $\unicode[STIX]{x1D708}_{h}=\unicode[STIX]{x1D708}_{\widetilde{h}}$
. By Proposition 4.4, this is equivalent to the following identity: for any
$\unicode[STIX]{x1D708}_{h}=\unicode[STIX]{x1D708}_{\widetilde{h}}$
. By Proposition 4.4, this is equivalent to the following identity: for any
![]() $x\in F$
,
$x\in F$
,
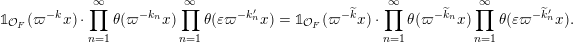 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(\unicode[STIX]{x1D71B}^{-k}x)\cdot \mathop{\prod }_{n=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-k_{n}}x)\mathop{\prod }_{n=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-k_{n}^{\prime }}x)=\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(\unicode[STIX]{x1D71B}^{-\widetilde{k}}x)\cdot \mathop{\prod }_{n=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-\widetilde{k}_{n}}x)\mathop{\prod }_{n=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-\widetilde{k}_{n}^{\prime }}x).\quad & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(\unicode[STIX]{x1D71B}^{-k}x)\cdot \mathop{\prod }_{n=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-k_{n}}x)\mathop{\prod }_{n=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-k_{n}^{\prime }}x)=\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(\unicode[STIX]{x1D71B}^{-\widetilde{k}}x)\cdot \mathop{\prod }_{n=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-\widetilde{k}_{n}}x)\mathop{\prod }_{n=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-\widetilde{k}_{n}^{\prime }}x).\quad & & \displaystyle\end{eqnarray}$$
Recall the identity (49). By taking the modulus and square of both sides of (54) and substituting
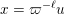 $x=\unicode[STIX]{x1D71B}^{-\ell }u$
with
$x=\unicode[STIX]{x1D71B}^{-\ell }u$
with
![]() $\ell \in \mathbb{Z}$
and
$\ell \in \mathbb{Z}$
and
![]() $u\in {\mathcal{O}}_{F}^{\times }$
, we obtain
$u\in {\mathcal{O}}_{F}^{\times }$
, we obtain
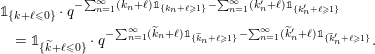 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D7D9}_{\{k+\ell \leqslant 0\}}\cdot q^{-\hspace{-0.9pt}\mathop{\sum }_{n=1}^{\infty }(k_{n}+\ell )\unicode[STIX]{x1D7D9}_{\{k_{n}+\ell \geqslant 1\}}-\mathop{\sum }_{n=1}^{\infty }(k_{n}^{\prime }+\ell )\unicode[STIX]{x1D7D9}_{\{k_{n}^{\prime }+\ell \geqslant 1\}}}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D7D9}_{\{\widetilde{k}+\ell \leqslant 0\}}\cdot q^{-\hspace{-0.9pt}\mathop{\sum }_{n=1}^{\infty }(\widetilde{k}_{n}+\ell )\unicode[STIX]{x1D7D9}_{\{\widetilde{k}_{n}+\ell \geqslant 1\}}-\mathop{\sum }_{n=1}^{\infty }(\widetilde{k}_{n}^{\prime }+\ell )\unicode[STIX]{x1D7D9}_{\{\widetilde{k}_{n}^{\prime }+\ell \geqslant 1\}}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D7D9}_{\{k+\ell \leqslant 0\}}\cdot q^{-\hspace{-0.9pt}\mathop{\sum }_{n=1}^{\infty }(k_{n}+\ell )\unicode[STIX]{x1D7D9}_{\{k_{n}+\ell \geqslant 1\}}-\mathop{\sum }_{n=1}^{\infty }(k_{n}^{\prime }+\ell )\unicode[STIX]{x1D7D9}_{\{k_{n}^{\prime }+\ell \geqslant 1\}}}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D7D9}_{\{\widetilde{k}+\ell \leqslant 0\}}\cdot q^{-\hspace{-0.9pt}\mathop{\sum }_{n=1}^{\infty }(\widetilde{k}_{n}+\ell )\unicode[STIX]{x1D7D9}_{\{\widetilde{k}_{n}+\ell \geqslant 1\}}-\mathop{\sum }_{n=1}^{\infty }(\widetilde{k}_{n}^{\prime }+\ell )\unicode[STIX]{x1D7D9}_{\{\widetilde{k}_{n}^{\prime }+\ell \geqslant 1\}}}.\end{eqnarray}$$
Claim 1:
![]() $k=\widetilde{k}$
.
$k=\widetilde{k}$
.
Indeed, if
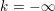 $k=-\infty$
, then the left-hand side of the identity (55) never vanishes. Consequently, so does the right-hand side. It follows that
$k=-\infty$
, then the left-hand side of the identity (55) never vanishes. Consequently, so does the right-hand side. It follows that
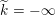 $\widetilde{k}=-\infty$
. If
$\widetilde{k}=-\infty$
. If
![]() $k\in \mathbb{Z}$
. Then the left-hand side of the identity (55) vanishes at
$k\in \mathbb{Z}$
. Then the left-hand side of the identity (55) vanishes at
 $\ell =1-k$
. Consequently, so does the right-hand side of (55) vanishes both at
$\ell =1-k$
. Consequently, so does the right-hand side of (55) vanishes both at
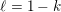 $\ell =1-k$
. It follows that
$\ell =1-k$
. It follows that
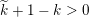 $\widetilde{k}+1-k>0$
or equivalently
$\widetilde{k}+1-k>0$
or equivalently
![]() $\widetilde{k}\geqslant k$
. By symmetry, we have
$\widetilde{k}\geqslant k$
. By symmetry, we have
![]() $k=\widetilde{k}$
.
$k=\widetilde{k}$
.
Claim 2:
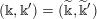 $(\Bbbk ,\Bbbk ^{\prime })=(\widetilde{\Bbbk },\widetilde{\Bbbk }^{\prime })$
.
$(\Bbbk ,\Bbbk ^{\prime })=(\widetilde{\Bbbk },\widetilde{\Bbbk }^{\prime })$
.
For simplifying notation, let us define
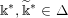 $\Bbbk ^{\ast },\widetilde{\Bbbk }^{\ast }\in \unicode[STIX]{x1D6E5}$
as follows: if
$\Bbbk ^{\ast },\widetilde{\Bbbk }^{\ast }\in \unicode[STIX]{x1D6E5}$
as follows: if
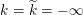 $k=\widetilde{k}=-\infty$
, then set
$k=\widetilde{k}=-\infty$
, then set
 $\Bbbk ^{\ast }:=\Bbbk ,\widetilde{\Bbbk }^{\ast }:=\widetilde{\Bbbk }$
; if
$\Bbbk ^{\ast }:=\Bbbk ,\widetilde{\Bbbk }^{\ast }:=\widetilde{\Bbbk }$
; if
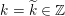 $k=\widetilde{k}\in \mathbb{Z}$
, then both
$k=\widetilde{k}\in \mathbb{Z}$
, then both
![]() $\Bbbk$
and
$\Bbbk$
and
![]() $\widetilde{\Bbbk }$
are finite sequences in
$\widetilde{\Bbbk }$
are finite sequences in
![]() $\mathbb{Z}_{{>}k}$
, set
$\mathbb{Z}_{{>}k}$
, set
![]() $\Bbbk ^{\ast }$
and
$\Bbbk ^{\ast }$
and
![]() $\widetilde{\Bbbk }^{\ast }$
by adding infinitely many
$\widetilde{\Bbbk }^{\ast }$
by adding infinitely many
![]() $k$
. Clearly, for proving
$k$
. Clearly, for proving
 $(\Bbbk ,\Bbbk ^{\prime })=(\widetilde{\Bbbk },\widetilde{\Bbbk }^{\prime })$
, it suffices to prove that
$(\Bbbk ,\Bbbk ^{\prime })=(\widetilde{\Bbbk },\widetilde{\Bbbk }^{\prime })$
, it suffices to prove that
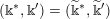 $(\Bbbk ^{\ast },\Bbbk ^{\prime })=(\widetilde{\Bbbk }^{\ast },\widetilde{\Bbbk }^{\prime })$
. By Remark 5.4, it suffices to prove that for any
$(\Bbbk ^{\ast },\Bbbk ^{\prime })=(\widetilde{\Bbbk }^{\ast },\widetilde{\Bbbk }^{\prime })$
. By Remark 5.4, it suffices to prove that for any
![]() $l\in \mathbb{Z}$
,
$l\in \mathbb{Z}$
,
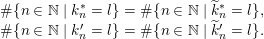 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\#\{n\in \mathbb{N}\mid k_{n}^{\ast }=l\}=\#\{n\in \mathbb{N}\mid \widetilde{k}_{n}^{\ast }=l\},\\ \#\{n\in \mathbb{N}\mid k_{n}^{\prime }=l\}=\#\{n\in \mathbb{N}\mid \widetilde{k}_{n}^{\prime }=l\}.\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\#\{n\in \mathbb{N}\mid k_{n}^{\ast }=l\}=\#\{n\in \mathbb{N}\mid \widetilde{k}_{n}^{\ast }=l\},\\ \#\{n\in \mathbb{N}\mid k_{n}^{\prime }=l\}=\#\{n\in \mathbb{N}\mid \widetilde{k}_{n}^{\prime }=l\}.\end{array}\right. & & \displaystyle\end{eqnarray}$$
Applying (43) to
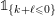 $\unicode[STIX]{x1D7D9}_{\{k+\ell \leqslant 0\}}$
and
$\unicode[STIX]{x1D7D9}_{\{k+\ell \leqslant 0\}}$
and
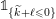 $\unicode[STIX]{x1D7D9}_{\{\widetilde{k}+\ell \leqslant 0\}}$
, we may write (54) as
$\unicode[STIX]{x1D7D9}_{\{\widetilde{k}+\ell \leqslant 0\}}$
, we may write (54) as
 $$\begin{eqnarray}\displaystyle q^{-\hspace{-0.9pt}\mathop{\sum }_{n=1}^{\infty }(k_{n}^{\ast }+\ell )\unicode[STIX]{x1D7D9}_{\{k_{n}^{\ast }+\ell \geqslant 1\}}-\mathop{\sum }_{n=1}^{\infty }(k_{n}^{\prime }+\ell )\unicode[STIX]{x1D7D9}_{\{k_{n}^{\prime }+\ell \geqslant 1\}}}=q^{-\hspace{-0.9pt}\mathop{\sum }_{n=1}^{\infty }(\widetilde{k}_{n}^{\ast }+\ell )\unicode[STIX]{x1D7D9}_{\{\widetilde{k}_{n}^{\ast }+\ell \geqslant 1\}}-\mathop{\sum }_{n=1}^{\infty }(\widetilde{k}_{n}^{\prime }+\ell )\unicode[STIX]{x1D7D9}_{\{\widetilde{k}_{n}^{\prime }+\ell \geqslant 1\}}}.\qquad & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle q^{-\hspace{-0.9pt}\mathop{\sum }_{n=1}^{\infty }(k_{n}^{\ast }+\ell )\unicode[STIX]{x1D7D9}_{\{k_{n}^{\ast }+\ell \geqslant 1\}}-\mathop{\sum }_{n=1}^{\infty }(k_{n}^{\prime }+\ell )\unicode[STIX]{x1D7D9}_{\{k_{n}^{\prime }+\ell \geqslant 1\}}}=q^{-\hspace{-0.9pt}\mathop{\sum }_{n=1}^{\infty }(\widetilde{k}_{n}^{\ast }+\ell )\unicode[STIX]{x1D7D9}_{\{\widetilde{k}_{n}^{\ast }+\ell \geqslant 1\}}-\mathop{\sum }_{n=1}^{\infty }(\widetilde{k}_{n}^{\prime }+\ell )\unicode[STIX]{x1D7D9}_{\{\widetilde{k}_{n}^{\prime }+\ell \geqslant 1\}}}.\qquad & & \displaystyle\end{eqnarray}$$
By Lemma 5.2 and Remark 5.4, the equality (57) implies that for any
![]() $l\in \mathbb{Z}$
, we have
$l\in \mathbb{Z}$
, we have
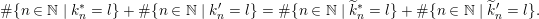 $$\begin{eqnarray}\displaystyle \#\{n\in \mathbb{N}\mid k_{n}^{\ast }=l\}+\#\{n\in \mathbb{N}\mid k_{n}^{\prime }=l\}=\#\{n\in \mathbb{N}\mid \widetilde{k}_{n}^{\ast }=l\}+\#\{n\in \mathbb{N}\mid \widetilde{k}_{n}^{\prime }=l\}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \#\{n\in \mathbb{N}\mid k_{n}^{\ast }=l\}+\#\{n\in \mathbb{N}\mid k_{n}^{\prime }=l\}=\#\{n\in \mathbb{N}\mid \widetilde{k}_{n}^{\ast }=l\}+\#\{n\in \mathbb{N}\mid \widetilde{k}_{n}^{\prime }=l\}. & & \displaystyle\end{eqnarray}$$
The identity (58) implies in particular that the two identities in (56) hold or are violated simultaneously. Now assume by contradiction that there exists
![]() $l_{0}\in \mathbb{Z}$
, such that the identities in (56) are violated. Obviously, such
$l_{0}\in \mathbb{Z}$
, such that the identities in (56) are violated. Obviously, such
![]() $l_{0}$
verifies
$l_{0}$
verifies
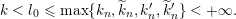 $$\begin{eqnarray}\displaystyle k<l_{0}\leqslant \max \{k_{n},\widetilde{k}_{n},k_{n}^{\prime },\widetilde{k}_{n}^{\prime }\}<+\infty . & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle k<l_{0}\leqslant \max \{k_{n},\widetilde{k}_{n},k_{n}^{\prime },\widetilde{k}_{n}^{\prime }\}<+\infty . & & \displaystyle \nonumber\end{eqnarray}$$
Now let
 $l_{\max }\in \mathbb{Z}$
be the largest
$l_{\max }\in \mathbb{Z}$
be the largest
![]() $l_{0}$
such that the identities in (56) are violated. Substituting
$l_{0}$
such that the identities in (56) are violated. Substituting
 $x=\unicode[STIX]{x1D71B}^{l_{\max }-1}u$
with
$x=\unicode[STIX]{x1D71B}^{l_{\max }-1}u$
with
![]() $u\in {\mathcal{O}}_{F}^{\times }$
into the identity (54), we obtain
$u\in {\mathcal{O}}_{F}^{\times }$
into the identity (54), we obtain
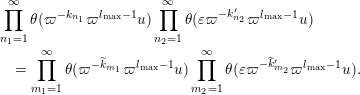 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\prod }_{n_{1}=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-k_{n_{1}}}\unicode[STIX]{x1D71B}^{l_{\max }-1}u)\mathop{\prod }_{n_{2}=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-k_{n_{2}}^{\prime }}\unicode[STIX]{x1D71B}^{l_{\max }-1}u)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\prod }_{m_{1}=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-\widetilde{k}_{m_{1}}}\unicode[STIX]{x1D71B}^{l_{\max }-1}u)\mathop{\prod }_{m_{2}=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-\widetilde{k}_{m_{2}}^{\prime }}\unicode[STIX]{x1D71B}^{l_{\max }-1}u).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\prod }_{n_{1}=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-k_{n_{1}}}\unicode[STIX]{x1D71B}^{l_{\max }-1}u)\mathop{\prod }_{n_{2}=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-k_{n_{2}}^{\prime }}\unicode[STIX]{x1D71B}^{l_{\max }-1}u)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\prod }_{m_{1}=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-\widetilde{k}_{m_{1}}}\unicode[STIX]{x1D71B}^{l_{\max }-1}u)\mathop{\prod }_{m_{2}=1}^{\infty }\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-\widetilde{k}_{m_{2}}^{\prime }}\unicode[STIX]{x1D71B}^{l_{\max }-1}u).\end{eqnarray}$$
By the assumption of
![]() $l_{\max }$
, we know that for any
$l_{\max }$
, we know that for any
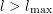 $l>l_{\max }$
,
$l>l_{\max }$
,
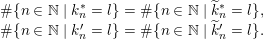 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\#\{n\in \mathbb{N}\mid k_{n}^{\ast }=l\}=\#\{n\in \mathbb{N}\mid \widetilde{k}_{n}^{\ast }=l\},\\ \#\{n\in \mathbb{N}\mid k_{n}^{\prime }=l\}=\#\{n\in \mathbb{N}\mid \widetilde{k}_{n}^{\prime }=l\}.\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\#\{n\in \mathbb{N}\mid k_{n}^{\ast }=l\}=\#\{n\in \mathbb{N}\mid \widetilde{k}_{n}^{\ast }=l\},\\ \#\{n\in \mathbb{N}\mid k_{n}^{\prime }=l\}=\#\{n\in \mathbb{N}\mid \widetilde{k}_{n}^{\prime }=l\}.\end{array}\right. & & \displaystyle\end{eqnarray}$$
Since
 $l_{\max }>k$
, by definition of
$l_{\max }>k$
, by definition of
![]() $\Bbbk ^{\ast }$
and
$\Bbbk ^{\ast }$
and
![]() $\widetilde{\Bbbk }^{\ast }$
we also have for any
$\widetilde{\Bbbk }^{\ast }$
we also have for any
 $l>l_{\max }$
,
$l>l_{\max }$
,
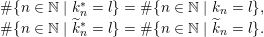 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\#\{n\in \mathbb{N}\mid k_{n}^{\ast }=l\}=\#\{n\in \mathbb{N}\mid k_{n}=l\},\\ \#\{n\in \mathbb{N}\mid \widetilde{k}_{n}^{\ast }=l\}=\#\{n\in \mathbb{N}\mid \widetilde{k}_{n}=l\}.\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\#\{n\in \mathbb{N}\mid k_{n}^{\ast }=l\}=\#\{n\in \mathbb{N}\mid k_{n}=l\},\\ \#\{n\in \mathbb{N}\mid \widetilde{k}_{n}^{\ast }=l\}=\#\{n\in \mathbb{N}\mid \widetilde{k}_{n}=l\}.\end{array}\right. & & \displaystyle\end{eqnarray}$$
By Proposition 4.5, the function
![]() $\unicode[STIX]{x1D703}$
never vanishes. Hence by the identities (60) and (61), we can remove simultaneously all those terms concerning
$\unicode[STIX]{x1D703}$
never vanishes. Hence by the identities (60) and (61), we can remove simultaneously all those terms concerning
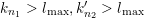 $k_{n_{1}}>l_{\max },k_{n_{2}}^{\prime }>l_{\max }$
and
$k_{n_{1}}>l_{\max },k_{n_{2}}^{\prime }>l_{\max }$
and
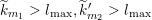 $\widetilde{k}_{m_{1}}>l_{\max },\widetilde{k}_{m_{2}}^{\prime }>l_{\max }$
from both sides of identity (59). Again by Proposition 4.5, for any
$\widetilde{k}_{m_{1}}>l_{\max },\widetilde{k}_{m_{2}}^{\prime }>l_{\max }$
from both sides of identity (59). Again by Proposition 4.5, for any
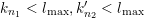 $k_{n_{1}}<l_{\max },k_{n_{2}}^{\prime }<l_{\max }$
and
$k_{n_{1}}<l_{\max },k_{n_{2}}^{\prime }<l_{\max }$
and
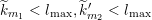 $\widetilde{k}_{m_{1}}<l_{\max },\widetilde{k}_{m_{2}}^{\prime }<l_{\max }$
, we have
$\widetilde{k}_{m_{1}}<l_{\max },\widetilde{k}_{m_{2}}^{\prime }<l_{\max }$
, we have
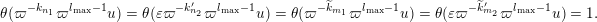 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-k_{n_{1}}}\unicode[STIX]{x1D71B}^{l_{\max }-1}u)=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-k_{n_{2}}^{\prime }}\unicode[STIX]{x1D71B}^{l_{\max }-1}u)=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-\widetilde{k}_{m_{1}}}\unicode[STIX]{x1D71B}^{l_{\max }-1}u)=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-\widetilde{k}_{m_{2}}^{\prime }}\unicode[STIX]{x1D71B}^{l_{\max }-1}u)=1. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-k_{n_{1}}}\unicode[STIX]{x1D71B}^{l_{\max }-1}u)=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-k_{n_{2}}^{\prime }}\unicode[STIX]{x1D71B}^{l_{\max }-1}u)=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-\widetilde{k}_{m_{1}}}\unicode[STIX]{x1D71B}^{l_{\max }-1}u)=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-\widetilde{k}_{m_{2}}^{\prime }}\unicode[STIX]{x1D71B}^{l_{\max }-1}u)=1. & & \displaystyle \nonumber\end{eqnarray}$$
Consequently, we may remove simultaneously all those terms concerning
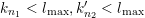 $k_{n_{1}}<l_{\max },k_{n_{2}}^{\prime }<l_{\max }$
and
$k_{n_{1}}<l_{\max },k_{n_{2}}^{\prime }<l_{\max }$
and
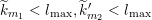 $\widetilde{k}_{m_{1}}<l_{\max },\widetilde{k}_{m_{2}}^{\prime }<l_{\max }$
from both sides of identity (59) as well. Then we arrive at the identity
$\widetilde{k}_{m_{1}}<l_{\max },\widetilde{k}_{m_{2}}^{\prime }<l_{\max }$
from both sides of identity (59) as well. Then we arrive at the identity
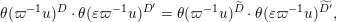 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-1}u)^{D}\cdot \unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-1}u)^{D^{\prime }}=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-1}u)^{\widetilde{D}}\cdot \unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-1}u)^{\widetilde{D^{\prime }}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-1}u)^{D}\cdot \unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-1}u)^{D^{\prime }}=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-1}u)^{\widetilde{D}}\cdot \unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-1}u)^{\widetilde{D^{\prime }}}, & & \displaystyle\end{eqnarray}$$
where
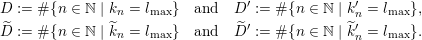 $$\begin{eqnarray}\displaystyle D & := & \displaystyle \#\{n\in \mathbb{N}\mid k_{n}=l_{\max }\}\quad \text{and}\quad D^{\prime }:=\#\{n\in \mathbb{N}\mid k_{n}^{\prime }=l_{\max }\},\nonumber\\ \displaystyle \widetilde{D} & := & \displaystyle \#\{n\in \mathbb{N}\mid \widetilde{k}_{n}=l_{\max }\}\quad \text{and}\quad \widetilde{D}^{\prime }:=\#\{n\in \mathbb{N}\mid \widetilde{k}_{n}^{\prime }=l_{\max }\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D & := & \displaystyle \#\{n\in \mathbb{N}\mid k_{n}=l_{\max }\}\quad \text{and}\quad D^{\prime }:=\#\{n\in \mathbb{N}\mid k_{n}^{\prime }=l_{\max }\},\nonumber\\ \displaystyle \widetilde{D} & := & \displaystyle \#\{n\in \mathbb{N}\mid \widetilde{k}_{n}=l_{\max }\}\quad \text{and}\quad \widetilde{D}^{\prime }:=\#\{n\in \mathbb{N}\mid \widetilde{k}_{n}^{\prime }=l_{\max }\}.\nonumber\end{eqnarray}$$
By definitions for
![]() $\unicode[STIX]{x1D6E5}[k]$
and
$\unicode[STIX]{x1D6E5}[k]$
and
![]() $\unicode[STIX]{x1D6E5}^{\sharp }[k]$
, we must have
$\unicode[STIX]{x1D6E5}^{\sharp }[k]$
, we must have
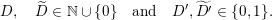 $$\begin{eqnarray}\displaystyle D,\quad \widetilde{D}\in \mathbb{N}\cup \{0\}\quad \text{and}\quad D^{\prime },\widetilde{D^{\prime }}\in \{0,1\}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D,\quad \widetilde{D}\in \mathbb{N}\cup \{0\}\quad \text{and}\quad D^{\prime },\widetilde{D^{\prime }}\in \{0,1\}. & & \displaystyle\end{eqnarray}$$
The identity (58) now implies that
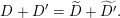 $$\begin{eqnarray}\displaystyle D+D^{\prime }=\widetilde{D}+\widetilde{D^{\prime }}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D+D^{\prime }=\widetilde{D}+\widetilde{D^{\prime }}. & & \displaystyle\end{eqnarray}$$
By definition of
![]() $l_{\max }$
, we have
$l_{\max }$
, we have
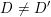 $D\neq D^{\prime }$
. Without loss of generality, we may assume that
$D\neq D^{\prime }$
. Without loss of generality, we may assume that
![]() $D^{\prime }=0$
and
$D^{\prime }=0$
and
![]() $\widetilde{D^{\prime }}=1$
. Then the identity (62) becomes
$\widetilde{D^{\prime }}=1$
. Then the identity (62) becomes
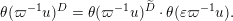 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-1}u)^{D}=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-1}u)^{\widetilde{D}}\cdot \unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-1}u). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-1}u)^{D}=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-1}u)^{\widetilde{D}}\cdot \unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-1}u). & & \displaystyle\end{eqnarray}$$
But now
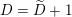 $D=\widetilde{D}+1$
and since
$D=\widetilde{D}+1$
and since
![]() $\unicode[STIX]{x1D703}$
never vanishes, the identity (65) is equivalent to
$\unicode[STIX]{x1D703}$
never vanishes, the identity (65) is equivalent to
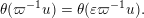 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-1}u)=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-1}u). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-1}u)=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-1}u). & & \displaystyle \nonumber\end{eqnarray}$$
Since
 $|\unicode[STIX]{x1D71B}^{-1}u|>1,\text{ord}_{F}(\unicode[STIX]{x1D71B}^{-1}u)=-1\equiv 1(\operatorname{mod}2)$
and
$|\unicode[STIX]{x1D71B}^{-1}u|>1,\text{ord}_{F}(\unicode[STIX]{x1D71B}^{-1}u)=-1\equiv 1(\operatorname{mod}2)$
and
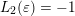 $L_{2}(\unicode[STIX]{x1D700})=-1$
, by Proposition 4.5, we have
$L_{2}(\unicode[STIX]{x1D700})=-1$
, by Proposition 4.5, we have
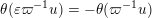 $\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-1}u)=-\unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-1}u)$
. Consequently, we would have
$\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-1}u)=-\unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-1}u)$
. Consequently, we would have
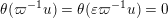 $\unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-1}u)=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-1}u)=0$
. This contradicts to the non-vanishing property of
$\unicode[STIX]{x1D703}(\unicode[STIX]{x1D71B}^{-1}u)=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-1}u)=0$
. This contradicts to the non-vanishing property of
![]() $\unicode[STIX]{x1D703}$
. Hence we complete the proof of Claim 2.
$\unicode[STIX]{x1D703}$
. Hence we complete the proof of Claim 2.
Combining Claims 1 and 2, we complete the proof of Proposition 5.3. ◻
6 Ergodic measures as limits of orbital measures: the Vershik–Kerov ergodic method
In this section, we recall the Vershik–Kerov ergodic method for dealing with ergodic measures for inductively compact groups. The general setting is as follows. Let
 $$\begin{eqnarray}\displaystyle K(1)\subset K(2)\subset \cdots \subset K(n)\subset \cdots \subset K(\infty ), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K(1)\subset K(2)\subset \cdots \subset K(n)\subset \cdots \subset K(\infty ), & & \displaystyle \nonumber\end{eqnarray}$$
be an increasing chain of topological groups such that for any
![]() $n\in \mathbb{N}$
, the group
$n\in \mathbb{N}$
, the group
![]() $K(n)$
is compact and
$K(n)$
is compact and
![]() $K(\infty )$
is the inductive limit:
$K(\infty )$
is the inductive limit:
 $$\begin{eqnarray}\displaystyle K(\infty )=\lim _{\longrightarrow }K(n). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K(\infty )=\lim _{\longrightarrow }K(n). & & \displaystyle \nonumber\end{eqnarray}$$
For any
![]() $n\in \mathbb{N}$
, let
$n\in \mathbb{N}$
, let
![]() $m_{K(n)}$
denote the normalized Haar measure of
$m_{K(n)}$
denote the normalized Haar measure of
![]() $K(n)$
. Fix a group action of
$K(n)$
. Fix a group action of
![]() $K(\infty )$
on a Polish space
$K(\infty )$
on a Polish space
![]() ${\mathcal{X}}$
.
${\mathcal{X}}$
.
Definition 6.1 (Orbital measures).
For any
![]() $x\in {\mathcal{X}}$
and any
$x\in {\mathcal{X}}$
and any
![]() $n\in \mathbb{N}$
, we define the
$n\in \mathbb{N}$
, we define the
![]() $K(n)$
-orbital measure generated by
$K(n)$
-orbital measure generated by
![]() $x$
, denoted by
$x$
, denoted by
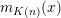 $m_{K(n)}(x)$
, as the unique
$m_{K(n)}(x)$
, as the unique
![]() $K(n)$
-invariant probability measure on
$K(n)$
-invariant probability measure on
![]() ${\mathcal{X}}$
supported on the
${\mathcal{X}}$
supported on the
![]() $K(n)$
-orbit
$K(n)$
-orbit
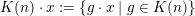 $K(n)\cdot x:=\{g\cdot x\mid g\in K(n)\}$
. In other words,
$K(n)\cdot x:=\{g\cdot x\mid g\in K(n)\}$
. In other words,
 $m_{K(n)}(x)$
is the image of
$m_{K(n)}(x)$
is the image of
![]() $m_{K(n)}$
under the map
$m_{K(n)}$
under the map
 $g\mapsto g\cdot x$
from
$g\mapsto g\cdot x$
from
![]() $K(n)$
to
$K(n)$
to
![]() ${\mathcal{X}}$
.
${\mathcal{X}}$
.
Definition 6.2. Let
 $\mathscr{L}^{K(\infty )}({\mathcal{X}})\subset {\mathcal{P}}({\mathcal{X}})$
be the set of probability measures
$\mathscr{L}^{K(\infty )}({\mathcal{X}})\subset {\mathcal{P}}({\mathcal{X}})$
be the set of probability measures
![]() $\unicode[STIX]{x1D707}$
on
$\unicode[STIX]{x1D707}$
on
![]() ${\mathcal{X}}$
such that there exists
${\mathcal{X}}$
such that there exists
![]() $x\in {\mathcal{X}}$
verifying
$x\in {\mathcal{X}}$
verifying
 $m_{K(n)}(x)\Longrightarrow \unicode[STIX]{x1D707}$
.
$m_{K(n)}(x)\Longrightarrow \unicode[STIX]{x1D707}$
.
Theorem 6.3 (Vershik [Reference VershikVer74, Theorem 1]).
The following inclusion holds:
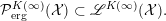 $$\begin{eqnarray}\displaystyle {\mathcal{P}}_{\text{erg}}^{K(\infty )}({\mathcal{X}})\subset \mathscr{L}^{K(\infty )}({\mathcal{X}}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{P}}_{\text{erg}}^{K(\infty )}({\mathcal{X}})\subset \mathscr{L}^{K(\infty )}({\mathcal{X}}). & & \displaystyle\end{eqnarray}$$
More precisely, if
![]() $\unicode[STIX]{x1D707}$
is an ergodic
$\unicode[STIX]{x1D707}$
is an ergodic
![]() $K(\infty )$
-invariant Borel probability measure on
$K(\infty )$
-invariant Borel probability measure on
![]() ${\mathcal{X}}$
, then for
${\mathcal{X}}$
, then for
![]() $\unicode[STIX]{x1D707}$
-almost every point
$\unicode[STIX]{x1D707}$
-almost every point
![]() $x\in {\mathcal{X}}$
, the weak convergence
$x\in {\mathcal{X}}$
, the weak convergence
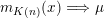 $m_{K(n)}(x)\Longrightarrow \unicode[STIX]{x1D707}$
holds.
$m_{K(n)}(x)\Longrightarrow \unicode[STIX]{x1D707}$
holds.
Vershik’s method in [Reference VershikVer74] was further developed in a series of papers [Reference Vershik and KerovVK81a, Reference Vershik and KerovVK81b, Reference Kerov and VershikKV86, Reference Olshanski and VershikOV96] by Kerov et al.
Remark 6.4. In general, the converse inclusion
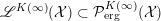 $\mathscr{L}^{K(\infty )}({\mathcal{X}})\subset {\mathcal{P}}_{\text{erg}}^{K(\infty )}({\mathcal{X}})$
does not hold. There is however a simple situation, see the note [Reference QiuQiu17], where
$\mathscr{L}^{K(\infty )}({\mathcal{X}})\subset {\mathcal{P}}_{\text{erg}}^{K(\infty )}({\mathcal{X}})$
does not hold. There is however a simple situation, see the note [Reference QiuQiu17], where
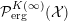 ${\mathcal{P}}_{\text{erg}}^{K(\infty )}({\mathcal{X}})$
always coincides with
${\mathcal{P}}_{\text{erg}}^{K(\infty )}({\mathcal{X}})$
always coincides with
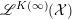 $\mathscr{L}^{K(\infty )}({\mathcal{X}})$
.
$\mathscr{L}^{K(\infty )}({\mathcal{X}})$
.
For simplifying notation, in what follows, we write
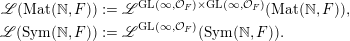 $$\begin{eqnarray}\displaystyle \mathscr{L}(\operatorname{Mat}(\mathbb{N},F)) & := & \displaystyle \mathscr{L}^{\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})}(\operatorname{Mat}(\mathbb{N},F)),\nonumber\\ \displaystyle \mathscr{L}(\operatorname{Sym}(\mathbb{N},F)) & := & \displaystyle \mathscr{L}^{\operatorname{GL}(\infty ,{\mathcal{O}}_{F})}(\operatorname{Sym}(\mathbb{N},F)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{L}(\operatorname{Mat}(\mathbb{N},F)) & := & \displaystyle \mathscr{L}^{\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})}(\operatorname{Mat}(\mathbb{N},F)),\nonumber\\ \displaystyle \mathscr{L}(\operatorname{Sym}(\mathbb{N},F)) & := & \displaystyle \mathscr{L}^{\operatorname{GL}(\infty ,{\mathcal{O}}_{F})}(\operatorname{Sym}(\mathbb{N},F)).\nonumber\end{eqnarray}$$
For any
![]() $n\in \mathbb{N}$
, we set
$n\in \mathbb{N}$
, we set
 $$\begin{eqnarray}\displaystyle \mathscr{ORB}_{n}(\operatorname{Mat}(n,F)):=\{m_{\operatorname{GL}(n,{\mathcal{O}}_{F})\times \operatorname{GL}(n,{\mathcal{O}}_{F})}(M)\mid M\in \operatorname{Mat}(n,F)\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{ORB}_{n}(\operatorname{Mat}(n,F)):=\{m_{\operatorname{GL}(n,{\mathcal{O}}_{F})\times \operatorname{GL}(n,{\mathcal{O}}_{F})}(M)\mid M\in \operatorname{Mat}(n,F)\}. & & \displaystyle \nonumber\end{eqnarray}$$
By identifying
 $\operatorname{Mat}(n,F)$
in a natural way with the subset of
$\operatorname{Mat}(n,F)$
in a natural way with the subset of
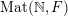 $\operatorname{Mat}(\mathbb{N},F)$
, we have
$\operatorname{Mat}(\mathbb{N},F)$
, we have
 ${\mathcal{P}}(\operatorname{Mat}(n,F))\subset {\mathcal{P}}(\operatorname{Mat}(\mathbb{N},F))$
. In particular,
${\mathcal{P}}(\operatorname{Mat}(n,F))\subset {\mathcal{P}}(\operatorname{Mat}(\mathbb{N},F))$
. In particular,
 $$\begin{eqnarray}\displaystyle \mathscr{ORB}_{n}(\operatorname{Mat}(n,F))\subset {\mathcal{P}}(\operatorname{Mat}(\mathbb{N},F)). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{ORB}_{n}(\operatorname{Mat}(n,F))\subset {\mathcal{P}}(\operatorname{Mat}(\mathbb{N},F)). & & \displaystyle \nonumber\end{eqnarray}$$
Definition 6.5. Let
 $\mathscr{ORB}_{\infty }(\operatorname{Mat}(\mathbb{N},F))$
denote the set of probability measures
$\mathscr{ORB}_{\infty }(\operatorname{Mat}(\mathbb{N},F))$
denote the set of probability measures
![]() $\unicode[STIX]{x1D707}$
on
$\unicode[STIX]{x1D707}$
on
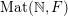 $\operatorname{Mat}(\mathbb{N},F)$
such that there exists a subsequence of positive integers
$\operatorname{Mat}(\mathbb{N},F)$
such that there exists a subsequence of positive integers
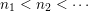 $n_{1}<n_{2}<\cdots \,$
and a sequence
$n_{1}<n_{2}<\cdots \,$
and a sequence
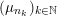 $(\unicode[STIX]{x1D707}_{n_{k}})_{k\in \mathbb{N}}$
of orbital measures with
$(\unicode[STIX]{x1D707}_{n_{k}})_{k\in \mathbb{N}}$
of orbital measures with
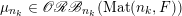 $\unicode[STIX]{x1D707}_{n_{k}}\in \mathscr{ORB}_{n_{k}}(\operatorname{Mat}(n_{k},F))$
, so that
$\unicode[STIX]{x1D707}_{n_{k}}\in \mathscr{ORB}_{n_{k}}(\operatorname{Mat}(n_{k},F))$
, so that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}_{n_{k}}\Longrightarrow \unicode[STIX]{x1D707}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}_{n_{k}}\Longrightarrow \unicode[STIX]{x1D707}. & & \displaystyle \nonumber\end{eqnarray}$$
Similarly, in the symmetric case, for any
![]() $n\in \mathbb{N}$
, we set
$n\in \mathbb{N}$
, we set
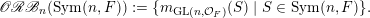 $$\begin{eqnarray}\displaystyle \mathscr{ORB}_{n}(\operatorname{Sym}(n,F)):=\{m_{\operatorname{GL}(n,{\mathcal{O}}_{F})}(S)\mid S\in \operatorname{Sym}(n,F)\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{ORB}_{n}(\operatorname{Sym}(n,F)):=\{m_{\operatorname{GL}(n,{\mathcal{O}}_{F})}(S)\mid S\in \operatorname{Sym}(n,F)\}. & & \displaystyle \nonumber\end{eqnarray}$$
By identifying
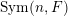 $\operatorname{Sym}(n,F)$
in a natural way with a subspace of
$\operatorname{Sym}(n,F)$
in a natural way with a subspace of
 $\operatorname{Sym}(\mathbb{N},F)$
, we have
$\operatorname{Sym}(\mathbb{N},F)$
, we have
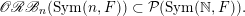 $$\begin{eqnarray}\displaystyle \mathscr{ORB}_{n}(\operatorname{Sym}(n,F))\subset {\mathcal{P}}(\operatorname{Sym}(\mathbb{N},F)). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{ORB}_{n}(\operatorname{Sym}(n,F))\subset {\mathcal{P}}(\operatorname{Sym}(\mathbb{N},F)). & & \displaystyle \nonumber\end{eqnarray}$$
Definition 6.6. Let
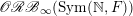 $\mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))$
denote the set of probability measures
$\mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))$
denote the set of probability measures
![]() $\unicode[STIX]{x1D708}$
on
$\unicode[STIX]{x1D708}$
on
 $\operatorname{Sym}(\mathbb{N},F)$
such that there exists a subsequence of positive integers
$\operatorname{Sym}(\mathbb{N},F)$
such that there exists a subsequence of positive integers
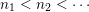 $n_{1}<n_{2}<\cdots \,$
and a sequence
$n_{1}<n_{2}<\cdots \,$
and a sequence
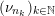 $(\unicode[STIX]{x1D708}_{n_{k}})_{k\in \mathbb{N}}$
of orbital measures with
$(\unicode[STIX]{x1D708}_{n_{k}})_{k\in \mathbb{N}}$
of orbital measures with
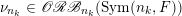 $\unicode[STIX]{x1D708}_{n_{k}}\in \mathscr{ORB}_{n_{k}}(\operatorname{Sym}(n_{k},F))$
, so that
$\unicode[STIX]{x1D708}_{n_{k}}\in \mathscr{ORB}_{n_{k}}(\operatorname{Sym}(n_{k},F))$
, so that
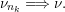 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D708}_{n_{k}}\Longrightarrow \unicode[STIX]{x1D708}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D708}_{n_{k}}\Longrightarrow \unicode[STIX]{x1D708}. & & \displaystyle \nonumber\end{eqnarray}$$
Remark 6.7. It is easy to see that we have
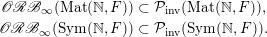 $$\begin{eqnarray}\displaystyle \mathscr{ORB}_{\infty }(\operatorname{Mat}(\mathbb{N},F)) & \subset & \displaystyle {\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F)),\nonumber\\ \displaystyle \mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F)) & \subset & \displaystyle {\mathcal{P}}_{\text{inv}}(\operatorname{Sym}(\mathbb{N},F)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{ORB}_{\infty }(\operatorname{Mat}(\mathbb{N},F)) & \subset & \displaystyle {\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F)),\nonumber\\ \displaystyle \mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F)) & \subset & \displaystyle {\mathcal{P}}_{\text{inv}}(\operatorname{Sym}(\mathbb{N},F)).\nonumber\end{eqnarray}$$
Proposition 6.8. The following two inclusions hold:
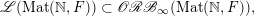 $$\begin{eqnarray}\displaystyle \mathscr{L}(\operatorname{Mat}(\mathbb{N},F)) & \subset & \displaystyle \mathscr{ORB}_{\infty }(\operatorname{Mat}(\mathbb{N},F)),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{L}(\operatorname{Mat}(\mathbb{N},F)) & \subset & \displaystyle \mathscr{ORB}_{\infty }(\operatorname{Mat}(\mathbb{N},F)),\end{eqnarray}$$
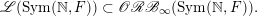 $$\begin{eqnarray}\displaystyle \mathscr{L}(\operatorname{Sym}(\mathbb{N},F)) & \subset & \displaystyle \mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F)).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{L}(\operatorname{Sym}(\mathbb{N},F)) & \subset & \displaystyle \mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F)).\end{eqnarray}$$
Proof. For any
 $n,m\in \mathbb{N}$
such that
$n,m\in \mathbb{N}$
such that
![]() $m\geqslant n$
, let
$m\geqslant n$
, let
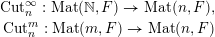 $$\begin{eqnarray}\displaystyle & \operatorname{Cut}_{n}^{\infty }:\operatorname{Mat}(\mathbb{N},F)\rightarrow \operatorname{Mat}(n,F), & \displaystyle \nonumber\\ \displaystyle & \operatorname{Cut}_{n}^{m}:\operatorname{Mat}(m,F)\rightarrow \operatorname{Mat}(n,F) & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \operatorname{Cut}_{n}^{\infty }:\operatorname{Mat}(\mathbb{N},F)\rightarrow \operatorname{Mat}(n,F), & \displaystyle \nonumber\\ \displaystyle & \operatorname{Cut}_{n}^{m}:\operatorname{Mat}(m,F)\rightarrow \operatorname{Mat}(n,F) & \displaystyle \nonumber\end{eqnarray}$$
be the maps of cutting the
![]() $n\times n$
left-upper corner.
$n\times n$
left-upper corner.
For simplifying notation, write
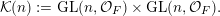 $$\begin{eqnarray}\displaystyle {\mathcal{K}}(n):=\operatorname{GL}(n,{\mathcal{O}}_{F})\times \operatorname{GL}(n,{\mathcal{O}}_{F}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{K}}(n):=\operatorname{GL}(n,{\mathcal{O}}_{F})\times \operatorname{GL}(n,{\mathcal{O}}_{F}). & & \displaystyle\end{eqnarray}$$
Let
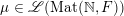 $\unicode[STIX]{x1D707}\in \mathscr{L}(\operatorname{Mat}(\mathbb{N},F))$
. By definition, there exists an infinite matrix
$\unicode[STIX]{x1D707}\in \mathscr{L}(\operatorname{Mat}(\mathbb{N},F))$
. By definition, there exists an infinite matrix
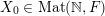 $X_{0}\in \operatorname{Mat}(\mathbb{N},F)$
and a subsequence
$X_{0}\in \operatorname{Mat}(\mathbb{N},F)$
and a subsequence
 $(n_{k})_{k\in \mathbb{N}}$
of positive integers such that
$(n_{k})_{k\in \mathbb{N}}$
of positive integers such that
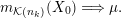 $$\begin{eqnarray}m_{{\mathcal{K}}(n_{k})}(X_{0})\Longrightarrow \unicode[STIX]{x1D707}.\end{eqnarray}$$
$$\begin{eqnarray}m_{{\mathcal{K}}(n_{k})}(X_{0})\Longrightarrow \unicode[STIX]{x1D707}.\end{eqnarray}$$
This is equivalent to saying that for any
![]() $N\in \mathbb{N}$
, we have
$N\in \mathbb{N}$
, we have
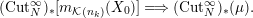 $$\begin{eqnarray}\displaystyle (\operatorname{Cut}_{N}^{\infty })_{\ast }[m_{{\mathcal{K}}(n_{k})}(X_{0})]\Longrightarrow (\operatorname{Cut}_{N}^{\infty })_{\ast }(\unicode[STIX]{x1D707}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\operatorname{Cut}_{N}^{\infty })_{\ast }[m_{{\mathcal{K}}(n_{k})}(X_{0})]\Longrightarrow (\operatorname{Cut}_{N}^{\infty })_{\ast }(\unicode[STIX]{x1D707}). & & \displaystyle\end{eqnarray}$$
Take
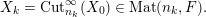 $$\begin{eqnarray}X_{k}=\operatorname{Cut}_{n_{k}}^{\infty }(X_{0})\in \operatorname{Mat}(n_{k},F).\end{eqnarray}$$
$$\begin{eqnarray}X_{k}=\operatorname{Cut}_{n_{k}}^{\infty }(X_{0})\in \operatorname{Mat}(n_{k},F).\end{eqnarray}$$
Then we have
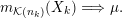 $$\begin{eqnarray}m_{{\mathcal{K}}(n_{k})}(X_{k})\Longrightarrow \unicode[STIX]{x1D707}.\end{eqnarray}$$
$$\begin{eqnarray}m_{{\mathcal{K}}(n_{k})}(X_{k})\Longrightarrow \unicode[STIX]{x1D707}.\end{eqnarray}$$
Indeed, it suffices to prove that for any
![]() $N\in \mathbb{N}$
, we have
$N\in \mathbb{N}$
, we have
 $$\begin{eqnarray}\displaystyle (\operatorname{Cut}_{N}^{\infty })_{\ast }[m_{{\mathcal{K}}(n_{k})}(X_{k})]\Longrightarrow (\operatorname{Cut}_{N}^{\infty })_{\ast }(\unicode[STIX]{x1D707}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\operatorname{Cut}_{N}^{\infty })_{\ast }[m_{{\mathcal{K}}(n_{k})}(X_{k})]\Longrightarrow (\operatorname{Cut}_{N}^{\infty })_{\ast }(\unicode[STIX]{x1D707}). & & \displaystyle\end{eqnarray}$$
For any
![]() $k\in \mathbb{N}$
, we clearly have
$k\in \mathbb{N}$
, we clearly have
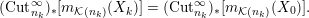 $$\begin{eqnarray}\displaystyle (\operatorname{Cut}_{n_{k}}^{\infty })_{\ast }[m_{{\mathcal{K}}(n_{k})}(X_{k})]=(\operatorname{Cut}_{n_{k}}^{\infty })_{\ast }[m_{{\mathcal{K}}(n_{k})}(X_{0})]. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\operatorname{Cut}_{n_{k}}^{\infty })_{\ast }[m_{{\mathcal{K}}(n_{k})}(X_{k})]=(\operatorname{Cut}_{n_{k}}^{\infty })_{\ast }[m_{{\mathcal{K}}(n_{k})}(X_{0})]. & & \displaystyle\end{eqnarray}$$
But if
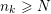 $n_{k}\geqslant N$
, we have
$n_{k}\geqslant N$
, we have
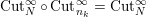 $\operatorname{Cut}_{N}^{\infty }\circ \operatorname{Cut}_{n_{k}}^{\infty }=\operatorname{Cut}_{N}^{\infty }$
. Combining with (72), we see that, once
$\operatorname{Cut}_{N}^{\infty }\circ \operatorname{Cut}_{n_{k}}^{\infty }=\operatorname{Cut}_{N}^{\infty }$
. Combining with (72), we see that, once
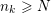 $n_{k}\geqslant N$
, we have
$n_{k}\geqslant N$
, we have
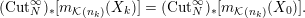 $$\begin{eqnarray}(\operatorname{Cut}_{N}^{\infty })_{\ast }[m_{{\mathcal{K}}(n_{k})}(X_{k})]=(\operatorname{Cut}_{N}^{\infty })_{\ast }[m_{{\mathcal{K}}(n_{k})}(X_{0})].\end{eqnarray}$$
$$\begin{eqnarray}(\operatorname{Cut}_{N}^{\infty })_{\ast }[m_{{\mathcal{K}}(n_{k})}(X_{k})]=(\operatorname{Cut}_{N}^{\infty })_{\ast }[m_{{\mathcal{K}}(n_{k})}(X_{0})].\end{eqnarray}$$
Now it is clear that (70) implies (71). The first inclusion (67) is proved. The proof of the second inclusion (68) is the same. ◻
7 Asymptotic multiplicativity for orbital integrals
7.1
 $\operatorname{GL}(n,{\mathcal{O}}_{F})\times \operatorname{GL}(n,{\mathcal{O}}_{F})$
-orbital integrals
$\operatorname{GL}(n,{\mathcal{O}}_{F})\times \operatorname{GL}(n,{\mathcal{O}}_{F})$
-orbital integrals
Recall Definition 42 and Lemma 4.2:
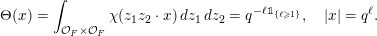 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}(x)=\int _{{\mathcal{O}}_{F}\times {\mathcal{O}}_{F}}\unicode[STIX]{x1D712}(z_{1}z_{2}\cdot x)\,dz_{1}\,dz_{2}=q^{-\ell \unicode[STIX]{x1D7D9}_{\{\ell \geqslant 1\}}},\quad |x|=q^{\ell }. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}(x)=\int _{{\mathcal{O}}_{F}\times {\mathcal{O}}_{F}}\unicode[STIX]{x1D712}(z_{1}z_{2}\cdot x)\,dz_{1}\,dz_{2}=q^{-\ell \unicode[STIX]{x1D7D9}_{\{\ell \geqslant 1\}}},\quad |x|=q^{\ell }. & & \displaystyle \nonumber\end{eqnarray}$$
In what follows, we use the notation (69).
Theorem 7.1. Let
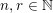 $n,r\in \mathbb{N}$
be such that
$n,r\in \mathbb{N}$
be such that
![]() $r\leqslant n$
. Suppose that
$r\leqslant n$
. Suppose that
![]() $D$
and
$D$
and
![]() $A$
are two diagonal matrices given by
$A$
are two diagonal matrices given by
 $$\begin{eqnarray}\displaystyle D=\operatorname{diag}(x_{1},\ldots ,x_{n}),\quad A=\operatorname{diag}(a_{1},\ldots ,a_{r},0,\ldots ,0) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D=\operatorname{diag}(x_{1},\ldots ,x_{n}),\quad A=\operatorname{diag}(a_{1},\ldots ,a_{r},0,\ldots ,0) & & \displaystyle \nonumber\end{eqnarray}$$
where
 $x_{1},\ldots ,x_{n},a_{1},\ldots ,a_{r}\in F$
. Then
$x_{1},\ldots ,x_{n},a_{1},\ldots ,a_{r}\in F$
. Then
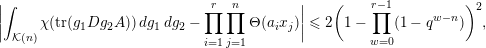 $$\begin{eqnarray}\displaystyle \biggl|\int _{{\mathcal{K}}(n)}\unicode[STIX]{x1D712}(\operatorname{tr}(g_{1}Dg_{2}A))\,dg_{1}\,dg_{2}-\mathop{\prod }_{i=1}^{r}\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D6E9}(a_{i}x_{j})\biggr|\leqslant 2\biggl(1-\mathop{\prod }_{w=0}^{r-1}(1-q^{w-n})\biggr)^{2}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \biggl|\int _{{\mathcal{K}}(n)}\unicode[STIX]{x1D712}(\operatorname{tr}(g_{1}Dg_{2}A))\,dg_{1}\,dg_{2}-\mathop{\prod }_{i=1}^{r}\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D6E9}(a_{i}x_{j})\biggr|\leqslant 2\biggl(1-\mathop{\prod }_{w=0}^{r-1}(1-q^{w-n})\biggr)^{2}, & & \displaystyle\end{eqnarray}$$
where
![]() $dg_{1}\,dg_{2}$
is the normalized Haar measure on
$dg_{1}\,dg_{2}$
is the normalized Haar measure on
![]() ${\mathcal{K}}(n)$
.
${\mathcal{K}}(n)$
.
In particular, for any
![]() $a\in F$
, we have
$a\in F$
, we have
 $$\begin{eqnarray}\displaystyle \biggl|\int _{{\mathcal{K}}(n)}\unicode[STIX]{x1D712}(a\cdot \operatorname{tr}(g_{1}Dg_{2}e_{11}))\,dg_{1}\,dg_{2}-\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D6E9}(ax_{j})\biggr|\leqslant 2q^{-2n}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \biggl|\int _{{\mathcal{K}}(n)}\unicode[STIX]{x1D712}(a\cdot \operatorname{tr}(g_{1}Dg_{2}e_{11}))\,dg_{1}\,dg_{2}-\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D6E9}(ax_{j})\biggr|\leqslant 2q^{-2n}. & & \displaystyle\end{eqnarray}$$
Remark 7.2. Obviously, we have
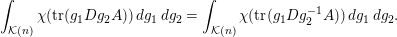 $$\begin{eqnarray}\displaystyle \int _{{\mathcal{K}}(n)}\unicode[STIX]{x1D712}(\operatorname{tr}(g_{1}Dg_{2}A))\,dg_{1}\,dg_{2}=\int _{{\mathcal{K}}(n)}\unicode[STIX]{x1D712}(\operatorname{tr}(g_{1}Dg_{2}^{-1}A))\,dg_{1}\,dg_{2}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{{\mathcal{K}}(n)}\unicode[STIX]{x1D712}(\operatorname{tr}(g_{1}Dg_{2}A))\,dg_{1}\,dg_{2}=\int _{{\mathcal{K}}(n)}\unicode[STIX]{x1D712}(\operatorname{tr}(g_{1}Dg_{2}^{-1}A))\,dg_{1}\,dg_{2}. & & \displaystyle \nonumber\end{eqnarray}$$
The following elementary lemma will be useful.
Lemma 7.3. Let
![]() $r\leqslant n$
be two positive integers. Define
$r\leqslant n$
be two positive integers. Define
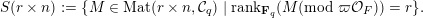 $$\begin{eqnarray}\displaystyle S(r\times n):=\{M\in \operatorname{Mat}(r\times n,{\mathcal{C}}_{q})\mid \operatorname{rank}_{\mathbf{F}_{q}}(M(\operatorname{mod}\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}))=r\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S(r\times n):=\{M\in \operatorname{Mat}(r\times n,{\mathcal{C}}_{q})\mid \operatorname{rank}_{\mathbf{F}_{q}}(M(\operatorname{mod}\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}))=r\}. & & \displaystyle \nonumber\end{eqnarray}$$
Then we have
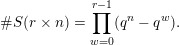 $$\begin{eqnarray}\displaystyle \#S(r\times n)=\mathop{\prod }_{w=0}^{r-1}(q^{n}-q^{w}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \#S(r\times n)=\mathop{\prod }_{w=0}^{r-1}(q^{n}-q^{w}). & & \displaystyle\end{eqnarray}$$
For any rectangular matrix
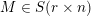 $M\in S(r\times n)$
, we have
$M\in S(r\times n)$
, we have
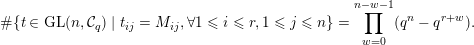 $$\begin{eqnarray}\displaystyle \#\{t\in \operatorname{GL}(n,{\mathcal{C}}_{q})\mid t_{ij}=M_{ij},\forall 1\leqslant i\leqslant r,1\leqslant j\leqslant n\}=\mathop{\prod }_{w=0}^{n-w-1}(q^{n}-q^{r+w}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \#\{t\in \operatorname{GL}(n,{\mathcal{C}}_{q})\mid t_{ij}=M_{ij},\forall 1\leqslant i\leqslant r,1\leqslant j\leqslant n\}=\mathop{\prod }_{w=0}^{n-w-1}(q^{n}-q^{r+w}). & & \displaystyle \nonumber\end{eqnarray}$$
In particular, the above cardinality does not depend on the choice of
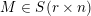 $M\in S(r\times n)$
.
$M\in S(r\times n)$
.
Proof of Theorem 7.1.
Fix
 $n,r\in \mathbb{N}$
and fix the two diagonal matrices
$n,r\in \mathbb{N}$
and fix the two diagonal matrices
![]() $D$
and
$D$
and
![]() $A$
. Let
$A$
. Let
 $T=T(n),T^{\prime }=T^{\prime }(n)$
be two independent copies of random matrices sampled uniformly from the finite set
$T=T(n),T^{\prime }=T^{\prime }(n)$
be two independent copies of random matrices sampled uniformly from the finite set
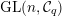 $\operatorname{GL}(n,{\mathcal{C}}_{q})$
, and let
$\operatorname{GL}(n,{\mathcal{C}}_{q})$
, and let
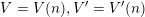 $V=V(n),V^{\prime }=V^{\prime }(n)$
be two independent random matrices sampled uniformly from
$V=V(n),V^{\prime }=V^{\prime }(n)$
be two independent random matrices sampled uniformly from
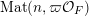 $\operatorname{Mat}(n,\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})$
and independent of
$\operatorname{Mat}(n,\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})$
and independent of
![]() $T,T^{\prime }$
. By Proposition 2.3, we have
$T,T^{\prime }$
. By Proposition 2.3, we have
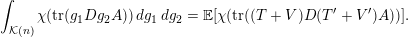 $$\begin{eqnarray}\displaystyle \int _{{\mathcal{K}}(n)}\unicode[STIX]{x1D712}(\operatorname{tr}(g_{1}Dg_{2}A))\,dg_{1}\,dg_{2}=\mathbb{E}[\unicode[STIX]{x1D712}(\operatorname{tr}((T+V)D(T^{\prime }+V^{\prime })A))]. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{{\mathcal{K}}(n)}\unicode[STIX]{x1D712}(\operatorname{tr}(g_{1}Dg_{2}A))\,dg_{1}\,dg_{2}=\mathbb{E}[\unicode[STIX]{x1D712}(\operatorname{tr}((T+V)D(T^{\prime }+V^{\prime })A))]. & & \displaystyle \nonumber\end{eqnarray}$$
Since the transposed random matrix
 $(T^{\prime }+V^{\prime })^{t}$
and the original random matrix
$(T^{\prime }+V^{\prime })^{t}$
and the original random matrix
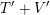 $T^{\prime }+V^{\prime }$
have the same distribution, we have
$T^{\prime }+V^{\prime }$
have the same distribution, we have
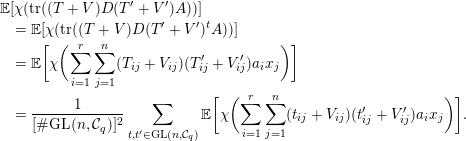 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{E}[\unicode[STIX]{x1D712}(\operatorname{tr}((T+V)D(T^{\prime }+V^{\prime })A))]\nonumber\\ \displaystyle & & \displaystyle \quad =\mathbb{E}[\unicode[STIX]{x1D712}(\operatorname{tr}((T+V)D(T^{\prime }+V^{\prime })^{t}A))]\nonumber\\ \displaystyle & & \displaystyle \quad =\mathbb{E}\biggl[\unicode[STIX]{x1D712}\biggl(\mathop{\sum }_{i=1}^{r}\mathop{\sum }_{j=1}^{n}(T_{ij}+V_{ij})(T_{ij}^{\prime }+V_{ij}^{\prime })a_{i}x_{j}\biggr)\biggr]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{[\#\text{GL}(n,{\mathcal{C}}_{q})]^{2}}\mathop{\sum }_{t,t^{\prime }\in \operatorname{GL}(n,{\mathcal{C}}_{q})}\mathbb{E}\biggl[\unicode[STIX]{x1D712}\biggl(\mathop{\sum }_{i=1}^{r}\mathop{\sum }_{j=1}^{n}(t_{ij}+V_{ij})(t_{ij}^{\prime }+V_{ij}^{\prime })a_{i}x_{j}\biggr)\biggr].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{E}[\unicode[STIX]{x1D712}(\operatorname{tr}((T+V)D(T^{\prime }+V^{\prime })A))]\nonumber\\ \displaystyle & & \displaystyle \quad =\mathbb{E}[\unicode[STIX]{x1D712}(\operatorname{tr}((T+V)D(T^{\prime }+V^{\prime })^{t}A))]\nonumber\\ \displaystyle & & \displaystyle \quad =\mathbb{E}\biggl[\unicode[STIX]{x1D712}\biggl(\mathop{\sum }_{i=1}^{r}\mathop{\sum }_{j=1}^{n}(T_{ij}+V_{ij})(T_{ij}^{\prime }+V_{ij}^{\prime })a_{i}x_{j}\biggr)\biggr]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{[\#\text{GL}(n,{\mathcal{C}}_{q})]^{2}}\mathop{\sum }_{t,t^{\prime }\in \operatorname{GL}(n,{\mathcal{C}}_{q})}\mathbb{E}\biggl[\unicode[STIX]{x1D712}\biggl(\mathop{\sum }_{i=1}^{r}\mathop{\sum }_{j=1}^{n}(t_{ij}+V_{ij})(t_{ij}^{\prime }+V_{ij}^{\prime })a_{i}x_{j}\biggr)\biggr].\nonumber\end{eqnarray}$$
By Lemma 7.3, we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{E}[\unicode[STIX]{x1D712}(\operatorname{tr}((T+V)D(T^{\prime }+V^{\prime })A))]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{[\#S(r\times n)]^{2}}\mathop{\sum }_{M,M^{\prime }\in S(r\times n)}\mathbb{E}\biggl[\unicode[STIX]{x1D712}\biggl(\mathop{\sum }_{i=1}^{r}\mathop{\sum }_{j=1}^{n}(M_{ij}+V_{ij})(M_{ij}^{\prime }+V_{ji}^{\prime })a_{i}x_{j}\biggr)\biggr].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{E}[\unicode[STIX]{x1D712}(\operatorname{tr}((T+V)D(T^{\prime }+V^{\prime })A))]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{[\#S(r\times n)]^{2}}\mathop{\sum }_{M,M^{\prime }\in S(r\times n)}\mathbb{E}\biggl[\unicode[STIX]{x1D712}\biggl(\mathop{\sum }_{i=1}^{r}\mathop{\sum }_{j=1}^{n}(M_{ij}+V_{ij})(M_{ij}^{\prime }+V_{ji}^{\prime })a_{i}x_{j}\biggr)\biggr].\nonumber\end{eqnarray}$$
For simplifying notation, for any pair of rectangular matrices
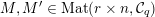 $M,M^{\prime }\in \operatorname{Mat}(r\times n,{\mathcal{C}}_{q})$
, we write
$M,M^{\prime }\in \operatorname{Mat}(r\times n,{\mathcal{C}}_{q})$
, we write
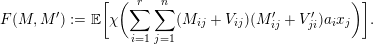 $$\begin{eqnarray}\displaystyle F(M,M^{\prime }):=\mathbb{E}\biggl[\unicode[STIX]{x1D712}\biggl(\mathop{\sum }_{i=1}^{r}\mathop{\sum }_{j=1}^{n}(M_{ij}+V_{ij})(M_{ij}^{\prime }+V_{ji}^{\prime })a_{i}x_{j}\biggr)\biggr]. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F(M,M^{\prime }):=\mathbb{E}\biggl[\unicode[STIX]{x1D712}\biggl(\mathop{\sum }_{i=1}^{r}\mathop{\sum }_{j=1}^{n}(M_{ij}+V_{ij})(M_{ij}^{\prime }+V_{ji}^{\prime })a_{i}x_{j}\biggr)\biggr]. & & \displaystyle \nonumber\end{eqnarray}$$
Then we may write
 $$\begin{eqnarray}\displaystyle \mathbb{E}[\unicode[STIX]{x1D712}(\operatorname{tr}((T+V)D(T^{\prime }+V^{\prime })A))]=\frac{1}{[\#S(r\times n)]^{2}}\underbrace{\biggl[\mathop{\sum }_{M,M^{\prime }\in \operatorname{Mat}(r\times n,{\mathcal{C}}_{q})}F(M,M^{\prime })+{\mathcal{E}}_{1}\biggr]}_{\text{denoted}~\text{by}~I}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{E}[\unicode[STIX]{x1D712}(\operatorname{tr}((T+V)D(T^{\prime }+V^{\prime })A))]=\frac{1}{[\#S(r\times n)]^{2}}\underbrace{\biggl[\mathop{\sum }_{M,M^{\prime }\in \operatorname{Mat}(r\times n,{\mathcal{C}}_{q})}F(M,M^{\prime })+{\mathcal{E}}_{1}\biggr]}_{\text{denoted}~\text{by}~I}, & & \displaystyle \nonumber\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle {\mathcal{E}}_{1}:=-\mathop{\sum }_{M,M^{\prime }\in \operatorname{Mat}(r\times n,{\mathcal{C}}_{q})\,\setminus \,S(r\times n)}F(M,M^{\prime }). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{E}}_{1}:=-\mathop{\sum }_{M,M^{\prime }\in \operatorname{Mat}(r\times n,{\mathcal{C}}_{q})\,\setminus \,S(r\times n)}F(M,M^{\prime }). & & \displaystyle \nonumber\end{eqnarray}$$
Note that if
![]() $M_{ij}$
and
$M_{ij}$
and
![]() $V_{ij}$
are sampled independently and uniformly from the finite set
$V_{ij}$
are sampled independently and uniformly from the finite set
![]() ${\mathcal{C}}_{q}$
and from the compact additive group
${\mathcal{C}}_{q}$
and from the compact additive group
![]() $\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
respectively, then
$\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
respectively, then
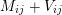 $M_{ij}+V_{ij}$
is uniformly distributed on
$M_{ij}+V_{ij}$
is uniformly distributed on
![]() ${\mathcal{O}}_{F}$
. It follows that
${\mathcal{O}}_{F}$
. It follows that
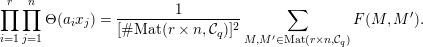 $$\begin{eqnarray}\displaystyle \mathop{\prod }_{i=1}^{r}\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D6E9}(a_{i}x_{j})=\frac{1}{[\#\text{Mat}(r\times n,{\mathcal{C}}_{q})]^{2}}\mathop{\sum }_{M,M^{\prime }\in \operatorname{Mat}(r\times n,{\mathcal{C}}_{q})}F(M,M^{\prime }). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\prod }_{i=1}^{r}\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D6E9}(a_{i}x_{j})=\frac{1}{[\#\text{Mat}(r\times n,{\mathcal{C}}_{q})]^{2}}\mathop{\sum }_{M,M^{\prime }\in \operatorname{Mat}(r\times n,{\mathcal{C}}_{q})}F(M,M^{\prime }). & & \displaystyle \nonumber\end{eqnarray}$$
Consequently,
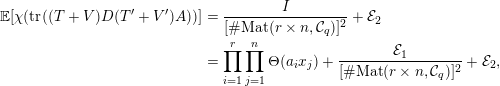 $$\begin{eqnarray}\displaystyle \mathbb{E}[\unicode[STIX]{x1D712}(\operatorname{tr}((T+V)D(T^{\prime }+V^{\prime })A))] & = & \displaystyle \frac{I}{[\#\text{Mat}(r\times n,{\mathcal{C}}_{q})]^{2}}+{\mathcal{E}}_{2}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\prod }_{i=1}^{r}\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D6E9}(a_{i}x_{j})+\frac{{\mathcal{E}}_{1}}{[\#\text{Mat}(r\times n,{\mathcal{C}}_{q})]^{2}}+{\mathcal{E}}_{2},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{E}[\unicode[STIX]{x1D712}(\operatorname{tr}((T+V)D(T^{\prime }+V^{\prime })A))] & = & \displaystyle \frac{I}{[\#\text{Mat}(r\times n,{\mathcal{C}}_{q})]^{2}}+{\mathcal{E}}_{2}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\prod }_{i=1}^{r}\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D6E9}(a_{i}x_{j})+\frac{{\mathcal{E}}_{1}}{[\#\text{Mat}(r\times n,{\mathcal{C}}_{q})]^{2}}+{\mathcal{E}}_{2},\nonumber\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle {\mathcal{E}}_{2}:=\frac{I}{[\#S(r\times n)]^{2}}-\frac{I}{[\#\text{Mat}(r\times n,{\mathcal{C}}_{q})]^{2}}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{E}}_{2}:=\frac{I}{[\#S(r\times n)]^{2}}-\frac{I}{[\#\text{Mat}(r\times n,{\mathcal{C}}_{q})]^{2}}. & & \displaystyle \nonumber\end{eqnarray}$$
Now let us estimate these error terms. By the obvious estimate
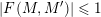 $|F(M,M^{\prime })|\leqslant 1$
, we have
$|F(M,M^{\prime })|\leqslant 1$
, we have
 $$\begin{eqnarray}\displaystyle |{\mathcal{E}}_{1}|\leqslant [\#(\operatorname{Mat}(r\times n,{\mathcal{C}}_{q})\,\setminus \,S(r\times n))]^{2}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |{\mathcal{E}}_{1}|\leqslant [\#(\operatorname{Mat}(r\times n,{\mathcal{C}}_{q})\,\setminus \,S(r\times n))]^{2}. & & \displaystyle \nonumber\end{eqnarray}$$
Note that
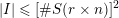 $|I|\leqslant [\#S(r\times n)]^{2}$
. Hence
$|I|\leqslant [\#S(r\times n)]^{2}$
. Hence
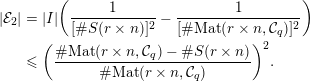 $$\begin{eqnarray}\displaystyle |{\mathcal{E}}_{2}| & = & \displaystyle |I|\biggl(\frac{1}{[\#S(r\times n)]^{2}}-\frac{1}{[\#\text{Mat}(r\times n,{\mathcal{C}}_{q})]^{2}}\biggr)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \biggl(\frac{\#\text{Mat}(r\times n,{\mathcal{C}}_{q})-\#S(r\times n)}{\#\text{Mat}(r\times n,{\mathcal{C}}_{q})}\biggr)^{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |{\mathcal{E}}_{2}| & = & \displaystyle |I|\biggl(\frac{1}{[\#S(r\times n)]^{2}}-\frac{1}{[\#\text{Mat}(r\times n,{\mathcal{C}}_{q})]^{2}}\biggr)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \biggl(\frac{\#\text{Mat}(r\times n,{\mathcal{C}}_{q})-\#S(r\times n)}{\#\text{Mat}(r\times n,{\mathcal{C}}_{q})}\biggr)^{2}.\nonumber\end{eqnarray}$$
Taking (75) into account, we get
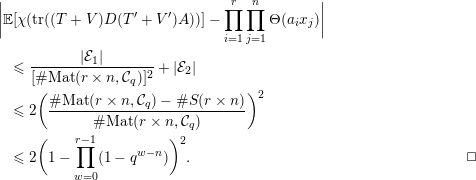 $$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\mathbb{E}[\unicode[STIX]{x1D712}(\operatorname{tr}((T+V)D(T^{\prime }+V^{\prime })A))]-\mathop{\prod }_{i=1}^{r}\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D6E9}(a_{i}x_{j})\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \frac{|{\mathcal{E}}_{1}|}{[\#\text{Mat}(r\times n,{\mathcal{C}}_{q})]^{2}}+|{\mathcal{E}}_{2}|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 2\biggl(\frac{\#\text{Mat}(r\times n,{\mathcal{C}}_{q})-\#S(r\times n)}{\#\text{Mat}(r\times n,{\mathcal{C}}_{q})}\biggr)^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 2\biggl(1-\mathop{\prod }_{w=0}^{r-1}(1-q^{w-n})\biggr)^{2}.\Box \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\mathbb{E}[\unicode[STIX]{x1D712}(\operatorname{tr}((T+V)D(T^{\prime }+V^{\prime })A))]-\mathop{\prod }_{i=1}^{r}\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D6E9}(a_{i}x_{j})\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \frac{|{\mathcal{E}}_{1}|}{[\#\text{Mat}(r\times n,{\mathcal{C}}_{q})]^{2}}+|{\mathcal{E}}_{2}|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 2\biggl(\frac{\#\text{Mat}(r\times n,{\mathcal{C}}_{q})-\#S(r\times n)}{\#\text{Mat}(r\times n,{\mathcal{C}}_{q})}\biggr)^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 2\biggl(1-\mathop{\prod }_{w=0}^{r-1}(1-q^{w-n})\biggr)^{2}.\Box \nonumber\end{eqnarray}$$
Theorem 7.4 (Uniform asymptotic multiplicativity).
Let
 $n,r\in \mathbb{N}$
be such that
$n,r\in \mathbb{N}$
be such that
![]() $r\leqslant n$
. Suppose that
$r\leqslant n$
. Suppose that
![]() $D$
and
$D$
and
![]() $A$
are two diagonal matrices given by
$A$
are two diagonal matrices given by
 $$\begin{eqnarray}D=\operatorname{diag}(x_{1},\ldots ,x_{n}),\quad A=\operatorname{diag}(a_{1},\ldots ,a_{r},0,\ldots ,0),\end{eqnarray}$$
$$\begin{eqnarray}D=\operatorname{diag}(x_{1},\ldots ,x_{n}),\quad A=\operatorname{diag}(a_{1},\ldots ,a_{r},0,\ldots ,0),\end{eqnarray}$$
where
 $x_{1},\ldots ,x_{n},a_{1},\ldots ,a_{r}\in F$
. Then
$x_{1},\ldots ,x_{n},a_{1},\ldots ,a_{r}\in F$
. Then
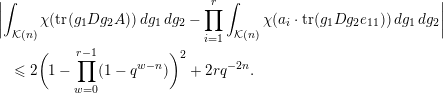 $$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\int _{{\mathcal{K}}(n)}\unicode[STIX]{x1D712}(\operatorname{tr}(g_{1}Dg_{2}A))\,dg_{1}\,dg_{2}-\mathop{\prod }_{i=1}^{r}\int _{{\mathcal{K}}(n)}\unicode[STIX]{x1D712}(a_{i}\cdot \operatorname{tr}(g_{1}Dg_{2}e_{11}))\,dg_{1}\,dg_{2}\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 2\biggl(1-\mathop{\prod }_{w=0}^{r-1}(1-q^{w-n})\biggr)^{2}+2rq^{-2n}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\int _{{\mathcal{K}}(n)}\unicode[STIX]{x1D712}(\operatorname{tr}(g_{1}Dg_{2}A))\,dg_{1}\,dg_{2}-\mathop{\prod }_{i=1}^{r}\int _{{\mathcal{K}}(n)}\unicode[STIX]{x1D712}(a_{i}\cdot \operatorname{tr}(g_{1}Dg_{2}e_{11}))\,dg_{1}\,dg_{2}\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 2\biggl(1-\mathop{\prod }_{w=0}^{r-1}(1-q^{w-n})\biggr)^{2}+2rq^{-2n}.\end{eqnarray}$$
Proof. By inequalities (73) and (74), we have
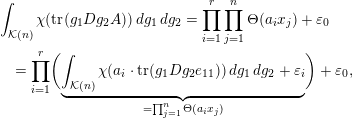 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{{\mathcal{K}}(n)}\unicode[STIX]{x1D712}(\operatorname{tr}(g_{1}Dg_{2}A))\,dg_{1}\,dg_{2}=\mathop{\prod }_{i=1}^{r}\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D6E9}(a_{i}x_{j})+\unicode[STIX]{x1D700}_{0}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\prod }_{i=1}^{r}\biggl(\underbrace{\int _{{\mathcal{K}}(n)}\unicode[STIX]{x1D712}(a_{i}\cdot \operatorname{tr}(g_{1}Dg_{2}e_{11}))\,dg_{1}\,dg_{2}+\unicode[STIX]{x1D700}_{i}}_{=\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D6E9}(a_{i}x_{j})}\biggr)+\unicode[STIX]{x1D700}_{0},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{{\mathcal{K}}(n)}\unicode[STIX]{x1D712}(\operatorname{tr}(g_{1}Dg_{2}A))\,dg_{1}\,dg_{2}=\mathop{\prod }_{i=1}^{r}\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D6E9}(a_{i}x_{j})+\unicode[STIX]{x1D700}_{0}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\prod }_{i=1}^{r}\biggl(\underbrace{\int _{{\mathcal{K}}(n)}\unicode[STIX]{x1D712}(a_{i}\cdot \operatorname{tr}(g_{1}Dg_{2}e_{11}))\,dg_{1}\,dg_{2}+\unicode[STIX]{x1D700}_{i}}_{=\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D6E9}(a_{i}x_{j})}\biggr)+\unicode[STIX]{x1D700}_{0},\nonumber\end{eqnarray}$$
with the errors
 $\unicode[STIX]{x1D700}_{0},\unicode[STIX]{x1D700}_{1},\ldots ,\unicode[STIX]{x1D700}_{r}$
controlled by
$\unicode[STIX]{x1D700}_{0},\unicode[STIX]{x1D700}_{1},\ldots ,\unicode[STIX]{x1D700}_{r}$
controlled by
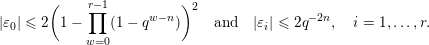 $$\begin{eqnarray}\displaystyle |\unicode[STIX]{x1D700}_{0}|\leqslant 2\biggl(1-\mathop{\prod }_{w=0}^{r-1}(1-q^{w-n})\biggr)^{2}\quad \text{and}\quad |\unicode[STIX]{x1D700}_{i}|\leqslant 2q^{-2n},\quad i=1,\ldots ,r. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\unicode[STIX]{x1D700}_{0}|\leqslant 2\biggl(1-\mathop{\prod }_{w=0}^{r-1}(1-q^{w-n})\biggr)^{2}\quad \text{and}\quad |\unicode[STIX]{x1D700}_{i}|\leqslant 2q^{-2n},\quad i=1,\ldots ,r. & & \displaystyle \nonumber\end{eqnarray}$$
Using the elementary inequalities
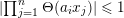 $|\!\prod _{j=1}^{n}\unicode[STIX]{x1D6E9}(a_{i}x_{j})|\leqslant 1$
and by a simple computation, we get
$|\!\prod _{j=1}^{n}\unicode[STIX]{x1D6E9}(a_{i}x_{j})|\leqslant 1$
and by a simple computation, we get
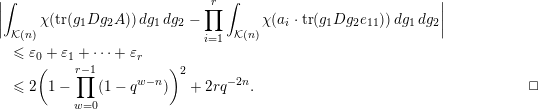 $$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\int _{{\mathcal{K}}(n)}\unicode[STIX]{x1D712}(\operatorname{tr}(g_{1}Dg_{2}A))\,dg_{1}\,dg_{2}-\mathop{\prod }_{i=1}^{r}\int _{{\mathcal{K}}(n)}\unicode[STIX]{x1D712}(a_{i}\cdot \operatorname{tr}(g_{1}Dg_{2}e_{11}))\,dg_{1}\,dg_{2}\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \unicode[STIX]{x1D700}_{0}+\unicode[STIX]{x1D700}_{1}+\cdots +\unicode[STIX]{x1D700}_{r}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 2\biggl(1-\mathop{\prod }_{w=0}^{r-1}(1-q^{w-n})\biggr)^{2}+2rq^{-2n}.\Box \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\int _{{\mathcal{K}}(n)}\unicode[STIX]{x1D712}(\operatorname{tr}(g_{1}Dg_{2}A))\,dg_{1}\,dg_{2}-\mathop{\prod }_{i=1}^{r}\int _{{\mathcal{K}}(n)}\unicode[STIX]{x1D712}(a_{i}\cdot \operatorname{tr}(g_{1}Dg_{2}e_{11}))\,dg_{1}\,dg_{2}\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \unicode[STIX]{x1D700}_{0}+\unicode[STIX]{x1D700}_{1}+\cdots +\unicode[STIX]{x1D700}_{r}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 2\biggl(1-\mathop{\prod }_{w=0}^{r-1}(1-q^{w-n})\biggr)^{2}+2rq^{-2n}.\Box \nonumber\end{eqnarray}$$
7.2
 $\operatorname{GL}(n,{\mathcal{O}}_{F})$
-orbital integrals
$\operatorname{GL}(n,{\mathcal{O}}_{F})$
-orbital integrals
Recall the definition (7) for the function
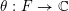 $\unicode[STIX]{x1D703}:F\rightarrow \mathbb{C}$
.
$\unicode[STIX]{x1D703}:F\rightarrow \mathbb{C}$
.
Theorem 7.5. Let
 $n,r\in \mathbb{N}$
be such that
$n,r\in \mathbb{N}$
be such that
![]() $r\leqslant n$
. Given two diagonal matrices
$r\leqslant n$
. Given two diagonal matrices
![]() $D$
and
$D$
and
![]() $A$
,
$A$
,
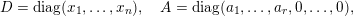 $$\begin{eqnarray}D=\operatorname{diag}(x_{1},\ldots ,x_{n}),\quad A=\operatorname{diag}(a_{1},\ldots ,a_{r},0,\ldots ,0),\end{eqnarray}$$
$$\begin{eqnarray}D=\operatorname{diag}(x_{1},\ldots ,x_{n}),\quad A=\operatorname{diag}(a_{1},\ldots ,a_{r},0,\ldots ,0),\end{eqnarray}$$
where
 $x_{1},\ldots ,x_{n},a_{1},\ldots ,a_{r}\in F$
, we have
$x_{1},\ldots ,x_{n},a_{1},\ldots ,a_{r}\in F$
, we have
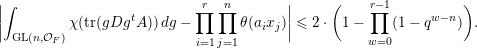 $$\begin{eqnarray}\displaystyle \biggl|\int _{\operatorname{GL}(n,{\mathcal{O}}_{F})}\unicode[STIX]{x1D712}(\operatorname{tr}(gDg^{t}A))\,dg-\mathop{\prod }_{i=1}^{r}\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D703}(a_{i}x_{j})\biggr|\leqslant 2\cdot \biggl(1-\mathop{\prod }_{w=0}^{r-1}(1-q^{w-n})\biggr). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \biggl|\int _{\operatorname{GL}(n,{\mathcal{O}}_{F})}\unicode[STIX]{x1D712}(\operatorname{tr}(gDg^{t}A))\,dg-\mathop{\prod }_{i=1}^{r}\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D703}(a_{i}x_{j})\biggr|\leqslant 2\cdot \biggl(1-\mathop{\prod }_{w=0}^{r-1}(1-q^{w-n})\biggr). & & \displaystyle\end{eqnarray}$$
In particular, for any
![]() $a\in F$
, we have
$a\in F$
, we have
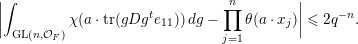 $$\begin{eqnarray}\displaystyle \biggl|\int _{\operatorname{GL}(n,{\mathcal{O}}_{F})}\unicode[STIX]{x1D712}(a\cdot \operatorname{tr}(gDg^{t}e_{11}))\,dg-\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D703}(a\cdot x_{j})\biggr|\leqslant 2q^{-n}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \biggl|\int _{\operatorname{GL}(n,{\mathcal{O}}_{F})}\unicode[STIX]{x1D712}(a\cdot \operatorname{tr}(gDg^{t}e_{11}))\,dg-\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D703}(a\cdot x_{j})\biggr|\leqslant 2q^{-n}. & & \displaystyle\end{eqnarray}$$
Proof. Fix
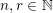 $n,r\in \mathbb{N}$
and fix the two diagonal matrices
$n,r\in \mathbb{N}$
and fix the two diagonal matrices
![]() $D$
and
$D$
and
![]() $A$
. Let
$A$
. Let
 $T=T(n)$
be a random matrix uniformly distributed on the finite set
$T=T(n)$
be a random matrix uniformly distributed on the finite set
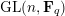 $\operatorname{GL}(n,\mathbf{F}_{q})$
, and let
$\operatorname{GL}(n,\mathbf{F}_{q})$
, and let
 $V=V(n)$
be a random matrix uniformly distributed on
$V=V(n)$
be a random matrix uniformly distributed on
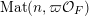 $\operatorname{Mat}(n,\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})$
and independent of
$\operatorname{Mat}(n,\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})$
and independent of
![]() $T$
. By Proposition 2.3, we have
$T$
. By Proposition 2.3, we have
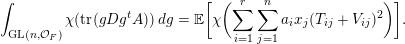 $$\begin{eqnarray}\displaystyle \int _{\operatorname{GL}(n,{\mathcal{O}}_{F})}\unicode[STIX]{x1D712}(\operatorname{tr}(gDg^{t}A))\,dg=\mathbb{E}\biggl[\unicode[STIX]{x1D712}\biggl(\mathop{\sum }_{i=1}^{r}\mathop{\sum }_{j=1}^{n}a_{i}x_{j}(T_{ij}+V_{ij})^{2}\biggr)\biggr]. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{\operatorname{GL}(n,{\mathcal{O}}_{F})}\unicode[STIX]{x1D712}(\operatorname{tr}(gDg^{t}A))\,dg=\mathbb{E}\biggl[\unicode[STIX]{x1D712}\biggl(\mathop{\sum }_{i=1}^{r}\mathop{\sum }_{j=1}^{n}a_{i}x_{j}(T_{ij}+V_{ij})^{2}\biggr)\biggr]. & & \displaystyle \nonumber\end{eqnarray}$$
By similar arguments as in the proof of Theorem 7.1, we may get the desired inequality (77). The second inequality (78) follows immediately by taking
![]() $e=1$
and
$e=1$
and
![]() $a_{1}=a$
.◻
$a_{1}=a$
.◻
Theorem 7.6 (Uniform asymptotic multiplicativity).
Let
 $n,r\in \mathbb{N}$
be such that
$n,r\in \mathbb{N}$
be such that
![]() $r\leqslant n$
. Given two diagonal matrices
$r\leqslant n$
. Given two diagonal matrices
![]() $D$
and
$D$
and
![]() $A$
,
$A$
,
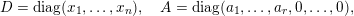 $$\begin{eqnarray}D=\operatorname{diag}(x_{1},\ldots ,x_{n}),\quad A=\operatorname{diag}(a_{1},\ldots ,a_{r},0,\ldots ,0),\end{eqnarray}$$
$$\begin{eqnarray}D=\operatorname{diag}(x_{1},\ldots ,x_{n}),\quad A=\operatorname{diag}(a_{1},\ldots ,a_{r},0,\ldots ,0),\end{eqnarray}$$
where
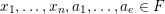 $x_{1},\ldots ,x_{n},a_{1},\ldots ,a_{e}\in F$
, we have
$x_{1},\ldots ,x_{n},a_{1},\ldots ,a_{e}\in F$
, we have
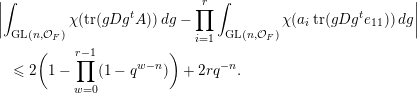 $$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\int _{\operatorname{GL}(n,{\mathcal{O}}_{F})}\unicode[STIX]{x1D712}(\operatorname{tr}(gDg^{t}A))\,dg-\mathop{\prod }_{i=1}^{r}\int _{\operatorname{GL}(n,{\mathcal{O}}_{F})}\unicode[STIX]{x1D712}(a_{i}\operatorname{tr}(gDg^{t}e_{11}))\,dg\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 2\biggl(1-\mathop{\prod }_{w=0}^{r-1}(1-q^{w-n})\biggr)+2rq^{-n}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\int _{\operatorname{GL}(n,{\mathcal{O}}_{F})}\unicode[STIX]{x1D712}(\operatorname{tr}(gDg^{t}A))\,dg-\mathop{\prod }_{i=1}^{r}\int _{\operatorname{GL}(n,{\mathcal{O}}_{F})}\unicode[STIX]{x1D712}(a_{i}\operatorname{tr}(gDg^{t}e_{11}))\,dg\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 2\biggl(1-\mathop{\prod }_{w=0}^{r-1}(1-q^{w-n})\biggr)+2rq^{-n}.\nonumber\end{eqnarray}$$
Proof. The proof is similar to that of Theorem 7.4. ◻
8 The completion of the classification of ergodic measures
8.1 The case of
 ${\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
${\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
Theorem 8.1 (Multiplicativity theorem for orbital limit measures).
Assume that
![]() $\unicode[STIX]{x1D707}$
is an element in
$\unicode[STIX]{x1D707}$
is an element in
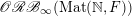 $\mathscr{ORB}_{\infty }(\operatorname{Mat}(\mathbb{N},F))$
. Then for any
$\mathscr{ORB}_{\infty }(\operatorname{Mat}(\mathbb{N},F))$
. Then for any
![]() $r\in \mathbb{N}$
and for any finite sequence
$r\in \mathbb{N}$
and for any finite sequence
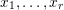 $x_{1},\ldots ,x_{r}$
in
$x_{1},\ldots ,x_{r}$
in
![]() $F$
, we have
$F$
, we have
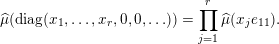 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}}(\operatorname{diag}(x_{1},\ldots ,x_{r},0,0,\ldots ))=\mathop{\prod }_{j=1}^{r}\widehat{\unicode[STIX]{x1D707}}(x_{j}e_{11}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}}(\operatorname{diag}(x_{1},\ldots ,x_{r},0,0,\ldots ))=\mathop{\prod }_{j=1}^{r}\widehat{\unicode[STIX]{x1D707}}(x_{j}e_{11}). & & \displaystyle\end{eqnarray}$$
In particular, we have
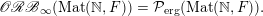 $$\begin{eqnarray}\displaystyle \mathscr{ORB}_{\infty }(\operatorname{Mat}(\mathbb{N},F))={\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F)). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{ORB}_{\infty }(\operatorname{Mat}(\mathbb{N},F))={\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F)). & & \displaystyle \nonumber\end{eqnarray}$$
Proof. Let
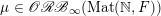 $\unicode[STIX]{x1D707}\in \mathscr{ORB}_{\infty }(\operatorname{Mat}(\mathbb{N},F))$
. Then by definition, there exists an increasing sequence
$\unicode[STIX]{x1D707}\in \mathscr{ORB}_{\infty }(\operatorname{Mat}(\mathbb{N},F))$
. Then by definition, there exists an increasing sequence
![]() $(n_{k})_{k\in \mathbb{N}}$
in
$(n_{k})_{k\in \mathbb{N}}$
in
![]() $\mathbb{N}$
and a sequence
$\mathbb{N}$
and a sequence
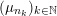 $(\unicode[STIX]{x1D707}_{n_{k}})_{k\in \mathbb{N}}$
of orbital measures with
$(\unicode[STIX]{x1D707}_{n_{k}})_{k\in \mathbb{N}}$
of orbital measures with
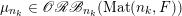 $\unicode[STIX]{x1D707}_{n_{k}}\in \mathscr{ORB}_{n_{k}}(\operatorname{Mat}(n_{k},F))$
, such that
$\unicode[STIX]{x1D707}_{n_{k}}\in \mathscr{ORB}_{n_{k}}(\operatorname{Mat}(n_{k},F))$
, such that
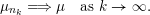 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}_{n_{k}}\Longrightarrow \unicode[STIX]{x1D707}\quad \text{as }k\rightarrow \infty . & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}_{n_{k}}\Longrightarrow \unicode[STIX]{x1D707}\quad \text{as }k\rightarrow \infty . & & \displaystyle\end{eqnarray}$$
Take any
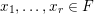 $x_{1},\ldots ,x_{r}\in F$
. By the inequality (76), we have
$x_{1},\ldots ,x_{r}\in F$
. By the inequality (76), we have
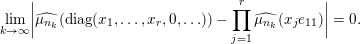 $$\begin{eqnarray}\displaystyle \lim _{k\rightarrow \infty }\biggl|\widehat{\unicode[STIX]{x1D707}_{n_{k}}}(\operatorname{diag}(x_{1},\ldots ,x_{r},0,\ldots ))-\mathop{\prod }_{j=1}^{r}\widehat{\unicode[STIX]{x1D707}_{n_{k}}}(x_{j}e_{11})\biggr|=0. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{k\rightarrow \infty }\biggl|\widehat{\unicode[STIX]{x1D707}_{n_{k}}}(\operatorname{diag}(x_{1},\ldots ,x_{r},0,\ldots ))-\mathop{\prod }_{j=1}^{r}\widehat{\unicode[STIX]{x1D707}_{n_{k}}}(x_{j}e_{11})\biggr|=0. & & \displaystyle\end{eqnarray}$$
Combining (80) and (81), we get the desired identity (79).
By Vershik’s Theorem 6.3 and Proposition 6.8, to obtain (81), we only need to prove the inclusion
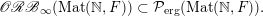 $$\begin{eqnarray}\displaystyle \mathscr{ORB}_{\infty }(\operatorname{Mat}(\mathbb{N},F))\subset {\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F)). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{ORB}_{\infty }(\operatorname{Mat}(\mathbb{N},F))\subset {\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F)). & & \displaystyle\end{eqnarray}$$
Recall the definition (36) of the affine map
![]() $\unicode[STIX]{x1D6F9}$
:
$\unicode[STIX]{x1D6F9}$
:
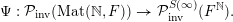 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F9}:{\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F))\rightarrow {\mathcal{P}}_{\text{inv}}^{S(\infty )}(F^{\mathbb{N}}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F9}:{\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F))\rightarrow {\mathcal{P}}_{\text{inv}}^{S(\infty )}(F^{\mathbb{N}}). & & \displaystyle \nonumber\end{eqnarray}$$
The identity (79) implies that for any
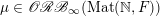 $\unicode[STIX]{x1D707}\in \mathscr{ORB}_{\infty }(\operatorname{Mat}(\mathbb{N},F))$
, the marginal measure on the diagonal matrices
$\unicode[STIX]{x1D707}\in \mathscr{ORB}_{\infty }(\operatorname{Mat}(\mathbb{N},F))$
, the marginal measure on the diagonal matrices
![]() $\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707})$
is a Bernoulli measure on
$\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707})$
is a Bernoulli measure on
![]() $F^{\mathbb{N}}$
. Consequently, by exactly the same argument as in the proof of Theorem 3.5, we can prove the desired inclusion (82).◻
$F^{\mathbb{N}}$
. Consequently, by exactly the same argument as in the proof of Theorem 3.5, we can prove the desired inclusion (82).◻
An immediate consequence of Theorem 8.1 and the argument as in the proof of Theorem 8.1 is the following Ismagilov–Olshanski multiplicativity in our setting.
Corollary 8.2 (Ismagilov–Olshanski multiplicativity).
An invariant probability measure
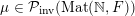 $\unicode[STIX]{x1D707}\in {\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F))$
is ergodic if and only if for any
$\unicode[STIX]{x1D707}\in {\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F))$
is ergodic if and only if for any
![]() $r\in \mathbb{N}$
and for any finite sequence
$r\in \mathbb{N}$
and for any finite sequence
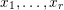 $x_{1},\ldots ,x_{r}$
in
$x_{1},\ldots ,x_{r}$
in
![]() $F$
, we have
$F$
, we have
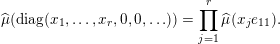 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}}(\operatorname{diag}(x_{1},\ldots ,x_{r},0,0,\ldots ))=\mathop{\prod }_{j=1}^{r}\widehat{\unicode[STIX]{x1D707}}(x_{j}e_{11}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}}(\operatorname{diag}(x_{1},\ldots ,x_{r},0,0,\ldots ))=\mathop{\prod }_{j=1}^{r}\widehat{\unicode[STIX]{x1D707}}(x_{j}e_{11}). & & \displaystyle \nonumber\end{eqnarray}$$
Remark 8.3. The reader may compare our method with the methods used in, for instance, Olshansk and Vershik [Reference Olshanski and VershikOV96]. The Olshanski–Vershik argument relies on the Ismagilov–Olshanski multiplicativity: the multiplicativity of the characteristic function is equivalent to the ergodicity of the corresponding probability measure. In different contexts, this multiplicativity is established, e.g., by Ismagilov [Reference IsmagilovIsm69, Reference IsmagilovIsm70], Nessonov [Reference NessonovNes86], Voiculescu [Reference VoiculescuVoi76], Olshanski [Reference Ol’shanskiiOl’78], Stratila and Voiculescu [Reference Strătilă and VoiculescuSV82], Pickrell [Reference PickrellPic90], Vershik and Kerov [Reference Vershik and KerovVK90], Olshanski [Reference Ol’shanskiiOl’90].
In our situation, the Ismagilov–Olshanski multiplicativity follows as a corollary.
Now we may concentrate on the classification of
 $\mathscr{ORB}_{\infty }(\operatorname{Mat}(\mathbb{N},F))$
. For this purpose, we need to study the weak convergence of probability measures on
$\mathscr{ORB}_{\infty }(\operatorname{Mat}(\mathbb{N},F))$
. For this purpose, we need to study the weak convergence of probability measures on
 $\operatorname{Mat}(\mathbb{N},F)$
. The following standard proposition implies that the weak convergence of probability measures on
$\operatorname{Mat}(\mathbb{N},F)$
. The following standard proposition implies that the weak convergence of probability measures on
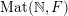 $\operatorname{Mat}(\mathbb{N},F)$
is equivalent to the locally uniform convergence of corresponding characteristic functions. For completeness, we include its proof in Appendix A.
$\operatorname{Mat}(\mathbb{N},F)$
is equivalent to the locally uniform convergence of corresponding characteristic functions. For completeness, we include its proof in Appendix A.
Proposition 8.4. A sequence of invariant probability measures
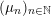 $(\unicode[STIX]{x1D707}_{n})_{n\in \mathbb{N}}$
in
$(\unicode[STIX]{x1D707}_{n})_{n\in \mathbb{N}}$
in
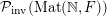 ${\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F))$
converges weakly to an invariant probability measure
${\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F))$
converges weakly to an invariant probability measure
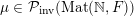 $\unicode[STIX]{x1D707}\in {\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F))$
if and only if for any
$\unicode[STIX]{x1D707}\in {\mathcal{P}}_{\text{inv}}(\operatorname{Mat}(\mathbb{N},F))$
if and only if for any
![]() $r\in \mathbb{N}$
and any
$r\in \mathbb{N}$
and any
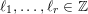 $\ell _{1},\ldots ,\ell _{r}\in \mathbb{Z}$
, we have
$\ell _{1},\ldots ,\ell _{r}\in \mathbb{Z}$
, we have
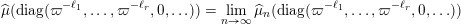 $$\begin{eqnarray}\widehat{\unicode[STIX]{x1D707}}(\operatorname{diag}(\unicode[STIX]{x1D71B}^{-\ell _{1}},\ldots ,\unicode[STIX]{x1D71B}^{-\ell _{r}},0,\ldots ))=\lim _{n\rightarrow \infty }\widehat{\unicode[STIX]{x1D707}}_{n}(\operatorname{diag}(\unicode[STIX]{x1D71B}^{-\ell _{1}},\ldots ,\unicode[STIX]{x1D71B}^{-\ell _{r}},0,\ldots ))\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\unicode[STIX]{x1D707}}(\operatorname{diag}(\unicode[STIX]{x1D71B}^{-\ell _{1}},\ldots ,\unicode[STIX]{x1D71B}^{-\ell _{r}},0,\ldots ))=\lim _{n\rightarrow \infty }\widehat{\unicode[STIX]{x1D707}}_{n}(\operatorname{diag}(\unicode[STIX]{x1D71B}^{-\ell _{1}},\ldots ,\unicode[STIX]{x1D71B}^{-\ell _{r}},0,\ldots ))\end{eqnarray}$$
and the convergence is uniform on any subset of type
 $$\begin{eqnarray}\{(\ell _{1},\ldots ,\ell _{r})\mid \ell _{1},\ldots ,\ell _{r}\in \mathbb{Z}_{{\leqslant}C}\}.\end{eqnarray}$$
$$\begin{eqnarray}\{(\ell _{1},\ldots ,\ell _{r})\mid \ell _{1},\ldots ,\ell _{r}\in \mathbb{Z}_{{\leqslant}C}\}.\end{eqnarray}$$
Lemma 8.5. Let
![]() $\unicode[STIX]{x1D707}$
be a Borel probability measure on
$\unicode[STIX]{x1D707}$
be a Borel probability measure on
 $\operatorname{Mat}(\mathbb{N},F)$
. The function
$\operatorname{Mat}(\mathbb{N},F)$
. The function
 $x\in F\mapsto \widehat{\unicode[STIX]{x1D707}}(xe_{11})\in \mathbb{C}$
is uniformly continuous. In particular, we have
$x\in F\mapsto \widehat{\unicode[STIX]{x1D707}}(xe_{11})\in \mathbb{C}$
is uniformly continuous. In particular, we have
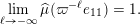 $$\begin{eqnarray}\displaystyle \lim _{\ell \rightarrow -\infty }\widehat{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D71B}^{-\ell }e_{11})=1. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{\ell \rightarrow -\infty }\widehat{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D71B}^{-\ell }e_{11})=1. & & \displaystyle \nonumber\end{eqnarray}$$
Proof. Note that the function
 $x\mapsto \widehat{\unicode[STIX]{x1D707}}(xe_{11})$
is the characteristic function of the marginal probability measure
$x\mapsto \widehat{\unicode[STIX]{x1D707}}(xe_{11})$
is the characteristic function of the marginal probability measure
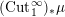 $(\operatorname{Cut}_{1}^{\infty })_{\ast }\unicode[STIX]{x1D707}$
on
$(\operatorname{Cut}_{1}^{\infty })_{\ast }\unicode[STIX]{x1D707}$
on
![]() $F$
. The uniform continuity of this function then follows immediately, see, e.g., Hewitt and Ross [Reference Hewitt and RossHR70, Theorem 31.5, p. 212].◻
$F$
. The uniform continuity of this function then follows immediately, see, e.g., Hewitt and Ross [Reference Hewitt and RossHR70, Theorem 31.5, p. 212].◻
Lemma 8.6. Assume that we are given a sequence of probability measures
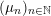 $(\unicode[STIX]{x1D707}_{n})_{n\in \mathbb{N}}$
, such that
$(\unicode[STIX]{x1D707}_{n})_{n\in \mathbb{N}}$
, such that
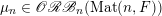 $\unicode[STIX]{x1D707}_{n}\in \mathscr{ORB}_{n}(\operatorname{Mat}(n,F))$
. A necessary and sufficient condition for this sequence to be tight is the following.
$\unicode[STIX]{x1D707}_{n}\in \mathscr{ORB}_{n}(\operatorname{Mat}(n,F))$
. A necessary and sufficient condition for this sequence to be tight is the following.
- (
 $C_{1}$
)
$C_{1}$
) -
There exists
 $\unicode[STIX]{x1D6FE}\in \mathbb{Z}$
, such that the supports
$\unicode[STIX]{x1D6FE}\in \mathbb{Z}$
, such that the supports
 $\operatorname{supp}(\unicode[STIX]{x1D707}_{n})$
are all contained in the following compact subset of
$\operatorname{supp}(\unicode[STIX]{x1D707}_{n})$
are all contained in the following compact subset of
 $\operatorname{Mat}(\mathbb{N},F)$
:
$\operatorname{Mat}(\mathbb{N},F)$
:  $$\begin{eqnarray}\displaystyle \{X\in \operatorname{Mat}(\mathbb{N},F)\mid |X_{ij}|\leqslant q^{\unicode[STIX]{x1D6FE}},\forall i,j\in \mathbb{N}\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \{X\in \operatorname{Mat}(\mathbb{N},F)\mid |X_{ij}|\leqslant q^{\unicode[STIX]{x1D6FE}},\forall i,j\in \mathbb{N}\}. & & \displaystyle \nonumber\end{eqnarray}$$
Proof. The above condition (
![]() $C_{1}$
) is clearly sufficient for the sequence to be tight. Now suppose that the sequence
$C_{1}$
) is clearly sufficient for the sequence to be tight. Now suppose that the sequence
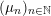 $(\unicode[STIX]{x1D707}_{n})_{n\in \mathbb{N}}$
is tight. By assumption, suppose that
$(\unicode[STIX]{x1D707}_{n})_{n\in \mathbb{N}}$
is tight. By assumption, suppose that
![]() $\unicode[STIX]{x1D707}_{n}$
is the
$\unicode[STIX]{x1D707}_{n}$
is the
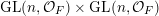 $\operatorname{GL}(n,{\mathcal{O}}_{F})\times \operatorname{GL}(n,{\mathcal{O}}_{F})$
-orbital measure supported on an orbit generated by
$\operatorname{GL}(n,{\mathcal{O}}_{F})\times \operatorname{GL}(n,{\mathcal{O}}_{F})$
-orbital measure supported on an orbit generated by
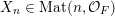 $X_{n}\in \operatorname{Mat}(n,{\mathcal{O}}_{F})$
. By Lemma 2.4, we may assume that
$X_{n}\in \operatorname{Mat}(n,{\mathcal{O}}_{F})$
. By Lemma 2.4, we may assume that
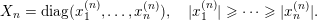 $$\begin{eqnarray}X_{n}=\operatorname{diag}(x_{1}^{(n)},\ldots ,x_{n}^{(n)}),\quad |x_{1}^{(n)}|\geqslant \cdots \geqslant |x_{n}^{(n)}|.\end{eqnarray}$$
$$\begin{eqnarray}X_{n}=\operatorname{diag}(x_{1}^{(n)},\ldots ,x_{n}^{(n)}),\quad |x_{1}^{(n)}|\geqslant \cdots \geqslant |x_{n}^{(n)}|.\end{eqnarray}$$
Assume by contradiction that the condition (
![]() $C_{1}$
) is not satisfied. Then there exists a subsequence
$C_{1}$
) is not satisfied. Then there exists a subsequence
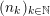 $(n_{k})_{k\in \mathbb{N}}$
of positive integers, such that
$(n_{k})_{k\in \mathbb{N}}$
of positive integers, such that
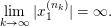 $$\begin{eqnarray}\displaystyle \lim _{k\rightarrow \infty }|x_{1}^{(n_{k})}|=\infty . & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{k\rightarrow \infty }|x_{1}^{(n_{k})}|=\infty . & & \displaystyle\end{eqnarray}$$
Passing to a subsequence if necessary, we may assume that there exists a probability measure
![]() $\unicode[STIX]{x1D707}$
on
$\unicode[STIX]{x1D707}$
on
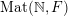 $\operatorname{Mat}(\mathbb{N},F)$
, such that
$\operatorname{Mat}(\mathbb{N},F)$
, such that
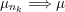 $\unicode[STIX]{x1D707}_{n_{k}}\Longrightarrow \unicode[STIX]{x1D707}$
. By Lemma 8.5, for any
$\unicode[STIX]{x1D707}_{n_{k}}\Longrightarrow \unicode[STIX]{x1D707}$
. By Lemma 8.5, for any
![]() $a\in F$
, we have
$a\in F$
, we have
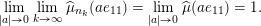 $$\begin{eqnarray}\displaystyle \lim _{|a|\rightarrow 0}\lim _{k\rightarrow \infty }\widehat{\unicode[STIX]{x1D707}}_{n_{k}}(ae_{11})=\lim _{|a|\rightarrow 0}\widehat{\unicode[STIX]{x1D707}}(ae_{11})=1. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{|a|\rightarrow 0}\lim _{k\rightarrow \infty }\widehat{\unicode[STIX]{x1D707}}_{n_{k}}(ae_{11})=\lim _{|a|\rightarrow 0}\widehat{\unicode[STIX]{x1D707}}(ae_{11})=1. & & \displaystyle \nonumber\end{eqnarray}$$
That is,
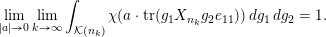 $$\begin{eqnarray}\displaystyle \lim _{|a|\rightarrow 0}\lim _{k\rightarrow \infty }\int _{{\mathcal{K}}(n_{k})}\unicode[STIX]{x1D712}(a\cdot \operatorname{tr}(g_{1}X_{n_{k}}g_{2}e_{11}))\,dg_{1}\,dg_{2}=1. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{|a|\rightarrow 0}\lim _{k\rightarrow \infty }\int _{{\mathcal{K}}(n_{k})}\unicode[STIX]{x1D712}(a\cdot \operatorname{tr}(g_{1}X_{n_{k}}g_{2}e_{11}))\,dg_{1}\,dg_{2}=1. & & \displaystyle\end{eqnarray}$$
By (74), the relation (84) implies that
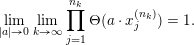 $$\begin{eqnarray}\displaystyle \lim _{|a|\rightarrow 0}\lim _{k\rightarrow \infty }\mathop{\prod }_{j=1}^{n_{k}}\unicode[STIX]{x1D6E9}(a\cdot x_{j}^{(n_{k})})=1. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{|a|\rightarrow 0}\lim _{k\rightarrow \infty }\mathop{\prod }_{j=1}^{n_{k}}\unicode[STIX]{x1D6E9}(a\cdot x_{j}^{(n_{k})})=1. & & \displaystyle\end{eqnarray}$$
Since
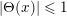 $|\unicode[STIX]{x1D6E9}(x)|\leqslant 1$
, for any
$|\unicode[STIX]{x1D6E9}(x)|\leqslant 1$
, for any
![]() $a\in F^{\times }$
, we have
$a\in F^{\times }$
, we have
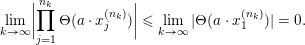 $$\begin{eqnarray}\displaystyle \lim _{k\rightarrow \infty }\biggl|\mathop{\prod }_{j=1}^{n_{k}}\unicode[STIX]{x1D6E9}(a\cdot x_{j}^{(n_{k})})\biggr|\leqslant \lim _{k\rightarrow \infty }|\unicode[STIX]{x1D6E9}(a\cdot x_{1}^{(n_{k})})|=0. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{k\rightarrow \infty }\biggl|\mathop{\prod }_{j=1}^{n_{k}}\unicode[STIX]{x1D6E9}(a\cdot x_{j}^{(n_{k})})\biggr|\leqslant \lim _{k\rightarrow \infty }|\unicode[STIX]{x1D6E9}(a\cdot x_{1}^{(n_{k})})|=0. & & \displaystyle \nonumber\end{eqnarray}$$
This contradicts to (85). Thus the condition (
![]() $C_{1}$
) is necessary for the sequence
$C_{1}$
) is necessary for the sequence
 $(\unicode[STIX]{x1D707}_{n})_{n\in \mathbb{N}}$
to be tight.◻
$(\unicode[STIX]{x1D707}_{n})_{n\in \mathbb{N}}$
to be tight.◻
Recall that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}=\{\Bbbk =(k_{j})_{j=1}^{\infty }\mid k_{j}\in \mathbb{Z}\cup \{-\infty \};k_{1}\geqslant k_{2}\geqslant \cdots \,\}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}=\{\Bbbk =(k_{j})_{j=1}^{\infty }\mid k_{j}\in \mathbb{Z}\cup \{-\infty \};k_{1}\geqslant k_{2}\geqslant \cdots \,\}, & & \displaystyle \nonumber\end{eqnarray}$$
as a subset of
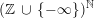 $(\mathbb{Z}\,\cup \,\{-\infty \})^{\mathbb{N}}$
, is assumed to be equipped with the subspace topology of Tychonoff’s product topology on
$(\mathbb{Z}\,\cup \,\{-\infty \})^{\mathbb{N}}$
, is assumed to be equipped with the subspace topology of Tychonoff’s product topology on
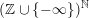 $(\mathbb{Z}\cup \{-\infty \})^{\mathbb{N}}$
.
$(\mathbb{Z}\cup \{-\infty \})^{\mathbb{N}}$
.
Lemma 8.7. Let
![]() $\ell \in \mathbb{Z}$
. Then
$\ell \in \mathbb{Z}$
. Then
 $$\begin{eqnarray}\displaystyle \Bbbk \mapsto f(\Bbbk ):=\mathop{\sum }_{j=1}^{\infty }(k_{j}+\ell )\unicode[STIX]{x1D7D9}_{\{k_{j}+\ell \geqslant 1\}} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Bbbk \mapsto f(\Bbbk ):=\mathop{\sum }_{j=1}^{\infty }(k_{j}+\ell )\unicode[STIX]{x1D7D9}_{\{k_{j}+\ell \geqslant 1\}} & & \displaystyle \nonumber\end{eqnarray}$$
defines a continuous map from
![]() $\unicode[STIX]{x1D6E5}$
to
$\unicode[STIX]{x1D6E5}$
to
 $\mathbb{Z}\cup \{+\infty \}$
.
$\mathbb{Z}\cup \{+\infty \}$
.
Proof. It suffices to prove Lemma 8.7 for
![]() $\ell =0$
. We want to prove that
$\ell =0$
. We want to prove that
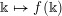 $\Bbbk \mapsto f(\Bbbk )$
is continuous at some point
$\Bbbk \mapsto f(\Bbbk )$
is continuous at some point
 $\Bbbk ^{(0)}=(k_{j}^{(0)})_{j\in \mathbb{N}}\in \unicode[STIX]{x1D6E5}$
.
$\Bbbk ^{(0)}=(k_{j}^{(0)})_{j\in \mathbb{N}}\in \unicode[STIX]{x1D6E5}$
.
Case 1:
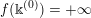 $f(\Bbbk ^{(0)})=+\infty$
. This means that
$f(\Bbbk ^{(0)})=+\infty$
. This means that
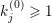 $k_{j}^{(0)}\geqslant 1$
for any
$k_{j}^{(0)}\geqslant 1$
for any
![]() $j\in \mathbb{N}$
. Consequently, for any
$j\in \mathbb{N}$
. Consequently, for any
![]() $A\in \mathbb{R}$
, we may take
$A\in \mathbb{R}$
, we may take
![]() $n$
large enough so that
$n$
large enough so that
 $\sum _{j=1}^{n}k_{j}^{(0)}>A$
. Then for any
$\sum _{j=1}^{n}k_{j}^{(0)}>A$
. Then for any
![]() $\Bbbk \in \unicode[STIX]{x1D6E5}$
sufficiently close to
$\Bbbk \in \unicode[STIX]{x1D6E5}$
sufficiently close to
![]() $\Bbbk ^{(0)}$
, we have
$\Bbbk ^{(0)}$
, we have
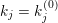 $k_{j}=k_{j}^{(0)}$
for
$k_{j}=k_{j}^{(0)}$
for
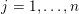 $j=1,\ldots ,n$
. For such
$j=1,\ldots ,n$
. For such
![]() $\Bbbk$
, we have
$\Bbbk$
, we have
 $f(\Bbbk )\geqslant \sum _{j=1}^{n}k_{j}>A$
.
$f(\Bbbk )\geqslant \sum _{j=1}^{n}k_{j}>A$
.
Case 2:
 $f(\Bbbk ^{(0)})<+\infty$
. Then choose
$f(\Bbbk ^{(0)})<+\infty$
. Then choose
![]() $n$
so that
$n$
so that
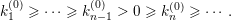 $$\begin{eqnarray}\displaystyle k_{1}^{(0)}\geqslant \cdots \geqslant k_{n-1}^{(0)}>0\geqslant k_{n}^{(0)}\geqslant \cdots \,. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle k_{1}^{(0)}\geqslant \cdots \geqslant k_{n-1}^{(0)}>0\geqslant k_{n}^{(0)}\geqslant \cdots \,. & & \displaystyle \nonumber\end{eqnarray}$$
For any
![]() $\Bbbk \in \unicode[STIX]{x1D6E5}$
sufficiently close to
$\Bbbk \in \unicode[STIX]{x1D6E5}$
sufficiently close to
![]() $\Bbbk ^{(0)}$
, we have
$\Bbbk ^{(0)}$
, we have
 $k_{j}=k_{j}^{(0)}$
for
$k_{j}=k_{j}^{(0)}$
for
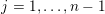 $j=1,\ldots ,n-1$
and
$j=1,\ldots ,n-1$
and
![]() $k_{n}\leqslant 0$
. For such
$k_{n}\leqslant 0$
. For such
![]() $\Bbbk$
, we have
$\Bbbk$
, we have
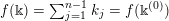 $f(\Bbbk )=\sum _{j=1}^{n-1}k_{j}=f(\Bbbk ^{(0)})$
.
$f(\Bbbk )=\sum _{j=1}^{n-1}k_{j}=f(\Bbbk ^{(0)})$
.
The proof of Lemma 8.7 is completed. ◻
Theorem 8.8. The map
![]() $\Bbbk \mapsto \unicode[STIX]{x1D707}_{\Bbbk }$
induces a bijection between
$\Bbbk \mapsto \unicode[STIX]{x1D707}_{\Bbbk }$
induces a bijection between
![]() $\unicode[STIX]{x1D6E5}$
and
$\unicode[STIX]{x1D6E5}$
and
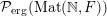 ${\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
.
${\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
.
Proof. The injectivity of the map
![]() $\Bbbk \mapsto \unicode[STIX]{x1D707}_{\Bbbk }$
from
$\Bbbk \mapsto \unicode[STIX]{x1D707}_{\Bbbk }$
from
![]() $\unicode[STIX]{x1D6E5}$
to
$\unicode[STIX]{x1D6E5}$
to
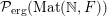 ${\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
has already been proved in Proposition 5.1. We only need to prove that the map is also surjective.
${\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
has already been proved in Proposition 5.1. We only need to prove that the map is also surjective.
Let
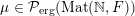 $\unicode[STIX]{x1D707}\in {\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
. By Theorem 8.1,
$\unicode[STIX]{x1D707}\in {\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
. By Theorem 8.1,
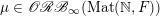 $\unicode[STIX]{x1D707}\in \mathscr{ORB}_{\infty }(\operatorname{Mat}(\mathbb{N},F))$
. Consequently, there exists a sequence
$\unicode[STIX]{x1D707}\in \mathscr{ORB}_{\infty }(\operatorname{Mat}(\mathbb{N},F))$
. Consequently, there exists a sequence
![]() $(n_{l})_{l\in \mathbb{N}}$
of positive integers and a sequence
$(n_{l})_{l\in \mathbb{N}}$
of positive integers and a sequence
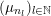 $(\unicode[STIX]{x1D707}_{n_{l}})_{l\in \mathbb{N}}$
of orbital measures such that
$(\unicode[STIX]{x1D707}_{n_{l}})_{l\in \mathbb{N}}$
of orbital measures such that
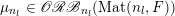 $\unicode[STIX]{x1D707}_{n_{l}}\in \mathscr{ORB}_{n_{l}}(\operatorname{Mat}(n_{l},F))$
and
$\unicode[STIX]{x1D707}_{n_{l}}\in \mathscr{ORB}_{n_{l}}(\operatorname{Mat}(n_{l},F))$
and
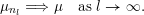 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}_{n_{l}}\Longrightarrow \unicode[STIX]{x1D707}\quad \text{as }l\rightarrow \infty . & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}_{n_{l}}\Longrightarrow \unicode[STIX]{x1D707}\quad \text{as }l\rightarrow \infty . & & \displaystyle\end{eqnarray}$$
By Lemma 2.4, we may assume that
![]() $\unicode[STIX]{x1D707}_{n_{l}}$
is the
$\unicode[STIX]{x1D707}_{n_{l}}$
is the
![]() ${\mathcal{K}}(n_{l})$
-orbital measure supported on the orbit
${\mathcal{K}}(n_{l})$
-orbital measure supported on the orbit
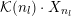 ${\mathcal{K}}(n_{l})\cdot X_{n_{l}}$
with
${\mathcal{K}}(n_{l})\cdot X_{n_{l}}$
with
 $$\begin{eqnarray}\displaystyle X_{n_{l}}=\operatorname{diag}(\unicode[STIX]{x1D71B}^{-k_{1}^{(n_{l})}},\ldots ,\unicode[STIX]{x1D71B}^{-k_{n_{l}}^{(n_{l})}}),\quad k_{1}^{(n_{l})}\geqslant \cdots \geqslant k_{n_{l}}^{(n_{l})}\geqslant -\infty . & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X_{n_{l}}=\operatorname{diag}(\unicode[STIX]{x1D71B}^{-k_{1}^{(n_{l})}},\ldots ,\unicode[STIX]{x1D71B}^{-k_{n_{l}}^{(n_{l})}}),\quad k_{1}^{(n_{l})}\geqslant \cdots \geqslant k_{n_{l}}^{(n_{l})}\geqslant -\infty . & & \displaystyle \nonumber\end{eqnarray}$$
By Lemma 8.6, the convergence (86) implies that
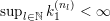 $\sup _{l\in \mathbb{N}}k_{1}^{(n_{l})}<\infty$
. Consequently, passing to a subsequence of
$\sup _{l\in \mathbb{N}}k_{1}^{(n_{l})}<\infty$
. Consequently, passing to a subsequence of
![]() $(n_{l})_{l\in \mathbb{N}}$
if necessary, we may assume that for any
$(n_{l})_{l\in \mathbb{N}}$
if necessary, we may assume that for any
![]() $j\in \mathbb{N}$
, there exists
$j\in \mathbb{N}$
, there exists
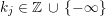 $k_{j}\in \mathbb{Z}\,\cup \,\{-\infty \}$
such that
$k_{j}\in \mathbb{Z}\,\cup \,\{-\infty \}$
such that
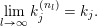 $$\begin{eqnarray}\displaystyle \lim _{l\rightarrow \infty }k_{j}^{(n_{l})}=k_{j}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{l\rightarrow \infty }k_{j}^{(n_{l})}=k_{j}. & & \displaystyle\end{eqnarray}$$
The convergence (86) and the relation (74) now imply that, for any
![]() $\ell \in \mathbb{Z}$
, we have
$\ell \in \mathbb{Z}$
, we have
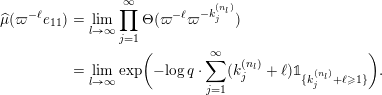 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D71B}^{-\ell }e_{11}) & = & \displaystyle \lim _{l\rightarrow \infty }\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D71B}^{-\ell }\unicode[STIX]{x1D71B}^{-k_{j}^{(n_{l})}})\nonumber\\ \displaystyle & = & \displaystyle \lim _{l\rightarrow \infty }\exp \biggl(-\text{log}\,q\cdot \mathop{\sum }_{j=1}^{\infty }(k_{j}^{(n_{l})}+\ell )\unicode[STIX]{x1D7D9}_{\{k_{j}^{(n_{l})}+\ell \geqslant 1\}}\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D71B}^{-\ell }e_{11}) & = & \displaystyle \lim _{l\rightarrow \infty }\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D71B}^{-\ell }\unicode[STIX]{x1D71B}^{-k_{j}^{(n_{l})}})\nonumber\\ \displaystyle & = & \displaystyle \lim _{l\rightarrow \infty }\exp \biggl(-\text{log}\,q\cdot \mathop{\sum }_{j=1}^{\infty }(k_{j}^{(n_{l})}+\ell )\unicode[STIX]{x1D7D9}_{\{k_{j}^{(n_{l})}+\ell \geqslant 1\}}\biggr).\nonumber\end{eqnarray}$$
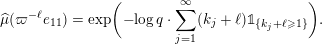 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D71B}^{-\ell }e_{11})=\exp \biggl(-\text{log}\,q\cdot \mathop{\sum }_{j=1}^{\infty }(k_{j}+\ell )\unicode[STIX]{x1D7D9}_{\{k_{j}+\ell \geqslant 1\}}\biggr). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D71B}^{-\ell }e_{11})=\exp \biggl(-\text{log}\,q\cdot \mathop{\sum }_{j=1}^{\infty }(k_{j}+\ell )\unicode[STIX]{x1D7D9}_{\{k_{j}+\ell \geqslant 1\}}\biggr). & & \displaystyle\end{eqnarray}$$
Let us define
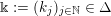 $\Bbbk :=(k_{j})_{j\in \mathbb{N}}\in \unicode[STIX]{x1D6E5}$
. Comparing (99) with the formula (40) in Proposition 4.1, we get
$\Bbbk :=(k_{j})_{j\in \mathbb{N}}\in \unicode[STIX]{x1D6E5}$
. Comparing (99) with the formula (40) in Proposition 4.1, we get
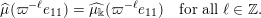 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D71B}^{-\ell }e_{11})=\widehat{\unicode[STIX]{x1D707}_{\Bbbk }}(\unicode[STIX]{x1D71B}^{-\ell }e_{11})\quad \text{for all }\ell \in \mathbb{Z}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D71B}^{-\ell }e_{11})=\widehat{\unicode[STIX]{x1D707}_{\Bbbk }}(\unicode[STIX]{x1D71B}^{-\ell }e_{11})\quad \text{for all }\ell \in \mathbb{Z}. & & \displaystyle\end{eqnarray}$$
But by the multiplicativity of
![]() $\widehat{\unicode[STIX]{x1D707}}$
established in Theorem 8.9 and the multiplicativity of
$\widehat{\unicode[STIX]{x1D707}}$
established in Theorem 8.9 and the multiplicativity of
![]() $\widehat{\unicode[STIX]{x1D707}}_{\Bbbk }$
established in Proposition 4.1, the above identity (89) implies
$\widehat{\unicode[STIX]{x1D707}}_{\Bbbk }$
established in Proposition 4.1, the above identity (89) implies
![]() $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{\Bbbk }$
.
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{\Bbbk }$
.
The proof of Theorem 8.8 is completed. ◻
8.2 The case of
 ${\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))$
${\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))$
Theorem 8.9 (Multiplicativity theorem for orbital limit measures).
Let
![]() $\unicode[STIX]{x1D708}$
be an element in
$\unicode[STIX]{x1D708}$
be an element in
 $\mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))$
. Then for any
$\mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))$
. Then for any
![]() $r\in \mathbb{N}$
and for any finite sequence
$r\in \mathbb{N}$
and for any finite sequence
 $(x_{1},\ldots ,x_{r})$
in
$(x_{1},\ldots ,x_{r})$
in
![]() $F$
, we have
$F$
, we have
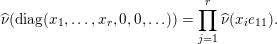 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(\operatorname{diag}(x_{1},\ldots ,x_{r},0,0,\ldots ))=\mathop{\prod }_{j=1}^{r}\widehat{\unicode[STIX]{x1D708}}(x_{i}e_{11}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(\operatorname{diag}(x_{1},\ldots ,x_{r},0,0,\ldots ))=\mathop{\prod }_{j=1}^{r}\widehat{\unicode[STIX]{x1D708}}(x_{i}e_{11}). & & \displaystyle \nonumber\end{eqnarray}$$
In particular, we have
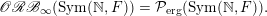 $$\begin{eqnarray}\displaystyle \mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))={\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F)). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F))={\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F)). & & \displaystyle \nonumber\end{eqnarray}$$
Proof. The proof is similar to that of Theorem 8.1. ◻
Corollary 8.10 (Ismagilov–Olshanski multiplicativity).
An invariant probability measure
 $\unicode[STIX]{x1D707}\in {\mathcal{P}}_{\text{inv}}(\operatorname{Sym}(\mathbb{N},F))$
is ergodic if and only if for any
$\unicode[STIX]{x1D707}\in {\mathcal{P}}_{\text{inv}}(\operatorname{Sym}(\mathbb{N},F))$
is ergodic if and only if for any
![]() $r\in \mathbb{N}$
and for any finite sequence
$r\in \mathbb{N}$
and for any finite sequence
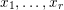 $x_{1},\ldots ,x_{r}$
in
$x_{1},\ldots ,x_{r}$
in
![]() $F$
, we have
$F$
, we have
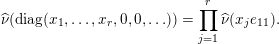 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(\operatorname{diag}(x_{1},\ldots ,x_{r},0,0,\ldots ))=\mathop{\prod }_{j=1}^{r}\widehat{\unicode[STIX]{x1D708}}(x_{j}e_{11}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(\operatorname{diag}(x_{1},\ldots ,x_{r},0,0,\ldots ))=\mathop{\prod }_{j=1}^{r}\widehat{\unicode[STIX]{x1D708}}(x_{j}e_{11}). & & \displaystyle \nonumber\end{eqnarray}$$
Lemma 8.11. Let
![]() $\unicode[STIX]{x1D708}$
be a Borel probability measure on
$\unicode[STIX]{x1D708}$
be a Borel probability measure on
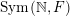 $\operatorname{Sym}(\mathbb{N},F)$
. Then we have
$\operatorname{Sym}(\mathbb{N},F)$
. Then we have
 $$\begin{eqnarray}\displaystyle \lim _{|x|\rightarrow 0}\widehat{\unicode[STIX]{x1D708}}(xe_{11})=1. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{|x|\rightarrow 0}\widehat{\unicode[STIX]{x1D708}}(xe_{11})=1. & & \displaystyle \nonumber\end{eqnarray}$$
Proof. The proof is similar to that of Lemma 8.5. ◻
Lemma 8.12. Assume that we are given a sequence of probability measures
![]() $(\unicode[STIX]{x1D708}_{n})_{n\in \mathbb{N}}$
, such that
$(\unicode[STIX]{x1D708}_{n})_{n\in \mathbb{N}}$
, such that
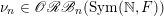 $\unicode[STIX]{x1D708}_{n}\in \mathscr{ORB}_{n}(\operatorname{Sym}(\mathbb{N},F))$
. The necessary and sufficient condition for this sequence to be tight is the following.
$\unicode[STIX]{x1D708}_{n}\in \mathscr{ORB}_{n}(\operatorname{Sym}(\mathbb{N},F))$
. The necessary and sufficient condition for this sequence to be tight is the following.
- (
 $C_{2}$
)
$C_{2}$
) -
There exists
 $\unicode[STIX]{x1D6FE}\in \mathbb{Z}$
, such that the supports
$\unicode[STIX]{x1D6FE}\in \mathbb{Z}$
, such that the supports
 $\operatorname{supp}(\unicode[STIX]{x1D708}_{n})$
are all contained in the following compact subset of
$\operatorname{supp}(\unicode[STIX]{x1D708}_{n})$
are all contained in the following compact subset of
 $\operatorname{Sym}(\mathbb{N},F)$
:
$\operatorname{Sym}(\mathbb{N},F)$
:  $$\begin{eqnarray}\displaystyle \{X\in \operatorname{Sym}(\mathbb{N},F)\mid |X_{ij}|\leqslant q^{\unicode[STIX]{x1D6FE}},\forall i,j\in \mathbb{N}\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \{X\in \operatorname{Sym}(\mathbb{N},F)\mid |X_{ij}|\leqslant q^{\unicode[STIX]{x1D6FE}},\forall i,j\in \mathbb{N}\}. & & \displaystyle \nonumber\end{eqnarray}$$
Proof. The above condition (
![]() $C_{2}$
) is clearly sufficient for the sequence to be tight. Now suppose that the sequence is tight, we shall prove that (
$C_{2}$
) is clearly sufficient for the sequence to be tight. Now suppose that the sequence is tight, we shall prove that (
![]() $C_{2}$
) is satisfied. By assumption, suppose that
$C_{2}$
) is satisfied. By assumption, suppose that
![]() $\unicode[STIX]{x1D708}_{n}$
is the
$\unicode[STIX]{x1D708}_{n}$
is the
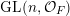 $\operatorname{GL}(n,{\mathcal{O}}_{F})$
-orbital measure supported on the orbit
$\operatorname{GL}(n,{\mathcal{O}}_{F})$
-orbital measure supported on the orbit
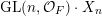 $\operatorname{GL}(n,{\mathcal{O}}_{F})\cdot X_{n}$
. By Lemma 2.7, we may assume that
$\operatorname{GL}(n,{\mathcal{O}}_{F})\cdot X_{n}$
. By Lemma 2.7, we may assume that
 $$\begin{eqnarray}X_{n}=\operatorname{diag}(x_{1}^{(n)},\ldots ,x_{n}^{(n)}),\quad |x_{1}^{(n)}|\geqslant \cdots \geqslant |x_{n}^{(n)}|.\end{eqnarray}$$
$$\begin{eqnarray}X_{n}=\operatorname{diag}(x_{1}^{(n)},\ldots ,x_{n}^{(n)}),\quad |x_{1}^{(n)}|\geqslant \cdots \geqslant |x_{n}^{(n)}|.\end{eqnarray}$$
Now we argue by contradiction. If the condition is not satisfied, then there exists a subsequence
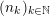 $(n_{k})_{k\in \mathbb{N}}$
of positive integers such that
$(n_{k})_{k\in \mathbb{N}}$
of positive integers such that
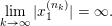 $$\begin{eqnarray}\displaystyle \lim _{k\rightarrow \infty }|x_{1}^{(n_{k})}|=\infty . & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{k\rightarrow \infty }|x_{1}^{(n_{k})}|=\infty . & & \displaystyle\end{eqnarray}$$
Passing to a subsequence if necessary, we may assume that there exists a probability measure
![]() $\unicode[STIX]{x1D708}$
on
$\unicode[STIX]{x1D708}$
on
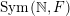 $\operatorname{Sym}(\mathbb{N},F)$
, such that
$\operatorname{Sym}(\mathbb{N},F)$
, such that
 $\unicode[STIX]{x1D708}_{n_{k}}\Longrightarrow \unicode[STIX]{x1D708}$
. By Lemma 8.11, for any
$\unicode[STIX]{x1D708}_{n_{k}}\Longrightarrow \unicode[STIX]{x1D708}$
. By Lemma 8.11, for any
![]() $a\in F$
, we have
$a\in F$
, we have
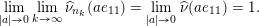 $$\begin{eqnarray}\displaystyle \lim _{|a|\rightarrow 0}\lim _{k\rightarrow \infty }\widehat{\unicode[STIX]{x1D708}}_{n_{k}}(ae_{11})=\lim _{|a|\rightarrow 0}\widehat{\unicode[STIX]{x1D708}}(ae_{11})=1. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{|a|\rightarrow 0}\lim _{k\rightarrow \infty }\widehat{\unicode[STIX]{x1D708}}_{n_{k}}(ae_{11})=\lim _{|a|\rightarrow 0}\widehat{\unicode[STIX]{x1D708}}(ae_{11})=1. & & \displaystyle \nonumber\end{eqnarray}$$
That is,
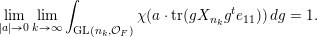 $$\begin{eqnarray}\displaystyle \lim _{|a|\rightarrow 0}\lim _{k\rightarrow \infty }\int _{\operatorname{GL}(n_{k},{\mathcal{O}}_{F})}\unicode[STIX]{x1D712}(a\cdot \operatorname{tr}(gX_{n_{k}}g^{t}e_{11}))\,dg=1. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{|a|\rightarrow 0}\lim _{k\rightarrow \infty }\int _{\operatorname{GL}(n_{k},{\mathcal{O}}_{F})}\unicode[STIX]{x1D712}(a\cdot \operatorname{tr}(gX_{n_{k}}g^{t}e_{11}))\,dg=1. & & \displaystyle\end{eqnarray}$$
By (78) in Theorem 7.5, the relation (91) implies that
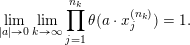 $$\begin{eqnarray}\displaystyle \lim _{|a|\rightarrow 0}\lim _{k\rightarrow \infty }\mathop{\prod }_{j=1}^{n_{k}}\unicode[STIX]{x1D703}(a\cdot x_{j}^{(n_{k})})=1. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{|a|\rightarrow 0}\lim _{k\rightarrow \infty }\mathop{\prod }_{j=1}^{n_{k}}\unicode[STIX]{x1D703}(a\cdot x_{j}^{(n_{k})})=1. & & \displaystyle\end{eqnarray}$$
Using the elementary inequality
 $|\unicode[STIX]{x1D703}(x)|\leqslant 1$
and (90) and Proposition 4.5, for any
$|\unicode[STIX]{x1D703}(x)|\leqslant 1$
and (90) and Proposition 4.5, for any
![]() $a\in F^{\times }$
, we have
$a\in F^{\times }$
, we have
 $$\begin{eqnarray}\displaystyle \lim _{k\rightarrow \infty }\biggl|\mathop{\prod }_{j=1}^{n_{k}}\unicode[STIX]{x1D703}(a\cdot x_{j}^{(n_{k})})\biggr|\leqslant \lim _{k\rightarrow \infty }|\unicode[STIX]{x1D703}(a\cdot x_{1}^{(n_{k})})|=0. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{k\rightarrow \infty }\biggl|\mathop{\prod }_{j=1}^{n_{k}}\unicode[STIX]{x1D703}(a\cdot x_{j}^{(n_{k})})\biggr|\leqslant \lim _{k\rightarrow \infty }|\unicode[STIX]{x1D703}(a\cdot x_{1}^{(n_{k})})|=0. & & \displaystyle \nonumber\end{eqnarray}$$
This contradicts to (92). Thus the condition (
![]() $C_{2}$
) is necessary for the sequence
$C_{2}$
) is necessary for the sequence
 $(\unicode[STIX]{x1D708}_{n})_{n\in \mathbb{N}}$
to be tight.◻
$(\unicode[STIX]{x1D708}_{n})_{n\in \mathbb{N}}$
to be tight.◻
8.2.1 Classification of
 ${\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))$
${\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))$
Recall that by Lemma 4.7, for any
![]() $a\in F$
and any
$a\in F$
and any
 $\Bbbk =(k_{j})_{j\in \mathbb{N}}\in \unicode[STIX]{x1D6E5}$
, we may define an infinite product
$\Bbbk =(k_{j})_{j\in \mathbb{N}}\in \unicode[STIX]{x1D6E5}$
, we may define an infinite product
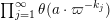 $\prod _{j=1}^{\infty }\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}})$
.
$\prod _{j=1}^{\infty }\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}})$
.
Lemma 8.13. Let
![]() $a\in F$
be a fixed element. Then
$a\in F$
be a fixed element. Then
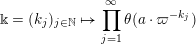 $$\begin{eqnarray}\displaystyle \Bbbk =(k_{j})_{j\in \mathbb{N}}\mapsto \mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}}) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Bbbk =(k_{j})_{j\in \mathbb{N}}\mapsto \mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}}) & & \displaystyle \nonumber\end{eqnarray}$$
defines a continuous map from
![]() $\unicode[STIX]{x1D6E5}$
to
$\unicode[STIX]{x1D6E5}$
to
![]() $\mathbb{C}$
.
$\mathbb{C}$
.
Proof. If
![]() $a=0$
, the assertion is obvious. Now assume that
$a=0$
, the assertion is obvious. Now assume that
 $|a|=q^{\unicode[STIX]{x1D6FE}}$
with
$|a|=q^{\unicode[STIX]{x1D6FE}}$
with
![]() $\unicode[STIX]{x1D6FE}\in \mathbb{Z}$
. Suppose that
$\unicode[STIX]{x1D6FE}\in \mathbb{Z}$
. Suppose that
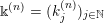 $\Bbbk ^{(n)}=(k_{j}^{(n)})_{j\in \mathbb{N}}$
converges to
$\Bbbk ^{(n)}=(k_{j}^{(n)})_{j\in \mathbb{N}}$
converges to
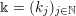 $\Bbbk =(k_{j})_{j\in \mathbb{N}}$
. That is, for any
$\Bbbk =(k_{j})_{j\in \mathbb{N}}$
. That is, for any
![]() $j\in N$
,
$j\in N$
,
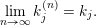 $$\begin{eqnarray}\displaystyle \lim _{n\rightarrow \infty }k_{j}^{(n)}=k_{j}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{n\rightarrow \infty }k_{j}^{(n)}=k_{j}. & & \displaystyle\end{eqnarray}$$
We need to show that
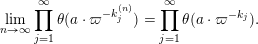 $$\begin{eqnarray}\displaystyle \lim _{n\rightarrow \infty }\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}^{(n)}})=\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{n\rightarrow \infty }\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}^{(n)}})=\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}}). & & \displaystyle\end{eqnarray}$$
First write
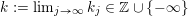 $k:=\lim _{j\rightarrow \infty }k_{j}\in \mathbb{Z}\cup \{-\infty \}$
.
$k:=\lim _{j\rightarrow \infty }k_{j}\in \mathbb{Z}\cup \{-\infty \}$
.
Case 1:
 $k+\unicode[STIX]{x1D6FE}\leqslant 0$
.
$k+\unicode[STIX]{x1D6FE}\leqslant 0$
.
In this case, there exists
![]() $j_{0}\in \mathbb{N}$
, such that
$j_{0}\in \mathbb{N}$
, such that
 $k_{j_{0}}+\unicode[STIX]{x1D6FE}\leqslant 0$
. Since
$k_{j_{0}}+\unicode[STIX]{x1D6FE}\leqslant 0$
. Since
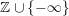 $\mathbb{Z}\cup \{-\infty \}$
is a discrete space, by (93), there exists
$\mathbb{Z}\cup \{-\infty \}$
is a discrete space, by (93), there exists
![]() $n_{0}\in \mathbb{N}$
, such that for any
$n_{0}\in \mathbb{N}$
, such that for any
![]() $n\geqslant n_{0}$
,
$n\geqslant n_{0}$
,
 $$\begin{eqnarray}\displaystyle \sup _{j\geqslant j_{0}}(k_{j}^{(n)}+\unicode[STIX]{x1D6FE})=k_{j_{0}}^{(n)}+\unicode[STIX]{x1D6FE}\leqslant 0. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \sup _{j\geqslant j_{0}}(k_{j}^{(n)}+\unicode[STIX]{x1D6FE})=k_{j_{0}}^{(n)}+\unicode[STIX]{x1D6FE}\leqslant 0. & & \displaystyle\end{eqnarray}$$
Hence by property (i) in Proposition 4.5, for any
![]() $j\geqslant j_{0}$
and
$j\geqslant j_{0}$
and
![]() $n\geqslant n_{0}$
, we have
$n\geqslant n_{0}$
, we have
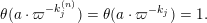 $$\begin{eqnarray}\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}^{(n)}})=\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}})=1.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}^{(n)}})=\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}})=1.\end{eqnarray}$$
Consequently, we have
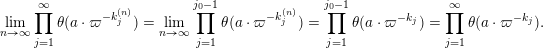 $$\begin{eqnarray}\displaystyle \lim _{n\rightarrow \infty }\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}^{(n)}})=\lim _{n\rightarrow \infty }\mathop{\prod }_{j=1}^{j_{0}-1}\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}^{(n)}})=\mathop{\prod }_{j=1}^{j_{0}-1}\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}})=\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{n\rightarrow \infty }\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}^{(n)}})=\lim _{n\rightarrow \infty }\mathop{\prod }_{j=1}^{j_{0}-1}\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}^{(n)}})=\mathop{\prod }_{j=1}^{j_{0}-1}\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}})=\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}}). & & \displaystyle \nonumber\end{eqnarray}$$
Case 2:
 $k+\unicode[STIX]{x1D6FE}>0$
.
$k+\unicode[STIX]{x1D6FE}>0$
.
In this case, by the previous argument, we have
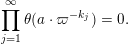 $$\begin{eqnarray}\displaystyle \mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}})=0. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}})=0. & & \displaystyle \nonumber\end{eqnarray}$$
By (93), for any
![]() $N\in \mathbb{N}$
, there exists
$N\in \mathbb{N}$
, there exists
![]() $n_{0}\in \mathbb{N}$
, such that for any
$n_{0}\in \mathbb{N}$
, such that for any
![]() $n\geqslant n_{0}$
and any
$n\geqslant n_{0}$
and any
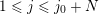 $1\leqslant j\leqslant j_{0}+N$
, we have
$1\leqslant j\leqslant j_{0}+N$
, we have
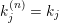 $k_{j}^{(n)}=k_{j}$
. This implies
$k_{j}^{(n)}=k_{j}$
. This implies
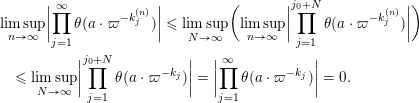 $$\begin{eqnarray}\displaystyle & & \displaystyle \limsup _{n\rightarrow \infty }\biggl|\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}^{(n)}})\biggr|\leqslant \limsup _{N\rightarrow \infty }\biggl(\limsup _{n\rightarrow \infty }\biggl|\mathop{\prod }_{j=1}^{j_{0}+N}\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}^{(n)}})\biggr|\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \limsup _{N\rightarrow \infty }\biggl|\mathop{\prod }_{j=1}^{j_{0}+N}\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}})\biggr|=\biggl|\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}})\biggr|=0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \limsup _{n\rightarrow \infty }\biggl|\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}^{(n)}})\biggr|\leqslant \limsup _{N\rightarrow \infty }\biggl(\limsup _{n\rightarrow \infty }\biggl|\mathop{\prod }_{j=1}^{j_{0}+N}\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}^{(n)}})\biggr|\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \limsup _{N\rightarrow \infty }\biggl|\mathop{\prod }_{j=1}^{j_{0}+N}\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}})\biggr|=\biggl|\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(a\cdot \unicode[STIX]{x1D71B}^{-k_{j}})\biggr|=0.\nonumber\end{eqnarray}$$
Hence the desired relation (94) holds. ◻
Theorem 8.14. Assume that
![]() $F$
is non-dyadic. Then the map
$F$
is non-dyadic. Then the map
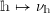 $h\mapsto \unicode[STIX]{x1D708}_{h}$
induces a bijection between
$h\mapsto \unicode[STIX]{x1D708}_{h}$
induces a bijection between
![]() $\unicode[STIX]{x1D6FA}$
and
$\unicode[STIX]{x1D6FA}$
and
 ${\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))$
.
${\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))$
.
Proof. The injectivity of the map
![]() $h\mapsto \unicode[STIX]{x1D708}_{h}$
from
$h\mapsto \unicode[STIX]{x1D708}_{h}$
from
![]() $\unicode[STIX]{x1D6FA}$
to
$\unicode[STIX]{x1D6FA}$
to
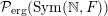 ${\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))$
has already been proved in Proposition 5.3. We only need to prove that the map is also surjective.
${\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))$
has already been proved in Proposition 5.3. We only need to prove that the map is also surjective.
Assume that
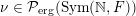 $\unicode[STIX]{x1D708}\in {\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))$
. Since
$\unicode[STIX]{x1D708}\in {\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))$
. Since
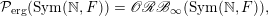 $$\begin{eqnarray}\displaystyle {\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))=\mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F)), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))=\mathscr{ORB}_{\infty }(\operatorname{Sym}(\mathbb{N},F)), & & \displaystyle \nonumber\end{eqnarray}$$
there exists a sequence
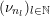 $(\unicode[STIX]{x1D708}_{n_{l}})_{l\in \mathbb{N}}$
of orbital measures satisfying
$(\unicode[STIX]{x1D708}_{n_{l}})_{l\in \mathbb{N}}$
of orbital measures satisfying
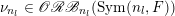 $\unicode[STIX]{x1D708}_{n_{l}}\in \mathscr{ORB}_{n_{l}}(\operatorname{Sym}(n_{l},F))$
such that
$\unicode[STIX]{x1D708}_{n_{l}}\in \mathscr{ORB}_{n_{l}}(\operatorname{Sym}(n_{l},F))$
such that
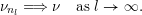 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D708}_{n_{l}}\Longrightarrow \unicode[STIX]{x1D708}\quad \text{as }l\rightarrow \infty . & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D708}_{n_{l}}\Longrightarrow \unicode[STIX]{x1D708}\quad \text{as }l\rightarrow \infty . & & \displaystyle\end{eqnarray}$$
By Lemma 2.7, we may assume that
![]() $\unicode[STIX]{x1D708}_{n_{l}}$
is the
$\unicode[STIX]{x1D708}_{n_{l}}$
is the
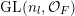 $\operatorname{GL}(n_{l},{\mathcal{O}}_{F})$
-orbital measure supported on the orbit
$\operatorname{GL}(n_{l},{\mathcal{O}}_{F})$
-orbital measure supported on the orbit
 $\operatorname{GL}(n_{l},{\mathcal{O}}_{F})\cdot X_{n_{l}}$
with
$\operatorname{GL}(n_{l},{\mathcal{O}}_{F})\cdot X_{n_{l}}$
with
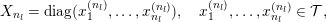 $$\begin{eqnarray}\displaystyle X_{n_{l}}=\operatorname{diag}(x_{1}^{(n_{l})},\ldots ,x_{n_{l}}^{(n_{l})}),\quad x_{1}^{(n_{l})},\ldots ,x_{n_{l}}^{(n_{l})}\in {\mathcal{T}}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X_{n_{l}}=\operatorname{diag}(x_{1}^{(n_{l})},\ldots ,x_{n_{l}}^{(n_{l})}),\quad x_{1}^{(n_{l})},\ldots ,x_{n_{l}}^{(n_{l})}\in {\mathcal{T}}, & & \displaystyle \nonumber\end{eqnarray}$$
where
![]() ${\mathcal{T}}$
is given in (26). If for any multi-setFootnote
1
${\mathcal{T}}$
is given in (26). If for any multi-setFootnote
1
![]() $B$
with elements in
$B$
with elements in
![]() $F$
, we denote by
$F$
, we denote by
![]() $B^{\ast }$
the multi-set of non-zero elements of
$B^{\ast }$
the multi-set of non-zero elements of
![]() $B$
. Then there exist
$B$
. Then there exist
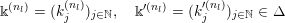 $$\begin{eqnarray}\displaystyle \Bbbk ^{(n_{l})}=(k_{j}^{(n_{l})})_{j\in \mathbb{N}},\quad \Bbbk ^{\prime (n_{l})}=(k_{j}^{\prime (n_{l})})_{j\in \mathbb{N}}\in \unicode[STIX]{x1D6E5} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Bbbk ^{(n_{l})}=(k_{j}^{(n_{l})})_{j\in \mathbb{N}},\quad \Bbbk ^{\prime (n_{l})}=(k_{j}^{\prime (n_{l})})_{j\in \mathbb{N}}\in \unicode[STIX]{x1D6E5} & & \displaystyle \nonumber\end{eqnarray}$$
such that the following two multi-sets coincide:
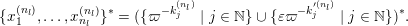 $$\begin{eqnarray}\displaystyle \{x_{1}^{(n_{l})},\ldots ,x_{n_{l}}^{(n_{l})}\}^{\ast }=(\{\unicode[STIX]{x1D71B}^{-k_{j}^{(n_{l})}}\mid j\in \mathbb{N}\}\cup \{\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-k_{j}^{\prime (n_{l})}}\mid j\in \mathbb{N}\})^{\ast }. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \{x_{1}^{(n_{l})},\ldots ,x_{n_{l}}^{(n_{l})}\}^{\ast }=(\{\unicode[STIX]{x1D71B}^{-k_{j}^{(n_{l})}}\mid j\in \mathbb{N}\}\cup \{\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-k_{j}^{\prime (n_{l})}}\mid j\in \mathbb{N}\})^{\ast }. & & \displaystyle \nonumber\end{eqnarray}$$
By Lemma 8.12, the weak convergence (96) implies that
 $$\begin{eqnarray}\sup _{l\in \mathbb{N}}k_{1}^{(n_{l})}<\infty \quad \text{and}\quad \sup _{l\in \mathbb{N}}k_{1}^{\prime (n_{l})}<\infty .\end{eqnarray}$$
$$\begin{eqnarray}\sup _{l\in \mathbb{N}}k_{1}^{(n_{l})}<\infty \quad \text{and}\quad \sup _{l\in \mathbb{N}}k_{1}^{\prime (n_{l})}<\infty .\end{eqnarray}$$
Consequently, passing to a subsequence if necessary, we may assume that for any
![]() $j\in \mathbb{N}$
, there exist
$j\in \mathbb{N}$
, there exist
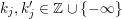 $k_{j},k_{j}^{\prime }\in \mathbb{Z}\cup \{-\infty \}$
and we have
$k_{j},k_{j}^{\prime }\in \mathbb{Z}\cup \{-\infty \}$
and we have
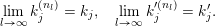 $$\begin{eqnarray}\displaystyle \lim _{l\rightarrow \infty }k_{j}^{(n_{l})}=k_{j},\quad \lim _{l\rightarrow \infty }k_{j}^{\prime (n_{l})}=k_{j}^{\prime }. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{l\rightarrow \infty }k_{j}^{(n_{l})}=k_{j},\quad \lim _{l\rightarrow \infty }k_{j}^{\prime (n_{l})}=k_{j}^{\prime }. & & \displaystyle\end{eqnarray}$$
Now by the weak convergence (96) and the relation (78), for any
![]() $x\in F$
, we have
$x\in F$
, we have
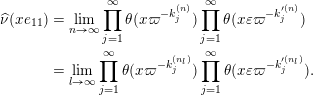 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(xe_{11}) & = & \displaystyle \lim _{n\rightarrow \infty }\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D71B}^{-k_{j}^{(n)}})\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-k_{j}^{\prime (n)}})\nonumber\\ \displaystyle & = & \displaystyle \lim _{l\rightarrow \infty }\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D71B}^{-k_{j}^{(n_{l})}})\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-k_{j}^{\prime (n_{l})}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(xe_{11}) & = & \displaystyle \lim _{n\rightarrow \infty }\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D71B}^{-k_{j}^{(n)}})\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-k_{j}^{\prime (n)}})\nonumber\\ \displaystyle & = & \displaystyle \lim _{l\rightarrow \infty }\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D71B}^{-k_{j}^{(n_{l})}})\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-k_{j}^{\prime (n_{l})}}).\nonumber\end{eqnarray}$$
By the continuity of the map in Lemma 8.13 and (97), we get
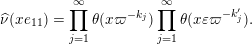 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(xe_{11})=\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D71B}^{-k_{j}})\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-k_{j}^{\prime }}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(xe_{11})=\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D71B}^{-k_{j}})\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-k_{j}^{\prime }}). & & \displaystyle\end{eqnarray}$$
Now by using the identity
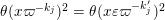 $\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D71B}^{-k_{j}})^{2}=\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-k_{j}^{\prime }})^{2}$
for any
$\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D71B}^{-k_{j}})^{2}=\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-k_{j}^{\prime }})^{2}$
for any
![]() $x\in F$
and
$x\in F$
and
![]() $j\in \mathbb{N}$
and by moving certain elements (in
$j\in \mathbb{N}$
and by moving certain elements (in
![]() $\mathbb{Z}$
and with multiplicities larger than
$\mathbb{Z}$
and with multiplicities larger than
![]() $1$
) from
$1$
) from
![]() $(k_{j}^{\prime })_{j\in \mathbb{N}}$
to the sequence
$(k_{j}^{\prime })_{j\in \mathbb{N}}$
to the sequence
![]() $(k_{j})_{j\in \mathbb{N}}$
, we get a new non-increasing sequence
$(k_{j})_{j\in \mathbb{N}}$
, we get a new non-increasing sequence
![]() $(\widetilde{k}_{j})_{j\in \mathbb{N}}$
and a new strictly decreasing sequence
$(\widetilde{k}_{j})_{j\in \mathbb{N}}$
and a new strictly decreasing sequence
![]() $(\widetilde{k}_{j}^{\prime })_{j\in \mathbb{N}}$
of finite or infinite lengths in
$(\widetilde{k}_{j}^{\prime })_{j\in \mathbb{N}}$
of finite or infinite lengths in
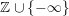 $\mathbb{Z}\cup \{-\infty \}$
such that the identity (98) is transformed to
$\mathbb{Z}\cup \{-\infty \}$
such that the identity (98) is transformed to
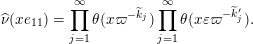 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(xe_{11})=\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D71B}^{-\widetilde{k}_{j}})\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-\widetilde{k}_{j}^{\prime }}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(xe_{11})=\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D71B}^{-\widetilde{k}_{j}})\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-\widetilde{k}_{j}^{\prime }}). & & \displaystyle\end{eqnarray}$$
Assume first that
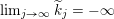 $\lim _{j\rightarrow \infty }\widetilde{k}_{j}=-\infty$
. Then
$\lim _{j\rightarrow \infty }\widetilde{k}_{j}=-\infty$
. Then
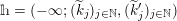 $$\begin{eqnarray}\displaystyle h=(-\infty ;(\widetilde{k}_{j})_{j\in \mathbb{N}},(\widetilde{k}_{j}^{\prime })_{j\in \mathbb{N}}) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h=(-\infty ;(\widetilde{k}_{j})_{j\in \mathbb{N}},(\widetilde{k}_{j}^{\prime })_{j\in \mathbb{N}}) & & \displaystyle \nonumber\end{eqnarray}$$
is an element in
![]() $\unicode[STIX]{x1D6FA}$
. Comparing (99) with the formula in Proposition 4.4, we get
$\unicode[STIX]{x1D6FA}$
. Comparing (99) with the formula in Proposition 4.4, we get
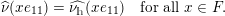 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(xe_{11})=\widehat{\unicode[STIX]{x1D708}_{h}}(xe_{11})\quad \text{for all }x\in F. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(xe_{11})=\widehat{\unicode[STIX]{x1D708}_{h}}(xe_{11})\quad \text{for all }x\in F. & & \displaystyle \nonumber\end{eqnarray}$$
But by the multiplicativity of
![]() $\widehat{\unicode[STIX]{x1D708}}$
established in Theorem 8.9 and the multiplicativity of
$\widehat{\unicode[STIX]{x1D708}}$
established in Theorem 8.9 and the multiplicativity of
![]() $\widehat{\unicode[STIX]{x1D708}}_{h}$
established in Proposition 4.4, the above identity implies
$\widehat{\unicode[STIX]{x1D708}}_{h}$
established in Proposition 4.4, the above identity implies
![]() $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}_{h}$
.
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}_{h}$
.
Assume now that
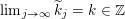 $\lim _{j\rightarrow \infty }\widetilde{k}_{j}=k\in \mathbb{Z}$
. Then using the relation (51), we have
$\lim _{j\rightarrow \infty }\widetilde{k}_{j}=k\in \mathbb{Z}$
. Then using the relation (51), we have
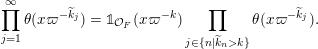 $$\begin{eqnarray}\displaystyle \mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D71B}^{-\widetilde{k}_{j}})=\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(x\unicode[STIX]{x1D71B}^{-k})\mathop{\prod }_{j\in \{n\mid \widetilde{k}_{n}>k\}}\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D71B}^{-\widetilde{k}_{j}}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D71B}^{-\widetilde{k}_{j}})=\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(x\unicode[STIX]{x1D71B}^{-k})\mathop{\prod }_{j\in \{n\mid \widetilde{k}_{n}>k\}}\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D71B}^{-\widetilde{k}_{j}}). & & \displaystyle\end{eqnarray}$$
Moreover, we also have
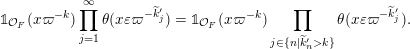 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(x\unicode[STIX]{x1D71B}^{-k})\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-\widetilde{k}_{j}^{\prime }})=\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(x\unicode[STIX]{x1D71B}^{-k})\mathop{\prod }_{j\in \{n\mid \widetilde{k}_{n}^{\prime }>k\}}\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-\widetilde{k}_{j}^{\prime }}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(x\unicode[STIX]{x1D71B}^{-k})\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-\widetilde{k}_{j}^{\prime }})=\unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(x\unicode[STIX]{x1D71B}^{-k})\mathop{\prod }_{j\in \{n\mid \widetilde{k}_{n}^{\prime }>k\}}\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-\widetilde{k}_{j}^{\prime }}). & & \displaystyle\end{eqnarray}$$
It suffices to check for
![]() $x\in F$
such that
$x\in F$
such that
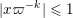 $|x\unicode[STIX]{x1D71B}^{-k}|\leqslant 1$
. For
$|x\unicode[STIX]{x1D71B}^{-k}|\leqslant 1$
. For
![]() $\widetilde{k}_{j}^{\prime }$
such that
$\widetilde{k}_{j}^{\prime }$
such that
![]() $\widetilde{k}_{j}^{\prime }\leqslant k$
(if they exist), we have
$\widetilde{k}_{j}^{\prime }\leqslant k$
(if they exist), we have
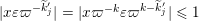 $|x\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-\widetilde{k}_{j}^{\prime }}|=|x\unicode[STIX]{x1D71B}^{-k}\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{k-\widetilde{k}_{j}^{\prime }}|\leqslant 1$
. Hence
$|x\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-\widetilde{k}_{j}^{\prime }}|=|x\unicode[STIX]{x1D71B}^{-k}\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{k-\widetilde{k}_{j}^{\prime }}|\leqslant 1$
. Hence
 $\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-\widetilde{k}_{j}^{\prime }})=1$
by property (i) in Proposition 4.5. The identity (101) is proved. Write
$\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-\widetilde{k}_{j}^{\prime }})=1$
by property (i) in Proposition 4.5. The identity (101) is proved. Write
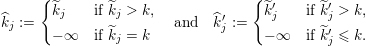 $$\begin{eqnarray}\displaystyle \widehat{k}_{j}:=\left\{\begin{array}{@{}ll@{}}\widetilde{k}_{j}\quad & \text{if }\widetilde{k}_{j}>k,\\ -\infty \quad & \text{if }\widetilde{k}_{j}=k\end{array}\right.\quad \text{and}\quad \widehat{k}_{j}^{\prime }:=\left\{\begin{array}{@{}ll@{}}\widetilde{k}_{j}^{\prime }\quad & \text{if }\widetilde{k}_{j}^{\prime }>k,\\ -\infty \quad & \text{if }\widetilde{k}_{j}^{\prime }\leqslant k.\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{k}_{j}:=\left\{\begin{array}{@{}ll@{}}\widetilde{k}_{j}\quad & \text{if }\widetilde{k}_{j}>k,\\ -\infty \quad & \text{if }\widetilde{k}_{j}=k\end{array}\right.\quad \text{and}\quad \widehat{k}_{j}^{\prime }:=\left\{\begin{array}{@{}ll@{}}\widetilde{k}_{j}^{\prime }\quad & \text{if }\widetilde{k}_{j}^{\prime }>k,\\ -\infty \quad & \text{if }\widetilde{k}_{j}^{\prime }\leqslant k.\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
Now,
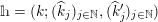 $h=(k;(\widehat{k}_{j})_{j\in \mathbb{N}},(\widehat{k}_{j}^{\prime })_{j\in \mathbb{N}})$
, being an element in
$h=(k;(\widehat{k}_{j})_{j\in \mathbb{N}},(\widehat{k}_{j}^{\prime })_{j\in \mathbb{N}})$
, being an element in
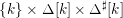 $\{k\}\times \unicode[STIX]{x1D6E5}[k]\times \unicode[STIX]{x1D6E5}^{\sharp }[k]$
, is an element of
$\{k\}\times \unicode[STIX]{x1D6E5}[k]\times \unicode[STIX]{x1D6E5}^{\sharp }[k]$
, is an element of
![]() $\unicode[STIX]{x1D6FA}$
. Combining (99)–(101), we obtain
$\unicode[STIX]{x1D6FA}$
. Combining (99)–(101), we obtain
 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(xe_{11}) & = & \displaystyle \mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D71B}^{-\widetilde{k}_{j}})\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-\widetilde{k}_{j}^{\prime }})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(x\unicode[STIX]{x1D71B}^{-k})\biggl[\mathop{\prod }_{j\in \{n\mid \widetilde{k}_{n}>k\}}\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D71B}^{-\widetilde{k}_{j}})\biggr]\biggl[\mathop{\prod }_{j\in \{n\mid \widetilde{k}_{n}^{\prime }>k\}}\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-\widetilde{k}_{j}^{\prime }})\biggr].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(xe_{11}) & = & \displaystyle \mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D71B}^{-\widetilde{k}_{j}})\mathop{\prod }_{j=1}^{\infty }\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-\widetilde{k}_{j}^{\prime }})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D7D9}_{{\mathcal{O}}_{F}}(x\unicode[STIX]{x1D71B}^{-k})\biggl[\mathop{\prod }_{j\in \{n\mid \widetilde{k}_{n}>k\}}\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D71B}^{-\widetilde{k}_{j}})\biggr]\biggl[\mathop{\prod }_{j\in \{n\mid \widetilde{k}_{n}^{\prime }>k\}}\unicode[STIX]{x1D703}(x\unicode[STIX]{x1D700}\unicode[STIX]{x1D71B}^{-\widetilde{k}_{j}^{\prime }})\biggr].\nonumber\end{eqnarray}$$
In this case, we also have
 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(xe_{11})=\widehat{\unicode[STIX]{x1D708}_{h}}(xe_{11})\quad \text{for all }x\in F. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D708}}(xe_{11})=\widehat{\unicode[STIX]{x1D708}_{h}}(xe_{11})\quad \text{for all }x\in F. & & \displaystyle \nonumber\end{eqnarray}$$
By the same argument as above in using the multiplicativities of
![]() $\widehat{\unicode[STIX]{x1D708}}$
and
$\widehat{\unicode[STIX]{x1D708}}$
and
![]() $\widehat{\unicode[STIX]{x1D708}}_{h}$
, we get
$\widehat{\unicode[STIX]{x1D708}}_{h}$
, we get
![]() $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}_{h}$
.
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}_{h}$
.
The proof of Theorem 8.14 is completed. ◻
9 Properties of the parametrization
9.1 The parametrizations are homeomorphisms
Proof of Theorem 1.3.
By Theorem 8.8, we only need to prove that the map
![]() $\Bbbk \mapsto \unicode[STIX]{x1D707}_{\Bbbk }$
from
$\Bbbk \mapsto \unicode[STIX]{x1D707}_{\Bbbk }$
from
![]() $\unicode[STIX]{x1D6E5}$
to
$\unicode[STIX]{x1D6E5}$
to
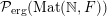 ${\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
and its inverse are both continuous. Note that since
${\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
and its inverse are both continuous. Note that since
![]() $\unicode[STIX]{x1D6E5}$
and
$\unicode[STIX]{x1D6E5}$
and
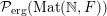 ${\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
are metrizable, their topologies are determined by convergence of sequences.
${\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F))$
are metrizable, their topologies are determined by convergence of sequences.
If a sequence
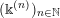 $(\Bbbk ^{(n)})_{n\in \mathbb{N}}$
converges in
$(\Bbbk ^{(n)})_{n\in \mathbb{N}}$
converges in
![]() $\unicode[STIX]{x1D6E5}$
to a point
$\unicode[STIX]{x1D6E5}$
to a point
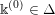 $\Bbbk ^{(0)}\in \unicode[STIX]{x1D6E5}$
, then
$\Bbbk ^{(0)}\in \unicode[STIX]{x1D6E5}$
, then
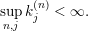 $$\begin{eqnarray}\displaystyle \sup _{n,j}k_{j}^{(n)}<\infty . & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \sup _{n,j}k_{j}^{(n)}<\infty . & & \displaystyle\end{eqnarray}$$
Consequently, the family of the measures
![]() $\unicode[STIX]{x1D707}_{\Bbbk ^{(n)}}$
, all being supported on a common compact subset of
$\unicode[STIX]{x1D707}_{\Bbbk ^{(n)}}$
, all being supported on a common compact subset of
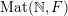 $\operatorname{Mat}(\mathbb{N},F)$
, is tight. Thus to prove that
$\operatorname{Mat}(\mathbb{N},F)$
, is tight. Thus to prove that
![]() $\unicode[STIX]{x1D707}_{\Bbbk ^{(n)}}$
converges weakly to
$\unicode[STIX]{x1D707}_{\Bbbk ^{(n)}}$
converges weakly to
![]() $\unicode[STIX]{x1D707}_{\Bbbk ^{(0)}}$
, it suffices to prove that the latter one is the unique accumulation point of the former family of measures. Now let
$\unicode[STIX]{x1D707}_{\Bbbk ^{(0)}}$
, it suffices to prove that the latter one is the unique accumulation point of the former family of measures. Now let
![]() $\unicode[STIX]{x1D707}$
be an accumulation point of the sequence
$\unicode[STIX]{x1D707}$
be an accumulation point of the sequence
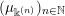 $(\unicode[STIX]{x1D707}_{\Bbbk ^{(n)}})_{n\in \mathbb{N}}$
. By definition, there exists a subsequence
$(\unicode[STIX]{x1D707}_{\Bbbk ^{(n)}})_{n\in \mathbb{N}}$
. By definition, there exists a subsequence
![]() $(n_{j})_{j\in \mathbb{N}}$
such that
$(n_{j})_{j\in \mathbb{N}}$
such that
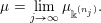 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}=\lim _{j\rightarrow \infty }\unicode[STIX]{x1D707}_{\Bbbk ^{(n_{j})}}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}=\lim _{j\rightarrow \infty }\unicode[STIX]{x1D707}_{\Bbbk ^{(n_{j})}}. & & \displaystyle \nonumber\end{eqnarray}$$
Since
 $\Bbbk ^{(n)}\longrightarrow \Bbbk ^{(0)}$
, by explicit formula (40) in Proposition 4.1 and Lemma 8.7, the characteristic function of
$\Bbbk ^{(n)}\longrightarrow \Bbbk ^{(0)}$
, by explicit formula (40) in Proposition 4.1 and Lemma 8.7, the characteristic function of
![]() $\unicode[STIX]{x1D707}$
is given by
$\unicode[STIX]{x1D707}$
is given by
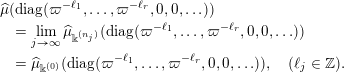 $$\begin{eqnarray}\displaystyle & & \displaystyle \widehat{\unicode[STIX]{x1D707}}(\operatorname{diag}(\unicode[STIX]{x1D71B}^{-\ell _{1}},\ldots ,\unicode[STIX]{x1D71B}^{-\ell _{r}},0,0,\ldots ))\nonumber\\ \displaystyle & & \displaystyle \quad =\lim _{j\rightarrow \infty }\widehat{\unicode[STIX]{x1D707}}_{\Bbbk ^{(n_{j})}}(\operatorname{diag}(\unicode[STIX]{x1D71B}^{-\ell _{1}},\ldots ,\unicode[STIX]{x1D71B}^{-\ell _{r}},0,0,\ldots ))\nonumber\\ \displaystyle & & \displaystyle \quad =\widehat{\unicode[STIX]{x1D707}}_{\Bbbk ^{(0)}}(\operatorname{diag}(\unicode[STIX]{x1D71B}^{-\ell _{1}},\ldots ,\unicode[STIX]{x1D71B}^{-\ell _{r}},0,0,\ldots )),\quad (\ell _{j}\in \mathbb{Z}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \widehat{\unicode[STIX]{x1D707}}(\operatorname{diag}(\unicode[STIX]{x1D71B}^{-\ell _{1}},\ldots ,\unicode[STIX]{x1D71B}^{-\ell _{r}},0,0,\ldots ))\nonumber\\ \displaystyle & & \displaystyle \quad =\lim _{j\rightarrow \infty }\widehat{\unicode[STIX]{x1D707}}_{\Bbbk ^{(n_{j})}}(\operatorname{diag}(\unicode[STIX]{x1D71B}^{-\ell _{1}},\ldots ,\unicode[STIX]{x1D71B}^{-\ell _{r}},0,0,\ldots ))\nonumber\\ \displaystyle & & \displaystyle \quad =\widehat{\unicode[STIX]{x1D707}}_{\Bbbk ^{(0)}}(\operatorname{diag}(\unicode[STIX]{x1D71B}^{-\ell _{1}},\ldots ,\unicode[STIX]{x1D71B}^{-\ell _{r}},0,0,\ldots )),\quad (\ell _{j}\in \mathbb{Z}).\nonumber\end{eqnarray}$$
This implies that we have
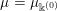 $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{\Bbbk ^{(0)}}$
.
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{\Bbbk ^{(0)}}$
.
Conversely, if
![]() $\unicode[STIX]{x1D707}_{\Bbbk ^{(n)}}$
converges to
$\unicode[STIX]{x1D707}_{\Bbbk ^{(n)}}$
converges to
![]() $\unicode[STIX]{x1D707}_{\Bbbk ^{(0)}}$
. By using the same argument as in the proof of Lemma 8.6, we can still get the relation (102). Again by compactness argument, it suffices to show that
$\unicode[STIX]{x1D707}_{\Bbbk ^{(0)}}$
. By using the same argument as in the proof of Lemma 8.6, we can still get the relation (102). Again by compactness argument, it suffices to show that
![]() $\Bbbk ^{(0)}$
is the unique accumulation point for the sequence
$\Bbbk ^{(0)}$
is the unique accumulation point for the sequence
![]() $\Bbbk ^{(n)}$
. But if
$\Bbbk ^{(n)}$
. But if
![]() $\Bbbk$
is an accumulation point of
$\Bbbk$
is an accumulation point of
![]() $\Bbbk ^{(n)}$
, then
$\Bbbk ^{(n)}$
, then
![]() $\unicode[STIX]{x1D707}_{\Bbbk }$
is an accumulation point of
$\unicode[STIX]{x1D707}_{\Bbbk }$
is an accumulation point of
![]() $\unicode[STIX]{x1D707}_{\Bbbk ^{(n)}}$
, whence
$\unicode[STIX]{x1D707}_{\Bbbk ^{(n)}}$
, whence
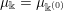 $\unicode[STIX]{x1D707}_{\Bbbk }=\unicode[STIX]{x1D707}_{\Bbbk ^{(0)}}$
. Combining with Proposition 5.1 we have
$\unicode[STIX]{x1D707}_{\Bbbk }=\unicode[STIX]{x1D707}_{\Bbbk ^{(0)}}$
. Combining with Proposition 5.1 we have
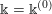 $\Bbbk =\Bbbk ^{(0)}$
.
$\Bbbk =\Bbbk ^{(0)}$
.
The proof of Theorem 1.3 is completed. ◻
Proof of Theorem 1.8.
By Theorem 8.14, we only need to prove that the map
![]() $h\mapsto \unicode[STIX]{x1D708}_{h}$
from
$h\mapsto \unicode[STIX]{x1D708}_{h}$
from
![]() $\unicode[STIX]{x1D6FA}$
to
$\unicode[STIX]{x1D6FA}$
to
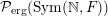 ${\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))$
and its inverse are both continuous. The proof of this part is similar to that of Theorem 1.3 as above. ◻
${\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F))$
and its inverse are both continuous. The proof of this part is similar to that of Theorem 1.3 as above. ◻
9.2 The parametrizations are semi-group homomorphisms
On
![]() $\unicode[STIX]{x1D6E5}$
is equipped with an Abelian semi-group structure. Given any two points
$\unicode[STIX]{x1D6E5}$
is equipped with an Abelian semi-group structure. Given any two points
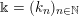 $\Bbbk =(k_{n})_{n\in \mathbb{N}}$
and
$\Bbbk =(k_{n})_{n\in \mathbb{N}}$
and
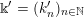 $\Bbbk ^{\prime }=(k_{n}^{\prime })_{n\in \mathbb{N}}$
in
$\Bbbk ^{\prime }=(k_{n}^{\prime })_{n\in \mathbb{N}}$
in
![]() $\unicode[STIX]{x1D6E5}$
, we define
$\unicode[STIX]{x1D6E5}$
, we define
 $\Bbbk \oplus _{\unicode[STIX]{x1D6E5}}\Bbbk ^{\prime }$
as follows.
$\Bbbk \oplus _{\unicode[STIX]{x1D6E5}}\Bbbk ^{\prime }$
as follows.
(i) If
 $\inf k_{n}=\inf k_{n}^{\prime }=-\infty$
, then we define
$\inf k_{n}=\inf k_{n}^{\prime }=-\infty$
, then we define
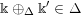 $\Bbbk \oplus _{\unicode[STIX]{x1D6E5}}\Bbbk ^{\prime }\in \unicode[STIX]{x1D6E5}$
to be the non-increasing rearrangement of the sequence
$\Bbbk \oplus _{\unicode[STIX]{x1D6E5}}\Bbbk ^{\prime }\in \unicode[STIX]{x1D6E5}$
to be the non-increasing rearrangement of the sequence
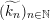 $(\widetilde{k_{n}})_{n\in \mathbb{N}}$
, where
$(\widetilde{k_{n}})_{n\in \mathbb{N}}$
, where
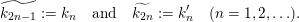 $$\begin{eqnarray}\widetilde{k_{2n-1}}:=k_{n}\quad \text{and}\quad \widetilde{k_{2n}}:=k_{n}^{\prime }\quad (n=1,2,\ldots ).\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{k_{2n-1}}:=k_{n}\quad \text{and}\quad \widetilde{k_{2n}}:=k_{n}^{\prime }\quad (n=1,2,\ldots ).\end{eqnarray}$$
(ii) If
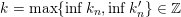 $k=\max \{\inf k_{n},\inf k_{n}^{\prime }\}\in \mathbb{Z}$
, then we define
$k=\max \{\inf k_{n},\inf k_{n}^{\prime }\}\in \mathbb{Z}$
, then we define
 $\Bbbk \oplus \Bbbk ^{\prime }\in \unicode[STIX]{x1D6E5}$
to be the non-increasing rearrangement of the sequence
$\Bbbk \oplus \Bbbk ^{\prime }\in \unicode[STIX]{x1D6E5}$
to be the non-increasing rearrangement of the sequence
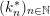 $(k_{n}^{\ast })_{n\in \mathbb{N}}$
, that is any sequence exhausting the integers larger than
$(k_{n}^{\ast })_{n\in \mathbb{N}}$
, that is any sequence exhausting the integers larger than
![]() $k$
and from
$k$
and from
![]() $\Bbbk$
and
$\Bbbk$
and
![]() $\Bbbk ^{\prime }$
, repeated with corresponding multiplicity. For instance, if
$\Bbbk ^{\prime }$
, repeated with corresponding multiplicity. For instance, if
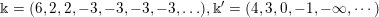 $\Bbbk =(6,2,2,-3,-3,-3,-3,\ldots ),\Bbbk ^{\prime }=(4,3,0,-1,-\infty ,\cdots \,)$
, then we define
$\Bbbk =(6,2,2,-3,-3,-3,-3,\ldots ),\Bbbk ^{\prime }=(4,3,0,-1,-\infty ,\cdots \,)$
, then we define
 $$\begin{eqnarray}\Bbbk \oplus _{\unicode[STIX]{x1D6E5}}\Bbbk ^{\prime }=(6,4,3,2,2,0,-1,-3,-3,-3,-3,\ldots ).\end{eqnarray}$$
$$\begin{eqnarray}\Bbbk \oplus _{\unicode[STIX]{x1D6E5}}\Bbbk ^{\prime }=(6,4,3,2,2,0,-1,-3,-3,-3,-3,\ldots ).\end{eqnarray}$$
Clearly, we have the following.
Proposition 9.1. The map
![]() $\Bbbk \mapsto \unicode[STIX]{x1D707}_{\Bbbk }$
defines a semi-group isomorphism between
$\Bbbk \mapsto \unicode[STIX]{x1D707}_{\Bbbk }$
defines a semi-group isomorphism between
 $(\unicode[STIX]{x1D6E5},\oplus _{\unicode[STIX]{x1D6E5}})$
and
$(\unicode[STIX]{x1D6E5},\oplus _{\unicode[STIX]{x1D6E5}})$
and
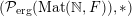 $({\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F)),\ast )$
. More precisely, we have
$({\mathcal{P}}_{\text{erg}}(\operatorname{Mat}(\mathbb{N},F)),\ast )$
. More precisely, we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}_{\Bbbk }\ast \unicode[STIX]{x1D707}_{\Bbbk ^{\prime }}=\unicode[STIX]{x1D707}_{\Bbbk \oplus _{\unicode[STIX]{x1D6E5}}\Bbbk ^{\prime }}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}_{\Bbbk }\ast \unicode[STIX]{x1D707}_{\Bbbk ^{\prime }}=\unicode[STIX]{x1D707}_{\Bbbk \oplus _{\unicode[STIX]{x1D6E5}}\Bbbk ^{\prime }}. & & \displaystyle \nonumber\end{eqnarray}$$
An Abelian semigroup structure
![]() $\oplus _{\unicode[STIX]{x1D6FA}}$
on
$\oplus _{\unicode[STIX]{x1D6FA}}$
on
![]() $\unicode[STIX]{x1D6FA}$
such that
$\unicode[STIX]{x1D6FA}$
such that
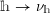 $h\rightarrow \unicode[STIX]{x1D708}_{h}$
defines semi-groups isomorphism between
$h\rightarrow \unicode[STIX]{x1D708}_{h}$
defines semi-groups isomorphism between
![]() $(\unicode[STIX]{x1D6FA},\oplus _{\unicode[STIX]{x1D6FA}})$
and
$(\unicode[STIX]{x1D6FA},\oplus _{\unicode[STIX]{x1D6FA}})$
and
 $({\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F)),\ast )$
is introduced in the same way.
$({\mathcal{P}}_{\text{erg}}(\operatorname{Sym}(\mathbb{N},F)),\ast )$
is introduced in the same way.
10 Proof of Proposition 4.5
In this section, we always assume that
![]() $F$
is non-dyadic. We will use the following change of variables in the integration over a local field. To introduce the formula for change of variables, we need the notion of
$F$
is non-dyadic. We will use the following change of variables in the integration over a local field. To introduce the formula for change of variables, we need the notion of
![]() $F$
-analytic functions. A function
$F$
-analytic functions. A function
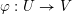 $\unicode[STIX]{x1D711}:U\rightarrow V$
, with
$\unicode[STIX]{x1D711}:U\rightarrow V$
, with
![]() $U,V$
open subsets of
$U,V$
open subsets of
![]() $F$
, is called
$F$
, is called
![]() $F$
-analytic, if in some neighbourhood of any point in
$F$
-analytic, if in some neighbourhood of any point in
![]() $U$
it is given by a convergent power series, it is called
$U$
it is given by a convergent power series, it is called
![]() $F$
-bi-analytic, if
$F$
-bi-analytic, if
![]() $\unicode[STIX]{x1D711}$
is invertible such that both
$\unicode[STIX]{x1D711}$
is invertible such that both
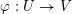 $\unicode[STIX]{x1D711}:U\rightarrow V$
and
$\unicode[STIX]{x1D711}:U\rightarrow V$
and
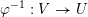 $\unicode[STIX]{x1D711}^{-1}:V\rightarrow U$
are
$\unicode[STIX]{x1D711}^{-1}:V\rightarrow U$
are
![]() $F$
-analytic.
$F$
-analytic.
Theorem 10.1 (Change of variables, see Schoissengeier [Reference SchoissengeierSch92]).
Let
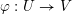 $\unicode[STIX]{x1D711}:U\rightarrow V$
be a
$\unicode[STIX]{x1D711}:U\rightarrow V$
be a
![]() $F$
-bi-analytic function. Then for any integrable function
$F$
-bi-analytic function. Then for any integrable function
 $f:U\rightarrow \mathbb{C}$
, we have
$f:U\rightarrow \mathbb{C}$
, we have
 $$\begin{eqnarray}\displaystyle \int _{U}f(\unicode[STIX]{x1D711}(x))|\unicode[STIX]{x1D711}^{\prime }(x)|\,dx=\int _{V}f(y)\,dy, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{U}f(\unicode[STIX]{x1D711}(x))|\unicode[STIX]{x1D711}^{\prime }(x)|\,dx=\int _{V}f(y)\,dy, & & \displaystyle \nonumber\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D711}^{\prime }$
is the formal derivative of
$\unicode[STIX]{x1D711}^{\prime }$
is the formal derivative of
![]() $\unicode[STIX]{x1D711}$
.
$\unicode[STIX]{x1D711}$
.
We will also need the following classical result from number theory concerning Gauss sums for finite field
![]() $\mathbf{F}_{q}$
. For the reader’s convenience, we include its standard proof in Appendix A.
$\mathbf{F}_{q}$
. For the reader’s convenience, we include its standard proof in Appendix A.
Denote by
![]() $\unicode[STIX]{x1D706}_{2}$
the unique multiplicative character for
$\unicode[STIX]{x1D706}_{2}$
the unique multiplicative character for
![]() $\mathbf{F}_{q}^{\times }$
of order
$\mathbf{F}_{q}^{\times }$
of order
![]() $2$
, that is,
$2$
, that is,
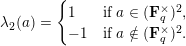 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}_{2}(a)=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }a\in (\mathbf{F}_{q}^{\times })^{2},\\ -1\quad & \text{if }a\notin (\mathbf{F}_{q}^{\times })^{2}.\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}_{2}(a)=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }a\in (\mathbf{F}_{q}^{\times })^{2},\\ -1\quad & \text{if }a\notin (\mathbf{F}_{q}^{\times })^{2}.\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
By convention, we extend the definition of
![]() $\unicode[STIX]{x1D706}_{2}$
to the whole finite field
$\unicode[STIX]{x1D706}_{2}$
to the whole finite field
![]() $\mathbf{F}_{q}$
by setting
$\mathbf{F}_{q}$
by setting
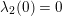 $\unicode[STIX]{x1D706}_{2}(0)=0$
.
$\unicode[STIX]{x1D706}_{2}(0)=0$
.
Denote the set of additive characters of
![]() $\mathbf{F}_{q}$
by
$\mathbf{F}_{q}$
by
![]() $\widehat{\mathbf{F}}_{q}$
. Given any
$\widehat{\mathbf{F}}_{q}$
. Given any
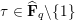 $\unicode[STIX]{x1D70F}\in \widehat{\mathbf{F}}_{q}\setminus \{1\}$
(that is,
$\unicode[STIX]{x1D70F}\in \widehat{\mathbf{F}}_{q}\setminus \{1\}$
(that is,
![]() $\unicode[STIX]{x1D70F}$
is a non-trivial character of
$\unicode[STIX]{x1D70F}$
is a non-trivial character of
![]() $\mathbf{F}_{q}$
) and any
$\mathbf{F}_{q}$
) and any
![]() $a\in \mathbf{F}_{q}$
, denote by
$a\in \mathbf{F}_{q}$
, denote by
![]() $\unicode[STIX]{x1D70F}_{a}$
the character of
$\unicode[STIX]{x1D70F}_{a}$
the character of
![]() $\mathbf{F}_{q}$
defined by
$\mathbf{F}_{q}$
defined by
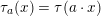 $\unicode[STIX]{x1D70F}_{a}(x)=\unicode[STIX]{x1D70F}(a\cdot x)$
. It is a standard fact that the map
$\unicode[STIX]{x1D70F}_{a}(x)=\unicode[STIX]{x1D70F}(a\cdot x)$
. It is a standard fact that the map
![]() $a\mapsto \unicode[STIX]{x1D70F}_{a}$
is an group isomorphism between
$a\mapsto \unicode[STIX]{x1D70F}_{a}$
is an group isomorphism between
![]() $\mathbf{F}_{q}$
and
$\mathbf{F}_{q}$
and
![]() $\widehat{\mathbf{F}}_{q}$
.
$\widehat{\mathbf{F}}_{q}$
.
Lemma 10.2 (Gauss sums).
Fix an element
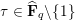 $\unicode[STIX]{x1D70F}\in \widehat{\mathbf{F}}_{q}\setminus \{1\}$
. Then for any
$\unicode[STIX]{x1D70F}\in \widehat{\mathbf{F}}_{q}\setminus \{1\}$
. Then for any
![]() $a\in \mathbf{F}_{q}^{\times }$
, we have
$a\in \mathbf{F}_{q}^{\times }$
, we have
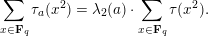 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}_{a}(x^{2})=\unicode[STIX]{x1D706}_{2}(a)\cdot \mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}(x^{2}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}_{a}(x^{2})=\unicode[STIX]{x1D706}_{2}(a)\cdot \mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}(x^{2}). & & \displaystyle\end{eqnarray}$$
Moreover,
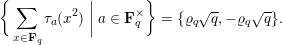 $$\begin{eqnarray}\displaystyle \bigg\{\mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}_{a}(x^{2})\biggm\vert\hspace{0.0pt}a\in \mathbf{F}_{q}^{\times }\bigg\}=\{\unicode[STIX]{x1D71A}_{q}\sqrt{q},-\unicode[STIX]{x1D71A}_{q}\sqrt{q}\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \bigg\{\mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}_{a}(x^{2})\biggm\vert\hspace{0.0pt}a\in \mathbf{F}_{q}^{\times }\bigg\}=\{\unicode[STIX]{x1D71A}_{q}\sqrt{q},-\unicode[STIX]{x1D71A}_{q}\sqrt{q}\}. & & \displaystyle \nonumber\end{eqnarray}$$
Denote by
![]() ${\mathcal{O}}_{F}^{\ast }$
the set of non-zero elements in
${\mathcal{O}}_{F}^{\ast }$
the set of non-zero elements in
![]() ${\mathcal{O}}_{F}$
and denote by
${\mathcal{O}}_{F}$
and denote by
![]() $({\mathcal{O}}_{F}^{\ast })^{2}$
the square elements in
$({\mathcal{O}}_{F}^{\ast })^{2}$
the square elements in
![]() ${\mathcal{O}}_{F}^{\ast }$
, that is,
${\mathcal{O}}_{F}^{\ast }$
, that is,
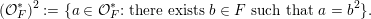 $$\begin{eqnarray}({\mathcal{O}}_{F}^{\ast })^{2}:=\{a\in {\mathcal{O}}_{F}^{\ast }:\text{ there exists }b\in F\text{ such that }a=b^{2}\}.\end{eqnarray}$$
$$\begin{eqnarray}({\mathcal{O}}_{F}^{\ast })^{2}:=\{a\in {\mathcal{O}}_{F}^{\ast }:\text{ there exists }b\in F\text{ such that }a=b^{2}\}.\end{eqnarray}$$
Denote the square function
![]() $x\mapsto x^{2}$
by
$x\mapsto x^{2}$
by
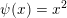 $\unicode[STIX]{x1D713}(x)=x^{2}$
.
$\unicode[STIX]{x1D713}(x)=x^{2}$
.
Proposition 10.3. There exists a partition
 $$\begin{eqnarray}{\mathcal{O}}_{F}^{\ast }=U_{1}\sqcup U_{2},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}_{F}^{\ast }=U_{1}\sqcup U_{2},\end{eqnarray}$$
such that the square function
 $\unicode[STIX]{x1D713}(x)=x^{2}$
induces two
$\unicode[STIX]{x1D713}(x)=x^{2}$
induces two
![]() $F$
-bi-analytic functions:
$F$
-bi-analytic functions:
 $$\begin{eqnarray}\unicode[STIX]{x1D713}:U_{i}\rightarrow ({\mathcal{O}}_{F}^{\ast })^{2},\quad i=1,2.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}:U_{i}\rightarrow ({\mathcal{O}}_{F}^{\ast })^{2},\quad i=1,2.\end{eqnarray}$$
Recall that by Lemma 2.5, the group
![]() $({\mathcal{O}}_{F}^{\times })^{2}$
is a disjoint union of
$({\mathcal{O}}_{F}^{\times })^{2}$
is a disjoint union of
 $(q-1)/2$
balls of radius
$(q-1)/2$
balls of radius
![]() $q^{-1}$
:
$q^{-1}$
:
 $$\begin{eqnarray}\displaystyle ({\mathcal{O}}_{F}^{\times })^{2}=\bigsqcup _{a\in ({\mathcal{C}}_{q}^{\times })^{2}}(a+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle ({\mathcal{O}}_{F}^{\times })^{2}=\bigsqcup _{a\in ({\mathcal{C}}_{q}^{\times })^{2}}(a+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}). & & \displaystyle \nonumber\end{eqnarray}$$
Lemma 10.4. Any element
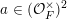 $a\in ({\mathcal{O}}_{F}^{\times })^{2}$
has two square roots
$a\in ({\mathcal{O}}_{F}^{\times })^{2}$
has two square roots
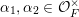 $\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2}\in {\mathcal{O}}_{F}^{\times }$
such that
$\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2}\in {\mathcal{O}}_{F}^{\times }$
such that
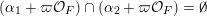 $(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})\cap (\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})=\emptyset$
and we have
$(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})\cap (\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})=\emptyset$
and we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})\subset a+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F},\quad i=1,2. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})\subset a+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F},\quad i=1,2. & & \displaystyle\end{eqnarray}$$
Moreover, we have two bijective maps:
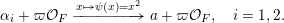 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}\xrightarrow[{}]{x\mapsto \unicode[STIX]{x1D713}(x)=x^{2}}a+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F},\quad i=1,2. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}\xrightarrow[{}]{x\mapsto \unicode[STIX]{x1D713}(x)=x^{2}}a+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F},\quad i=1,2. & & \displaystyle\end{eqnarray}$$
Proof. For any
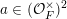 $a\in ({\mathcal{O}}_{F}^{\times })^{2}$
, there exist exactly two elements
$a\in ({\mathcal{O}}_{F}^{\times })^{2}$
, there exist exactly two elements
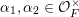 $\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2}\in {\mathcal{O}}_{F}^{\times }$
, such that
$\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2}\in {\mathcal{O}}_{F}^{\times }$
, such that
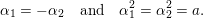 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{1}=-\unicode[STIX]{x1D6FC}_{2}\quad \text{and}\quad \unicode[STIX]{x1D6FC}_{1}^{2}=\unicode[STIX]{x1D6FC}_{2}^{2}=a.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{1}=-\unicode[STIX]{x1D6FC}_{2}\quad \text{and}\quad \unicode[STIX]{x1D6FC}_{1}^{2}=\unicode[STIX]{x1D6FC}_{2}^{2}=a.\end{eqnarray}$$
Hence
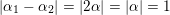 $|\unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D6FC}_{2}|=|2\unicode[STIX]{x1D6FC}|=|\unicode[STIX]{x1D6FC}|=1$
and
$|\unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D6FC}_{2}|=|2\unicode[STIX]{x1D6FC}|=|\unicode[STIX]{x1D6FC}|=1$
and
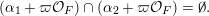 $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})\cap (\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})=\emptyset . & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})\cap (\unicode[STIX]{x1D6FC}_{2}+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})=\emptyset . & & \displaystyle \nonumber\end{eqnarray}$$
For any
![]() $z\in {\mathcal{O}}_{F}$
and
$z\in {\mathcal{O}}_{F}$
and
![]() $i=1,2$
, we have
$i=1,2$
, we have
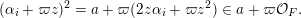 $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D71B}z)^{2}=a+\unicode[STIX]{x1D71B}(2z\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D71B}z^{2})\in a+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D71B}z)^{2}=a+\unicode[STIX]{x1D71B}(2z\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D71B}z^{2})\in a+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}. & & \displaystyle \nonumber\end{eqnarray}$$
This proves (104).
By Hensel’s lemma (24), for
![]() $i=1,2$
, if
$i=1,2$
, if
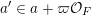 $a^{\prime }\in a+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
, then there exists
$a^{\prime }\in a+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
, then there exists
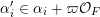 $\unicode[STIX]{x1D6FC}_{i}^{\prime }\in \unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
such that
$\unicode[STIX]{x1D6FC}_{i}^{\prime }\in \unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
such that
 $(\unicode[STIX]{x1D6FC}_{i}^{\prime })^{2}=a^{\prime }$
. Hence the maps (105) for
$(\unicode[STIX]{x1D6FC}_{i}^{\prime })^{2}=a^{\prime }$
. Hence the maps (105) for
![]() $i=1,2$
are both surjective. Now fix
$i=1,2$
are both surjective. Now fix
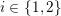 $i\in \{1,2\}$
. If
$i\in \{1,2\}$
. If
 $\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2}\in \unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
are such that
$\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2}\in \unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
are such that
![]() $\unicode[STIX]{x1D6FF}_{1}^{2}=\unicode[STIX]{x1D6FF}_{2}^{2}$
, then either
$\unicode[STIX]{x1D6FF}_{1}^{2}=\unicode[STIX]{x1D6FF}_{2}^{2}$
, then either
![]() $\unicode[STIX]{x1D6FF}_{1}=\unicode[STIX]{x1D6FF}_{2}$
or
$\unicode[STIX]{x1D6FF}_{1}=\unicode[STIX]{x1D6FF}_{2}$
or
 $\unicode[STIX]{x1D6FF}_{1}=-\unicode[STIX]{x1D6FF}_{2}$
. However, if
$\unicode[STIX]{x1D6FF}_{1}=-\unicode[STIX]{x1D6FF}_{2}$
. However, if
 $\unicode[STIX]{x1D6FF}_{1}=-\unicode[STIX]{x1D6FF}_{2}$
, then
$\unicode[STIX]{x1D6FF}_{1}=-\unicode[STIX]{x1D6FF}_{2}$
, then
 $$\begin{eqnarray}|\unicode[STIX]{x1D6FF}_{1}-\unicode[STIX]{x1D6FF}_{2}|=|2\unicode[STIX]{x1D6FF}_{1}|=|2||\unicode[STIX]{x1D6FF}_{1}|=1.\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D6FF}_{1}-\unicode[STIX]{x1D6FF}_{2}|=|2\unicode[STIX]{x1D6FF}_{1}|=|2||\unicode[STIX]{x1D6FF}_{1}|=1.\end{eqnarray}$$
This contradicts to the following estimate:
 $$\begin{eqnarray}|\unicode[STIX]{x1D6FF}_{1}-\unicode[STIX]{x1D6FF}_{2}|=|(\unicode[STIX]{x1D6FF}_{1}-\unicode[STIX]{x1D6FC}_{i})-(\unicode[STIX]{x1D6FF}_{2}-\unicode[STIX]{x1D6FC}_{i})|\leqslant \max (|\unicode[STIX]{x1D6FF}_{1}-\unicode[STIX]{x1D6FC}_{i}|,|\unicode[STIX]{x1D6FF}_{2}-\unicode[STIX]{x1D6FC}_{i}|)\leqslant q^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D6FF}_{1}-\unicode[STIX]{x1D6FF}_{2}|=|(\unicode[STIX]{x1D6FF}_{1}-\unicode[STIX]{x1D6FC}_{i})-(\unicode[STIX]{x1D6FF}_{2}-\unicode[STIX]{x1D6FC}_{i})|\leqslant \max (|\unicode[STIX]{x1D6FF}_{1}-\unicode[STIX]{x1D6FC}_{i}|,|\unicode[STIX]{x1D6FF}_{2}-\unicode[STIX]{x1D6FC}_{i}|)\leqslant q^{-1}.\end{eqnarray}$$
Hence we must have
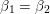 $\unicode[STIX]{x1D6FD}_{1}=\unicode[STIX]{x1D6FD}_{2}$
. This proves the injectivity of the map (105).◻
$\unicode[STIX]{x1D6FD}_{1}=\unicode[STIX]{x1D6FD}_{2}$
. This proves the injectivity of the map (105).◻
Proof of Proposition 10.3.
Clearly, we have
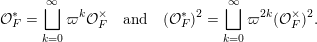 $$\begin{eqnarray}{\mathcal{O}}_{F}^{\ast }=\bigsqcup _{k=0}^{\infty }\unicode[STIX]{x1D71B}^{k}{\mathcal{O}}_{F}^{\times }\quad \text{and}\quad ({\mathcal{O}}_{F}^{\ast })^{2}=\bigsqcup _{k=0}^{\infty }\unicode[STIX]{x1D71B}^{2k}({\mathcal{O}}_{F}^{\times })^{2}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}_{F}^{\ast }=\bigsqcup _{k=0}^{\infty }\unicode[STIX]{x1D71B}^{k}{\mathcal{O}}_{F}^{\times }\quad \text{and}\quad ({\mathcal{O}}_{F}^{\ast })^{2}=\bigsqcup _{k=0}^{\infty }\unicode[STIX]{x1D71B}^{2k}({\mathcal{O}}_{F}^{\times })^{2}.\end{eqnarray}$$
For any
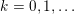 $k=0,1,\ldots$
, the square map
$k=0,1,\ldots$
, the square map
![]() $\unicode[STIX]{x1D711}$
maps
$\unicode[STIX]{x1D711}$
maps
![]() $\unicode[STIX]{x1D71B}^{k}{\mathcal{O}}_{F}^{\times }$
surjectively into
$\unicode[STIX]{x1D71B}^{k}{\mathcal{O}}_{F}^{\times }$
surjectively into
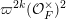 $\unicode[STIX]{x1D71B}^{2k}({\mathcal{O}}_{F}^{\times })^{2}$
. For proving Proposition 10.3, it suffices to prove that for any
$\unicode[STIX]{x1D71B}^{2k}({\mathcal{O}}_{F}^{\times })^{2}$
. For proving Proposition 10.3, it suffices to prove that for any
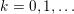 $k=0,1,\ldots$
, the set
$k=0,1,\ldots$
, the set
![]() $\unicode[STIX]{x1D71B}^{k}{\mathcal{O}}_{F}^{\times }$
can be divided into two parts, such that the square map
$\unicode[STIX]{x1D71B}^{k}{\mathcal{O}}_{F}^{\times }$
can be divided into two parts, such that the square map
![]() $\unicode[STIX]{x1D713}$
maps each part surjectively into
$\unicode[STIX]{x1D713}$
maps each part surjectively into
 $\unicode[STIX]{x1D71B}^{2k}({\mathcal{O}}_{F}^{\times })^{2}$
and the restriction of
$\unicode[STIX]{x1D71B}^{2k}({\mathcal{O}}_{F}^{\times })^{2}$
and the restriction of
![]() $\unicode[STIX]{x1D713}$
on each part is
$\unicode[STIX]{x1D713}$
on each part is
![]() $F$
-bi-analytic.
$F$
-bi-analytic.
We only need to prove this assertion for
![]() $k=0$
, since the other
$k=0$
, since the other
![]() $k\geqslant 1$
can be reduced to the case
$k\geqslant 1$
can be reduced to the case
![]() $k=0$
by a suitable dilation. By Lemma 10.4,
$k=0$
by a suitable dilation. By Lemma 10.4,
![]() ${\mathcal{O}}_{F}^{\times }$
can be divided into two parts
${\mathcal{O}}_{F}^{\times }$
can be divided into two parts
 ${\mathcal{O}}_{F}^{\times }=V_{1}\,\sqcup \,V_{2}$
, such that the two maps
${\mathcal{O}}_{F}^{\times }=V_{1}\,\sqcup \,V_{2}$
, such that the two maps
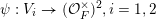 $\unicode[STIX]{x1D713}:V_{i}\rightarrow ({\mathcal{O}}_{F}^{\times })^{2},i=1,2$
are both bijective. The analyticity of the inverse maps
$\unicode[STIX]{x1D713}:V_{i}\rightarrow ({\mathcal{O}}_{F}^{\times })^{2},i=1,2$
are both bijective. The analyticity of the inverse maps
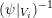 $(\unicode[STIX]{x1D713}|_{V_{i}})^{-1}$
follows from the Inverse Mapping Theorem in non-Archimedean setting, see, e.g., Abhyankar [Reference AbhyankarAbh64, p. 87].◻
$(\unicode[STIX]{x1D713}|_{V_{i}})^{-1}$
follows from the Inverse Mapping Theorem in non-Archimedean setting, see, e.g., Abhyankar [Reference AbhyankarAbh64, p. 87].◻
Corollary 10.5. For any integrable function
 $f:{\mathcal{O}}_{F}\rightarrow \mathbb{C}$
, we have
$f:{\mathcal{O}}_{F}\rightarrow \mathbb{C}$
, we have
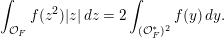 $$\begin{eqnarray}\displaystyle \int _{{\mathcal{O}}_{F}}f(z^{2})|z|\,dz=2\int _{({\mathcal{O}}_{F}^{\ast })^{2}}f(y)\,dy. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{{\mathcal{O}}_{F}}f(z^{2})|z|\,dz=2\int _{({\mathcal{O}}_{F}^{\ast })^{2}}f(y)\,dy. & & \displaystyle\end{eqnarray}$$
Proof. Note that since
![]() $F$
is non-dyadic,
$F$
is non-dyadic,
![]() $2\in {\mathcal{O}}_{F}^{\times }$
. Using the notation in Proposition 10.3 and Theorem 10.1
$2\in {\mathcal{O}}_{F}^{\times }$
. Using the notation in Proposition 10.3 and Theorem 10.1
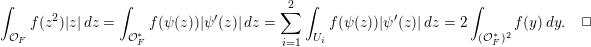 $$\begin{eqnarray}\displaystyle \int _{{\mathcal{O}}_{F}}f(z^{2})|z|\,dz=\int _{{\mathcal{O}}_{F}^{\ast }}f(\unicode[STIX]{x1D713}(z))|\unicode[STIX]{x1D713}^{\prime }(z)|\,dz=\mathop{\sum }_{i=1}^{2}\int _{U_{i}}f(\unicode[STIX]{x1D713}(z))|\unicode[STIX]{x1D713}^{\prime }(z)|\,dz=2\int _{({\mathcal{O}}_{F}^{\ast })^{2}}f(y)\,dy.\square & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{{\mathcal{O}}_{F}}f(z^{2})|z|\,dz=\int _{{\mathcal{O}}_{F}^{\ast }}f(\unicode[STIX]{x1D713}(z))|\unicode[STIX]{x1D713}^{\prime }(z)|\,dz=\mathop{\sum }_{i=1}^{2}\int _{U_{i}}f(\unicode[STIX]{x1D713}(z))|\unicode[STIX]{x1D713}^{\prime }(z)|\,dz=2\int _{({\mathcal{O}}_{F}^{\ast })^{2}}f(y)\,dy.\square & & \displaystyle \nonumber\end{eqnarray}$$
Proof of Proposition 4.5.
Property (i) in Proposition 4.5 is trivial. We proceed with the proof of properties (ii) and (iii).
For any
![]() $x\in F^{\ast }$
, define
$x\in F^{\ast }$
, define
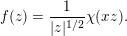 $$\begin{eqnarray}f(z)=\frac{1}{|z|^{1/2}}\unicode[STIX]{x1D712}(xz).\end{eqnarray}$$
$$\begin{eqnarray}f(z)=\frac{1}{|z|^{1/2}}\unicode[STIX]{x1D712}(xz).\end{eqnarray}$$
Then by substituting
![]() $f$
into the identity (106), we get
$f$
into the identity (106), we get
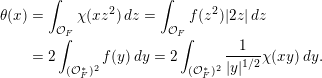 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(x) & = & \displaystyle \int _{{\mathcal{O}}_{F}}\unicode[STIX]{x1D712}(xz^{2})\,dz=\int _{{\mathcal{O}}_{F}}f(z^{2})|2z|\,dz\nonumber\\ \displaystyle & = & \displaystyle 2\int _{({\mathcal{O}}_{F}^{\ast })^{2}}f(y)\,dy=2\int _{({\mathcal{O}}_{F}^{\ast })^{2}}\frac{1}{|y|^{1/2}}\unicode[STIX]{x1D712}(xy)\,dy.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(x) & = & \displaystyle \int _{{\mathcal{O}}_{F}}\unicode[STIX]{x1D712}(xz^{2})\,dz=\int _{{\mathcal{O}}_{F}}f(z^{2})|2z|\,dz\nonumber\\ \displaystyle & = & \displaystyle 2\int _{({\mathcal{O}}_{F}^{\ast })^{2}}f(y)\,dy=2\int _{({\mathcal{O}}_{F}^{\ast })^{2}}\frac{1}{|y|^{1/2}}\unicode[STIX]{x1D712}(xy)\,dy.\end{eqnarray}$$
Define
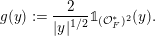 $$\begin{eqnarray}\displaystyle g(y):=\frac{2}{|y|^{1/2}}\unicode[STIX]{x1D7D9}_{({\mathcal{O}}_{F}^{\ast })^{2}}(y). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g(y):=\frac{2}{|y|^{1/2}}\unicode[STIX]{x1D7D9}_{({\mathcal{O}}_{F}^{\ast })^{2}}(y). & & \displaystyle\end{eqnarray}$$
It is a standard fact that
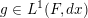 $g\in L^{1}(F,dx)$
. The identity (107) can now be rewritten as
$g\in L^{1}(F,dx)$
. The identity (107) can now be rewritten as
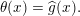 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(x)=\widehat{g}(x). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(x)=\widehat{g}(x). & & \displaystyle \nonumber\end{eqnarray}$$
Since we have
 $$\begin{eqnarray}\displaystyle ({\mathcal{O}}_{F}^{\ast })^{2}=\text{}\bigsqcup _{k=0}^{\infty }\unicode[STIX]{x1D71B}^{2k}({\mathcal{O}}_{F}^{\times })^{2}=\text{}\bigsqcup _{k=0}^{\infty }\text{}\bigsqcup _{a\in ({\mathcal{C}}_{q}^{\times })^{2}}(\unicode[STIX]{x1D71B}^{2k}a+\unicode[STIX]{x1D71B}^{2k+1}{\mathcal{O}}_{F}), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle ({\mathcal{O}}_{F}^{\ast })^{2}=\text{}\bigsqcup _{k=0}^{\infty }\unicode[STIX]{x1D71B}^{2k}({\mathcal{O}}_{F}^{\times })^{2}=\text{}\bigsqcup _{k=0}^{\infty }\text{}\bigsqcup _{a\in ({\mathcal{C}}_{q}^{\times })^{2}}(\unicode[STIX]{x1D71B}^{2k}a+\unicode[STIX]{x1D71B}^{2k+1}{\mathcal{O}}_{F}), & & \displaystyle \nonumber\end{eqnarray}$$
the function
![]() $g$
defined by formula (108) can be written in the form
$g$
defined by formula (108) can be written in the form
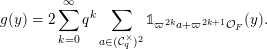 $$\begin{eqnarray}\displaystyle g(y)=2\mathop{\sum }_{k=0}^{\infty }q^{k}\mathop{\sum }_{a\in ({\mathcal{C}}_{q}^{\times })^{2}}\unicode[STIX]{x1D7D9}_{\unicode[STIX]{x1D71B}^{2k}a+\unicode[STIX]{x1D71B}^{2k+1}{\mathcal{O}}_{F}}(y). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g(y)=2\mathop{\sum }_{k=0}^{\infty }q^{k}\mathop{\sum }_{a\in ({\mathcal{C}}_{q}^{\times })^{2}}\unicode[STIX]{x1D7D9}_{\unicode[STIX]{x1D71B}^{2k}a+\unicode[STIX]{x1D71B}^{2k+1}{\mathcal{O}}_{F}}(y). & & \displaystyle \nonumber\end{eqnarray}$$
Consequently, we have
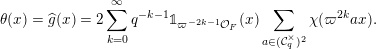 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(x)=\widehat{g}(x)=2\mathop{\sum }_{k=0}^{\infty }q^{-k-1}\unicode[STIX]{x1D7D9}_{\unicode[STIX]{x1D71B}^{-2k-1}{\mathcal{O}}_{F}}(x)\mathop{\sum }_{a\in ({\mathcal{C}}_{q}^{\times })^{2}}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{2k}ax). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(x)=\widehat{g}(x)=2\mathop{\sum }_{k=0}^{\infty }q^{-k-1}\unicode[STIX]{x1D7D9}_{\unicode[STIX]{x1D71B}^{-2k-1}{\mathcal{O}}_{F}}(x)\mathop{\sum }_{a\in ({\mathcal{C}}_{q}^{\times })^{2}}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{2k}ax). & & \displaystyle\end{eqnarray}$$
Property (ii) in Proposition 4.5
. If
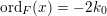 $\text{ord}_{F}(x)=-2k_{0}$
with
$\text{ord}_{F}(x)=-2k_{0}$
with
![]() $k_{0}\geqslant 1$
, then
$k_{0}\geqslant 1$
, then
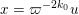 $x=\unicode[STIX]{x1D71B}^{-2k_{0}}u$
with
$x=\unicode[STIX]{x1D71B}^{-2k_{0}}u$
with
![]() $u\in {\mathcal{O}}_{F}^{\times }$
. Substituting
$u\in {\mathcal{O}}_{F}^{\times }$
. Substituting
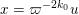 $x=\unicode[STIX]{x1D71B}^{-2k_{0}}u$
into (109) and using the assumption (28) on
$x=\unicode[STIX]{x1D71B}^{-2k_{0}}u$
into (109) and using the assumption (28) on
![]() $\unicode[STIX]{x1D712}$
, we obtain
$\unicode[STIX]{x1D712}$
, we obtain
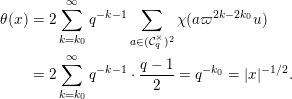 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(x) & = & \displaystyle 2\mathop{\sum }_{k=k_{0}}^{\infty }q^{-k-1}\mathop{\sum }_{a\in ({\mathcal{C}}_{q}^{\times })^{2}}\unicode[STIX]{x1D712}(a\unicode[STIX]{x1D71B}^{2k-2k_{0}}u)\nonumber\\ \displaystyle & = & \displaystyle 2\mathop{\sum }_{k=k_{0}}^{\infty }q^{-k-1}\cdot \frac{q-1}{2}=q^{-k_{0}}=|x|^{-1/2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(x) & = & \displaystyle 2\mathop{\sum }_{k=k_{0}}^{\infty }q^{-k-1}\mathop{\sum }_{a\in ({\mathcal{C}}_{q}^{\times })^{2}}\unicode[STIX]{x1D712}(a\unicode[STIX]{x1D71B}^{2k-2k_{0}}u)\nonumber\\ \displaystyle & = & \displaystyle 2\mathop{\sum }_{k=k_{0}}^{\infty }q^{-k-1}\cdot \frac{q-1}{2}=q^{-k_{0}}=|x|^{-1/2}.\nonumber\end{eqnarray}$$
We thus complete the proof of property (ii) in Proposition 4.5.
Property (iii) in Proposition 4.5
. If
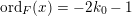 $\text{ord}_{F}(x)=-2k_{0}-1$
with
$\text{ord}_{F}(x)=-2k_{0}-1$
with
![]() $k_{0}\geqslant 0$
, then
$k_{0}\geqslant 0$
, then
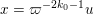 $x=\unicode[STIX]{x1D71B}^{-2k_{0}-1}u$
with
$x=\unicode[STIX]{x1D71B}^{-2k_{0}-1}u$
with
![]() $u\in {\mathcal{O}}_{F}^{\times }$
. By substituting
$u\in {\mathcal{O}}_{F}^{\times }$
. By substituting
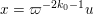 $x=\unicode[STIX]{x1D71B}^{-2k_{0}-1}u$
into (109) and using the fact that
$x=\unicode[STIX]{x1D71B}^{-2k_{0}-1}u$
into (109) and using the fact that
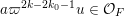 $a\unicode[STIX]{x1D71B}^{2k-2k_{0}-1}u\in {\mathcal{O}}_{F}$
for any
$a\unicode[STIX]{x1D71B}^{2k-2k_{0}-1}u\in {\mathcal{O}}_{F}$
for any
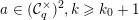 $a\in ({\mathcal{C}}_{q}^{\times })^{2},k\geqslant k_{0}+1$
and the assumption (28) on the choice of
$a\in ({\mathcal{C}}_{q}^{\times })^{2},k\geqslant k_{0}+1$
and the assumption (28) on the choice of
![]() $\unicode[STIX]{x1D712}$
, we obtain
$\unicode[STIX]{x1D712}$
, we obtain
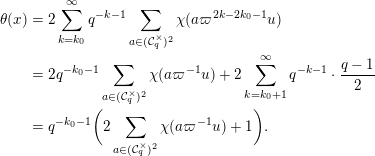 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(x) & = & \displaystyle 2\mathop{\sum }_{k=k_{0}}^{\infty }q^{-k-1}\mathop{\sum }_{a\in ({\mathcal{C}}_{q}^{\times })^{2}}\unicode[STIX]{x1D712}(a\unicode[STIX]{x1D71B}^{2k-2k_{0}-1}u)\nonumber\\ \displaystyle & = & \displaystyle 2q^{-k_{0}-1}\mathop{\sum }_{a\in ({\mathcal{C}}_{q}^{\times })^{2}}\unicode[STIX]{x1D712}(a\unicode[STIX]{x1D71B}^{-1}u)+2\mathop{\sum }_{k=k_{0}+1}^{\infty }q^{-k-1}\cdot \frac{q-1}{2}\nonumber\\ \displaystyle & = & \displaystyle q^{-k_{0}-1}\biggl(2\mathop{\sum }_{a\in ({\mathcal{C}}_{q}^{\times })^{2}}\unicode[STIX]{x1D712}(a\unicode[STIX]{x1D71B}^{-1}u)+1\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(x) & = & \displaystyle 2\mathop{\sum }_{k=k_{0}}^{\infty }q^{-k-1}\mathop{\sum }_{a\in ({\mathcal{C}}_{q}^{\times })^{2}}\unicode[STIX]{x1D712}(a\unicode[STIX]{x1D71B}^{2k-2k_{0}-1}u)\nonumber\\ \displaystyle & = & \displaystyle 2q^{-k_{0}-1}\mathop{\sum }_{a\in ({\mathcal{C}}_{q}^{\times })^{2}}\unicode[STIX]{x1D712}(a\unicode[STIX]{x1D71B}^{-1}u)+2\mathop{\sum }_{k=k_{0}+1}^{\infty }q^{-k-1}\cdot \frac{q-1}{2}\nonumber\\ \displaystyle & = & \displaystyle q^{-k_{0}-1}\biggl(2\mathop{\sum }_{a\in ({\mathcal{C}}_{q}^{\times })^{2}}\unicode[STIX]{x1D712}(a\unicode[STIX]{x1D71B}^{-1}u)+1\biggr).\end{eqnarray}$$
Now define a function
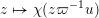 $z\mapsto \unicode[STIX]{x1D712}(z\unicode[STIX]{x1D71B}^{-1}u)$
for
$z\mapsto \unicode[STIX]{x1D712}(z\unicode[STIX]{x1D71B}^{-1}u)$
for
![]() $z\in {\mathcal{O}}_{F}$
. Since this function takes same value on every coset of
$z\in {\mathcal{O}}_{F}$
. Since this function takes same value on every coset of
![]() $\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
in
$\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
in
![]() ${\mathcal{O}}_{F}$
, we define a non-trivial additive character
${\mathcal{O}}_{F}$
, we define a non-trivial additive character
![]() $\unicode[STIX]{x1D70F}$
on
$\unicode[STIX]{x1D70F}$
on
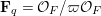 $\mathbf{F}_{q}={\mathcal{O}}_{F}/\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
by the following formula:
$\mathbf{F}_{q}={\mathcal{O}}_{F}/\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
by the following formula:
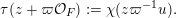 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}(z+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}):=\unicode[STIX]{x1D712}(z\unicode[STIX]{x1D71B}^{-1}u). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}(z+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}):=\unicode[STIX]{x1D712}(z\unicode[STIX]{x1D71B}^{-1}u). & & \displaystyle \nonumber\end{eqnarray}$$
Thus we have
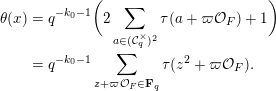 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(x) & = & \displaystyle q^{-k_{0}-1}\biggl(2\mathop{\sum }_{a\in ({\mathcal{C}}_{q}^{\times })^{2}}\unicode[STIX]{x1D70F}(a+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})+1\biggr)\nonumber\\ \displaystyle & = & \displaystyle q^{-k_{0}-1}\mathop{\sum }_{z+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}(z^{2}+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(x) & = & \displaystyle q^{-k_{0}-1}\biggl(2\mathop{\sum }_{a\in ({\mathcal{C}}_{q}^{\times })^{2}}\unicode[STIX]{x1D70F}(a+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})+1\biggr)\nonumber\\ \displaystyle & = & \displaystyle q^{-k_{0}-1}\mathop{\sum }_{z+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}(z^{2}+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}).\end{eqnarray}$$
Indeed, the second equality in (111) follows from the fact that for every element in
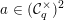 $a\in ({\mathcal{C}}_{q}^{\times })^{2}$
, there exist exactly two distinct square roots:
$a\in ({\mathcal{C}}_{q}^{\times })^{2}$
, there exist exactly two distinct square roots:
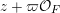 $z+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
and
$z+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
and
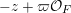 $-z+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
, that is,
$-z+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}$
, that is,
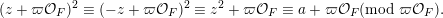 $$\begin{eqnarray}\displaystyle (z+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})^{2}\equiv (-z+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})^{2}\equiv z^{2}+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}\equiv a+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}(\operatorname{mod}\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (z+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})^{2}\equiv (-z+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})^{2}\equiv z^{2}+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}\equiv a+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}(\operatorname{mod}\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}). & & \displaystyle \nonumber\end{eqnarray}$$
Now by applying Theorem 10.2, we have
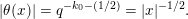 $$\begin{eqnarray}\displaystyle |\unicode[STIX]{x1D703}(x)|=q^{-k_{0}-(1/2)}=|x|^{-1/2}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\unicode[STIX]{x1D703}(x)|=q^{-k_{0}-(1/2)}=|x|^{-1/2}. & & \displaystyle \nonumber\end{eqnarray}$$
Now assume that
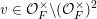 $v\in {\mathcal{O}}_{F}^{\times }\setminus ({\mathcal{O}}_{F}^{\times })^{2}$
. Then by changing
$v\in {\mathcal{O}}_{F}^{\times }\setminus ({\mathcal{O}}_{F}^{\times })^{2}$
. Then by changing
![]() $x$
to
$x$
to
![]() $vx$
(equivalently, changing
$vx$
(equivalently, changing
![]() $u$
to
$u$
to
![]() $v\cdot u$
) in (110) and applying (103), we obtain
$v\cdot u$
) in (110) and applying (103), we obtain
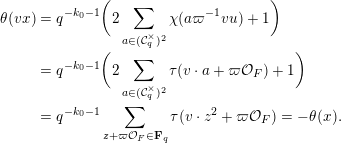 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(vx) & = & \displaystyle q^{-k_{0}-1}\biggl(2\mathop{\sum }_{a\in ({\mathcal{C}}_{q}^{\times })^{2}}\unicode[STIX]{x1D712}(a\unicode[STIX]{x1D71B}^{-1}vu)+1\biggr)\nonumber\\ \displaystyle & = & \displaystyle q^{-k_{0}-1}\biggl(2\mathop{\sum }_{a\in ({\mathcal{C}}_{q}^{\times })^{2}}\unicode[STIX]{x1D70F}(v\cdot a+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})+1\biggr)\nonumber\\ \displaystyle & = & \displaystyle q^{-k_{0}-1}\mathop{\sum }_{z+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}(v\cdot z^{2}+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})=-\unicode[STIX]{x1D703}(x).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(vx) & = & \displaystyle q^{-k_{0}-1}\biggl(2\mathop{\sum }_{a\in ({\mathcal{C}}_{q}^{\times })^{2}}\unicode[STIX]{x1D712}(a\unicode[STIX]{x1D71B}^{-1}vu)+1\biggr)\nonumber\\ \displaystyle & = & \displaystyle q^{-k_{0}-1}\biggl(2\mathop{\sum }_{a\in ({\mathcal{C}}_{q}^{\times })^{2}}\unicode[STIX]{x1D70F}(v\cdot a+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})+1\biggr)\nonumber\\ \displaystyle & = & \displaystyle q^{-k_{0}-1}\mathop{\sum }_{z+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F}\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}(v\cdot z^{2}+\unicode[STIX]{x1D71B}{\mathcal{O}}_{F})=-\unicode[STIX]{x1D703}(x).\nonumber\end{eqnarray}$$
We thus complete the proof of property (iii) in Proposition 4.5. ◻
Acknowledgements
We are deeply grateful to Grigori Olshanski for helpful discussions. We are also deeply grateful to Alexei Klimenko for useful discussions and for suggesting to us a simpler proof of Lemma 8.7 than our original one. We are deeply grateful to the anonymous referee for many very helpful suggestions on improving the presentation, in particular, for the suggestion to add § 2.1.2. This work started as ‘research in pairs’ at the CIRM, and we are deeply grateful to the CIRM for its warm hospitality.
Appendix A
A.1 Proof of Proposition 8.4
Lemma A.1. Let
![]() $m\in \mathbb{N}$
be a positive integer. Suppose that
$m\in \mathbb{N}$
be a positive integer. Suppose that
 $(\unicode[STIX]{x1D70E}_{n})_{n\in \mathbb{N}}$
is a sequence of probability measures on
$(\unicode[STIX]{x1D70E}_{n})_{n\in \mathbb{N}}$
is a sequence of probability measures on
![]() $F^{m}$
, such that
$F^{m}$
, such that
 $$\begin{eqnarray}\lim _{n\rightarrow \infty }\widehat{\unicode[STIX]{x1D70E}}_{n}(x)=\unicode[STIX]{x1D719}(x)\quad \text{for all }x\in F^{m}.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{n\rightarrow \infty }\widehat{\unicode[STIX]{x1D70E}}_{n}(x)=\unicode[STIX]{x1D719}(x)\quad \text{for all }x\in F^{m}.\end{eqnarray}$$
Assume that the function
![]() $\unicode[STIX]{x1D719}$
is continuous at the origin
$\unicode[STIX]{x1D719}$
is continuous at the origin
![]() $0\in F^{m}$
. Then there exists a probability measure
$0\in F^{m}$
. Then there exists a probability measure
![]() $\unicode[STIX]{x1D70E}$
on
$\unicode[STIX]{x1D70E}$
on
![]() $F^{m}$
, such that
$F^{m}$
, such that
 $\widehat{\unicode[STIX]{x1D70E}}(x)=\unicode[STIX]{x1D719}(x)$
and
$\widehat{\unicode[STIX]{x1D70E}}(x)=\unicode[STIX]{x1D719}(x)$
and
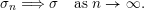 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}_{n}\Longrightarrow \unicode[STIX]{x1D70E}\quad \text{as }n\rightarrow \infty . & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}_{n}\Longrightarrow \unicode[STIX]{x1D70E}\quad \text{as }n\rightarrow \infty . & & \displaystyle\end{eqnarray}$$
Proof. First we show that under the hypothesis of Lemma A.1, the sequence of probability measures
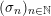 $(\unicode[STIX]{x1D70E}_{n})_{n\in \mathbb{N}}$
is tight. By using Fubini’s theorem and Lemma 3.3, for any
$(\unicode[STIX]{x1D70E}_{n})_{n\in \mathbb{N}}$
is tight. By using Fubini’s theorem and Lemma 3.3, for any
![]() $k\in \mathbb{N}$
, we have
$k\in \mathbb{N}$
, we have
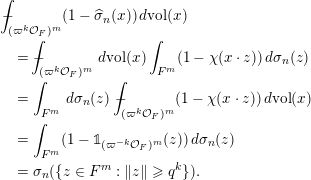 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x2A0D}_{(\unicode[STIX]{x1D71B}^{k}{\mathcal{O}}_{F})^{m}}(1-\widehat{\unicode[STIX]{x1D70E}}_{n}(x))\,d\text{vol}(x)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x2A0D}_{(\unicode[STIX]{x1D71B}^{k}{\mathcal{O}}_{F})^{m}}\,d\text{vol}(x)\int _{F^{m}}(1-\unicode[STIX]{x1D712}(x\cdot z))\,d\unicode[STIX]{x1D70E}_{n}(z)\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{F^{m}}\,d\unicode[STIX]{x1D70E}_{n}(z)~\unicode[STIX]{x2A0D}_{(\unicode[STIX]{x1D71B}^{k}{\mathcal{O}}_{F})^{m}}(1-\unicode[STIX]{x1D712}(x\cdot z))\,d\text{vol}(x)\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{F^{m}}(1-\unicode[STIX]{x1D7D9}_{(\unicode[STIX]{x1D71B}^{-k}{\mathcal{O}}_{F})^{m}}(z))\,d\unicode[STIX]{x1D70E}_{n}(z)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D70E}_{n}(\{z\in F^{m}:\Vert z\Vert \geqslant q^{k}\}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x2A0D}_{(\unicode[STIX]{x1D71B}^{k}{\mathcal{O}}_{F})^{m}}(1-\widehat{\unicode[STIX]{x1D70E}}_{n}(x))\,d\text{vol}(x)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x2A0D}_{(\unicode[STIX]{x1D71B}^{k}{\mathcal{O}}_{F})^{m}}\,d\text{vol}(x)\int _{F^{m}}(1-\unicode[STIX]{x1D712}(x\cdot z))\,d\unicode[STIX]{x1D70E}_{n}(z)\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{F^{m}}\,d\unicode[STIX]{x1D70E}_{n}(z)~\unicode[STIX]{x2A0D}_{(\unicode[STIX]{x1D71B}^{k}{\mathcal{O}}_{F})^{m}}(1-\unicode[STIX]{x1D712}(x\cdot z))\,d\text{vol}(x)\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{F^{m}}(1-\unicode[STIX]{x1D7D9}_{(\unicode[STIX]{x1D71B}^{-k}{\mathcal{O}}_{F})^{m}}(z))\,d\unicode[STIX]{x1D70E}_{n}(z)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D70E}_{n}(\{z\in F^{m}:\Vert z\Vert \geqslant q^{k}\}).\nonumber\end{eqnarray}$$
By bounded convergence theorem, we have
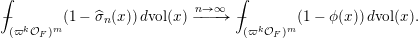 $$\begin{eqnarray}\unicode[STIX]{x2A0D}_{(\unicode[STIX]{x1D71B}^{k}{\mathcal{O}}_{F})^{m}}(1-\widehat{\unicode[STIX]{x1D70E}}_{n}(x))\,d\text{vol}(x)\xrightarrow[{}]{n\rightarrow \infty }\unicode[STIX]{x2A0D}_{(\unicode[STIX]{x1D71B}^{k}{\mathcal{O}}_{F})^{m}}(1-\unicode[STIX]{x1D719}(x))\,d\text{vol}(x).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2A0D}_{(\unicode[STIX]{x1D71B}^{k}{\mathcal{O}}_{F})^{m}}(1-\widehat{\unicode[STIX]{x1D70E}}_{n}(x))\,d\text{vol}(x)\xrightarrow[{}]{n\rightarrow \infty }\unicode[STIX]{x2A0D}_{(\unicode[STIX]{x1D71B}^{k}{\mathcal{O}}_{F})^{m}}(1-\unicode[STIX]{x1D719}(x))\,d\text{vol}(x).\end{eqnarray}$$
By assumption,
![]() $\unicode[STIX]{x1D719}$
is continuous at
$\unicode[STIX]{x1D719}$
is continuous at
![]() $0$
. Since
$0$
. Since
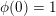 $\unicode[STIX]{x1D719}(0)=1$
, for any
$\unicode[STIX]{x1D719}(0)=1$
, for any
![]() $\unicode[STIX]{x1D700}>0$
there exists
$\unicode[STIX]{x1D700}>0$
there exists
![]() $k$
large enough such that
$k$
large enough such that
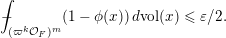 $$\begin{eqnarray}\unicode[STIX]{x2A0D}_{(\unicode[STIX]{x1D71B}^{k}{\mathcal{O}}_{F})^{m}}(1-\unicode[STIX]{x1D719}(x))\,d\text{vol}(x)\leqslant \unicode[STIX]{x1D700}/2.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2A0D}_{(\unicode[STIX]{x1D71B}^{k}{\mathcal{O}}_{F})^{m}}(1-\unicode[STIX]{x1D719}(x))\,d\text{vol}(x)\leqslant \unicode[STIX]{x1D700}/2.\end{eqnarray}$$
Fix such an integer
![]() $k\in \mathbb{N}$
, and choose
$k\in \mathbb{N}$
, and choose
![]() $n_{0}\in \mathbb{N}$
such that for any
$n_{0}\in \mathbb{N}$
such that for any
![]() $n\geqslant n_{0}$
, we have
$n\geqslant n_{0}$
, we have
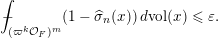 $$\begin{eqnarray}\unicode[STIX]{x2A0D}_{(\unicode[STIX]{x1D71B}^{k}{\mathcal{O}}_{F})^{m}}(1-\widehat{\unicode[STIX]{x1D70E}}_{n}(x))\,d\text{vol}(x)\leqslant \unicode[STIX]{x1D700}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2A0D}_{(\unicode[STIX]{x1D71B}^{k}{\mathcal{O}}_{F})^{m}}(1-\widehat{\unicode[STIX]{x1D70E}}_{n}(x))\,d\text{vol}(x)\leqslant \unicode[STIX]{x1D700}.\end{eqnarray}$$
That is, for any
![]() $n\geqslant n_{0}$
, we have
$n\geqslant n_{0}$
, we have
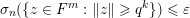 $\unicode[STIX]{x1D70E}_{n}(\{z\in F^{m}:\Vert z\Vert \geqslant q^{k}\})\leqslant \unicode[STIX]{x1D700}$
. Note that we may choose
$\unicode[STIX]{x1D70E}_{n}(\{z\in F^{m}:\Vert z\Vert \geqslant q^{k}\})\leqslant \unicode[STIX]{x1D700}$
. Note that we may choose
![]() $k^{\prime }$
large enough such that
$k^{\prime }$
large enough such that
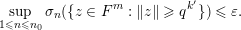 $$\begin{eqnarray}\sup _{1\leqslant n\leqslant n_{0}}\unicode[STIX]{x1D70E}_{n}(\{z\in F^{m}:\Vert z\Vert \geqslant q^{k^{\prime }}\})\leqslant \unicode[STIX]{x1D700}.\end{eqnarray}$$
$$\begin{eqnarray}\sup _{1\leqslant n\leqslant n_{0}}\unicode[STIX]{x1D70E}_{n}(\{z\in F^{m}:\Vert z\Vert \geqslant q^{k^{\prime }}\})\leqslant \unicode[STIX]{x1D700}.\end{eqnarray}$$
Hence by taking
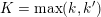 $K=\max (k,k^{\prime })$
, we get
$K=\max (k,k^{\prime })$
, we get
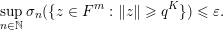 $$\begin{eqnarray}\sup _{n\in \mathbb{N}}\unicode[STIX]{x1D70E}_{n}(\{z\in F^{m}:\Vert z\Vert \geqslant q^{K}\})\leqslant \unicode[STIX]{x1D700}.\end{eqnarray}$$
$$\begin{eqnarray}\sup _{n\in \mathbb{N}}\unicode[STIX]{x1D70E}_{n}(\{z\in F^{m}:\Vert z\Vert \geqslant q^{K}\})\leqslant \unicode[STIX]{x1D700}.\end{eqnarray}$$
This proves the tightness of the sequence
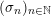 $(\unicode[STIX]{x1D70E}_{n})_{n\in \mathbb{N}}$
.
$(\unicode[STIX]{x1D70E}_{n})_{n\in \mathbb{N}}$
.
Now, for proving (A.1), we only need to show that any weakly convergent subsequence
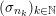 $(\unicode[STIX]{x1D70E}_{n_{k}})_{k\in \mathbb{N}}$
has the same limit point
$(\unicode[STIX]{x1D70E}_{n_{k}})_{k\in \mathbb{N}}$
has the same limit point
![]() $\unicode[STIX]{x1D70E}$
. Indeed, assume that
$\unicode[STIX]{x1D70E}$
. Indeed, assume that
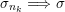 $\unicode[STIX]{x1D70E}_{n_{k}}\Longrightarrow \unicode[STIX]{x1D70E}$
. Then
$\unicode[STIX]{x1D70E}_{n_{k}}\Longrightarrow \unicode[STIX]{x1D70E}$
. Then
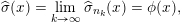 $$\begin{eqnarray}\widehat{\unicode[STIX]{x1D70E}}(x)=\lim _{k\rightarrow \infty }\widehat{\unicode[STIX]{x1D70E}}_{n_{k}}(x)=\unicode[STIX]{x1D719}(x),\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\unicode[STIX]{x1D70E}}(x)=\lim _{k\rightarrow \infty }\widehat{\unicode[STIX]{x1D70E}}_{n_{k}}(x)=\unicode[STIX]{x1D719}(x),\end{eqnarray}$$
which does not depend on the choice of the subsequence. We now complete the proof by using the fact that the measure is uniquely determined by its characteristic function. ◻
Lemma A.2. Let
![]() $m\in \mathbb{N}$
be a positive integer. Suppose that
$m\in \mathbb{N}$
be a positive integer. Suppose that
 $(\unicode[STIX]{x1D70E}_{n})_{n\in \mathbb{N}}$
and
$(\unicode[STIX]{x1D70E}_{n})_{n\in \mathbb{N}}$
and
![]() $\unicode[STIX]{x1D70E}$
are probability measures on
$\unicode[STIX]{x1D70E}$
are probability measures on
![]() $F^{m}$
. Then
$F^{m}$
. Then
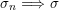 $\unicode[STIX]{x1D70E}_{n}\Longrightarrow \unicode[STIX]{x1D70E}$
as
$\unicode[STIX]{x1D70E}_{n}\Longrightarrow \unicode[STIX]{x1D70E}$
as
![]() $n\rightarrow \infty$
if and only if
$n\rightarrow \infty$
if and only if
![]() $\widehat{\unicode[STIX]{x1D70E}}_{n}(x)$
converges uniformly to
$\widehat{\unicode[STIX]{x1D70E}}_{n}(x)$
converges uniformly to
![]() $\widehat{\unicode[STIX]{x1D70E}}(x)$
for
$\widehat{\unicode[STIX]{x1D70E}}(x)$
for
![]() $x$
in any compact subset of
$x$
in any compact subset of
![]() $F^{m}$
.
$F^{m}$
.
Proof. Assume first that
![]() $\widehat{\unicode[STIX]{x1D70E}}_{n}(x)$
converges uniformly to
$\widehat{\unicode[STIX]{x1D70E}}_{n}(x)$
converges uniformly to
![]() $\widehat{\unicode[STIX]{x1D70E}}(x)$
on any compact subset of
$\widehat{\unicode[STIX]{x1D70E}}(x)$
on any compact subset of
![]() $F^{m}$
. Then, by Lemma A.1,
$F^{m}$
. Then, by Lemma A.1,
 $\unicode[STIX]{x1D70E}_{n}\Longrightarrow \unicode[STIX]{x1D70E}$
as
$\unicode[STIX]{x1D70E}_{n}\Longrightarrow \unicode[STIX]{x1D70E}$
as
![]() $n\rightarrow \infty$
.
$n\rightarrow \infty$
.
Conversely, assume that
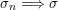 $\unicode[STIX]{x1D70E}_{n}\Longrightarrow \unicode[STIX]{x1D70E}$
as
$\unicode[STIX]{x1D70E}_{n}\Longrightarrow \unicode[STIX]{x1D70E}$
as
![]() $n\rightarrow \infty$
. For any
$n\rightarrow \infty$
. For any
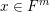 $x\in F^{m}$
, the function
$x\in F^{m}$
, the function
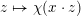 $z\mapsto \unicode[STIX]{x1D712}(x\cdot z)$
is bounded and continuous, hence
$z\mapsto \unicode[STIX]{x1D712}(x\cdot z)$
is bounded and continuous, hence
![]() $\widehat{\unicode[STIX]{x1D70E}}_{n}(x)$
converges to
$\widehat{\unicode[STIX]{x1D70E}}_{n}(x)$
converges to
![]() $\widehat{\unicode[STIX]{x1D70E}}(x)$
. By the Arzelà–Ascoli theorem, for proving the uniform convergence of
$\widehat{\unicode[STIX]{x1D70E}}(x)$
. By the Arzelà–Ascoli theorem, for proving the uniform convergence of
![]() $\widehat{\unicode[STIX]{x1D70E}}_{n}$
on any compact subset, it suffices to prove the sequence of characteristic functions
$\widehat{\unicode[STIX]{x1D70E}}_{n}$
on any compact subset, it suffices to prove the sequence of characteristic functions
![]() $\widehat{\unicode[STIX]{x1D70E}}_{n}$
is equicontinuous on any compact subset of
$\widehat{\unicode[STIX]{x1D70E}}_{n}$
is equicontinuous on any compact subset of
![]() $F^{m}$
. In fact, let us prove that these characteristic functions are equicontinuous on the whole space
$F^{m}$
. In fact, let us prove that these characteristic functions are equicontinuous on the whole space
![]() $F^{m}$
. For any
$F^{m}$
. For any
![]() $\unicode[STIX]{x1D700}>0$
, since the sequence
$\unicode[STIX]{x1D700}>0$
, since the sequence
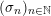 $(\unicode[STIX]{x1D70E}_{n})_{n\in \mathbb{N}}$
of probability measures is tight, there exists
$(\unicode[STIX]{x1D70E}_{n})_{n\in \mathbb{N}}$
of probability measures is tight, there exists
![]() $k\in \mathbb{N}$
large enough, such that
$k\in \mathbb{N}$
large enough, such that
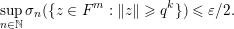 $$\begin{eqnarray}\sup _{n\in \mathbb{N}}\unicode[STIX]{x1D70E}_{n}(\{z\in F^{m}:\Vert z\Vert \geqslant q^{k}\})\leqslant \unicode[STIX]{x1D700}/2.\end{eqnarray}$$
$$\begin{eqnarray}\sup _{n\in \mathbb{N}}\unicode[STIX]{x1D70E}_{n}(\{z\in F^{m}:\Vert z\Vert \geqslant q^{k}\})\leqslant \unicode[STIX]{x1D700}/2.\end{eqnarray}$$
Now if
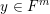 $y\in F^{m}$
is such that
$y\in F^{m}$
is such that
 $\Vert y\Vert \leqslant q^{-k}$
, then for any
$\Vert y\Vert \leqslant q^{-k}$
, then for any
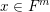 $x\in F^{m}$
, we have
$x\in F^{m}$
, we have
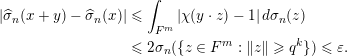 $$\begin{eqnarray}\displaystyle |\widehat{\unicode[STIX]{x1D70E}}_{n}(x+y)-\widehat{\unicode[STIX]{x1D70E}}_{n}(x)| & {\leqslant} & \displaystyle \int _{F^{m}}|\unicode[STIX]{x1D712}(y\cdot z)-1|\,d\unicode[STIX]{x1D70E}_{n}(z)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 2\unicode[STIX]{x1D70E}_{n}(\{z\in F^{m}:\Vert z\Vert \geqslant q^{k}\})\leqslant \unicode[STIX]{x1D700}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\widehat{\unicode[STIX]{x1D70E}}_{n}(x+y)-\widehat{\unicode[STIX]{x1D70E}}_{n}(x)| & {\leqslant} & \displaystyle \int _{F^{m}}|\unicode[STIX]{x1D712}(y\cdot z)-1|\,d\unicode[STIX]{x1D70E}_{n}(z)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 2\unicode[STIX]{x1D70E}_{n}(\{z\in F^{m}:\Vert z\Vert \geqslant q^{k}\})\leqslant \unicode[STIX]{x1D700}.\nonumber\end{eqnarray}$$
This proves the equicontinuity of the sequence
 $(\widehat{\unicode[STIX]{x1D70E}}_{n})_{n\in \mathbb{N}}$
and completes the proof of Lemma A.2.◻
$(\widehat{\unicode[STIX]{x1D70E}}_{n})_{n\in \mathbb{N}}$
and completes the proof of Lemma A.2.◻
Now we may prove Proposition 8.4 by using the following two points.
-
– Characteristic functions
 $\widehat{\unicode[STIX]{x1D707}}_{n}$
and
$\widehat{\unicode[STIX]{x1D707}}_{n}$
and
 $\widehat{\unicode[STIX]{x1D707}}$
are all invariant under the action of the group
$\widehat{\unicode[STIX]{x1D707}}$
are all invariant under the action of the group
 ${\mathcal{K}}(\infty )=\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
.
${\mathcal{K}}(\infty )=\operatorname{GL}(\infty ,{\mathcal{O}}_{F})\times \operatorname{GL}(\infty ,{\mathcal{O}}_{F})$
. -
– Checking the convergence
 $\unicode[STIX]{x1D707}_{n}\Longrightarrow \unicode[STIX]{x1D707}$
is equivalent to checking, for all
$\unicode[STIX]{x1D707}_{n}\Longrightarrow \unicode[STIX]{x1D707}$
is equivalent to checking, for all
 $r\in \mathbb{N}$
, the convergence
$r\in \mathbb{N}$
, the convergence
 $(\operatorname{Cut}_{r}^{\infty })_{\ast }\unicode[STIX]{x1D707}_{n}\Longrightarrow (\operatorname{Cut}_{r}^{\infty })_{\ast }\unicode[STIX]{x1D707}$
.
$(\operatorname{Cut}_{r}^{\infty })_{\ast }\unicode[STIX]{x1D707}_{n}\Longrightarrow (\operatorname{Cut}_{r}^{\infty })_{\ast }\unicode[STIX]{x1D707}$
.
A.2 Proof of Lemma 10.2
Let
![]() $a\in \mathbf{F}_{q}^{\times }$
. First we claim that
$a\in \mathbf{F}_{q}^{\times }$
. First we claim that
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}_{a}(x^{2})=\mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D706}_{2}(x)\unicode[STIX]{x1D70F}_{a}(x). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}_{a}(x^{2})=\mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D706}_{2}(x)\unicode[STIX]{x1D70F}_{a}(x). & & \displaystyle\end{eqnarray}$$
Indeed,
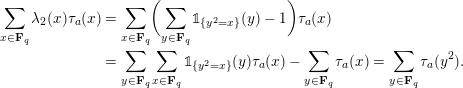 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D706}_{2}(x)\unicode[STIX]{x1D70F}_{a}(x) & = & \displaystyle \mathop{\sum }_{x\in \mathbf{F}_{q}}\biggl(\mathop{\sum }_{y\in \mathbf{F}_{q}}\unicode[STIX]{x1D7D9}_{\{y^{2}=x\}}(y)-1\biggr)\unicode[STIX]{x1D70F}_{a}(x)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{y\in \mathbf{F}_{q}}\mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D7D9}_{\{y^{2}=x\}}(y)\unicode[STIX]{x1D70F}_{a}(x)-\mathop{\sum }_{y\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}_{a}(x)=\mathop{\sum }_{y\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}_{a}(y^{2}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D706}_{2}(x)\unicode[STIX]{x1D70F}_{a}(x) & = & \displaystyle \mathop{\sum }_{x\in \mathbf{F}_{q}}\biggl(\mathop{\sum }_{y\in \mathbf{F}_{q}}\unicode[STIX]{x1D7D9}_{\{y^{2}=x\}}(y)-1\biggr)\unicode[STIX]{x1D70F}_{a}(x)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{y\in \mathbf{F}_{q}}\mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D7D9}_{\{y^{2}=x\}}(y)\unicode[STIX]{x1D70F}_{a}(x)-\mathop{\sum }_{y\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}_{a}(x)=\mathop{\sum }_{y\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}_{a}(y^{2}).\nonumber\end{eqnarray}$$
Consequently, by using the fact that
![]() $\unicode[STIX]{x1D706}_{2}$
is a multiplicative character of
$\unicode[STIX]{x1D706}_{2}$
is a multiplicative character of
![]() $\mathbf{F}_{q}^{\times }$
, we have
$\mathbf{F}_{q}^{\times }$
, we have
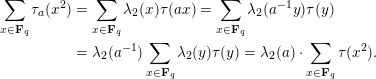 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}_{a}(x^{2}) & = & \displaystyle \mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D706}_{2}(x)\unicode[STIX]{x1D70F}(ax)=\mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D706}_{2}(a^{-1}y)\unicode[STIX]{x1D70F}(y)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D706}_{2}(a^{-1})\mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D706}_{2}(y)\unicode[STIX]{x1D70F}(y)=\unicode[STIX]{x1D706}_{2}(a)\cdot \mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}(x^{2}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}_{a}(x^{2}) & = & \displaystyle \mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D706}_{2}(x)\unicode[STIX]{x1D70F}(ax)=\mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D706}_{2}(a^{-1}y)\unicode[STIX]{x1D70F}(y)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D706}_{2}(a^{-1})\mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D706}_{2}(y)\unicode[STIX]{x1D70F}(y)=\unicode[STIX]{x1D706}_{2}(a)\cdot \mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}(x^{2}).\nonumber\end{eqnarray}$$
Hence the identity (103) is proved.
Let us now show that
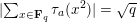 $|\!\sum _{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}_{a}(x^{2})|=\sqrt{q}$
. Indeed, by (A.2), we have
$|\!\sum _{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}_{a}(x^{2})|=\sqrt{q}$
. Indeed, by (A.2), we have
 $$\begin{eqnarray}\displaystyle \biggl|\mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}_{a}(x^{2})\biggr|^{2} & = & \displaystyle \mathop{\sum }_{x,y\in \mathbf{F}_{q}}\unicode[STIX]{x1D706}_{2}(x)\unicode[STIX]{x1D706}_{2}(y)\overline{\unicode[STIX]{x1D70F}_{a}(x)}\unicode[STIX]{x1D70F}_{a}(y)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{x\in \mathbf{F}_{q}^{\times }}\mathop{\sum }_{y\in \mathbf{F}_{q}}\unicode[STIX]{x1D706}_{2}(x)\unicode[STIX]{x1D706}_{2}(y)\unicode[STIX]{x1D70F}_{a}(y-x).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \biggl|\mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}_{a}(x^{2})\biggr|^{2} & = & \displaystyle \mathop{\sum }_{x,y\in \mathbf{F}_{q}}\unicode[STIX]{x1D706}_{2}(x)\unicode[STIX]{x1D706}_{2}(y)\overline{\unicode[STIX]{x1D70F}_{a}(x)}\unicode[STIX]{x1D70F}_{a}(y)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{x\in \mathbf{F}_{q}^{\times }}\mathop{\sum }_{y\in \mathbf{F}_{q}}\unicode[STIX]{x1D706}_{2}(x)\unicode[STIX]{x1D706}_{2}(y)\unicode[STIX]{x1D70F}_{a}(y-x).\nonumber\end{eqnarray}$$
For fixed
![]() $x\in \mathbf{F}_{q}^{\times }$
, by change of variables
$x\in \mathbf{F}_{q}^{\times }$
, by change of variables
![]() $y=xz$
, we get
$y=xz$
, we get
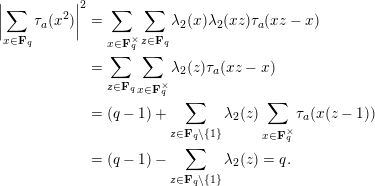 $$\begin{eqnarray}\displaystyle \biggl|\mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}_{a}(x^{2})\biggr|^{2} & = & \displaystyle \mathop{\sum }_{x\in \mathbf{F}_{q}^{\times }}\mathop{\sum }_{z\in \mathbf{F}_{q}}\unicode[STIX]{x1D706}_{2}(x)\unicode[STIX]{x1D706}_{2}(xz)\unicode[STIX]{x1D70F}_{a}(xz-x)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{z\in \mathbf{F}_{q}}\mathop{\sum }_{x\in \mathbf{F}_{q}^{\times }}\unicode[STIX]{x1D706}_{2}(z)\unicode[STIX]{x1D70F}_{a}(xz-x)\nonumber\\ \displaystyle & = & \displaystyle (q-1)+\mathop{\sum }_{z\in \mathbf{F}_{q}\setminus \{1\}}\unicode[STIX]{x1D706}_{2}(z)\mathop{\sum }_{x\in \mathbf{F}_{q}^{\times }}\unicode[STIX]{x1D70F}_{a}(x(z-1))\nonumber\\ \displaystyle & = & \displaystyle (q-1)-\mathop{\sum }_{z\in \mathbf{F}_{q}\setminus \{1\}}\unicode[STIX]{x1D706}_{2}(z)=q.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \biggl|\mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}_{a}(x^{2})\biggr|^{2} & = & \displaystyle \mathop{\sum }_{x\in \mathbf{F}_{q}^{\times }}\mathop{\sum }_{z\in \mathbf{F}_{q}}\unicode[STIX]{x1D706}_{2}(x)\unicode[STIX]{x1D706}_{2}(xz)\unicode[STIX]{x1D70F}_{a}(xz-x)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{z\in \mathbf{F}_{q}}\mathop{\sum }_{x\in \mathbf{F}_{q}^{\times }}\unicode[STIX]{x1D706}_{2}(z)\unicode[STIX]{x1D70F}_{a}(xz-x)\nonumber\\ \displaystyle & = & \displaystyle (q-1)+\mathop{\sum }_{z\in \mathbf{F}_{q}\setminus \{1\}}\unicode[STIX]{x1D706}_{2}(z)\mathop{\sum }_{x\in \mathbf{F}_{q}^{\times }}\unicode[STIX]{x1D70F}_{a}(x(z-1))\nonumber\\ \displaystyle & = & \displaystyle (q-1)-\mathop{\sum }_{z\in \mathbf{F}_{q}\setminus \{1\}}\unicode[STIX]{x1D706}_{2}(z)=q.\nonumber\end{eqnarray}$$
For concluding the proof, we need to show that
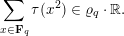 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}(x^{2})\in \unicode[STIX]{x1D71A}_{q}\cdot \mathbb{R}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}(x^{2})\in \unicode[STIX]{x1D71A}_{q}\cdot \mathbb{R}. & & \displaystyle\end{eqnarray}$$
However, if
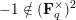 $-1\notin (\mathbf{F}_{q}^{\times })^{2}$
, then
$-1\notin (\mathbf{F}_{q}^{\times })^{2}$
, then
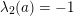 $\unicode[STIX]{x1D706}_{2}(a)=-1$
and we have
$\unicode[STIX]{x1D706}_{2}(a)=-1$
and we have
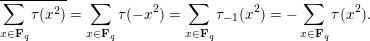 $$\begin{eqnarray}\displaystyle \overline{\mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}(x^{2})}=\mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}(-x^{2})=\mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}_{-1}(x^{2})=-\mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}(x^{2}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{\mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}(x^{2})}=\mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}(-x^{2})=\mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}_{-1}(x^{2})=-\mathop{\sum }_{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}(x^{2}). & & \displaystyle \nonumber\end{eqnarray}$$
It follows that
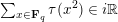 $\sum _{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}(x^{2})\in i\mathbb{R}$
. By similar argument, we can show that if
$\sum _{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}(x^{2})\in i\mathbb{R}$
. By similar argument, we can show that if
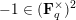 $-1\in (\mathbf{F}_{q}^{\times })^{2}$
, then
$-1\in (\mathbf{F}_{q}^{\times })^{2}$
, then
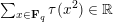 $\sum _{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}(x^{2})\in \mathbb{R}$
. By definition of
$\sum _{x\in \mathbf{F}_{q}}\unicode[STIX]{x1D70F}(x^{2})\in \mathbb{R}$
. By definition of
![]() $\unicode[STIX]{x1D71A}_{q}$
and the cyclic structure of the group
$\unicode[STIX]{x1D71A}_{q}$
and the cyclic structure of the group
![]() $\mathbf{F}_{q}^{\times }$
, we get the desired relation (A.3).
$\mathbf{F}_{q}^{\times }$
, we get the desired relation (A.3).