Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kebekus, Stefan
and
Kovács, Sándor J.
2010.
The structure of surfaces and threefolds mapping to the moduli stack of canonically polarized varieties.
Duke Mathematical Journal,
Vol. 155,
Issue. 1,
Hacking, Paul
and
Prokhorov, Yuri
2010.
Smoothable del Pezzo surfaces with quotient singularities.
Compositio Mathematica,
Vol. 146,
Issue. 1,
p.
169.
Greb, Daniel
Kebekus, Stefan
Kovács, Sándor J
and
Peternell, Thomas
2011.
Differential forms on log canonical spaces.
Publications mathématiques de l'IHÉS,
Vol. 114,
Issue. 1,
p.
87.
Jabbusch, Kelly
and
Kebekus, Stefan
2011.
Families over special base manifolds and a conjecture of Campana.
Mathematische Zeitschrift,
Vol. 269,
Issue. 3-4,
p.
847.
Namikawa, Yoshinori
2013.
On the structure of homogeneous symplectic varieties of complete intersection.
Inventiones mathematicae,
Vol. 193,
Issue. 1,
p.
159.
Araujo, Carolina
and
Druel, Stéphane
2013.
On Fano foliations.
Advances in Mathematics,
Vol. 238,
Issue. ,
p.
70.
Kebekus, Stefan
2013.
Pull-back morphisms for reflexive differential forms.
Advances in Mathematics,
Vol. 245,
Issue. ,
p.
78.
Druel, Stéphane
2014.
The Zariski-Lipman conjecture for log canonical spaces.
Bulletin of the London Mathematical Society,
Vol. 46,
Issue. 4,
p.
827.
Roulleau, Xavier
and
Rousseau, Erwan
2014.
Canonical surfaces with big cotangent bundle.
Duke Mathematical Journal,
Vol. 163,
Issue. 7,
Kebekus, Stefan
and
Peternell, Thomas
2016.
Foliation Theory in Algebraic Geometry.
p.
73.
Druel, Stéphane
2018.
A decomposition theorem for singular spaces with trivial canonical class of dimension at most five.
Inventiones mathematicae,
Vol. 211,
Issue. 1,
p.
245.
Sieder, Philip
2018.
Varieties with ample tangent sheaves.
manuscripta mathematica,
Vol. 157,
Issue. 1-2,
p.
257.
Graf, Patrick
2018.
Algebraic approximation of Kähler threefolds of Kodaira dimension zero.
Mathematische Annalen,
Vol. 371,
Issue. 1-2,
p.
487.
Cadorel, Benoît
Rousseau, Erwan
and
Taji, Behrouz
2019.
Hyperbolicity of singular spaces.
Journal de l’École polytechnique — Mathématiques,
Vol. 6,
Issue. ,
p.
1.
Claudon, Benoît
Höring, Andreas
and
Lin, Hsueh-Yung
2019.
The fundamental group of compact Kähler
threefolds.
Geometry & Topology,
Vol. 23,
Issue. 7,
p.
3233.
HEUVER, S.
2020.
EXTENSION THEOREMS FOR DIFFERENTIAL FORMS ON LOW-DIMENSIONAL GIT QUOTIENTS.
Transformation Groups,
Vol. 25,
Issue. 1,
p.
81.
Mistretta, Ernesto C.
2020.
Holomorphic symmetric differentials and a birational characterization of abelian varieties.
Mathematische Nachrichten,
Vol. 293,
Issue. 11,
p.
2175.
Kebekus, Stefan
and
Schnell, Christian
2021.
Extending holomorphic forms from the regular locus of a complex space to a resolution of singularities.
Journal of the American Mathematical Society,
Vol. 34,
Issue. 2,
p.
315.
Druel, Stéphane
2021.
Codimension 1 foliations with numerically trivial canonical class on singular spaces.
Duke Mathematical Journal,
Vol. 170,
Issue. 1,
Kawakami, Tatsuro
2021.
Bogomolov–Sommese type vanishing for globally F-regular threefolds.
Mathematische Zeitschrift,
Vol. 299,
Issue. 3-4,
p.
1821.

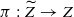 , we study the problem of extending the pull-back
, we study the problem of extending the pull-back 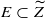 . For log canonical pairs and for certain values of
. For log canonical pairs and for certain values of 