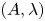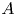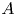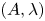1. Introduction
Let ![]() $(A,\lambda )$ be a principally polarized abelian variety of positive dimension over the field of algebraic numbers
$(A,\lambda )$ be a principally polarized abelian variety of positive dimension over the field of algebraic numbers ![]() $\bar {\mathbb {Q}}$. Let
$\bar {\mathbb {Q}}$. Let ![]() $\Theta$ be an effective symmetric ample divisor on
$\Theta$ be an effective symmetric ample divisor on ![]() $A$ that defines the principal polarization
$A$ that defines the principal polarization ![]() $\lambda$ and put
$\lambda$ and put ![]() $L=\mathcal {O}_A(\Theta )$.
$L=\mathcal {O}_A(\Theta )$.
We are interested in the Néron–Tate height ![]() $\mathrm {h}'_L(\Theta )$ of the cycle
$\mathrm {h}'_L(\Theta )$ of the cycle ![]() $\Theta$. The Néron–Tate height of higher-dimensional cycles was first constructed by Philippon [Reference PhilipponPhi91] and soon afterwards re-obtained using different methods by, among others, Gubler [Reference GublerGub94], Bost et al. [Reference BostBos96b, Reference Bost, Gillet and SouléBGS94] and Zhang [Reference ZhangZha95]. The Néron–Tate height
$\Theta$. The Néron–Tate height of higher-dimensional cycles was first constructed by Philippon [Reference PhilipponPhi91] and soon afterwards re-obtained using different methods by, among others, Gubler [Reference GublerGub94], Bost et al. [Reference BostBos96b, Reference Bost, Gillet and SouléBGS94] and Zhang [Reference ZhangZha95]. The Néron–Tate height ![]() $\mathrm {h}'_L(\Theta )$ is non-negative and is an invariant of the pair
$\mathrm {h}'_L(\Theta )$ is non-negative and is an invariant of the pair ![]() $(A,\lambda )$.
$(A,\lambda )$.
Another natural invariant of ![]() $(A,\lambda )$ is the stable Faltings height
$(A,\lambda )$ is the stable Faltings height ![]() $\mathrm {h}_F(A)$ of
$\mathrm {h}_F(A)$ of ![]() $A$ introduced by Faltings in [Reference FaltingsFal83] as a key tool in his proof of the Mordell conjecture. It is natural to ask how
$A$ introduced by Faltings in [Reference FaltingsFal83] as a key tool in his proof of the Mordell conjecture. It is natural to ask how ![]() $\mathrm {h}'_L(\Theta )$ and
$\mathrm {h}'_L(\Theta )$ and ![]() $\mathrm {h}_F(A)$ are related.
$\mathrm {h}_F(A)$ are related.
Let ![]() $k \subset \bar {\mathbb {Q}}$ be a number field and assume that the pair
$k \subset \bar {\mathbb {Q}}$ be a number field and assume that the pair ![]() $(A,L)$ is defined over
$(A,L)$ is defined over ![]() $k$. In [Reference AutissierAut06, Reference HindryHin93], Hindry and Autissier proved an identity relating
$k$. In [Reference AutissierAut06, Reference HindryHin93], Hindry and Autissier proved an identity relating ![]() $\mathrm {h}'_L(\Theta )$ and
$\mathrm {h}'_L(\Theta )$ and ![]() $\mathrm {h}_F(A)$ under the assumption that
$\mathrm {h}_F(A)$ under the assumption that ![]() $A$ has everywhere good reduction over
$A$ has everywhere good reduction over ![]() $k$. In order to state their result, we introduce some notation.
$k$. In order to state their result, we introduce some notation.
Let ![]() $s$ be a non-zero global section of
$s$ be a non-zero global section of ![]() $L$. Let
$L$. Let ![]() $M(k)_\infty$ denote the set of complex embeddings of
$M(k)_\infty$ denote the set of complex embeddings of ![]() $k$. For each
$k$. For each ![]() $v \in M(k)_\infty$, we put the standard euclidean metric on
$v \in M(k)_\infty$, we put the standard euclidean metric on ![]() $\bar {k}_v\cong \mathbb {C}$. Let
$\bar {k}_v\cong \mathbb {C}$. Let ![]() $\|\cdot \|_v$ be a canonical metric on
$\|\cdot \|_v$ be a canonical metric on ![]() $L_v=L \otimes \bar {k}_v$ (i.e. a smooth hermitian metric with a translation-invariant curvature form). We then consider the local archimedean invariants
$L_v=L \otimes \bar {k}_v$ (i.e. a smooth hermitian metric with a translation-invariant curvature form). We then consider the local archimedean invariants
where ![]() $\mu _{H,v}$ denotes the Haar measure on the complex torus
$\mu _{H,v}$ denotes the Haar measure on the complex torus ![]() $A(\bar {k}_v)$, normalized to give
$A(\bar {k}_v)$, normalized to give ![]() $A(\bar {k}_v)$ unit volume, and where
$A(\bar {k}_v)$ unit volume, and where
 \begin{equation} \|s\|_{v,L^2} = \biggl( \int_{A(\bar{k}_v)} \|s\|_v^2 \, d \mu_{H,v} \biggr)^{1/2} \end{equation}
\begin{equation} \|s\|_{v,L^2} = \biggl( \int_{A(\bar{k}_v)} \|s\|_v^2 \, d \mu_{H,v} \biggr)^{1/2} \end{equation}
is the ![]() $L^2$-norm of
$L^2$-norm of ![]() $s$. Here and below we denote by
$s$. Here and below we denote by ![]() $\log$ the natural logarithm. The real number
$\log$ the natural logarithm. The real number ![]() $I(A_v,\lambda _v)$ does not depend on the choice of
$I(A_v,\lambda _v)$ does not depend on the choice of ![]() $\Theta$ or
$\Theta$ or ![]() $s$ or
$s$ or ![]() $\|\cdot \|_v$ (we verify this in § 12.4). We have
$\|\cdot \|_v$ (we verify this in § 12.4). We have ![]() $I(A_v,\lambda _v) > 0$ by the Jensen inequality.
$I(A_v,\lambda _v) > 0$ by the Jensen inequality.
In [Reference AutissierAut06, Théorème 3.1] and [Reference HindryHin93, formula (A.17)], we find the following result. Assume that ![]() $A$ has everywhere good reduction over
$A$ has everywhere good reduction over ![]() $k$. Write
$k$. Write ![]() $\kappa _0=\log (\pi \sqrt {2})$ and let
$\kappa _0=\log (\pi \sqrt {2})$ and let ![]() $g=\dim (A)$. Then the equality
$g=\dim (A)$. Then the equality
 \begin{equation} \mathrm{h}_F(A) = 2g \, \mathrm{h}'_L(\Theta) - \kappa_0 \, g + \frac{2}{[k:\mathbb{Q}]} \sum_{v \in M(k)_\infty} I(A_v,\lambda_v) \end{equation}
\begin{equation} \mathrm{h}_F(A) = 2g \, \mathrm{h}'_L(\Theta) - \kappa_0 \, g + \frac{2}{[k:\mathbb{Q}]} \sum_{v \in M(k)_\infty} I(A_v,\lambda_v) \end{equation}
holds in ![]() $\mathbb {R}$. Formula (1.3) is obtained in both [Reference AutissierAut06, Reference HindryHin93] as the result of a calculation in Gillet–Soulé's arithmetic intersection theory, combined with Moret-Bailly's celebrated key formula for abelian schemes [Reference Moret-BaillyMor85].
$\mathbb {R}$. Formula (1.3) is obtained in both [Reference AutissierAut06, Reference HindryHin93] as the result of a calculation in Gillet–Soulé's arithmetic intersection theory, combined with Moret-Bailly's celebrated key formula for abelian schemes [Reference Moret-BaillyMor85].
In [Reference AutissierAut06, Question], it is asked whether an extension of (1.3) might hold for arbitrary principally polarized abelian varieties over ![]() $\bar {\mathbb {Q}}$ of the following shape. Assume that the abelian variety
$\bar {\mathbb {Q}}$ of the following shape. Assume that the abelian variety ![]() $A$ has semistable reduction over
$A$ has semistable reduction over ![]() $k$. Let
$k$. Let ![]() $M(k)_0$ denote the set of non-archimedean places of
$M(k)_0$ denote the set of non-archimedean places of ![]() $k$ and, for
$k$ and, for ![]() $v \in M(k)_0$, denote by
$v \in M(k)_0$, denote by ![]() $Nv$ the cardinality of the residue field at
$Nv$ the cardinality of the residue field at ![]() $v$. Then, for each
$v$. Then, for each ![]() $v \in M(k)_0$, there should exist a natural local invariant
$v \in M(k)_0$, there should exist a natural local invariant ![]() $\alpha _v \in \mathbb {Q}_{\geqslant 0}$ of
$\alpha _v \in \mathbb {Q}_{\geqslant 0}$ of ![]() $(A,\lambda )$ at
$(A,\lambda )$ at ![]() $v$ such that the equality
$v$ such that the equality
 \begin{equation} \mathrm{h}_F(A) = 2g \, \mathrm{h}'_L(\Theta) - \kappa_0 \, g + \frac{2}{[k:\mathbb{Q}]} \bigg( \sum_{v \in M(k)_0} \alpha_v \log Nv+\sum_{v \in M(k)_\infty} I(A_v,\lambda_v) \bigg) \end{equation}
\begin{equation} \mathrm{h}_F(A) = 2g \, \mathrm{h}'_L(\Theta) - \kappa_0 \, g + \frac{2}{[k:\mathbb{Q}]} \bigg( \sum_{v \in M(k)_0} \alpha_v \log Nv+\sum_{v \in M(k)_\infty} I(A_v,\lambda_v) \bigg) \end{equation}
holds in ![]() $\mathbb {R}$. The local invariant
$\mathbb {R}$. The local invariant ![]() $\alpha _v$ should vanish if and only if
$\alpha _v$ should vanish if and only if ![]() $A$ has good reduction at
$A$ has good reduction at ![]() $v$.
$v$.
In [Reference AutissierAut06], Autissier established the identity (1.4) for elliptic curves, for Jacobians of genus two curves and for arbitrary products of these. In [Reference de JongdJ18, Theorem 1.6], the first-named author exhibited natural ![]() $\alpha _v \in \mathbb {Q}_{\geqslant 0}$, and established (1.4), for all Jacobians and for arbitrary products of these. In both [Reference AutissierAut06, Reference de JongdJ18], the local non-archimedean invariants
$\alpha _v \in \mathbb {Q}_{\geqslant 0}$, and established (1.4), for all Jacobians and for arbitrary products of these. In both [Reference AutissierAut06, Reference de JongdJ18], the local non-archimedean invariants ![]() $\alpha _v$ are expressed in terms of the combinatorics of the dual graph of the underlying semistable curve at
$\alpha _v$ are expressed in terms of the combinatorics of the dual graph of the underlying semistable curve at ![]() $v$.
$v$.
1.1 Main result
The goal of this paper is to give a complete affirmative answer to [Reference AutissierAut06, Question]. This is established by combining Theorems A and B below.
Let ![]() $v \in M(k)_0$ be a non-archimedean place of
$v \in M(k)_0$ be a non-archimedean place of ![]() $k$. Let
$k$. Let ![]() $A^\mathrm {an}_v$ be the Berkovich analytification of
$A^\mathrm {an}_v$ be the Berkovich analytification of ![]() $A$ over the completion
$A$ over the completion ![]() $\mathbb {C}_v$ of the algebraic closure of the completion
$\mathbb {C}_v$ of the algebraic closure of the completion ![]() $k_v$ of
$k_v$ of ![]() $k$ at
$k$ at ![]() $v$. Similar to the archimedean setting, the analytification
$v$. Similar to the archimedean setting, the analytification ![]() $L_v^\mathrm {an}$ of
$L_v^\mathrm {an}$ of ![]() $L$ at
$L$ at ![]() $v$ can be endowed with a canonical metric
$v$ can be endowed with a canonical metric ![]() $\|\cdot \|_{v}$; we refer to § 5 for a review of the construction and main properties of such canonical metrics.
$\|\cdot \|_{v}$; we refer to § 5 for a review of the construction and main properties of such canonical metrics.
Analogous to (1.1), we define
where
is the supremum norm of ![]() $s$ and where
$s$ and where ![]() $\mu _{H,v}$ is the pushforward into
$\mu _{H,v}$ is the pushforward into ![]() $A_v^\mathrm {an}$ of the Haar measure of unit volume on the canonical skeleton of
$A_v^\mathrm {an}$ of the Haar measure of unit volume on the canonical skeleton of ![]() $A_v^\mathrm {an}$. The canonical skeleton of
$A_v^\mathrm {an}$. The canonical skeleton of ![]() $A_v^\mathrm {an}$ is a natural real torus contained in
$A_v^\mathrm {an}$ is a natural real torus contained in ![]() $A_v^\mathrm {an}$ and to which
$A_v^\mathrm {an}$ and to which ![]() $A_v^\mathrm {an}$ has a natural deformation retraction.
$A_v^\mathrm {an}$ has a natural deformation retraction.
The invariant ![]() $I(A_v,\lambda _v)$ is independent of the choice of
$I(A_v,\lambda _v)$ is independent of the choice of ![]() $L$, the choice of canonical metric
$L$, the choice of canonical metric ![]() $\|\cdot \|_v$ and the choice of global section
$\|\cdot \|_v$ and the choice of global section ![]() $s$ (we verify this in § 7.2). It follows from the definition that
$s$ (we verify this in § 7.2). It follows from the definition that ![]() $I(A_v,\lambda _v) \geqslant 0$ and equality is obtained if
$I(A_v,\lambda _v) \geqslant 0$ and equality is obtained if ![]() $A$ has good reduction at
$A$ has good reduction at ![]() $v$ (we verify this in § 10.1).
$v$ (we verify this in § 10.1).
Our first result is as follows.
Theorem A Let ![]() $(A,\lambda )$ be a principally polarized abelian variety over
$(A,\lambda )$ be a principally polarized abelian variety over ![]() $\bar {\mathbb {Q}}$. Assume that
$\bar {\mathbb {Q}}$. Assume that ![]() $A$ has semistable reduction over the number field
$A$ has semistable reduction over the number field ![]() $k$ and set
$k$ and set ![]() $g=\dim (A)$. Let
$g=\dim (A)$. Let ![]() $\Theta$ be a symmetric effective ample divisor on
$\Theta$ be a symmetric effective ample divisor on ![]() $A$ that defines the polarization
$A$ that defines the polarization ![]() $\lambda$ and put
$\lambda$ and put ![]() $L=\mathcal {O}_A(\Theta )$. Then the equality
$L=\mathcal {O}_A(\Theta )$. Then the equality
 \[ \mathrm{h}_F(A) = 2g \, \mathrm{h}'_L(\Theta) - \kappa_0 \, g + \frac{2}{[k:\mathbb{Q}]} \bigg( \sum_{v \in M(k)_0} I(A_v,\lambda_v) \log Nv \, + \sum_{v \in M(k)_\infty} I(A_v,\lambda_v) \bigg) \]
\[ \mathrm{h}_F(A) = 2g \, \mathrm{h}'_L(\Theta) - \kappa_0 \, g + \frac{2}{[k:\mathbb{Q}]} \bigg( \sum_{v \in M(k)_0} I(A_v,\lambda_v) \log Nv \, + \sum_{v \in M(k)_\infty} I(A_v,\lambda_v) \bigg) \]
holds in ![]() $\mathbb {R}$.
$\mathbb {R}$.
Note that the sum over ![]() $M(k)_0$ is indeed finite since
$M(k)_0$ is indeed finite since ![]() $A$ has good reduction at almost all
$A$ has good reduction at almost all ![]() $v \in M(k)_0$. An important ingredient in our proof of Theorem A is Moret-Bailly's well-known key formula [Reference Moret-BaillyMor85] or more precisely Bost's version [Reference BostBos96b] of the key formula in the number field setting that expresses the stable Faltings height of a polarized abelian variety in terms of a so-called Moret-Bailly model of it. We review the notion of Moret-Bailly models, and state Bost's version of the key formula, in § 13.
$v \in M(k)_0$. An important ingredient in our proof of Theorem A is Moret-Bailly's well-known key formula [Reference Moret-BaillyMor85] or more precisely Bost's version [Reference BostBos96b] of the key formula in the number field setting that expresses the stable Faltings height of a polarized abelian variety in terms of a so-called Moret-Bailly model of it. We review the notion of Moret-Bailly models, and state Bost's version of the key formula, in § 13.
1.2 Tropical moments
As we discuss next, for all non-archimedean places ![]() $v$ the term
$v$ the term ![]() $I(A_v,\lambda _v)$ can be expressed as a ‘tropical moment’ of a principally polarized tropical abelian variety canonically associated to
$I(A_v,\lambda _v)$ can be expressed as a ‘tropical moment’ of a principally polarized tropical abelian variety canonically associated to ![]() $A$ at
$A$ at ![]() $v$. This gives a concrete interpretation of the terms
$v$. This gives a concrete interpretation of the terms ![]() $I(A_v,\lambda _v)$ and makes it possible to calculate the terms
$I(A_v,\lambda _v)$ and makes it possible to calculate the terms ![]() $I(A_v,\lambda _v)$ explicitly.
$I(A_v,\lambda _v)$ explicitly.
A principally polarized tropical abelian variety is a tuple ![]() $(X,Y,\Phi,b)$, where
$(X,Y,\Phi,b)$, where ![]() $X, Y$ are finitely generated free abelian groups,
$X, Y$ are finitely generated free abelian groups, ![]() $\Phi \colon Y \xrightarrow {\sim } X$ is an isomorphism and
$\Phi \colon Y \xrightarrow {\sim } X$ is an isomorphism and ![]() $b \colon Y \times X \to \mathbb {R}$ is a bilinear map such that
$b \colon Y \times X \to \mathbb {R}$ is a bilinear map such that ![]() $b(\cdot,\Phi (\cdot ))$ is positive definite. When
$b(\cdot,\Phi (\cdot ))$ is positive definite. When ![]() $(X,Y,\Phi,b)$ is a principally polarized tropical abelian variety, we have a natural associated inclusion
$(X,Y,\Phi,b)$ is a principally polarized tropical abelian variety, we have a natural associated inclusion ![]() $Y \hookrightarrow X_\mathbb {R}^*$, where we write
$Y \hookrightarrow X_\mathbb {R}^*$, where we write ![]() $X_\mathbb {R}^* = \operatorname {Hom}(X,\mathbb {R})$. The cokernel
$X_\mathbb {R}^* = \operatorname {Hom}(X,\mathbb {R})$. The cokernel ![]() $\Sigma = X_\mathbb {R}^*/Y$ is a real torus and the bilinear map
$\Sigma = X_\mathbb {R}^*/Y$ is a real torus and the bilinear map ![]() $b$ naturally induces a norm
$b$ naturally induces a norm ![]() $\|\cdot \|$ on
$\|\cdot \|$ on ![]() $X_\mathbb {R}^*$. We usually simply write
$X_\mathbb {R}^*$. We usually simply write ![]() $\Sigma$ for a principally polarized tropical abelian variety if the underlying data
$\Sigma$ for a principally polarized tropical abelian variety if the underlying data ![]() $(X,Y,\Phi,b)$ are understood.
$(X,Y,\Phi,b)$ are understood.
Associated to the principally polarized tropical abelian variety ![]() $\Sigma$, we have its Voronoi polytope centered at the origin
$\Sigma$, we have its Voronoi polytope centered at the origin
The tropical moment of ![]() $\Sigma$ is defined to be the value of the integral
$\Sigma$ is defined to be the value of the integral
Here ![]() $\mu _L$ denotes the Lebesgue measure on
$\mu _L$ denotes the Lebesgue measure on ![]() $X_\mathbb {R}^*$, normalized to give
$X_\mathbb {R}^*$, normalized to give ![]() $\textrm {Vor}(0)$ unit volume.
$\textrm {Vor}(0)$ unit volume.
Let ![]() $v \in M(k)_0$ be a non-archimedean place of
$v \in M(k)_0$ be a non-archimedean place of ![]() $k$. By Raynaud's classical theory of non-archimedean uniformization, see for example [Reference Baker and RabinoffBR15, Reference Bosch and LütkebohmertBL91, Reference Foster, Rabinoff, Shokrieh and SotoFRSS18] or §§ 6–7, the canonical skeleton
$k$. By Raynaud's classical theory of non-archimedean uniformization, see for example [Reference Baker and RabinoffBR15, Reference Bosch and LütkebohmertBL91, Reference Foster, Rabinoff, Shokrieh and SotoFRSS18] or §§ 6–7, the canonical skeleton ![]() $\Sigma _v$ of the Berkovich analytic space
$\Sigma _v$ of the Berkovich analytic space ![]() $A_v^\mathrm {an}$ is naturally equipped with a structure of a principally polarized tropical abelian variety.
$A_v^\mathrm {an}$ is naturally equipped with a structure of a principally polarized tropical abelian variety.
Theorem B Let ![]() $v \in M(k)_0$. The following statements hold.
$v \in M(k)_0$. The following statements hold.
(a) The local non-archimedean term
 $I(A_v,\lambda _v)$ is equal to half the tropical moment of the canonical skeleton
$I(A_v,\lambda _v)$ is equal to half the tropical moment of the canonical skeleton  $\Sigma _v$.
$\Sigma _v$.(b) The term
 $I(A_v,\lambda _v)$ vanishes if and only if
$I(A_v,\lambda _v)$ vanishes if and only if  $A$ has good reduction at
$A$ has good reduction at  $v$.
$v$.(c)
 $I(A_v,\lambda _v)$ is a rational number.
$I(A_v,\lambda _v)$ is a rational number.
Parts (b) and (c) of the theorem follow easily from part (a). Indeed, it is clear that the tropical moment of ![]() $\Sigma _v$ vanishes if and only if
$\Sigma _v$ vanishes if and only if ![]() $\Sigma _v$ is a point. The latter holds if and only if
$\Sigma _v$ is a point. The latter holds if and only if ![]() $A$ has good reduction at
$A$ has good reduction at ![]() $v$.
$v$.
Next, the underlying bilinear form of the principally polarized tropical abelian variety ![]() $\Sigma _v$ is defined in terms of the discrete valuation corresponding to
$\Sigma _v$ is defined in terms of the discrete valuation corresponding to ![]() $v$ and is, in particular,
$v$ and is, in particular, ![]() $\mathbb {Z}$-valued. This implies that the Voronoi polytope associated to
$\mathbb {Z}$-valued. This implies that the Voronoi polytope associated to ![]() $\Sigma _v$ is a rational polyhedron and this gives that the tropical moment of
$\Sigma _v$ is a rational polyhedron and this gives that the tropical moment of ![]() $\Sigma _v$ is a rational number.
$\Sigma _v$ is a rational number.
In the following we discuss a few applications of Theorems A and B.
1.3 Lower bounds for the stable Faltings height
First, as ![]() $\mathrm {h}'_L(\Theta )$ is non-negative, Theorem A immediately implies the following lower bound for the stable Faltings height of
$\mathrm {h}'_L(\Theta )$ is non-negative, Theorem A immediately implies the following lower bound for the stable Faltings height of ![]() $A$.
$A$.
Corollary Assume that ![]() $A$ has semistable reduction over the number field
$A$ has semistable reduction over the number field ![]() $k$ and set
$k$ and set ![]() $g=\dim (A)$. Then the lower bound
$g=\dim (A)$. Then the lower bound
 \begin{equation} \mathrm{h}_F(A) \geqslant - \kappa_0 \, g + \frac{2}{[k:\mathbb{Q}]} \bigg(\sum_{v \in M(k)_0} I(A_v,\lambda_v) \log Nv + \sum_{v \in M(k)_\infty} I(A_v,\lambda_v) \bigg) \end{equation}
\begin{equation} \mathrm{h}_F(A) \geqslant - \kappa_0 \, g + \frac{2}{[k:\mathbb{Q}]} \bigg(\sum_{v \in M(k)_0} I(A_v,\lambda_v) \log Nv + \sum_{v \in M(k)_\infty} I(A_v,\lambda_v) \bigg) \end{equation}holds.
With the terms ![]() $I(A_v,\lambda _v)$ interpreted as half the tropical moments of the canonical skeleta
$I(A_v,\lambda _v)$ interpreted as half the tropical moments of the canonical skeleta ![]() $\Sigma _v$, Wagener obtained the lower bound (1.7) in his 2016 PhD thesis [Reference WagenerWag16, Théorème A]. As for each
$\Sigma _v$, Wagener obtained the lower bound (1.7) in his 2016 PhD thesis [Reference WagenerWag16, Théorème A]. As for each ![]() $v \in M(k)_0$ we have
$v \in M(k)_0$ we have ![]() $I(A_v,\lambda _v) \geqslant 0$, the lower bound (1.7) improves upon the well-known lower bound
$I(A_v,\lambda _v) \geqslant 0$, the lower bound (1.7) improves upon the well-known lower bound
 \begin{equation} \mathrm{h}_F(A) \geqslant - \kappa_0 \, g + \frac{2}{[k:\mathbb{Q}]} \sum_{v \in M(k)_\infty} I(A_v,\lambda_v) \end{equation}
\begin{equation} \mathrm{h}_F(A) \geqslant - \kappa_0 \, g + \frac{2}{[k:\mathbb{Q}]} \sum_{v \in M(k)_\infty} I(A_v,\lambda_v) \end{equation}
for ![]() $\mathrm {h}_F(A)$ due to Bost [Reference BostBos96a, Reference Gaudron and RémondGR14]. We recall that (1.8) can in turn be used to obtain refinements of Masser's ‘matrix lemma’ [Reference MasserMas85]. See, for example, [Reference AutissierAut13] and the references therein.
$\mathrm {h}_F(A)$ due to Bost [Reference BostBos96a, Reference Gaudron and RémondGR14]. We recall that (1.8) can in turn be used to obtain refinements of Masser's ‘matrix lemma’ [Reference MasserMas85]. See, for example, [Reference AutissierAut13] and the references therein.
1.4 Elliptic curves
Let ![]() $\Sigma$ be a circle of circumference
$\Sigma$ be a circle of circumference ![]() $\sqrt {\ell }$. A small calculation yields that the tropical moment of
$\sqrt {\ell }$. A small calculation yields that the tropical moment of ![]() $\Sigma$ is equal to
$\Sigma$ is equal to ![]() $\frac {1}{12}\ell$. This has the following application. Let
$\frac {1}{12}\ell$. This has the following application. Let ![]() $(A,\lambda )$ be an elliptic curve with semistable reduction over the number field
$(A,\lambda )$ be an elliptic curve with semistable reduction over the number field ![]() $k$. Let
$k$. Let ![]() $\Theta$ be an effective symmetric divisor on
$\Theta$ be an effective symmetric divisor on ![]() $A$ that defines the principal polarization
$A$ that defines the principal polarization ![]() $\lambda$ and put
$\lambda$ and put ![]() $L=\mathcal {O}_A(\Theta )$. Then
$L=\mathcal {O}_A(\Theta )$. Then ![]() $\Theta$ is a two-torsion point of
$\Theta$ is a two-torsion point of ![]() $A$, which gives
$A$, which gives ![]() $\mathrm {h}'_L(\Theta )=0$. If
$\mathrm {h}'_L(\Theta )=0$. If ![]() $A$ has bad reduction at
$A$ has bad reduction at ![]() $v \in M(k)_0$, then
$v \in M(k)_0$, then ![]() $\Sigma _v$ is a circle of circumference
$\Sigma _v$ is a circle of circumference ![]() $\sqrt {\operatorname {ord}_v \Delta _v}$, where
$\sqrt {\operatorname {ord}_v \Delta _v}$, where ![]() $\Delta _v$ is the minimal discriminant of
$\Delta _v$ is the minimal discriminant of ![]() $A$ at
$A$ at ![]() $v$. We conclude using Theorem B that
$v$. We conclude using Theorem B that ![]() $I(A_v,\lambda _v)=\frac {1}{24}\operatorname {ord}_v \Delta _v$ if
$I(A_v,\lambda _v)=\frac {1}{24}\operatorname {ord}_v \Delta _v$ if ![]() $v \in M(k)_0$.
$v \in M(k)_0$.
Next, let ![]() $v \in M(k)_\infty$ and write
$v \in M(k)_\infty$ and write ![]() $A(\bar {k}_v) = \mathbb {C}/(\mathbb {Z}+\tau _v \mathbb {Z})$, where
$A(\bar {k}_v) = \mathbb {C}/(\mathbb {Z}+\tau _v \mathbb {Z})$, where ![]() $\tau _v \in \mathbb {H}$ with
$\tau _v \in \mathbb {H}$ with ![]() $\mathbb {H}$ the Siegel upper half plane. For
$\mathbb {H}$ the Siegel upper half plane. For ![]() $\tau \in \mathbb {H}$, we set
$\tau \in \mathbb {H}$, we set ![]() $q={e}^{2\pi \sqrt {-1}\tau }$ and let
$q={e}^{2\pi \sqrt {-1}\tau }$ and let ![]() $\Delta (\tau )=q \prod _{n=1}^\infty (1-q^n)^{24}$ be the usual discriminant modular form. By [Reference AutissierAut06, Proposition 2.1], we have
$\Delta (\tau )=q \prod _{n=1}^\infty (1-q^n)^{24}$ be the usual discriminant modular form. By [Reference AutissierAut06, Proposition 2.1], we have ![]() $I(A_v,\lambda _v) = -\frac {1}{24} \log (|\Delta (\tau _v)|(2 \,\mathrm {Im}\, \tau _v)^6)$.
$I(A_v,\lambda _v) = -\frac {1}{24} \log (|\Delta (\tau _v)|(2 \,\mathrm {Im}\, \tau _v)^6)$.
Let ![]() $\mathrm {h}_F(A)$ be the stable Faltings height of
$\mathrm {h}_F(A)$ be the stable Faltings height of ![]() $A$. Applying Theorem A, we find that
$A$. Applying Theorem A, we find that
This recovers the well-known Faltings–Silverman formula for the stable Faltings height of an elliptic curve; cf. [Reference DeligneDel85, Exemple 1.4 and Remarque 1.5] or [Reference FaltingsFal84, Theorem 7] or [Reference SilvermanSil84, Proposition 1.1].
1.5 Jacobians
Let ![]() $\Gamma$ be a compact connected metric graph. Let
$\Gamma$ be a compact connected metric graph. Let ![]() $r(p,q)$ denote the effective resistance between points
$r(p,q)$ denote the effective resistance between points ![]() $p, q \in \Gamma$. Fix
$p, q \in \Gamma$. Fix ![]() $q \in \Gamma$ and set
$q \in \Gamma$ and set ![]() $f(x) = \frac {1}{2}r(x,q)$. Following [Reference Baker and FaberBF06, Reference Baker and RumelyBR07], we set
$f(x) = \frac {1}{2}r(x,q)$. Following [Reference Baker and FaberBF06, Reference Baker and RumelyBR07], we set
The real number ![]() $\tau (\Gamma )$ is independent of the choice of
$\tau (\Gamma )$ is independent of the choice of ![]() $q$. Let
$q$. Let ![]() $\operatorname {Jac}(\Gamma )$ denote the tropical Jacobian of
$\operatorname {Jac}(\Gamma )$ denote the tropical Jacobian of ![]() $\Gamma$ as in [Reference Mikhalkin and ZharkovMZ08]. Then
$\Gamma$ as in [Reference Mikhalkin and ZharkovMZ08]. Then ![]() $\operatorname {Jac}(\Gamma )$ is a principally polarized tropical abelian variety canonically associated to
$\operatorname {Jac}(\Gamma )$ is a principally polarized tropical abelian variety canonically associated to ![]() $\Gamma$. We have shown in [Reference de Jong and ShokriehdJS18, Theorem B] that its tropical moment is equal to
$\Gamma$. We have shown in [Reference de Jong and ShokriehdJS18, Theorem B] that its tropical moment is equal to
where ![]() $\ell (\Gamma )$ is the total length of
$\ell (\Gamma )$ is the total length of ![]() $\Gamma$ and
$\Gamma$ and ![]() $\tau (\Gamma )$ is the tau invariant of
$\tau (\Gamma )$ is the tau invariant of ![]() $\Gamma$ as in (1.9).
$\Gamma$ as in (1.9).
This leads to the following application. Let ![]() $C$ be a smooth projective geometrically connected curve of genus
$C$ be a smooth projective geometrically connected curve of genus ![]() $g \geqslant 2$ with semistable reduction over
$g \geqslant 2$ with semistable reduction over ![]() $k$ and let
$k$ and let ![]() $(J,\lambda )$ be its Jacobian. Let
$(J,\lambda )$ be its Jacobian. Let ![]() $v \in M(k)_0$. Let
$v \in M(k)_0$. Let ![]() $\Gamma _v$ be the dual graph of the geometric special fiber
$\Gamma _v$ be the dual graph of the geometric special fiber ![]() $\mathcal {C}_{\bar {v}}$ of the minimal regular model
$\mathcal {C}_{\bar {v}}$ of the minimal regular model ![]() $\mathcal {C}$ of
$\mathcal {C}$ of ![]() $C$ at
$C$ at ![]() $v$, endowed with its canonical metric structure as in [Reference ZhangZha93]. In particular,
$v$, endowed with its canonical metric structure as in [Reference ZhangZha93]. In particular, ![]() $\Gamma _v$ is a compact connected metric graph and its total length
$\Gamma _v$ is a compact connected metric graph and its total length ![]() $\ell (\Gamma _v)$ equals the number of singular points of
$\ell (\Gamma _v)$ equals the number of singular points of ![]() $\mathcal {C}_{\bar {v}}$. By [Reference Faltings and ChaiFC90, Theorem III.8.3], the tropical Jacobian
$\mathcal {C}_{\bar {v}}$. By [Reference Faltings and ChaiFC90, Theorem III.8.3], the tropical Jacobian ![]() $\operatorname {Jac}(\Gamma _v)$ of
$\operatorname {Jac}(\Gamma _v)$ of ![]() $\Gamma _v$ is isometric with the principally polarized tropical abelian variety
$\Gamma _v$ is isometric with the principally polarized tropical abelian variety ![]() $\Sigma _v$ determined by
$\Sigma _v$ determined by ![]() $(J,\lambda )$ at
$(J,\lambda )$ at ![]() $v$.
$v$.
Using (1.10) and Theorem B, the formula from Theorem A specializes into the formula
 \begin{equation} \mathrm{h}_F(J) = 2g \, \mathrm{h}'_L(\Theta) - \kappa_0 \, g + \frac{1}{[k:\mathbb{Q}]} \sum_{v \in M(k)_0} \bigl(\tfrac{1}{8}\ell(\Gamma_v) -\tfrac{1}{2}\tau(\Gamma_v) \bigr) \log Nv +
\frac{2}{[k:\mathbb{Q}]} \sum_{v \in M(k)_\infty} I(J_v,\lambda_v) \end{equation}
\begin{equation} \mathrm{h}_F(J) = 2g \, \mathrm{h}'_L(\Theta) - \kappa_0 \, g + \frac{1}{[k:\mathbb{Q}]} \sum_{v \in M(k)_0} \bigl(\tfrac{1}{8}\ell(\Gamma_v) -\tfrac{1}{2}\tau(\Gamma_v) \bigr) \log Nv +
\frac{2}{[k:\mathbb{Q}]} \sum_{v \in M(k)_\infty} I(J_v,\lambda_v) \end{equation}
for the stable Faltings height of ![]() $J$. This recovers [Reference de JongdJ18, Theorem 1.6].
$J$. This recovers [Reference de JongdJ18, Theorem 1.6].
Note that ![]() $\mathrm {h}_F(J)$ is equal to the stable Faltings height
$\mathrm {h}_F(J)$ is equal to the stable Faltings height ![]() $\mathrm {h}_F(C)$ of the curve
$\mathrm {h}_F(C)$ of the curve ![]() $C$ itself; cf. [Reference PazukiPaz19, Proposition 6.5]. In the case that
$C$ itself; cf. [Reference PazukiPaz19, Proposition 6.5]. In the case that ![]() $g=2$, the formula in (1.11) reproves [Reference AutissierAut06, Théorème 5.1] and gives a uniform explanation for the entries in the table that follows directly upon [Reference AutissierAut06, Théorème 5.1]. We refer to [Reference de Jong and ShokriehdJS18, § 9] for more details about the
$g=2$, the formula in (1.11) reproves [Reference AutissierAut06, Théorème 5.1] and gives a uniform explanation for the entries in the table that follows directly upon [Reference AutissierAut06, Théorème 5.1]. We refer to [Reference de Jong and ShokriehdJS18, § 9] for more details about the ![]() $g=2$ case.
$g=2$ case.
1.6 The function field case
A slight variation of our arguments yields the following counterpart in the function field setting.
Let ![]() $S$ be a smooth projective connected curve over an algebraically closed field and let
$S$ be a smooth projective connected curve over an algebraically closed field and let ![]() $F$ denote the function field of
$F$ denote the function field of ![]() $S$. Let
$S$. Let ![]() $(A,\lambda )$ be a principally polarized abelian variety of dimension
$(A,\lambda )$ be a principally polarized abelian variety of dimension ![]() $g$ with semistable reduction over
$g$ with semistable reduction over ![]() $F$ and let
$F$ and let ![]() $\pi \colon G \to S$ denote the connected component of the Néron model of
$\pi \colon G \to S$ denote the connected component of the Néron model of ![]() $A$ over
$A$ over ![]() $S$ with zero section
$S$ with zero section ![]() $e \colon S \to G$. Let
$e \colon S \to G$. Let ![]() $\mathrm {h}(A) = \deg e^* \Omega ^g_{G/S}$ in
$\mathrm {h}(A) = \deg e^* \Omega ^g_{G/S}$ in ![]() $\mathbb {Z}$ denote the modular degree of
$\mathbb {Z}$ denote the modular degree of ![]() $A$.
$A$.
Let ![]() $\Theta$ be a symmetric effective ample divisor on
$\Theta$ be a symmetric effective ample divisor on ![]() $A$ defining the principal polarization
$A$ defining the principal polarization ![]() $\lambda$ and denote by
$\lambda$ and denote by ![]() $\mathrm {h}'_L(\Theta )$ the Néron–Tate height of
$\mathrm {h}'_L(\Theta )$ the Néron–Tate height of ![]() $\Theta$ with respect to the line bundle
$\Theta$ with respect to the line bundle ![]() $L=\mathcal {O}_A(\Theta )$. Then the equality
$L=\mathcal {O}_A(\Theta )$. Then the equality
holds. Here ![]() $|S|$ denotes the set of closed points of
$|S|$ denotes the set of closed points of ![]() $S$ and
$S$ and ![]() $I(A_v,\lambda _v)$ is half the tropical moment of the canonical skeleton of the Berkovich analytification of
$I(A_v,\lambda _v)$ is half the tropical moment of the canonical skeleton of the Berkovich analytification of ![]() $A$ at
$A$ at ![]() $v$.
$v$.
From the fact that ![]() $I(A_v,\lambda _v) \in \mathbb {Q}$, we obtain
$I(A_v,\lambda _v) \in \mathbb {Q}$, we obtain ![]() $\mathrm {h}'_L(\Theta ) \in \mathbb {Q}$, a fact that seems not clear a priori. Moreover, as the right-hand side of (1.12) is clearly non-negative, we obtain another proof of the well-known fact that
$\mathrm {h}'_L(\Theta ) \in \mathbb {Q}$, a fact that seems not clear a priori. Moreover, as the right-hand side of (1.12) is clearly non-negative, we obtain another proof of the well-known fact that ![]() $\mathrm {h}(A) \geqslant 0$; cf. [Reference Faltings and ChaiFC90, Proposition V.2.2] or [Reference Moret-BaillyMor85, Chapitre XI, 4.5]. We leave the details of the proof of (1.12) to the interested reader.
$\mathrm {h}(A) \geqslant 0$; cf. [Reference Faltings and ChaiFC90, Proposition V.2.2] or [Reference Moret-BaillyMor85, Chapitre XI, 4.5]. We leave the details of the proof of (1.12) to the interested reader.
1.7 Structure of the paper
Sections 2–9 are mostly preliminary. In these sections we review basic notions and results concerning semistable models, cubical structures, Berkovich analytification, model metrics, admissible metrics, Green's functions, canonical metrics, Raynaud extensions, non-archimedean uniformization, non-archimedean theta functions and tropicalization of abelian varieties.
In § 10 we investigate the relationship between canonical metrics and cubical line bundles on semistable models and in § 11 we prove Theorem B. In § 12 we introduce the main relevant structures on the archimedean side needed for our proof of Theorem A and in § 13 we recall the stable Faltings height and state Bost's key formula for it.
In § 14 we review the notion of Néron–Tate heights of cycles on abelian varieties over number fields and prove a local decomposition formula for the height of a theta divisor. In § 15 we finally give our proof of Theorem A.
Notation and terminology
When ![]() $R$ is a discrete valuation ring with fraction field
$R$ is a discrete valuation ring with fraction field ![]() $F$, we denote its maximal ideal by
$F$, we denote its maximal ideal by ![]() $\mathfrak {m}_R$, its residue field by
$\mathfrak {m}_R$, its residue field by ![]() $\tilde {F}$ and we let
$\tilde {F}$ and we let ![]() $\varpi$ denote a generator of
$\varpi$ denote a generator of ![]() $\mathfrak {m}_R$. Unless mentioned otherwise, we endow
$\mathfrak {m}_R$. Unless mentioned otherwise, we endow ![]() $F$ with the unique non-archimedean absolute value
$F$ with the unique non-archimedean absolute value ![]() $|\cdot | \colon F \to \mathbb {R}$ whose valuation ring is
$|\cdot | \colon F \to \mathbb {R}$ whose valuation ring is ![]() $R$ and that is normalized such that
$R$ and that is normalized such that ![]() $|\varpi |={e}^{-1}$.
$|\varpi |={e}^{-1}$.
When ![]() $M$ is a free rank-one
$M$ is a free rank-one ![]() $R$-module and
$R$-module and ![]() $s$ is a non-zero element of
$s$ is a non-zero element of ![]() $M\otimes _R F$, we write
$M\otimes _R F$, we write ![]() $\operatorname {ord}(s)$ for the multiplicity of
$\operatorname {ord}(s)$ for the multiplicity of ![]() $s$, by which we mean the largest integer
$s$, by which we mean the largest integer ![]() $e$ such that
$e$ such that ![]() $s$ is contained in
$s$ is contained in ![]() $M \otimes \mathfrak {m}_R^e$.
$M \otimes \mathfrak {m}_R^e$.
When ![]() $\mathcal {X}$ is an integral noetherian scheme, and
$\mathcal {X}$ is an integral noetherian scheme, and ![]() $\mathcal {L}$ is a line bundle on
$\mathcal {L}$ is a line bundle on ![]() $\mathcal {X}$, we call a rational section of
$\mathcal {X}$, we call a rational section of ![]() $\mathcal {L}$ any element of the stalk
$\mathcal {L}$ any element of the stalk ![]() $\mathcal {L}_\eta$. Here
$\mathcal {L}_\eta$. Here ![]() $\eta$ is the generic point of
$\eta$ is the generic point of ![]() $\mathcal {X}$. Let
$\mathcal {X}$. Let ![]() $\xi \in \mathcal {X}$ and let
$\xi \in \mathcal {X}$ and let ![]() $K=\mathcal {O}_{\mathcal {X},\eta }$ be the function field of
$K=\mathcal {O}_{\mathcal {X},\eta }$ be the function field of ![]() $\mathcal {X}$. The fraction field of the local ring
$\mathcal {X}$. The fraction field of the local ring ![]() $\mathcal {O}_{\mathcal {X},\xi }$ of
$\mathcal {O}_{\mathcal {X},\xi }$ of ![]() $\mathcal {X}$ at
$\mathcal {X}$ at ![]() $\xi$ coincides with
$\xi$ coincides with ![]() $K$ and the natural map
$K$ and the natural map ![]() $\mathcal {L}_\xi \otimes _{\mathcal {O}_{\mathcal {X},\xi }} K \to \mathcal {L}_\eta$ is an isomorphism. When
$\mathcal {L}_\xi \otimes _{\mathcal {O}_{\mathcal {X},\xi }} K \to \mathcal {L}_\eta$ is an isomorphism. When ![]() $\mathcal {O}_{\mathcal {X},\xi }$ is a discrete valuation ring and
$\mathcal {O}_{\mathcal {X},\xi }$ is a discrete valuation ring and ![]() $s$ is a non-zero rational section of
$s$ is a non-zero rational section of ![]() $\mathcal {L}$, we obtain via the natural isomorphism
$\mathcal {L}$, we obtain via the natural isomorphism ![]() $\mathcal {L}_\xi \otimes _{\mathcal {O}_{\mathcal {X},\xi }} K \xrightarrow {\sim } \mathcal {L}_\eta$ a well-defined multiplicity
$\mathcal {L}_\xi \otimes _{\mathcal {O}_{\mathcal {X},\xi }} K \xrightarrow {\sim } \mathcal {L}_\eta$ a well-defined multiplicity ![]() $\operatorname {ord}_{\xi,\mathcal {L}} (s) \in \mathbb {Z}$ of
$\operatorname {ord}_{\xi,\mathcal {L}} (s) \in \mathbb {Z}$ of ![]() $s$ at
$s$ at ![]() $\xi$.
$\xi$.
When ![]() $V$ is a scheme over
$V$ is a scheme over ![]() $\mathbb {C}$ or over an algebraically closed non-archimedean valued field, we denote by
$\mathbb {C}$ or over an algebraically closed non-archimedean valued field, we denote by ![]() $V^\mathrm {an}$ the associated complex or Berkovich analytic space.
$V^\mathrm {an}$ the associated complex or Berkovich analytic space.
When ![]() $k$ is a number field, we denote by
$k$ is a number field, we denote by ![]() $M(k)_0$ the set of non-archimedean places of
$M(k)_0$ the set of non-archimedean places of ![]() $k$, by
$k$, by ![]() $M(k)_\infty$ the set of complex embeddings of
$M(k)_\infty$ the set of complex embeddings of ![]() $k$ and we set
$k$ and we set ![]() $M(k) = M(k)_0 \sqcup M(k)_\infty$.
$M(k) = M(k)_0 \sqcup M(k)_\infty$.
2. Semistable group schemes
Let ![]() $S$ be a locally noetherian scheme. Let
$S$ be a locally noetherian scheme. Let ![]() $\pi \colon \mathcal {A} \to S$ be a smooth commutative group scheme of finite type over
$\pi \colon \mathcal {A} \to S$ be a smooth commutative group scheme of finite type over ![]() $S$ with zero section
$S$ with zero section ![]() $e \colon S \to \mathcal {A}$. We call the identity component of
$e \colon S \to \mathcal {A}$. We call the identity component of ![]() $\mathcal {A}$ the open subscheme of
$\mathcal {A}$ the open subscheme of ![]() $\mathcal {A}$ formed by taking the union of all fiberwise identity components. The group scheme
$\mathcal {A}$ formed by taking the union of all fiberwise identity components. The group scheme ![]() $\mathcal {A}$ is called semistable if the identity component of
$\mathcal {A}$ is called semistable if the identity component of ![]() $\mathcal {A}$ is a semiabelian group scheme.
$\mathcal {A}$ is a semiabelian group scheme.
Let ![]() $\mathcal {L}$ be a line bundle on
$\mathcal {L}$ be a line bundle on ![]() $\mathcal {A}$. A rigidification of
$\mathcal {A}$. A rigidification of ![]() $\mathcal {L}$ is an isomorphism of line bundles
$\mathcal {L}$ is an isomorphism of line bundles ![]() $\mathcal {O}_S \xrightarrow {\sim } e^*\mathcal {L}$. For each
$\mathcal {O}_S \xrightarrow {\sim } e^*\mathcal {L}$. For each ![]() $I \subset \{1,2,3\}$, let
$I \subset \{1,2,3\}$, let ![]() $m_I \colon \mathcal {A} \times _S \mathcal {A} \times _S \mathcal {A} \to \mathcal {A}$ be the morphism given functorially on points by sending
$m_I \colon \mathcal {A} \times _S \mathcal {A} \times _S \mathcal {A} \to \mathcal {A}$ be the morphism given functorially on points by sending ![]() $(x_1,x_2, x_3)$ to
$(x_1,x_2, x_3)$ to ![]() $\sum _{i \in I} x_i$. Write
$\sum _{i \in I} x_i$. Write ![]() $\mathcal {D}_3(\mathcal {L})$ for the line bundle
$\mathcal {D}_3(\mathcal {L})$ for the line bundle ![]() $\mathcal {D}_3(\mathcal {L}) = \bigotimes _{\varnothing \neq I \subset \{1,2,3\}} m_I^*\mathcal {L}^{\otimes (-1)^{\sharp I}}$ on
$\mathcal {D}_3(\mathcal {L}) = \bigotimes _{\varnothing \neq I \subset \{1,2,3\}} m_I^*\mathcal {L}^{\otimes (-1)^{\sharp I}}$ on ![]() $\mathcal {A} \times _S \mathcal {A} \times _S \mathcal {A}$. A cubical structure on
$\mathcal {A} \times _S \mathcal {A} \times _S \mathcal {A}$. A cubical structure on ![]() $\mathcal {L}$ is an isomorphism
$\mathcal {L}$ is an isomorphism ![]() $\mathcal {O}_{\mathcal {A}^3}\xrightarrow {\sim }\mathcal {D}_3(\mathcal {L})$ satisfying suitable symmetry and cocycle conditions as described in [Reference Moret-BaillyMor85, Définition I.2.4.5]. A line bundle
$\mathcal {O}_{\mathcal {A}^3}\xrightarrow {\sim }\mathcal {D}_3(\mathcal {L})$ satisfying suitable symmetry and cocycle conditions as described in [Reference Moret-BaillyMor85, Définition I.2.4.5]. A line bundle ![]() $\mathcal {L}$ on
$\mathcal {L}$ on ![]() $\mathcal {A}$ endowed with a cubical structure is called a cubical line bundle. A cubical line bundle is canonically rigidified.
$\mathcal {A}$ endowed with a cubical structure is called a cubical line bundle. A cubical line bundle is canonically rigidified.
By the theorem of the cube, each rigidified line bundle on an abelian variety over a field has a unique cubical structure.
2.1 Cubical extensions
Assume that ![]() $S$ is the spectrum of a discrete valuation ring
$S$ is the spectrum of a discrete valuation ring ![]() $R$ and assume that the generic fiber of
$R$ and assume that the generic fiber of ![]() $\mathcal {A}$ is an abelian variety
$\mathcal {A}$ is an abelian variety ![]() $A$. Let
$A$. Let ![]() $L$ be a cubical (that is, rigidified) line bundle on
$L$ be a cubical (that is, rigidified) line bundle on ![]() $A$. A cubical line bundle
$A$. A cubical line bundle ![]() $\mathcal {L}$ on
$\mathcal {L}$ on ![]() $\mathcal {A}$ extending the cubical line bundle
$\mathcal {A}$ extending the cubical line bundle ![]() $L$ is unique up to isomorphism, once one exists, by [Reference Moret-BaillyMor85, Théorème II.1.1]. We have the following two important existence results for cubical extensions. Let
$L$ is unique up to isomorphism, once one exists, by [Reference Moret-BaillyMor85, Théorème II.1.1]. We have the following two important existence results for cubical extensions. Let ![]() $\Phi _\mathcal {A}$ denote the group of connected components of the special fiber of
$\Phi _\mathcal {A}$ denote the group of connected components of the special fiber of ![]() $\mathcal {A}$ and let
$\mathcal {A}$ and let ![]() $n \in \mathbb {Z}_{>0}$ be such that
$n \in \mathbb {Z}_{>0}$ be such that ![]() $n \cdot \Phi _\mathcal {A}=0$.
$n \cdot \Phi _\mathcal {A}=0$.
Lemma 2.1 The cubical line bundle ![]() $L^{\otimes 2n}$ extends as a cubical line bundle over
$L^{\otimes 2n}$ extends as a cubical line bundle over ![]() $\mathcal {A}$.
$\mathcal {A}$.
Proof. This is [Reference Moret-BaillyMor85, Proposition II.1.2.1].
Lemma 2.2 Let ![]() $R \to R'$ be a finite extension and let
$R \to R'$ be a finite extension and let ![]() $F'$ be the fraction field of
$F'$ be the fraction field of ![]() $R'$. Let
$R'$. Let ![]() $e$ denote the ramification index of
$e$ denote the ramification index of ![]() $R \to R'$. Assume that
$R \to R'$. Assume that ![]() $2n | e$ if
$2n | e$ if ![]() $n$ is even and
$n$ is even and ![]() $n|e$ if
$n|e$ if ![]() $n$ is odd. Then the cubical line bundle
$n$ is odd. Then the cubical line bundle ![]() $L_{F'}$ on
$L_{F'}$ on ![]() $A_{F'}$ extends as a cubical line bundle over the group scheme
$A_{F'}$ extends as a cubical line bundle over the group scheme ![]() $\mathcal {A} \times _R R'$.
$\mathcal {A} \times _R R'$.
Proof. This is [Reference Moret-BaillyMor85, Proposition II.1.2.2].
3. Berkovich analytification
The purpose of this section is to set terminology and recall some basic notions concerning Berkovich spaces. We use [Reference BerkovichBer90, Reference Chambert-LoirCha11, Reference Chambert-LoirCha06, Reference Chambert-Loir and ThuillierCT09, Reference GublerGub10, Reference GublerGub07] as our main references.
3.1 Berkovich analytic spaces
Let ![]() $R$ be a complete discrete valuation ring, with fraction field
$R$ be a complete discrete valuation ring, with fraction field ![]() $F$, and let
$F$, and let ![]() $\mathbb {F}$ be the completion of an algebraic closure of
$\mathbb {F}$ be the completion of an algebraic closure of ![]() $F$, endowed with the unique extension of
$F$, endowed with the unique extension of ![]() $|\cdot |$ as an absolute value on
$|\cdot |$ as an absolute value on ![]() $\mathbb {F}$. We write
$\mathbb {F}$. We write ![]() $\mathbb {F}^\circ$ for the valuation ring of
$\mathbb {F}^\circ$ for the valuation ring of ![]() $\mathbb {F}$ and
$\mathbb {F}$ and ![]() $\tilde {\mathbb {F}}$ for the residue field of
$\tilde {\mathbb {F}}$ for the residue field of ![]() $\mathbb {F}^\circ$. When
$\mathbb {F}^\circ$. When ![]() $V$ is a separated scheme of finite type over
$V$ is a separated scheme of finite type over ![]() $F$, we are interested in the Berkovich analytification of the
$F$, we are interested in the Berkovich analytification of the ![]() $\mathbb {F}$-scheme
$\mathbb {F}$-scheme ![]() $V_\mathbb {F}$, denoted by
$V_\mathbb {F}$, denoted by ![]() $V^\mathrm {an}$. The step of passing to
$V^\mathrm {an}$. The step of passing to ![]() $\mathbb {F}$ first is natural for our purposes and moreover some of the references that we use only consider Berkovich analytic spaces over algebraically closed fields.
$\mathbb {F}$ first is natural for our purposes and moreover some of the references that we use only consider Berkovich analytic spaces over algebraically closed fields.
We recall that the underlying set of ![]() $V^\mathrm {an}$ consists of pairs
$V^\mathrm {an}$ consists of pairs ![]() $x=(y,|\cdot |)$, where
$x=(y,|\cdot |)$, where ![]() $y$ is a point of
$y$ is a point of ![]() $V_\mathbb {F}$ and where
$V_\mathbb {F}$ and where ![]() $|\cdot | \colon \kappa (y) \to \mathbb {R}$ is an absolute value on the residue field at
$|\cdot | \colon \kappa (y) \to \mathbb {R}$ is an absolute value on the residue field at ![]() $y$ that extends the given absolute value on
$y$ that extends the given absolute value on ![]() $\mathbb {F}$. The point
$\mathbb {F}$. The point ![]() $y$ is called the center of
$y$ is called the center of ![]() $x$. The space
$x$. The space ![]() $V^\mathrm {an}$ contains the set
$V^\mathrm {an}$ contains the set ![]() $V^\mathrm {alg}=V(\mathbb {F})$ of algebraic points of
$V^\mathrm {alg}=V(\mathbb {F})$ of algebraic points of ![]() $V$ naturally as a dense subset. The underlying topological space of
$V$ naturally as a dense subset. The underlying topological space of ![]() $V^\mathrm {an}$ is Hausdorff, locally compact, locally contractible and path-connected if
$V^\mathrm {an}$ is Hausdorff, locally compact, locally contractible and path-connected if ![]() $V_\mathbb {F}$ is connected. The construction
$V_\mathbb {F}$ is connected. The construction ![]() $V \mapsto V^\mathrm {an}$ is functorial; for example, when
$V \mapsto V^\mathrm {an}$ is functorial; for example, when ![]() $L$ is a line bundle on
$L$ is a line bundle on ![]() $V$, analytification produces a line bundle
$V$, analytification produces a line bundle ![]() $L^\mathrm {an}$ on
$L^\mathrm {an}$ on ![]() $V^\mathrm {an}$.
$V^\mathrm {an}$.
Assume that ![]() $V$ is geometrically integral and let
$V$ is geometrically integral and let ![]() $\mathbb {F}(V)$ denote the function field of
$\mathbb {F}(V)$ denote the function field of ![]() $V_\mathbb {F}$. Let
$V_\mathbb {F}$. Let ![]() $y \in V_\mathbb {F}$ and let
$y \in V_\mathbb {F}$ and let ![]() $\mathcal {O}_{V_\mathbb {F},y}$ denote the local ring of
$\mathcal {O}_{V_\mathbb {F},y}$ denote the local ring of ![]() $V_\mathbb {F}$ at
$V_\mathbb {F}$ at ![]() $y$. For each
$y$. For each ![]() $x \in V^\mathrm {an}$ with center
$x \in V^\mathrm {an}$ with center ![]() $y$, pullback along the canonical map
$y$, pullback along the canonical map ![]() $\mathcal {O}_{V_\mathbb {F},y} \to \kappa (y)$ gives rise to a multiplicative seminorm on
$\mathcal {O}_{V_\mathbb {F},y} \to \kappa (y)$ gives rise to a multiplicative seminorm on ![]() $\mathbb {F}(V) = \operatorname {Frac} \mathcal {O}_{V_\mathbb {F},y}$. We denote this seminorm by
$\mathbb {F}(V) = \operatorname {Frac} \mathcal {O}_{V_\mathbb {F},y}$. We denote this seminorm by ![]() $|\cdot |_x$. For
$|\cdot |_x$. For ![]() $f \in \mathbb {F}(V)$, we sometimes write
$f \in \mathbb {F}(V)$, we sometimes write ![]() $|f(x)|$ instead of
$|f(x)|$ instead of ![]() $|f|_x$.
$|f|_x$.
3.2 Reduction map
Let ![]() $V$ be a geometrically integral and projective
$V$ be a geometrically integral and projective ![]() $F$-scheme. Write
$F$-scheme. Write ![]() $S = \operatorname {Spec} R$. One way of obtaining
$S = \operatorname {Spec} R$. One way of obtaining ![]() $V^\mathrm {an}$ as an analytic space is as follows [Reference GublerGub07, § 2.7]. Let
$V^\mathrm {an}$ as an analytic space is as follows [Reference GublerGub07, § 2.7]. Let ![]() $\mathcal {V}$ be an integral scheme and let
$\mathcal {V}$ be an integral scheme and let ![]() $\mathcal {V} \to S$ be a projective and flat morphism with generic fiber isomorphic to
$\mathcal {V} \to S$ be a projective and flat morphism with generic fiber isomorphic to ![]() $V$. By base change and
$V$. By base change and ![]() $\varpi$-adic completion, one obtains from
$\varpi$-adic completion, one obtains from ![]() $\mathcal {V}$ an admissible formal scheme
$\mathcal {V}$ an admissible formal scheme ![]() $\mathfrak {V}$ over
$\mathfrak {V}$ over ![]() $\mathbb {F}^\circ$. The analytic space
$\mathbb {F}^\circ$. The analytic space ![]() $V^\mathrm {an}$ is naturally identified with the generic fiber of
$V^\mathrm {an}$ is naturally identified with the generic fiber of ![]() $\mathfrak {V}$. The special fiber of
$\mathfrak {V}$. The special fiber of ![]() $\mathfrak {V}$ is naturally identified with the
$\mathfrak {V}$ is naturally identified with the ![]() $\tilde {\mathbb {F}}$-scheme
$\tilde {\mathbb {F}}$-scheme ![]() $\mathcal {V}_{\tilde {\mathbb {F}}}$. By virtue of these identifications, we obtain by [Reference BerkovichBer90, § 2.4] a canonical reduction map
$\mathcal {V}_{\tilde {\mathbb {F}}}$. By virtue of these identifications, we obtain by [Reference BerkovichBer90, § 2.4] a canonical reduction map ![]() $\operatorname {red}_\mathcal {V} \colon V^\mathrm {an} \to \mathcal {V}_{\tilde {\mathbb {F}}}$. The reduction map
$\operatorname {red}_\mathcal {V} \colon V^\mathrm {an} \to \mathcal {V}_{\tilde {\mathbb {F}}}$. The reduction map ![]() $\operatorname {red}_\mathcal {V}$ is surjective and, if
$\operatorname {red}_\mathcal {V}$ is surjective and, if ![]() $\xi$ is a generic point of
$\xi$ is a generic point of ![]() $\mathcal {V}_{\tilde {\mathbb {F}}}$, there exists a unique
$\mathcal {V}_{\tilde {\mathbb {F}}}$, there exists a unique ![]() $x \in V^\mathrm {an}$ such that
$x \in V^\mathrm {an}$ such that ![]() $\operatorname {red}_\mathcal {V}(x) = \xi$; see [Reference BerkovichBer90, Proposition 2.4.4]. We call this point the Shilov point corresponding to
$\operatorname {red}_\mathcal {V}(x) = \xi$; see [Reference BerkovichBer90, Proposition 2.4.4]. We call this point the Shilov point corresponding to ![]() $\xi$, denoted by
$\xi$, denoted by ![]() $x_\xi$.
$x_\xi$.
4. Metrics and Green's functions
We continue with the setting of § 3 and review the notions of metrics and Green's functions.
4.1 Model metrics
Let ![]() $L$ be a line bundle on
$L$ be a line bundle on ![]() $V$ and let
$V$ and let ![]() $L^\mathrm {an}$ be its analytification over
$L^\mathrm {an}$ be its analytification over ![]() $\mathbb {F}$. One has a natural notion of continuous metrics on
$\mathbb {F}$. One has a natural notion of continuous metrics on ![]() $L^\mathrm {an}$. An important class of continuous metrics on
$L^\mathrm {an}$. An important class of continuous metrics on ![]() $L^\mathrm {an}$ is provided by models of (tensor powers of)
$L^\mathrm {an}$ is provided by models of (tensor powers of) ![]() $L$, as follows: let
$L$, as follows: let ![]() $\mathcal {V} \to S$ be an integral, projective and flat model of
$\mathcal {V} \to S$ be an integral, projective and flat model of ![]() $V$ and let
$V$ and let ![]() $\mathcal {L}$ be a line bundle on
$\mathcal {L}$ be a line bundle on ![]() $\mathcal {V}$ whose restriction to
$\mathcal {V}$ whose restriction to ![]() $V$ is equal to
$V$ is equal to ![]() $L$. There exists a continuous metric
$L$. There exists a continuous metric ![]() $\|\cdot \|_{\mathcal {L}}$ on
$\|\cdot \|_{\mathcal {L}}$ on ![]() $L^\mathrm {an}$ uniquely determined by the following property. Let
$L^\mathrm {an}$ uniquely determined by the following property. Let ![]() $s$ be a non-zero rational section of
$s$ be a non-zero rational section of ![]() $L$ and view
$L$ and view ![]() $s$ as a rational section of
$s$ as a rational section of ![]() $\mathcal {L}$ on
$\mathcal {L}$ on ![]() $\mathcal {V}$. Let
$\mathcal {V}$. Let ![]() $x \in V^\mathrm {an}$ and write
$x \in V^\mathrm {an}$ and write ![]() $\xi = \operatorname {red}_\mathcal {V}(x)$, viewed as a point on
$\xi = \operatorname {red}_\mathcal {V}(x)$, viewed as a point on ![]() $\mathcal {V}$. Then
$\mathcal {V}$. Then ![]() $\|s(x)\|_\mathcal {L}$ is given by the following prescription. Let
$\|s(x)\|_\mathcal {L}$ is given by the following prescription. Let ![]() $U$ be an open neighborhood of
$U$ be an open neighborhood of ![]() $\xi$ in
$\xi$ in ![]() $\mathcal {V}$ such that
$\mathcal {V}$ such that ![]() $\mathcal {L}$ is trivialized on
$\mathcal {L}$ is trivialized on ![]() $U$. Let
$U$. Let ![]() $t$ be a trivializing element of
$t$ be a trivializing element of ![]() $\mathcal {L}(U)$ and let
$\mathcal {L}(U)$ and let ![]() $f \in F(V)$ be the unique rational function on
$f \in F(V)$ be the unique rational function on ![]() $U$ satisfying
$U$ satisfying ![]() $s = f \cdot t$ on
$s = f \cdot t$ on ![]() $U$. Then we put
$U$. Then we put ![]() $\|s(x)\|_\mathcal {L} = |f(x)|$.
$\|s(x)\|_\mathcal {L} = |f(x)|$.
A small verification shows that the assignment ![]() $(s,x) \mapsto \|s(x)\|_\mathcal {L}$ is well defined and, in particular, is independent of the choice of
$(s,x) \mapsto \|s(x)\|_\mathcal {L}$ is well defined and, in particular, is independent of the choice of ![]() $U$ and of the trivializing section
$U$ and of the trivializing section ![]() $t$. One calls
$t$. One calls ![]() $\|\cdot \|_{\mathcal {L}}$ the model metric on
$\|\cdot \|_{\mathcal {L}}$ the model metric on ![]() $L^\mathrm {an}$ determined by the model
$L^\mathrm {an}$ determined by the model ![]() $(\mathcal {V},\mathcal {L})$ of
$(\mathcal {V},\mathcal {L})$ of ![]() $(V,L)$. More generally, a model metric on
$(V,L)$. More generally, a model metric on ![]() $L^\mathrm {an}$ is any metric that is obtained by taking
$L^\mathrm {an}$ is any metric that is obtained by taking ![]() $e$th roots of a model metric determined by some model of
$e$th roots of a model metric determined by some model of ![]() $L^{\otimes e}$ for some
$L^{\otimes e}$ for some ![]() $e \in \mathbb {Z}_{>0}$. The notion of model metrics can be extended to the setting of formal models of
$e \in \mathbb {Z}_{>0}$. The notion of model metrics can be extended to the setting of formal models of ![]() $V$, but our assumption that
$V$, but our assumption that ![]() $V$ is projective ensures that for our purposes we do not need them.
$V$ is projective ensures that for our purposes we do not need them.
4.2 Semipositive and admissible metrics
Let ![]() $\|\cdot \|$ be a continuous metric on
$\|\cdot \|$ be a continuous metric on ![]() $L^\mathrm {an}$. We call the metric
$L^\mathrm {an}$. We call the metric ![]() $\|\cdot \|$ semipositive if
$\|\cdot \|$ semipositive if ![]() $\|\cdot \|$ is obtained as a uniform limit of model metrics on
$\|\cdot \|$ is obtained as a uniform limit of model metrics on ![]() $L^\mathrm {an}$ associated to pairs
$L^\mathrm {an}$ associated to pairs ![]() $(\mathcal {V},\mathcal {L})$ consisting of an integral projective flat model
$(\mathcal {V},\mathcal {L})$ consisting of an integral projective flat model ![]() $\mathcal {V}$ of
$\mathcal {V}$ of ![]() $V$ and a model
$V$ and a model ![]() $\mathcal {L}$ of some tensor power
$\mathcal {L}$ of some tensor power ![]() $L^{\otimes e}$ as above, such that for each
$L^{\otimes e}$ as above, such that for each ![]() $(\mathcal {V},\mathcal {L})$, the first Chern class
$(\mathcal {V},\mathcal {L})$, the first Chern class ![]() $c_1(\mathcal {L})$ has non-negative intersection with all complete curves in the special fiber of
$c_1(\mathcal {L})$ has non-negative intersection with all complete curves in the special fiber of ![]() $\mathcal {V}$. We call the metric
$\mathcal {V}$. We call the metric ![]() $\|\cdot \|$ admissible if
$\|\cdot \|$ admissible if ![]() $\|\cdot \|$ can be written as a quotient of two semipositive metrics. We call the metric
$\|\cdot \|$ can be written as a quotient of two semipositive metrics. We call the metric ![]() $\|\cdot \|$ bounded continuous if there exists a pair
$\|\cdot \|$ bounded continuous if there exists a pair ![]() $(\mathcal {V},\mathcal {L})$, where
$(\mathcal {V},\mathcal {L})$, where ![]() $\mathcal {L}$ extends
$\mathcal {L}$ extends ![]() $L$ such that the quotient
$L$ such that the quotient ![]() $\| \cdot \|/\| \cdot \|_{\mathcal {L}}$ is a bounded and continuous function on
$\| \cdot \|/\| \cdot \|_{\mathcal {L}}$ is a bounded and continuous function on ![]() $V^\mathrm {an}$. An admissible metric is bounded continuous.
$V^\mathrm {an}$. An admissible metric is bounded continuous.
We refer to [Reference Chambert-LoirCha11, Reference Chambert-LoirCha06, Reference Chambert-Loir and ThuillierCT09, Reference ZhangZha95] for more precise definitions and extensive discussions. The definitions of semipositive and admissible metrics given in [Reference GublerGub10, Reference GublerGub07] are more involved, and work more generally for proper schemes ![]() $V$, but coincide with the current definitions since we are assuming that
$V$, but coincide with the current definitions since we are assuming that ![]() $V$ is projective. An important class of admissible metrics is given by the canonical metrics on a rigidified symmetric ample line bundle on an abelian variety over
$V$ is projective. An important class of admissible metrics is given by the canonical metrics on a rigidified symmetric ample line bundle on an abelian variety over ![]() $F$. We discuss these canonical metrics in § 5.
$F$. We discuss these canonical metrics in § 5.
4.3 Green's functions
Let ![]() $D$ be an effective Cartier divisor on
$D$ be an effective Cartier divisor on ![]() $V$. Following [Reference Chambert-Loir and ThuillierCT09, § 2], a Green's function with respect to
$V$. Following [Reference Chambert-Loir and ThuillierCT09, § 2], a Green's function with respect to ![]() $D$ is any continuous function
$D$ is any continuous function ![]() $g_D \colon V^\mathrm {an} \setminus \operatorname {Supp}(D) \to \mathbb {R}$ obtained as follows: put
$g_D \colon V^\mathrm {an} \setminus \operatorname {Supp}(D) \to \mathbb {R}$ obtained as follows: put ![]() $L=\mathcal {O}_V(D)$ and let
$L=\mathcal {O}_V(D)$ and let ![]() $\|\cdot \|$ be any admissible metric on
$\|\cdot \|$ be any admissible metric on ![]() $L^\mathrm {an}$. The divisor
$L^\mathrm {an}$. The divisor ![]() $D$ determines a canonical global section
$D$ determines a canonical global section ![]() $s_D$ of
$s_D$ of ![]() $L$. Then, for each
$L$. Then, for each ![]() $x \in V^\mathrm {an} \setminus \operatorname {Supp}(D)$, we put
$x \in V^\mathrm {an} \setminus \operatorname {Supp}(D)$, we put ![]() $g_D(x) = -\log \! \|s_D(x)\|$. The notion of a Green's function readily generalizes to arbitrary Cartier divisors on
$g_D(x) = -\log \! \|s_D(x)\|$. The notion of a Green's function readily generalizes to arbitrary Cartier divisors on ![]() $V$. When
$V$. When ![]() $g_D \colon V^\mathrm {an} \setminus \operatorname {Supp}(D) \to \mathbb {R}$ is a Green's function on
$g_D \colon V^\mathrm {an} \setminus \operatorname {Supp}(D) \to \mathbb {R}$ is a Green's function on ![]() $V^\mathrm {an}$ with respect to the Cartier divisor
$V^\mathrm {an}$ with respect to the Cartier divisor ![]() $D$, the restriction of
$D$, the restriction of ![]() $g_D$ to
$g_D$ to ![]() $V^\mathrm {alg} \setminus \operatorname {Supp}(D)$ is a Weil function on
$V^\mathrm {alg} \setminus \operatorname {Supp}(D)$ is a Weil function on ![]() $V^\mathrm {alg}$ with respect to
$V^\mathrm {alg}$ with respect to ![]() $D$ in the sense of [Reference LangLan83, § 10.2].
$D$ in the sense of [Reference LangLan83, § 10.2].
5. Canonical metrics
Let ![]() $A$ be an abelian variety over
$A$ be an abelian variety over ![]() $F$ and let
$F$ and let ![]() $L$ be a rigidified ample line bundle on
$L$ be a rigidified ample line bundle on ![]() $A$ that we assume moreover to be symmetric. We thus have a unique isomorphism of rigidified line bundles
$A$ that we assume moreover to be symmetric. We thus have a unique isomorphism of rigidified line bundles ![]() $[-1]^*L \xrightarrow {\sim } L$. Gubler constructed in [Reference GublerGub07, § 3.3] a canonical metric
$[-1]^*L \xrightarrow {\sim } L$. Gubler constructed in [Reference GublerGub07, § 3.3] a canonical metric ![]() $\|\cdot \|_L$ on
$\|\cdot \|_L$ on ![]() $L^\mathrm {an}$ using formal model metrics and taking uniform limits. The discussion in [Reference ZhangZha95, § 2] shows that
$L^\mathrm {an}$ using formal model metrics and taking uniform limits. The discussion in [Reference ZhangZha95, § 2] shows that ![]() $\|\cdot \|_L$ can alternatively be obtained by working with model metrics obtained from integral projective flat models of
$\|\cdot \|_L$ can alternatively be obtained by working with model metrics obtained from integral projective flat models of ![]() $A$ and taking uniform limits of such.
$A$ and taking uniform limits of such.
5.1 Axiomatic characterization
This leads to the following characterization of ![]() $\|\cdot \|_L$; cf. [Reference ZhangZha95, Theorem 2.2]. Let
$\|\cdot \|_L$; cf. [Reference ZhangZha95, Theorem 2.2]. Let ![]() $m \in \mathbb {Z}_{>0}$ and denote by
$m \in \mathbb {Z}_{>0}$ and denote by ![]() $[m] \colon A \to A$ the multiplication-by-
$[m] \colon A \to A$ the multiplication-by-![]() $m$. We have a unique isomorphism
$m$. We have a unique isomorphism ![]() $\varphi _m \colon [m]^*L \xrightarrow {\sim } L^{ \otimes m^2}$ of rigidified line bundles on
$\varphi _m \colon [m]^*L \xrightarrow {\sim } L^{ \otimes m^2}$ of rigidified line bundles on ![]() $A$ (see, for instance, [Reference Moret-BaillyMor85, Proposition I.5.5]). The canonical metric
$A$ (see, for instance, [Reference Moret-BaillyMor85, Proposition I.5.5]). The canonical metric ![]() $\|\cdot \|_L$ is the unique bounded continuous metric on
$\|\cdot \|_L$ is the unique bounded continuous metric on ![]() $L^\mathrm {an}$ that has the property that the isomorphism
$L^\mathrm {an}$ that has the property that the isomorphism ![]() $\varphi _m$ is an isometry with respect to the canonically induced metrics on
$\varphi _m$ is an isometry with respect to the canonically induced metrics on ![]() $[m]^*L$ and
$[m]^*L$ and ![]() $L^{\otimes m^2}$.
$L^{\otimes m^2}$.
The canonical metric ![]() $\|\cdot \|_L$ is independent of the choice of
$\|\cdot \|_L$ is independent of the choice of ![]() $m$ and is invariant under extensions of the base field
$m$ and is invariant under extensions of the base field ![]() $F$. As can be verified immediately, if the given rigidification of
$F$. As can be verified immediately, if the given rigidification of ![]() $L$ is multiplied by a scalar
$L$ is multiplied by a scalar ![]() $\lambda \in F^\times$, then the canonical metric on
$\lambda \in F^\times$, then the canonical metric on ![]() $L$ associated to the new rigidification is obtained by multiplying
$L$ associated to the new rigidification is obtained by multiplying ![]() $\|\cdot \|_L$ by
$\|\cdot \|_L$ by ![]() $|\lambda |$. Furthermore, for each
$|\lambda |$. Furthermore, for each ![]() $n \in \mathbb {Z}_{>0}$, the canonical metric on the symmetric rigidified ample line bundle
$n \in \mathbb {Z}_{>0}$, the canonical metric on the symmetric rigidified ample line bundle ![]() $L^{\otimes n}$ is given by
$L^{\otimes n}$ is given by ![]() $\|\cdot \|_L^{\otimes n}$.
$\|\cdot \|_L^{\otimes n}$.
In § 10, we see how ![]() $\|\cdot \|_L$ is connected to the Néron model of
$\|\cdot \|_L$ is connected to the Néron model of ![]() $A$ over the valuation ring of
$A$ over the valuation ring of ![]() $F$. We discuss here a special case. If
$F$. We discuss here a special case. If ![]() $A$ has good reduction over the valuation ring
$A$ has good reduction over the valuation ring ![]() $R$ of
$R$ of ![]() $F$, then, by [Reference Moret-BaillyMor85, II.3.5 and VI.2.1], the line bundle
$F$, then, by [Reference Moret-BaillyMor85, II.3.5 and VI.2.1], the line bundle ![]() $L$ extends uniquely as a cubical symmetric ample line bundle
$L$ extends uniquely as a cubical symmetric ample line bundle ![]() $\mathcal {L}$ over the Néron model of
$\mathcal {L}$ over the Néron model of ![]() $A$ over
$A$ over ![]() $R$, which now is an abelian scheme over
$R$, which now is an abelian scheme over ![]() $R$. In this case
$R$. In this case ![]() $\|\cdot \|_L$ is just the model metric associated to
$\|\cdot \|_L$ is just the model metric associated to ![]() $\mathcal {L}$. The metric
$\mathcal {L}$. The metric ![]() $\|\cdot \|_L$ is in general not a model metric, but it is always an admissible metric [Reference Chambert-LoirCha11, Reference GublerGub07, Reference ZhangZha95].
$\|\cdot \|_L$ is in general not a model metric, but it is always an admissible metric [Reference Chambert-LoirCha11, Reference GublerGub07, Reference ZhangZha95].
5.2 Translation by a two-torsion point
We continue to assume that ![]() $L$ is symmetric, ample and rigidified. As our considerations are analytic in nature, we work over the field
$L$ is symmetric, ample and rigidified. As our considerations are analytic in nature, we work over the field ![]() $\mathbb {F}$. Let
$\mathbb {F}$. Let ![]() $y \in A[2]$ be a two-torsion point of
$y \in A[2]$ be a two-torsion point of ![]() $A$ and write
$A$ and write ![]() $T_y \colon A \xrightarrow {\sim } A$ for translation along
$T_y \colon A \xrightarrow {\sim } A$ for translation along ![]() $y$. We have that
$y$. We have that ![]() $T_y^*L$ is a symmetric ample line bundle on
$T_y^*L$ is a symmetric ample line bundle on ![]() $A$.
$A$.
Lemma 5.1 Let ![]() $\|\cdot \|_L$ be the canonical metric on
$\|\cdot \|_L$ be the canonical metric on ![]() $L^\mathrm {an}$. Then the pullback metric
$L^\mathrm {an}$. Then the pullback metric ![]() $T_y^*\|\cdot \|_L$ is a canonical metric on
$T_y^*\|\cdot \|_L$ is a canonical metric on ![]() $T_y^*L^\mathrm {an}$.
$T_y^*L^\mathrm {an}$.
Proof. It suffices to show that ![]() $T_y^* \|\cdot \|_L^{\otimes 4}$ is a canonical metric on
$T_y^* \|\cdot \|_L^{\otimes 4}$ is a canonical metric on ![]() $(T_y^*L^\mathrm {an})^{\otimes 4}$. As the metric
$(T_y^*L^\mathrm {an})^{\otimes 4}$. As the metric ![]() $T_y^* \|\cdot \|_L^{\otimes 4}$ is bounded continuous, it suffices to show that there exists an isomorphism
$T_y^* \|\cdot \|_L^{\otimes 4}$ is bounded continuous, it suffices to show that there exists an isomorphism ![]() $[2]^* (T_y^*L)^{\otimes 4} \xrightarrow {\sim } (T_y^*L)^{\otimes 16}$ that is an isometry for the metrics induced from
$[2]^* (T_y^*L)^{\otimes 4} \xrightarrow {\sim } (T_y^*L)^{\otimes 16}$ that is an isometry for the metrics induced from ![]() $\|\cdot \|_L$. We may construct such an isomorphism as follows. Starting from the isomorphism
$\|\cdot \|_L$. We may construct such an isomorphism as follows. Starting from the isomorphism ![]() $\varphi _2 \colon [2]^*L \xrightarrow {\sim } L^{\otimes 4}$, we obtain by pullback along
$\varphi _2 \colon [2]^*L \xrightarrow {\sim } L^{\otimes 4}$, we obtain by pullback along ![]() $T_y$ an isomorphism
$T_y$ an isomorphism ![]() $[2]^*L = T_y^*[2]^*L \xrightarrow {\sim } (T_y^*L)^{\otimes 4}$. From this, we obtain by pullback along
$[2]^*L = T_y^*[2]^*L \xrightarrow {\sim } (T_y^*L)^{\otimes 4}$. From this, we obtain by pullback along ![]() $[2]$ an isomorphism
$[2]$ an isomorphism ![]() $[4]^*L \xrightarrow {\sim } [2]^*(T_y^*L)^{\otimes 4}$. On the other hand, we have, again starting from the isomorphism
$[4]^*L \xrightarrow {\sim } [2]^*(T_y^*L)^{\otimes 4}$. On the other hand, we have, again starting from the isomorphism ![]() $\varphi _2 \colon [2]^*L \xrightarrow {\sim } L^{\otimes 4}$, by pullback along
$\varphi _2 \colon [2]^*L \xrightarrow {\sim } L^{\otimes 4}$, by pullback along ![]() $[2]$, an isomorphism
$[2]$, an isomorphism ![]() $\varphi _4 \colon [4]^*L \xrightarrow {\sim } L^{\otimes 16}$ and then by pullback along
$\varphi _4 \colon [4]^*L \xrightarrow {\sim } L^{\otimes 16}$ and then by pullback along ![]() $T_y$ an isomorphism
$T_y$ an isomorphism ![]() $[4]^*L = T_y^*[4]^*L \xrightarrow {\sim } (T_y^*L)^{\otimes 16}$. Combining the results of applying
$[4]^*L = T_y^*[4]^*L \xrightarrow {\sim } (T_y^*L)^{\otimes 16}$. Combining the results of applying ![]() $[2]^* \circ T_y^*$, respectively
$[2]^* \circ T_y^*$, respectively ![]() $T_y^* \circ [2]^*$, to
$T_y^* \circ [2]^*$, to ![]() $\varphi _2$, we find an isomorphism
$\varphi _2$, we find an isomorphism ![]() $[2]^* (T_y^*L)^{\otimes 4} \xrightarrow {\sim } (T_y^*L)^{\otimes 16}$. This isomorphism is by construction an isometry for the induced metrics from
$[2]^* (T_y^*L)^{\otimes 4} \xrightarrow {\sim } (T_y^*L)^{\otimes 16}$. This isomorphism is by construction an isometry for the induced metrics from ![]() $\|\cdot \|_L$.
$\|\cdot \|_L$.
5.3 Néron functions
Let ![]() $s$ be a non-zero rational section of the rigidified symmetric ample line bundle
$s$ be a non-zero rational section of the rigidified symmetric ample line bundle ![]() $L$ and write
$L$ and write ![]() $D=\operatorname {div}_L s$. Following [Reference LangLan83, § 11.1], we call a Néron function with respect to
$D=\operatorname {div}_L s$. Following [Reference LangLan83, § 11.1], we call a Néron function with respect to ![]() $D$ any Weil function
$D$ any Weil function ![]() $\Lambda \colon A^\mathrm {alg} \setminus \operatorname {Supp}(D) \to \mathbb {R}$ with respect to
$\Lambda \colon A^\mathrm {alg} \setminus \operatorname {Supp}(D) \to \mathbb {R}$ with respect to ![]() $D$ such that there exists a rational function
$D$ such that there exists a rational function ![]() $h$ on
$h$ on ![]() $A$ whose divisor is equal to
$A$ whose divisor is equal to ![]() $-[2]^*D+4D$ and such that, away from the support of
$-[2]^*D+4D$ and such that, away from the support of ![]() $\operatorname {div} h$, the identity
$\operatorname {div} h$, the identity
is satisfied. For the notion of Weil function, we refer to [Reference LangLan83, § 10.2].
We note that the isomorphism ![]() $\varphi _2 \colon [2]^*L \xrightarrow {\sim } L^{\otimes 4}$ of line bundles from § 5.1 allows us to view the rational section
$\varphi _2 \colon [2]^*L \xrightarrow {\sim } L^{\otimes 4}$ of line bundles from § 5.1 allows us to view the rational section ![]() $s^{\otimes 4} \otimes [2]^*s^{\otimes -1}$ of the rigidified trivial line bundle
$s^{\otimes 4} \otimes [2]^*s^{\otimes -1}$ of the rigidified trivial line bundle ![]() $L^{\otimes 4} \otimes [2]^*L^{\otimes -1}$ as a rational function
$L^{\otimes 4} \otimes [2]^*L^{\otimes -1}$ as a rational function ![]() $h$ on
$h$ on ![]() $A$ whose divisor is equal to
$A$ whose divisor is equal to ![]() $-[2]^*D+4D$. The fact that
$-[2]^*D+4D$. The fact that ![]() $\varphi _2$ is an isometry for the canonical metrics translates into the identity
$\varphi _2$ is an isometry for the canonical metrics translates into the identity
on ![]() $A^\mathrm {an}$ wherever each of the three terms is defined.
$A^\mathrm {an}$ wherever each of the three terms is defined.
Write ![]() $g_D$ for the Green's function
$g_D$ for the Green's function ![]() $-\log \|s\|_L$ on
$-\log \|s\|_L$ on ![]() $A^\mathrm {an}$ (cf. § 4.3). The restriction of
$A^\mathrm {an}$ (cf. § 4.3). The restriction of ![]() $g_D$ to
$g_D$ to ![]() $A^\mathrm {alg} \setminus \operatorname {Supp}(D)$ is a Weil function with respect to
$A^\mathrm {alg} \setminus \operatorname {Supp}(D)$ is a Weil function with respect to ![]() $D$. We conclude from (5.2) that the restriction of
$D$. We conclude from (5.2) that the restriction of ![]() $g_D$ to
$g_D$ to ![]() $A^\mathrm {alg} \setminus \operatorname {Supp}(D)$ is in fact a Néron function with respect to
$A^\mathrm {alg} \setminus \operatorname {Supp}(D)$ is in fact a Néron function with respect to ![]() $D$. It is shown in [Reference LangLan83, § 11.1] that a Néron function with respect to
$D$. It is shown in [Reference LangLan83, § 11.1] that a Néron function with respect to ![]() $D$ is unique up to an additive constant.
$D$ is unique up to an additive constant.
6. Raynaud extensions
Let ![]() $R$ be a complete discrete valuation ring with fraction field
$R$ be a complete discrete valuation ring with fraction field ![]() $F$. We briefly discuss the theory of Raynaud extensions for polarized abelian varieties over
$F$. We briefly discuss the theory of Raynaud extensions for polarized abelian varieties over ![]() $F$, following [Reference Faltings and ChaiFC90, Chapter II].
$F$, following [Reference Faltings and ChaiFC90, Chapter II].
Assume that we are given an abelian variety ![]() $A$ over
$A$ over ![]() $F$ with split semistable reduction, and a rigidified ample line bundle
$F$ with split semistable reduction, and a rigidified ample line bundle ![]() $L$ on
$L$ on ![]() $A$, determining a polarization
$A$, determining a polarization ![]() $\lambda _{A,L} \colon A \to A^t$ of
$\lambda _{A,L} \colon A \to A^t$ of ![]() $A$. Write
$A$. Write ![]() $S = \operatorname {Spec} R$ and let
$S = \operatorname {Spec} R$ and let ![]() $v$ denote the closed point of
$v$ denote the closed point of ![]() $S$. Let
$S$. Let ![]() $G$ denote the identity component of the Néron model of
$G$ denote the identity component of the Néron model of ![]() $A$ over
$A$ over ![]() $S$. By our assumptions, the scheme
$S$. By our assumptions, the scheme ![]() $G$ is a semiabelian scheme over
$G$ is a semiabelian scheme over ![]() $S$. By [Reference Moret-BaillyMor85, II.3.5 and VI.2.1], the group scheme
$S$. By [Reference Moret-BaillyMor85, II.3.5 and VI.2.1], the group scheme ![]() $G$ is endowed with a unique cubical ample extension
$G$ is endowed with a unique cubical ample extension ![]() $\mathcal {L}_G$ of
$\mathcal {L}_G$ of ![]() $L$. The Raynaud extension construction [Reference Faltings and ChaiFC90, II.1–2] can be applied to the pair
$L$. The Raynaud extension construction [Reference Faltings and ChaiFC90, II.1–2] can be applied to the pair ![]() $(G,\mathcal {L}_G)$ to yield a canonical short exact sequence, for the fppf topology, of commutative group schemes
$(G,\mathcal {L}_G)$ to yield a canonical short exact sequence, for the fppf topology, of commutative group schemes
over ![]() $S$. Here
$S$. Here ![]() $T$ is a split torus and
$T$ is a split torus and ![]() $\mathcal {B}$ an abelian scheme. The Raynaud construction produces an ample cubical line bundle
$\mathcal {B}$ an abelian scheme. The Raynaud construction produces an ample cubical line bundle ![]() $\tilde {\mathcal {L}}_{\tilde {G}}$ on
$\tilde {\mathcal {L}}_{\tilde {G}}$ on ![]() $\tilde {G}$ and an isomorphism
$\tilde {G}$ and an isomorphism ![]() $\tilde {G}_v \xrightarrow {\sim } G_v$ of special fibers. In particular, the formal completions of
$\tilde {G}_v \xrightarrow {\sim } G_v$ of special fibers. In particular, the formal completions of ![]() $G$ and
$G$ and ![]() $\tilde {G}$ are identified.
$\tilde {G}$ are identified.
Let ![]() $G^t$ denote the identity component of the Néron model of the dual abelian variety
$G^t$ denote the identity component of the Néron model of the dual abelian variety ![]() $A^t$. We similarly have, associated to
$A^t$. We similarly have, associated to ![]() $G^t$, a Raynaud extension
$G^t$, a Raynaud extension
over ![]() $S$ with
$S$ with ![]() $T^t$ a split torus. Let
$T^t$ a split torus. Let ![]() $\underline {X} = \mathcal {H}om(T,\mathbb {G}_m)$ and
$\underline {X} = \mathcal {H}om(T,\mathbb {G}_m)$ and ![]() $\underline {Y} = \mathcal {H}om(T^t,\mathbb {G}_m)$, both viewed as étale group schemes over
$\underline {Y} = \mathcal {H}om(T^t,\mathbb {G}_m)$, both viewed as étale group schemes over ![]() $S$. For
$S$. For ![]() $u \in \underline {X}(S)$, we usually denote by
$u \in \underline {X}(S)$, we usually denote by ![]() $\chi ^u \colon T \to \mathbb {G}_m$ the corresponding character. From extension (6.1), we obtain an associated pushout diagram
$\chi ^u \colon T \to \mathbb {G}_m$ the corresponding character. From extension (6.1), we obtain an associated pushout diagram

in the category of commutative ![]() $S$-group schemes with the fppf topology. The pushout construction gives rise to a morphism
$S$-group schemes with the fppf topology. The pushout construction gives rise to a morphism ![]() $\Omega \colon \underline {X} \to \mathcal {B}^t$ of group schemes by sending
$\Omega \colon \underline {X} \to \mathcal {B}^t$ of group schemes by sending ![]() $u$ to the class of the algebraically trivial line bundle on
$u$ to the class of the algebraically trivial line bundle on ![]() $\mathcal {B}$ determined by the
$\mathcal {B}$ determined by the ![]() $\mathbb {G}_m$-torsor
$\mathbb {G}_m$-torsor ![]() $\tilde {G}_u$. Similarly, the extension (
$\tilde {G}_u$. Similarly, the extension (
) determines an assignment ![]() $u' \mapsto e_{u'}$ and a morphism of group schemes
$u' \mapsto e_{u'}$ and a morphism of group schemes ![]() $\Omega ' \colon \underline {Y} \to \mathcal {B}$.
$\Omega ' \colon \underline {Y} \to \mathcal {B}$.
The polarization ![]() $\lambda _{A,L} \colon A \to A^t$ associated to
$\lambda _{A,L} \colon A \to A^t$ associated to ![]() $L$ extends canonically into an isogeny
$L$ extends canonically into an isogeny ![]() $\lambda _{G,L} \colon G \to G^t$. Functoriality of the Raynaud extension gives an isogeny
$\lambda _{G,L} \colon G \to G^t$. Functoriality of the Raynaud extension gives an isogeny ![]() $\lambda _{T,L} \colon T \to T^t$, an isogeny
$\lambda _{T,L} \colon T \to T^t$, an isogeny ![]() $\lambda _{\tilde {G},L} \colon \tilde {G} \to \tilde {G}^t$ and a polarization
$\lambda _{\tilde {G},L} \colon \tilde {G} \to \tilde {G}^t$ and a polarization ![]() $\lambda _{\mathcal {B},L} \colon \mathcal {B} \to \mathcal {B}^t$. These morphisms fit together into a morphism of short exact sequences of commutative group schemes
$\lambda _{\mathcal {B},L} \colon \mathcal {B} \to \mathcal {B}^t$. These morphisms fit together into a morphism of short exact sequences of commutative group schemes

over ![]() $S$. The morphism
$S$. The morphism ![]() $\lambda _{T,L}$ induces by pullback a morphism
$\lambda _{T,L}$ induces by pullback a morphism ![]() $\Phi \colon \underline {Y} \to \underline {X}$ of group schemes and the diagram
$\Phi \colon \underline {Y} \to \underline {X}$ of group schemes and the diagram

commutes. If ![]() $L$ defines a principal polarization, then
$L$ defines a principal polarization, then ![]() $\Phi \colon \underline {Y} \to \underline {X}$ and each of the maps
$\Phi \colon \underline {Y} \to \underline {X}$ and each of the maps ![]() $\lambda$ in (
$\lambda$ in (
) is an isomorphism.
In addition to the above canonical data associated to ![]() $(A,L)$, we may and do pick some non-canonical further data as follows. For these extra data, a finite extension of the field
$(A,L)$, we may and do pick some non-canonical further data as follows. For these extra data, a finite extension of the field ![]() $F$ may be needed, but this is harmless for our purposes. Denote the generic fibers of
$F$ may be needed, but this is harmless for our purposes. Denote the generic fibers of ![]() $\tilde {G}$ and
$\tilde {G}$ and ![]() $\mathcal {B}$ by
$\mathcal {B}$ by ![]() $E$ and
$E$ and ![]() $B$, respectively. Let
$B$, respectively. Let ![]() $q \colon E \to B$ be the map induced by
$q \colon E \to B$ be the map induced by ![]() $\mathfrak {q} \colon \tilde {G} \to \mathcal {B}$. Set
$\mathfrak {q} \colon \tilde {G} \to \mathcal {B}$. Set ![]() $X=\underline {X}(F)$,
$X=\underline {X}(F)$, ![]() $Y=\underline {Y}(F)$. First of all, we may and do pick an injective lift
$Y=\underline {Y}(F)$. First of all, we may and do pick an injective lift

of the map ![]() $\Omega '_\eta$. Similarly, we may pick an injective lift
$\Omega '_\eta$. Similarly, we may pick an injective lift ![]() $\upsilon ^t \colon X \to E^t(F)$ of the quotient map
$\upsilon ^t \colon X \to E^t(F)$ of the quotient map ![]() $E^t(F) \to B^t(F)$. We view
$E^t(F) \to B^t(F)$. We view ![]() $Y$ as a subgroup of
$Y$ as a subgroup of ![]() $E(F)$ and
$E(F)$ and ![]() $X$ as a subgroup of
$X$ as a subgroup of ![]() $E^t(F)$ via the maps
$E^t(F)$ via the maps ![]() $\upsilon$,
$\upsilon$, ![]() $\upsilon ^t$. We can arrange that
$\upsilon ^t$. We can arrange that ![]() $e_u(u')=e_{u'}(u)$ for
$e_u(u')=e_{u'}(u)$ for ![]() $u \in X$,
$u \in X$, ![]() $u' \in Y$.
$u' \in Y$.
Let ![]() $\mathcal {P}$ denote the Poincaré bundle on
$\mathcal {P}$ denote the Poincaré bundle on ![]() $\mathcal {B} \times _S \mathcal {B}^t$, endowed with its canonical rigidification, and let
$\mathcal {B} \times _S \mathcal {B}^t$, endowed with its canonical rigidification, and let ![]() $P$ be its generic fiber. We may further suppose that the map
$P$ be its generic fiber. We may further suppose that the map
defines a trivialization of the invertible sheaf ![]() $(\Omega '_\eta \times \Omega _\eta )^*P$ on
$(\Omega '_\eta \times \Omega _\eta )^*P$ on ![]() $Y \times X$.
$Y \times X$.
Next, we may and do pick an ample cubical line bundle ![]() $\mathcal {M}$ on
$\mathcal {M}$ on ![]() $\mathcal {B}$ such that
$\mathcal {B}$ such that ![]() $\mathcal {M}$ determines the polarization
$\mathcal {M}$ determines the polarization ![]() $\lambda _{\mathcal {B},L} \colon \mathcal {B} \to \mathcal {B}^t$ and such that
$\lambda _{\mathcal {B},L} \colon \mathcal {B} \to \mathcal {B}^t$ and such that ![]() $\mathfrak {q}^* \mathcal {M}$ is identified with
$\mathfrak {q}^* \mathcal {M}$ is identified with ![]() $\tilde {\mathcal {L}}_{\tilde {G}}$ as cubical line bundles. Denote by
$\tilde {\mathcal {L}}_{\tilde {G}}$ as cubical line bundles. Denote by ![]() $M$ the generic fiber of
$M$ the generic fiber of ![]() $\mathcal {M}$, which is thus a rigidified ample line bundle on
$\mathcal {M}$, which is thus a rigidified ample line bundle on ![]() $B$. If
$B$. If ![]() $L$ determines a principal polarization, then so does
$L$ determines a principal polarization, then so does ![]() $M$.
$M$.
Let ![]() $m_\mathcal {B} \colon \mathcal {B} \times _S \mathcal {B} \to \mathcal {B}$ denote the additively written group operation of
$m_\mathcal {B} \colon \mathcal {B} \times _S \mathcal {B} \to \mathcal {B}$ denote the additively written group operation of ![]() $\mathcal {B}$ and denote by
$\mathcal {B}$ and denote by ![]() $p_1, p_2 \colon \mathcal {B} \times _S \mathcal {B} \to \mathcal {B}$ the projections onto the first, respectively the second, factor. We have a canonical identification
$p_1, p_2 \colon \mathcal {B} \times _S \mathcal {B} \to \mathcal {B}$ the projections onto the first, respectively the second, factor. We have a canonical identification
of rigidified line bundles on ![]() $\mathcal {B} \times _S \mathcal {B}$.
$\mathcal {B} \times _S \mathcal {B}$.
Finally, we may and do, pick, given our choices of ![]() $\upsilon, \upsilon '$ and
$\upsilon, \upsilon '$ and ![]() $\mathcal {M}$, a trivialization
$\mathcal {M}$, a trivialization ![]() $c \colon Y \to M$ of the rigidified line bundle
$c \colon Y \to M$ of the rigidified line bundle ![]() $(\Omega '_\eta )^*M$ on
$(\Omega '_\eta )^*M$ on ![]() $Y$ such that via the restriction of the canonical identification given by (6.6) to the generic fiber, the trivialization
$Y$ such that via the restriction of the canonical identification given by (6.6) to the generic fiber, the trivialization ![]() $c$ satisfies the relation
$c$ satisfies the relation
for all ![]() $u', v' \in Y$.
$u', v' \in Y$.
We call the data ![]() $(M,\Phi,c)$ a triple associated to the rigidified ample line bundle
$(M,\Phi,c)$ a triple associated to the rigidified ample line bundle ![]() $L$. For
$L$. For ![]() $u \in X$, we denote by
$u \in X$, we denote by ![]() $E_u$ the rigidified line bundle determined by the generic fiber of
$E_u$ the rigidified line bundle determined by the generic fiber of ![]() $\tilde {G}_u$. By [Reference Foster, Rabinoff, Shokrieh and SotoFRSS18, Theorem 3.6], two triples
$\tilde {G}_u$. By [Reference Foster, Rabinoff, Shokrieh and SotoFRSS18, Theorem 3.6], two triples ![]() $(M_1,\Phi _1,c_1)$ and
$(M_1,\Phi _1,c_1)$ and ![]() $(M_2,\Phi _2,c_2)$ define the same rigidified line bundle if and only if
$(M_2,\Phi _2,c_2)$ define the same rigidified line bundle if and only if ![]() $\Phi _1= \Phi _2$ and there exists
$\Phi _1= \Phi _2$ and there exists ![]() $u \in X$ such that
$u \in X$ such that ![]() $M_1 \otimes M_2^{-1} \cong E_u$ and
$M_1 \otimes M_2^{-1} \cong E_u$ and ![]() $c_1 \otimes c_2^{-1} \cong \varepsilon _u$. Here, for
$c_1 \otimes c_2^{-1} \cong \varepsilon _u$. Here, for ![]() $u \in X$, we denote by
$u \in X$, we denote by ![]() $\varepsilon _u \colon Y \to E_u(F)$ the composite of the inclusion
$\varepsilon _u \colon Y \to E_u(F)$ the composite of the inclusion ![]() $\upsilon \colon Y \to E(F)$ and the map
$\upsilon \colon Y \to E(F)$ and the map ![]() $e_u \colon E(F) \to E_u(F)$. It is straightforward to extend the notion of associated triple to the setting of rigidified ample line bundles defined over
$e_u \colon E(F) \to E_u(F)$. It is straightforward to extend the notion of associated triple to the setting of rigidified ample line bundles defined over ![]() $\mathbb {F}$.
$\mathbb {F}$.
Denote by ![]() $\|\cdot \|_M$ the model metric on
$\|\cdot \|_M$ the model metric on ![]() $M^\mathrm {an}$ derived from
$M^\mathrm {an}$ derived from ![]() $\mathcal {M}$ and by
$\mathcal {M}$ and by ![]() $\|\cdot \|_P$ the model metric on
$\|\cdot \|_P$ the model metric on ![]() $P^\mathrm {an}$ derived from
$P^\mathrm {an}$ derived from ![]() $\mathcal {P}$. By construction, the rigidification of
$\mathcal {P}$. By construction, the rigidification of ![]() $M$ is an isometry for the metric
$M$ is an isometry for the metric ![]() $\|\cdot \|_M$ and the canonical rigidification of
$\|\cdot \|_M$ and the canonical rigidification of ![]() $P$ is an isometry for the metric
$P$ is an isometry for the metric ![]() $\|\cdot \|_P$. For
$\|\cdot \|_P$. For ![]() $u' \in Y$,
$u' \in Y$, ![]() $v \in X$, we put
$v \in X$, we put
Then ![]() $b$ is a
$b$ is a ![]() $\mathbb {Z}$-valued bilinear map on
$\mathbb {Z}$-valued bilinear map on ![]() $Y \times X$ and
$Y \times X$ and ![]() $c_\mathrm {trop}$ is a
$c_\mathrm {trop}$ is a ![]() $\mathbb {Z}$-valued function on
$\mathbb {Z}$-valued function on ![]() $Y$. From (6.6) and (6.7), we derive the fundamental identity
$Y$. From (6.6) and (6.7), we derive the fundamental identity
for all ![]() $u', v' \in Y$. The assumption that
$u', v' \in Y$. The assumption that ![]() $L$ is ample implies that the map
$L$ is ample implies that the map ![]() $Y \times Y \to \mathbb {Z}$ given by sending
$Y \times Y \to \mathbb {Z}$ given by sending ![]() $(u',v') \in Y \times Y$ to
$(u',v') \in Y \times Y$ to ![]() $b(u',\Phi (v'))$ is positive definite.
$b(u',\Phi (v'))$ is positive definite.
The tuple ![]() $(X,Y,\Phi,b)$ constitutes a polarized tropical abelian variety. Let
$(X,Y,\Phi,b)$ constitutes a polarized tropical abelian variety. Let ![]() $X^*=\operatorname {Hom}(X,\mathbb {Z})$ and
$X^*=\operatorname {Hom}(X,\mathbb {Z})$ and ![]() $X^*_\mathbb {R} = X^* \otimes \mathbb {R} = \operatorname {Hom}(X,\mathbb {R})$. The bilinear map
$X^*_\mathbb {R} = X^* \otimes \mathbb {R} = \operatorname {Hom}(X,\mathbb {R})$. The bilinear map ![]() $b$ realizes
$b$ realizes ![]() $Y$ as a subgroup of
$Y$ as a subgroup of ![]() $X^*$ of finite index. We write
$X^*$ of finite index. We write ![]() $\Sigma$ for the real torus
$\Sigma$ for the real torus ![]() $X_\mathbb {R}^*/Y$. We note that
$X_\mathbb {R}^*/Y$. We note that ![]() $\Sigma$ is a point if and only if
$\Sigma$ is a point if and only if ![]() $A$ has good reduction over
$A$ has good reduction over ![]() $R$.
$R$.
7. Non-archimedean uniformization of abelian varieties
In [Reference BerkovichBer90, § 6.5], the classical rigid analytic uniformization of abelian varieties (see [Reference Bosch and LütkebohmertBL91] for a thorough treatment) is established in the context of Berkovich analytic spaces. We discuss the matter here briefly. Our main references are [Reference Foster, Rabinoff, Shokrieh and SotoFRSS18, Reference GublerGub10]. We continue with the notation and assumptions from § 6. The map ![]() $\upsilon$ from (6.5) induces, upon analytification, an exact sequence
$\upsilon$ from (6.5) induces, upon analytification, an exact sequence
of analytic groups. We refer to the map ![]() $p \colon E^\mathrm {an} \to A^\mathrm {an}$ as the non-archimedean uniformization of
$p \colon E^\mathrm {an} \to A^\mathrm {an}$ as the non-archimedean uniformization of ![]() $A$ and we call the group
$A$ and we call the group ![]() $Y$ the group of periods of
$Y$ the group of periods of ![]() $A^\mathrm {an}$. We have a canonical isomorphism
$A^\mathrm {an}$. We have a canonical isomorphism ![]() $p^*L^\mathrm {an} \xrightarrow {\sim } q^*M^\mathrm {an}$ of rigidified analytic line bundles on
$p^*L^\mathrm {an} \xrightarrow {\sim } q^*M^\mathrm {an}$ of rigidified analytic line bundles on ![]() $E^\mathrm {an}$.
$E^\mathrm {an}$.
7.1 Tropicalization
Let ![]() $\langle \cdot,\cdot \rangle \colon X \times X_\mathbb {R}^* \to \mathbb {R}$ denote the natural evaluation pairing. The tropicalization map
$\langle \cdot,\cdot \rangle \colon X \times X_\mathbb {R}^* \to \mathbb {R}$ denote the natural evaluation pairing. The tropicalization map ![]() $\mathrm {trop} \colon T^\mathrm {an} \to X_\mathbb {R}^*$ is given by the rule
$\mathrm {trop} \colon T^\mathrm {an} \to X_\mathbb {R}^*$ is given by the rule
The tropicalization map is a surjective homomorphism and extends in a natural way to a surjective homomorphism ![]() $\mathrm {trop} \colon E^\mathrm {an} \to X_\mathbb {R}^*$ by setting
$\mathrm {trop} \colon E^\mathrm {an} \to X_\mathbb {R}^*$ by setting
Here ![]() $\| \cdot \|_{E_u}$ is the model metric on
$\| \cdot \|_{E_u}$ is the model metric on ![]() $E_u^\mathrm {an}$ determined by the
$E_u^\mathrm {an}$ determined by the ![]() $\mathbb {G}_m$-torsor
$\mathbb {G}_m$-torsor ![]() $\tilde {G}_u$ on
$\tilde {G}_u$ on ![]() $\mathcal {B}$.
$\mathcal {B}$.
Write ![]() $\Sigma = X_\mathbb {R}^*/Y$. The homomorphism
$\Sigma = X_\mathbb {R}^*/Y$. The homomorphism ![]() $\mathrm {trop} \colon E^\mathrm {an} \to X_\mathbb {R}^*$ gives rise to a morphism of short exact sequences
$\mathrm {trop} \colon E^\mathrm {an} \to X_\mathbb {R}^*$ gives rise to a morphism of short exact sequences

The map ![]() $\tau \colon A^\mathrm {an} \to \Sigma$ turns out to be a deformation retraction. Following [Reference Foster, Rabinoff, Shokrieh and SotoFRSS18, § 4] and [Reference GublerGub10, Example 7.2], there exists a natural section
$\tau \colon A^\mathrm {an} \to \Sigma$ turns out to be a deformation retraction. Following [Reference Foster, Rabinoff, Shokrieh and SotoFRSS18, § 4] and [Reference GublerGub10, Example 7.2], there exists a natural section ![]() $\sigma \colon X_\mathbb {R}^* \to E^\mathrm {an}$ of
$\sigma \colon X_\mathbb {R}^* \to E^\mathrm {an}$ of ![]() $\mathrm {trop}$. We denote by
$\mathrm {trop}$. We denote by ![]() $\iota \colon \Sigma \to A^\mathrm {an}$ the resulting section of
$\iota \colon \Sigma \to A^\mathrm {an}$ the resulting section of ![]() $\tau$. We usually view
$\tau$. We usually view ![]() $\Sigma =X_\mathbb {R}^*/Y$ as a subspace of
$\Sigma =X_\mathbb {R}^*/Y$ as a subspace of ![]() $A^\mathrm {an}$ via the map
$A^\mathrm {an}$ via the map ![]() $\iota$. When viewed as a subspace of
$\iota$. When viewed as a subspace of ![]() $A^\mathrm {an}$ via
$A^\mathrm {an}$ via ![]() $\iota$, we call
$\iota$, we call ![]() $\Sigma$ the canonical skeleton of
$\Sigma$ the canonical skeleton of ![]() $A^\mathrm {an}$.
$A^\mathrm {an}$.
Lemma 7.1 The restriction of the retraction map ![]() $\tau \colon A^\mathrm {an} \to \Sigma =X_\mathbb {R}^*/Y$ to
$\tau \colon A^\mathrm {an} \to \Sigma =X_\mathbb {R}^*/Y$ to ![]() $A(F)$ induces an isomorphism of groups
$A(F)$ induces an isomorphism of groups ![]() $A(F)/G(R) \xrightarrow {\sim } X^*/Y$.
$A(F)/G(R) \xrightarrow {\sim } X^*/Y$.
Proof. We have canonical identifications (cf. [Reference Faltings and ChaiFC90, p. 78])
 \begin{align*} A(F)/G(R) & = E(F)/\upsilon(Y) \cdot G(R) \\ & = \tilde{G}(F)/\upsilon(Y) \cdot G(R) \\ & = \tilde{G}(F)/ \upsilon(Y) \cdot \tilde{G}(R) \end{align*}
\begin{align*} A(F)/G(R) & = E(F)/\upsilon(Y) \cdot G(R) \\ & = \tilde{G}(F)/\upsilon(Y) \cdot G(R) \\ & = \tilde{G}(F)/ \upsilon(Y) \cdot \tilde{G}(R) \end{align*}and
 \begin{align*} \tilde{G}(F)/\tilde{G}(R) & = T(F) / T(R) \\ & = \operatorname{Hom}(X, F^*/R^*). \end{align*}
\begin{align*} \tilde{G}(F)/\tilde{G}(R) & = T(F) / T(R) \\ & = \operatorname{Hom}(X, F^*/R^*). \end{align*}
The restriction of the tropicalization map ![]() $\mathrm {trop} \colon E^\mathrm {an} \to X_\mathbb {R}^*$ to
$\mathrm {trop} \colon E^\mathrm {an} \to X_\mathbb {R}^*$ to ![]() $E(F)=\tilde {G}(F)$ induces an isomorphism of groups
$E(F)=\tilde {G}(F)$ induces an isomorphism of groups ![]() $\tilde {G}(F)/\tilde {G}(R)=\operatorname {Hom}(X,F^*/R^*) \xrightarrow {\sim } X^*$. This descends to an isomorphism
$\tilde {G}(F)/\tilde {G}(R)=\operatorname {Hom}(X,F^*/R^*) \xrightarrow {\sim } X^*$. This descends to an isomorphism ![]() $\tilde {G}(F)/ \upsilon (Y) \cdot \tilde {G}(R) \xrightarrow {\sim } X^*/Y$. Since, by construction, the retraction map
$\tilde {G}(F)/ \upsilon (Y) \cdot \tilde {G}(R) \xrightarrow {\sim } X^*/Y$. Since, by construction, the retraction map ![]() $\tau \colon A^\mathrm {an} \to \Sigma$ descends from
$\tau \colon A^\mathrm {an} \to \Sigma$ descends from ![]() $\mathrm {trop}$, we see that
$\mathrm {trop}$, we see that ![]() $\tau$ sends
$\tau$ sends ![]() $A(F)$ onto
$A(F)$ onto ![]() $X^*/Y$ with kernel
$X^*/Y$ with kernel ![]() $G(R)$.
$G(R)$.
Let ![]() $\mathcal {N}$ be the Néron model of
$\mathcal {N}$ be the Néron model of ![]() $A$ over
$A$ over ![]() $S = \operatorname {Spec} R$, let
$S = \operatorname {Spec} R$, let ![]() $\Phi _\mathcal {N}$ be the group of components of its special fiber and let
$\Phi _\mathcal {N}$ be the group of components of its special fiber and let ![]() $\mathrm {sp} \colon \mathcal {N}(R) \to \Phi _\mathcal {N}$ denote the specialization map. We note that
$\mathrm {sp} \colon \mathcal {N}(R) \to \Phi _\mathcal {N}$ denote the specialization map. We note that ![]() $\mathrm {sp}$ induces a group isomorphism
$\mathrm {sp}$ induces a group isomorphism ![]() $\mathcal {N}(R)/G(R) \xrightarrow {\sim } \Phi _\mathcal {N}$. As
$\mathcal {N}(R)/G(R) \xrightarrow {\sim } \Phi _\mathcal {N}$. As ![]() $\mathcal {N}(R)=A(F)$, we immediately deduce from Lemma 7.1 the following.
$\mathcal {N}(R)=A(F)$, we immediately deduce from Lemma 7.1 the following.
Corollary 7.2 The map ![]() $\Phi _\mathcal {N} \to X^*/Y$ that sends
$\Phi _\mathcal {N} \to X^*/Y$ that sends ![]() $\mathrm {sp}(x)$ for
$\mathrm {sp}(x)$ for ![]() $x \in \mathcal {N}(R)$ to
$x \in \mathcal {N}(R)$ to ![]() $\tau (x)$ is a group isomorphism.
$\tau (x)$ is a group isomorphism.
Compare with [Reference Faltings and ChaiFC90, Corollary III.8.2].
This has the following consequence. Let ![]() $\mathcal {V}$ be a projective integral model of
$\mathcal {V}$ be a projective integral model of ![]() $A$ containing
$A$ containing ![]() $\mathcal {N}$ as an open subscheme. In particular, we have an open immersion
$\mathcal {N}$ as an open subscheme. In particular, we have an open immersion ![]() $\mathcal {N}_{\tilde {\mathbb {F}}} \hookrightarrow \mathcal {V}_{\tilde {\mathbb {F}}}$ of special fibers. Let
$\mathcal {N}_{\tilde {\mathbb {F}}} \hookrightarrow \mathcal {V}_{\tilde {\mathbb {F}}}$ of special fibers. Let ![]() $\xi \in \Phi _\mathcal {N}$ and let
$\xi \in \Phi _\mathcal {N}$ and let ![]() $x_\xi \in A^\mathrm {an}$ denote the Shilov point determined by the generic point of the irreducible component corresponding to
$x_\xi \in A^\mathrm {an}$ denote the Shilov point determined by the generic point of the irreducible component corresponding to ![]() $\xi$ in
$\xi$ in ![]() $\mathcal {V}_{\tilde {\mathbb {F}}}$. Then
$\mathcal {V}_{\tilde {\mathbb {F}}}$. Then ![]() $x_\xi$ is an element of the canonical skeleton
$x_\xi$ is an element of the canonical skeleton ![]() $\Sigma$ of
$\Sigma$ of ![]() $A^\mathrm {an}$.
$A^\mathrm {an}$.
7.2 The invariant  $I(A,\lambda )$
$I(A,\lambda )$
Let ![]() $\lambda \colon A \xrightarrow {\sim } A^t$ be a principal polarization of
$\lambda \colon A \xrightarrow {\sim } A^t$ be a principal polarization of ![]() $A$ and let
$A$ and let ![]() $L$ be any rigidified symmetric ample line bundle on
$L$ be any rigidified symmetric ample line bundle on ![]() $A$ determining
$A$ determining ![]() $\lambda$. Let
$\lambda$. Let ![]() $s$ be a non-zero global section of
$s$ be a non-zero global section of ![]() $L$. Let
$L$. Let ![]() $\|\cdot \|_L$ denote the canonical metric on
$\|\cdot \|_L$ denote the canonical metric on ![]() $L^\mathrm {an}$.
$L^\mathrm {an}$.
We define
where
is the supremum norm of ![]() $s$ and where
$s$ and where ![]() $\mu _{H}$ is the pushforward, along the inclusion
$\mu _{H}$ is the pushforward, along the inclusion ![]() $\iota \colon \Sigma \hookrightarrow A^\mathrm {an}$, of the Haar measure of unit volume on the canonical skeleton
$\iota \colon \Sigma \hookrightarrow A^\mathrm {an}$, of the Haar measure of unit volume on the canonical skeleton ![]() $\Sigma$ of
$\Sigma$ of ![]() $A^\mathrm {an}$.
$A^\mathrm {an}$.
Lemma 7.3 The quantity ![]() $I(A,\lambda )$ is independent of the choice of symmetric ample line bundle
$I(A,\lambda )$ is independent of the choice of symmetric ample line bundle ![]() $L$, of section
$L$, of section ![]() $s$ and of rigidification of
$s$ and of rigidification of ![]() $L$ and hence defines an invariant of the principally polarized abelian variety
$L$ and hence defines an invariant of the principally polarized abelian variety ![]() $(A,\lambda )$.
$(A,\lambda )$.
Proof. Choose one symmetric ample line bundle ![]() $L$ on
$L$ on ![]() $A$ determining
$A$ determining ![]() $\lambda$. A change of rigidification results in a replacement of
$\lambda$. A change of rigidification results in a replacement of ![]() $\|\cdot \|_L$ by a scalar multiple of
$\|\cdot \|_L$ by a scalar multiple of ![]() $\|\cdot \|_L$. Moreover, the space
$\|\cdot \|_L$. Moreover, the space ![]() $H^0(A,L)$ of global sections of
$H^0(A,L)$ of global sections of ![]() $L$ is one-dimensional. It follows immediately that the quantity
$L$ is one-dimensional. It follows immediately that the quantity ![]() $I(A,\lambda )$ as defined in (7.4) is independent of the choice of rigidification of
$I(A,\lambda )$ as defined in (7.4) is independent of the choice of rigidification of ![]() $L$ and of section
$L$ and of section ![]() $s$. Now any other symmetric ample line bundle on
$s$. Now any other symmetric ample line bundle on ![]() $A$ determining
$A$ determining ![]() $\lambda$ is given by
$\lambda$ is given by ![]() $T_y^*L$ for some two-torsion point
$T_y^*L$ for some two-torsion point ![]() $y$ of
$y$ of ![]() $A$. By Lemma 5.1, the pullback
$A$. By Lemma 5.1, the pullback ![]() $T_y^*\|\cdot \|_L$ of the canonical metric on
$T_y^*\|\cdot \|_L$ of the canonical metric on ![]() $L^\mathrm {an}$ is a canonical metric on
$L^\mathrm {an}$ is a canonical metric on ![]() $T_y^*L^\mathrm {an}$. As the measure
$T_y^*L^\mathrm {an}$. As the measure ![]() $\mu _H$ is translation-invariant, we obtain that the quantity
$\mu _H$ is translation-invariant, we obtain that the quantity ![]() $I(A,\lambda )$ is also independent of the choice of
$I(A,\lambda )$ is also independent of the choice of ![]() $L$.
$L$.
8. Non-archimedean theta functions
We briefly review the theory of non-archimedean theta functions. A reference for this section is [Reference Foster, Rabinoff, Shokrieh and SotoFRSS18, §§ 3–4]. We continue with the notation and assumptions from §§ 6 and 7. In particular, we work with a symmetric rigidified ample line bundle ![]() $L$ on the abelian variety
$L$ on the abelian variety ![]() $A$ over the complete discretely valued field
$A$ over the complete discretely valued field ![]() $F$.
$F$.
Recall that we have a polarized tropical abelian variety ![]() $(X,Y,\Phi,b)$ associated to the pair
$(X,Y,\Phi,b)$ associated to the pair ![]() $(A,L)$ by Raynaud's construction. The bilinear map
$(A,L)$ by Raynaud's construction. The bilinear map ![]() $b$ gives rise to an inner product
$b$ gives rise to an inner product ![]() $[\cdot,\cdot ]$ on
$[\cdot,\cdot ]$ on ![]() $X_\mathbb {R}^*$. In these terms, the identity in (6.9) can be rewritten as
$X_\mathbb {R}^*$. In these terms, the identity in (6.9) can be rewritten as
Recall that we have a canonical isomorphism ![]() $p^*L^\mathrm {an} \xrightarrow {\sim } q^*M^\mathrm {an}$ of rigidified analytic line bundles on
$p^*L^\mathrm {an} \xrightarrow {\sim } q^*M^\mathrm {an}$ of rigidified analytic line bundles on ![]() $E^\mathrm {an}$. Following [Reference Foster, Rabinoff, Shokrieh and SotoFRSS18, Definition 3.14], a theta function for
$E^\mathrm {an}$. Following [Reference Foster, Rabinoff, Shokrieh and SotoFRSS18, Definition 3.14], a theta function for ![]() $L$ is any global section
$L$ is any global section ![]() $f \in H^0(E^\mathrm {an},q^*M^\mathrm {an})$ that descends to a section of
$f \in H^0(E^\mathrm {an},q^*M^\mathrm {an})$ that descends to a section of ![]() $L^\mathrm {an}$ along
$L^\mathrm {an}$ along ![]() $p$.
$p$.
If ![]() $L$ defines a principal polarization, we call
$L$ defines a principal polarization, we call ![]() $f$ a Riemann theta function for
$f$ a Riemann theta function for ![]() $L$. A Riemann theta function is unique up to translations by elements from
$L$. A Riemann theta function is unique up to translations by elements from ![]() $Y$ and up to multiplication by scalars.
$Y$ and up to multiplication by scalars.
Let ![]() $f$ be a non-zero theta function for
$f$ be a non-zero theta function for ![]() $L$. For a suitable triple
$L$. For a suitable triple ![]() $(M,\Phi,c)$ associated to
$(M,\Phi,c)$ associated to ![]() $L$, we have a functional equation
$L$, we have a functional equation
for ![]() $z \in E^\mathrm {an}$ and
$z \in E^\mathrm {an}$ and ![]() $u' \in Y$; see [Reference Foster, Rabinoff, Shokrieh and SotoFRSS18, Proposition 3.13]. By (6.8) and (7.2), this yields the functional equation
$u' \in Y$; see [Reference Foster, Rabinoff, Shokrieh and SotoFRSS18, Proposition 3.13]. By (6.8) and (7.2), this yields the functional equation
for ![]() $z \in E^\mathrm {an}$ and
$z \in E^\mathrm {an}$ and ![]() $u' \in Y$. The function
$u' \in Y$. The function ![]() $f$ does not vanish on the image of the section
$f$ does not vanish on the image of the section ![]() $\sigma \colon X_\mathbb {R}^* \to E^\mathrm {an}$. Following [Reference Foster, Rabinoff, Shokrieh and SotoFRSS18, § 4.3], we define
$\sigma \colon X_\mathbb {R}^* \to E^\mathrm {an}$. Following [Reference Foster, Rabinoff, Shokrieh and SotoFRSS18, § 4.3], we define
The map ![]() $\bar {f}$ is called the tropicalization of the theta function
$\bar {f}$ is called the tropicalization of the theta function ![]() $f$. From (8.3), we obtain the relation
$f$. From (8.3), we obtain the relation
for ![]() $\nu \in X_\mathbb {R}^*$,
$\nu \in X_\mathbb {R}^*$, ![]() $u' \in Y$.
$u' \in Y$.
A tropical cocycle on ![]() $X_\mathbb {R}^*$ with respect to the
$X_\mathbb {R}^*$ with respect to the ![]() $Y$-action by translations is any function
$Y$-action by translations is any function ![]() $\mathbf {z} \colon Y \times X_\mathbb {R}^* \to \mathbb {R}$ that satisfies
$\mathbf {z} \colon Y \times X_\mathbb {R}^* \to \mathbb {R}$ that satisfies
Let ![]() $(M,\Phi,c)$ be a triple for
$(M,\Phi,c)$ be a triple for ![]() $L$. From (8.1), one deduces that the function
$L$. From (8.1), one deduces that the function ![]() $c_\mathrm {trop}(u') + \langle \Phi (u'), \nu \rangle$ that appears in (8.5) is a tropical cocycle on
$c_\mathrm {trop}(u') + \langle \Phi (u'), \nu \rangle$ that appears in (8.5) is a tropical cocycle on ![]() $X_\mathbb {R}^*$ with respect to
$X_\mathbb {R}^*$ with respect to ![]() $Y$.
$Y$.
8.1 Tropical Riemann theta function
Following [Reference Foster, Rabinoff, Shokrieh and SotoFRSS18], the tropical Riemann theta function associated to ![]() $(A,L)$ is the function
$(A,L)$ is the function ![]() $\Psi \colon X^*_\mathbb {R} \to \mathbb {R}$ given by
$\Psi \colon X^*_\mathbb {R} \to \mathbb {R}$ given by
 \begin{align} \Psi(\nu) & = \min_{u' \in Y} \bigl\{ \tfrac{1}{2} [u',u'] + [u',\nu] \bigr\} \nonumber\\ & = \min_{u' \in Y} \bigl\{ \tfrac{1}{2} [u',u'] + \langle \Phi(u'),\nu \rangle \bigr\} \end{align}
\begin{align} \Psi(\nu) & = \min_{u' \in Y} \bigl\{ \tfrac{1}{2} [u',u'] + [u',\nu] \bigr\} \nonumber\\ & = \min_{u' \in Y} \bigl\{ \tfrac{1}{2} [u',u'] + \langle \Phi(u'),\nu \rangle \bigr\} \end{align}
for ![]() $\nu \in X^*_\mathbb {R}$. We note that
$\nu \in X^*_\mathbb {R}$. We note that ![]() $\Psi =-\Theta$, where
$\Psi =-\Theta$, where ![]() $\Theta$ is the theta function considered in [Reference Mikhalkin and ZharkovMZ08]. As is easily checked, we have a functional equation
$\Theta$ is the theta function considered in [Reference Mikhalkin and ZharkovMZ08]. As is easily checked, we have a functional equation
for all ![]() $\nu \in X^*_\mathbb {R}$ and
$\nu \in X^*_\mathbb {R}$ and ![]() $u' \in Y$.
$u' \in Y$.
8.2 Translations of line bundles
Let ![]() $z' \in E^t(F)$. We denote by
$z' \in E^t(F)$. We denote by ![]() $L_{z'}$ the rigidified translation-invariant line bundle on
$L_{z'}$ the rigidified translation-invariant line bundle on ![]() $B$ corresponding to
$B$ corresponding to ![]() $q'(z') \in B^t(F)$ and let
$q'(z') \in B^t(F)$ and let ![]() $L_{z'}^\times$ denote the associated
$L_{z'}^\times$ denote the associated ![]() $\mathbb {G}_m$-torsor. We may view
$\mathbb {G}_m$-torsor. We may view ![]() $L_{z'}^\times$ as an extension of
$L_{z'}^\times$ as an extension of ![]() $B$ by
$B$ by ![]() $\mathbb {G}_m$. For
$\mathbb {G}_m$. For ![]() $u' \in Y$, we have canonical identifications of fibers
$u' \in Y$, we have canonical identifications of fibers
As is explained in [Reference Foster, Rabinoff, Shokrieh and SotoFRSS18, § 3.5], we can view the assignment ![]() $u' \mapsto e_{u'}(z')$ for
$u' \mapsto e_{u'}(z')$ for ![]() $u' \in Y$ naturally as a homomorphism
$u' \in Y$ naturally as a homomorphism ![]() $Y \to L_{z'}^{\times,\mathrm {an}}$. We denote this homomorphism by
$Y \to L_{z'}^{\times,\mathrm {an}}$. We denote this homomorphism by ![]() $c_{z'}$. The rigidified line bundle
$c_{z'}$. The rigidified line bundle ![]() $L_{z'}$ has a unique rigidified extension over
$L_{z'}$ has a unique rigidified extension over ![]() $\mathcal {B}$. We denote by
$\mathcal {B}$. We denote by ![]() $\|\cdot \|_{L_{z'}}$ the associated model metric on
$\|\cdot \|_{L_{z'}}$ the associated model metric on ![]() $L_{z'}^\mathrm {an}$. We set
$L_{z'}^\mathrm {an}$. We set ![]() $c_{z',\mathrm {trop}}(u') = - \log \! \| c_{z'}(u') \|_{L_{z'}}$ for
$c_{z',\mathrm {trop}}(u') = - \log \! \| c_{z'}(u') \|_{L_{z'}}$ for ![]() $u' \in Y$.
$u' \in Y$.
Lemma 8.1 Let ![]() $z \in E(F)$ and set
$z \in E(F)$ and set ![]() $z' = \lambda _{E,L}(z)$. The equality
$z' = \lambda _{E,L}(z)$. The equality ![]() $c_{z',\mathrm {trop}}(u') = \langle \Phi (u'),\mathrm {trop}(z) \rangle$ holds.
$c_{z',\mathrm {trop}}(u') = \langle \Phi (u'),\mathrm {trop}(z) \rangle$ holds.
Proof. Let ![]() $\mathrm {trop}' \colon E^{t,\mathrm {an}} \to Y^*_\mathbb {R}$ denote the tropicalization map of
$\mathrm {trop}' \colon E^{t,\mathrm {an}} \to Y^*_\mathbb {R}$ denote the tropicalization map of ![]() $E^{t,\mathrm {an}}$. We compute
$E^{t,\mathrm {an}}$. We compute
 \begin{align*} c_{z',\mathrm{trop}}(u')& ={-} \log\! \| c_{z'}(u') \|_{L_{z'}} \\ & ={-}\log\! \| e_{u'} (\lambda_{E,L}(z) \|_{E^t_{u'}} \\ & = \langle u', \mathrm{trop}'(\lambda_{E,L}(z)) \rangle \\ & = \langle u', \Phi^*(\mathrm{trop}(z)) \rangle \\ & = \langle \Phi(u'),\mathrm{trop}(z) \rangle. \end{align*}
\begin{align*} c_{z',\mathrm{trop}}(u')& ={-} \log\! \| c_{z'}(u') \|_{L_{z'}} \\ & ={-}\log\! \| e_{u'} (\lambda_{E,L}(z) \|_{E^t_{u'}} \\ & = \langle u', \mathrm{trop}'(\lambda_{E,L}(z)) \rangle \\ & = \langle u', \Phi^*(\mathrm{trop}(z)) \rangle \\ & = \langle \Phi(u'),\mathrm{trop}(z) \rangle. \end{align*}The lemma follows.
It is straightforward to extend the definitions of ![]() $c_{z'}$ and
$c_{z'}$ and ![]() $c_{z',\mathrm {trop}}$ to the setting that
$c_{z',\mathrm {trop}}$ to the setting that ![]() $z' \in E^{t,\mathrm {alg}}$. For each
$z' \in E^{t,\mathrm {alg}}$. For each ![]() $y \in A^\mathrm {alg}$, we denote by
$y \in A^\mathrm {alg}$, we denote by ![]() $T_y$ the translation along
$T_y$ the translation along ![]() $y$.
$y$.
Lemma 8.2 Assume that ![]() $(M,\Phi,c)$ is a triple for
$(M,\Phi,c)$ is a triple for ![]() $L$. Let
$L$. Let ![]() $z \in E^\mathrm {alg}$ and set
$z \in E^\mathrm {alg}$ and set ![]() $z' = \lambda _{E,L}(z)$. Further, set
$z' = \lambda _{E,L}(z)$. Further, set ![]() $y=p(z)$,
$y=p(z)$, ![]() $w=q(z)$ and write
$w=q(z)$ and write ![]() $c' = c \otimes c_{z'}$. Then
$c' = c \otimes c_{z'}$. Then ![]() $T_w^* M \cong M \otimes L_{z'}$ and
$T_w^* M \cong M \otimes L_{z'}$ and ![]() $(T_w^*M,\Phi,c')$ is a triple for the translated line bundle
$(T_w^*M,\Phi,c')$ is a triple for the translated line bundle ![]() $T_y^*L$.
$T_y^*L$.
Proof. This is [Reference Foster, Rabinoff, Shokrieh and SotoFRSS18, Proposition 3.9].
8.3 Tropicalization of Riemann theta functions
We assume in this section that ![]() $L$ defines a principal polarization. It is shown in [Reference Foster, Rabinoff, Shokrieh and SotoFRSS18] that the tropicalization of a Riemann theta function associated to
$L$ defines a principal polarization. It is shown in [Reference Foster, Rabinoff, Shokrieh and SotoFRSS18] that the tropicalization of a Riemann theta function associated to ![]() $L$ is a translate of the tropical Riemann theta function, up to an additive constant. In this section we review this result and discuss some of the details.
$L$ is a translate of the tropical Riemann theta function, up to an additive constant. In this section we review this result and discuss some of the details.
Let ![]() $f$ be a non-zero Riemann theta function for
$f$ be a non-zero Riemann theta function for ![]() $L$. Let
$L$. Let ![]() $(M,\Phi,c)$ be a triple associated to
$(M,\Phi,c)$ be a triple associated to ![]() $L$ such that the tropical cocycle of
$L$ such that the tropical cocycle of ![]() $f$ is given by
$f$ is given by ![]() $c_\mathrm {trop}(u') + \langle \Phi (u'), \nu \rangle$.
$c_\mathrm {trop}(u') + \langle \Phi (u'), \nu \rangle$.
Proposition 8.3 There exists an element ![]() $z_0 \in E^\mathrm {alg}$ such that the following four properties are satisfied. Let
$z_0 \in E^\mathrm {alg}$ such that the following four properties are satisfied. Let ![]() $y=p(z_0)$.
$y=p(z_0)$.
(a) Let
 $z' = \lambda _{E,L}(z_0)$, let
$z' = \lambda _{E,L}(z_0)$, let  $w = q(z_0)$ and write
$w = q(z_0)$ and write  $c'=c \otimes c_{z'}$ and
$c'=c \otimes c_{z'}$ and  $M'=M \otimes L_{z'}$. The line bundle
$M'=M \otimes L_{z'}$. The line bundle  $M'$ is symmetric and, under the canonical identification of line bundles
$M'$ is symmetric and, under the canonical identification of line bundles  $M'^{\otimes 2} = (\mathrm {id},\lambda _{B,L})^* P$ on
$M'^{\otimes 2} = (\mathrm {id},\lambda _{B,L})^* P$ on  $B$ derived from (6.6), we have
$B$ derived from (6.6), we have  $c'(u')^{\otimes 2} = t(u',\Phi (u'))$ for
$c'(u')^{\otimes 2} = t(u',\Phi (u'))$ for  $u' \in Y$, the identity
$u' \in Y$, the identity  $c'_\mathrm {trop}(u') = \frac {1}{2}[u',u']$ holds for
$c'_\mathrm {trop}(u') = \frac {1}{2}[u',u']$ holds for  $u' \in Y$ and
$u' \in Y$ and  $(M',\Phi,c')$ is a triple for
$(M',\Phi,c')$ is a triple for  $T_y^*L$.
$T_y^*L$.(b) The line bundle
 $T_y^*L$ is symmetric.
$T_y^*L$ is symmetric.(c) The function
 $T_{z_0}^*f$ is a theta function for the line bundle
$T_{z_0}^*f$ is a theta function for the line bundle  $T_y^*L$.
$T_y^*L$.(d) The tropicalization
 $\overline {T_{z_0}^*f}$ of the theta function
$\overline {T_{z_0}^*f}$ of the theta function  $T_{z_0}^*f$ is equal to the tropical Riemann theta function
$T_{z_0}^*f$ is equal to the tropical Riemann theta function  $\Psi$, up to an additive constant.
$\Psi$, up to an additive constant.
Proof. The existence of an element ![]() $z_0 \in E^\mathrm {alg}$ such that property (a) holds is guaranteed by combining Lemma 8.2 and [Reference Foster, Rabinoff, Shokrieh and SotoFRSS18, Proposition 3.18]. Property (b) follows from the symmetry of
$z_0 \in E^\mathrm {alg}$ such that property (a) holds is guaranteed by combining Lemma 8.2 and [Reference Foster, Rabinoff, Shokrieh and SotoFRSS18, Proposition 3.18]. Property (b) follows from the symmetry of ![]() $M'$ and property (c) is clear. As to property (d), we note that [Reference Foster, Rabinoff, Shokrieh and SotoFRSS18, Theorem 4.9] states that the tropicalization
$M'$ and property (c) is clear. As to property (d), we note that [Reference Foster, Rabinoff, Shokrieh and SotoFRSS18, Theorem 4.9] states that the tropicalization ![]() $\bar {f}$ of
$\bar {f}$ of ![]() $f$ is equal to a translate of the tropical Riemann theta function
$f$ is equal to a translate of the tropical Riemann theta function ![]() $\Psi$, up to an additive constant. This means that for suitable
$\Psi$, up to an additive constant. This means that for suitable ![]() $\kappa ' \in X_\mathbb {R}^*$, we have that
$\kappa ' \in X_\mathbb {R}^*$, we have that ![]() $T_{\kappa '}^*\bar {f}$ is equal to
$T_{\kappa '}^*\bar {f}$ is equal to ![]() $\Psi$, up to an additive constant. Let
$\Psi$, up to an additive constant. Let ![]() $\kappa =\mathrm {trop}(z_0)$. We claim that
$\kappa =\mathrm {trop}(z_0)$. We claim that ![]() $\kappa '=\kappa$. By Lemma 8.1, we have that
$\kappa '=\kappa$. By Lemma 8.1, we have that ![]() $c_{z',\mathrm {trop}}(u') = \langle \Phi (u'),\kappa \rangle = [u',\kappa ]$ for
$c_{z',\mathrm {trop}}(u') = \langle \Phi (u'),\kappa \rangle = [u',\kappa ]$ for ![]() $u' \in Y$. Since, for
$u' \in Y$. Since, for ![]() $c'=c \otimes c_{z'}$, we have
$c'=c \otimes c_{z'}$, we have ![]() $c'_\mathrm {trop}(u') = \frac {1}{2}[u',u']$ by (a), we deduce that
$c'_\mathrm {trop}(u') = \frac {1}{2}[u',u']$ by (a), we deduce that ![]() $c_\mathrm {trop}(u') = c'_\mathrm {trop}(u') - c_{z',\mathrm {trop}}(u') = \frac {1}{2} [ u', u' ] - [u',\kappa ]$ for
$c_\mathrm {trop}(u') = c'_\mathrm {trop}(u') - c_{z',\mathrm {trop}}(u') = \frac {1}{2} [ u', u' ] - [u',\kappa ]$ for ![]() $u' \in Y$. We see that
$u' \in Y$. We see that ![]() $\bar {f}$ has tropical cocycle
$\bar {f}$ has tropical cocycle ![]() $\frac {1}{2} [ u', u' ] + [u',-\kappa +\nu ]$. As is easily verified, this is the tropical cocycle of the translated tropical Riemann theta function
$\frac {1}{2} [ u', u' ] + [u',-\kappa +\nu ]$. As is easily verified, this is the tropical cocycle of the translated tropical Riemann theta function ![]() $T_{-\kappa }^*\Psi$. Reasoning as in the proof of [Reference Foster, Rabinoff, Shokrieh and SotoFRSS18, Theorem 4.9], we may conclude that
$T_{-\kappa }^*\Psi$. Reasoning as in the proof of [Reference Foster, Rabinoff, Shokrieh and SotoFRSS18, Theorem 4.9], we may conclude that ![]() $\bar {f}= T_{-\kappa }^*\Psi$, up to an additive constant. This gives that
$\bar {f}= T_{-\kappa }^*\Psi$, up to an additive constant. This gives that ![]() $\overline {T_{z_0}^*f} = T_\kappa ^*\bar {f}$ is equal to
$\overline {T_{z_0}^*f} = T_\kappa ^*\bar {f}$ is equal to ![]() $\Psi$, up to an additive constant, and we see that property (d) holds.
$\Psi$, up to an additive constant, and we see that property (d) holds.
9. Canonical metrics and theta functions
Let ![]() $L$ be a rigidified symmetric ample line bundle on
$L$ be a rigidified symmetric ample line bundle on ![]() $A$ defining a principal polarization of
$A$ defining a principal polarization of ![]() $A$. In this section we make the following assumption.
$A$. In this section we make the following assumption.
The rigidified line bundle
 $L$ has an associated triple
$L$ has an associated triple  $(M,\Phi,c)$ with
$(M,\Phi,c)$ with  $M$ a symmetric rigidified ample line bundle on
$M$ a symmetric rigidified ample line bundle on  $B$ such that under the identification of rigidified line bundles
$B$ such that under the identification of rigidified line bundles  $M^{\otimes 2} = (\mathrm {id},\lambda _{B,L})^* P$ on
$M^{\otimes 2} = (\mathrm {id},\lambda _{B,L})^* P$ on  $B$ derived from (6.6), we have
$B$ derived from (6.6), we have  $c(u')^{\otimes 2} = t(u',\Phi (u'))$ for
$c(u')^{\otimes 2} = t(u',\Phi (u'))$ for  $u' \in Y$.
$u' \in Y$.
Proposition 8.3 shows that this assumption is verified upon replacing ![]() $L$ by a suitable translate.
$L$ by a suitable translate.
Proposition 9.1 Let ![]() $s$ be a non-zero global section of
$s$ be a non-zero global section of ![]() $L^\mathrm {an}$ and let
$L^\mathrm {an}$ and let ![]() $f$ be a theta function of
$f$ be a theta function of ![]() $L$ corresponding to
$L$ corresponding to ![]() $s$. Let
$s$. Let ![]() $x \in A^\mathrm {an}$, choose
$x \in A^\mathrm {an}$, choose ![]() $z \in E^\mathrm {an}$ such that
$z \in E^\mathrm {an}$ such that ![]() $p(z)=x$ and assume that
$p(z)=x$ and assume that ![]() $s$ does not vanish at
$s$ does not vanish at ![]() $x$. The equality
$x$. The equality
holds.
Proof. Our assumption implies that ![]() $c_\mathrm {trop}(u')= \frac {1}{2}[u',u']$ for
$c_\mathrm {trop}(u')= \frac {1}{2}[u',u']$ for ![]() $u' \in Y$. We have
$u' \in Y$. We have ![]() $\langle \Phi (u'),\mathrm {trop}(z) \rangle = [\mathrm {trop}(z),u']$ for
$\langle \Phi (u'),\mathrm {trop}(z) \rangle = [\mathrm {trop}(z),u']$ for ![]() $z \in E^\mathrm {an}$ and
$z \in E^\mathrm {an}$ and ![]() $u' \in Y$. The functional equation (8.3) therefore translates into
$u' \in Y$. The functional equation (8.3) therefore translates into
for ![]() $z \in E^\mathrm {an}$ and
$z \in E^\mathrm {an}$ and ![]() $u' \in Y$. It follows that the right-hand side of (9.1) is independent of the choice of
$u' \in Y$. It follows that the right-hand side of (9.1) is independent of the choice of ![]() $z \in E^\mathrm {an}$ such that
$z \in E^\mathrm {an}$ such that ![]() $p(z)=x$. As
$p(z)=x$. As ![]() $A^\mathrm {alg}$ is dense in
$A^\mathrm {alg}$ is dense in ![]() $A^\mathrm {an}$, it suffices by continuity to verify equality (9.1) for
$A^\mathrm {an}$, it suffices by continuity to verify equality (9.1) for ![]() $x \in A^\mathrm {alg}$.
$x \in A^\mathrm {alg}$.
Write ![]() $D=\operatorname {div}_L s$. We have seen in § 5.3 that the restriction of
$D=\operatorname {div}_L s$. We have seen in § 5.3 that the restriction of ![]() $-\log \|s(x)\|_L$ to
$-\log \|s(x)\|_L$ to ![]() $A^\mathrm {alg}$ defines a Néron function for
$A^\mathrm {alg}$ defines a Néron function for ![]() $D$. Also, a Néron function for
$D$. Also, a Néron function for ![]() $D$ is unique up to an additive constant.
$D$ is unique up to an additive constant.
Let ![]() $\Lambda (x)$ denote the restriction of the right-hand side of (9.1) to
$\Lambda (x)$ denote the restriction of the right-hand side of (9.1) to ![]() $A^\mathrm {alg}$. The compatibility of the rigidifications of
$A^\mathrm {alg}$. The compatibility of the rigidifications of ![]() $p^*L$ and
$p^*L$ and ![]() $q^*M$ at the origin along the isomorphism
$q^*M$ at the origin along the isomorphism ![]() $p^*L \xrightarrow {\sim } q^*M$ implies that the continuous function
$p^*L \xrightarrow {\sim } q^*M$ implies that the continuous function ![]() $-\log \! \| s(p(z)) \|_L + \log \! \|f(z)\|_{q^*M}$ evaluates as zero when
$-\log \! \| s(p(z)) \|_L + \log \! \|f(z)\|_{q^*M}$ evaluates as zero when ![]() $z=0$. Hence, in order to prove (9.1) for
$z=0$. Hence, in order to prove (9.1) for ![]() $x \in A^\mathrm {alg}$, it suffices to show that
$x \in A^\mathrm {alg}$, it suffices to show that ![]() $\Lambda (x)$ is a Néron function for
$\Lambda (x)$ is a Néron function for ![]() $D$.
$D$.
First of all, we have that ![]() $\Lambda (x)$ defines a Weil function for
$\Lambda (x)$ defines a Weil function for ![]() $D$ on
$D$ on ![]() $A^\mathrm {alg} \setminus \operatorname {Supp}(D)$. It is therefore left to show that there is a rational function
$A^\mathrm {alg} \setminus \operatorname {Supp}(D)$. It is therefore left to show that there is a rational function ![]() $h$ on
$h$ on ![]() $A$ with
$A$ with ![]() $\operatorname {div} h = -[2]^*D + 4 D$ such that
$\operatorname {div} h = -[2]^*D + 4 D$ such that
for ![]() $x \in A^\mathrm {alg}$ away from the support of
$x \in A^\mathrm {alg}$ away from the support of ![]() $-[2]^*D + 4 D$. We note that
$-[2]^*D + 4 D$. We note that
Let ![]() $\mathcal {M}$ denote the unique cubical extension of the rigidified line bundle
$\mathcal {M}$ denote the unique cubical extension of the rigidified line bundle ![]() $M$ over the abelian scheme
$M$ over the abelian scheme ![]() $\mathcal {B}$. Then
$\mathcal {B}$. Then ![]() $\mathcal {M}$ is symmetric and it follows that there is a unique isomorphism of rigidified line bundles
$\mathcal {M}$ is symmetric and it follows that there is a unique isomorphism of rigidified line bundles ![]() $[2]^*\mathcal {M} \xrightarrow {\sim } \mathcal {M}^{\otimes 4}$ on
$[2]^*\mathcal {M} \xrightarrow {\sim } \mathcal {M}^{\otimes 4}$ on ![]() $\mathcal {B}$. The restriction of this isomorphism to
$\mathcal {B}$. The restriction of this isomorphism to ![]() $B^\mathrm {an}$ is by construction an isometry for the model metric
$B^\mathrm {an}$ is by construction an isometry for the model metric ![]() $\|\cdot \|_M$ associated to
$\|\cdot \|_M$ associated to ![]() $\mathcal {M}$ on
$\mathcal {M}$ on ![]() $M^\mathrm {an}$ on
$M^\mathrm {an}$ on ![]() $B^\mathrm {an}$. We also note that the model metric
$B^\mathrm {an}$. We also note that the model metric ![]() $\|\cdot \|_M$ equals the canonical metric on
$\|\cdot \|_M$ equals the canonical metric on ![]() $M^\mathrm {an}$. Let
$M^\mathrm {an}$. Let ![]() $g(z) = f(z)^4 \cdot f(2z)^{-1}$, viewed as a meromorphic function on
$g(z) = f(z)^4 \cdot f(2z)^{-1}$, viewed as a meromorphic function on ![]() $E$. We conclude that
$E$. We conclude that
We claim that the function ![]() $g(z)$ is
$g(z)$ is ![]() $Y$-invariant. Indeed, by the functional equation (8.2), we have
$Y$-invariant. Indeed, by the functional equation (8.2), we have
for ![]() $u' \in Y$ and
$u' \in Y$ and ![]() $z \in E^\mathrm {an}$. As
$z \in E^\mathrm {an}$. As ![]() $e_u(z)$ is bilinear, we have
$e_u(z)$ is bilinear, we have ![]() $e_{\Phi (u')}(z)^{\otimes 4} = e_{\Phi (2u')}(2z)$ and the condition
$e_{\Phi (u')}(z)^{\otimes 4} = e_{\Phi (2u')}(2z)$ and the condition ![]() $c(u')^{\otimes 2} = t(u',\Phi (u'))$ for
$c(u')^{\otimes 2} = t(u',\Phi (u'))$ for ![]() $u' \in Y$ implies that
$u' \in Y$ implies that ![]() $c(u')^{\otimes 4} = c(2u')$, up to canonical identifications. The claim follows. As a result, we may identify
$c(u')^{\otimes 4} = c(2u')$, up to canonical identifications. The claim follows. As a result, we may identify ![]() $g$ with
$g$ with ![]() $p^*h$. Combining (9.4) and (9.5), we obtain (9.3).
$p^*h$. Combining (9.4) and (9.5), we obtain (9.3).
Remark 9.1 The formula in Proposition 9.1 may be compared with the formulas for Néron functions associated to ![]() $L$ given in [Reference HindryHin93, Théorème D], and in [Reference HindryHin93, Théorème C] and [Reference WernerWer97, Corollary 3.6] in the situation that
$L$ given in [Reference HindryHin93, Théorème D], and in [Reference HindryHin93, Théorème C] and [Reference WernerWer97, Corollary 3.6] in the situation that ![]() $A$ has toric reduction.
$A$ has toric reduction.
10. Semistable models and canonical metric
Recall that we assume that ![]() $A$ has semistable reduction over
$A$ has semistable reduction over ![]() $F$. Let
$F$. Let ![]() $\mathcal {N}$ denote the Néron model of
$\mathcal {N}$ denote the Néron model of ![]() $A$ over
$A$ over ![]() $R$. Then
$R$. Then ![]() $\mathcal {N}$ is a semistable model of
$\mathcal {N}$ is a semistable model of ![]() $A$ over
$A$ over ![]() $R$. When
$R$. When ![]() $D$ is a prime divisor on
$D$ is a prime divisor on ![]() $A$, we denote by
$A$, we denote by ![]() $\bar {D}$ its Zariski closure on
$\bar {D}$ its Zariski closure on ![]() $\mathcal {N}$. This is a prime divisor on
$\mathcal {N}$. This is a prime divisor on ![]() $\mathcal {N}$. We extend the assignment
$\mathcal {N}$. We extend the assignment ![]() $D \mapsto \bar {D}$ by linearity to the set of all divisors on
$D \mapsto \bar {D}$ by linearity to the set of all divisors on ![]() $A$. Following [Reference LangLan83, § 11.5], if
$A$. Following [Reference LangLan83, § 11.5], if ![]() $D$ is a divisor on
$D$ is a divisor on ![]() $A$, we call the associated divisor
$A$, we call the associated divisor ![]() $\bar {D}$ on
$\bar {D}$ on ![]() $\mathcal {N}$ the thickening of
$\mathcal {N}$ the thickening of ![]() $D$ on
$D$ on ![]() $\mathcal {N}$.
$\mathcal {N}$.
For each ![]() $w \in A(F)$, we write
$w \in A(F)$, we write ![]() $\bar {w}$ for the section of
$\bar {w}$ for the section of ![]() $\mathcal {N}$ corresponding to
$\mathcal {N}$ corresponding to ![]() $w$. Let
$w$. Let ![]() $\Phi _{\mathcal {N}}$ denote the group of connected components of the special fiber of
$\Phi _{\mathcal {N}}$ denote the group of connected components of the special fiber of ![]() $\mathcal {N}$. Let
$\mathcal {N}$. Let ![]() $n \in \mathbb {Z}_{>0}$ be such that
$n \in \mathbb {Z}_{>0}$ be such that ![]() $n \cdot \Phi _{\mathcal {N}} =0$ and write
$n \cdot \Phi _{\mathcal {N}} =0$ and write ![]() $M=L^{\otimes 2n}$. By Lemma 2.1, the cubical line bundle
$M=L^{\otimes 2n}$. By Lemma 2.1, the cubical line bundle ![]() $M$ admits a unique cubical extension
$M$ admits a unique cubical extension ![]() $\mathcal {M}$ over
$\mathcal {M}$ over ![]() $\mathcal {N}$.
$\mathcal {N}$.
The next result is essentially a classical result due to Néron (see, for example, [Reference LangLan83, § 11.5] or [Reference Moret-BaillyMor85, § III.1.3]).
Proposition 10.1 Let ![]() $s$ be a non-zero rational section of
$s$ be a non-zero rational section of ![]() $L$. Write
$L$. Write ![]() $t=s^{\otimes 2n}$ and view
$t=s^{\otimes 2n}$ and view ![]() $t$ as a rational section of the cubical line bundle
$t$ as a rational section of the cubical line bundle ![]() $\mathcal {M}$ over
$\mathcal {M}$ over ![]() $\mathcal {N}$. Write
$\mathcal {N}$. Write ![]() $D = \operatorname {div}_L s$ and let
$D = \operatorname {div}_L s$ and let ![]() $\bar {D}$ denote the thickening of
$\bar {D}$ denote the thickening of ![]() $D$ in
$D$ in ![]() $\mathcal {N}$. Let
$\mathcal {N}$. Let ![]() $x \in A(F)$ and let
$x \in A(F)$ and let ![]() $\bar {x}$ denote the closure of
$\bar {x}$ denote the closure of ![]() $x$ in
$x$ in ![]() $\mathcal {N}$. Let
$\mathcal {N}$. Let ![]() $\xi \in \Phi _{\mathcal {N}}$ be such that
$\xi \in \Phi _{\mathcal {N}}$ be such that ![]() $x$ specializes to
$x$ specializes to ![]() $\xi$. Assume that
$\xi$. Assume that ![]() $x \notin \operatorname {Supp}(D)$. Then the equality
$x \notin \operatorname {Supp}(D)$. Then the equality
holds. Here ![]() $(\bar {x} \cdot \bar {D})$ denotes the intersection multiplicity of the
$(\bar {x} \cdot \bar {D})$ denotes the intersection multiplicity of the ![]() $1$-cycle
$1$-cycle ![]() $\bar {x}$ with the divisor
$\bar {x}$ with the divisor ![]() $\bar {D}$ on the regular scheme
$\bar {D}$ on the regular scheme ![]() $\mathcal {N}$.
$\mathcal {N}$.
Proof. Write ![]() $E =\operatorname {div}_\mathcal {M}(t)$, viewed as a Cartier divisor on
$E =\operatorname {div}_\mathcal {M}(t)$, viewed as a Cartier divisor on ![]() $\mathcal {N}$. Following [Reference Moret-BaillyMor85, §§ III.1.2–4], we consider the map
$\mathcal {N}$. Following [Reference Moret-BaillyMor85, §§ III.1.2–4], we consider the map ![]() $\langle t,\cdot \rangle \colon A(F) \setminus \operatorname {Supp}(D) \to \mathbb {R}$ given by setting
$\langle t,\cdot \rangle \colon A(F) \setminus \operatorname {Supp}(D) \to \mathbb {R}$ given by setting ![]() $\langle t,w \rangle = (\bar {w} \cdot E)$, where
$\langle t,w \rangle = (\bar {w} \cdot E)$, where ![]() $(\bar {w} \cdot E)$ denotes the intersection multiplicity of the
$(\bar {w} \cdot E)$ denotes the intersection multiplicity of the ![]() $1$-cycle
$1$-cycle ![]() $\bar {w}$ with the divisor
$\bar {w}$ with the divisor ![]() $E$ on
$E$ on ![]() $\mathcal {N}$. The discussion in [Reference Moret-BaillyMor85, §§ III.1.2–4] shows that
$\mathcal {N}$. The discussion in [Reference Moret-BaillyMor85, §§ III.1.2–4] shows that ![]() $\langle t,\cdot \rangle$ extends uniquely as a Weil function on
$\langle t,\cdot \rangle$ extends uniquely as a Weil function on ![]() $A^\mathrm {alg}$ with respect to the divisor
$A^\mathrm {alg}$ with respect to the divisor ![]() $2n D$. We claim that
$2n D$. We claim that ![]() $\langle t,w \rangle$ is actually a Néron function with respect to
$\langle t,w \rangle$ is actually a Néron function with respect to ![]() $2n D$. Let
$2n D$. Let ![]() $h$ as in § 5.3 be the rational function on
$h$ as in § 5.3 be the rational function on ![]() $A$ corresponding to the rational section
$A$ corresponding to the rational section ![]() $s^{\otimes 4} \otimes [2]^*s^{\otimes -1}$ of the rigidified trivial line bundle
$s^{\otimes 4} \otimes [2]^*s^{\otimes -1}$ of the rigidified trivial line bundle ![]() $L^{\otimes 4} \otimes [2]^*L^{\otimes -1}$. Let
$L^{\otimes 4} \otimes [2]^*L^{\otimes -1}$. Let ![]() $w \in A(F)$ and assume that
$w \in A(F)$ and assume that ![]() $w$ is not contained in the support of
$w$ is not contained in the support of ![]() $\operatorname {div} h$. Observe that
$\operatorname {div} h$. Observe that ![]() $[2] \colon A \to A$ extends as the multiplication-by-two map of the commutative group scheme
$[2] \colon A \to A$ extends as the multiplication-by-two map of the commutative group scheme ![]() $\mathcal {N}$. We compute
$\mathcal {N}$. We compute
 \begin{align*} 4\langle t, w \rangle - \langle t,2w \rangle & = 4(\bar{w} \cdot E) - (\overline{[2](w)} \cdot E ) \\ & =4(\bar{w} \cdot E) - (([2] \circ \bar{w}) \cdot E ) \\ & = 4(\bar{w} \cdot E) - (\bar{w} \cdot [2]^*E) \\ & = (\bar{w} \cdot (4E - [2]^*E) ). \end{align*}
\begin{align*} 4\langle t, w \rangle - \langle t,2w \rangle & = 4(\bar{w} \cdot E) - (\overline{[2](w)} \cdot E ) \\ & =4(\bar{w} \cdot E) - (([2] \circ \bar{w}) \cdot E ) \\ & = 4(\bar{w} \cdot E) - (\bar{w} \cdot [2]^*E) \\ & = (\bar{w} \cdot (4E - [2]^*E) ). \end{align*}
Now, as ![]() $\mathcal {M}$ is a cubical extension of
$\mathcal {M}$ is a cubical extension of ![]() $L^{\otimes 2n}$, we have that the
$L^{\otimes 2n}$, we have that the ![]() $(2n)$th tensor power of the isomorphism
$(2n)$th tensor power of the isomorphism ![]() $\varphi \colon L^{\otimes 4} \xrightarrow {\sim } [2]^*L$ extends into an isomorphism of line bundles
$\varphi \colon L^{\otimes 4} \xrightarrow {\sim } [2]^*L$ extends into an isomorphism of line bundles ![]() $\mathcal {M}^{\otimes 4} \xrightarrow {\sim } [2]^* \mathcal {M}$ over
$\mathcal {M}^{\otimes 4} \xrightarrow {\sim } [2]^* \mathcal {M}$ over ![]() $\mathcal {N}$. It follows that
$\mathcal {N}$. It follows that ![]() $4E - [2]^*E$ coincides with
$4E - [2]^*E$ coincides with ![]() $2n \operatorname {div} h$, where
$2n \operatorname {div} h$, where ![]() $h$ is now viewed as a rational function on the integral scheme
$h$ is now viewed as a rational function on the integral scheme ![]() $\mathcal {N}$. We find that
$\mathcal {N}$. We find that
and, since ![]() $(\bar {w} \cdot \operatorname {div} h) = -\log |h(w)|$, we conclude that
$(\bar {w} \cdot \operatorname {div} h) = -\log |h(w)|$, we conclude that
This shows that ![]() $\langle t,w \rangle$ is a Néron function with respect to the divisor
$\langle t,w \rangle$ is a Néron function with respect to the divisor ![]() $2n D$. Comparison with (5.2) and the uniqueness of Néron functions up to additive constants yield that
$2n D$. Comparison with (5.2) and the uniqueness of Néron functions up to additive constants yield that ![]() $\langle t,\cdot \rangle = -2n \log \! \|s\|_L$ as functions on
$\langle t,\cdot \rangle = -2n \log \! \|s\|_L$ as functions on ![]() $A^\mathrm {alg} \setminus \operatorname {Supp}(D)$. Explicitly, we have
$A^\mathrm {alg} \setminus \operatorname {Supp}(D)$. Explicitly, we have ![]() $E= 2n \bar {D} + \sum _{\zeta \in \Phi _{\mathcal {N}}} \operatorname {ord}_{\zeta,\mathcal {M}}(t) \cdot \bar {\zeta }$. For
$E= 2n \bar {D} + \sum _{\zeta \in \Phi _{\mathcal {N}}} \operatorname {ord}_{\zeta,\mathcal {M}}(t) \cdot \bar {\zeta }$. For ![]() $x \in A(F)$ and
$x \in A(F)$ and ![]() $\xi \in \Phi _\mathcal {N}$ as in the proposition, this gives
$\xi \in \Phi _\mathcal {N}$ as in the proposition, this gives ![]() $\langle t,x \rangle = (\bar {x} \cdot E) = 2n \,(\bar {x} \cdot \bar {D}) + \operatorname {ord}_{\xi,\mathcal {M}}(t)$. The equality in (10.1) follows.
$\langle t,x \rangle = (\bar {x} \cdot E) = 2n \,(\bar {x} \cdot \bar {D}) + \operatorname {ord}_{\xi,\mathcal {M}}(t)$. The equality in (10.1) follows.
Now let ![]() $\mathcal {A}$ be any semistable model of
$\mathcal {A}$ be any semistable model of ![]() $A$ over
$A$ over ![]() $R$. Let
$R$. Let ![]() $\mathcal {N}$ be the Néron model of
$\mathcal {N}$ be the Néron model of ![]() $A$. As both
$A$. As both ![]() $\mathcal {A}$ and
$\mathcal {A}$ and ![]() $\mathcal {N}$ are semistable models of
$\mathcal {N}$ are semistable models of ![]() $A$ over
$A$ over ![]() $R$, the natural map
$R$, the natural map ![]() $\mathcal {A} \to \mathcal {N}$ given by the Néron mapping property is an open immersion.
$\mathcal {A} \to \mathcal {N}$ given by the Néron mapping property is an open immersion.
Assume that ![]() $L$ has a cubical extension
$L$ has a cubical extension ![]() $\mathcal {L}$ over
$\mathcal {L}$ over ![]() $\mathcal {A}$. Let
$\mathcal {A}$. Let ![]() $s$ be a non-zero rational section of
$s$ be a non-zero rational section of ![]() $L$ and view
$L$ and view ![]() $s$ as a rational section of the cubical line bundle
$s$ as a rational section of the cubical line bundle ![]() $\mathcal {L}$ over
$\mathcal {L}$ over ![]() $\mathcal {A}$. We have the following variant of Proposition 10.1. Note that we similarly have a notion of thickening of divisors on
$\mathcal {A}$. We have the following variant of Proposition 10.1. Note that we similarly have a notion of thickening of divisors on ![]() $A$ in
$A$ in ![]() $\mathcal {A}$.
$\mathcal {A}$.
Proposition 10.2 Write ![]() $D = \operatorname {div}_L s$ and let
$D = \operatorname {div}_L s$ and let ![]() $\bar {D}$ denote the thickening of
$\bar {D}$ denote the thickening of ![]() $D$ in
$D$ in ![]() $\mathcal {A}$. Let
$\mathcal {A}$. Let ![]() $\xi \in \Phi _\mathcal {A}$ and let
$\xi \in \Phi _\mathcal {A}$ and let ![]() $x \in A(F)$ be such that its Zariski closure
$x \in A(F)$ be such that its Zariski closure ![]() $\bar {x}$ in
$\bar {x}$ in ![]() $\mathcal {A}$ intersects the irreducible component corresponding to
$\mathcal {A}$ intersects the irreducible component corresponding to ![]() $\xi$. Assume that
$\xi$. Assume that ![]() $x \notin \operatorname {Supp}(D)$. Then the equality
$x \notin \operatorname {Supp}(D)$. Then the equality
holds. Here ![]() $(\bar {x} \cdot \bar {D})$ denotes the intersection multiplicity of the
$(\bar {x} \cdot \bar {D})$ denotes the intersection multiplicity of the ![]() $1$-cycle
$1$-cycle ![]() $\bar {x}$ with the divisor
$\bar {x}$ with the divisor ![]() $\bar {D}$ on the regular scheme
$\bar {D}$ on the regular scheme ![]() $\mathcal {A}$.
$\mathcal {A}$.
Proof. Let ![]() $n \in \mathbb {Z}_{>0}$ be such that
$n \in \mathbb {Z}_{>0}$ be such that ![]() $n \cdot \Phi _{\mathcal {N}} =0$ and let
$n \cdot \Phi _{\mathcal {N}} =0$ and let ![]() $\mathcal {M}$ denote the cubical extension of the line bundle
$\mathcal {M}$ denote the cubical extension of the line bundle ![]() $M=L^{\otimes 2n}$ over
$M=L^{\otimes 2n}$ over ![]() $\mathcal {N}$ whose existence is guaranteed by Lemma 2.1. Then
$\mathcal {N}$ whose existence is guaranteed by Lemma 2.1. Then ![]() $\mathcal {M}|_\mathcal {A} = \mathcal {L}^{\otimes 2n}$ by uniqueness of cubical extensions. Noting that
$\mathcal {M}|_\mathcal {A} = \mathcal {L}^{\otimes 2n}$ by uniqueness of cubical extensions. Noting that ![]() $\operatorname {ord}_{\xi,\mathcal {M}}(s^{\otimes 2n}) = 2n \operatorname {ord}_{\xi,\mathcal {L}}(s)$, we find the required equality by applying Proposition 10.1.
$\operatorname {ord}_{\xi,\mathcal {M}}(s^{\otimes 2n}) = 2n \operatorname {ord}_{\xi,\mathcal {L}}(s)$, we find the required equality by applying Proposition 10.1.
10.1 Evaluations at Shilov points
Let ![]() $A^\mathrm {an}$ denote the Berkovich analytification of
$A^\mathrm {an}$ denote the Berkovich analytification of ![]() $A$. Let
$A$. Let ![]() $\mathcal {V}$ be a projective integral model of
$\mathcal {V}$ be a projective integral model of ![]() $A$ containing
$A$ containing ![]() $\mathcal {N}$ and hence
$\mathcal {N}$ and hence ![]() $\mathcal {A}$ as an open subscheme. Let
$\mathcal {A}$ as an open subscheme. Let ![]() $\xi \in \Phi _\mathcal {A}$. It follows from what we have said at the end of § 7.1 that the Shilov point
$\xi \in \Phi _\mathcal {A}$. It follows from what we have said at the end of § 7.1 that the Shilov point ![]() $x_\xi$ of
$x_\xi$ of ![]() $A^\mathrm {an}$ determined by the generic point of
$A^\mathrm {an}$ determined by the generic point of ![]() $\xi$ in the special fiber
$\xi$ in the special fiber ![]() $\mathcal {V}_{\tilde {\mathbb {F}}}$ is an element of the canonical skeleton
$\mathcal {V}_{\tilde {\mathbb {F}}}$ is an element of the canonical skeleton ![]() $\Sigma$ of
$\Sigma$ of ![]() $A^\mathrm {an}$.
$A^\mathrm {an}$.
Let ![]() $\tau \colon A^\mathrm {an} \to \Sigma$ be the reduction map onto
$\tau \colon A^\mathrm {an} \to \Sigma$ be the reduction map onto ![]() $\Sigma$.
$\Sigma$.
Proposition 10.3 The equalities
hold.
Proof. Write ![]() $D = \operatorname {div}_L s$ and let
$D = \operatorname {div}_L s$ and let ![]() $\bar {D}$ denote the thickening of
$\bar {D}$ denote the thickening of ![]() $D$ in
$D$ in ![]() $\mathcal {A}$. Let
$\mathcal {A}$. Let ![]() $x$ be any closed point of
$x$ be any closed point of ![]() $A$ with
$A$ with ![]() $x \notin \operatorname {Supp}(D)$ such that its Zariski closure
$x \notin \operatorname {Supp}(D)$ such that its Zariski closure ![]() $\bar {x}$ in
$\bar {x}$ in ![]() $\mathcal {A}$ intersects the irreducible component
$\mathcal {A}$ intersects the irreducible component ![]() $X$ corresponding to
$X$ corresponding to ![]() $\xi$. From Proposition 10.2, we readily obtain the equality
$\xi$. From Proposition 10.2, we readily obtain the equality
This can be seen by taking a finite extension ![]() $F'$ of
$F'$ of ![]() $F$ such that
$F$ such that ![]() $x$ extends as a section over the valuation ring of
$x$ extends as a section over the valuation ring of ![]() $F'$.
$F'$.
Denote by ![]() $\Omega$ (respectively,
$\Omega$ (respectively, ![]() $\Omega '$) the inverse image of
$\Omega '$) the inverse image of ![]() $X$ (respectively,
$X$ (respectively, ![]() $X \setminus \operatorname {Supp}(\bar {D})$) under the reduction map
$X \setminus \operatorname {Supp}(\bar {D})$) under the reduction map ![]() $\mathrm {red}_{\mathcal {V}} \colon A^\mathrm {an} \to \mathcal {V}_{\tilde {\mathbb {F}}}$. We note that
$\mathrm {red}_{\mathcal {V}} \colon A^\mathrm {an} \to \mathcal {V}_{\tilde {\mathbb {F}}}$. We note that ![]() $X \setminus \operatorname {Supp}(\bar {D}) \subset X \subset \mathcal {A}_{\tilde {\mathbb {F}}} \subset \mathcal {V}_{\tilde {\mathbb {F}}}$ are open immersions, that
$X \setminus \operatorname {Supp}(\bar {D}) \subset X \subset \mathcal {A}_{\tilde {\mathbb {F}}} \subset \mathcal {V}_{\tilde {\mathbb {F}}}$ are open immersions, that ![]() $\Omega$ (respectively,
$\Omega$ (respectively, ![]() $\Omega '$) is the Raynaud generic fiber of the formal completion of
$\Omega '$) is the Raynaud generic fiber of the formal completion of ![]() $\mathcal {A}$ along
$\mathcal {A}$ along ![]() $X$ (respectively,
$X$ (respectively, ![]() $X \setminus \operatorname {Supp}(\bar {D})$), that both
$X \setminus \operatorname {Supp}(\bar {D})$), that both ![]() $\Omega$ and
$\Omega$ and ![]() $\Omega '$ contain the Shilov point
$\Omega '$ contain the Shilov point ![]() $x_\xi$ corresponding to
$x_\xi$ corresponding to ![]() $X$ and that
$X$ and that ![]() $\Omega$ is exactly the set of
$\Omega$ is exactly the set of ![]() $x \in A^\mathrm {an}$ such that
$x \in A^\mathrm {an}$ such that ![]() $\tau (x) = x_\xi$.
$\tau (x) = x_\xi$.
Denote by ![]() $\Omega _0$ (respectively,
$\Omega _0$ (respectively, ![]() $\Omega '_0$) the set of algebraic points of
$\Omega '_0$) the set of algebraic points of ![]() $\Omega$ (respectively,
$\Omega$ (respectively, ![]() $\Omega '$). Then
$\Omega '$). Then ![]() $\Omega _0$ (respectively,
$\Omega _0$ (respectively, ![]() $\Omega '_0$) is dense in
$\Omega '_0$) is dense in ![]() $\Omega$ (respectively,
$\Omega$ (respectively, ![]() $\Omega '$). Equation (10.4) gives
$\Omega '$). Equation (10.4) gives
As ![]() $\Omega _0$ is dense in
$\Omega _0$ is dense in ![]() $\Omega$, this implies that
$\Omega$, this implies that
Equation (10.4) also gives
On the one hand, the combination of (10.5) and (10.6) gives
On the other hand, as ![]() $\Omega '_0$ is dense in
$\Omega '_0$ is dense in ![]() $\Omega '$, and
$\Omega '$, and ![]() $\Omega '$ contains
$\Omega '$ contains ![]() $x_\xi$, (10.6) implies by continuity that
$x_\xi$, (10.6) implies by continuity that
This proves the proposition.
Corollary 10.4 For all ![]() $y \in \Sigma$, one has the equality
$y \in \Sigma$, one has the equality
In particular, the equality
holds.
Proof. For each torsion point ![]() $x \in \Sigma$, there exist a finite extension
$x \in \Sigma$, there exist a finite extension ![]() $F'$ of
$F'$ of ![]() $F$ and a semistable model
$F$ and a semistable model ![]() $\mathcal {A}'$ of
$\mathcal {A}'$ of ![]() $A$ over the valuation ring of
$A$ over the valuation ring of ![]() $F'$ such that
$F'$ such that ![]() $x=x_{\xi '}$ for some
$x=x_{\xi '}$ for some ![]() $\xi ' \in \Phi _{\mathcal {A}'}$. By Lemma 2.2, upon a further base change, we may assume that
$\xi ' \in \Phi _{\mathcal {A}'}$. By Lemma 2.2, upon a further base change, we may assume that ![]() $\mathcal {A}'$ admits a cubical extension
$\mathcal {A}'$ admits a cubical extension ![]() $\mathcal {L}'$ of
$\mathcal {L}'$ of ![]() $L$. Proposition 10.3 therefore gives
$L$. Proposition 10.3 therefore gives
for all ![]() $y \in \Sigma _{\mathrm {tor}}$. We obtain (10.7) by density of
$y \in \Sigma _{\mathrm {tor}}$. We obtain (10.7) by density of ![]() $\Sigma _{\mathrm {tor}}$ and by continuity. Equation (10.8) is immediate from (10.7).
$\Sigma _{\mathrm {tor}}$ and by continuity. Equation (10.8) is immediate from (10.7).
Assume that ![]() $L$ defines a principal polarization
$L$ defines a principal polarization ![]() $\lambda \colon A \xrightarrow {\sim } A^t$. Consider the invariant
$\lambda \colon A \xrightarrow {\sim } A^t$. Consider the invariant ![]() $I(A,\lambda )$ as in (7.4).
$I(A,\lambda )$ as in (7.4).
Corollary 10.5 The formula
holds. In particular, ![]() $I(A,\lambda )$ vanishes if
$I(A,\lambda )$ vanishes if ![]() $A$ has good reduction.
$A$ has good reduction.
10.2 Direct images
Let ![]() $\pi \colon \mathcal {A} \to S=\operatorname {Spec} R$ denote the structure morphism of the semistable model
$\pi \colon \mathcal {A} \to S=\operatorname {Spec} R$ denote the structure morphism of the semistable model ![]() $\mathcal {A}$. The sheaf
$\mathcal {A}$. The sheaf ![]() $\pi _*\mathcal {L}$ is coherent, by [Reference Moret-BaillyMor85, Lemme VI.1.4.2], and torsion-free and, hence, locally free. We assume from now on that
$\pi _*\mathcal {L}$ is coherent, by [Reference Moret-BaillyMor85, Lemme VI.1.4.2], and torsion-free and, hence, locally free. We assume from now on that ![]() $\pi _*\mathcal {L}$ is in fact a line bundle on
$\pi _*\mathcal {L}$ is in fact a line bundle on ![]() $S$, that is, the generic fiber
$S$, that is, the generic fiber ![]() $L$ of
$L$ of ![]() $\mathcal {L}$ determines a principal polarization of
$\mathcal {L}$ determines a principal polarization of ![]() $A$. We may view
$A$. We may view ![]() $s$ also as a non-zero rational section of the sheaf
$s$ also as a non-zero rational section of the sheaf ![]() $\pi _*\mathcal {L}$.
$\pi _*\mathcal {L}$.
Proposition 10.6 Assume that ![]() $\pi _*\mathcal {L}$ is a line bundle. Let
$\pi _*\mathcal {L}$ is a line bundle. Let ![]() $v$ denote the closed point of
$v$ denote the closed point of ![]() $S$. Then
$S$. Then ![]() $\operatorname {ord}_v (s) = \min _{\xi \in \Phi _\mathcal {A}} \operatorname {ord}_{\xi,\mathcal {L}} (s)$.
$\operatorname {ord}_v (s) = \min _{\xi \in \Phi _\mathcal {A}} \operatorname {ord}_{\xi,\mathcal {L}} (s)$.
Proof. Let ![]() $a=\operatorname {ord}_v (s)$ and set
$a=\operatorname {ord}_v (s)$ and set ![]() $s'=\varpi ^{-a}s$. Let
$s'=\varpi ^{-a}s$. Let ![]() $M=H^0(S,\pi _*\mathcal {L})$. By assumption,
$M=H^0(S,\pi _*\mathcal {L})$. By assumption, ![]() $M$ is a free rank-one
$M$ is a free rank-one ![]() $R$-module and
$R$-module and ![]() $s'$ is a generator of
$s'$ is a generator of ![]() $M$. Let
$M$. Let ![]() $\xi \in \Phi _\mathcal {A}$. The
$\xi \in \Phi _\mathcal {A}$. The ![]() $R$-module
$R$-module ![]() $M$ is canonically identified with the
$M$ is canonically identified with the ![]() $R$-module
$R$-module ![]() $H^0(\mathcal {A},\mathcal {L})$ and this gives
$H^0(\mathcal {A},\mathcal {L})$ and this gives ![]() $\operatorname {ord}_\xi (s') \geqslant 0$. Since
$\operatorname {ord}_\xi (s') \geqslant 0$. Since ![]() $\operatorname {ord}_\xi (s')=-a+\operatorname {ord}_\xi (s)$, we conclude that
$\operatorname {ord}_\xi (s')=-a+\operatorname {ord}_\xi (s)$, we conclude that ![]() $\operatorname {ord}_\xi (s) \geqslant a$. We are left to prove that there exists a
$\operatorname {ord}_\xi (s) \geqslant a$. We are left to prove that there exists a ![]() $\xi \in \Phi _\mathcal {A}$ such that
$\xi \in \Phi _\mathcal {A}$ such that ![]() $\operatorname {ord}_\xi (s)=a$. Suppose that for all
$\operatorname {ord}_\xi (s)=a$. Suppose that for all ![]() $\xi \in \Phi _\mathcal {A}$, we have
$\xi \in \Phi _\mathcal {A}$, we have ![]() $\operatorname {ord}_\xi (s)>a$. Then
$\operatorname {ord}_\xi (s)>a$. Then ![]() $\operatorname {ord}_\xi (\varpi ^{-1}s') \geqslant 0$ for all
$\operatorname {ord}_\xi (\varpi ^{-1}s') \geqslant 0$ for all ![]() $\xi$ and hence
$\xi$ and hence ![]() $\varpi ^{-1}s' \in H^0(\mathcal {A},\mathcal {L})=M$. It follows that
$\varpi ^{-1}s' \in H^0(\mathcal {A},\mathcal {L})=M$. It follows that ![]() $M = \mathfrak {m}_R \cdot M$. This contradicts Nakayama's lemma.
$M = \mathfrak {m}_R \cdot M$. This contradicts Nakayama's lemma.
Define ![]() $\|s\|_{\pi _* \mathcal {L}}$ via the formula
$\|s\|_{\pi _* \mathcal {L}}$ via the formula ![]() $\operatorname {ord}_v (s) = -\log \! \|s\|_{\pi _* \mathcal {L}}$.
$\operatorname {ord}_v (s) = -\log \! \|s\|_{\pi _* \mathcal {L}}$.
Corollary 10.7 The equality
holds.
Proof. By Proposition 10.6, we have
By Proposition 10.3, this can be rewritten as
As the left-hand side is independent of the choice of semistable model of ![]() $A$ with cubical extension of
$A$ with cubical extension of ![]() $L$, we find that for any semistable model
$L$, we find that for any semistable model ![]() $\mathcal {A}'$ of
$\mathcal {A}'$ of ![]() $A$ with cubical extension
$A$ with cubical extension ![]() $\mathcal {L}'$ of
$\mathcal {L}'$ of ![]() $L$ over the valuation ring of any finite extension
$L$ over the valuation ring of any finite extension ![]() $F'$ of
$F'$ of ![]() $F$ that
$F$ that
For each torsion point ![]() $x \in \Sigma$, there exist a finite extension
$x \in \Sigma$, there exist a finite extension ![]() $F'$ of
$F'$ of ![]() $F$ and a semistable model
$F$ and a semistable model ![]() $\mathcal {A}'$ of
$\mathcal {A}'$ of ![]() $A$ over the valuation ring of
$A$ over the valuation ring of ![]() $F'$ such that
$F'$ such that ![]() $x=x_{\xi '}$ for some
$x=x_{\xi '}$ for some ![]() $\xi ' \in \Phi _{\mathcal {A}'}$. By Lemma 2.2, upon a further base change, we may assume that
$\xi ' \in \Phi _{\mathcal {A}'}$. By Lemma 2.2, upon a further base change, we may assume that ![]() $\mathcal {A}'$ admits a cubical extension
$\mathcal {A}'$ admits a cubical extension ![]() $\mathcal {L}'$ of
$\mathcal {L}'$ of ![]() $L$. We thus actually find that
$L$. We thus actually find that
By continuity and the density of ![]() $\Sigma _{\mathrm {tor}}$ in
$\Sigma _{\mathrm {tor}}$ in ![]() $\Sigma$, we deduce that
$\Sigma$, we deduce that
This finishes the proof of the corollary.
11. Proof of Theorem B
We continue to assume that the rigidified symmetric ample line bundle ![]() $L$ defines a principal polarization
$L$ defines a principal polarization ![]() $\lambda$ on
$\lambda$ on ![]() $A$. Let
$A$. Let ![]() $(X,Y,\Phi,b)$ be the principally polarized tropical abelian variety associated to
$(X,Y,\Phi,b)$ be the principally polarized tropical abelian variety associated to ![]() $(A,L)$ by Raynaud's uniformization theory and let
$(A,L)$ by Raynaud's uniformization theory and let ![]() $\Sigma = X_\mathbb {R}^*/Y$ be the associated polarized real torus as at the end of § 6. Let
$\Sigma = X_\mathbb {R}^*/Y$ be the associated polarized real torus as at the end of § 6. Let ![]() $[\cdot,\cdot ]$ denote the induced inner product on
$[\cdot,\cdot ]$ denote the induced inner product on ![]() $X_\mathbb {R}^*$.
$X_\mathbb {R}^*$.
We recall from § 8.1 that the tropical Riemann theta function associated to ![]() $(A,L)$ is the function
$(A,L)$ is the function ![]() $\Psi \colon X^*_\mathbb {R} \to \mathbb {R}$ given by
$\Psi \colon X^*_\mathbb {R} \to \mathbb {R}$ given by
for ![]() $\nu \in X^*_\mathbb {R}$. Let
$\nu \in X^*_\mathbb {R}$. Let ![]() $\|\cdot \|$ denote the norm associated to
$\|\cdot \|$ denote the norm associated to ![]() $[\cdot,\cdot ]$ on
$[\cdot,\cdot ]$ on ![]() $X_\mathbb {R}^*$. The modified tropical Riemann theta function is defined to be the function
$X_\mathbb {R}^*$. The modified tropical Riemann theta function is defined to be the function
The function ![]() $\|\Psi \|$ is
$\|\Psi \|$ is ![]() $Y$-invariant and hence descends to
$Y$-invariant and hence descends to ![]() $\Sigma$. Explicitly, we have
$\Sigma$. Explicitly, we have
for all ![]() $\nu \in X^*_\mathbb {R}$.
$\nu \in X^*_\mathbb {R}$.
We have the following result about the invariant ![]() $I(A,\lambda )$ as defined in (7.4).
$I(A,\lambda )$ as defined in (7.4).
Theorem 11.1 The formula
holds. Here ![]() $\mu _H$ is the Haar measure of unit volume on the real torus
$\mu _H$ is the Haar measure of unit volume on the real torus ![]() $\Sigma$.
$\Sigma$.
It is not hard to see that the integral ![]() $\int _\Sigma \| \Psi \| \, d \mu _H$ equals half the tropical moment of
$\int _\Sigma \| \Psi \| \, d \mu _H$ equals half the tropical moment of ![]() $\Sigma$. Thus, Theorem 11.1 implies part (a) of Theorem B.
$\Sigma$. Thus, Theorem 11.1 implies part (a) of Theorem B.
Proof of Theorem 11.1 Let ![]() $s$ be a non-zero global section of
$s$ be a non-zero global section of ![]() $L$ and let
$L$ and let ![]() $f$ be a theta function corresponding to
$f$ be a theta function corresponding to ![]() $s$. By Proposition 8.3, there exists an element
$s$. By Proposition 8.3, there exists an element ![]() $z_0 \in E^\mathrm {alg}$ such that the following four properties hold. Let
$z_0 \in E^\mathrm {alg}$ such that the following four properties hold. Let ![]() $y=p(z_0)$ and put
$y=p(z_0)$ and put ![]() $L'=T_y^*L$.
$L'=T_y^*L$.
(a) The line bundle
 $L'$ has an associated triple
$L'$ has an associated triple  $(M',\Phi,c')$ with
$(M',\Phi,c')$ with  $M'$ a symmetric rigidified line bundle that as a line bundle is isomorphic with
$M'$ a symmetric rigidified line bundle that as a line bundle is isomorphic with  $T_w^*M$, where
$T_w^*M$, where  $w=q(z_0)$, such that under the canonical identification of line bundles
$w=q(z_0)$, such that under the canonical identification of line bundles  $M'^{\otimes 2} = (\mathrm {id},\lambda _{B,L})^* P$ on
$M'^{\otimes 2} = (\mathrm {id},\lambda _{B,L})^* P$ on  $B$ derived from (6.6) and the symmetry of
$B$ derived from (6.6) and the symmetry of  $M'$, we have
$M'$, we have  $c'(u')^{\otimes 2} = t(u',\Phi (u'))$ for
$c'(u')^{\otimes 2} = t(u',\Phi (u'))$ for  $u' \in Y$.
$u' \in Y$.(b) The line bundle
 $L'$ is symmetric.
$L'$ is symmetric.(c) The function
 $T_{z_0}^*f$ is a theta function for the symmetric line bundle
$T_{z_0}^*f$ is a theta function for the symmetric line bundle  $L'$ corresponding to the section
$L'$ corresponding to the section  $T_y^*s$.
$T_y^*s$.(d) The tropicalization
 $\overline {T_{z_0}^*f}$ of the theta function
$\overline {T_{z_0}^*f}$ of the theta function  $T_{z_0}^*f$ is equal to the tropical Riemann theta function
$T_{z_0}^*f$ is equal to the tropical Riemann theta function  $\Psi$, up to an additive constant.
$\Psi$, up to an additive constant.
By the invariance property expressed in Lemma 7.3, in order to compute ![]() $I(A,\lambda )$ we may replace the line bundle
$I(A,\lambda )$ we may replace the line bundle ![]() $L$ by the line bundle
$L$ by the line bundle ![]() $L'=T_y^*L$. We may therefore assume that the following is verified for
$L'=T_y^*L$. We may therefore assume that the following is verified for ![]() $L$ and
$L$ and ![]() $f$: there exists a triple
$f$: there exists a triple ![]() $(M,\Phi,c)$ for
$(M,\Phi,c)$ for ![]() $L$ such that:
$L$ such that:
(i) under the identification of rigidified line bundles
 $M^{\otimes 2} = (\mathrm {id},\lambda _{B,L})^* P$ on
$M^{\otimes 2} = (\mathrm {id},\lambda _{B,L})^* P$ on  $B$ derived from (6.6), we have
$B$ derived from (6.6), we have  $c(u')^{\otimes 2} = t(u',\Phi (u'))$ for
$c(u')^{\otimes 2} = t(u',\Phi (u'))$ for  $u' \in Y$;
$u' \in Y$;(ii) the tropicalization
 $\bar {f}$ is equal to the tropical Riemann theta function
$\bar {f}$ is equal to the tropical Riemann theta function  $\Psi$, up to an additive constant.
$\Psi$, up to an additive constant.
Write ![]() $\bar {f} = \Psi + \gamma$, where
$\bar {f} = \Psi + \gamma$, where ![]() $\gamma \in \mathbb {R}$. Let
$\gamma \in \mathbb {R}$. Let ![]() $x \in \Sigma$ and let
$x \in \Sigma$ and let ![]() $z \in X_\mathbb {R}^*$ be such that
$z \in X_\mathbb {R}^*$ be such that ![]() $p(z)=x$. By condition (i), we may apply Proposition 9.1 and conclude that
$p(z)=x$. By condition (i), we may apply Proposition 9.1 and conclude that
 \begin{align} -\log\! \|s(x)\|_L & = \tfrac{1}{2}[z,z] + \bar{f}(z) \nonumber\\ & = \tfrac{1}{2}[z,z] + \Psi(z) + \gamma \nonumber\\ & = \| \Psi \|(x) + \gamma. \end{align}
\begin{align} -\log\! \|s(x)\|_L & = \tfrac{1}{2}[z,z] + \bar{f}(z) \nonumber\\ & = \tfrac{1}{2}[z,z] + \Psi(z) + \gamma \nonumber\\ & = \| \Psi \|(x) + \gamma. \end{align}
As ![]() $\inf _{y \in \Sigma } \| \Psi \|(y)= \|\Psi \|(0) = 0$, we deduce that
$\inf _{y \in \Sigma } \| \Psi \|(y)= \|\Psi \|(0) = 0$, we deduce that
Using Corollary 10.5, we find that
 \begin{align} I(A,\lambda) & = \log \sup_{y \in \Sigma} \|s(y)\|_L - \int_{\Sigma} \log\! \|s\|_L \, d \mu_H \nonumber\\ &= \int_{\Sigma} \| \Psi \| \, d \mu_H, \end{align}
\begin{align} I(A,\lambda) & = \log \sup_{y \in \Sigma} \|s(y)\|_L - \int_{\Sigma} \log\! \|s\|_L \, d \mu_H \nonumber\\ &= \int_{\Sigma} \| \Psi \| \, d \mu_H, \end{align}which proves the theorem.
12. Complex abelian varieties
The purpose of this section is to discuss several intrinsic hermitian metrics associated to line bundles on complex abelian varieties. Let ![]() $A$ be an abelian variety over
$A$ be an abelian variety over ![]() $\mathbb {C}$ of dimension
$\mathbb {C}$ of dimension ![]() $g$.
$g$.
12.1 Faltings metric and  $L^2$-metric
$L^2$-metric
Let ![]() $\alpha$ be an element of the fiber
$\alpha$ be an element of the fiber ![]() $0^*\Omega _{A/\mathbb {C}}^g$ of the canonical line bundle
$0^*\Omega _{A/\mathbb {C}}^g$ of the canonical line bundle ![]() $\Omega _{A/\mathbb {C}}^g$ at the origin. Evaluation at the origin gives an isomorphism
$\Omega _{A/\mathbb {C}}^g$ at the origin. Evaluation at the origin gives an isomorphism ![]() $H^0(A,\Omega ^g_{A/\mathbb {C}}) \xrightarrow {\sim } 0^*\Omega _{A/\mathbb {C}}^g$ of
$H^0(A,\Omega ^g_{A/\mathbb {C}}) \xrightarrow {\sim } 0^*\Omega _{A/\mathbb {C}}^g$ of ![]() $\mathbb {C}$-vector spaces and this allows us to view
$\mathbb {C}$-vector spaces and this allows us to view ![]() $\alpha$ as an element of
$\alpha$ as an element of ![]() $H^0(A,\Omega ^g_{A/\mathbb {C}})$. We define the Faltings norm of
$H^0(A,\Omega ^g_{A/\mathbb {C}})$. We define the Faltings norm of ![]() $\alpha$ by the equation
$\alpha$ by the equation
 \begin{equation} \|\alpha\|_{\mathrm{Fa}}^2 = \frac{ \sqrt{-1}^{g^2} }{2^g} \int_{A(\mathbb{C})} \alpha \wedge \bar{\alpha}. \end{equation}
\begin{equation} \|\alpha\|_{\mathrm{Fa}}^2 = \frac{ \sqrt{-1}^{g^2} }{2^g} \int_{A(\mathbb{C})} \alpha \wedge \bar{\alpha}. \end{equation}Remark 12.1 We warn the reader that in the literature there appear several variants of the normalization factor ![]() $\sqrt {-1}^{g^2} 2^{-g}$ in front of the integral in (12.1). Our normalization is compatible with the original source [Reference FaltingsFal83], and with [Reference AutissierAut06], but unfortunately not with [Reference BostBos96b], where the normalization factor is
$\sqrt {-1}^{g^2} 2^{-g}$ in front of the integral in (12.1). Our normalization is compatible with the original source [Reference FaltingsFal83], and with [Reference AutissierAut06], but unfortunately not with [Reference BostBos96b], where the normalization factor is ![]() $\sqrt {-1}^{g^2} (2\pi )^{-g}$.
$\sqrt {-1}^{g^2} (2\pi )^{-g}$.
Let ![]() $L$ be an ample line bundle on
$L$ be an ample line bundle on ![]() $A$. Let
$A$. Let ![]() $\|\cdot \|$ be a smooth hermitian metric on
$\|\cdot \|$ be a smooth hermitian metric on ![]() $L^\mathrm {an}$. The associated
$L^\mathrm {an}$. The associated ![]() $L^2$-metric on
$L^2$-metric on ![]() $H^0(A^\mathrm {an},L^\mathrm {an})$ is defined as follows: let
$H^0(A^\mathrm {an},L^\mathrm {an})$ is defined as follows: let ![]() $s$ be a global section of
$s$ be a global section of ![]() $L^\mathrm {an}$. We put
$L^\mathrm {an}$. We put
where ![]() $\mu _H$ denotes the Haar measure on
$\mu _H$ denotes the Haar measure on ![]() $A^\mathrm {an}$, normalized to give
$A^\mathrm {an}$, normalized to give ![]() $A^\mathrm {an}$ total mass equal to one.
$A^\mathrm {an}$ total mass equal to one.
12.2 Canonical metrics
Assume now that ![]() $L$ is ample and rigidified. By [Reference Moret-BaillyMor85, § II.2], there exists a unique smooth hermitian metric
$L$ is ample and rigidified. By [Reference Moret-BaillyMor85, § II.2], there exists a unique smooth hermitian metric ![]() $\|\cdot \|_L$ on
$\|\cdot \|_L$ on ![]() $L^\mathrm {an}$ such that the canonical cubical structure on
$L^\mathrm {an}$ such that the canonical cubical structure on ![]() $L$ provided by the theorem of the cube is an isometry. The metric
$L$ provided by the theorem of the cube is an isometry. The metric ![]() $\|\cdot \|_L$ is called the canonical metric on
$\|\cdot \|_L$ is called the canonical metric on ![]() $L^\mathrm {an}$. Equivalently, the metric
$L^\mathrm {an}$. Equivalently, the metric ![]() $\|\cdot \|_L$ can be characterized as the unique smooth hermitian metric on
$\|\cdot \|_L$ can be characterized as the unique smooth hermitian metric on ![]() $L^\mathrm {an}$ such that (a) the given rigidification at the origin is an isometry and (b) the curvature form of
$L^\mathrm {an}$ such that (a) the given rigidification at the origin is an isometry and (b) the curvature form of ![]() $\|\cdot \|_L$ is translation-invariant. See [Reference Moret-BaillyMor85, Proposition II.2.1].
$\|\cdot \|_L$ is translation-invariant. See [Reference Moret-BaillyMor85, Proposition II.2.1].
As can be verified immediately, if the given rigidification of ![]() $L$ is multiplied by a scalar
$L$ is multiplied by a scalar ![]() $\lambda \in \mathbb {C}^\times$, then the canonical metric on
$\lambda \in \mathbb {C}^\times$, then the canonical metric on ![]() $L$ associated to the new rigidification is obtained by multiplying
$L$ associated to the new rigidification is obtained by multiplying ![]() $\|\cdot \|_L$ by
$\|\cdot \|_L$ by ![]() $|\lambda |$. Further, let
$|\lambda |$. Further, let ![]() $s$ be a non-zero rational section of
$s$ be a non-zero rational section of ![]() $L$ and write
$L$ and write ![]() $D=\operatorname {div}_L s$. We note that the map
$D=\operatorname {div}_L s$. We note that the map ![]() $-\log \|s\|_L \colon A^\mathrm {an} \setminus \operatorname {Supp}(D^\mathrm {an}) \to \mathbb {R}$ is a Néron function on
$-\log \|s\|_L \colon A^\mathrm {an} \setminus \operatorname {Supp}(D^\mathrm {an}) \to \mathbb {R}$ is a Néron function on ![]() $A$ with respect to
$A$ with respect to ![]() $D$ in the sense of [Reference LangLan83, § 11.1].
$D$ in the sense of [Reference LangLan83, § 11.1].
Assume now that ![]() $L$ is moreover symmetric. We have a unique isomorphism
$L$ is moreover symmetric. We have a unique isomorphism ![]() $[-1]^*L \xrightarrow {\sim } L$ of rigidified line bundles and, further, by applying the theorem of the cube, a unique isomorphism of rigidified line bundles
$[-1]^*L \xrightarrow {\sim } L$ of rigidified line bundles and, further, by applying the theorem of the cube, a unique isomorphism of rigidified line bundles ![]() $\varphi _2 \colon [2]^*L \xrightarrow {\sim } L^{\otimes 4}$. The fact that the canonical cubical structure on
$\varphi _2 \colon [2]^*L \xrightarrow {\sim } L^{\otimes 4}$. The fact that the canonical cubical structure on ![]() $L$ is an isometry for
$L$ is an isometry for ![]() $\|\cdot \|_L$ implies that
$\|\cdot \|_L$ implies that ![]() $\varphi _2$ is an isometry for the metrics induced by
$\varphi _2$ is an isometry for the metrics induced by ![]() $\|\cdot \|_L$ on
$\|\cdot \|_L$ on ![]() $[2]^*L$ and
$[2]^*L$ and ![]() $L^{\otimes 4}$.
$L^{\otimes 4}$.
12.3 Translation by a two-torsion point
We continue to assume that ![]() $L$ is symmetric, rigidified and ample. Let
$L$ is symmetric, rigidified and ample. Let ![]() $y \in A[2]$ be a two-torsion point and write
$y \in A[2]$ be a two-torsion point and write ![]() $T_y \colon A \to A$ for translation along
$T_y \colon A \to A$ for translation along ![]() $y$. We have that
$y$. We have that ![]() $T_y^*L$ is a symmetric ample line bundle.
$T_y^*L$ is a symmetric ample line bundle.
Lemma 12.1 Let ![]() $\|\cdot \|_L$ be the canonical metric on
$\|\cdot \|_L$ be the canonical metric on ![]() $L^\mathrm {an}$. Then the pullback metric
$L^\mathrm {an}$. Then the pullback metric ![]() $T_y^* \|\cdot \|_L$ is a canonical metric on
$T_y^* \|\cdot \|_L$ is a canonical metric on ![]() $T_y^*L^\mathrm {an}$.
$T_y^*L^\mathrm {an}$.
Proof. This can be shown exactly analogously to Lemma 5.1. Alternatively, it is clear that ![]() $T_y^* \|\cdot \|_L$ is a smooth hermitian metric on
$T_y^* \|\cdot \|_L$ is a smooth hermitian metric on ![]() $T_y^*L$ whose curvature form is translation-invariant. This also proves the lemma.
$T_y^*L$ whose curvature form is translation-invariant. This also proves the lemma.
12.4 The invariant  $I(A,\lambda )$
$I(A,\lambda )$
Let ![]() $\lambda \colon A \xrightarrow {\sim } A^t$ be a principal polarization of
$\lambda \colon A \xrightarrow {\sim } A^t$ be a principal polarization of ![]() $A$ and let
$A$ and let ![]() $L$ be any symmetric ample line bundle on
$L$ be any symmetric ample line bundle on ![]() $A$ determining
$A$ determining ![]() $\lambda$. Let
$\lambda$. Let ![]() $s$ be a non-zero global section of
$s$ be a non-zero global section of ![]() $L$ and fix a rigidification of
$L$ and fix a rigidification of ![]() $L$. Let
$L$. Let ![]() $\|\cdot \|_L$ denote the associated canonical metric on
$\|\cdot \|_L$ denote the associated canonical metric on ![]() $L^\mathrm {an}$.
$L^\mathrm {an}$.
We define
where ![]() $\mu _H$ denotes the Haar measure on
$\mu _H$ denotes the Haar measure on ![]() $A^\mathrm {an}$, normalized to give
$A^\mathrm {an}$, normalized to give ![]() $A^\mathrm {an}$ total mass equal to one.
$A^\mathrm {an}$ total mass equal to one.
Lemma 12.2 The quantity ![]() $I(A,\lambda )$ is independent of the choice of line bundle
$I(A,\lambda )$ is independent of the choice of line bundle ![]() $L$, of section
$L$, of section ![]() $s$ and of rigidification of
$s$ and of rigidification of ![]() $L$ and hence defines an invariant of the principally polarized complex abelian variety
$L$ and hence defines an invariant of the principally polarized complex abelian variety ![]() $(A,\lambda )$.
$(A,\lambda )$.
Proof. Choose one symmetric ample line bundle ![]() $L$ on
$L$ on ![]() $A$ determining
$A$ determining ![]() $\lambda$. A change of rigidification results in a replacement of
$\lambda$. A change of rigidification results in a replacement of ![]() $\|\cdot \|_L$ by a scalar multiple of
$\|\cdot \|_L$ by a scalar multiple of ![]() $\|\cdot \|_L$. Moreover, the space
$\|\cdot \|_L$. Moreover, the space ![]() $H^0(A,L)$ of global sections of
$H^0(A,L)$ of global sections of ![]() $L$ is one-dimensional. It follows immediately that the quantity
$L$ is one-dimensional. It follows immediately that the quantity ![]() $I(A,\lambda )$ as defined in (12.3) is independent of the choice of rigidification of
$I(A,\lambda )$ as defined in (12.3) is independent of the choice of rigidification of ![]() $L$ and of section
$L$ and of section ![]() $s$. Now any other symmetric ample line bundle on
$s$. Now any other symmetric ample line bundle on ![]() $A$ determining
$A$ determining ![]() $\lambda$ is given by
$\lambda$ is given by ![]() $T_y^*L$ for some two-torsion point
$T_y^*L$ for some two-torsion point ![]() $y$ of
$y$ of ![]() $A$. By Lemma 12.1 and the translation-invariance of
$A$. By Lemma 12.1 and the translation-invariance of ![]() $\mu _H$, we find that the quantity
$\mu _H$, we find that the quantity ![]() $I(A,\lambda )$ is also independent of the choice of
$I(A,\lambda )$ is also independent of the choice of ![]() $L$.
$L$.
13. Stable Faltings height and key formula
The purpose of this section is to review the definition of the stable Faltings height of an abelian variety defined over the field ![]() $\bar {\mathbb {Q}}$ of algebraic numbers and to state Bost's formula [Reference BostBos96b] for it. We start by recalling the general notion of Arakelov degree.
$\bar {\mathbb {Q}}$ of algebraic numbers and to state Bost's formula [Reference BostBos96b] for it. We start by recalling the general notion of Arakelov degree.
13.1 Arakelov degree
Let ![]() $k$ be a number field. Let
$k$ be a number field. Let ![]() $S$ denote the spectrum of the ring of integers
$S$ denote the spectrum of the ring of integers ![]() $\mathcal {O}_k$ of
$\mathcal {O}_k$ of ![]() $k$. Let
$k$. Let ![]() $\mathcal {V} \to S$ be a flat morphism of finite type with smooth generic fiber. A hermitian line bundle on
$\mathcal {V} \to S$ be a flat morphism of finite type with smooth generic fiber. A hermitian line bundle on ![]() $\mathcal {V}$ is the data of a line bundle
$\mathcal {V}$ is the data of a line bundle ![]() $\mathcal {L}$ on
$\mathcal {L}$ on ![]() $\mathcal {V}$ together with smooth hermitian metrics on the
$\mathcal {V}$ together with smooth hermitian metrics on the ![]() $\mathcal {L}_v$ for
$\mathcal {L}_v$ for ![]() $v \in M(k)_\infty$. A hermitian line bundle on
$v \in M(k)_\infty$. A hermitian line bundle on ![]() $S$ can be identified with a projective rank-one
$S$ can be identified with a projective rank-one ![]() $\mathcal {O}_k$-module
$\mathcal {O}_k$-module ![]() $\mathcal {M}$ together with hermitian metrics
$\mathcal {M}$ together with hermitian metrics ![]() $\|\cdot \|_v$ on the
$\|\cdot \|_v$ on the ![]() $\bar {k}_v$-vector spaces
$\bar {k}_v$-vector spaces ![]() $\mathcal {M}_v$ for all
$\mathcal {M}_v$ for all ![]() $v \in M(k)_\infty$. Let
$v \in M(k)_\infty$. Let ![]() $\bar {\mathcal {M}}= (\mathcal {M}, (\|\cdot \|_v)_{v \in M(k)_\infty })$ be a hermitian line bundle on
$\bar {\mathcal {M}}= (\mathcal {M}, (\|\cdot \|_v)_{v \in M(k)_\infty })$ be a hermitian line bundle on ![]() $S$. Its Arakelov degree is given by choosing a non-zero element
$S$. Its Arakelov degree is given by choosing a non-zero element ![]() $s$ of
$s$ of ![]() $\mathcal {M}$ and by setting
$\mathcal {M}$ and by setting
Here ![]() $Nv$ denotes the cardinality of the residue field at
$Nv$ denotes the cardinality of the residue field at ![]() $v$. The Arakelov degree
$v$. The Arakelov degree ![]() $\widehat {\deg } \,\bar {\mathcal {M}}$ is independent of the choice of the section
$\widehat {\deg } \,\bar {\mathcal {M}}$ is independent of the choice of the section ![]() $s$, by the product formula.
$s$, by the product formula.
13.2 Stable Faltings height
Let ![]() $A$ be an abelian variety of dimension
$A$ be an abelian variety of dimension ![]() $g$ over the number field
$g$ over the number field ![]() $k$. Let
$k$. Let ![]() $G$ be the identity component of the Néron model of
$G$ be the identity component of the Néron model of ![]() $A$ over
$A$ over ![]() $S=\operatorname {Spec} \mathcal {O}_k$, let
$S=\operatorname {Spec} \mathcal {O}_k$, let ![]() $e \colon S \to G$ denote the zero section of
$e \colon S \to G$ denote the zero section of ![]() $G$ and set
$G$ and set ![]() $\omega _{G/S}= e^* \Omega ^g_{G/S}$. Then
$\omega _{G/S}= e^* \Omega ^g_{G/S}$. Then ![]() $\omega _{G/S}$ is a line bundle on
$\omega _{G/S}$ is a line bundle on ![]() $S$. We endow
$S$. We endow ![]() $\omega _{G/S}$ canonically with the structure of a hermitian line bundle
$\omega _{G/S}$ canonically with the structure of a hermitian line bundle ![]() $\overline {\omega _{G/S}}$ on
$\overline {\omega _{G/S}}$ on ![]() $S$ by using the metrics (12.1) on all
$S$ by using the metrics (12.1) on all ![]() $v \in M(k)_\infty$. The Faltings height
$v \in M(k)_\infty$. The Faltings height ![]() $\mathrm {h}_F(A)$ of
$\mathrm {h}_F(A)$ of ![]() $A$ over
$A$ over ![]() $k$ is given by the Arakelov degree
$k$ is given by the Arakelov degree
Finally, let ![]() $A$ be an abelian variety over
$A$ be an abelian variety over ![]() $\bar {\mathbb {Q}}$ and let
$\bar {\mathbb {Q}}$ and let ![]() $k \subset \bar {\mathbb {Q}}$ be a number field such that
$k \subset \bar {\mathbb {Q}}$ be a number field such that ![]() $A$ has semistable reduction over
$A$ has semistable reduction over ![]() $k$. We let the stable Faltings height of
$k$. We let the stable Faltings height of ![]() $A$ be the Faltings height of
$A$ be the Faltings height of ![]() $A$ over
$A$ over ![]() $k$ given by (13.2). The stable Faltings height is independent of the choice of the number field
$k$ given by (13.2). The stable Faltings height is independent of the choice of the number field ![]() $k \subset \bar {\mathbb {Q}}$.
$k \subset \bar {\mathbb {Q}}$.
13.3 Moret-Bailly models
We make a slight variation upon [Reference BostBos96b, § 4.3]. Let ![]() $S$ be a connected Dedekind scheme and let
$S$ be a connected Dedekind scheme and let ![]() $\pi \colon \mathcal {A} \to S$ be a semistable group scheme. Let
$\pi \colon \mathcal {A} \to S$ be a semistable group scheme. Let ![]() $\mathcal {L}$ be a line bundle on
$\mathcal {L}$ be a line bundle on ![]() $\mathcal {A}$. Let
$\mathcal {A}$. Let ![]() $A$ be the generic fiber of
$A$ be the generic fiber of ![]() $\mathcal {A}$ and
$\mathcal {A}$ and ![]() $L$ the generic fiber of
$L$ the generic fiber of ![]() $\mathcal {L}$. Assume that
$\mathcal {L}$. Assume that ![]() $A$ is an abelian variety and assume that
$A$ is an abelian variety and assume that ![]() $L$ is a rigidified symmetric and ample line bundle on
$L$ is a rigidified symmetric and ample line bundle on ![]() $A$. We denote by
$A$. We denote by ![]() $K(L^{\otimes 2})$ the kernel of the polarization
$K(L^{\otimes 2})$ the kernel of the polarization ![]() $\lambda _{L^{\otimes 2}} \colon A \to A^t$ associated to
$\lambda _{L^{\otimes 2}} \colon A \to A^t$ associated to ![]() $L^{\otimes 2}$. We call
$L^{\otimes 2}$. We call ![]() $(\mathcal {A},\mathcal {L})$ a Moret-Bailly model of
$(\mathcal {A},\mathcal {L})$ a Moret-Bailly model of ![]() $(A,L)$ if the line bundle
$(A,L)$ if the line bundle ![]() $\mathcal {L}$ is a cubical extension of
$\mathcal {L}$ is a cubical extension of ![]() $L$ and the group scheme
$L$ and the group scheme ![]() $K(L^{\otimes 2})$ extends as a finite flat subgroup scheme of
$K(L^{\otimes 2})$ extends as a finite flat subgroup scheme of ![]() $\mathcal {A}$ over
$\mathcal {A}$ over ![]() $S$. Denote by
$S$. Denote by ![]() $F$ the function field of
$F$ the function field of ![]() $S$. Starting from the Néron model of
$S$. Starting from the Néron model of ![]() $A$ over
$A$ over ![]() $S$, and using Lemma 2.2, one may readily construct Moret-Bailly models, at the cost of replacing
$S$, and using Lemma 2.2, one may readily construct Moret-Bailly models, at the cost of replacing ![]() $F$ by a suitable finite field extension. See, for instance, [Reference BostBos96b, Theorem 4.10(i)] and its proof.
$F$ by a suitable finite field extension. See, for instance, [Reference BostBos96b, Theorem 4.10(i)] and its proof.
13.4 Bost's formula for the stable Faltings height
The aim of this section is to display Bost's formula [Reference BostBos96b, Theorem 4.10(v)] for the stable Faltings height of a principally polarized abelian variety, based on Moret-Bailly's key formula. We refer to [Reference Moret-BaillyMor85, Chapitre VIII] for the original key formula. We restrict ourselves to the principally polarized case but mention that the results of [Reference BostBos96b] pertain to polarizations of arbitrary degree.
Let ![]() $A$ be an abelian variety with semistable reduction over the number field
$A$ be an abelian variety with semistable reduction over the number field ![]() $k$. Let
$k$. Let ![]() $L$ be a rigidified symmetric ample line bundle on
$L$ be a rigidified symmetric ample line bundle on ![]() $A$. Let
$A$. Let ![]() $S$ be the spectrum of the ring of integers of
$S$ be the spectrum of the ring of integers of ![]() $k$ and let
$k$ and let ![]() $\pi \colon \mathcal {A} \to S$ be a semistable group scheme with generic fiber
$\pi \colon \mathcal {A} \to S$ be a semistable group scheme with generic fiber ![]() $A$ and equipped with a line bundle
$A$ and equipped with a line bundle ![]() $\mathcal {L}$ extending the line bundle
$\mathcal {L}$ extending the line bundle ![]() $L$ on
$L$ on ![]() $A$. We note that
$A$. We note that ![]() $\mathcal {L}$ is canonically endowed with a structure of a hermitian line bundle
$\mathcal {L}$ is canonically endowed with a structure of a hermitian line bundle ![]() $\bar {\mathcal {L}}$, by taking the canonical metrics
$\bar {\mathcal {L}}$, by taking the canonical metrics ![]() $\|\cdot \|_{L,v}$ from § 12.1 on
$\|\cdot \|_{L,v}$ from § 12.1 on ![]() $\mathcal {L}_v$ at all
$\mathcal {L}_v$ at all ![]() $v \in M(k)_\infty$.
$v \in M(k)_\infty$.
Assume that ![]() $(\mathcal {A},\mathcal {L})$ is a Moret-Bailly model of
$(\mathcal {A},\mathcal {L})$ is a Moret-Bailly model of ![]() $(A,L)$ as in § 13.3 and assume further that
$(A,L)$ as in § 13.3 and assume further that ![]() $L$ defines a principal polarization. Then the sheaf
$L$ defines a principal polarization. Then the sheaf ![]() $\pi _* \mathcal {L}$ is invertible [Reference Moret-BaillyMor85, Chapitre VI]. Further, the line bundle
$\pi _* \mathcal {L}$ is invertible [Reference Moret-BaillyMor85, Chapitre VI]. Further, the line bundle ![]() $\pi _*\mathcal {L}$ on
$\pi _*\mathcal {L}$ on ![]() $S$ has a canonical structure of a hermitian line bundle
$S$ has a canonical structure of a hermitian line bundle ![]() $\overline {\pi _*\mathcal {L}}$, as follows: for each
$\overline {\pi _*\mathcal {L}}$, as follows: for each ![]() $v \in M(k)_\infty$, one chooses the
$v \in M(k)_\infty$, one chooses the ![]() $L^2$-metric (12.2) derived from the canonical metric
$L^2$-metric (12.2) derived from the canonical metric ![]() $\|\cdot \|_{L,v}$. Write
$\|\cdot \|_{L,v}$. Write ![]() $\kappa _0 = \log (\pi \sqrt {2})$ as before. The following is a special case of Bost's formula from [Reference BostBos96b, Theorem 4.10(v)].
$\kappa _0 = \log (\pi \sqrt {2})$ as before. The following is a special case of Bost's formula from [Reference BostBos96b, Theorem 4.10(v)].
Theorem 13.1 Let ![]() $A$ be an abelian variety over
$A$ be an abelian variety over ![]() $k$ and let
$k$ and let ![]() $L$ be a symmetric rigidified ample line bundle on
$L$ be a symmetric rigidified ample line bundle on ![]() $A$. Assume that
$A$. Assume that ![]() $L$ determines a principal polarization of
$L$ determines a principal polarization of ![]() $A$. Assume that
$A$. Assume that ![]() $(A,L)$ extends into a Moret-Bailly model
$(A,L)$ extends into a Moret-Bailly model ![]() $(\mathcal {A},\mathcal {L})$ over
$(\mathcal {A},\mathcal {L})$ over ![]() $S$. Then the equality
$S$. Then the equality
holds in ![]() $\mathbb {R}$. Here
$\mathbb {R}$. Here ![]() $g$ denotes the dimension of
$g$ denotes the dimension of ![]() $A$.
$A$.
Remark 13.1 The formula in Theorem 13.1 is slightly different from the one in [Reference BostBos96b, Theorem 4.10(v)]. This is due to a difference in normalization of the Faltings metric (12.1): see Remark 12.1.
14. Néron–Tate heights
The purpose of this section is to review the notion of Néron–Tate heights of cycles on a polarized abelian variety over a number field. The main references for this section are [Reference Chambert-Loir and ThuillierCT09, Reference GublerGub10, Reference ZhangZha95].
14.1 Adelic absolute values
Let ![]() $k$ be a number field and let
$k$ be a number field and let ![]() $S$ be the spectrum of the ring of integers
$S$ be the spectrum of the ring of integers ![]() $\mathcal {O}_k$ of
$\mathcal {O}_k$ of ![]() $k$. For each
$k$. For each ![]() $v \in M(k)_\infty$, we choose the standard euclidean metrics
$v \in M(k)_\infty$, we choose the standard euclidean metrics ![]() $|\cdot |_v$ on all
$|\cdot |_v$ on all ![]() $\bar {k}_v\cong \mathbb {C}$. For each
$\bar {k}_v\cong \mathbb {C}$. For each ![]() $v \in M(k)_0$, we let
$v \in M(k)_0$, we let ![]() $k_v$ denote the completion of
$k_v$ denote the completion of ![]() $k$ at
$k$ at ![]() $v$, choose a uniformizer
$v$, choose a uniformizer ![]() $\varpi _v$, fix the completion
$\varpi _v$, fix the completion ![]() $\mathbb {C}_v$ of an algebraic closure of
$\mathbb {C}_v$ of an algebraic closure of ![]() $k_v$ and fix on
$k_v$ and fix on ![]() $\mathbb {C}_v$ a corresponding absolute value
$\mathbb {C}_v$ a corresponding absolute value ![]() $|\cdot |_v$ such that
$|\cdot |_v$ such that ![]() $|\varpi _v|_v=(Nv)^{-1}$ with
$|\varpi _v|_v=(Nv)^{-1}$ with ![]() $Nv$ the cardinality of the residue field at
$Nv$ the cardinality of the residue field at ![]() $v$. These normalizations ensure that the resulting collection of absolute values
$v$. These normalizations ensure that the resulting collection of absolute values ![]() $(|\cdot |_v)_{v \in M(k)}$ on
$(|\cdot |_v)_{v \in M(k)}$ on ![]() $k$ satisfies the product formula.
$k$ satisfies the product formula.
14.2 Adelic line bundles
Let ![]() $V$ be a geometrically integral normal projective variety over
$V$ be a geometrically integral normal projective variety over ![]() $k$ and let
$k$ and let ![]() $L$ be a line bundle on
$L$ be a line bundle on ![]() $V$. We refer to [Reference Chambert-LoirCha11, Reference ZhangZha95] for a general discussion of how suitable collections of admissible metrics on
$V$. We refer to [Reference Chambert-LoirCha11, Reference ZhangZha95] for a general discussion of how suitable collections of admissible metrics on ![]() $L_v^\mathrm {an}$ on
$L_v^\mathrm {an}$ on ![]() $V_v^\mathrm {an}$ for all
$V_v^\mathrm {an}$ for all ![]() $v \in M(k)$ (we call the resulting data an admissible adelic line bundle on
$v \in M(k)$ (we call the resulting data an admissible adelic line bundle on ![]() $V$) give rise to a notion of height of integral cycles on
$V$) give rise to a notion of height of integral cycles on ![]() $V$ with respect to
$V$ with respect to ![]() $L$. We discuss the case of abelian varieties in some detail, referring to [Reference ZhangZha95] for proofs.
$L$. We discuss the case of abelian varieties in some detail, referring to [Reference ZhangZha95] for proofs.
14.3 Adelic intersections
Let ![]() $A$ be an abelian variety over
$A$ be an abelian variety over ![]() $k$. Let
$k$. Let ![]() $L$ be a rigidified symmetric ample line bundle on
$L$ be a rigidified symmetric ample line bundle on ![]() $A$. Given our choices of absolute values in § 14.1, we obtain, at each
$A$. Given our choices of absolute values in § 14.1, we obtain, at each ![]() $v \in M(k)$, a canonical metric
$v \in M(k)$, a canonical metric ![]() $\|\cdot \|_{L,v}$ on
$\|\cdot \|_{L,v}$ on ![]() $L_v^\mathrm {an}$ on
$L_v^\mathrm {an}$ on ![]() $A_v^{\mathrm {an}}$. We refer to § 12.2 for the complex embeddings and to § 5.1 for the non-archimedean places.
$A_v^{\mathrm {an}}$. We refer to § 12.2 for the complex embeddings and to § 5.1 for the non-archimedean places.
The resulting adelic line bundle ![]() $\hat {L} =(L,(\|\cdot \|_{L,v})_{v \in M(k)})$ is admissible. In particular, for each integral cycle
$\hat {L} =(L,(\|\cdot \|_{L,v})_{v \in M(k)})$ is admissible. In particular, for each integral cycle ![]() $Z$ on
$Z$ on ![]() $A$, the self-intersection number
$A$, the self-intersection number ![]() $\langle \hat {L} \cdots \hat {L} | Z \rangle$ is well defined. The Néron–Tate height of
$\langle \hat {L} \cdots \hat {L} | Z \rangle$ is well defined. The Néron–Tate height of ![]() $Z$ with respect to
$Z$ with respect to ![]() $L$ is defined to be the normalized intersection number
$L$ is defined to be the normalized intersection number
where ![]() $d=\dim Z$. One can use formula (14.1) to define the Néron–Tate height of any effective cycle
$d=\dim Z$. One can use formula (14.1) to define the Néron–Tate height of any effective cycle ![]() $Z$ of pure dimension
$Z$ of pure dimension ![]() $d$ on
$d$ on ![]() $A$. We have the following properties:
$A$. We have the following properties: ![]() $\mathrm {h}'_L(Z) \geqslant 0$ and, for all
$\mathrm {h}'_L(Z) \geqslant 0$ and, for all ![]() $n \in \mathbb {Z}_{>0}$, we have
$n \in \mathbb {Z}_{>0}$, we have ![]() $\mathrm {h}'_L([n]_*Z)=n^2\,\mathrm {h}'_L(Z)$. In particular, if
$\mathrm {h}'_L([n]_*Z)=n^2\,\mathrm {h}'_L(Z)$. In particular, if ![]() $Z$ is an abelian subvariety of
$Z$ is an abelian subvariety of ![]() $A$, then
$A$, then ![]() $\mathrm {h}'_L(Z)=0$. The real number
$\mathrm {h}'_L(Z)=0$. The real number ![]() $\mathrm {h}'_L(Z)$ is independent of the chosen rigidification of
$\mathrm {h}'_L(Z)$ is independent of the chosen rigidification of ![]() $L$. This is verified in § 14.5 below.
$L$. This is verified in § 14.5 below.
14.4 Chambert-Loir measure
Let ![]() $Z$ be an integral cycle on
$Z$ be an integral cycle on ![]() $A$ and let
$A$ and let ![]() $v \in M(k)$. Associated to
$v \in M(k)$. Associated to ![]() $\hat {L}$,
$\hat {L}$, ![]() $Z$ and
$Z$ and ![]() $v$, one has a canonical measure
$v$, one has a canonical measure ![]() $c_1(\hat {L})_v^d \wedge \delta _Z$ on
$c_1(\hat {L})_v^d \wedge \delta _Z$ on ![]() $A^\mathrm {an}_v$ introduced by Chambert-Loir [Reference Chambert-LoirCha11, Reference Chambert-LoirCha06]. For
$A^\mathrm {an}_v$ introduced by Chambert-Loir [Reference Chambert-LoirCha11, Reference Chambert-LoirCha06]. For ![]() $v \in M(k)_\infty$, the measure
$v \in M(k)_\infty$, the measure ![]() $c_1(\hat {L})_v^d \wedge \delta _Z$ is just obtained, as the notation suggests, by taking the
$c_1(\hat {L})_v^d \wedge \delta _Z$ is just obtained, as the notation suggests, by taking the ![]() $d$-fold wedge of the first Chern form of
$d$-fold wedge of the first Chern form of ![]() $(L_v,\|\cdot \|_{L,v})$ and wedging the result with the Dirac current
$(L_v,\|\cdot \|_{L,v})$ and wedging the result with the Dirac current ![]() $\delta _{Z_v}$ at
$\delta _{Z_v}$ at ![]() $Z_v$. For
$Z_v$. For ![]() $v \in M(k)_0$, the measure
$v \in M(k)_0$, the measure ![]() $c_1(\hat {L})_v^d \wedge \delta _Z$ is defined in terms of intersection theory. The measure
$c_1(\hat {L})_v^d \wedge \delta _Z$ is defined in terms of intersection theory. The measure ![]() $c_1(\hat {L})_v^d \wedge \delta _Z$ is independent of the choice of rigidification on
$c_1(\hat {L})_v^d \wedge \delta _Z$ is independent of the choice of rigidification on ![]() $L$. We refer to
$L$. We refer to ![]() $c_1(\hat {L})_v^d \wedge \delta _Z$ as the Chambert-Loir measure associated to
$c_1(\hat {L})_v^d \wedge \delta _Z$ as the Chambert-Loir measure associated to ![]() $\hat {L}$,
$\hat {L}$, ![]() $Z$ and
$Z$ and ![]() $v$.
$v$.
As follows from [Reference Chambert-Loir and ThuillierCT09, Théorème 4.1], the Chambert-Loir measure satisfies the following property. Let ![]() $s$ be a non-zero rational section of
$s$ be a non-zero rational section of ![]() $L$ such that
$L$ such that ![]() $Z$ is not contained in the support of
$Z$ is not contained in the support of ![]() $\operatorname {div}_L s$. Then, for each
$\operatorname {div}_L s$. Then, for each ![]() $v \in M(k)$, the Green's function
$v \in M(k)$, the Green's function ![]() $\log \! \|s\|_{L,v}$ is integrable against the measure
$\log \! \|s\|_{L,v}$ is integrable against the measure ![]() $c_1(\hat {L})_v^d \wedge \delta _Z$. Moreover, one has the recursive formula
$c_1(\hat {L})_v^d \wedge \delta _Z$. Moreover, one has the recursive formula
 \begin{equation} \langle \hat{L} \cdots \hat{L}\, | \, Z \rangle = \langle \hat{L} \cdots \hat{L} \, | \, \operatorname{div}_Z(s) \rangle - \sum_{v \in M(k)} \int_{A_v^\mathrm{an}} \log\! \|s\|_{L,v} \, c_1(\hat{L})_v^d \wedge \delta_Z. \end{equation}
\begin{equation} \langle \hat{L} \cdots \hat{L}\, | \, Z \rangle = \langle \hat{L} \cdots \hat{L} \, | \, \operatorname{div}_Z(s) \rangle - \sum_{v \in M(k)} \int_{A_v^\mathrm{an}} \log\! \|s\|_{L,v} \, c_1(\hat{L})_v^d \wedge \delta_Z. \end{equation}14.5 Independence of rigidification
At this point we may verify that ![]() $\mathrm {h}'_L(Z)$ or equivalently
$\mathrm {h}'_L(Z)$ or equivalently ![]() $\langle \hat {L} \cdots \hat {L}\, | \, Z \rangle$ is independent of the choice of rigidification of
$\langle \hat {L} \cdots \hat {L}\, | \, Z \rangle$ is independent of the choice of rigidification of ![]() $L$. We note that if we change the given rigidification of
$L$. We note that if we change the given rigidification of ![]() $L$ by multiplying it by a scalar
$L$ by multiplying it by a scalar ![]() $\lambda \in k^\times$, we have that at each
$\lambda \in k^\times$, we have that at each ![]() $v \in M(k)$ the new canonical metric is obtained by multiplying the given canonical metric
$v \in M(k)$ the new canonical metric is obtained by multiplying the given canonical metric ![]() $\|\cdot \|_{L,v}$ by
$\|\cdot \|_{L,v}$ by ![]() $|\lambda |_v$. It follows by the product formula that the term
$|\lambda |_v$. It follows by the product formula that the term
 \begin{equation} \sum_{v \in M(k)} \int_{A_v^\mathrm{an}} \log\! \|s\|_{L,v} \, c_1(\hat{L})_v^d \wedge \delta_Z \end{equation}
\begin{equation} \sum_{v \in M(k)} \int_{A_v^\mathrm{an}} \log\! \|s\|_{L,v} \, c_1(\hat{L})_v^d \wedge \delta_Z \end{equation}
from (14.2) is independent of the choice of rigidification of ![]() $L$. By (14.2), we are then reduced, using induction on
$L$. By (14.2), we are then reduced, using induction on ![]() $\dim (Z)$, to the case that
$\dim (Z)$, to the case that ![]() $Z=P \in A(k)$ is a rational point of
$Z=P \in A(k)$ is a rational point of ![]() $A$. Let
$A$. Let ![]() $s$ be a non-zero rational section of
$s$ be a non-zero rational section of ![]() $L$ such that
$L$ such that ![]() $P$ does not lie on the support of
$P$ does not lie on the support of ![]() $\operatorname {div}_L s$. In this case, (14.2) becomes
$\operatorname {div}_L s$. In this case, (14.2) becomes
expressing the Néron–Tate height with respect to ![]() $L$ of the point
$L$ of the point ![]() $P$ as a sum of evaluations of the local Néron functions
$P$ as a sum of evaluations of the local Néron functions ![]() $-\log \|s\|_{L,v}$. The product formula then shows that
$-\log \|s\|_{L,v}$. The product formula then shows that ![]() $\mathrm {h}'_L(P)$ is independent of the chosen rigidification of
$\mathrm {h}'_L(P)$ is independent of the chosen rigidification of ![]() $L$.
$L$.
14.6 Connection with the Néron model
Assume that ![]() $A$ has semistable reduction over
$A$ has semistable reduction over ![]() $k$ and let
$k$ and let ![]() $\mathcal {N}$ be the Néron model of
$\mathcal {N}$ be the Néron model of ![]() $A$ over
$A$ over ![]() $S$. Let
$S$. Let ![]() $n \in \mathbb {Z}_{>0}$ be such that for each
$n \in \mathbb {Z}_{>0}$ be such that for each ![]() $v \in M(k)_0$, the group of connected components of
$v \in M(k)_0$, the group of connected components of ![]() $\mathcal {N}$ at
$\mathcal {N}$ at ![]() $v$ is annihilated by
$v$ is annihilated by ![]() $n$. Let
$n$. Let ![]() $M=L^{\otimes 2n}$. By Lemma 2.1, the cubical line bundle
$M=L^{\otimes 2n}$. By Lemma 2.1, the cubical line bundle ![]() $M$ admits a cubical extension
$M$ admits a cubical extension ![]() $\mathcal {M}$ over
$\mathcal {M}$ over ![]() $\mathcal {N}$. We obtain a hermitian line bundle
$\mathcal {N}$. We obtain a hermitian line bundle ![]() $\bar {\mathcal {M}}$ on
$\bar {\mathcal {M}}$ on ![]() $\mathcal {N}$ by endowing
$\mathcal {N}$ by endowing ![]() $M$ at each complex embedding with the canonical metric (cf. § 12.2). Let
$M$ at each complex embedding with the canonical metric (cf. § 12.2). Let ![]() $P \in A(k)$ and denote by
$P \in A(k)$ and denote by ![]() $\bar {P}$ the section of
$\bar {P}$ the section of ![]() $\mathcal {N}$ over
$\mathcal {N}$ over ![]() $S$ induced by
$S$ induced by ![]() $P$. Proposition 10.1 readily gives that
$P$. Proposition 10.1 readily gives that
Combining with (14.4), we obtain
Compare with [Reference BostBos96b, Theorem 4.10(ii)] and [Reference Moret-BaillyMor85, § III.4.4].
14.7 Néron–Tate height of a theta divisor
Let ![]() $v \in M(k)_0$. In [Reference GublerGub10], Gubler calculated the Chambert-Loir measures
$v \in M(k)_0$. In [Reference GublerGub10], Gubler calculated the Chambert-Loir measures ![]() $c_1(\hat {L})_v^d \wedge \delta _Z$ on
$c_1(\hat {L})_v^d \wedge \delta _Z$ on ![]() $A^\mathrm {an}_v$ explicitly, using tropical geometry. We need the following special case, where we take
$A^\mathrm {an}_v$ explicitly, using tropical geometry. We need the following special case, where we take ![]() $Z$ to be
$Z$ to be ![]() $A$ itself. Let
$A$ itself. Let ![]() $\iota _v \colon \Sigma _v \hookrightarrow A_v^{\mathrm {an}}$ denote the inclusion of the canonical skeleton into
$\iota _v \colon \Sigma _v \hookrightarrow A_v^{\mathrm {an}}$ denote the inclusion of the canonical skeleton into ![]() $A_v^{\mathrm {an}}$; cf. § 7. Let
$A_v^{\mathrm {an}}$; cf. § 7. Let ![]() $g=\dim (A)$ and let
$g=\dim (A)$ and let ![]() $\mu _{H,v}$ be the Haar measure of
$\mu _{H,v}$ be the Haar measure of ![]() $\Sigma _v$, normalized to give
$\Sigma _v$, normalized to give ![]() $\Sigma _v$ total mass equal to one. Then, by [Reference GublerGub10, Corollary 7.3], we have the identity
$\Sigma _v$ total mass equal to one. Then, by [Reference GublerGub10, Corollary 7.3], we have the identity
of measures on ![]() $A_v^\mathrm {an}$. For
$A_v^\mathrm {an}$. For ![]() $v \in M(k)_\infty$, a very similar identity holds, namely
$v \in M(k)_\infty$, a very similar identity holds, namely
where now ![]() $\mu _{H,v}$ is the Haar measure on the complex torus
$\mu _{H,v}$ is the Haar measure on the complex torus ![]() $A_v^\mathrm {an}$, normalized to give
$A_v^\mathrm {an}$, normalized to give ![]() $A_v^\mathrm {an}$ total mass equal to one. These identities lead to the following expression for the Néron–Tate height of a theta divisor.
$A_v^\mathrm {an}$ total mass equal to one. These identities lead to the following expression for the Néron–Tate height of a theta divisor.
Theorem 14.1 Let ![]() $s$ be a non-zero global section of
$s$ be a non-zero global section of ![]() $L$. Write
$L$. Write ![]() $\Theta = \operatorname {div} s$. Then the identity
$\Theta = \operatorname {div} s$. Then the identity
 \[ g \,[k:\mathbb{Q}]\, \mathrm{h}_L'(\Theta) = \sum_{v \in M(k)_0} \int_{A_v^\mathrm{an}} \log\! \|s\|_{L,v} \, d \mu_{H,v} + \sum_{v \in M(k)_\infty} \int_{A_v^\mathrm{an}} \log\! \|s\|_{L,v} \, d \mu_{H,v} \]
\[ g \,[k:\mathbb{Q}]\, \mathrm{h}_L'(\Theta) = \sum_{v \in M(k)_0} \int_{A_v^\mathrm{an}} \log\! \|s\|_{L,v} \, d \mu_{H,v} + \sum_{v \in M(k)_\infty} \int_{A_v^\mathrm{an}} \log\! \|s\|_{L,v} \, d \mu_{H,v} \]holds.
Proof. As the Néron–Tate height of ![]() $A$ vanishes, we have
$A$ vanishes, we have ![]() $\langle \hat {L} \cdots \hat {L}\, | \, A \rangle = 0$. By (14.2) applied to
$\langle \hat {L} \cdots \hat {L}\, | \, A \rangle = 0$. By (14.2) applied to ![]() $Z=A$ and the global section
$Z=A$ and the global section ![]() $s$, we find that
$s$, we find that
 \[ \langle \hat{L} \cdots \hat{L} \, | \, \Theta \rangle = \sum_{v \in M(k)} \int_{A_v^\mathrm{an}} \log\! \|s\|_{L,v} \, c_{1}(\hat{L})^g_v. \]
\[ \langle \hat{L} \cdots \hat{L} \, | \, \Theta \rangle = \sum_{v \in M(k)} \int_{A_v^\mathrm{an}} \log\! \|s\|_{L,v} \, c_{1}(\hat{L})^g_v. \]
We also have ![]() $\langle \hat {L} \cdots \hat {L} \, | \, \Theta \rangle = [k:\mathbb {Q}] \, \mathrm {h}_L'(\Theta )\cdot g \cdot \deg _L (A)$. Using (14.7) and (14.8), we find the required identity.
$\langle \hat {L} \cdots \hat {L} \, | \, \Theta \rangle = [k:\mathbb {Q}] \, \mathrm {h}_L'(\Theta )\cdot g \cdot \deg _L (A)$. Using (14.7) and (14.8), we find the required identity.
15. Proof of Theorem A
In this section we prove Theorem A. We repeat the statement for convenience. Let ![]() $k$ be a number field. Let
$k$ be a number field. Let ![]() $(A,\lambda )$ be a principally polarized abelian variety of positive dimension with semistable reduction over
$(A,\lambda )$ be a principally polarized abelian variety of positive dimension with semistable reduction over ![]() $k$. Let
$k$. Let ![]() $L$ be a symmetric ample line bundle on
$L$ be a symmetric ample line bundle on ![]() $A$ that determines the principal polarization
$A$ that determines the principal polarization ![]() $\lambda$, let
$\lambda$, let ![]() $s$ be a non-zero global section of
$s$ be a non-zero global section of ![]() $L$ and write
$L$ and write ![]() $\Theta = \operatorname {div} s$.
$\Theta = \operatorname {div} s$.
Let ![]() $\mathrm {h}'_L(\Theta )$ be the Néron–Tate height (14.1) of
$\mathrm {h}'_L(\Theta )$ be the Néron–Tate height (14.1) of ![]() $\Theta$ and let
$\Theta$ and let ![]() $\mathrm {h}_F(A)$ be the stable Faltings height (13.2) of
$\mathrm {h}_F(A)$ be the stable Faltings height (13.2) of ![]() $A$. For
$A$. For ![]() $v \in M(k)_\infty$, let
$v \in M(k)_\infty$, let ![]() $I(A_v,\lambda _v)$ be the invariant defined in (1.1) and, for
$I(A_v,\lambda _v)$ be the invariant defined in (1.1) and, for ![]() $v \in M(k)_0$, let
$v \in M(k)_0$, let ![]() $I(A_v,\lambda _v)$ be the invariant defined in (1.5).
$I(A_v,\lambda _v)$ be the invariant defined in (1.5).
Write ![]() $\kappa _0=\log (\pi \sqrt {2})$ and set
$\kappa _0=\log (\pi \sqrt {2})$ and set ![]() $g=\dim (A)$.
$g=\dim (A)$.
Theorem 15.1 The equality
 \[ \mathrm{h}_F(A) = 2g \,\mathrm{h}'_L(\Theta) - \kappa_0 \, g + \frac{2}{[k:\mathbb{Q}]}\bigg( \sum_{v \in M(k)_0} I(A_v,\lambda_v) \log Nv + \sum_{v \in M(k)_\infty} I(A_v,\lambda_v) \bigg) \]
\[ \mathrm{h}_F(A) = 2g \,\mathrm{h}'_L(\Theta) - \kappa_0 \, g + \frac{2}{[k:\mathbb{Q}]}\bigg( \sum_{v \in M(k)_0} I(A_v,\lambda_v) \log Nv + \sum_{v \in M(k)_\infty} I(A_v,\lambda_v) \bigg) \]
holds in ![]() $\mathbb {R}$.
$\mathbb {R}$.
Proof. We are allowed to replace ![]() $k$ by a finite field extension. Hence, we may assume that
$k$ by a finite field extension. Hence, we may assume that ![]() $(A,L)$ has a Moret-Bailly model
$(A,L)$ has a Moret-Bailly model ![]() $(\mathcal {A},\mathcal {L})$ over the ring of integers of
$(\mathcal {A},\mathcal {L})$ over the ring of integers of ![]() $k$.
$k$.
For each ![]() $v \in M(k)_0$, we let
$v \in M(k)_0$, we let ![]() $k_v$ denote the completion of
$k_v$ denote the completion of ![]() $k$ at
$k$ at ![]() $v$, choose a uniformizer
$v$, choose a uniformizer ![]() $\varpi _v$, fix the completion
$\varpi _v$, fix the completion ![]() $\mathbb {C}_v$ of an algebraic closure of
$\mathbb {C}_v$ of an algebraic closure of ![]() $k_v$ and fix on
$k_v$ and fix on ![]() $\mathbb {C}_v$ a corresponding absolute value
$\mathbb {C}_v$ a corresponding absolute value ![]() $|\cdot |_v$ such that
$|\cdot |_v$ such that ![]() $|\varpi _v|_v=(Nv)^{-1}$ with
$|\varpi _v|_v=(Nv)^{-1}$ with ![]() $Nv$ the cardinality of the residue field at
$Nv$ the cardinality of the residue field at ![]() $v$.
$v$.
For each ![]() $v \in M(k)_\infty$, we choose the standard euclidean metrics
$v \in M(k)_\infty$, we choose the standard euclidean metrics ![]() $|\cdot |_v$ on all
$|\cdot |_v$ on all ![]() $\bar {k}_v\cong \mathbb {C}$.
$\bar {k}_v\cong \mathbb {C}$.
We fix a rigidification on ![]() $L$. For each
$L$. For each ![]() $v \in M(k)$, we let
$v \in M(k)$, we let ![]() $\|\cdot \|_{L,v}$ denote the canonical metric on
$\|\cdot \|_{L,v}$ denote the canonical metric on ![]() $L^\mathrm {an}_v$ on
$L^\mathrm {an}_v$ on ![]() $A_v^{\mathrm {an}}$ determined by the absolute value
$A_v^{\mathrm {an}}$ determined by the absolute value ![]() $|\cdot |_v$.
$|\cdot |_v$.
Let ![]() $S$ be the spectrum of the ring of integers of
$S$ be the spectrum of the ring of integers of ![]() $k$ and let
$k$ and let ![]() $\pi \colon \mathcal {A} \to S$ denote the structure morphism. Set
$\pi \colon \mathcal {A} \to S$ denote the structure morphism. Set ![]() $\mathrm {h}^*_F(A) = \mathrm {h}_F(A)+ \kappa _0 g$. By Theorem 13.1 (the key formula), we find that
$\mathrm {h}^*_F(A) = \mathrm {h}_F(A)+ \kappa _0 g$. By Theorem 13.1 (the key formula), we find that
Here the Arakelov degree is taken over ![]() $S$ and the metrics at the complex embeddings are the
$S$ and the metrics at the complex embeddings are the ![]() $L^2$-metrics (12.2).
$L^2$-metrics (12.2).
We are going to calculate the Arakelov degree in the right-hand side of (15.1) explicitly. View ![]() $s$ as a rational section of the invertible sheaf
$s$ as a rational section of the invertible sheaf ![]() $\pi _* \mathcal {L}$ on
$\pi _* \mathcal {L}$ on ![]() $S$. By (13.1), we have
$S$. By (13.1), we have
Let ![]() $v \in M(k)_0$. Let
$v \in M(k)_0$. Let ![]() $\Sigma _v$ be the canonical skeleton of
$\Sigma _v$ be the canonical skeleton of ![]() $A_v^\mathrm {an}$ and let
$A_v^\mathrm {an}$ and let ![]() $\mu _{H,v}$ denote the Haar measure of unit volume on
$\mu _{H,v}$ denote the Haar measure of unit volume on ![]() $\Sigma _v$. By Corollary 10.7, we have, taking care of the identity
$\Sigma _v$. By Corollary 10.7, we have, taking care of the identity ![]() $|\varpi _v|_v=(Nv)^{-1}$ for the absolute value at
$|\varpi _v|_v=(Nv)^{-1}$ for the absolute value at ![]() $v$,
$v$,
 \begin{align} \operatorname{ord}_v(s) \log Nv & ={-} \log \Bigl(\sup_{x \in \Sigma_v} \|s(x)\|_{L,v} \Bigr)\nonumber\\ & ={-} \biggl( \int_{A_v^\mathrm{an}} \log\! \|s\|_{L,v} \, d \mu_{H,v} + I(A_v,\lambda_v) \log Nv \biggr). \end{align}
\begin{align} \operatorname{ord}_v(s) \log Nv & ={-} \log \Bigl(\sup_{x \in \Sigma_v} \|s(x)\|_{L,v} \Bigr)\nonumber\\ & ={-} \biggl( \int_{A_v^\mathrm{an}} \log\! \|s\|_{L,v} \, d \mu_{H,v} + I(A_v,\lambda_v) \log Nv \biggr). \end{align} Now let ![]() $v \in M(k)_\infty$. From (1.1) and (12.2), we obtain
$v \in M(k)_\infty$. From (1.1) and (12.2), we obtain
 \begin{align} \log\! \|s\|_v & = \frac{1}{2} \log \int_{A_v^{\mathrm{an}}} \|s\|_{L,v}^2 \, d \mu_{H,v} \nonumber\\ & = \int_{A_v^{\mathrm{an}}} \log\! \|s\|_{L,v} \, d \mu_{H,v} + I(A_v,\lambda_v). \end{align}
\begin{align} \log\! \|s\|_v & = \frac{1}{2} \log \int_{A_v^{\mathrm{an}}} \|s\|_{L,v}^2 \, d \mu_{H,v} \nonumber\\ & = \int_{A_v^{\mathrm{an}}} \log\! \|s\|_{L,v} \, d \mu_{H,v} + I(A_v,\lambda_v). \end{align}Combining (15.1)–(15.4), we find that
 \begin{align*} [k:\mathbb{Q}]\, \mathrm{h}^*_F(A) & = 2 \sum_{v \in M(k)_0} \biggl( \int_{A_v^\mathrm{an}} \log\! \|s\|_{L,v} \, d \mu_{H,v} + I(A_v,\lambda_v)\log Nv \biggr)\nonumber \\ & \quad + 2 \sum_{v \in M(k)_\infty} \biggl(\int_{A_v^{\mathrm{an}}} \log\! \|s\|_{L,v} \, d \mu_{H,v} + I(A_v,\lambda_v) \biggr). \end{align*}
\begin{align*} [k:\mathbb{Q}]\, \mathrm{h}^*_F(A) & = 2 \sum_{v \in M(k)_0} \biggl( \int_{A_v^\mathrm{an}} \log\! \|s\|_{L,v} \, d \mu_{H,v} + I(A_v,\lambda_v)\log Nv \biggr)\nonumber \\ & \quad + 2 \sum_{v \in M(k)_\infty} \biggl(\int_{A_v^{\mathrm{an}}} \log\! \|s\|_{L,v} \, d \mu_{H,v} + I(A_v,\lambda_v) \biggr). \end{align*}Using Theorem 14.1, we obtain
This proves Theorem A.
Acknowledgements
We thank Lars Halle, David Holmes, Johannes Nicaise and Xinyi Yuan for helpful remarks. We especially thank the anonymous referee for valuable suggestions that constituted a major simplification of some of the arguments leading to the proof of our main result. The second-named author was partially supported by a NSF CAREER grant DMS-2044564.