Article contents
A formula for certain Shalika germs of ramified unitary groups
Published online by Cambridge University Press: 19 January 2017
Abstract
In this article, for nilpotent orbits of ramified quasi-split unitary groups with two Jordan blocks, we give closed formulas for their Shalika germs at certain equi-valued elements with half-integral depth previously studied by Hales. Associated with these elements are hyperelliptic curves defined over the residue field, and the numbers we obtain can be expressed in terms of Frobenius eigenvalues on the first 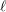 $\ell$ -adic cohomology of the curves, generalizing previous result of Hales on stable subregular Shalika germs. These Shalika germ formulas imply new results on stability and endoscopic transfer of nilpotent orbital integrals of ramified unitary groups. We also describe how the same numbers appear in the local character expansions of specific supercuspidal representations and consequently dimensions of degenerate Whittaker models.
$\ell$ -adic cohomology of the curves, generalizing previous result of Hales on stable subregular Shalika germs. These Shalika germ formulas imply new results on stability and endoscopic transfer of nilpotent orbital integrals of ramified unitary groups. We also describe how the same numbers appear in the local character expansions of specific supercuspidal representations and consequently dimensions of degenerate Whittaker models.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author 2017
References
- 3
- Cited by

