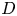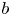1. Introduction
1.1
This article studies how ![]() $D$-module operations interact with singular support. The main technical result, Theorem 2.5.1, shows that
$D$-module operations interact with singular support. The main technical result, Theorem 2.5.1, shows that ![]() $D$-module operations preserve a certain numerical obstruction to holonomicity. This result generalizes the usual preservation of holonomic
$D$-module operations preserve a certain numerical obstruction to holonomicity. This result generalizes the usual preservation of holonomic ![]() $D$-modules under such operations, which is essentially equivalent to the
$D$-modules under such operations, which is essentially equivalent to the ![]() $b$-function lemma: see [Reference KashiwaraKas76] or [Reference BernsteinBer].
$b$-function lemma: see [Reference KashiwaraKas76] or [Reference BernsteinBer].
1.2 Exactness properties
Our main application is Theorem 3.4.1, which states that, inasmuch as the assertion makes sense (see § 1.3), ![]() $f_!$ is left
$f_!$ is left ![]() $t$-exact for an affine morphism
$t$-exact for an affine morphism ![]() $f:X \to Y$.
$f:X \to Y$.
This is certainly an old folklore result. It is standard for holonomic ![]() $D$-modules, where it is a consequence of the usual
$D$-modules, where it is a consequence of the usual ![]() $b$-function lemma. It is also easy to show for
$b$-function lemma. It is also easy to show for ![]() $Y = \operatorname {Spec}(k)$, or for a map of curves. Otherwise, it does not seem to follow from existing foundational results in the literature, which is surprising for something so basic.
$Y = \operatorname {Spec}(k)$, or for a map of curves. Otherwise, it does not seem to follow from existing foundational results in the literature, which is surprising for something so basic.
1.3
We remark that, as just stated, this result does not quite make sense.
Let, for example, ![]() $D(X)$ denote the derived category of
$D(X)$ denote the derived category of ![]() $D$-modules on
$D$-modules on ![]() $X$. There is a standard pullback functor
$X$. There is a standard pullback functor ![]() $f^!:D(Y) \to D(X)$ for
$f^!:D(Y) \to D(X)$ for ![]() $D$-modules. For
$D$-modules. For ![]() ${\cal F} \in D(X)$,
${\cal F} \in D(X)$, ![]() $f_!({\cal F}) \in D(Y)$ should corepresent the functor
$f_!({\cal F}) \in D(Y)$ should corepresent the functor ![]() ${\cal G} \mapsto \operatorname {Hom}_{D(X)}({\cal F},f^!({\cal G}))$, but this functor is not necessarily corepresentable. We say that
${\cal G} \mapsto \operatorname {Hom}_{D(X)}({\cal F},f^!({\cal G}))$, but this functor is not necessarily corepresentable. We say that ![]() $f_!({\cal F})$ is defined whenever this functor is corepresentable.
$f_!({\cal F})$ is defined whenever this functor is corepresentable.
Recall that standard ![]() $D$-module theory shows that
$D$-module theory shows that ![]() $f_!({\cal F})$ is defined when
$f_!({\cal F})$ is defined when ![]() ${\cal F}$ is holonomic, or when
${\cal F}$ is holonomic, or when ![]() $f$ is proper (in which case it coincides with the
$f$ is proper (in which case it coincides with the ![]() $D$-module pushforward
$D$-module pushforward ![]() $f_{*,{\rm dR}}({\cal F})$).
$f_{*,{\rm dR}}({\cal F})$).
One version of Theorem 3.4.1 states that if ![]() $f$ is affine,
$f$ is affine, ![]() ${\cal F} \in D(X)^{\geq 0}$, and
${\cal F} \in D(X)^{\geq 0}$, and ![]() $f_!({\cal F})$ is defined, then
$f_!({\cal F})$ is defined, then ![]() $f_!({\cal F}) \in D(Y)^{\geq 0}$; for technical reasons, we also need to assume that
$f_!({\cal F}) \in D(Y)^{\geq 0}$; for technical reasons, we also need to assume that ![]() ${\cal F}$ is coherent (in the applications we have in mind, one can readily remove this hypothesis). We remark that for coherent
${\cal F}$ is coherent (in the applications we have in mind, one can readily remove this hypothesis). We remark that for coherent ![]() ${\cal F}$,
${\cal F}$, ![]() $f_!({\cal F})$ being defined is equivalent to
$f_!({\cal F})$ being defined is equivalent to ![]() $f_{*,{\rm dR}}({\cal F})$ being coherent on
$f_{*,{\rm dR}}({\cal F})$ being coherent on ![]() $Y$; in this case,
$Y$; in this case, ![]() $f_!({\cal F}) = {\mathbb {D}} f_{*,{\rm dR}} {\mathbb {D}} ({\cal F})$ for
$f_!({\cal F}) = {\mathbb {D}} f_{*,{\rm dR}} {\mathbb {D}} ({\cal F})$ for ![]() ${\mathbb {D}}$ the relevant Verdier duality functors.
${\mathbb {D}}$ the relevant Verdier duality functors.
More generally, we prove a somewhat more technical version of this theorem using pro-categories, which allows us to remove the hypothesis that ![]() $f_!({\cal F})$ is defined. The author finds this to be a more satisfying formulation, but we remark that the use of pro-categories in this paper is not so significant.
$f_!({\cal F})$ is defined. The author finds this to be a more satisfying formulation, but we remark that the use of pro-categories in this paper is not so significant.
1.4
Finally, there is the question of applications of this left ![]() $t$-exactness.
$t$-exactness.
In fact, one commonly finds affine morphisms ![]() $f$ and non-holonomic
$f$ and non-holonomic ![]() $D$-modules
$D$-modules ![]() ${\cal F}$ with
${\cal F}$ with ![]() $f_!({\cal F})$ being defined in geometric representation theory. Moreover, in such situations,
$f_!({\cal F})$ being defined in geometric representation theory. Moreover, in such situations, ![]() $f_!({\cal F})$ typically coincides with
$f_!({\cal F})$ typically coincides with ![]() $f_{*,{\rm dR}}({\cal F})$, and therefore one can deduce
$f_{*,{\rm dR}}({\cal F})$, and therefore one can deduce ![]() $t$-exactness results from our result (for affine
$t$-exactness results from our result (for affine ![]() $f$, it is easy to see
$f$, it is easy to see ![]() $f_{*,{\rm dR}}$ is right
$f_{*,{\rm dR}}$ is right ![]() $t$-exact).
$t$-exact).
For example, this situation occurs for the Fourier–Deligne transform, and the results here can be used to show its ![]() $t$-exactness in a conceptual way.Footnote 1
$t$-exactness in a conceptual way.Footnote 1
We include another example, due to [Reference Bezrukavnikov, Braverman and MirkovicBBM04], in Appendix A. A related example in infinite-dimensional Lie theory is given in [Reference RaskinRas21, Theorem 2.7.1].Footnote 2
Finally, see [Reference Bezrukavnikov and Yom DinBY18, Theorem 5.4] for another instance of this phenomenon.
1.5 Categorical conventions
As was already remarked above, we use derived categories of pro-![]() $D$-modules in § 3. It is well known that it is inconvenient to use triangulated categories when working with pro-complexes, and better to use more sophisticated homotopical methods.
$D$-modules in § 3. It is well known that it is inconvenient to use triangulated categories when working with pro-complexes, and better to use more sophisticated homotopical methods.
In § 2, which is the core of the paper, it is manifestly adequate to merely consider the triangulated category of ![]() $D$-modules on
$D$-modules on ![]() $X$. Indeed, the key point is Lemma 2.7.1, and this lemma is not about complexes; the reductions used in the remainder of the section only use standard homological algebra methods.
$X$. Indeed, the key point is Lemma 2.7.1, and this lemma is not about complexes; the reductions used in the remainder of the section only use standard homological algebra methods.
To keep consistent conventions in this paper, we will formally use the language of differential graded (DG) categories throughout this paper. Because this language is not relevant until § 3, we refer to § 3.2 for more details and references on our precise formalism.
1.6 Notation
We let ![]() $k$ denote a field of characteristic zero.
$k$ denote a field of characteristic zero.
By a variety, we mean a reduced, separated, finite type ![]() $k$-scheme.
$k$-scheme.
For ![]() $X$ a variety over
$X$ a variety over ![]() $k$, we let
$k$, we let ![]() $D(X)$ denote the DG category of
$D(X)$ denote the DG category of ![]() $D$-modules on
$D$-modules on ![]() $X$. For
$X$. For ![]() $f:X \to Y$, we let
$f:X \to Y$, we let ![]() $f^!:D(Y) \to D(X)$ and
$f^!:D(Y) \to D(X)$ and ![]() $f_{*,{\rm dR}}:D(X) \to D(Y)$ denote the standard
$f_{*,{\rm dR}}:D(X) \to D(Y)$ denote the standard ![]() $D$-module pullback and pushforward operations. We let
$D$-module pullback and pushforward operations. We let ![]() $f_!$ and
$f_!$ and ![]() $f^{*,{\rm dR}}$ denote their left adjoints (where appropriate).
$f^{*,{\rm dR}}$ denote their left adjoints (where appropriate).
Remark 1.6.1 We refer the reader to [Reference Gaitsgory and RozenblyumGR17, § III.4] for a detailed development of ![]() $D$-module theory in the DG formalism. For the reader's convenience, we remark that in [Reference Gaitsgory and RozenblyumGR17], our category
$D$-module theory in the DG formalism. For the reader's convenience, we remark that in [Reference Gaitsgory and RozenblyumGR17], our category ![]() $D(X)$ is denoted
$D(X)$ is denoted ![]() $\operatorname {Crys}(X)$, our functor
$\operatorname {Crys}(X)$, our functor ![]() $f^!$ is denoted
$f^!$ is denoted ![]() $f_{{\rm dR}}^!$, and our functor
$f_{{\rm dR}}^!$, and our functor ![]() $f_{*,{\rm dR}}$ is denoted
$f_{*,{\rm dR}}$ is denoted ![]() $f_{{\rm dR},*}$. The comparison with the classical theory of
$f_{{\rm dR},*}$. The comparison with the classical theory of ![]() $D$-modules (as developed, for example, in [Reference BernsteinBer] or [Reference KashiwaraKas95, § 2]) is given in [Reference Gaitsgory and RozenblyumGR17, § III.4.4].
$D$-modules (as developed, for example, in [Reference BernsteinBer] or [Reference KashiwaraKas95, § 2]) is given in [Reference Gaitsgory and RozenblyumGR17, § III.4.4].
We highlight that [Reference Gaitsgory and RozenblyumGR17, Theorem III.4.2.1.2] encodes base-change properties of ![]() $D$-module functors, as is extensively discussed in [Reference Gaitsgory and RozenblyumGR17]. In its symmetric monoidal form, which is a special case of [Reference Gaitsgory and RozenblyumGR17, Corollary III.3.6.1.3], this result also encodes the projection formula.
$D$-module functors, as is extensively discussed in [Reference Gaitsgory and RozenblyumGR17]. In its symmetric monoidal form, which is a special case of [Reference Gaitsgory and RozenblyumGR17, Corollary III.3.6.1.3], this result also encodes the projection formula.
Remark 1.6.2 As in [Reference Gaitsgory and RozenblyumGR17], with caveats, the forgetful functor from ![]() $D$-modules to quasi-coherent sheaves intertwines the upper-
$D$-modules to quasi-coherent sheaves intertwines the upper-![]() $!$ functor for
$!$ functor for ![]() $D$-modules with Grothendieck's upper-
$D$-modules with Grothendieck's upper-![]() $!$ functor for quasi-coherent sheaves. The two caveats are that one should consider the forgetful functor taking the underlying right (as opposed to left)
$!$ functor for quasi-coherent sheaves. The two caveats are that one should consider the forgetful functor taking the underlying right (as opposed to left) ![]() $D_X$-module, and that for singular
$D_X$-module, and that for singular ![]() $X$, it is better to work with ind-coherent sheaves than quasi-coherent sheaves (as is always the case when considering Grothendieck's functor).
$X$, it is better to work with ind-coherent sheaves than quasi-coherent sheaves (as is always the case when considering Grothendieck's functor).
By contrast, the quasi-coherent sheaf underlying ![]() $f_{*,{\rm dR}}({\cal F})$ is quite sensitive to the connection on
$f_{*,{\rm dR}}({\cal F})$ is quite sensitive to the connection on ![]() ${\cal F}$, leading to the asymmetric notation.
${\cal F}$, leading to the asymmetric notation.
We use ![]() $-\overset {!}{\otimes }-$ to denote the standard symmetric monoidal product on
$-\overset {!}{\otimes }-$ to denote the standard symmetric monoidal product on ![]() $D(X)$. We recall that
$D(X)$. We recall that ![]() ${\cal F} \overset {!}{\otimes } {\cal G} = \Delta ^!({\cal F} \boxtimes {\cal G})$ for
${\cal F} \overset {!}{\otimes } {\cal G} = \Delta ^!({\cal F} \boxtimes {\cal G})$ for ![]() ${\cal F},{\cal G} \in D(X)$. We refer to [Reference Gaitsgory and RozenblyumGR17, § III.3.6.1] for the construction in the DG formalism.
${\cal F},{\cal G} \in D(X)$. We refer to [Reference Gaitsgory and RozenblyumGR17, § III.3.6.1] for the construction in the DG formalism.
We let ![]() $D(X)^{\geq i}$ and
$D(X)^{\geq i}$ and ![]() $D(X)^{\leq i}$ respectively denote the subcategoriesFootnote 3 of complexes
$D(X)^{\leq i}$ respectively denote the subcategoriesFootnote 3 of complexes ![]() ${\cal F} \in D(X)$ with
${\cal F} \in D(X)$ with ![]() $H^j({\cal F}) = 0$ for
$H^j({\cal F}) = 0$ for ![]() $j< i$ and
$j< i$ and ![]() $j>i$, respectively. We let
$j>i$, respectively. We let ![]() $D(X)^{\heartsuit } = D(X)^{\geq 0} \cap D(X)^{\leq 0}$ denote the heart of the
$D(X)^{\heartsuit } = D(X)^{\geq 0} \cap D(X)^{\leq 0}$ denote the heart of the ![]() $t$-structure, that is, the abelian category of
$t$-structure, that is, the abelian category of ![]() $D$-modules. We let
$D$-modules. We let ![]() $\tau ^{\geq i}$ and
$\tau ^{\geq i}$ and ![]() $\tau ^{\leq i}$ denote the corresponding truncation functors.
$\tau ^{\leq i}$ denote the corresponding truncation functors.
We let ![]() $D(X)^c \subseteq D(X)$ denote the DG subcategory of coherent complexes, that is, bounded complexes with locally coherentFootnote 4 cohomologies. Recall that
$D(X)^c \subseteq D(X)$ denote the DG subcategory of coherent complexes, that is, bounded complexes with locally coherentFootnote 4 cohomologies. Recall that ![]() $D(X)$ is compactly generatedFootnote 5 with compact objects
$D(X)$ is compactly generatedFootnote 5 with compact objects ![]() $D(X)^c$, that is,
$D(X)^c$, that is, ![]() $D(X) = \mathsf {Ind}(D(X)^c)$ for
$D(X) = \mathsf {Ind}(D(X)^c)$ for ![]() $\mathsf {Ind}$ denoting the ind-category;Footnote 6 cf. [Reference Gaitsgory and RozenblyumGR17, Corollary III.4.1.6.4].Footnote 7
$\mathsf {Ind}$ denoting the ind-category;Footnote 6 cf. [Reference Gaitsgory and RozenblyumGR17, Corollary III.4.1.6.4].Footnote 7
We let ![]() ${\mathbb {D}}:D(X)^c \xrightarrow {\simeq } D(X)^{c,{\rm op}}$ denote the Verdier duality functor. We refer to [Reference Gaitsgory and RozenblyumGR17, § III.4.2.2.5] for its construction in the DG formalism.
${\mathbb {D}}:D(X)^c \xrightarrow {\simeq } D(X)^{c,{\rm op}}$ denote the Verdier duality functor. We refer to [Reference Gaitsgory and RozenblyumGR17, § III.4.2.2.5] for its construction in the DG formalism.
We let ![]() $\mathsf {Vect}$ denote the DG category of chain complexes of vector spaces. For
$\mathsf {Vect}$ denote the DG category of chain complexes of vector spaces. For ![]() ${\cal C}$ a DG category and
${\cal C}$ a DG category and ![]() ${\cal F},{\cal G} \in {\cal C}$, we let
${\cal F},{\cal G} \in {\cal C}$, we let ![]() $\underline {\operatorname {Hom}}_{{\cal C}}({\cal F},{\cal G}) \in \mathsf {Vect}$ denote the chain complex of maps between
$\underline {\operatorname {Hom}}_{{\cal C}}({\cal F},{\cal G}) \in \mathsf {Vect}$ denote the chain complex of maps between ![]() ${\cal F}$ and
${\cal F}$ and ![]() ${\cal G}$.
${\cal G}$.
2. Holonomic defect
2.1
In this section we introduce a generalization of the holonomic condition on a ![]() $D$-module and show that it is preserved under
$D$-module and show that it is preserved under ![]() $D$-module operations.
$D$-module operations.
The method is standard. The main point is Lemma 2.7.1, which is a generalization of the fact that pushforward along an open embedding preserves holonomic objects, which is essentially equivalent to the usual ![]() $b$-function lemma. The main difference is that we cannot use finite-length methods. See also Remark 2.7.2 for indications on a different approach.
$b$-function lemma. The main difference is that we cannot use finite-length methods. See also Remark 2.7.2 for indications on a different approach.
The presentation is based on [Reference KashiwaraKas76, Reference GinzburgGin86].
2.2 Gabber–Kashiwara–Sato (GKS) filtration
We begin by reviewing some material from [Reference GinzburgGin86, § 1].
Definition 2.2.1 Let ![]() $X$ be a variety and let
$X$ be a variety and let ![]() ${\cal F} \in D(X)^{\heartsuit }$ be a coherent
${\cal F} \in D(X)^{\heartsuit }$ be a coherent ![]() $D$-module. For an integer
$D$-module. For an integer ![]() $i$, we let
$i$, we let
We extend this definition to general ![]() ${\cal F}$ by ind-extension. That is, if we write
${\cal F}$ by ind-extension. That is, if we write ![]() ${\cal F}$ as a filtered colimit
${\cal F}$ as a filtered colimit ![]() $\operatorname {colim}_j {\cal F}_j$ with each
$\operatorname {colim}_j {\cal F}_j$ with each ![]() ${\cal F}_j$ coherent (as can always be done), we take
${\cal F}_j$ coherent (as can always be done), we take ![]() $F_i^{{\rm GKS}} {\cal F} := \operatorname {colim}_j F_i^{{\rm GKS}} {\cal F}_j$.
$F_i^{{\rm GKS}} {\cal F} := \operatorname {colim}_j F_i^{{\rm GKS}} {\cal F}_j$.
Remark 2.2.2 Formula (2.2.1) is valid for general ![]() ${\cal F}$ if one interprets
${\cal F}$ if one interprets ![]() ${\mathbb {D}}$ as an equivalence between
${\mathbb {D}}$ as an equivalence between ![]() $D(X)$ and the DG category of pro-coherent
$D(X)$ and the DG category of pro-coherent ![]() $D$-modules equipped with the
$D$-modules equipped with the ![]() $t$-structure of § 3.3.
$t$-structure of § 3.3.
Note that ![]() $F_{\bullet }^{{\rm GKS}}$ is an increasing filtration on
$F_{\bullet }^{{\rm GKS}}$ is an increasing filtration on ![]() ${\cal F}$. Because
${\cal F}$. Because ![]() ${\mathbb {D}} {\cal F}$ is in cohomological degrees
${\mathbb {D}} {\cal F}$ is in cohomological degrees ![]() $[-\dim X,0]$, we have
$[-\dim X,0]$, we have ![]() $F_i^{{\rm GKS}} {\cal F} = 0$ for
$F_i^{{\rm GKS}} {\cal F} = 0$ for ![]() $i<0$, and
$i<0$, and ![]() $F_i^{{\rm GKS}} {\cal F} = {\cal F}$ for
$F_i^{{\rm GKS}} {\cal F} = {\cal F}$ for ![]() $i \geq \dim X$. Formation of the GKS filtration is functorial for
$i \geq \dim X$. Formation of the GKS filtration is functorial for ![]() $D$-module morphisms, that is, a map
$D$-module morphisms, that is, a map ![]() ${\cal F}_1 \to {\cal F}_2 \in D(X)^{\heartsuit }$ sends
${\cal F}_1 \to {\cal F}_2 \in D(X)^{\heartsuit }$ sends ![]() $F_i^{{\rm GKS}} {\cal F}_1$ to
$F_i^{{\rm GKS}} {\cal F}_1$ to ![]() $F_i^{{\rm GKS}} {\cal F}_2$.
$F_i^{{\rm GKS}} {\cal F}_2$.
Note that if ![]() ${\cal F} = \operatorname {colim}_j {\cal F}_j$ is a filtered colimit in
${\cal F} = \operatorname {colim}_j {\cal F}_j$ is a filtered colimit in ![]() $D(X)^{\heartsuit }$, then
$D(X)^{\heartsuit }$, then ![]() $F_i^{{\rm GKS}} {\cal F} = \operatorname {colim}_j F_i^{{\rm GKS}} {\cal F}_j$.
$F_i^{{\rm GKS}} {\cal F} = \operatorname {colim}_j F_i^{{\rm GKS}} {\cal F}_j$.
Lemma 2.2.3 Formation of ![]() $F_{\bullet }^{{\rm GKS}}$ commutes with open restriction and pushforwards along closed embeddings.
$F_{\bullet }^{{\rm GKS}}$ commutes with open restriction and pushforwards along closed embeddings.
Proof. Each of these functors is ![]() $t$-exact and commutes with Verdier duality.
$t$-exact and commutes with Verdier duality.
Therefore, many results about this filtration reduce to the case of smooth ![]() $X$ by taking Zariski local closed embeddings into affine space. The key property in the smooth case is given in the following theorem.
$X$ by taking Zariski local closed embeddings into affine space. The key property in the smooth case is given in the following theorem.
Theorem 2.2.4 If ![]() $X$ is smooth, then a local section
$X$ is smooth, then a local section ![]() $s$ of
$s$ of ![]() ${\cal F}$ lies in
${\cal F}$ lies in ![]() $F_i^{{\rm GKS}} {\cal F}$ if and only if the
$F_i^{{\rm GKS}} {\cal F}$ if and only if the ![]() $D$-module generated by it has singular support with dimension
$D$-module generated by it has singular support with dimension ![]() $\leq \dim X + i$.Footnote 8
$\leq \dim X + i$.Footnote 8
See [Reference GinzburgGin86, Proposition V.14]. Note that it is equivalent to say that ![]() $F_i^{{\rm GKS}} {\cal F}$ is the maximal submodule of
$F_i^{{\rm GKS}} {\cal F}$ is the maximal submodule of ![]() ${\cal F}$ with singular support of dimension
${\cal F}$ with singular support of dimension ![]() $\leq \dim X+i$.
$\leq \dim X+i$.
2.3 Holonomic defect
For ![]() $\delta \in {\mathbb {Z}}^{\geq 0}$, we say that
$\delta \in {\mathbb {Z}}^{\geq 0}$, we say that ![]() ${\cal F} \in D(X)^{\heartsuit }$ has holonomic defect
${\cal F} \in D(X)^{\heartsuit }$ has holonomic defect ![]() $\leq \delta$ if
$\leq \delta$ if ![]() $F_{\delta }^{{\rm GKS}} {\cal F} = {\cal F}$.
$F_{\delta }^{{\rm GKS}} {\cal F} = {\cal F}$.
Example 2.3.1 A coherent ![]() $D$-module
$D$-module ![]() ${\cal F}$ has holonomic defect
${\cal F}$ has holonomic defect ![]() $\leq 0$ if and only if
$\leq 0$ if and only if ![]() ${\cal F}$ is holonomic. Indeed, this follows by reduction to the smooth case and Theorem 2.2.4.
${\cal F}$ is holonomic. Indeed, this follows by reduction to the smooth case and Theorem 2.2.4.
Example 2.3.2 Every ![]() ${\cal F}$ has holonomic defect
${\cal F}$ has holonomic defect ![]() $\leq \dim X$.
$\leq \dim X$.
Example 2.3.3 If ![]() $X$ is smooth and
$X$ is smooth and ![]() ${\cal F}$ is coherent, then by Theorem 2.2.4,
${\cal F}$ is coherent, then by Theorem 2.2.4, ![]() ${\cal F}$ has holonomic defect
${\cal F}$ has holonomic defect ![]() $\leq \delta$ if and only if
$\leq \delta$ if and only if ![]() ${\cal F}$ has singular support with dimension
${\cal F}$ has singular support with dimension ![]() $\leq \dim X + \delta$.
$\leq \dim X + \delta$.
Lemma 2.3.4 The subcategory of ![]() $D(X)^{\heartsuit }$ consisting of objects with holonomic defect
$D(X)^{\heartsuit }$ consisting of objects with holonomic defect ![]() $\leq \delta$ is closed under submodules, quotient modules, and extensions.
$\leq \delta$ is closed under submodules, quotient modules, and extensions.
Proof. The argument reduces to the case of ![]() $X$ smooth, and then follows from Theorem 2.2.4 and standard facts about singular support.
$X$ smooth, and then follows from Theorem 2.2.4 and standard facts about singular support.
Lemma 2.3.5 Holonomic defect is preserved under filtered colimits, and ![]() ${\cal F} \in D(X)^{\heartsuit }$ has holonomic defect
${\cal F} \in D(X)^{\heartsuit }$ has holonomic defect ![]() $\leq \delta$ if and only if
$\leq \delta$ if and only if ![]() ${\cal F} = \operatorname {colim} {\cal F}_i$ with
${\cal F} = \operatorname {colim} {\cal F}_i$ with ![]() ${\cal F}_i$ coherent of holonomic defect
${\cal F}_i$ coherent of holonomic defect ![]() $\leq \delta$.
$\leq \delta$.
Proof. The first part is clear since formation of ![]() $F_{\bullet }^{{\rm GKS}}$ commutes with filtered colimits. For the second part, write
$F_{\bullet }^{{\rm GKS}}$ commutes with filtered colimits. For the second part, write ![]() ${\cal F} = \operatorname {colim}_i {\cal F}_i^{\prime }$ with
${\cal F} = \operatorname {colim}_i {\cal F}_i^{\prime }$ with ![]() ${\cal F}_i^{\prime }$ coherent, and then set
${\cal F}_i^{\prime }$ coherent, and then set ![]() ${\cal F}_i = F_{\delta }^{{\rm GKS}} {\cal F}_i^{\prime }$.
${\cal F}_i = F_{\delta }^{{\rm GKS}} {\cal F}_i^{\prime }$.
2.4
More generally, for ![]() ${\cal F} \in D(X)$ a complex of
${\cal F} \in D(X)$ a complex of ![]() $D$-modules, we say that
$D$-modules, we say that ![]() ${\cal F}$ has holonomic defect
${\cal F}$ has holonomic defect ![]() $\leq \delta$ if all of its cohomology groups do. By Lemmas 2.3.4 and 2.3.5, this defines a DG subcategory of
$\leq \delta$ if all of its cohomology groups do. By Lemmas 2.3.4 and 2.3.5, this defines a DG subcategory of ![]() $D(X)$ closed under (homotopy) colimits (equivalently, under cones, shifts, and arbitrary direct sums).
$D(X)$ closed under (homotopy) colimits (equivalently, under cones, shifts, and arbitrary direct sums).
2.5
The following theorem is the main result of this section.
Theorem 2.5.1 If ![]() $f:X \to Y$ is a morphism and
$f:X \to Y$ is a morphism and ![]() ${\cal F} \in D(X)$ (respectively,
${\cal F} \in D(X)$ (respectively, ![]() ${\cal G} \in D(Y)$) has holonomic defect
${\cal G} \in D(Y)$) has holonomic defect ![]() $\leq \delta$, then
$\leq \delta$, then ![]() $f_{*,{\rm dR}}({\cal F})$ (respectively,
$f_{*,{\rm dR}}({\cal F})$ (respectively, ![]() $f^!({\cal G})$) does as well. Moreover, for
$f^!({\cal G})$) does as well. Moreover, for ![]() ${\cal F}$ coherent as above,
${\cal F}$ coherent as above, ![]() ${\mathbb {D}} {\cal F}$ has holonomic defect
${\mathbb {D}} {\cal F}$ has holonomic defect ![]() $\leq \delta$ as well.
$\leq \delta$ as well.
This theorem generalizes the preservation of holonomic objects under ![]() $D$-module operations, so the proof must follow similar lines. It is given below.
$D$-module operations, so the proof must follow similar lines. It is given below.
2.6 Verdier duality
The compatibility with Verdier duality in Theorem 2.5.1 is well known. Indeed, the result immediately reduces to ![]() $X$ being smooth, and then we have the following proposition.
$X$ being smooth, and then we have the following proposition.
Proposition 2.6.1 For coherent ![]() ${\cal F} \in D(X)^{\heartsuit }$ with singular support of dimension
${\cal F} \in D(X)^{\heartsuit }$ with singular support of dimension ![]() $\leq \dim X+i$, we have
$\leq \dim X+i$, we have ![]() $H^{-j} {\mathbb {D}} {\cal F} = 0$ unless
$H^{-j} {\mathbb {D}} {\cal F} = 0$ unless ![]() $0\leq j \leq i$. Moreover,
$0\leq j \leq i$. Moreover, ![]() $H^{-j} {\mathbb {D}} {\cal F}$ has holonomic defect
$H^{-j} {\mathbb {D}} {\cal F}$ has holonomic defect ![]() $\leq j$.
$\leq j$.
See, for example, [Reference KashiwaraKas76, Theorem 2.3].
2.7 Affine open embeddings
The main case of Theorem 2.5.1 is pushforward along an open embedding.
Lemma 2.7.1 Let ![]() $X$ be a smooth variety and let
$X$ be a smooth variety and let ![]() $f:X \to {\mathbb {A}}^1$ be a function. Let
$f:X \to {\mathbb {A}}^1$ be a function. Let ![]() $U = \{f \neq 0\}$ be the corresponding basic open and let
$U = \{f \neq 0\}$ be the corresponding basic open and let ![]() $j:U \hookrightarrow X$ denote the corresponding affine open embedding.
$j:U \hookrightarrow X$ denote the corresponding affine open embedding.
Then ![]() $j_{*,{\rm dR}}$ preserves the property of having holonomic defect
$j_{*,{\rm dR}}$ preserves the property of having holonomic defect ![]() $\leq \delta$.
$\leq \delta$.
Remark 2.7.2 The argument that follows is a version of the standard proof in the holonomic setting via ![]() $b$-functions. Victor Ginzburg communicated to us that the proof of the holonomic version of Lemma 2.7.1 via the Bernstein filtration and Hilbert polynomials has a more straightforward generalization. This argument, which follows early work [Reference BernsteinBer72] in the subject, is easily extracted from [Reference Hotta, Takeuchi and TanisakiHTT08, § 3.2.2].
$b$-functions. Victor Ginzburg communicated to us that the proof of the holonomic version of Lemma 2.7.1 via the Bernstein filtration and Hilbert polynomials has a more straightforward generalization. This argument, which follows early work [Reference BernsteinBer72] in the subject, is easily extracted from [Reference Hotta, Takeuchi and TanisakiHTT08, § 3.2.2].
Proof of Lemma 2.7.1 Step 1. We may obviously assume ![]() $X$ is connected and affine and that
$X$ is connected and affine and that ![]() $f$ is non-constant.
$f$ is non-constant.
We let ![]() $D_X$ and
$D_X$ and ![]() $D_U$ denote the respective rings of global differential operators (as opposed to the sheaves of differential operators). Because
$D_U$ denote the respective rings of global differential operators (as opposed to the sheaves of differential operators). Because ![]() $X$ and
$X$ and ![]() $U$ are affine, we may consider
$U$ are affine, we may consider ![]() $D$-modules on either of these schemes as modules over these rings.
$D$-modules on either of these schemes as modules over these rings.
Let ![]() ${\cal F} \in D_U - \mathsf {mod}^{\heartsuit } \simeq D(U)^{\heartsuit }$. Because we are working with modules rather than sheaves, considering
${\cal F} \in D_U - \mathsf {mod}^{\heartsuit } \simeq D(U)^{\heartsuit }$. Because we are working with modules rather than sheaves, considering ![]() ${\cal F}$ as a
${\cal F}$ as a ![]() $D_X$-module by restriction is the same as considering the sheaf
$D_X$-module by restriction is the same as considering the sheaf ![]() $j_{*,{\rm dR}}({\cal F}) \in D(X)^{\heartsuit }$.
$j_{*,{\rm dR}}({\cal F}) \in D(X)^{\heartsuit }$.
For ![]() $s \in {\cal F}$, we write
$s \in {\cal F}$, we write ![]() $\operatorname {SS}_U(s) \subseteq T^* U$ for the singular support of
$\operatorname {SS}_U(s) \subseteq T^* U$ for the singular support of ![]() $D_U \cdot s$ and
$D_U \cdot s$ and ![]() $\operatorname {SS}_X(s) \subseteq T^* X$ for the singular support of
$\operatorname {SS}_X(s) \subseteq T^* X$ for the singular support of ![]() $D_X \cdot s$. Note that
$D_X \cdot s$. Note that ![]() $\operatorname {SS}_X(s)|_{T^* U} = \operatorname {SS}_U(s)$. We always understand singular support as a reduced subscheme.
$\operatorname {SS}_X(s)|_{T^* U} = \operatorname {SS}_U(s)$. We always understand singular support as a reduced subscheme.
We want to show that if every section ![]() $s \in {\cal F}$ has
$s \in {\cal F}$ has ![]() $\dim \operatorname {SS}_U(s) \leq \dim U + \delta = \dim X + \delta$, then the same is true of
$\dim \operatorname {SS}_U(s) \leq \dim U + \delta = \dim X + \delta$, then the same is true of ![]() $\dim SS_X(s)$.
$\dim SS_X(s)$.
Step 2. First, we observe that there is a ![]() $D_X$-submodule
$D_X$-submodule ![]() ${\cal G} \subseteq {\cal F}$ such that every section of
${\cal G} \subseteq {\cal F}$ such that every section of ![]() ${\cal G}$ has singular support with dimension
${\cal G}$ has singular support with dimension ![]() $\leq \dim X + \delta$, and which is a lattice, that is,
$\leq \dim X + \delta$, and which is a lattice, that is, ![]() ${\cal G} \otimes _{{\cal O}_X} {\cal O}_U \xrightarrow {\simeq } {\cal F}$.
${\cal G} \otimes _{{\cal O}_X} {\cal O}_U \xrightarrow {\simeq } {\cal F}$.
Indeed, we can take ![]() ${\cal G} = F_{\delta }^{{\rm GKS}} {\cal F}$, where the GKS filtration is with
${\cal G} = F_{\delta }^{{\rm GKS}} {\cal F}$, where the GKS filtration is with ![]() ${\cal F}$ considered as a
${\cal F}$ considered as a ![]() $D_X$-module. Because the GKS filtration commutes with open restriction, we must have
$D_X$-module. Because the GKS filtration commutes with open restriction, we must have ![]() ${\cal G}|_U = {\cal F}$.
${\cal G}|_U = {\cal F}$.
(Note that by Theorem 2.2.4, we are trying to show that ![]() ${\cal G} = {\cal F}$.)
${\cal G} = {\cal F}$.)
Step 3. We begin with some preliminary constructions.
Let ![]() $\lambda$ be an indeterminate. We write
$\lambda$ be an indeterminate. We write ![]() ${\mathbb {A}}_{\lambda }^1$ for
${\mathbb {A}}_{\lambda }^1$ for ![]() $\operatorname {Spec}(k[\lambda ])$. We let
$\operatorname {Spec}(k[\lambda ])$. We let ![]() $k^{\prime }$ denote the fraction field
$k^{\prime }$ denote the fraction field ![]() $k(\lambda )$ of
$k(\lambda )$ of ![]() $k[\lambda ]$. We use similar notation for a base-change to
$k[\lambda ]$. We use similar notation for a base-change to ![]() $k^{\prime }$; for example,
$k^{\prime }$; for example, ![]() $X^{\prime }$ or
$X^{\prime }$ or ![]() ${\cal F}^{\prime }$, etc. We always consider
${\cal F}^{\prime }$, etc. We always consider ![]() $X^{\prime }$ and
$X^{\prime }$ and ![]() $U^{\prime }$ as schemes over
$U^{\prime }$ as schemes over ![]() $k^{\prime }$, so, for example, their cotangent bundles are understood relative to
$k^{\prime }$, so, for example, their cotangent bundles are understood relative to ![]() $k^{\prime }$, and
$k^{\prime }$, and ![]() $D_X^{\prime } = D_{X^{\prime }}$.
$D_X^{\prime } = D_{X^{\prime }}$.
We now recall that there is certain standard object ![]() ${\cal O}_{U^{\prime }}f^{\lambda } \in D(U^{\prime })^{\heartsuit }$ which is
${\cal O}_{U^{\prime }}f^{\lambda } \in D(U^{\prime })^{\heartsuit }$ which is ![]() $({\cal O}_{U^{\prime }},\nabla = d+\lambda (df\!{/}\!f))$. We denote the basis vector of
$({\cal O}_{U^{\prime }},\nabla = d+\lambda (df\!{/}\!f))$. We denote the basis vector of ![]() $\Gamma (U^{\prime },{\cal O}_{U^{\prime }}f^{\lambda }) \in D_U^{\prime } - \mathsf {mod}^{\heartsuit }$ also by
$\Gamma (U^{\prime },{\cal O}_{U^{\prime }}f^{\lambda }) \in D_U^{\prime } - \mathsf {mod}^{\heartsuit }$ also by ![]() $f^{\lambda }$.
$f^{\lambda }$.
We similarly let ![]() ${\cal F}^{\prime }f^{\lambda }$ denote the tensor product of
${\cal F}^{\prime }f^{\lambda }$ denote the tensor product of ![]() ${\cal F}^{\prime }$ with
${\cal F}^{\prime }$ with ![]() ${\cal O}_{U^{\prime }}f^{\lambda }$ over
${\cal O}_{U^{\prime }}f^{\lambda }$ over ![]() ${\cal O}_{U^{\prime }}$, equipped with its standard
${\cal O}_{U^{\prime }}$, equipped with its standard ![]() $D_{U^{\prime }}$-module structure. Explicitly, this
$D_{U^{\prime }}$-module structure. Explicitly, this ![]() $D_U^{\prime }$-module has the same underlying
$D_U^{\prime }$-module has the same underlying ![]() $\Gamma (U^{\prime },{\cal O}_{U^{\prime }})$-module as
$\Gamma (U^{\prime },{\cal O}_{U^{\prime }})$-module as ![]() ${\cal F}^{\prime }$, except that we write this identification as
${\cal F}^{\prime }$, except that we write this identification as
Then the action of vector fields is modified: for ![]() $\xi$ a vector field and
$\xi$ a vector field and ![]() $s\in {\cal F}^{\prime }$, we have
$s\in {\cal F}^{\prime }$, we have
Step 4. We first show that the result is true for ![]() ${\cal F}^{\prime } f^{\lambda }$, that is, that every section has
${\cal F}^{\prime } f^{\lambda }$, that is, that every section has ![]() $SS_{X^{\prime }}$ with dimension
$SS_{X^{\prime }}$ with dimension ![]() $\leq \dim X + \delta$.
$\leq \dim X + \delta$.
First, note that the singular support in ![]() $U^{\prime }$ of any section has dimension
$U^{\prime }$ of any section has dimension ![]() $\leq \dim X + \delta$: this follows because
$\leq \dim X + \delta$: this follows because ![]() ${\cal O}_{U^{\prime }}f^{\lambda }$ is lisse on
${\cal O}_{U^{\prime }}f^{\lambda }$ is lisse on ![]() $U^{\prime }$ (that is, a vector bundle when considered as a mere quasi-coherent sheaf).
$U^{\prime }$ (that is, a vector bundle when considered as a mere quasi-coherent sheaf).
We have a canonical field automorphism ![]() $\gamma \in \operatorname {Aut}(k^{\prime }/k)$ sending
$\gamma \in \operatorname {Aut}(k^{\prime }/k)$ sending ![]() $\lambda \mapsto \lambda +1$. Of course, anything obtained by extension of scalars from
$\lambda \mapsto \lambda +1$. Of course, anything obtained by extension of scalars from ![]() $k$ to
$k$ to ![]() $k^{\prime }$ also carries such an automorphism
$k^{\prime }$ also carries such an automorphism ![]() $\gamma$; in particular,
$\gamma$; in particular, ![]() $D_X^{\prime }$ does (it sends a differential operator
$D_X^{\prime }$ does (it sends a differential operator ![]() $P(\lambda )$ to
$P(\lambda )$ to ![]() $P(\lambda +1)$).
$P(\lambda +1)$).
Similarly, ![]() ${\cal F}^{\prime }$ has such an automorphism: note that this is not an automorphism as a
${\cal F}^{\prime }$ has such an automorphism: note that this is not an automorphism as a ![]() $D_X^{\prime }$-module, but rather intertwines the standard action with the one obtained by twisting by the automorphism
$D_X^{\prime }$-module, but rather intertwines the standard action with the one obtained by twisting by the automorphism ![]() $\gamma$ of
$\gamma$ of ![]() $D_X^{\prime }$. That is,
$D_X^{\prime }$. That is, ![]() $\gamma (P \cdot s) = \gamma (P) \cdot \gamma (s)$ for
$\gamma (P \cdot s) = \gamma (P) \cdot \gamma (s)$ for ![]() $P \in D_X^{\prime }$ and
$P \in D_X^{\prime }$ and ![]() $s \in {\cal F}^{\prime }$.
$s \in {\cal F}^{\prime }$.
Define ![]() $\gamma$ on the
$\gamma$ on the ![]() $D_X^{\prime }$-module
$D_X^{\prime }$-module ![]() ${\cal O}_{U^{\prime }}f^{\lambda }$ by setting
${\cal O}_{U^{\prime }}f^{\lambda }$ by setting
for ![]() $g$ a function on
$g$ a function on ![]() $U^{\prime }$. Again, this morphism intertwines the actions of
$U^{\prime }$. Again, this morphism intertwines the actions of ![]() $D_X^{\prime }$ up to the automorphism
$D_X^{\prime }$ up to the automorphism ![]() $\gamma$ of
$\gamma$ of ![]() $D_X^{\prime }$.
$D_X^{\prime }$.
Tensoring, we obtain an automorphism ![]() $\gamma$ of
$\gamma$ of ![]() ${\cal F}^{\prime } f^{\lambda }$ with similar semi-linearity.
${\cal F}^{\prime } f^{\lambda }$ with similar semi-linearity.
By the semi-linearity, we have
where we are using ![]() $\gamma$ to indicate the induced automorphism of
$\gamma$ to indicate the induced automorphism of ![]() $T^* X^{\prime }$. In particular, we find that
$T^* X^{\prime }$. In particular, we find that
Now let ![]() ${\cal G} = F_{\delta }^{{\rm GKS}} ({\cal F}^{\prime } f^{\lambda })$,Footnote 9 where the GKS filtration is taken with
${\cal G} = F_{\delta }^{{\rm GKS}} ({\cal F}^{\prime } f^{\lambda })$,Footnote 9 where the GKS filtration is taken with ![]() ${\cal F}^{\prime } f^{\lambda }$ considered as a
${\cal F}^{\prime } f^{\lambda }$ considered as a ![]() $D_X^{\prime }$-module. By the above and Theorem 2.2.4,
$D_X^{\prime }$-module. By the above and Theorem 2.2.4, ![]() $s f^{\lambda } \in {\cal G}$ if and only if
$s f^{\lambda } \in {\cal G}$ if and only if ![]() $\gamma (s f^{\lambda }) \in {\cal G}$.
$\gamma (s f^{\lambda }) \in {\cal G}$.
For any ![]() $s \in {\cal F}$ (as opposed to
$s \in {\cal F}$ (as opposed to ![]() ${\cal F}^{\prime }$), we clearly have
${\cal F}^{\prime }$), we clearly have ![]() $\gamma (s f^{\lambda }) = s f^{\lambda +1}$. Since
$\gamma (s f^{\lambda }) = s f^{\lambda +1}$. Since ![]() ${\cal G}$ is a lattice (by Step 2),
${\cal G}$ is a lattice (by Step 2), ![]() $\gamma ^N(s) = s f^{\lambda +N} \in {\cal G}$ for
$\gamma ^N(s) = s f^{\lambda +N} \in {\cal G}$ for ![]() $N \gg 0$. But by the above, this means that
$N \gg 0$. But by the above, this means that ![]() $s \in {\cal G}$. Since
$s \in {\cal G}$. Since ![]() ${\cal F}^{\prime } f^{\lambda }$ is
${\cal F}^{\prime } f^{\lambda }$ is ![]() $k^{\prime }$-spanned by such vectors, this means that
$k^{\prime }$-spanned by such vectors, this means that ![]() ${\cal G} = {\cal F}^{\prime } f^{\lambda }$, as desired.
${\cal G} = {\cal F}^{\prime } f^{\lambda }$, as desired.
Step 5. We now show that the result is true for our original ![]() ${\cal F}$. Let
${\cal F}$. Let ![]() $s \in {\cal F}$; we want to show
$s \in {\cal F}$; we want to show ![]() $\dim \operatorname {SS}_X(s) \leq \dim X+\delta$.
$\dim \operatorname {SS}_X(s) \leq \dim X+\delta$.
We now write ![]() ${\cal F} f^{\lambda }$ for the corresponding
${\cal F} f^{\lambda }$ for the corresponding ![]() $D_X[\lambda ]$-module (as opposed to the fiber over the generic point in
$D_X[\lambda ]$-module (as opposed to the fiber over the generic point in ![]() ${\mathbb {A}}_{\lambda }^1$, which is what we called by this name previously). Note that
${\mathbb {A}}_{\lambda }^1$, which is what we called by this name previously). Note that ![]() ${\cal F} f^{\lambda } = {\cal F} \otimes _k k[\lambda ]$ as a
${\cal F} f^{\lambda } = {\cal F} \otimes _k k[\lambda ]$ as a ![]() ${\cal O}_X[\lambda ]$-module.
${\cal O}_X[\lambda ]$-module.
Let ![]() ${\cal F}_0$ be the
${\cal F}_0$ be the ![]() $D_X[\lambda ]$ submodule generated by
$D_X[\lambda ]$ submodule generated by ![]() $s f^{\lambda }$. Equip
$s f^{\lambda }$. Equip ![]() ${\cal F}_0$ with the filtration
${\cal F}_0$ with the filtration ![]() $F_i {\cal F}_0 = D_X^{\leq i}[\lambda ]s f^{\lambda }$, where
$F_i {\cal F}_0 = D_X^{\leq i}[\lambda ]s f^{\lambda }$, where ![]() $D_X^{\leq i}$ are differential operators of order
$D_X^{\leq i}$ are differential operators of order ![]() $\leq i$.
$\leq i$.
Then ![]() $\operatorname {gr}_{\bullet }({\cal F}_0)$ is the structure sheaf of some closed subscheme
$\operatorname {gr}_{\bullet }({\cal F}_0)$ is the structure sheaf of some closed subscheme ![]() $Z \subseteq T^*X \times {\mathbb {A}}_{\lambda }^1$. We have seen that the base-change of
$Z \subseteq T^*X \times {\mathbb {A}}_{\lambda }^1$. We have seen that the base-change of ![]() $Z$ to the generic point of
$Z$ to the generic point of ![]() ${\mathbb {A}}_{\lambda }^1$ has dimension
${\mathbb {A}}_{\lambda }^1$ has dimension ![]() $\leq \dim X + \delta$, so the same is true for its fibers at closed points with only finitely many possible exceptions.
$\leq \dim X + \delta$, so the same is true for its fibers at closed points with only finitely many possible exceptions.
Choose a negative integer ![]() $-N$ not among this finite number of exceptions. Then the coherent
$-N$ not among this finite number of exceptions. Then the coherent ![]() $D_X$-module
$D_X$-module ![]() ${\cal F}_0/(\lambda +N)$ has singular support contained in
${\cal F}_0/(\lambda +N)$ has singular support contained in ![]() $Z \times _{{\mathbb {A}}_{\lambda }^1} \{-N\}$, so has dimension
$Z \times _{{\mathbb {A}}_{\lambda }^1} \{-N\}$, so has dimension ![]() $\leq \dim X + \delta$. We have the obvious morphism of
$\leq \dim X + \delta$. We have the obvious morphism of ![]() $D_U$-modules (in particular, of
$D_U$-modules (in particular, of ![]() $D_X$-modules):
$D_X$-modules):
 \[ \begin{gathered} ({\cal F} f^{\lambda})/(\lambda+N) \to {\cal F} \\ \sum_{i = 0}^r \sigma_i \lambda^i f^{\lambda} \mapsto \sum_{i = 0}^r f^{{-}N} \cdot \sigma_i \cdot ({-}N)^i,\quad \sigma_i \in {\cal F} , \end{gathered} \]
\[ \begin{gathered} ({\cal F} f^{\lambda})/(\lambda+N) \to {\cal F} \\ \sum_{i = 0}^r \sigma_i \lambda^i f^{\lambda} \mapsto \sum_{i = 0}^r f^{{-}N} \cdot \sigma_i \cdot ({-}N)^i,\quad \sigma_i \in {\cal F} , \end{gathered} \]
inducing a map ![]() ${\cal F}_0/(\lambda +N)$ to
${\cal F}_0/(\lambda +N)$ to ![]() ${\cal F}$ sending the generator to
${\cal F}$ sending the generator to ![]() $f^{-N} s$. By functoriality of the GKS filtration (or standard singular support analysis), this means that
$f^{-N} s$. By functoriality of the GKS filtration (or standard singular support analysis), this means that ![]() $f^{-N} s \in F_{\delta }^{{\rm GKS}} {\cal F}$, and since
$f^{-N} s \in F_{\delta }^{{\rm GKS}} {\cal F}$, and since ![]() $F_{\delta }^{{\rm GKS}} {\cal F}$ is a
$F_{\delta }^{{\rm GKS}} {\cal F}$ is a ![]() $D_X$-module, this means that
$D_X$-module, this means that ![]() $s \in F_{\delta }^{{\rm GKS}} {\cal F}$ as well.
$s \in F_{\delta }^{{\rm GKS}} {\cal F}$ as well.
2.8 Preservation of holonomic defect
We now proceed to prove Theorem 2.5.1. The argument is straightforward at this point, and we proceed in cases.
2.9
First, we treat pushforwards along an open embedding ![]() $j:U \to X$.
$j:U \to X$.
Suppose ![]() $X$ is smooth and affine. We proceed by induction on the number
$X$ is smooth and affine. We proceed by induction on the number ![]() $n$ of basic affine opens required to cover
$n$ of basic affine opens required to cover ![]() $U$. For
$U$. For ![]() $n = 1$, the result is treated by Lemma 2.7.1.
$n = 1$, the result is treated by Lemma 2.7.1.
The inductive step is a standard Čech argument.
For ![]() $n>1$,
$n>1$, ![]() $U$ admits a cover by some
$U$ admits a cover by some ![]() $U_1$ and
$U_1$ and ![]() $U_2$ where
$U_2$ where ![]() $U_1$ is a basic affine open and
$U_1$ is a basic affine open and ![]() $U_2$ admits a cover by
$U_2$ admits a cover by ![]() $n-1$ basic affine opens. Let
$n-1$ basic affine opens. Let ![]() $j_i:U_i \to U$ denote the embeddings and let
$j_i:U_i \to U$ denote the embeddings and let ![]() $j_{12}:U_1 \cap U_2 \to U$.
$j_{12}:U_1 \cap U_2 \to U$.
Fix ![]() ${\cal F} \in D(U)$ with holonomic defect
${\cal F} \in D(U)$ with holonomic defect ![]() $\leq \delta$. Note that
$\leq \delta$. Note that
(where this fiber product is a homotopyFootnote 10 fiber product). By induction, ![]() $j_{?,*,{\rm dR}}j_?^!({\cal F})$ has holonomic defect
$j_{?,*,{\rm dR}}j_?^!({\cal F})$ has holonomic defect ![]() $\leq \delta$. Now recall from § 2.4 that
$\leq \delta$. Now recall from § 2.4 that ![]() $D$-modules with holonomic defect
$D$-modules with holonomic defect ![]() $\leq \delta$ are a DG subcategory and therefore closed under finite limits.
$\leq \delta$ are a DG subcategory and therefore closed under finite limits.
Finally, for general ![]() $X$, note that the problem is Zariski local, so we may assume
$X$, note that the problem is Zariski local, so we may assume ![]() $X$ is affine. Take a closed embedding
$X$ is affine. Take a closed embedding ![]() $X \subseteq {\mathbb {A}}^N$. If
$X \subseteq {\mathbb {A}}^N$. If ![]() $U = X \setminus Z$, then we have
$U = X \setminus Z$, then we have ![]() $U \hookrightarrow {\mathbb {A}}^N\setminus Z \hookrightarrow {\mathbb {A}}^N$, with the first map being closed and the second being open between smooth affine schemes. Therefore, this pushforward preserves having holonomic defect
$U \hookrightarrow {\mathbb {A}}^N\setminus Z \hookrightarrow {\mathbb {A}}^N$, with the first map being closed and the second being open between smooth affine schemes. Therefore, this pushforward preserves having holonomic defect ![]() $\leq \delta$. Clearly this implies the result for the pushforward along
$\leq \delta$. Clearly this implies the result for the pushforward along ![]() $U \hookrightarrow X$.
$U \hookrightarrow X$.
2.10
Next, we treat restrictions to closed subschemes.
Let ![]() $i:Z \hookrightarrow X$ be closed and let
$i:Z \hookrightarrow X$ be closed and let ![]() $j:U = X\setminus Z \hookrightarrow X$. Then we have an exact triangle:
$j:U = X\setminus Z \hookrightarrow X$. Then we have an exact triangle:
If ![]() ${\cal F}$ has holonomic defect
${\cal F}$ has holonomic defect ![]() $\leq \delta$, we have shown the same for
$\leq \delta$, we have shown the same for ![]() $j_{*,{\rm dR}}j^!({\cal F})$, so
$j_{*,{\rm dR}}j^!({\cal F})$, so ![]() $i_{*,{\rm dR}}i^!({\cal F})$ has holonomic defect
$i_{*,{\rm dR}}i^!({\cal F})$ has holonomic defect ![]() $\leq \delta$, which is equivalent to
$\leq \delta$, which is equivalent to ![]() $i^!({\cal F})$ having holonomic defect
$i^!({\cal F})$ having holonomic defect ![]() $\leq \delta$.
$\leq \delta$.
2.11
We can now show the result for restrictions in general.
If ![]() $f:X \to Y$ is smooth of relative dimension
$f:X \to Y$ is smooth of relative dimension ![]() $d$, then
$d$, then ![]() $f^{*,{\rm dR}}[d] = f^![-d]$ commutes with Verdier duality and is
$f^{*,{\rm dR}}[d] = f^![-d]$ commutes with Verdier duality and is ![]() $t$-exact. Therefore, it commutes with formation of the GKS filtration, and therefore preserves the property of having holonomic defect
$t$-exact. Therefore, it commutes with formation of the GKS filtration, and therefore preserves the property of having holonomic defect ![]() $\leq \delta$.
$\leq \delta$.
The case of general ![]() $f:X \to Y$ is immediately reduced to the case of affine varieties (since holonomic defect is Zariski local). We can then find a commutative diagram:
$f:X \to Y$ is immediately reduced to the case of affine varieties (since holonomic defect is Zariski local). We can then find a commutative diagram:

with the horizontal arrows being closed embeddings. This reduces to the case where ![]() $X$ and
$X$ and ![]() $Y$ are smooth.
$Y$ are smooth.
Then we can factor ![]() $f$ through the graph as
$f$ through the graph as ![]() $X \to X \times Y \xrightarrow {p_1} Y$. The former map is a closed embedding, and the latter is smooth because
$X \to X \times Y \xrightarrow {p_1} Y$. The former map is a closed embedding, and the latter is smooth because ![]() $X$ is. We have treated each of these cases, so we obtain the result.
$X$ is. We have treated each of these cases, so we obtain the result.
2.12
Next, we treat pushforwards along a proper morphism ![]() $f:X \to Y$ between smooth varieties.
$f:X \to Y$ between smooth varieties.
This case does not need the work we have done so far. Let ![]() ${\cal F} \in D(X)^{\heartsuit }$ with holonomic defect
${\cal F} \in D(X)^{\heartsuit }$ with holonomic defect ![]() $\leq \delta$ be given. By Lemma 2.3.5, we may assume
$\leq \delta$ be given. By Lemma 2.3.5, we may assume ![]() ${\cal F}$ is coherent, so the hypothesis is that
${\cal F}$ is coherent, so the hypothesis is that ![]() ${\cal F}$ has singular support
${\cal F}$ has singular support ![]() $\operatorname {SS}_X({\cal F})$ with dimension
$\operatorname {SS}_X({\cal F})$ with dimension ![]() $\dim X + \delta$.
$\dim X + \delta$.
Recall that ![]() $\operatorname {SS}_Y(H^i(f_{*,{\rm dR}}({\cal F})))$ is bounded in terms of
$\operatorname {SS}_Y(H^i(f_{*,{\rm dR}}({\cal F})))$ is bounded in terms of ![]() $\operatorname {SS}_X({\cal F})$. More precisely, if we take the diagram
$\operatorname {SS}_X({\cal F})$. More precisely, if we take the diagram

then the singular support of these cohomologies is contained in ![]() $\alpha (\beta ^{-1}\operatorname {SS}_X({\cal F}))$ (see, for example, [Reference KashiwaraKas76, Theorem 4.2]).
$\alpha (\beta ^{-1}\operatorname {SS}_X({\cal F}))$ (see, for example, [Reference KashiwaraKas76, Theorem 4.2]).
Because ![]() $\operatorname {SS}_X({\cal F})$ is coisotropic by [Reference GabberGab81], we have
$\operatorname {SS}_X({\cal F})$ is coisotropic by [Reference GabberGab81], we have
by usual symplectic geometry. This immediately gives the claim.
2.13
Now observe that preservation of holonomic defect under pushforward along a general morphism ![]() $f:X \to Y$ between smooth varieties follows: by Nagata's compactification theorem (see, for example, [Reference ConradCon07]), there exist a scheme
$f:X \to Y$ between smooth varieties follows: by Nagata's compactification theorem (see, for example, [Reference ConradCon07]), there exist a scheme ![]() $\overline {X}{}$ and a factorization
$\overline {X}{}$ and a factorization
of ![]() $f$ with
$f$ with ![]() $\overline {f}{}$ proper and
$\overline {f}{}$ proper and ![]() $j$ an open embedding. Moreover, by resolution of singularities [Reference HironakaHir64, Main Theorem I], we may take
$j$ an open embedding. Moreover, by resolution of singularities [Reference HironakaHir64, Main Theorem I], we may take ![]() $\overline {X}{}$ to be smooth.Footnote 11 Then the result follows in this case from our earlier work.
$\overline {X}{}$ to be smooth.Footnote 11 Then the result follows in this case from our earlier work.
2.14
We can now treat a general pushforward along ![]() $f:X \to Y$ a morphism between possibly singular varieties.
$f:X \to Y$ a morphism between possibly singular varieties.
The problem is Zariski local on ![]() $Y$, so we may assume
$Y$, so we may assume ![]() $Y$ is affine.
$Y$ is affine.
Next, we reduce to the case where ![]() $X$ is affine. It suffices to observe that the subcategory of
$X$ is affine. It suffices to observe that the subcategory of ![]() $D(X)$ of
$D(X)$ of ![]() $D$-modules of holonomic defect
$D$-modules of holonomic defect ![]() $\leq \delta$ is generated under colimitsFootnote 12 by objects of the form
$\leq \delta$ is generated under colimitsFootnote 12 by objects of the form ![]() $j_{*,{\rm dR}}({\cal F})$ for
$j_{*,{\rm dR}}({\cal F})$ for ![]() $j:U \to X$ an affine open and
$j:U \to X$ an affine open and ![]() ${\cal F}$ of holonomic defect
${\cal F}$ of holonomic defect ![]() $\leq \delta$. This observation follows by induction on the number of affines required to cover
$\leq \delta$. This observation follows by induction on the number of affines required to cover ![]() $X$ by a Čech argument exactly as in § 2.9, and the fact (shown above) that pushforward along an open embedding preserves holonomic defect.
$X$ by a Čech argument exactly as in § 2.9, and the fact (shown above) that pushforward along an open embedding preserves holonomic defect.
When ![]() $X$ and
$X$ and ![]() $Y$ are affine, we can find a commutative diagram (2.11.1) as before. This reduces to the case with
$Y$ are affine, we can find a commutative diagram (2.11.1) as before. This reduces to the case with ![]() $X$ and
$X$ and ![]() $Y$ smooth, which we have already treated.
$Y$ smooth, which we have already treated.
3. Cohomological bounds
3.1
The main result of this section says that ![]() $f_!$ is left
$f_!$ is left ![]() $t$-exact for an affine morphism
$t$-exact for an affine morphism ![]() $f$. We also show that for
$f$. We also show that for ![]() $i:X \to Y$ a closed embedding,
$i:X \to Y$ a closed embedding, ![]() $i^{*,{\rm dR}}$ has cohomological amplitude
$i^{*,{\rm dR}}$ has cohomological amplitude ![]() $\geq -\dim (Y)+\dim (X)$, that is,
$\geq -\dim (Y)+\dim (X)$, that is, ![]() $i^{*,{\rm dR}}[-\dim (Y)+\dim (X)]$ is left
$i^{*,{\rm dR}}[-\dim (Y)+\dim (X)]$ is left ![]() $t$-exact. Since
$t$-exact. Since ![]() $f_!$ and
$f_!$ and ![]() $i^{*,{\rm dR}}$ are not necessarily defined on non-holonomic
$i^{*,{\rm dR}}$ are not necessarily defined on non-holonomic ![]() $D$-modules, we use the language of pro-categories to formulate this result.
$D$-modules, we use the language of pro-categories to formulate this result.
3.2
As was remarked in the introduction, we use some language from higher category theory in order to discuss pro-categories.
We use the theory of ![]() $\infty$-categories developed in [Reference LurieLur09]. In particular, we refer to [Reference LurieLur09, § 5.3] for a discussion of ind-categories in this formalism and we refer to [Reference LurieLur12, § 1.4.4] for the theory in the stable setting. There is a dual notion of pro-category: see [Reference LurieLur09, Remark 7.1.6.2].
$\infty$-categories developed in [Reference LurieLur09]. In particular, we refer to [Reference LurieLur09, § 5.3] for a discussion of ind-categories in this formalism and we refer to [Reference LurieLur12, § 1.4.4] for the theory in the stable setting. There is a dual notion of pro-category: see [Reference LurieLur09, Remark 7.1.6.2].
We apply this theory in the setting of DG categories. We follow [Reference Gaitsgory and RozenblyumGR17, § I.1.10.3] in our terminology here, and in particular in viewing DG categories as ![]() $\infty$-categories with additional structure.
$\infty$-categories with additional structure.
Remark 3.2.1 The reader may alter the treatment that follows in many possible ways to avoid the theory of ![]() $\infty$-categories.
$\infty$-categories.
First, the reader may use ‘strict’ DG categories, that is, usual categories enriched over chain complexes, and standard models for the relevant ind/pro-categories (see, for example, [Reference DrinfeldDri04, § 4]).
Alternatively, the reader may simply assume that we are given ![]() $D$-modules on which
$D$-modules on which ![]() $!$-pushforwards are defined and proceed accordingly.
$!$-pushforwards are defined and proceed accordingly.
Finally, the reader may note that, for example, in Theorem 3.4.1, the functor in question takes values in ![]() $\mathsf {Pro}(D(Y)^c) \simeq D(Y)^{{\rm op}}$. Therefore, the use of pro-categories is inessential, and can be replaced by the use of a non-standard
$\mathsf {Pro}(D(Y)^c) \simeq D(Y)^{{\rm op}}$. Therefore, the use of pro-categories is inessential, and can be replaced by the use of a non-standard ![]() $t$-structure on
$t$-structure on ![]() $D(Y)$. We spell out this reformulation in Remark 3.4.3 below.
$D(Y)$. We spell out this reformulation in Remark 3.4.3 below.
In what follows, we omit the prefix ![]() $\infty$ to avoid clutter, so, for example, ‘category’ means ‘
$\infty$ to avoid clutter, so, for example, ‘category’ means ‘![]() $\infty$-category’.
$\infty$-category’.
3.3 Pro-categories
We refer to [Reference LurieLur11, § 3.1] and [Reference Gaitsgory and RozenblyumGR17, § III.1.3.1] for the material that follows.
For ![]() ${\cal C}$ an accessibleFootnote 13 category, we have the corresponding pro-category
${\cal C}$ an accessibleFootnote 13 category, we have the corresponding pro-category ![]() $\mathsf {Pro}({\cal C})$. If
$\mathsf {Pro}({\cal C})$. If ![]() ${\cal C}$ is a DG category,
${\cal C}$ is a DG category, ![]() $\mathsf {Pro}({\cal C})$ is as well. If
$\mathsf {Pro}({\cal C})$ is as well. If ![]() ${\cal C}$ admits small colimits, then so does
${\cal C}$ admits small colimits, then so does ![]() $\mathsf {Pro}({\cal C})$. For
$\mathsf {Pro}({\cal C})$. For ![]() $F:{\cal C} \to {\cal D}$, there is an induced functor
$F:{\cal C} \to {\cal D}$, there is an induced functor ![]() $\mathsf {Pro}({\cal C}) \to \mathsf {Pro}({\cal D})$, which we denote again by
$\mathsf {Pro}({\cal C}) \to \mathsf {Pro}({\cal D})$, which we denote again by ![]() $F$ where there is no risk for confusion.
$F$ where there is no risk for confusion.
For any functor ![]() $G:{\cal D} \to {\cal C}$ commuting with finite colimits (for example, a DG functor), the induced functor
$G:{\cal D} \to {\cal C}$ commuting with finite colimits (for example, a DG functor), the induced functor ![]() $\mathsf {Pro}({\cal D}) \to \mathsf {Pro}({\cal C})$ admits a left adjoint
$\mathsf {Pro}({\cal D}) \to \mathsf {Pro}({\cal C})$ admits a left adjoint ![]() $F$. We say that
$F$. We say that ![]() $F$ is defined on an object
$F$ is defined on an object ![]() ${\cal F} \in {\cal C}$ if
${\cal F} \in {\cal C}$ if ![]() $F({\cal F}) \in {\cal D} \subseteq \mathsf {Pro}({\cal D})$. (This coincides with the usual notion of a left adjoint being defined on some object.)
$F({\cal F}) \in {\cal D} \subseteq \mathsf {Pro}({\cal D})$. (This coincides with the usual notion of a left adjoint being defined on some object.)
If ![]() ${\cal C}$ is a DG category equipped with a
${\cal C}$ is a DG category equipped with a ![]() $t$-structure, then
$t$-structure, then ![]() $\mathsf {Pro}({\cal C})$ inherits one as well. It is characterized by the equality
$\mathsf {Pro}({\cal C})$ inherits one as well. It is characterized by the equality ![]() $\mathsf {Pro}({\cal C})^{\leq 0} = \mathsf {Pro}({\cal C}^{\leq 0})$. Truncation functors are the pro-extensions of the truncation functors on
$\mathsf {Pro}({\cal C})^{\leq 0} = \mathsf {Pro}({\cal C}^{\leq 0})$. Truncation functors are the pro-extensions of the truncation functors on ![]() ${\cal C}$. In particular, we find that
${\cal C}$. In particular, we find that ![]() ${\cal C}$ is closed under truncations and inherits its given
${\cal C}$ is closed under truncations and inherits its given ![]() $t$-structure. We also find that
$t$-structure. We also find that ![]() $\mathsf {Pro}({\cal C})^{\geq 0} = \mathsf {Pro}({\cal C}^{\geq 0})$: if
$\mathsf {Pro}({\cal C})^{\geq 0} = \mathsf {Pro}({\cal C}^{\geq 0})$: if ![]() ${\cal F} = \operatorname {lim}_i {\cal F}_i \in \mathsf {Pro}({\cal C})^{\geq 0}$, then
${\cal F} = \operatorname {lim}_i {\cal F}_i \in \mathsf {Pro}({\cal C})^{\geq 0}$, then ![]() ${\cal F} = \tau ^{\geq 0} {\cal F} = \operatorname {lim}_i \tau ^{\geq 0} {\cal F}_i$.
${\cal F} = \tau ^{\geq 0} {\cal F} = \operatorname {lim}_i \tau ^{\geq 0} {\cal F}_i$.
3.4 Affine morphisms
For ![]() $f:X \to Y$, we have the functor
$f:X \to Y$, we have the functor ![]() $f_!:\mathsf {Pro}(D(X)) \to \mathsf {Pro}(D(Y))$ left adjoint to
$f_!:\mathsf {Pro}(D(X)) \to \mathsf {Pro}(D(Y))$ left adjoint to ![]() $f^!$.
$f^!$.
Theorem 3.4.1 For ![]() $f$ affine, the induced functor
$f$ affine, the induced functor ![]() $f_!:D(X)^c \to \mathsf {Pro}(D(Y))$ is left
$f_!:D(X)^c \to \mathsf {Pro}(D(Y))$ is left ![]() $t$-exact.
$t$-exact.
Remark 3.4.2 Before giving the argument, we spell out the meaning of this result without the language of pro-categories. Suppose ![]() ${\cal F} \in D(X)^{c,\geq 0}$ is coherent and in cohomological degrees
${\cal F} \in D(X)^{c,\geq 0}$ is coherent and in cohomological degrees ![]() $\geq 0$. Let
$\geq 0$. Let ![]() ${\cal G} \in D(Y)$ be arbitrary, and suppose we are given a morphism
${\cal G} \in D(Y)$ be arbitrary, and suppose we are given a morphism ![]() $\alpha :{\cal F} \to f^!({\cal G})$. Then the theorem is equivalent to asserting that when
$\alpha :{\cal F} \to f^!({\cal G})$. Then the theorem is equivalent to asserting that when ![]() $f$ is affine, there necessarily exist
$f$ is affine, there necessarily exist ![]() ${\cal G}_0 \in D(Y)^{\geq 0}$, a morphism
${\cal G}_0 \in D(Y)^{\geq 0}$, a morphism ![]() $\beta :{\cal G}_0\to {\cal G} \in D(Y)$, and a factorization
$\beta :{\cal G}_0\to {\cal G} \in D(Y)$, and a factorization
of ![]() $\alpha$. In particular, the assertion of Theorem 3.4.1 can be reformulated using only triangulated categories.
$\alpha$. In particular, the assertion of Theorem 3.4.1 can be reformulated using only triangulated categories.
Remark 3.4.3 Here is another, somewhat more classical reformation of the assertion. Define the non-standard ![]() $t$-structure on
$t$-structure on ![]() $D(X)$ by defining
$D(X)$ by defining ![]() $D(X)^{\overset {ns}{\leq } 0}$ to be generated under filtered colimits by coherent objects of
$D(X)^{\overset {ns}{\leq } 0}$ to be generated under filtered colimits by coherent objects of ![]() $D(X)$ whose Verdier duals lie in usual cohomological degrees
$D(X)$ whose Verdier duals lie in usual cohomological degrees ![]() $\geq 0$. In these terms, Theorem 3.4.1 is equivalent (essentially by (3.4.1) below) to the assertion that for
$\geq 0$. In these terms, Theorem 3.4.1 is equivalent (essentially by (3.4.1) below) to the assertion that for ![]() $f$ affine,
$f$ affine, ![]() $f_{*,{\rm dR}}$ is right
$f_{*,{\rm dR}}$ is right ![]() $t$-exact for these non-standard
$t$-exact for these non-standard ![]() $t$-structures, that is,
$t$-structures, that is, ![]() $f_{*,{\rm dR}}$ maps
$f_{*,{\rm dR}}$ maps ![]() $D(X)^{\overset {ns}{\leq } 0}$ to
$D(X)^{\overset {ns}{\leq } 0}$ to ![]() $D(Y)^{\overset {ns}{\leq } 0}$.
$D(Y)^{\overset {ns}{\leq } 0}$.
Proof of Theorem 3.4.1 The problem isFootnote 14 Zariski local on ![]() $Y$, so we may assume
$Y$, so we may assume ![]() $X$ and
$X$ and ![]() $Y$ are affine.
$Y$ are affine.
Note that ![]() $D$-module pushforward along closed embeddings remains fully faithful on pro-categories: the identity
$D$-module pushforward along closed embeddings remains fully faithful on pro-categories: the identity ![]() $i^!i_{*,{\rm dR}} = \operatorname {id}$ induces the same for the pro-functors. Therefore, the same argument as in § 2.11 allows us to assume
$i^!i_{*,{\rm dR}} = \operatorname {id}$ induces the same for the pro-functors. Therefore, the same argument as in § 2.11 allows us to assume ![]() $X$ and
$X$ and ![]() $Y$ are smooth.
$Y$ are smooth.
Recall that we have a Verdier duality equivalence ![]() ${\mathbb {D}}:D(X)^{{\rm op}} \xrightarrow {\simeq } \mathsf {Pro}(D(X)^c)$ induced by the usual Verdier duality equivalence
${\mathbb {D}}:D(X)^{{\rm op}} \xrightarrow {\simeq } \mathsf {Pro}(D(X)^c)$ induced by the usual Verdier duality equivalence ![]() ${\mathbb {D}}:D(X)^c \xrightarrow {\simeq } D(X)^{c,{\rm op}}$, and similarly for
${\mathbb {D}}:D(X)^c \xrightarrow {\simeq } D(X)^{c,{\rm op}}$, and similarly for ![]() $Y$.
$Y$.
We then claim that
This follows formally from the fact that ![]() $f_{*,{\rm dR}}$ and
$f_{*,{\rm dR}}$ and ![]() $f^!$ are dual functors in the sense of [Reference GaitsgoryGai12], but we give a direct proof below. Note that in this formula,
$f^!$ are dual functors in the sense of [Reference GaitsgoryGai12], but we give a direct proof below. Note that in this formula, ![]() $f_{*,{\rm dR}} {\mathbb {D}}({\cal F}) \in D(Y)$, and we are then using
$f_{*,{\rm dR}} {\mathbb {D}}({\cal F}) \in D(Y)$, and we are then using ![]() ${\mathbb {D}}$ to convert it to a pro-coherent object. Since this object is pro-coherent, it suffices to observe that for
${\mathbb {D}}$ to convert it to a pro-coherent object. Since this object is pro-coherent, it suffices to observe that for ![]() ${\cal G} \in D(Y)^c$, we have
${\cal G} \in D(Y)^c$, we have
 \[ \begin{aligned} \underline{\operatorname{Hom}}_{\mathsf{Pro}(D(Y)^c)}({\mathbb{D}} f_{*,{\rm dR}} {\mathbb{D}} ({\cal F}), {\cal G}) &= \underline{\operatorname{Hom}}_{D(Y)}({\mathbb{D}} {\cal G}, f_{*,{\rm dR}} {\mathbb{D}} ({\cal F})) = \Gamma_{{\rm dR}}(Y, f_{*,{\rm dR}} {\mathbb{D}}({\cal F}) \overset{!}{\otimes} {\cal G}) \\ &=\Gamma_{{\rm dR}}(X, {\mathbb{D}}({\cal F}) \overset{!}{\otimes} f^!({\cal G})) = \underline{\operatorname{Hom}}_{D(X)}({\cal F},f^!({\cal G})). \end{aligned} \]
\[ \begin{aligned} \underline{\operatorname{Hom}}_{\mathsf{Pro}(D(Y)^c)}({\mathbb{D}} f_{*,{\rm dR}} {\mathbb{D}} ({\cal F}), {\cal G}) &= \underline{\operatorname{Hom}}_{D(Y)}({\mathbb{D}} {\cal G}, f_{*,{\rm dR}} {\mathbb{D}} ({\cal F})) = \Gamma_{{\rm dR}}(Y, f_{*,{\rm dR}} {\mathbb{D}}({\cal F}) \overset{!}{\otimes} {\cal G}) \\ &=\Gamma_{{\rm dR}}(X, {\mathbb{D}}({\cal F}) \overset{!}{\otimes} f^!({\cal G})) = \underline{\operatorname{Hom}}_{D(X)}({\cal F},f^!({\cal G})). \end{aligned} \]
Here ![]() $\Gamma _{{\rm dR}}$ is the complex of de Rham cochains of a
$\Gamma _{{\rm dR}}$ is the complex of de Rham cochains of a ![]() $D$-module, and we are repeatedly using the formulaFootnote 15 that if
$D$-module, and we are repeatedly using the formulaFootnote 15 that if ![]() ${\cal F}_1$ is coherent, then
${\cal F}_1$ is coherent, then
Now suppose that ![]() ${\cal F} \in D(X)^{c,\heartsuit }$ is coherent and in cohomological degrees
${\cal F} \in D(X)^{c,\heartsuit }$ is coherent and in cohomological degrees ![]() $\geq 0$. Note that
$\geq 0$. Note that ![]() ${\mathbb {D}} {\cal F}$ carries the canonical filtration with subquotients
${\mathbb {D}} {\cal F}$ carries the canonical filtration with subquotients ![]() $(H^{-j}{\mathbb {D}}{\cal F})[j]$. By Proposition 2.6.1,
$(H^{-j}{\mathbb {D}}{\cal F})[j]$. By Proposition 2.6.1, ![]() $H^{-j} {\mathbb {D}} {\cal F}$ has holonomic defect
$H^{-j} {\mathbb {D}} {\cal F}$ has holonomic defect ![]() $\leq j$. By Theorem 2.5.1,
$\leq j$. By Theorem 2.5.1, ![]() $f_{*,{\rm dR}} H^{-j} {\mathbb {D}} {\cal F}$ has holonomic defect
$f_{*,{\rm dR}} H^{-j} {\mathbb {D}} {\cal F}$ has holonomic defect ![]() $\leq j$ as well. Moreover, by affineness of
$\leq j$ as well. Moreover, by affineness of ![]() $f$, the latter complex is in cohomological degrees
$f$, the latter complex is in cohomological degrees ![]() $\leq 0$.
$\leq 0$.
Note that by Proposition 2.6.1, if ![]() ${\cal G} \in D(Y)^{\heartsuit }$ has holonomic defect
${\cal G} \in D(Y)^{\heartsuit }$ has holonomic defect ![]() $\leq \delta$, then
$\leq \delta$, then ![]() ${\mathbb {D}} {\cal G} \in \mathsf {Pro}(D(Y)^c)$ is in cohomological degrees
${\mathbb {D}} {\cal G} \in \mathsf {Pro}(D(Y)^c)$ is in cohomological degrees ![]() $[-\delta ,0]$: indeed, this immediately reduces to the coherent case.
$[-\delta ,0]$: indeed, this immediately reduces to the coherent case.
Therefore, ![]() ${\mathbb {D}} H^{-k} f_{*,{\rm dR}} H^{-j} {\mathbb {D}} {\cal F}$ is in cohomological degrees
${\mathbb {D}} H^{-k} f_{*,{\rm dR}} H^{-j} {\mathbb {D}} {\cal F}$ is in cohomological degrees ![]() $[-j,0]$ for every
$[-j,0]$ for every ![]() $k$, which means
$k$, which means ![]() ${\mathbb {D}} (H^{-k} (f_{*,{\rm dR}} H^{-j} {\mathbb {D}} {\cal F})[k])$ is in cohomological degrees
${\mathbb {D}} (H^{-k} (f_{*,{\rm dR}} H^{-j} {\mathbb {D}} {\cal F})[k])$ is in cohomological degrees ![]() $[-j+k,k]$. This complex vanishes unless
$[-j+k,k]$. This complex vanishes unless ![]() $k\geq 0$, so
$k\geq 0$, so ![]() ${\mathbb {D}} f_{*,{\rm dR}} H^{-j} {\mathbb {D}} {\cal F}$ is in cohomological degrees
${\mathbb {D}} f_{*,{\rm dR}} H^{-j} {\mathbb {D}} {\cal F}$ is in cohomological degrees ![]() $\geq -j$. Finally, this means that
$\geq -j$. Finally, this means that ![]() ${\mathbb {D}} ((f_{*,{\rm dR}} H^{-j} {\mathbb {D}} {\cal F})[j])$ is in cohomological degrees
${\mathbb {D}} ((f_{*,{\rm dR}} H^{-j} {\mathbb {D}} {\cal F})[j])$ is in cohomological degrees ![]() $\geq 0$, so the same follows for
$\geq 0$, so the same follows for ![]() ${\mathbb {D}} f_{*,{\rm dR}} {\mathbb {D}}({\cal F}) = f_!({\cal F})$.
${\mathbb {D}} f_{*,{\rm dR}} {\mathbb {D}}({\cal F}) = f_!({\cal F})$.
Remark 3.4.4 More generally, this argument shows that if ![]() $f$ is a possibly non-affine morphism between varieties
$f$ is a possibly non-affine morphism between varieties ![]() $X$ and
$X$ and ![]() $Y$ such that
$Y$ such that ![]() $f_*:\mathsf {QCoh}(X) \to \mathsf {QCoh}(Y)$ has amplitude
$f_*:\mathsf {QCoh}(X) \to \mathsf {QCoh}(Y)$ has amplitude ![]() $\leq n$, then
$\leq n$, then ![]() $f_!:D(X)^c \to \mathsf {Pro}(D(Y))$ has amplitude
$f_!:D(X)^c \to \mathsf {Pro}(D(Y))$ has amplitude ![]() $\geq -n$. (Here
$\geq -n$. (Here ![]() $\mathsf {QCoh}$ denotes the DG category of quasi-coherent sheaves and
$\mathsf {QCoh}$ denotes the DG category of quasi-coherent sheaves and ![]() $f_*$ is the standard pushforward functor for such.)
$f_*$ is the standard pushforward functor for such.)
3.5 Closed embeddings
Similarly, we have the following theorem.
Theorem 3.5.1 For ![]() $i:X \to Y$ a closed embedding,
$i:X \to Y$ a closed embedding, ![]() $i^{*,{\rm dR}}:D(Y)^c \to \mathsf {Pro}(D(X))$ has cohomological amplitude
$i^{*,{\rm dR}}:D(Y)^c \to \mathsf {Pro}(D(X))$ has cohomological amplitude ![]() $\geq -\dim (Y)+\dim (X)$.
$\geq -\dim (Y)+\dim (X)$.
Appendix A. Exactness properties of Kostant's functor
A.1
In this appendix, we briefly give an application of Theorem 3.4.1 to representation theory. The result below is a toy model of the applications in [Reference RaskinRas21].
A.2
Let ![]() ${\mathfrak g}$ be a semi-simple Lie algebra, let
${\mathfrak g}$ be a semi-simple Lie algebra, let ![]() ${\mathfrak b},{\mathfrak b}^- \subseteq {\mathfrak g}$ be opposed Borels with radicals
${\mathfrak b},{\mathfrak b}^- \subseteq {\mathfrak g}$ be opposed Borels with radicals ![]() ${\mathfrak n}$ and
${\mathfrak n}$ and ![]() ${\mathfrak n}^-$. Let
${\mathfrak n}^-$. Let ![]() $\psi :{\mathfrak n}^- \to k$ be a non-degenerate character, that is,
$\psi :{\mathfrak n}^- \to k$ be a non-degenerate character, that is, ![]() $\psi$ is non-zero on weight spaces corresponding to negative simple roots.
$\psi$ is non-zero on weight spaces corresponding to negative simple roots.
Let ![]() ${\mathfrak g} - \mathsf {mod}$ denote the DG category of
${\mathfrak g} - \mathsf {mod}$ denote the DG category of ![]() ${\mathfrak g}$-modules. Let
${\mathfrak g}$-modules. Let ![]() $\Psi ^{{\rm {\rm fin}}}:{\mathfrak g} - \mathsf {mod} \to \mathsf {Vect}$ be the functor computing Lie algebra homology of
$\Psi ^{{\rm {\rm fin}}}:{\mathfrak g} - \mathsf {mod} \to \mathsf {Vect}$ be the functor computing Lie algebra homology of ![]() ${\mathfrak n}^-$ twisted by
${\mathfrak n}^-$ twisted by ![]() $\psi$. That is,
$\psi$. That is, ![]() $M \in {\mathfrak g} - \mathsf {mod}$ maps to
$M \in {\mathfrak g} - \mathsf {mod}$ maps to ![]() ${C_{\bullet }({\mathfrak n}^-,M \otimes \psi )}$, where
${C_{\bullet }({\mathfrak n}^-,M \otimes \psi )}$, where ![]() $M \otimes \psi$ indicates the
$M \otimes \psi$ indicates the ![]() ${\mathfrak n}^-$-module with the same underlying vector space as
${\mathfrak n}^-$-module with the same underlying vector space as ![]() $M$ but action twisted as
$M$ but action twisted as ![]() $x \overset {{\rm new}}{\cdot } v := x \overset {{\rm old}}{\cdot } v + \psi (x)$ for
$x \overset {{\rm new}}{\cdot } v := x \overset {{\rm old}}{\cdot } v + \psi (x)$ for ![]() $x \in {\mathfrak n}^-$ and
$x \in {\mathfrak n}^-$ and ![]() $v \in M$.
$v \in M$.
Let ![]() ${\mathfrak g} - \mathsf {mod}^N \subseteq {\mathfrak g} - \mathsf {mod}$ be the full subcategory consisting of complexes such that
${\mathfrak g} - \mathsf {mod}^N \subseteq {\mathfrak g} - \mathsf {mod}$ be the full subcategory consisting of complexes such that ![]() ${\mathfrak n}$ acts locally nilpotently on cohomology.
${\mathfrak n}$ acts locally nilpotently on cohomology.
Theorem A.2.1 The functor ![]() $\Psi ^{{\rm fin}}$ is exact when restricted to
$\Psi ^{{\rm fin}}$ is exact when restricted to ![]() ${\mathfrak g} - \mathsf {mod}^N$.
${\mathfrak g} - \mathsf {mod}^N$.
Remark A.2.2 This theorem is well known (cf. [Reference KostantKos78]) when we replace ![]() ${\mathfrak g} - \mathsf {mod}^N$ by the Bernstein–Gelfand–Gelfand category
${\mathfrak g} - \mathsf {mod}^N$ by the Bernstein–Gelfand–Gelfand category ![]() ${\cal O}$. Indeed, because the latter category is Artinian, it suffices to verify that
${\cal O}$. Indeed, because the latter category is Artinian, it suffices to verify that ![]() $\Psi ^{{\rm fin}}(L_{\lambda }) \in \mathsf {Vect}^{\heartsuit }$ for any
$\Psi ^{{\rm fin}}(L_{\lambda }) \in \mathsf {Vect}^{\heartsuit }$ for any ![]() $\lambda$, where
$\lambda$, where ![]() $L_{\lambda }$ is the simple of highest weight
$L_{\lambda }$ is the simple of highest weight ![]() $\lambda$. But this is easy to see: either
$\lambda$. But this is easy to see: either ![]() $L_{\lambda }$ is a Verma module and therefore free over
$L_{\lambda }$ is a Verma module and therefore free over ![]() $U({\mathfrak n}^-)$, or
$U({\mathfrak n}^-)$, or ![]() $L_{\lambda }$ is partially integrable, in which case
$L_{\lambda }$ is partially integrable, in which case ![]() $\Psi ^{{\rm fin}}(L_{\lambda }) = 0$.
$\Psi ^{{\rm fin}}(L_{\lambda }) = 0$.
However, this method does not work in the above setting, since ![]() ${\mathfrak g} - \mathsf {mod}^N$ is not Artinian (the Cartan subalgebra may not act locally finitely). I do not know another reference for this result in this generality.
${\mathfrak g} - \mathsf {mod}^N$ is not Artinian (the Cartan subalgebra may not act locally finitely). I do not know another reference for this result in this generality.
Example A.2.3 As a very simple case of Theorem A.2.1, note that the universal Verma module ![]() $M^{\operatorname {univ}} := U({\mathfrak g}) \otimes _{U({\mathfrak n})} k$ is an object of
$M^{\operatorname {univ}} := U({\mathfrak g}) \otimes _{U({\mathfrak n})} k$ is an object of ![]() ${\mathfrak g} - \mathsf {mod}^{N,\heartsuit }$. As
${\mathfrak g} - \mathsf {mod}^{N,\heartsuit }$. As ![]() $M^{\operatorname {univ}}$ is free over
$M^{\operatorname {univ}}$ is free over ![]() $U({\mathfrak n}^-)$ by the triangular decomposition and the Poincaré–Birkhoff–Witt theorem,
$U({\mathfrak n}^-)$ by the triangular decomposition and the Poincaré–Birkhoff–Witt theorem, ![]() $\Psi ^{{\rm fin}}(M^{\operatorname {univ}})$ is concentrated in degree
$\Psi ^{{\rm fin}}(M^{\operatorname {univ}})$ is concentrated in degree ![]() $0$.
$0$.
In fact, by functoriality, for ![]() $Z({\mathfrak g})$ the center of
$Z({\mathfrak g})$ the center of ![]() $U({\mathfrak g})$,
$U({\mathfrak g})$, ![]() $\Psi ^{{\rm fin}}(M^{\operatorname {univ}})$ is canonically a
$\Psi ^{{\rm fin}}(M^{\operatorname {univ}})$ is canonically a ![]() $(Z({\mathfrak g}),\operatorname {Sym}({\mathfrak t}))$-bimodule. Moreover, the above reasoning shows that it is free of rank one for the
$(Z({\mathfrak g}),\operatorname {Sym}({\mathfrak t}))$-bimodule. Moreover, the above reasoning shows that it is free of rank one for the ![]() $\operatorname {Sym}({\mathfrak t})$-action. By construction, the induced homomorphism
$\operatorname {Sym}({\mathfrak t})$-action. By construction, the induced homomorphism ![]() $Z({\mathfrak g}) \to \operatorname {Sym}({\mathfrak t})$ is the Harish-Chandra morphism.
$Z({\mathfrak g}) \to \operatorname {Sym}({\mathfrak t})$ is the Harish-Chandra morphism.
Proof of Theorem A.2.1 Step 1. We will use some notions from group actions on categories. The reader may skip this background material and refer back to it as needed. We refer to [Reference BeraldoBer17, § 2] for details on what follows.
Let ![]() $\mathsf {DGCat}_{{\rm cont}}$ denote the symmetric monoidal category of presentableFootnote 16 DG categories under colimit-preserving DG functors; the symmetric monoidal structure is discussed in [Reference Gaitsgory and RozenblyumGR17, § I.10.4].
$\mathsf {DGCat}_{{\rm cont}}$ denote the symmetric monoidal category of presentableFootnote 16 DG categories under colimit-preserving DG functors; the symmetric monoidal structure is discussed in [Reference Gaitsgory and RozenblyumGR17, § I.10.4].
Let ![]() $\mathsf {Sch}^{{\rm f.t.}}$ denote the category of finite type
$\mathsf {Sch}^{{\rm f.t.}}$ denote the category of finite type ![]() $k$-schemes. The functor
$k$-schemes. The functor ![]() $D(-):\mathsf {Sch}^{{\rm f.t.}} \to \mathsf {DGCat}_{{\rm cont}}$ from [Reference Gaitsgory and RozenblyumGR17, § III.4] carries a canonical symmetric monoidal structure. Therefore,
$D(-):\mathsf {Sch}^{{\rm f.t.}} \to \mathsf {DGCat}_{{\rm cont}}$ from [Reference Gaitsgory and RozenblyumGR17, § III.4] carries a canonical symmetric monoidal structure. Therefore, ![]() $D(G) \in \mathsf {Alg}(\mathsf {DGCat}_{{\rm cont}})$ has a canonical monoidal structure; the underlying monoidal product sends
$D(G) \in \mathsf {Alg}(\mathsf {DGCat}_{{\rm cont}})$ has a canonical monoidal structure; the underlying monoidal product sends ![]() ${\cal F},{\cal G} \in D(G)$ to
${\cal F},{\cal G} \in D(G)$ to ![]() $m_{*,{\rm dR}}({\cal F} \boxtimes {\cal G})$ for
$m_{*,{\rm dR}}({\cal F} \boxtimes {\cal G})$ for ![]() $m:G \times G \to G$ the group multiplication.
$m:G \times G \to G$ the group multiplication.
By definition, a (strong) action of ![]() $G$ on
$G$ on ![]() ${\cal C} \in \mathsf {DGCat}_{{\rm cont}}$ is an action of
${\cal C} \in \mathsf {DGCat}_{{\rm cont}}$ is an action of ![]() $D(G)$ on
$D(G)$ on ![]() ${\cal C}$, where
${\cal C}$, where ![]() $D(G)$ is thought of as an algebra object in
$D(G)$ is thought of as an algebra object in ![]() $\mathsf {DGCat}_{{\rm cont}}$.
$\mathsf {DGCat}_{{\rm cont}}$.
For ![]() $G$ acting on
$G$ acting on ![]() ${\cal C}$, recall from [Reference BeraldoBer17] that there is a full subcategory
${\cal C}$, recall from [Reference BeraldoBer17] that there is a full subcategory ![]() ${\cal C}^N \subseteq {\cal C}$ of
${\cal C}^N \subseteq {\cal C}$ of ![]() $N$-equivariant objects. (In general, equivariant objects are not a full subcategory, but this is the case for unipotent groups.) Moreover, this embedding functor admits a right adjoint
$N$-equivariant objects. (In general, equivariant objects are not a full subcategory, but this is the case for unipotent groups.) Moreover, this embedding functor admits a right adjoint ![]() $\operatorname {Av}_*^N:{\cal C} \to {\cal C}^N$ that is continuous.
$\operatorname {Av}_*^N:{\cal C} \to {\cal C}^N$ that is continuous.
As in [Reference BeraldoBer17, § 2.5], the character ![]() $N^- \to {\mathbb {G}}_a$ obtained by exponentiating
$N^- \to {\mathbb {G}}_a$ obtained by exponentiating ![]() $\psi$ also defines a twisted notion of invariants for
$\psi$ also defines a twisted notion of invariants for ![]() $N^-$, which we denote
$N^-$, which we denote ![]() ${\cal C}^{N^-,\psi }$. Again,
${\cal C}^{N^-,\psi }$. Again, ![]() ${\cal C}^{N^-,\psi }$ is a certain full subcategory of
${\cal C}^{N^-,\psi }$ is a certain full subcategory of ![]() ${\cal C}$, and the embedding admits a right adjoint that commutes with colimits, which we denote
${\cal C}$, and the embedding admits a right adjoint that commutes with colimits, which we denote ![]() $\operatorname {Av}_*^{N^-,\psi }$.
$\operatorname {Av}_*^{N^-,\psi }$.
In what follows, we will be particularly interested in the functor ![]() $\operatorname {Av}_*^{N^-,\psi }:{\cal C}^N \to {\cal C}^{N^-,\psi }$. (The notation is slightly abusive; we are also letting
$\operatorname {Av}_*^{N^-,\psi }:{\cal C}^N \to {\cal C}^{N^-,\psi }$. (The notation is slightly abusive; we are also letting ![]() $\operatorname {Av}_*^{N^-,\psi }$ denote the composition
$\operatorname {Av}_*^{N^-,\psi }$ denote the composition ![]() ${\cal C}^N \to {\cal C} \xrightarrow {\operatorname {Av}_*^{N^-,\psi }} {\cal C}^{N^-,\psi }$.)
${\cal C}^N \to {\cal C} \xrightarrow {\operatorname {Av}_*^{N^-,\psi }} {\cal C}^{N^-,\psi }$.)
Step 2. Let ![]() $\operatorname {Loc}:{\mathfrak g} - \mathsf {mod} \to D(G)$ denote the functor
$\operatorname {Loc}:{\mathfrak g} - \mathsf {mod} \to D(G)$ denote the functor ![]() ${\cal F} \mapsto D_G \otimes _{U({\mathfrak g})} {\cal F}$ for
${\cal F} \mapsto D_G \otimes _{U({\mathfrak g})} {\cal F}$ for ![]() $D_G \in D(G)^{\heartsuit }$ the
$D_G \in D(G)^{\heartsuit }$ the ![]() $D$-module of differential operators. We remark that if we think of
$D$-module of differential operators. We remark that if we think of ![]() ${\mathfrak g} - \mathsf {mod}$ as the category of weakly equivariant
${\mathfrak g} - \mathsf {mod}$ as the category of weakly equivariant ![]() $D$-modules on
$D$-modules on ![]() $G$,
$G$, ![]() $\operatorname {Loc}$ is the functor of forgetting the weak equivariance structure. The notation indicates that
$\operatorname {Loc}$ is the functor of forgetting the weak equivariance structure. The notation indicates that ![]() $\operatorname {Loc}$ may also be thought of as the localization functor for
$\operatorname {Loc}$ may also be thought of as the localization functor for ![]() $G$ acting on itself.
$G$ acting on itself.
Below, we will upgrade this functor to a map of categories acted on strongly by ![]() $G$.
$G$.
Step 3. Recall that when ![]() $G$ acts on
$G$ acts on ![]() ${\cal C}$, there is a DG category
${\cal C}$, there is a DG category ![]() ${\cal C}^{G,w} \in \mathsf {DGCat}_{{\rm cont}}$ of weakly equivariant objects in
${\cal C}^{G,w} \in \mathsf {DGCat}_{{\rm cont}}$ of weakly equivariant objects in ![]() ${\cal C}$; see [Reference BeraldoBer17, § 2.2]. We remind the reader that
${\cal C}$; see [Reference BeraldoBer17, § 2.2]. We remind the reader that ![]() ${\cal C}^{G,w}$ is equipped with a canonical functor
${\cal C}^{G,w}$ is equipped with a canonical functor ![]() $\operatorname {Oblv}:{\cal C}^{G,w} \to {\cal C}$.
$\operatorname {Oblv}:{\cal C}^{G,w} \to {\cal C}$.
Consider ![]() $D(G)$ as a bimodule over itself and form
$D(G)$ as a bimodule over itself and form ![]() $D(G)^{G,w}$ the weak invariants for the right action of
$D(G)^{G,w}$ the weak invariants for the right action of ![]() $G$; the left action of
$G$; the left action of ![]() $G$ on itself equips
$G$ on itself equips ![]() $D(G)^{G,w}$ with a canonical
$D(G)^{G,w}$ with a canonical ![]() $G$-action.
$G$-action.
By [Reference Gaitsgory and RozenblyumGR17, § IV.3 Proposition-Construction 5.1.2] and the definitions, there is a canonical equivalence ![]() $D(G)^{G,w} \simeq {\mathfrak g} - \mathsf {mod}$ normalized by having
$D(G)^{G,w} \simeq {\mathfrak g} - \mathsf {mod}$ normalized by having ![]() $\operatorname {Oblv}(U({\mathfrak g})) = D_G \in D(G)^{\heartsuit }$. Under this equivalence,
$\operatorname {Oblv}(U({\mathfrak g})) = D_G \in D(G)^{\heartsuit }$. Under this equivalence, ![]() $\operatorname {Loc}$ constructed above corresponds to the forgetful functor
$\operatorname {Loc}$ constructed above corresponds to the forgetful functor ![]() $\operatorname {Oblv}:D(G)^{G,w} \to D(G)$, making it clear that
$\operatorname {Oblv}:D(G)^{G,w} \to D(G)$, making it clear that ![]() $\operatorname {Loc}$ is canonically
$\operatorname {Loc}$ is canonically ![]() $G$-equivariant.
$G$-equivariant.
Step 4. Note that the subcategory we denoted ![]() ${\mathfrak g} - \mathsf {mod}^N \subseteq {\mathfrak g} - \mathsf {mod}$ is in fact the
${\mathfrak g} - \mathsf {mod}^N \subseteq {\mathfrak g} - \mathsf {mod}$ is in fact the ![]() $N$-equivariant category for our
$N$-equivariant category for our ![]() $G$-action on
$G$-action on ![]() ${\mathfrak g} - \mathsf {mod}$. Indeed, this
${\mathfrak g} - \mathsf {mod}$. Indeed, this ![]() $N$-equivariant category embeds fully faithfully into
$N$-equivariant category embeds fully faithfully into ![]() ${\mathfrak g} - \mathsf {mod}$ and is closed under truncations, so this claim may be checked at the abelian categorical level where it is standard (see, for example, [Reference Frenkel and GaitsgoryFG06, § 20.4]).
${\mathfrak g} - \mathsf {mod}$ and is closed under truncations, so this claim may be checked at the abelian categorical level where it is standard (see, for example, [Reference Frenkel and GaitsgoryFG06, § 20.4]).
Similarly, ![]() ${\mathfrak g} - \mathsf {mod}^{N^-,\psi }$ is the full subcategory of objects
${\mathfrak g} - \mathsf {mod}^{N^-,\psi }$ is the full subcategory of objects ![]() $M \in {\mathfrak g} - \mathsf {mod}$ such that
$M \in {\mathfrak g} - \mathsf {mod}$ such that ![]() ${\mathfrak n}$ acts locally nilpotently on the cohomology of
${\mathfrak n}$ acts locally nilpotently on the cohomology of ![]() $M \otimes -\psi$. (We use
$M \otimes -\psi$. (We use ![]() $-\otimes -\psi$ similarly to
$-\otimes -\psi$ similarly to ![]() $\otimes \psi$, but for the inverse character.)
$\otimes \psi$, but for the inverse character.)
Step 5. We now have a commutative diagram

where the horizontal arrows are induced by the functor ![]() $\operatorname {Loc}$ considered above and the vertical arrows are the
$\operatorname {Loc}$ considered above and the vertical arrows are the ![]() $*$-averaging functors discussed above.
$*$-averaging functors discussed above.
We claim the left vertical arrow is ![]() $t$-exact up to shift by the dimension, that is, it maps objects in
$t$-exact up to shift by the dimension, that is, it maps objects in ![]() ${\mathfrak g} - \mathsf {mod}^{N,\heartsuit }$ to objects in cohomological degree
${\mathfrak g} - \mathsf {mod}^{N,\heartsuit }$ to objects in cohomological degree ![]() $\dim (N)$.
$\dim (N)$.
The localization functors ![]() $\operatorname {Loc}^N$ and
$\operatorname {Loc}^N$ and ![]() $\operatorname {Loc}^{N^-,\psi }$ are clearly
$\operatorname {Loc}^{N^-,\psi }$ are clearly ![]() $t$-exact, since this is evident for
$t$-exact, since this is evident for ![]() $\operatorname {Loc}$ itself. Moreover, the
$\operatorname {Loc}$ itself. Moreover, the ![]() $*$-averaging functor on the right coincides with the
$*$-averaging functor on the right coincides with the ![]() $!$-averaging functor up to cohomological shift
$!$-averaging functor up to cohomological shift ![]() $2\dim N$ by [Reference Bezrukavnikov, Braverman and MirkovicBBM04, Theorem 1.5 (1)].Footnote 17
$2\dim N$ by [Reference Bezrukavnikov, Braverman and MirkovicBBM04, Theorem 1.5 (1)].Footnote 17
The ![]() $*$-averaging functor has cohomological amplitude
$*$-averaging functor has cohomological amplitude ![]() $\leq \dim N$ because
$\leq \dim N$ because ![]() $N^-$ is affine, and the
$N^-$ is affine, and the ![]() $!$-averaging functor has amplitude
$!$-averaging functor has amplitude ![]() $\geq -\dim N$ by Theorem 3.4.1. We remark that because
$\geq -\dim N$ by Theorem 3.4.1. We remark that because ![]() $D(G/N)$ is compactly generated with compact objects closed under truncations and mapping to compact objects in
$D(G/N)$ is compactly generated with compact objects closed under truncations and mapping to compact objects in ![]() $D(G)$, we are justified in passing from coherent objects to arbitrary ones here. (Note that the
$D(G)$, we are justified in passing from coherent objects to arbitrary ones here. (Note that the ![]() $D$-modules arising by localization here are not necessarily holonomic!) Identifying the functors after shift then gives the result.
$D$-modules arising by localization here are not necessarily holonomic!) Identifying the functors after shift then gives the result.
Step 6. Let ![]() $\operatorname {ind}_{{\mathfrak n}}^{{\mathfrak g}}(\psi ) \in {\mathfrak g} - \mathsf {mod}^{N^-,\psi ,\heartsuit }$ be the standard induced module.
$\operatorname {ind}_{{\mathfrak n}}^{{\mathfrak g}}(\psi ) \in {\mathfrak g} - \mathsf {mod}^{N^-,\psi ,\heartsuit }$ be the standard induced module.
Note that for ![]() $M \in {\mathfrak g} - \mathsf {mod}$, we have
$M \in {\mathfrak g} - \mathsf {mod}$, we have
Here ![]() $C^{\bullet }({\mathfrak n}^-,-)$ is the cohomological Chevalley complex.
$C^{\bullet }({\mathfrak n}^-,-)$ is the cohomological Chevalley complex.
By Skryabin's theorem,Footnote 18 the functor ![]() $C^{\bullet }({\mathfrak n}^-,(-) \otimes -\psi )$ is
$C^{\bullet }({\mathfrak n}^-,(-) \otimes -\psi )$ is ![]() $t$-exact on
$t$-exact on ![]() ${\mathfrak g} - \mathsf {mod}^{N^-,\psi }$.
${\mathfrak g} - \mathsf {mod}^{N^-,\psi }$.
For ![]() $M \in {\mathfrak g} - \mathsf {mod}^{N,\heartsuit }$,
$M \in {\mathfrak g} - \mathsf {mod}^{N,\heartsuit }$, ![]() $\operatorname {Av}_*^{N^-,\psi }(M)[\dim N] \in {\mathfrak g} - \mathsf {mod}^{N^-,\psi ,\heartsuit }$ by Step 5.
$\operatorname {Av}_*^{N^-,\psi }(M)[\dim N] \in {\mathfrak g} - \mathsf {mod}^{N^-,\psi ,\heartsuit }$ by Step 5.
Noting that Lie algebra homology and cohomology coincide up to shift by ![]() $\dim N$, and switching the role of
$\dim N$, and switching the role of ![]() $\psi$ and
$\psi$ and ![]() $-\psi$, we obtain the desired result.
$-\psi$, we obtain the desired result.
Acknowledgements
We are grateful to Dennis Gaitsgory, Victor Ginzburg, and Masaki Kashiwara for useful correspondence on the subject of this article. The methods owe a great deal to [Reference BernsteinBer, Reference GinzburgGin86, Reference KashiwaraKas76].