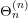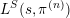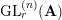Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kaplan, Eyal
2023.
Rankin–Selberg Integrals and L-Functions for Covering Groups of General Linear Groups.
International Mathematics Research Notices,
Vol. 2023,
Issue. 15,
p.
13332.
Luo, Caihua
2024.
An asymptotic expansion of (k, c)-functions for $$\textrm{GL}_{n}(F)$$.
Mathematische Zeitschrift,
Vol. 306,
Issue. 2,
Ginzburg, David
and
Soudry, David
2024.
A New Regularized Siegel-Weil Type Formula. Part I.
Geometric and Functional Analysis,
Vol. 34,
Issue. 1,
p.
60.
Jin, Yubo
and
Yan, Pan
2025.
L-functions for Sp(2n) × GL(k) via Non-unique Models.
International Mathematics Research Notices,
Vol. 2025,
Issue. 5,