Hostname: page-component-76c49bb84f-qtd2s Total loading time: 0 Render date: 2025-07-03T15:19:35.996Z Has data issue: false hasContentIssue false
  • English
  • Français

Generators in formal deformations of categories

Part of: Homological algebra Categories and geometry Algebraic geometry: Foundations

Published online by Cambridge University Press:  30 August 2018

Anthony Blanc ,
Ludmil Katzarkov  and
Pranav Pandit
Anthony Blanc
Affiliation:
Max Planck Institute for Mathematics, 53111 Bonn, Deutschland, Germany email ablanc@mpim-bonn.mpg.de
Ludmil Katzarkov
Affiliation:
Universität Wien, Fakultät für Mathematik, 1090 Wien, Österreich, Austria email pranav.pandit@univie.ac.at National Research University Higher School of Economics, Russian Federation, Laboratory of Mirror Symmetry NRU HSE, Moscow, Russia email lkatzarkov@gmail.com
Pranav Pandit
Affiliation:
Universität Wien, Fakultät für Mathematik, 1090 Wien, Österreich, Austria email pranav.pandit@univie.ac.at
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we use the theory of formal moduli problems developed by Lurie in order to study the space of formal deformations of a 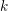$k$-linear 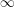$\infty$-category for a field 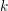$k$. Our main result states that if 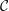${\mathcal{C}}$ is a 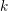$k$-linear 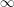$\infty$-category which has a compact generator whose groups of self-extensions vanish for sufficiently high positive degrees, then every formal deformation of 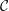${\mathcal{C}}$ has zero curvature and moreover admits a compact generator.

Keywords

deformation theorydg-categoriesE2 -algebrascompact generators

MSC classification

Primary: 14A22: Noncommutative algebraic geometry 18F99: None of the above, but in this section 18G55: Homotopical algebra

Information

Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 10 , October 2018 , pp. 2055 - 2089
Copyright
© The Authors 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alonso Tarrío, L., Jeremías López, A., Pérez Rodríguez, M. and Vale Gonsalves, M. J., On the existence of a compact generator on the derived category of a noetherian formal scheme , Appl. Categ. Structures 19 (2011), 865–877.Google Scholar
Blanc, A., Katzarkov, L. and Pandit, P., Generators in formal deformations: examples and applications, in preparation.Google Scholar
Cohn, L., Differential graded categories are k-linear stable infinity categories, Preprint (2013), arXiv:1308.2587 [math.AT].Google Scholar
Francis, J., The tangent complex and Hochschild cohomology of E n -rings , Compositio Math. 149 (2013), 430–480.Google Scholar
Keller, B. and Lowen, W., On Hochschild cohomology and Morita deformations , Int. Math. Res. Not. IMRN 2009 (2009), 3221–3235.Google Scholar
Kontsevich, M. and Soibelman, Y., Deformation theory, Vol. 1, Unpublished book draft (2005), www.math.ksu.edu/soibel/Book-vol1.ps.Google Scholar
Lowen, W., Hochschild cohomology, the characteristic morphism and derived deformations , Compos. Math. 144 (2008), 1557–1580.Google Scholar
Lowen, W. and Van den Bergh, M., The curvature problem for formal and infinitesimal deformations, Preprint (2015), arXiv:1505.03698 [math.KT].Google Scholar
Lurie, J., Higher topos theory, Annals of Mathematics Studies, vol. 170 (Princeton University Press, Princeton, NJ, 2009).Google Scholar
Lurie, J., Derived algebraic geometry IX: closed immersions, last update June 2011,www.math.harvard.edu/∼lurie.Google Scholar
Lurie, J., Derived algebraic geometry X: formal moduli problems, last update September 2011, www.math.harvard.edu/∼lurie.Google Scholar
Lurie, J., Derived algebraic geometry XII: proper morphisms, completions and the Grothendieck existence theorem, last update November 2011, www.math.harvard.edu/∼lurie.Google Scholar
Lurie, J., Higher algebra, last update September 2017, www.math.harvard.edu/∼lurie.Google Scholar
Petit, F., DG affinity of DQ-modules , Int. Math. Res. Not. IMRN 2012 (2012), 1414–1438.Google Scholar
Preygel, A., Thom-Sebastiani and duality for matrix factorizations, and results on the higher structures of the Hochschild invariants, PhD thesis, Massachusetts Institute of Technology (2012).Google Scholar
Robalo, M., Motivic Homotopy Theory of noncommutative Spaces, PhD thesis, Université Montpellier 2 (2014).Google Scholar