Article contents
A geometric p-adic Simpson correspondence in rank one
Published online by Cambridge University Press: 21 May 2024
Abstract
For any smooth proper rigid space 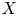 $X$ over a complete algebraically closed extension
$X$ over a complete algebraically closed extension 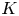 $K$ of
$K$ of 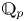 $\mathbb {Q}_p$ we give a geometrisation of the
$\mathbb {Q}_p$ we give a geometrisation of the 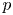 $p$-adic Simpson correspondence of rank one in terms of analytic moduli spaces: the
$p$-adic Simpson correspondence of rank one in terms of analytic moduli spaces: the 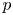 $p$-adic character variety is canonically an étale twist of the moduli space of topologically torsion Higgs line bundles over the Hitchin base. This also eliminates the choice of an exponential. The key idea is to relate both sides to moduli spaces of
$p$-adic character variety is canonically an étale twist of the moduli space of topologically torsion Higgs line bundles over the Hitchin base. This also eliminates the choice of an exponential. The key idea is to relate both sides to moduli spaces of 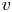 $v$-line bundles. As an application, we study a major open question in
$v$-line bundles. As an application, we study a major open question in 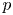 $p$-adic non-abelian Hodge theory raised by Faltings, namely which Higgs bundles correspond to continuous representations under the
$p$-adic non-abelian Hodge theory raised by Faltings, namely which Higgs bundles correspond to continuous representations under the 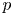 $p$-adic Simpson correspondence. We answer this question in rank one by describing the essential image of the continuous characters
$p$-adic Simpson correspondence. We answer this question in rank one by describing the essential image of the continuous characters 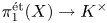 $\pi ^{{\mathrm {\acute {e}t}}}_1(X)\to K^\times$ in terms of moduli spaces: for projective
$\pi ^{{\mathrm {\acute {e}t}}}_1(X)\to K^\times$ in terms of moduli spaces: for projective 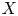 $X$ over
$X$ over 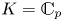 $K=\mathbb {C}_p$, it is given by Higgs line bundles with vanishing Chern classes like in complex geometry. However, in general, the correct condition is the strictly stronger assumption that the underlying line bundle is a topologically torsion element in the topological group
$K=\mathbb {C}_p$, it is given by Higgs line bundles with vanishing Chern classes like in complex geometry. However, in general, the correct condition is the strictly stronger assumption that the underlying line bundle is a topologically torsion element in the topological group 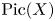 $\operatorname {Pic}(X)$.
$\operatorname {Pic}(X)$.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2024 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
References
- 4
- Cited by


