Hostname: page-component-7dd5485656-glrdx Total loading time: 0 Render date: 2025-10-30T16:30:00.087Z Has data issue: false hasContentIssue false
  • English
  • Français

Gonality of abstract modular curves in positive characteristic

Part of: Abelian varieties and schemes Curves

Published online by Cambridge University Press:  29 July 2016

Anna Cadoret  and
Akio Tamagawa
Anna Cadoret
Affiliation:
Centre de Mathématiques Laurent Schwartz, Ecole Polytechnique, 91128 Palaiseau, France email anna.cadoret@math.polytechnique.fr
Akio Tamagawa
Affiliation:
Research Institute for Mathematical Sciences, Kyoto University, Kyoto 606-8502, Japan email tamagawa@kurims.kyoto-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 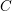$C$ be a smooth, separated and geometrically connected curve over a finitely generated field 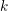$k$ of characteristic 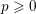$p\geqslant 0$ , 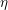$\unicode[STIX]{x1D702}$ the generic point of 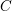$C$ and 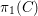$\unicode[STIX]{x1D70B}_{1}(C)$ its étale fundamental group. Let 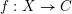$f:X\rightarrow C$ be a smooth proper morphism, and 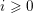$i\geqslant 0$ , 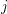$j$ integers. To the family of continuous 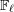$\mathbb{F}_{\ell }$ -linear representations 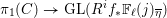$\unicode[STIX]{x1D70B}_{1}(C)\rightarrow \text{GL}(R^{i}f_{\ast }\mathbb{F}_{\ell }(j)_{\overline{\unicode[STIX]{x1D702}}})$ (where 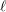$\ell$ runs over primes 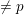$\neq p$ ), one can attach families of abstract modular curves 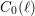$C_{0}(\ell )$ and 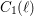$C_{1}(\ell )$ , which, in this setting, are the analogues of the usual modular curves 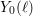$Y_{0}(\ell )$ and 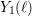$Y_{1}(\ell )$ . If 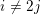$i\not =2j$ , it is conjectured that the geometric and arithmetic gonalities of these abstract modular curves go to infinity with 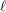$\ell$ (for the geometric gonality, under a certain necessary condition). We prove the conjecture for the arithmetic gonality of the abstract modular curves 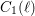$C_{1}(\ell )$ . We also obtain partial results for the growth of the geometric gonality of 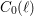$C_{0}(\ell )$ and 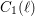$C_{1}(\ell )$ . The common strategy underlying these results consists in reducing by specialization theory to the case where the base field 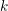$k$ is finite in order to apply techniques of counting rational points.

Keywords

curves over finite fieldsgonality in positive characteristicétale fundamental groupétale cohomology

MSC classification

Primary: 14H30: Coverings, fundamental group 14K99: None of the above, but in this section
Secondary: 14K10: Algebraic moduli, classification

Information

Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 11 , November 2016 , pp. 2405 - 2442
Copyright
© The Authors 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abramovich, D., A linear lower bound on the gonality of modular curves , Int. Math. Res. Not. IMRN 20 (1996), 1005–1011.CrossRefGoogle Scholar
Arbarello, E., Cornalba, M. and Griffith, P. A., Geometry of algebraic curves: Vol. II, Grundlehren der mathematischen Wissenschaften, vol. 268 (Springer, 2011).CrossRefGoogle Scholar
Berthelot, P., Altération des variétés algébriques (d’après A.J. de Jong) , in Séminaire Bourbaki 1995/1996, Vol. 815, Astérisque, vol. 241 (Société Mathématique de France, 1997), 273–311.Google Scholar
Cadoret, A., Note on the gonality of abstract modular curves , in The arithmetic of fundamental groups – PIA 2010, MATCH–HGS Contributions in Mathematical and Computational Science, vol. 2, ed. Stix, J. (Springer, 2012), 89–106.Google Scholar
Cadoret, A. and Tamagawa, A., Torsion of abelian schemes and rational points on moduli spaces , in Algebraic number theory and related topics, RIMS Kôkyûroku Bessatsu, vol. B12, eds Asada, M., Nakamura, H. and Takahashi, H. (RIMS, Kyoto, 2009), 7–29.Google Scholar
Cadoret, A. and Tamagawa, A., On a weak variant of the geometric torsion conjecture , J. Algebra 346 (2011), 227–247.Google Scholar
Cadoret, A. and Tamagawa, A., Uniform boundedness of p-primary torsion of abelian schemes , Invent. Math. 188 (2012), 83–125.Google Scholar
Cadoret, A. and Tamagawa, A., A uniform open image theorem for ℓ-adic representations I , Duke Math. J. 161 (2012), 2605–2634.Google Scholar
Cadoret, A. and Tamagawa, A., A uniform open image theorem for ℓ-adic representations II , Duke Math. J. 162 (2013), 2301–2344.Google Scholar
Cadoret, A. and Tamagawa, A., On the geometric image of $\mathbb{F}_{\ell }$ -linear representations of étale fundamental groups, Preprint (2014).Google Scholar
Cadoret, A. and Tamagawa, A., Genus of abstract modular curves with level- $\ell$ structures, Preprint (2014).Google Scholar
Cornelissen, G., Kato, F. and Kool, J., A combinatorial Li–Yau inequality and rational points on curves , Math. Ann. 361 (2015), 211–256.Google Scholar
Deligne, P., Théorie de Hodge, II , Publ. Math. Inst. Hautes Études Sci. 40 (1971), 5–57.Google Scholar
Deligne, P., La conjecture de Weil II , Publ. Math. Inst. Hautes Études Sci. 52 (1980), 137–252.CrossRefGoogle Scholar
Ellenberg, J., Elsholtz, C., Hall, C. and Kowalski, E., Non-simple abelian varieties in a family: algebraic and analytic approaches , J. Lond. Math. Soc. (2) 80 (2009), 135–154.Google Scholar
Dieudonné, J. and Grothendieck, A., Éléments de géométrie algébrique IV, Étude locale des schémas et des morphismes de schémas – troisième partie , Publ. Math. Inst. Hautes Études Sci. 28 (1966).Google Scholar
Ellenberg, J., Hall, C. and Kowalski, E., Expander graphs, gonality and variation of Galois representations , Duke Math. J. 161 (2012), 1233–1275.CrossRefGoogle Scholar
Faltings, G., Diophantine approximation on abelian varieties , Ann. of Math. (2) 133 (1991), 549–576.Google Scholar
Faltings, G. and Wüstholz, G., Rational points, Aspects of Mathematics, E6 (Vieweg, 1984).Google Scholar
Frey, G., Curves with infinitely many points of finite degree , Israel J. Math. 85 (1994), 79–83.CrossRefGoogle Scholar
Hall, C., Big symplectic or orthogonal monodromy groups modulo ℓ , Duke Math. J. 141 (2008), 179–203.Google Scholar
Hrushovsky, E., The Mordell–Lang conjecture for function fields , J. Amer. Math. Soc. 9 (1996), 667–690.Google Scholar
Kamienny, S., Torsion points on elliptic curves over fields of higher degree , Int. Math. Res. Not. IMRN 6 (1992), 129–133.CrossRefGoogle Scholar
Lang, S. and Néron, A., Rational points of abelian varieties over function fields , Amer. J. Math. 81 (1959), 95–118.Google Scholar
Mazur, B., Modular curves and the Eisenstein ideal , Publ. Math. Inst. Hautes Études Sci. 47 (1977), 33–186.Google Scholar
Mazur, B., Rational isogenies of prime degree (with an appendix by D. Goldfeld) , Invent. Math. 44 (1978), 129–162.Google Scholar
Merel, L., Bornes pour la torsion des courbes elliptiques sur les corps de nombres , Invent. Math. 124 (1996), 437–449.CrossRefGoogle Scholar
Milne, J. S., Jacobian varieties , in Arithmetic geometry, eds Cornell, G. and Silverman, J. H. (Springer, 1986), 167–212.Google Scholar
Momose, F., Isogenies of prime degree over number fields , Compositio Math. 97 (1995), 329–348.Google Scholar
Orgogozo, F., Sur les propriétés d’uniformité des images directes en cohomologie étale, Preprint (2013).Google Scholar
Orgogozo, F. and Vidal, I., Le théorème de spécialisation du groupe fondamental , in Courbes semi-stables et groupe fondamental en géométrie algébrique, Progress in Mathematics, vol. 187, eds Bost, J.-B., Loeser, F. and Raynaud, M. (Birkhäuser, 2000), 169–184.Google Scholar
Pink, R., l-adic algebraic monodromy groups, cocharacters, and the Mumford–Tate conjecture , J. Reine Angew. Math. 495 (1998), 187–237.Google Scholar
Poonen, B., Gonality of modular curves in characteristic p , Math. Res. Lett. 14 (2007), 691–701.Google Scholar
Rapoport, M. and Zink, T., Über die lokale Zetafunktion von Shimuravarietäten. Monodromiefiltration und verschwindende Zyklen in ungleicher Charakteristik , Invent. Math. 68 (1982), 21–101.Google Scholar
Schweizer, A., On the uniform boundedness conjecture for Drinfeld modules , Math. Z. 244 (2003), 601–614.Google Scholar
Serre, J.-P., Corps locaux (Hermann, 1968).Google Scholar
Grothendieck, A. et al. , Revêtements étales et groupe fondamental (SGA 1), Lecture Notes in Mathematics, vol. 224 (Springer, 1971).Google Scholar
Grothendieck, A. et al. , Schémas en groupes II (SGA 3 – II), Lecture Notes in Mathematics, vol. 152 (Springer, 1962–1964).Google Scholar
Grothendieck, A. et al. , Théorie des topos et cohomologie étale des schémas (SGA 4), tome 3, Lecture Notes in Mathematics, vol. 305 (Springer, 1973).Google Scholar
L. Szpiro (ed.), Séminaire sur les pinceaux arithmétiques: la conjecture de Mordell, Astérisque, vol. 127 (Société Mathématique de France, 1985).Google Scholar
Tamagawa, A., Fundamental groups and geometry of curves in positive characteristic , in Arithmetic fundamental groups and noncommutative algebra, Proceedings of Symposia in Pure Mathematics, vol. 70, eds Fried, M. D. and Ihara, Y. (American Mathematical Society, Providence, RI, 2002), 297–333.Google Scholar
Tate, J., Endomorphisms of abelian varieties over finite fields , Invent. Math. 2 (1966), 134–144.CrossRefGoogle Scholar
Zarhin, Ju. G., Endomorphisms of abelian varieties and points of finite order in characteristic p , Mat. Zametki 21 (1977), 737–744 (in Russian).Google Scholar