Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Forstnerič, Franc
2017.
Hyperbolic Complex Contact Structures on $$\mathbb {C}^{2n+1}$$ C 2 n + 1.
The Journal of Geometric Analysis,
Vol. 27,
Issue. 4,
p.
3166.
Alarcón, Antonio
and
Castro-Infantes, Ildefonso
2017.
Complete minimal surfaces densely lying in
arbitrary domains of ℝn.
Geometry & Topology,
Vol. 22,
Issue. 1,
p.
571.
ALARCÓN, ANTONIO
and
FORSTNERIČ, FRANC
2019.
NEW COMPLEX ANALYTIC METHODS IN THE THEORY OF MINIMAL SURFACES: A SURVEY.
Journal of the Australian Mathematical Society,
Vol. 106,
Issue. 03,
p.
287.
Forstnerič, Franc
2019.
A properly embedded holomorphic disc in the ball with finite area and dense boundary.
Mathematische Annalen,
Vol. 373,
Issue. 1-2,
p.
719.
Fornæss, John Erik
Forstnerič, Franc
and
Wold, Erlend F.
2020.
Advancements in Complex Analysis.
p.
133.
Vitagliano, Luca
and
Wade, Aïssa
2020.
Holomorphic Jacobi manifolds.
International Journal of Mathematics,
Vol. 31,
Issue. 03,
p.
2050024.
Forstnerič, Franc
2021.
The Calabi–Yau Property of Superminimal Surfaces in Self-Dual Einstein Four-Manifolds.
The Journal of Geometric Analysis,
Vol. 31,
Issue. 5,
p.
4754.
Alarcón, Antonio
Forstnerič, Franc
and
Lárusson, Finnur
2022.
Holomorphic Legendrian curves in ℂℙ3 and
superminimal surfaces in 𝕊4.
Geometry & Topology,
Vol. 25,
Issue. 7,
p.
3507.
Luza, Maycol Falla
and
Rosas, Rudy
2022.
Distributions, First Integrals and Legendrian Foliations.
Bulletin of the Brazilian Mathematical Society, New Series,
Vol. 53,
Issue. 4,
p.
1157.
Forstnerič, Franc
2022.
Mergelyan approximation theorem for holomorphic Legendrian curves.
Analysis & PDE,
Vol. 15,
Issue. 4,
p.
983.
Forstnerič, Franc
2023.
Recent developments on Oka manifolds.
Indagationes Mathematicae,
Vol. 34,
Issue. 2,
p.
367.
Forstnerič, Franc
2023.
Proper superminimal surfaces of given conformal types in the hyperbolic four-space.
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. 32,
Issue. 1,
p.
145.
Bhowmick, Aritra
and
Datta, Mahuya
2023.
Existence of horizontal immersions in fat distributions.
International Journal of Mathematics,
Vol. 34,
Issue. 10,
Svetina, Andrej
2024.
Approximation of holomorphic Legendrian curves with jet-interpolation.
Journal of Mathematical Analysis and Applications,
Vol. 531,
Issue. 2,
p.
127839.
Bhowmick, Aritra
2024.
On horizontal immersions of discs in fat distributions of type (4,6).
Journal of Topology and Analysis,
Vol. 16,
Issue. 01,
p.
125.
Alarcón, Antonio
and
Forstnerič, Franc
2025.
Oka-1 manifolds.
Mathematische Zeitschrift,
Vol. 311,
Issue. 2,
Svetina, Andrej
2025.
Holomorphic Legendrian Curves in Convex Domains.
The Journal of Geometric Analysis,
Vol. 35,
Issue. 1,
Alarcón, Antonio
and
Hidalgo, Jorge
2025.
Holomorphic null curves in the special linear group.
Transactions of the American Mathematical Society,
Andrist, Rafael B.
and
Huang, Gaofeng
2026.
Direct Products for the Hamiltonian Density Property.
The Journal of Geometric Analysis,
Vol. 36,
Issue. 1,
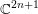 $\mathbb{C}^{2n+1}$ for any
$\mathbb{C}^{2n+1}$ for any 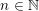 $n\in \mathbb{N}$ . We provide several approximation and desingularization results which enable us to prove general existence theorems, settling some of the open problems in the subject. In particular, we show that every open Riemann surface
$n\in \mathbb{N}$ . We provide several approximation and desingularization results which enable us to prove general existence theorems, settling some of the open problems in the subject. In particular, we show that every open Riemann surface 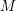 $M$ admits a proper holomorphic Legendrian embedding
$M$ admits a proper holomorphic Legendrian embedding 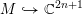 $M{\hookrightarrow}\mathbb{C}^{2n+1}$ , and we prove that for every compact bordered Riemann surface
$M{\hookrightarrow}\mathbb{C}^{2n+1}$ , and we prove that for every compact bordered Riemann surface 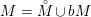 $M={M\unicode[STIX]{x0030A}}\,\cup \,bM$ there exists a topological embedding
$M={M\unicode[STIX]{x0030A}}\,\cup \,bM$ there exists a topological embedding 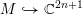 $M{\hookrightarrow}\mathbb{C}^{2n+1}$ whose restriction to the interior is a complete holomorphic Legendrian embedding
$M{\hookrightarrow}\mathbb{C}^{2n+1}$ whose restriction to the interior is a complete holomorphic Legendrian embedding 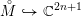 ${M\unicode[STIX]{x0030A}}{\hookrightarrow}\mathbb{C}^{2n+1}$ . As a consequence, we infer that every complex contact manifold
${M\unicode[STIX]{x0030A}}{\hookrightarrow}\mathbb{C}^{2n+1}$ . As a consequence, we infer that every complex contact manifold  $W$ carries relatively compact holomorphic Legendrian curves, normalized by any given bordered Riemann surface, which are complete with respect to any Riemannian metric on
$W$ carries relatively compact holomorphic Legendrian curves, normalized by any given bordered Riemann surface, which are complete with respect to any Riemannian metric on 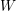 $W$ .
$W$ .
