Hostname: page-component-76c49bb84f-xk4dl Total loading time: 0 Render date: 2025-07-01T21:01:01.876Z Has data issue: false hasContentIssue false
  • English
  • Français

Howe–Moore type theorems for quantum groups and rigid $C^{\ast }$-tensor categories

Part of: Linear algebraic groups and related topics Categories with structure

Published online by Cambridge University Press:  30 October 2017

Yuki Arano ,
Tim de Laat  and
Jonas Wahl
Yuki Arano
Affiliation:
Department of Mathematics, Kyoto University, Kitashirakawa Oiwake-cho, Sakyo-ku, Kyoto 606-8502, Japan email y.arano@math.kyoto-u.ac.jp
Tim de Laat
Affiliation:
Mathematisches Institut, Westfälische Wilhelms-Universität Münster, Einsteinstrasse 62, 48149 Münster, Germany email tim.delaat@uni-muenster.de
Jonas Wahl
Affiliation:
KU Leuven, Department of Mathematics, Celestijnenlaan 200B – Box 2400, B-3001 Leuven, Belgium email jonas.wahl@kuleuven.be
Get access Rights & Permissions [Opens in a new window]

Abstract

We formulate and study Howe–Moore type properties in the setting of quantum groups and in the setting of rigid 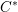$C^{\ast }$-tensor categories. We say that a rigid 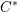$C^{\ast }$-tensor category 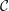${\mathcal{C}}$ has the Howe–Moore property if every completely positive multiplier on 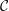${\mathcal{C}}$ has a limit at infinity. We prove that the representation categories of 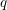$q$-deformations of connected compact simple Lie groups with trivial center satisfy the Howe–Moore property. As an immediate consequence, we deduce the Howe–Moore property for Temperley–Lieb–Jones standard invariants with principal graph 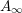$A_{\infty }$. These results form a special case of a more general result on the convergence of completely bounded multipliers on the aforementioned categories. This more general result also holds for the representation categories of the free orthogonal quantum groups and for the Kazhdan–Wenzl categories. Additionally, in the specific case of the quantum groups 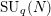$\text{SU}_{q}(N)$, we are able, using a result of the first-named author, to give an explicit characterization of the central states on the quantum coordinate algebra of 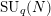$\text{SU}_{q}(N)$, which coincide with the completely positive multipliers on the representation category of 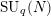$\text{SU}_{q}(N)$.

Keywords

C∗ -tensor categoriesquantum groupsHowe–Moore property

MSC classification

Primary: 18D10: Monoidal categories (= multiplicative categories), symmetric monoidal categories, braided categories 20G42: Quantum groups (quantized function algebras) and their representations

Information

Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 2 , February 2018 , pp. 328 - 341
Copyright
© The Authors 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Arano, Y., Unitary spherical representations of Drinfeld doubles , J. Reine Angew. Math. (2016), published ahead of print, doi:10.1515/crelle-2015-0079.Google Scholar
Arano, Y., Comparison of unitary duals of Drinfeld doubles and complex semisimple Lie groups , Comm. Math. Phys. 351 (2017), 1137–1147.Google Scholar
Bader, U. and Gelander, T., Equicontinuous actions of semisimple groups , Groups Geom. Dyn. 11 (2017), 1003–1039.CrossRefGoogle Scholar
Burger, M. and Mozes, S., Groups acting on trees: from local to global structure , Publ. Math. Inst. Hautes Études Sci. 92 (2000), 113–150.Google Scholar
Ciobotaru, C., A unified proof of the Howe–Moore property , J. Lie Theory 25 (2015), 65–89.Google Scholar
Daws, M., Skalski, A. and Viselter, A., Around Property (T) for quantum groups , Comm. Math. Phys. 353 (2017), 69–118.Google Scholar
De Commer, K., Freslon, A. and Yamashita, M., CCAP for universal discrete quantum groups , Comm. Math. Phys. 331 (2014), 677–701.Google Scholar
Ellis, R. and Nerurkar, M., Weakly almost periodic flows , Trans. Amer. Math. Soc. 313 (1989), 103–119.Google Scholar
Ghosh, S. K. and Jones, C., Annular representation theory for rigid C ∗ -tensor categories , J. Funct. Anal. 270 (2016), 1537–1584.Google Scholar
Hayashi, T. and Yamagami, S., Amenable tensor categories and their realizations as AFD bimodules , J. Funct. Anal. 172 (2000), 19–75.Google Scholar
Helgason, S., Groups and geometric analysis: integral geometry, invariant differential operators, and spherical functions (Academic Press, Orlando, FL, 1984).Google Scholar
Howe, R. E. and Moore, C. C., Asymptotic properties of unitary representations , J. Funct. Anal. 32 (1979), 72–96.Google Scholar
Jones, V. F. R., Index for subfactors , Invent. Math. 72 (1983), 1–25.CrossRefGoogle Scholar
Jones, V. F. R., Planar algebras, I, Preprint (1999), arXiv:math.QA/9909027.Google Scholar
Jones, V. F. R., Morrison, S. and Snyder, N., The classification of subfactors of index at most 5 , Bull. Amer. Math. Soc. 51 (2014), 277–327.Google Scholar
Jordans, B. P. A., A classification of SU(d)-type C ∗ -tensor categories , Internat. J. Math. 25 (2014), 14050081.CrossRefGoogle Scholar
Kac, V., Infinite-dimensional Lie algebras, third edition (Cambridge University Press, Cambridge, 1990).CrossRefGoogle Scholar
Kazhdan, D. A. and Wenzl, H., Reconstructing monoidal categories , in I. M. Gel’fand seminar, Advances in Soviet Mathematics, vol. 16 (American Mathematical Society, Providence, RI, 1993), 111–136.Google Scholar
Klimyk, A. and Schmüdgen, K., Quantum groups and their representations (Springer, Berlin, 1997).Google Scholar
Kustermans, J. and Vaes, S., Locally compact quantum groups , Ann. Sci. Éc. Norm. Supér. (4) 33 (2000), 837–934.CrossRefGoogle Scholar
Lubotzky, A. and Mozes, S., Asymptotic properties of unitary representations of tree automorphisms , in Harmonic analysis and discrete potential theory, Frascati, 1991 (Plenum, New York, 1992), 289–298.Google Scholar
Masuda, T., Classification of Roberts actions of strongly amenable $C^{\ast }$ -tensor categories on the injective factor of type $\mathit{III}_{1}$ , Preprint (2016), arXiv:1611.00476.Google Scholar
Neshveyev, S. and Tuset, L., Compact quantum groups and their representation categories (Société Mathématique de France, Paris, 2013).Google Scholar
Neshveyev, S. and Yamashita, M., Drinfeld center and representation theory for monoidal categories , Comm. Math. Phys. 345 (2016), 385–434.Google Scholar
Ocneanu, A., Chirality for operator algebras , in Subfactors, Kyuzeso, 1993 (World Scientific, River Edge, NJ, 1994), 39–63.Google Scholar
Popa, S., Classification of amenable subfactor of type II , Acta Math. 172 (1994), 163–255.Google Scholar
Popa, S., An axiomatization of the lattice of higher relative commutants of a subfactor , Invent. Math. 120 (1995), 347–389.Google Scholar
Popa, S. and Vaes, S., Representation theory for subfactors, 𝜆-lattices and C ∗ -tensor categories , Comm. Math. Phys. 340 (2015), 1239–1280.Google Scholar
Veech, W. A., Weakly almost periodic functions on semisimple Lie groups , Monatsh. Math. 88 (1979), 55–68.Google Scholar
Woronowicz, S. L., Twisted SU(2) group. An example of a noncommutative differential calculus , Publ. Res. Inst. Math. Sci. 23 (1987), 117–181.CrossRefGoogle Scholar
Zimmer, R. J., Ergodic theory and semisimple groups (Birkhäuser, Basel, 1984).Google Scholar