Article contents
Motivic and real étale stable homotopy theory
Published online by Cambridge University Press: 20 March 2018
Abstract
Let 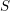 $S$ be a Noetherian scheme of finite dimension and denote by
$S$ be a Noetherian scheme of finite dimension and denote by 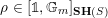 $\unicode[STIX]{x1D70C}\in [\unicode[STIX]{x1D7D9},\mathbb{G}_{m}]_{\mathbf{SH}(S)}$ the (additive inverse of the) morphism corresponding to
$\unicode[STIX]{x1D70C}\in [\unicode[STIX]{x1D7D9},\mathbb{G}_{m}]_{\mathbf{SH}(S)}$ the (additive inverse of the) morphism corresponding to 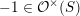 $-1\in {\mathcal{O}}^{\times }(S)$ . Here
$-1\in {\mathcal{O}}^{\times }(S)$ . Here 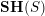 $\mathbf{SH}(S)$ denotes the motivic stable homotopy category. We show that the category obtained by inverting
$\mathbf{SH}(S)$ denotes the motivic stable homotopy category. We show that the category obtained by inverting 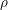 $\unicode[STIX]{x1D70C}$ in
$\unicode[STIX]{x1D70C}$ in 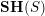 $\mathbf{SH}(S)$ is canonically equivalent to the (simplicial) local stable homotopy category of the site
$\mathbf{SH}(S)$ is canonically equivalent to the (simplicial) local stable homotopy category of the site 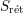 $S_{\text{r}\acute{\text{e}}\text{t}}$ , by which we mean the small real étale site of
$S_{\text{r}\acute{\text{e}}\text{t}}$ , by which we mean the small real étale site of 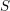 $S$ , comprised of étale schemes over
$S$ , comprised of étale schemes over 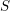 $S$ with the real étale topology. One immediate application is that
$S$ with the real étale topology. One immediate application is that 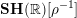 $\mathbf{SH}(\mathbb{R})[\unicode[STIX]{x1D70C}^{-1}]$ is equivalent to the classical stable homotopy category. In particular this computes all the stable homotopy sheaves of the
$\mathbf{SH}(\mathbb{R})[\unicode[STIX]{x1D70C}^{-1}]$ is equivalent to the classical stable homotopy category. In particular this computes all the stable homotopy sheaves of the 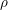 $\unicode[STIX]{x1D70C}$ -local sphere (over
$\unicode[STIX]{x1D70C}$ -local sphere (over 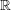 $\mathbb{R}$ ). As further applications we show that
$\mathbb{R}$ ). As further applications we show that 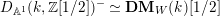 $D_{\mathbb{A}^{1}}(k,\mathbb{Z}[1/2])^{-}\simeq \mathbf{DM}_{W}(k)[1/2]$ (improving a result of Ananyevskiy–Levine–Panin), reprove Röndigs’ result that
$D_{\mathbb{A}^{1}}(k,\mathbb{Z}[1/2])^{-}\simeq \mathbf{DM}_{W}(k)[1/2]$ (improving a result of Ananyevskiy–Levine–Panin), reprove Röndigs’ result that 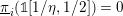 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/\unicode[STIX]{x1D702},1/2])=0$ for
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/\unicode[STIX]{x1D702},1/2])=0$ for 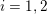 $i=1,2$ and establish some new rigidity results.
$i=1,2$ and establish some new rigidity results.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author 2018
References
- 32
- Cited by

