Article contents
Nearby Lagrangian fibers and Whitney sphere links
Published online by Cambridge University Press: 20 February 2018
Abstract
Let 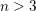 $n>3$ , and let
$n>3$ , and let 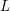 $L$ be a Lagrangian embedding of
$L$ be a Lagrangian embedding of 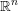 $\mathbb{R}^{n}$ into the cotangent bundle
$\mathbb{R}^{n}$ into the cotangent bundle  $T^{\ast }\mathbb{R}^{n}$ of
$T^{\ast }\mathbb{R}^{n}$ of 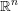 $\mathbb{R}^{n}$ that agrees with the cotangent fiber
$\mathbb{R}^{n}$ that agrees with the cotangent fiber 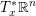 $T_{x}^{\ast }\mathbb{R}^{n}$ over a point
$T_{x}^{\ast }\mathbb{R}^{n}$ over a point 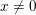 $x\neq 0$ outside a compact set. Assume that
$x\neq 0$ outside a compact set. Assume that 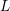 $L$ is disjoint from the cotangent fiber at the origin. The projection of
$L$ is disjoint from the cotangent fiber at the origin. The projection of 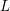 $L$ to the base extends to a map of the
$L$ to the base extends to a map of the  $n$ -sphere
$n$ -sphere 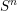 $S^{n}$ into
$S^{n}$ into 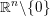 $\mathbb{R}^{n}\setminus \{0\}$ . We show that this map is homotopically trivial, answering a question of Eliashberg. We give a number of generalizations of this result, including homotopical constraints on embedded Lagrangian disks in the complement of another Lagrangian submanifold, and on two-component links of immersed Lagrangian spheres with one double point in
$\mathbb{R}^{n}\setminus \{0\}$ . We show that this map is homotopically trivial, answering a question of Eliashberg. We give a number of generalizations of this result, including homotopical constraints on embedded Lagrangian disks in the complement of another Lagrangian submanifold, and on two-component links of immersed Lagrangian spheres with one double point in 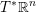 $T^{\ast }\mathbb{R}^{n}$ , under suitable dimension and Maslov index hypotheses. The proofs combine techniques from Ekholm and Smith [Exact Lagrangian immersions with a single double point, J. Amer. Math. Soc. 29 (2016), 1–59] and Ekholm and Smith [Exact Lagrangian immersions with one double point revisited, Math. Ann. 358 (2014), 195–240] with symplectic field theory.
$T^{\ast }\mathbb{R}^{n}$ , under suitable dimension and Maslov index hypotheses. The proofs combine techniques from Ekholm and Smith [Exact Lagrangian immersions with a single double point, J. Amer. Math. Soc. 29 (2016), 1–59] and Ekholm and Smith [Exact Lagrangian immersions with one double point revisited, Math. Ann. 358 (2014), 195–240] with symplectic field theory.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- © The Authors 2018
References
- 1
- Cited by

