Hostname: page-component-68c7f8b79f-qcl88 Total loading time: 0 Render date: 2025-12-17T08:45:43.054Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear Hodge flows in symplectic geometry

Part of: Symplectic geometry, contact geometry Parabolic equations and systems

Published online by Cambridge University Press:  17 December 2025

Weiyong He Open the ORCID record for Weiyong He [Opens in a new window]
Weiyong He*
Affiliation:
University of Oregon , Department of Mathematics, Eugene, OR 97403, USA whe@uoregon.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a symplectic class $$\left[ \omega \right]$$ on a four torus 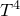$${T^4}$$ (or a 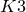$$K3$$ surface), a folklore problem in symplectic geometry is whether symplectic forms in $$\left[ \omega \right]$$ are isotopic to each other. We introduce a family of nonlinear Hodge heat flows on compact symplectic four manifolds to approach this problem, which is an adaption of nonlinear Hodge theory in symplectic geometry. As a particular example, we study a conformal Hodge heat flow in detail. We prove a stability result of the flow near an almost Kähler structure 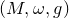$$\left( {M,\omega ,g} \right)$$. We also prove that, if 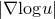$$\left| {\nabla {\rm{log}}u} \right|$$ stays bounded along the flow, then the flow exists for all time for any initial symplectic form 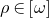$$\rho \in \left[ \omega \right]$$ and it converges to $$\omega $$ smoothly along the flow with uniform control, where 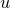$$u$$ is the volume potential of 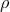$$\rho $$.

Keywords

uniqueness of symplectic structurenonlinear Hodge flowsthe conformal Hodge flow

MSC classification

Primary: 53D05: Symplectic manifolds, general
Secondary: 35K40: Second-order parabolic systems

Information

Type
Research Article
Information
Compositio Mathematica , Volume 161 , Issue 10 , October 2025 , pp. 2461 - 2492
Check for updates
Copyright
© The Author(s), 2025. The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Donaldson, S., Moment maps and diffeomorphisms, Asian J. Math. 3 (1999), 1–16.CrossRefGoogle Scholar
Donaldson, S., Two-forms on four-manifolds and elliptic equations, in Inspired by S. S. Chern, A Memorial Volume in Honor of A Great Mathematician, Nankai Tracts in Mathematics, vol. 11 (World Scientific Publishing, Hackensack, NJ, 2006), 153–172.CrossRefGoogle Scholar
Fei, T. and Phong, D. H., Symplectic geometric flows, Pure Appl. Math. Q. 19 (2023), 1853–1871.CrossRefGoogle Scholar
Fei, T., Phong, D. H., Picard, S. and Zhang, X., Geometric flows for the type IIA string, Camb. J. Math. 9 (2021), 693–807.CrossRefGoogle Scholar
Fine, J. and Yao, C. J., Hypersymplectic 4-manifolds, the -Laplacian flow, and extension assuming bounded scalar curvature, Duke Math. J. 167 (2018), 3533–3589.CrossRefGoogle Scholar
Hamilton, R., The inverse function theorem of Nash and Moser, Bull. Amer. Math. Soc. (N.S.) 7 (1982), 65–222.CrossRefGoogle Scholar
He, W. Y., Evolution equations for nondegenerate two forms, Int. Math. Res. Not. IMRN 2021 (2021), 4349–4391.CrossRefGoogle Scholar
He, W. Y. and Li, B., The harmonic heat flow of almost complex structures, Trans. Amer. Math. Soc. 374 (2021), 6179–6199.CrossRefGoogle Scholar
Krom, R., The Donaldson geometric flow is a smooth semiflow, Preprint (1987), arXiv:1512.09199Google Scholar
Krom, R. and Salamon, D., The Donaldson geometric flow for symplectic four-manifolds, J. Symplectic Geom. 17 (2019), 381–417.CrossRefGoogle Scholar
Le, H. V. and Wang, G. F., Anti-complexified Ricci flow on compact symplectic manifolds, J. Reine Angew. Math. 530 (2001), 17–31.Google Scholar
Li, T. J. and Liu, A., Uniqueness of symplectic canonical class, surface cone and symplectic cone of manifolds with $\begin{align*}{b^ + } = 1\end{align*}$ , J. Differential Geom. 58 (2001), 331–370.CrossRefGoogle Scholar
McDuff, D., Examples of symplectic structures, Invent. Math. 89 (1987), 13–36.CrossRefGoogle Scholar
McDuff, D. and Salamon, D., Introduction to symplectic topology, Oxford Graduate Texts in Mathematics, vol. 27 (Oxford University Press, Oxford, 2017).CrossRefGoogle Scholar
Salamon, D., Uniqueness of symplectic structures, Acta Math. Vietnam. 38 (2013), 123–144.CrossRefGoogle Scholar
Scott, C., $\begin{align*}{L^p}\end{align*}$ theory of differential forms on manifolds, Trans. Amer. Math. Soc. 347 (1995), 2075–2096.Google Scholar
Shi, W. X., Deforming the metric on complete Riemannian manifolds, J. Differential Geom. 30 (1989), 223–301.Google Scholar
Streets, J. and Tian, G., Symplectic curvature flow, J. Reine Angew. Math. 2014 (2014), 143–185.CrossRefGoogle Scholar