Hostname: page-component-784d4fb959-g549k Total loading time: 0 Render date: 2025-07-16T10:43:58.621Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical dimension and a Kawamata–Viehweg–Nadel-type vanishing theorem on compact Kähler manifolds

Part of: Holomorphic fiber spaces (Co)homology theory

Published online by Cambridge University Press:  27 August 2014

Junyan Cao
Junyan Cao*
Affiliation:
KIAS, 85 Hoegiro, Dongdaemun-gu, Seoul 130-722, Republic of Korea email junyan@kias.re.kr, jycao136@yahoo.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 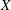$X$ be a compact Kähler manifold and let 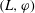$(L,{\it\varphi})$ be a pseudo-effective line bundle on 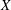$X$. We first define a notion of numerical dimension for pseudo-effective line bundles with singular metrics, and then discuss the properties of this numerical dimension. Finally, we prove a very general Kawamata–Viehweg–Nadel-type vanishing theorem on an arbitrary compact Kähler manifold.

Keywords

vanishing theoremcompact Kähler manifoldsNadel vanishing theorempseudo-effective line bundle

MSC classification

Primary: 32L20: Vanishing theorems 14F17: Vanishing theorems

Information

Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 11 , November 2014 , pp. 1869 - 1902
Copyright
© The Author 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Berndtsson, B., The openness conjecture for plurisubharmonic functions, Preprint (2013),arXiv:1305.5781.Google Scholar
Bonavero, L., Inégalités de morse holomorphes singulières, J. Geom. Anal. 8 (1998), 409–425; MR 1707735 (2000k:32020).CrossRefGoogle Scholar
Boucksom, S., Cones positifs des variétés complexes compactes, PhD thesis, Université Joseph Fourier, Grenoble (2002).Google Scholar
Demailly, J.-P., A numerical criterion for very ample line bundles, J. Differential Geom. 37 (1993), 323–374; MR 1205448 (94d:14007).CrossRefGoogle Scholar
Demailly, J.-P., Analytic methods in algebraic geometry, Surveys of Modern Mathematics, vol. 1 (International Press, Somerville, MA, 2012); MR 2978333.Google Scholar
Demailly, J.-P., Ein, L. and Lazarsfeld, R., A subadditivity property of multiplier ideals, Michigan Math. J. 48 (2000), 137–156; dedicated to William Fulton on the occasion of his 60th birthday; MR 1786484 (2002a:14016).Google Scholar
Demailly, J.-P. and Păun, M., Numerical characterization of the Kähler cone of a compact Kähler manifold, Ann. of Math. (2) 159 (2004), 1247–1274; MR 2113021 (2005i:32020).Google Scholar
Demailly, J.-P. and Peternell, T., A Kawamata-Viehweg vanishing theorem on compact Kähler manifolds, J. Differential Geom. 63 (2003), 231–277; MR 2015548 (2004m:32040).Google Scholar
Demailly, J.-P., Peternell, T. and Schneider, M., Compact complex manifolds with numerically effective tangent bundles, J. Algebraic Geom. 3 (1994), 295–345; MR 1257325 (95f:32037).Google Scholar
Demailly, J.-P., Peternell, T. and Schneider, M., Pseudo-effective line bundles on compact Kähler manifolds, Internat. J. Math. 12 (2001), 689–741; MR 1875649 (2003a:32032).Google Scholar
Enoki, I., Kawamata-Viehweg vanishing theorem for compact Kähler manifolds, in Einstein Metrics and Yang-Mills Connections (Sanda, 1990), Lecture Notes in Pure and Applied Mathematics, vol. 145 (Marcel Dekker, New York, 1993), 59–68; MR 1215279 (94f:32063).Google Scholar
Favre, C. and Jonsson, M., Valuations and multiplier ideals, J. Amer. Math. Soc. 18 (2005), 655–684; MR 2138140 (2007b:14004).CrossRefGoogle Scholar
Küronya, A., Asymptotic cohomological functions on projective varieties, Amer. J. Math. 128 (2006), 1475–1519; MR 2275909 (2007k:14009).Google Scholar
Matsumura, S.-i., An injectivity theorem with multiplier ideal sheaves of singular metrics with transcendental singularities, Preprint (2013), arXiv:1308.2033.Google Scholar
Mourougane, C., Versions kählériennes du théorème d’annulation de Bogomolov-Sommese, C. R. Acad. Sci. Paris Sér. I Math. 321 (1995), 1459–1462; MR 1366101 (96k:32066).Google Scholar
Nadel, A., Multiplier ideal sheaves and Kähler–Einstein metrics of positive scalar curvature, Ann. of Math. (2) 132 (1990), 549–596; MR 1078269 (92d:32038).Google Scholar
Trapani, S., Divisorial Zariski decomposition and algebraic Morse inequalities, Proc. Amer. Math. Soc. 139 (2011), 177–183; MR 2729081 (2012a:32019).Google Scholar
Tsuji, H., Extension of log pluricanonical forms from subvarieties, Preprint (2007),arXiv:0709.2710.Google Scholar