Article contents
Odd zeta motive and linear forms in odd zeta values
Published online by Cambridge University Press: 30 October 2017
Abstract
We study a family of mixed Tate motives over 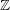 $\mathbb{Z}$ whose periods are linear forms in the zeta values
$\mathbb{Z}$ whose periods are linear forms in the zeta values 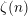 $\unicode[STIX]{x1D701}(n)$ . They naturally include the Beukers–Rhin–Viola integrals for
$\unicode[STIX]{x1D701}(n)$ . They naturally include the Beukers–Rhin–Viola integrals for 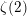 $\unicode[STIX]{x1D701}(2)$ and the Ball–Rivoal linear forms in odd zeta values. We give a general integral formula for the coefficients of the linear forms and a geometric interpretation of the vanishing of the coefficients of a given parity. The main underlying result is a geometric construction of a minimal ind-object in the category of mixed Tate motives over
$\unicode[STIX]{x1D701}(2)$ and the Ball–Rivoal linear forms in odd zeta values. We give a general integral formula for the coefficients of the linear forms and a geometric interpretation of the vanishing of the coefficients of a given parity. The main underlying result is a geometric construction of a minimal ind-object in the category of mixed Tate motives over 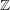 $\mathbb{Z}$ which contains all the non-trivial extensions between simple objects. In a joint appendix with Don Zagier, we prove the compatibility between the structure of the motives considered here and the representations of their periods as sums of series.
$\mathbb{Z}$ which contains all the non-trivial extensions between simple objects. In a joint appendix with Don Zagier, we prove the compatibility between the structure of the motives considered here and the representations of their periods as sums of series.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- © The Author 2017
References
- 4
- Cited by

