Hostname: page-component-7dd5485656-zlgnt Total loading time: 0 Render date: 2025-10-29T07:57:34.995Z Has data issue: false hasContentIssue false
  • English
  • Français

On mod 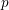$p$ local-global compatibility for 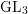$\text{GL}_{3}$ in the ordinary case

Part of: Algebraic number theory: local and $p$-adic fields Discontinuous groups and automorphic forms Lie groups

Published online by Cambridge University Press:  25 August 2017

Florian Herzig ,
Daniel Le  and
Stefano Morra
Florian Herzig
Affiliation:
Department of Mathematics, University of Toronto, 40 St. George Street, Toronto, ON M5S 2E4, Canada email herzig@math.toronto.edu
Daniel Le
Affiliation:
Department of Mathematics, University of Toronto, 40 St. George Street, Toronto, ON M5S 2E4, Canada email le@math.toronto.edu
Stefano Morra
Affiliation:
Institut Montpelliérain Alexander Grothendieck, Université de Montpellier, Case courrier 051, Place Eugène Bataillon, 34095 Montpellier Cedex, France email stefano.morra@umontpellier.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Suppose that 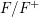$F/F^{+}$ is a CM extension of number fields in which the prime 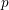$p$ splits completely and every other prime is unramified. Fix a place 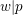$w|p$ of 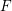$F$ . Suppose that 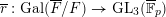$\overline{r}:\operatorname{Gal}(\overline{F}/F)\rightarrow \text{GL}_{3}(\overline{\mathbb{F}}_{p})$ is a continuous irreducible Galois representation such that 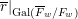$\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})}$ is upper-triangular, maximally non-split, and generic. If $\overline{r}$ is automorphic, and some suitable technical conditions hold, we show that 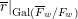$\overline{r}|_{\operatorname{Gal}(\overline{F}_{w}/F_{w})}$ can be recovered from the 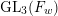$\text{GL}_{3}(F_{w})$ -action on a space of mod 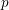$p$ automorphic forms on a compact unitary group. On the way we prove results about weights in Serre’s conjecture for $\overline{r}$ , show the existence of an ordinary lifting of $\overline{r}$ , and prove the freeness of certain Taylor–Wiles patched modules in this context. We also show the existence of many Galois representations $\overline{r}$ to which our main theorem applies.

Keywords

Galois representationsmod p Langlands programSerre-type conjectures

MSC classification

Primary: 11F80: Galois representations
Secondary: 11S37: Langlands-Weil conjectures, nonabelian class field theory 22E50: Representations of Lie and linear algebraic groups over local fields

Information

Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 11 , November 2017 , pp. 2215 - 2286
Copyright
© The Authors 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Andersen, H. H., Extensions of simple modules for finite Chevalley groups , J. Algebra 111 (1987), 388–403; MR 916175 (89b:20089).Google Scholar
Barnet-Lamb, T., Gee, T. and Geraghty, D., Congruences between Hilbert modular forms: constructing ordinary lifts , Duke Math. J. 161 (2012), 1521–1580; MR 2931274.CrossRefGoogle Scholar
Barnet-Lamb, T., Gee, T., Geraghty, D. and Taylor, R., Potential automorphy and change of weight , Ann. of Math. (2) 179 (2014), 501–609; MR 3152941.Google Scholar
Bellaïche, J. and Chenevier, G., Families of Galois representations and Selmer groups , Astérisque 324 (2009), MR 2656025 (2011m:11105).Google Scholar
Breuil, C., Représentations p-adiques semi-stables et transversalité de Griffiths , Math. Ann. 307 (1997), 191–224; MR 1428871 (98b:14016).Google Scholar
Breuil, C., Construction de représentations p-adiques semi-stables , Ann. Sci. Éc. Norm. Supér. (4) 31 (1998), 281–327; MR 1621389 (99k:14034).CrossRefGoogle Scholar
Breuil, C., Représentations semi-stables et modules fortement divisibles , Invent. Math. 136 (1999), 89–122; MR 1681105 (2000c:14024).Google Scholar
Breuil, C., Une application de corps des normes , Compos. Math. 117 (1999), 189–203; MR 1695849 (2000f:11157).Google Scholar
Breuil, C., Sur quelques représentations modulaires et p-adiques de GL2(Q p ). I , Compos. Math. 138 (2003), 165–188; MR 2018825 (2004k:11062).Google Scholar
Breuil, C., Diagrammes de Diamond et (𝜙, 𝛤)-modules , Israel J. Math. 182 (2011), 349–382; MR 2783977 (2012f:22026).Google Scholar
Breuil, C. and Diamond, F., Formes modulaires de Hilbert modulo p et valeurs d’extensions entre caractères galoisiens , Ann. Sci. Éc. Norm. Supér. (4) 47 (2014), 905–974; MR 3294620.Google Scholar
Breuil, C. and Herzig, F., Ordinary representations of G (ℚ p ) and fundamental algebraic representations , Duke Math. J. 164 (2015), 1271–1352; MR 3347316.Google Scholar
Breuil, C. and Paškūnas, V., Towards a modulo p Langlands correspondence for GL2 , Mem. Amer. Math. Soc. 216 (2012), vi+114; MR 2931521.Google Scholar
Caraiani, A., Emerton, M., Gee, T., Geraghty, D., Paškūnas, V. and Shin, S. W., Patching and the p-adic local Langlands correspondence , Camb. J. Math. 4 (2016), 197–287; MR 3529394.Google Scholar
Caruso, X., Conjecture de l’inertie modérée de Serre, PhD thesis, Université Paris 13 (2005), http://tel.archives-ouvertes.fr/tel-00011202.Google Scholar
Caruso, X., Représentations semi-stables de torsion dans le case er < p - 1 , J. Reine Angew. Math. 594 (2006), 35–92; MR 2248152 (2007d:11061).Google Scholar
Caruso, X., F p -représentations semi-stables , Ann. Inst. Fourier (Grenoble) 61 (2011), 1683–1747; MR 2951749.Google Scholar
Caruso, X. and Liu, T., Quasi-semi-stable representations , Bull. Soc. Math. France 137 (2009), 185–223; MR 2543474 (2011c:11086).Google Scholar
Clozel, L., Harris, M. and Taylor, R., Automorphy for some l-adic lifts of automorphic mod l Galois representations , Publ. Math. Inst. Hautes Études Sci. 108 (2008), 1–181; MR 2470687 (2010j:11082).Google Scholar
Colmez, P., Représentations de GL2(Q p ) et (𝜙, 𝛤)-modules , Astérisque 330 (2010), 281–509; MR 2642409 (2011j:11224).Google Scholar
Conrad, B., Diamond, F. and Taylor, R., Modularity of certain potentially Barsotti–Tate Galois representations , J. Amer. Math. Soc. 12 (1999), 521–567; MR 1639612 (99i:11037).Google Scholar
Diamond, F., The Taylor–Wiles construction and multiplicity one , Invent. Math. 128 (1997), 379–391; MR 1440309 (98c:11047).Google Scholar
Emerton, M., Local-global compatibility in the  $p$ -adic Langlands programme for  $\text{GL}_{2/\mathbb{Q}}$ , Preprint (2011), http://www.math.uchicago.edu/∼emerton/pdffiles/lg.pdf.Google Scholar
Emerton, M. and Gee, T., A geometric perspective on the Breuil–Mézard conjecture , J. Inst. Math. Jussieu 13 (2014), 183–223; MR 3134019.Google Scholar
Emerton, M., Gee, T. and Herzig, F., Weight cycling and Serre-type conjectures for unitary groups , Duke Math. J. 162 (2013), 1649–1722; MR 3079258.Google Scholar
Emerton, M., Gee, T. and Savitt, D., Lattices in the cohomology of Shimura curves , Invent. Math. 200 (2015), 1–96; MR 3323575.Google Scholar
Fontaine, J.-M., Représentations p-adiques des corps locaux. I , in The Grothendieck Festschrift, Vol. II, Progress in Mathematics, vol. 87 (Birkhäuser Boston, Boston, MA, 1990), 249–309; MR 1106901 (92i:11125).Google Scholar
Fontaine, J.-M. and Laffaille, G., Construction de représentations p-adiques , Ann. Sci. Éc. Norm. Supér. (4) 15 (1982), 547–608; MR 707328 (85c:14028).CrossRefGoogle Scholar
Gao, H. and Liu, T., A note on potential diagonalizability of crystalline representations , Math. Ann. 360 (2014), 481–487; MR 3263170.Google Scholar
Gee, T. and Geraghty, D., Companion forms for unitary and symplectic groups , Duke Math. J. 161 (2012), 247–303; MR 2876931.Google Scholar
Gee, T., Herzig, F. and Savitt, D., General Serre weight conjectures, Preprint (2016), arXiv:math.NT/1509.02527v2.Google Scholar
Harris, M. and Taylor, R., The Geometry and Cohomology of Some Simple Shimura Varieties, Annals of Mathematics Studies, vol. 151 (Princeton University Press, Princeton, NJ, 2001); MR 1876802 (2002m:11050).Google Scholar
Henniart, G., Une caractérisation de la correspondance de Langlands locale pour GL(n) , Bull. Soc. Math. France 130 (2002), 587–602; MR 1947454 (2004d:22013).Google Scholar
Herzig, F., The weight in a Serre-type conjecture for tame n-dimensional Galois representations , Duke Math. J. 149 (2009), 37–116; MR 2541127 (2010f:11083).Google Scholar
Herzig, F., The classification of irreducible admissible mod p representations of a p-adic GL n , Invent. Math. 186 (2011), 373–434; MR 2845621.CrossRefGoogle Scholar
Humphreys, J. E., Modular Representations of Finite Groups of Lie Type, London Mathematical Society Lecture Note Series, vol. 326 (Cambridge University Press, Cambridge, 2006); MR 2199819 (2007f:20023).Google Scholar
Jantzen, J. C., Representations of algebraic groups, Mathematical Surveys and Monographs, vol. 107, second edition (American Mathematical Society, Providence, RI, 2003);MR 2015057 (2004h:20061).Google Scholar
Keller, B., Chain complexes and stable categories , Manuscripta Math. 67 (1990), 379–417; MR 1052551 (91h:18006).Google Scholar
Le, D., Lattices in the cohomology of $U(3)$ arithmetic manifolds, Preprint (2015),arXiv:math.NT/1507.04766.Google Scholar
Le, D., Hung, B. V. L., Levin, B. and Morra, S., Potentially crystalline deformation rings and Serre weight conjectures (Shapes and Shadows), Preprint (2015),arXiv:math.NT/1512.06380.Google Scholar
Liu, T., On lattices in semi-stable representations: a proof of a conjecture of Breuil , Compos. Math. 144 (2008), 61–88; MR 2388556 (2009c:14087).Google Scholar
Morra, S. and Park, C., Serre weights for three dimensional ordinary Galois representations, Preprint (2014).Google Scholar
Paskunas, V., On the restriction of representations of GL2(F) to a Borel subgroup , Compos. Math. 143 (2007), 1533–1544; MR 2371380 (2009a:22013).Google Scholar
Roche, A., Types and Hecke algebras for principal series representations of split reductive p-adic groups , Ann. Sci. Éc. Norm. Supér. (4) 31 (1998), 361–413; MR 1621409 (99d:22028).Google Scholar
Taylor, R., Automorphy for some l-adic lifts of automorphic mod l Galois representations. II , Publ. Math. Inst. Hautes Études Sci. 108 (2008), 183–239; MR 2470688 (2010j:11085).CrossRefGoogle Scholar
Thorne, J., On the automorphy of l-adic Galois representations with small residual image , J. Inst. Math. Jussieu 11 (2012), 855–920; MR 2979825.Google Scholar
Wintenberger, J.-P., Le corps des normes de certaines extensions infinies de corps locaux; applications , Ann. Sci. Éc. Norm. Supér. (4) 16 (1983), 59–89; MR 719763 (85e:11098).Google Scholar