Hostname: page-component-7dd5485656-zklqj Total loading time: 0 Render date: 2025-10-26T20:44:05.007Z Has data issue: false hasContentIssue false
  • English
  • Français

On p-adic uniformization of abelian varieties with good reduction

Part of: Abelian varieties and schemes Arithmetic algebraic geometry Algebraic groups

Published online by Cambridge University Press:  05 September 2022

Adrian Iovita ,
Jackson S. Morrow  and
Alexandru Zaharescu
Adrian Iovita
Affiliation:
Department of Mathematics and Statistics, Concordia University, Montréal, Québec, Canada adrian.iovita@concordia.ca Dipartimento di Matematica, Universita degli Studi di Padova, Padova, Italy
Jackson S. Morrow
Affiliation:
Department of Mathematics, University of California, 749 Evans Hall, Berkeley, CA 94720, USA jacksonmorrow@berkeley.edu
Alexandru Zaharescu
Affiliation:
Department of Mathematics, University of Illinois Urbana-Champaign, 1409 West Green Street, Urbana, IL 61801, USA zaharesc@illinois.edu “Simion Stoilow” Institute of Mathematics of the Romanian Academy, P.O. Box 1-764, RO-014700 Bucharest, Romania
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 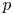$p$ be a rational prime, let 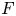$F$ denote a finite, unramified extension of 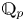${{\mathbb {Q}}}_p$, let 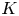$K$ be the maximal unramified extension of 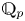${{\mathbb {Q}}}_p$, 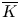${{\overline {K}}}$ some fixed algebraic closure of 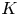$K$, and 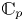${{\mathbb {C}}}_p$ be the completion of 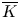${{\overline {K}}}$. Let 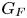$G_F$ be the absolute Galois group of 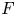$F$. Let 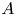$A$ be an abelian variety defined over 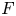$F$, with good reduction. Classically, the Fontaine integral was seen as a Hodge–Tate comparison morphism, i.e. as a map 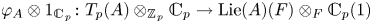$\varphi _{A} \otimes 1_{{{\mathbb {C}}}_p}\colon T_p(A)\otimes _{{{\mathbb {Z}}}_p}{{\mathbb {C}}}_p\to \operatorname {Lie}(A)(F)\otimes _F{{\mathbb {C}}}_p(1)$, and as such it is surjective and has a large kernel. This paper starts with the observation that if we do not tensor 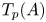$T_p(A)$ with 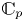${{\mathbb {C}}}_p$, then the Fontaine integral is often injective. In particular, it is proved that if 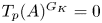$T_p(A)^{G_K} = 0$, then 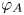$\varphi _A$ is injective. As an application, we extend the Fontaine integral to a perfectoid like universal cover of 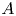$A$ and show that if 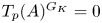$T_p(A)^{G_K} = 0$, then 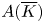$A(\overline {K})$ has a type of 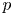$p$-adic uniformization, which resembles the classical complex uniformization.

Keywords

p-adic uniformizationabelian varietiesFontaine integration

MSC classification

Primary: 11G10: Abelian varieties of dimension $> 1$
Secondary: 14K20: Analytic theory; abelian integrals and differentials 11G25: Varieties over finite and local fields 14L05: Formal groups, $p$-divisible groups

Information

Type
Research Article
Information
Compositio Mathematica , Volume 158 , Issue 7 , July 2022 , pp. 1449 - 1476
Check for updates
Copyright
© 2022 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

With an appendix by Yeuk Hay Joshua Lam and Alexander Petrov

References

Berkovich, V. G., Spectral theory and analytic geometry over non-Archimedean fields, Mathematical Surveys and Monographs, vol. 33 (American Mathematical Society, Providence, RI, 1990); MR 1070709.Google Scholar
Berkovich, V. G., Étale cohomology for non-Archimedean analytic spaces, Publ. Math. Inst. Hautes Études Sci. 78 (1993), 5–161 (1994); MR 1259429.CrossRefGoogle Scholar
Berkovich, V. G., Smooth $p$-adic analytic spaces are locally contractible, Invent. Math. 137 (1999), 1–84; MR 1702143.CrossRefGoogle Scholar
Blakestad, C., Gvirtz, D., Heuer, B., Shchedrina, D., Shimizu, K., Wear, P. and Yao, Z., Perfectoid covers of abelian varieties, Math. Res. Lett., to appear. Preprint (2020), arXiv:1804.04455.Google Scholar
Bloch, S. and Kato, K., L-functions and Tamagawa numbers of motives (Birkhäuser, Boston, MA, 2007), 333–400.Google Scholar
Bosch, S. and Lütkebohmert, W., Stable reduction and uniformization of abelian varieties. II, Invent. Math. 78 (1984), 257–297; MR 767194.CrossRefGoogle Scholar
Bosch, S. and Lütkebohmert, W., Stable reduction and uniformization of abelian varieties. I, Math. Ann. 270 (1985), 349–379.CrossRefGoogle Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron models, Ergebnisse der Mathematik und ihrer Grenzgebiete (3), vol. 21 (Springer, Berlin, 1990); MR 1045822 (91i:14034).CrossRefGoogle Scholar
Coleman, R. F., Hodge–Tate periods and $p$-adic abelian integrals, Invent. Math. 78 (1984), 351–379.CrossRefGoogle Scholar
Coleman, R. F., Torsion points on curves and $p$-adic abelian integrals, Ann. Math. 121 (1985), 111–168.CrossRefGoogle Scholar
Coleman, R. and Iovita, A., The Frobenius and monodromy operators for curves and abelian varieties, Duke Math. J. 97 (1999), 171–215.CrossRefGoogle Scholar
Colmez, P., Périodes $p$-adiques des variétés abéliennes, Math. Ann. 292 (1992), 629–644.CrossRefGoogle Scholar
Colmez, P., Exposé II (appendice) : Les nombres algébriques sont denses dans $B^{+}_{\text {dR}}$, in Périodes $p$-adiques, Astérisque, vol. 223 (Société Mathématique de France, 1994).Google Scholar
Colmez, P., Intégration sur les variétés $p$-adiques, Astérisque 248 (1998); MR 1645429.Google Scholar
Fargues, L., Groupes analytiques rigides $p$-divisibles, Math. Ann. 374 (2019), 723–791; MR 3961325.CrossRefGoogle Scholar
Fontaine, J.-M., Formes Différentielles et Modules de Tate des Variétés abéliennes sur les Corps Locaux, Invent. Math. 65 (1981/82), 379–410.CrossRefGoogle Scholar
Fontaine, J.-M., Sur certains types de représentations $p$-adiques du groupe de Galois d'un corps local; construction d'un anneau de Barsotti-Tate, Ann. of Math. (2) 115 (1982), 529–577; MR 657238.CrossRefGoogle Scholar
Fontaine, J.-M., Représentations $p$-adiques semi-stables, in Périodes $p$-adiques, Astérisque, vol. 223 (Société Mathématique de France, 1994), 113–184; MR 1293972.Google Scholar
Fontaine, J.-M., Presque $C_p$-représentations, Doc. Math., Extra Vol., Kazuya Kato's Fiftieth Birthday (2003), 285–385.Google Scholar
Fesenko, I. B. and Vostokov, S. V., Local fields and their extensions, second edition, Translations of Mathematical Monographs, vol. 121 (American Mathematical Society, Providence, RI, 2002); MR 1915966.Google Scholar
Heuer, B., Pro-étale uniformisation of abelian varieties, Preprint (2021), arXiv:2105.12604.Google Scholar
Hrushovski, E. and Loeser, F., Non-Archimedean tame topology and stably dominated types, Annals of Mathematics Studies, vol. 225 (Princeton University Press, 2016).CrossRefGoogle Scholar
Huber, R., A generalization of formal schemes and rigid analytic varieties, Math. Z. 217 (1994), 513–551.CrossRefGoogle Scholar
Iovita, A. and Zaharescu, A., Completions of R.A.T.-valued fields of rational functions, J. Number Theory 50 (1995), 202–205; MR 1316815.CrossRefGoogle Scholar
Iovita, A. and Zaharescu, A., Galois theory of $B^{+}_{\text {dR}}$, Compos. Math. 117 (1999), 1–33.CrossRefGoogle Scholar
Katz, N. M., Crystalline cohomology, Dieudonné modules, and Jacobi sums, in Automorphic forms, representation theory and arithmetic (Bombay, 1979), Tata Institute Of Fundamental Research Studies In Mathematics, vol. 10 (Tata Institute of Fundamental Research, Bombay, 1981), 165–246; MR 633662.CrossRefGoogle Scholar
Ozeki, Y., Torsion points of abelian varieties with values in infinite extensions over a $p$-adic field, Publ. Res. Inst. Math. Sci. 45 (2010), 1011–1031.CrossRefGoogle Scholar
Pilloni, V. and Stroh, B., Cohomologie cohérente et représentations Galoisiennes, Ann. Math. Qué. 40 (2016), 167–202.CrossRefGoogle Scholar
Raynaud, M., Variétés abéliennes et géométrie rigide, in Actes du congrès international des mathématiciens (Nice, 1970), Vol. 1 (Gauthier-Villars, Paris, 1971), 473–477; MR 0427326.Google Scholar
Scholze, P., Perfectoid spaces, Publ. Math. Inst. Hautes Études Sci. 116 (2012), 245–313; MR 3090258.CrossRefGoogle Scholar
Scholze, P., Etale cohomology of diamonds, Preprint (2021), arXiv:1709.07343.Google Scholar
Scholze, P. and Weinstein, J., Moduli of $p$-divisible groups, Camb. J. Math. 1 (2013), 145–237.CrossRefGoogle Scholar
Scholze, P. and Weinstein, J., Berkeley lectures on P-adic geometry, Annals of Mathematics Studies, vol. 389 (Princeton University Press, Princeton, NJ 2020).Google Scholar
Sen, S., Continuous cohomology and $\textit{p}$-adic Galois representations, Invent. Math. 62 (1980/81), 89–116; MR 595584.CrossRefGoogle Scholar
Serre, J.-P., Abelian $\ell$-adic representations and elliptic curves, revised reprint of the 1968 original, Research Notes in Mathematics, vol. 7 (AK Peters, Wellesley, MA, 1998); MR 1484415.Google Scholar
Tate, J., $\textit{p}$-Divisible groups, Proceedings of a conference on local fields (Springer, 1967), 158–183.CrossRefGoogle Scholar
Tate, J., A review of non-Archimedean elliptic functions, in Elliptic curves, modular forms, & Fermat's last theorem, Series in Number Theory, vol. I (International Press, Cambridge, MA, 1995), 162–184; MR 1363501.Google Scholar