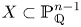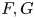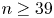1. Introduction
Let ![]() $X\subseteq \mathbb {P}^{n-1}_\mathbb {Q}$ denote a projective complete intersection variety. In particular, let
$X\subseteq \mathbb {P}^{n-1}_\mathbb {Q}$ denote a projective complete intersection variety. In particular, let ![]() $X$ correspond to the zero locus of a system of
$X$ correspond to the zero locus of a system of ![]() $R$ homogeneous polynomials of degree
$R$ homogeneous polynomials of degree ![]() $d$ defined over
$d$ defined over ![]() $\mathbb {Q}$. Let
$\mathbb {Q}$. Let
where
denotes the singular locus of the variety ![]() $X$. Furthermore, we define
$X$. Furthermore, we define ![]() $\underline {x}$ to be a non-singular point of
$\underline {x}$ to be a non-singular point of ![]() $X$ if
$X$ if
A long-standing result of Birch [Reference BirchBir61] establishes the Hasse principle as long as
While the case of lower-degree hypersurfaces ![]() $(R=1)$ has seen several breakthroughs in recent times, the case of general complete intersections has seen relatively lower success. In the case of a pair of quadrics over
$(R=1)$ has seen several breakthroughs in recent times, the case of general complete intersections has seen relatively lower success. In the case of a pair of quadrics over ![]() $\mathbb {Q}$, Munshi [Reference MunshiMun15] verified the Hasse principle when
$\mathbb {Q}$, Munshi [Reference MunshiMun15] verified the Hasse principle when ![]() $n\geq 11$, provided that their intersection is non-singular. Instead of proving the Hasse principle, Heath-Brown and Pierce [Reference Heath-Brown and PierceHP17] and Pierce, Schindler and Wood [Reference Pierce, Schindler and WoodPSW16] considered the question of representations of almost every integer tuple by systems of quadrics. In this context, [Reference Heath-Brown and PierceHP17] dealt with a smooth pair of quadrics in
$n\geq 11$, provided that their intersection is non-singular. Instead of proving the Hasse principle, Heath-Brown and Pierce [Reference Heath-Brown and PierceHP17] and Pierce, Schindler and Wood [Reference Pierce, Schindler and WoodPSW16] considered the question of representations of almost every integer tuple by systems of quadrics. In this context, [Reference Heath-Brown and PierceHP17] dealt with a smooth pair of quadrics in ![]() $n\geq 5$ variables and [Reference Pierce, Schindler and WoodPSW16] dealt with a system of three quadrics in
$n\geq 5$ variables and [Reference Pierce, Schindler and WoodPSW16] dealt with a system of three quadrics in ![]() $n\geq 10$ variables.
$n\geq 10$ variables.
There have been two recent notable breakthroughs. Myerson [Reference MyersonMye18, Reference MyersonMye19] improved the square dependence on ![]() $R$ in Birch's result to a linear one. When
$R$ in Birch's result to a linear one. When ![]() $d=2$ and
$d=2$ and ![]() $3$, these results improve the lower bound to
$3$, these results improve the lower bound to ![]() $n-\sigma \geq 8R$ and
$n-\sigma \geq 8R$ and ![]() $25R$, respectively. This is a significant improvement when
$25R$, respectively. This is a significant improvement when ![]() $R$ is large. However, when
$R$ is large. However, when ![]() $R$ is small (say
$R$ is small (say ![]() $2$), it fails to improve upon Birch's bounds. Typically, one expects better understanding of the distribution of rational points when
$2$), it fails to improve upon Birch's bounds. Typically, one expects better understanding of the distribution of rational points when ![]() $d$ and
$d$ and ![]() $R$ are relatively small. When
$R$ are relatively small. When ![]() $R=1$, this is facilitated by an analytic technique called Kloosterman refinement, which allows one to use the Poisson summation formula in an effective way. A recent breakthrough was obtained in the second author's work [Reference VisheVis23], where a two-dimensional version of Farey dissection was developed in the function field setting. Unfortunately, so far the method there does not extend to the
$R=1$, this is facilitated by an analytic technique called Kloosterman refinement, which allows one to use the Poisson summation formula in an effective way. A recent breakthrough was obtained in the second author's work [Reference VisheVis23], where a two-dimensional version of Farey dissection was developed in the function field setting. Unfortunately, so far the method there does not extend to the ![]() $\mathbb {Q}$ setting. The only other available version which works in the context here is due to Munshi [Reference MunshiMun15]; however, it does not generalise very effectively beyond the case of two quadrics. The aforementioned works [Reference Heath-Brown and PierceHP17] and [Reference Pierce, Schindler and WoodPSW16] also obtain a version of Kloosterman refinement for a system of forms, but these methods are only specific to the case of almost every representable integer tuples and are not applicable for proving the Hasse principle.
$\mathbb {Q}$ setting. The only other available version which works in the context here is due to Munshi [Reference MunshiMun15]; however, it does not generalise very effectively beyond the case of two quadrics. The aforementioned works [Reference Heath-Brown and PierceHP17] and [Reference Pierce, Schindler and WoodPSW16] also obtain a version of Kloosterman refinement for a system of forms, but these methods are only specific to the case of almost every representable integer tuples and are not applicable for proving the Hasse principle.
The main purpose of this work is to provide a route to Kloosterman refinement for a system of forms over ![]() $\mathbb {Q}$. In particular, the method here should improve upon the current results as long as the defining forms
$\mathbb {Q}$. In particular, the method here should improve upon the current results as long as the defining forms ![]() $F$ and
$F$ and ![]() $G$ of
$G$ of ![]() $X$ are not two quadrics or a cubic and a quadric.
$X$ are not two quadrics or a cubic and a quadric.
We now define the setting in this paper. Let ![]() $F(\underline {x}),G(\underline {x})\in \mathbb {Z}[x_1,\ldots,x_n]$ be two homogeneous cubic forms in
$F(\underline {x}),G(\underline {x})\in \mathbb {Z}[x_1,\ldots,x_n]$ be two homogeneous cubic forms in ![]() $n$ variables and with integer coefficients, and let
$n$ variables and with integer coefficients, and let ![]() $X$ denote the smooth projective variety defined by their simultaneous zero locus. The long-standing result by Birch
$X$ denote the smooth projective variety defined by their simultaneous zero locus. The long-standing result by Birch ![]() $n\geq 49$ is yet to be improved in the current setting (a pair of cubics). In the case of a system of diagonal cubic forms, one can obtain significantly stronger results. In particular, Brüdern and Wooley [Reference Brüdern and WooleyBW07, Reference Brüdern and WooleyBW16] proved that the Hasse principle is true for a smooth system of
$n\geq 49$ is yet to be improved in the current setting (a pair of cubics). In the case of a system of diagonal cubic forms, one can obtain significantly stronger results. In particular, Brüdern and Wooley [Reference Brüdern and WooleyBW07, Reference Brüdern and WooleyBW16] proved that the Hasse principle is true for a smooth system of ![]() $R$ diagonal cubic forms in
$R$ diagonal cubic forms in ![]() $n$ variables provided that
$n$ variables provided that ![]() $n\geq 6R+1$.
$n\geq 6R+1$.
In this paper, we will use a combination of Kloosterman refinement and a two-dimensional version of averaged van der Corput differencing to improve upon Birch's result. In particular, we aim to prove the following result.
Theorem 1.1 Let ![]() $X:=X_{F,G}\subset \mathbb {P}^{n-1}_\mathbb {Q}$ be a smooth complete intersection variety defined by a system of two cubic forms
$X:=X_{F,G}\subset \mathbb {P}^{n-1}_\mathbb {Q}$ be a smooth complete intersection variety defined by a system of two cubic forms ![]() $F$ and
$F$ and ![]() $G$. Then
$G$. Then ![]() $X$ satisfies the Hasse principle provided that
$X$ satisfies the Hasse principle provided that ![]() $n\geq 39$.
$n\geq 39$.
To the best of the authors’ knowledge, this is the first known improvement of Birch's result in this case. As is the typical feature of the methods used here, with some more work the result can be easily extended to cover the cases of singular varieties, as long as ![]() $n-\sigma \geq 40$. However, here we will stick to the non-singular setting. The limitation of the method here is
$n-\sigma \geq 40$. However, here we will stick to the non-singular setting. The limitation of the method here is ![]() $n\geq 38$. Akin to the work [Reference Marmon and VisheMV19] of Marmon and the second author, saving an extra variable variable will require substantially new technical input which we will not attempt to obtain here.
$n\geq 38$. Akin to the work [Reference Marmon and VisheMV19] of Marmon and the second author, saving an extra variable variable will require substantially new technical input which we will not attempt to obtain here.
For those familiar with circle method techniques, there are two key bounds here that facilitate Theorem 1.1. The first improvement comes from developing a two-dimensional version of averaged van der Corput differencing, which will be obtained in § 4. This followed by Weyl differencing could hand us Theorem 1.1 when ![]() $n\geq 43$. Our key innovation comes from combining an averaged van der Corput process with a version of Kloosterman refinement. This combination saves us
$n\geq 43$. Our key innovation comes from combining an averaged van der Corput process with a version of Kloosterman refinement. This combination saves us ![]() $4$ extra variables. To compare our results with the other potential existing methods, the method of Munshi [Reference MunshiMun15] has to be combined with some version of differencing to be applicable here. Assuming ideal bounds, our rough calculations show that if one were to combine the ideas in the second author's work [Reference Marmon and VisheMV19] along with Munshi's method [Reference MunshiMun15] one may be able to establish Theorem 1.1 for
$4$ extra variables. To compare our results with the other potential existing methods, the method of Munshi [Reference MunshiMun15] has to be combined with some version of differencing to be applicable here. Assuming ideal bounds, our rough calculations show that if one were to combine the ideas in the second author's work [Reference Marmon and VisheMV19] along with Munshi's method [Reference MunshiMun15] one may be able to establish Theorem 1.1 for ![]() $n\geq 46$. If one were to instead combine [Reference MunshiMun15] with our technique in § 4, one may save an extra variable over the Weyl bound (
$n\geq 46$. If one were to instead combine [Reference MunshiMun15] with our technique in § 4, one may save an extra variable over the Weyl bound (![]() $n\geq 42$). A key difference between our method with that of [Reference MunshiMun15] is that the latter uses a larger total modulus (the parameter
$n\geq 42$). A key difference between our method with that of [Reference MunshiMun15] is that the latter uses a larger total modulus (the parameter ![]() $Q$ appearing in this paper) than our method. This is wasteful if one is dealing with forms in many variables, rendering the method not ideal to deal with complete intersections which are not defined by two quadrics.
$Q$ appearing in this paper) than our method. This is wasteful if one is dealing with forms in many variables, rendering the method not ideal to deal with complete intersections which are not defined by two quadrics.
We now give a more detailed outline of the key ideas. From now on, we will assume that ![]() $X$ is a complete intersection of two cubics which contains a non-singular adelic point, i.e. that
$X$ is a complete intersection of two cubics which contains a non-singular adelic point, i.e. that
where given any variety ![]() $X$, let
$X$, let
Given a smooth weight function ![]() $\omega \in \mathrm {C}^\infty _c(\mathbb {R}^n)$, and a large parameter
$\omega \in \mathrm {C}^\infty _c(\mathbb {R}^n)$, and a large parameter ![]() $1\leq P$, we define the following smooth counting function:
$1\leq P$, we define the following smooth counting function:
 \[ N(P):=N_\omega(P):=\sum_{\substack{\underline{x}\in\mathbb{Z}^n,\\ F(\underline{x})= G(\underline{x}) = 0}} \omega(\underline{x}/P). \]
\[ N(P):=N_\omega(P):=\sum_{\substack{\underline{x}\in\mathbb{Z}^n,\\ F(\underline{x})= G(\underline{x}) = 0}} \omega(\underline{x}/P). \]
Our main tool in proving Theorem 1.1 is the asymptotic formula for ![]() $N(P)$ obtained in Theorem 1.2. Before stating it, let us define the weight function
$N(P)$ obtained in Theorem 1.2. Before stating it, let us define the weight function ![]() $\omega$ in the following way. We will choose
$\omega$ in the following way. We will choose ![]() $\omega$ to be a smooth weight function, centred at a non-singular point
$\omega$ to be a smooth weight function, centred at a non-singular point ![]() $\underline {x}_0\in X(\mathbb {R})$ with the additional property that its support is a ‘small’ region around
$\underline {x}_0\in X(\mathbb {R})$ with the additional property that its support is a ‘small’ region around ![]() $\underline {x}_0$. Upon recalling (1.2), it is easy to see that the existence of such a point is guaranteed by our earlier assumption that
$\underline {x}_0$. Upon recalling (1.2), it is easy to see that the existence of such a point is guaranteed by our earlier assumption that ![]() $X$ has a non-singular adelic point. In particular, the point
$X$ has a non-singular adelic point. In particular, the point ![]() $\underline {x}_0\in X(\mathbb {R})$ must have
$\underline {x}_0\in X(\mathbb {R})$ must have
Using homogeneity of ![]() $F$ and
$F$ and ![]() $G$, we may further assume that
$G$, we may further assume that ![]() $|\underline {x}_0|<1$. This condition is superficial, and only assumed to make the implied constants appearing in our argument simpler. Let
$|\underline {x}_0|<1$. This condition is superficial, and only assumed to make the implied constants appearing in our argument simpler. Let
 \[ \gamma(\underline{x}):=\begin{cases} \prod_j e^{-1/(1-x_j)^2} & \text{if } |\underline{x}|<1,\\ 0 & \text{else,} \end{cases} \]
\[ \gamma(\underline{x}):=\begin{cases} \prod_j e^{-1/(1-x_j)^2} & \text{if } |\underline{x}|<1,\\ 0 & \text{else,} \end{cases} \]
denote a non-negative smooth function supported in the hypercube ![]() $[-1,1]^n$. Given a parameter
$[-1,1]^n$. Given a parameter ![]() $0<\rho <1$ to be suitably decided later, we define
$0<\rho <1$ to be suitably decided later, we define
We are now set to state our main counting result, which directly implies Theorem 1.1.
Theorem 1.2 Let ![]() $X\subset \mathbb {P}^{n-1}_\mathbb {Q}$ be a smooth complete intersection variety defined by a system of two cubic forms
$X\subset \mathbb {P}^{n-1}_\mathbb {Q}$ be a smooth complete intersection variety defined by a system of two cubic forms ![]() $F,G$. Then provided that
$F,G$. Then provided that ![]() $n\geq 39$ and
$n\geq 39$ and ![]() $X_{\mathrm {ns}}(\mathbb {A}_\mathbb {Q}) \neq \emptyset$, there exist
$X_{\mathrm {ns}}(\mathbb {A}_\mathbb {Q}) \neq \emptyset$, there exist ![]() $C_X>0$ and some
$C_X>0$ and some ![]() $\rho _0\in (0,1]$, such that for each
$\rho _0\in (0,1]$, such that for each ![]() $0<\rho \leq \rho _0$, there exists
$0<\rho \leq \rho _0$, there exists ![]() $\delta _0:=\delta _0(\rho )>0$ such that
$\delta _0:=\delta _0(\rho )>0$ such that
Our main tool here will be provided by the circle method. It begins with by writing the counting function ![]() $N(P)$ as an integral of a suitable exponential sum:
$N(P)$ as an integral of a suitable exponential sum:
 \[ N(P):=N_\omega(P):=\sum_{\substack{\underline{x}\in\mathbb{Z}^n,\\ F(\underline{x})= G(\underline{x}) = 0}} \omega(\underline{x}/P)=\int_0^1 \int_0^1 K(\alpha_1,\alpha_2)\, d\alpha_1\,d\alpha_2, \]
\[ N(P):=N_\omega(P):=\sum_{\substack{\underline{x}\in\mathbb{Z}^n,\\ F(\underline{x})= G(\underline{x}) = 0}} \omega(\underline{x}/P)=\int_0^1 \int_0^1 K(\alpha_1,\alpha_2)\, d\alpha_1\,d\alpha_2, \]
where
denotes the corresponding exponential sum.
In the traditional circle method, the unit square ![]() $I:=[0,1]^2$ is split into major arcs
$I:=[0,1]^2$ is split into major arcs ![]() $\mathfrak {M}$ which consist of the points in
$\mathfrak {M}$ which consist of the points in ![]() $I$ which are ‘close’ to a rational point
$I$ which are ‘close’ to a rational point ![]() ${\underline {a}}/q$, where
${\underline {a}}/q$, where ![]() ${\underline {a}}=(a_1,a_2)\in \mathbb {Z}^2$ of ‘small’ denominator
${\underline {a}}=(a_1,a_2)\in \mathbb {Z}^2$ of ‘small’ denominator ![]() $q$, and minor arcs
$q$, and minor arcs ![]() $\mathfrak {m}=I\backslash \mathfrak {M}$. The limitation of the process usually occurs while bounding the integral
$\mathfrak {m}=I\backslash \mathfrak {M}$. The limitation of the process usually occurs while bounding the integral
When ![]() $R=1$, Kloosterman's revolutionary idea [Reference KloostermanKlo27] was to apply Farey dissection to partition
$R=1$, Kloosterman's revolutionary idea [Reference KloostermanKlo27] was to apply Farey dissection to partition ![]() $[0,1]$ and use it to bound the minor arc contribution. This allows us to treat the minor arcs in a similar way to the major arcs. This idea essentially allows us, upon setting
$[0,1]$ and use it to bound the minor arc contribution. This allows us to treat the minor arcs in a similar way to the major arcs. This idea essentially allows us, upon setting ![]() $\alpha :=a/q+z$ and fixing the value of
$\alpha :=a/q+z$ and fixing the value of ![]() $z$, to consider averages of the corresponding one-dimensional analogues of the exponential sums averaged over the set
$z$, to consider averages of the corresponding one-dimensional analogues of the exponential sums averaged over the set ![]() $\{ {a}/{q}+z:\gcd (a,q)=1\}$. The extra average over
$\{ {a}/{q}+z:\gcd (a,q)=1\}$. The extra average over ![]() $a$ allows us to save an extra factor of size
$a$ allows us to save an extra factor of size ![]() $O(q^{1/2})$, when
$O(q^{1/2})$, when ![]() $q$ is sufficiently large and
$q$ is sufficiently large and ![]() $z$ relatively small.
$z$ relatively small.
When ![]() $R=2$, finding an analogue of Farey dissection which can be used to attain Kloosterman refinement over
$R=2$, finding an analogue of Farey dissection which can be used to attain Kloosterman refinement over ![]() $\mathbb {Q}$ has proved to be major problem. In [Reference VisheVis23], the second author has managed to find such an analogue in the function field setting, but how to use these ideas when working over
$\mathbb {Q}$ has proved to be major problem. In [Reference VisheVis23], the second author has managed to find such an analogue in the function field setting, but how to use these ideas when working over ![]() $\mathbb {Q}$ remains elusive. The path to Kloosterman refinement in this paper will not focus on innovations to Farey dissection, and will instead focus on improving van der Corput differencing.
$\mathbb {Q}$ remains elusive. The path to Kloosterman refinement in this paper will not focus on innovations to Farey dissection, and will instead focus on improving van der Corput differencing.
In the setting of that we will discuss (pair of two cubics), the Poisson summation formula cannot be applied directly. To be more precise, it is possible to apply Poisson summation, but the bound that it gives is trivial due to the corresponding exponential integral bound behaving badly when the degrees of our forms become too large.
We therefore must use a differencing argument (such as van der Corput) to bound ![]() $|K(\alpha )|$ by a sum with polynomials of lower degree. To do this, one essentially starts by using Cauchy's inequality to bound
$|K(\alpha )|$ by a sum with polynomials of lower degree. To do this, one essentially starts by using Cauchy's inequality to bound
 \begin{equation} \bigg|\int_{\mathfrak{m}} K(\underline{\alpha})\,d\underline{\alpha}\bigg|\ll \bigg(\int_{\mathfrak{m}}|K(\underline{\alpha})|^2\,d\underline{\alpha}\bigg)^{1/2}. \end{equation}
\begin{equation} \bigg|\int_{\mathfrak{m}} K(\underline{\alpha})\,d\underline{\alpha}\bigg|\ll \bigg(\int_{\mathfrak{m}}|K(\underline{\alpha})|^2\,d\underline{\alpha}\bigg)^{1/2}. \end{equation}
This leads us for a fixed integer ![]() $q$ and a fixed small
$q$ and a fixed small ![]() $\underline {z}\in I$ to consider the averages of the form
$\underline {z}\in I$ to consider the averages of the form
 \begin{equation} \int_{|\underline{z}|< q^{-1}Q^{-1/2}}\sum_{\substack{{\underline{a}}\bmod{q}\\ ({\underline{a}},q)=1} }|K({\underline{a}}/q+\underline{z})|^2\,d\underline{z}, \end{equation}
\begin{equation} \int_{|\underline{z}|< q^{-1}Q^{-1/2}}\sum_{\substack{{\underline{a}}\bmod{q}\\ ({\underline{a}},q)=1} }|K({\underline{a}}/q+\underline{z})|^2\,d\underline{z}, \end{equation}
where ![]() $Q$ is a suitable parameter to be fixed later. This parameter
$Q$ is a suitable parameter to be fixed later. This parameter ![]() $Q$ arises from using a two-dimensional version of Dirichlet approximation theorem. We further develop a two-dimensional version of averaged van der Corput differencing used by [Reference HanselmannHan12], [Reference Heath-BrownHea07], and [Reference Marmon and VisheMV19] to estimate the averages of
$Q$ arises from using a two-dimensional version of Dirichlet approximation theorem. We further develop a two-dimensional version of averaged van der Corput differencing used by [Reference HanselmannHan12], [Reference Heath-BrownHea07], and [Reference Marmon and VisheMV19] to estimate the averages of ![]() $|K({\underline {a}}/q+\underline {z})|^2$ over
$|K({\underline {a}}/q+\underline {z})|^2$ over ![]() $\underline {z}$. This leads us to considering quadratic exponential sums for a system of differenced quadratic forms
$\underline {z}$. This leads us to considering quadratic exponential sums for a system of differenced quadratic forms
The extra averaging over ![]() ${\underline {a}}$ in (1.7) leads us to a saving of the size
${\underline {a}}$ in (1.7) leads us to a saving of the size ![]() $O(q)$ in the estimation of
$O(q)$ in the estimation of ![]() $\sum _{{\underline {a}}}|K({\underline {a}}/q+\underline {z})|^2$, and in light of the squaring technique used in (1.6), it overall saves us a factor of size
$\sum _{{\underline {a}}}|K({\underline {a}}/q+\underline {z})|^2$, and in light of the squaring technique used in (1.6), it overall saves us a factor of size ![]() $O(q^{1/2})$ when
$O(q^{1/2})$ when ![]() $q$ is square-free.
$q$ is square-free.
The methods developed here are versatile and can be readily adapted to deal with general complete intersections. While dealing with averages of squares of corresponding exponential sums next to rationals of type ![]() $(a_1,\ldots,a_R)/q$, where
$(a_1,\ldots,a_R)/q$, where ![]() $q$ is square-free, we would be able to save a factor of size
$q$ is square-free, we would be able to save a factor of size ![]() $O(q^{R/4})$ over the bounds coming from averaged van der Corput differencing along with pointwise Poisson summation. To the best of the authors’ knowledge, this is the first known version of Kloosterman refinement which generalises this way over
$O(q^{R/4})$ over the bounds coming from averaged van der Corput differencing along with pointwise Poisson summation. To the best of the authors’ knowledge, this is the first known version of Kloosterman refinement which generalises this way over ![]() $\mathbb {Q}$. This method could be further combined with any further versions of Kloosterman refinement in the contexts where a degree-lowering squaring technique is essential. For instance, in the function field setting, this method could potentially be combined with the method in the aforementioned work by the second author [Reference VisheVis23] to be able to save a factor of size
$\mathbb {Q}$. This method could be further combined with any further versions of Kloosterman refinement in the contexts where a degree-lowering squaring technique is essential. For instance, in the function field setting, this method could potentially be combined with the method in the aforementioned work by the second author [Reference VisheVis23] to be able to save a factor of size ![]() $O(q^{(R-1)/4+1/2})$ instead.
$O(q^{(R-1)/4+1/2})$ instead.
2. Background on a pair of quadrics
Exponential sums for a pair of quadrics will feature prominently in this work. Let ![]() $Q_1(\underline {x}), Q_2(\underline {x})$ be a pair of quadratic forms in
$Q_1(\underline {x}), Q_2(\underline {x})$ be a pair of quadratic forms in ![]() $n$ variables with integer coefficients and consider the variety defined by
$n$ variables with integer coefficients and consider the variety defined by
![]() $\underline {x}\in \overline {\mathbb {Q}}^n$. Let
$\underline {x}\in \overline {\mathbb {Q}}^n$. Let ![]() $\mathrm {Sing}_K(V)$ to be the (projective) singular locus of
$\mathrm {Sing}_K(V)$ to be the (projective) singular locus of ![]() $V$ over field
$V$ over field ![]() $K$. When
$K$. When ![]() $Q_1$ and
$Q_1$ and ![]() $Q_2$ intersect properly, namely, if
$Q_2$ intersect properly, namely, if ![]() $V$ is of projective dimension
$V$ is of projective dimension ![]() $n-3$, then we can express the singular locus of
$n-3$, then we can express the singular locus of ![]() $V$ as follows:
$V$ as follows:
We say that the intersection variety of ![]() $Q_1(\underline {x})$ and
$Q_1(\underline {x})$ and ![]() $Q_2(\underline {x})$,
$Q_2(\underline {x})$, ![]() $V$, is non-singular if
$V$, is non-singular if ![]() $\dim \mathrm {Sing}_K (V)=-1$ and singular otherwise. It should be noted that (2.1) only truly encapsulates the set of singular points when
$\dim \mathrm {Sing}_K (V)=-1$ and singular otherwise. It should be noted that (2.1) only truly encapsulates the set of singular points when ![]() $Q_1,Q_2$ have a proper intersection over
$Q_1,Q_2$ have a proper intersection over ![]() $K$ (that is, the forms
$K$ (that is, the forms ![]() $Q_1(\underline {x})$,
$Q_1(\underline {x})$, ![]() $Q_2(\underline {x})$ share no common factor over K). However,
$Q_2(\underline {x})$ share no common factor over K). However, ![]() $\mathrm {Sing}_K(V)$ is still a well-defined set with a well-defined dimension, even when
$\mathrm {Sing}_K(V)$ is still a well-defined set with a well-defined dimension, even when ![]() $Q_1$ and
$Q_1$ and ![]() $Q_2$ intersect improperly, and so we will also use this definition in this case.
$Q_2$ intersect improperly, and so we will also use this definition in this case.
We will now begin by noting a slight generalisation of [Reference Marmon and VisheMV19, Lemma 4.1] in the context of two quadrics, which will be vital in various stages of this paper.
Lemma 2.1 Let ![]() $Q_1,Q_2$ be a pair of quadratic forms defining a complete intersection
$Q_1,Q_2$ be a pair of quadratic forms defining a complete intersection ![]() $X=V(Q_1,Q_2)$. Let
$X=V(Q_1,Q_2)$. Let ![]() $\Pi$ be a collection of primes such that
$\Pi$ be a collection of primes such that ![]() $\#\Pi =r\geq 0$ and define
$\#\Pi =r\geq 0$ and define ![]() $\Pi _a:=\{p\in \Pi \,|\, p>a\}$ for every
$\Pi _a:=\{p\in \Pi \,|\, p>a\}$ for every ![]() $a\in \mathbb {N}$. Then there exists a constant
$a\in \mathbb {N}$. Then there exists a constant ![]() $c'=c'(n)$ and a set of primitive linearly independent vectors
$c'=c'(n)$ and a set of primitive linearly independent vectors
satisfying the following property for any integer ![]() $0\leq \eta \leq n-1$, any subset
$0\leq \eta \leq n-1$, any subset ![]() $\emptyset \neq I\subset \{1,2\}$ and any
$\emptyset \neq I\subset \{1,2\}$ and any ![]() $\upsilon \in \{\infty \}\cup \Pi _{2c'}$: The subspace
$\upsilon \in \{\infty \}\cup \Pi _{2c'}$: The subspace ![]() $\Lambda _\eta \subset \mathbb {P}^{n-1}_{\mathbb {F}_\upsilon }$ spanned by the images of
$\Lambda _\eta \subset \mathbb {P}^{n-1}_{\mathbb {F}_\upsilon }$ spanned by the images of ![]() $\underline {e}_1,\ldots,\underline {e}_{n-\eta }$ is such that
$\underline {e}_1,\ldots,\underline {e}_{n-\eta }$ is such that
and
Here given ![]() $\emptyset \neq I\subseteq \{1,2\}$, let
$\emptyset \neq I\subseteq \{1,2\}$, let ![]() $X_I$ denote the complete intersection variety defined by the forms
$X_I$ denote the complete intersection variety defined by the forms ![]() $\{F_i:i\in I\}$. Moreover, the basis vectors
$\{F_i:i\in I\}$. Moreover, the basis vectors ![]() $\underline {e}_i$ can be chosen so that
$\underline {e}_i$ can be chosen so that
for every ![]() $i=1,\ldots, n$ and
$i=1,\ldots, n$ and
for some constant ![]() $L=O_n(r+1).$
$L=O_n(r+1).$
Proof. Note that the statement of this lemma is identical to that of [Reference Marmon and VisheMV19, Lemma 4.1] except that in the latter there is an additional assumption that the closed subscheme ![]() $X_I\subset \mathbb {P}^{n-1}_{\mathbb {Z}}$ defined by
$X_I\subset \mathbb {P}^{n-1}_{\mathbb {Z}}$ defined by ![]() $F_i=0$ for all
$F_i=0$ for all ![]() $i\in I$ satisfies
$i\in I$ satisfies
This is equivalent to the case when ![]() $X_1$ and
$X_1$ and ![]() $X_2$ intersect properly. Therefore, it is enough to consider different cases where we have an improper intersection. In each of these particular cases, somewhat softer argument works.
$X_2$ intersect properly. Therefore, it is enough to consider different cases where we have an improper intersection. In each of these particular cases, somewhat softer argument works.
In the trivial case when ![]() $Q_1=Q_2=0$, the singular locus would be of dimension
$Q_1=Q_2=0$, the singular locus would be of dimension ![]() $n-1$ and, therefore, any basis
$n-1$ and, therefore, any basis ![]() $\underline {e}_1,\ldots,\underline {e}_n$ will work.
$\underline {e}_1,\ldots,\underline {e}_n$ will work.
When ![]() $Q_2=\lambda Q_1$, where
$Q_2=\lambda Q_1$, where ![]() $\lambda \in K$ and
$\lambda \in K$ and ![]() $Q_1$ a non-zero quadratic form, our singular locus would consist of the hypersurface
$Q_1$ a non-zero quadratic form, our singular locus would consist of the hypersurface ![]() $Q_1=0$ of dimension
$Q_1=0$ of dimension ![]() $n-2$. Here, we may apply [Reference Marmon and VisheMV19, Lemma 4.1] only to the hypersurface
$n-2$. Here, we may apply [Reference Marmon and VisheMV19, Lemma 4.1] only to the hypersurface ![]() $X_1$ to find a basis
$X_1$ to find a basis ![]() $\underline {e}_1,\ldots,\underline {e}_n$ which is chosen such that (2.2) and (2.3) hold for
$\underline {e}_1,\ldots,\underline {e}_n$ which is chosen such that (2.2) and (2.3) hold for ![]() $I=\{1\}$. This choice will clearly work for all
$I=\{1\}$. This choice will clearly work for all ![]() $I\subset \{1,2\}$.
$I\subset \{1,2\}$.
In the remaining case when ![]() $Q_1=L_1L_2,Q_2=L_1L_3$, where
$Q_1=L_1L_2,Q_2=L_1L_3$, where ![]() $L_i=\underline {v}_i\cdot \underline {x}$ and
$L_i=\underline {v}_i\cdot \underline {x}$ and ![]() $L_2$ is not a scalar multiple of
$L_2$ is not a scalar multiple of ![]() $L_3$. In this case, it is easy to check that the singular locus of
$L_3$. In this case, it is easy to check that the singular locus of ![]() $X_1\cap X_2$ to is the hyperplane
$X_1\cap X_2$ to is the hyperplane ![]() $L_1=0$ (of dimension
$L_1=0$ (of dimension ![]() $n-2$). Here, we may apply [Reference Marmon and VisheMV19, Lemma 4.1] to the single variety defined by the cubic form
$n-2$). Here, we may apply [Reference Marmon and VisheMV19, Lemma 4.1] to the single variety defined by the cubic form ![]() $L_1L_2L_3=0$. The basis
$L_1L_2L_3=0$. The basis ![]() $\Lambda$ that we get from this process will work here as well.
$\Lambda$ that we get from this process will work here as well.
Since ![]() $Q_1$ and
$Q_1$ and ![]() $Q_2$ are quadratic forms, we may also define
$Q_2$ are quadratic forms, we may also define ![]() $M_1$,
$M_1$, ![]() $M_2$ to be their respective associated coefficient matrices defined as follows: if
$M_2$ to be their respective associated coefficient matrices defined as follows: if
 \[ Q_i(\underline{x}):=\sum_{j=1}^n\sum_{k=j}^n b_{j,k}^{(i)} x_j x_k, \]
\[ Q_i(\underline{x}):=\sum_{j=1}^n\sum_{k=j}^n b_{j,k}^{(i)} x_j x_k, \]
then
 \begin{equation} (M_i)_{j,k}:=
\begin{cases} b_{j,k}^{(i)} & \text{ if } j=k\\
\frac{1}{2}b_{j,k}^{(i)} & \text{ if } j< k \\
\frac{1}{2}b_{k,j}^{(i)} & \text{ if } j> k. \end{cases}
\end{equation}
\begin{equation} (M_i)_{j,k}:=
\begin{cases} b_{j,k}^{(i)} & \text{ if } j=k\\
\frac{1}{2}b_{j,k}^{(i)} & \text{ if } j< k \\
\frac{1}{2}b_{k,j}^{(i)} & \text{ if } j> k. \end{cases}
\end{equation}
We clearly have that ![]() $M_1,M_2\in M_n(\mathbb {Z}/2)$, the set of
$M_1,M_2\in M_n(\mathbb {Z}/2)$, the set of ![]() $n\times n$ matrices with coefficients of the form
$n\times n$ matrices with coefficients of the form ![]() $a/2$,
$a/2$, ![]() $a\in \mathbb {Z}$, since
$a\in \mathbb {Z}$, since ![]() $b_{k,j}\in \mathbb {Z}$. For the rest of this section (and, in fact, the rest of the paper by Remark 3.1), we will assume without loss of generality that
$b_{k,j}\in \mathbb {Z}$. For the rest of this section (and, in fact, the rest of the paper by Remark 3.1), we will assume without loss of generality that ![]() $M_1,M_2\in M_n(\mathbb {Z})$. This is because even if
$M_1,M_2\in M_n(\mathbb {Z})$. This is because even if ![]() $M_1,M_2\not \in M_n(\mathbb {Z})$, we certainly have
$M_1,M_2\not \in M_n(\mathbb {Z})$, we certainly have ![]() $2M_1, 2M_2\in M_n(\mathbb {Z})$, and so we may work with
$2M_1, 2M_2\in M_n(\mathbb {Z})$, and so we may work with ![]() $2Q_1$,
$2Q_1$, ![]() $2Q_2$ and relabel instead.
$2Q_2$ and relabel instead.
We are now ready to prove the following generalisation of [Reference Heath-Brown and PierceHP17, Proposition 2.1]. This will be particularly helpful for us when we are working with exponential sums of the form
 \[ \sideset{}{^*}\sum_{{\underline{a}}}^q \sum_{\underline{x}}^q e_{q}(a_1Q_1(\underline{x})+a_2Q_2(\underline{x})+\underline{c}\cdot\underline{x}), \]
\[ \sideset{}{^*}\sum_{{\underline{a}}}^q \sum_{\underline{x}}^q e_{q}(a_1Q_1(\underline{x})+a_2Q_2(\underline{x})+\underline{c}\cdot\underline{x}), \]
where ![]() $q$ is square-full, in § 5.3. Here, as is standard, the
$q$ is square-full, in § 5.3. Here, as is standard, the ![]() $*$ next to the sum denotes that the sum is over
$*$ next to the sum denotes that the sum is over ![]() $({\underline {a}},q)=1$, and
$({\underline {a}},q)=1$, and ![]() $e_q(x):=\exp (2\pi i x/q)$.
$e_q(x):=\exp (2\pi i x/q)$.
Proposition 2.2 Let ![]() $\nu$ either denote a finite prime
$\nu$ either denote a finite prime ![]() $\nu \gg _n 1$ or the infinite prime, let
$\nu \gg _n 1$ or the infinite prime, let ![]() $\mathbb {F}_\nu$ either denote the corresponding finite field or
$\mathbb {F}_\nu$ either denote the corresponding finite field or ![]() $\mathbb {Q}$, and let
$\mathbb {Q}$, and let
where ![]() $V$ is defined as above. Let
$V$ is defined as above. Let ![]() ${\underline {a}}\in \mathbb {F}_\nu ^2\backslash (0,0)$ and
${\underline {a}}\in \mathbb {F}_\nu ^2\backslash (0,0)$ and ![]() $a_1M_1+a_2M_2$ be the matrix associated to the quadratic form
$a_1M_1+a_2M_2$ be the matrix associated to the quadratic form ![]() $a_1Q_1+a_2Q_2$. Then
$a_1Q_1+a_2Q_2$. Then
for any such ![]() ${\underline {a}}$. Furthermore, there exists a set
${\underline {a}}$. Furthermore, there exists a set ![]() $\Gamma =\{\gamma _1,\ldots,\gamma _k\}\subset \overline {\mathbb {F}}_\nu$ such that
$\Gamma =\{\gamma _1,\ldots,\gamma _k\}\subset \overline {\mathbb {F}}_\nu$ such that ![]() $1\leq i\leq k\leq n$ and
$1\leq i\leq k\leq n$ and
unless ![]() $a_2=0$ or
$a_2=0$ or ![]() $a_1= \gamma a_2$ for some
$a_1= \gamma a_2$ for some ![]() $\gamma \in \Gamma$.
$\gamma \in \Gamma$.
Proof. Let ![]() $M_1$ and
$M_1$ and ![]() $M_2$ denote the integer matrices defining the forms
$M_2$ denote the integer matrices defining the forms ![]() $Q_1$ and
$Q_1$ and ![]() $Q_2$, respectively. We first note that for
$Q_2$, respectively. We first note that for ![]() $s_{\nu }(Q_1,Q_2)=-1$, we recover (2.9) from [Reference Heath-Brown and PierceHP17, Proposition 2.1]. In this case, may also use [Reference Heath-Brown and PierceHP17, Proposition 2.1] to simultaneously diagonalise
$s_{\nu }(Q_1,Q_2)=-1$, we recover (2.9) from [Reference Heath-Brown and PierceHP17, Proposition 2.1]. In this case, may also use [Reference Heath-Brown and PierceHP17, Proposition 2.1] to simultaneously diagonalise ![]() $M_1$,
$M_1$, ![]() $M_2$, letting us instead work with
$M_2$, letting us instead work with
 \[ Q_i'(\underline{x}):=\sum_{j=1}^n\lambda_{i,j}x_j^2, \quad M_i':= \mathrm{Diag}(\underline{\lambda_{i}}). \]
\[ Q_i'(\underline{x}):=\sum_{j=1}^n\lambda_{i,j}x_j^2, \quad M_i':= \mathrm{Diag}(\underline{\lambda_{i}}). \]
In particular, we have
for every ![]() ${\underline {a}}\in \mathbb {F}^2_{\nu }\backslash (0,0)$. Next, we note that
${\underline {a}}\in \mathbb {F}^2_{\nu }\backslash (0,0)$. Next, we note that ![]() $\mathrm {Rank}(a_1M_1'+a_2M_2')< n$ if and only if there is some
$\mathrm {Rank}(a_1M_1'+a_2M_2')< n$ if and only if there is some ![]() $j\in \{1,\ldots, n\}$ such that
$j\in \{1,\ldots, n\}$ such that ![]() $a_1\lambda _{1,j}+a_2\lambda _{2,j}=0$, which imposes the desired restriction on
$a_1\lambda _{1,j}+a_2\lambda _{2,j}=0$, which imposes the desired restriction on ![]() $(a_1,a_2)$ provided that
$(a_1,a_2)$ provided that ![]() $(\lambda _{1,j},\lambda _{2,j})\neq (0,0)$. However, if
$(\lambda _{1,j},\lambda _{2,j})\neq (0,0)$. However, if ![]() $(\lambda _{1,j},\lambda _{2,j})=(0,0)$, then it is easy to see from the definition of
$(\lambda _{1,j},\lambda _{2,j})=(0,0)$, then it is easy to see from the definition of ![]() $Q_i'(\underline {x})$ that
$Q_i'(\underline {x})$ that
for every ![]() $m\in \overline {\mathbb {F}}_{\nu }$ (provided
$m\in \overline {\mathbb {F}}_{\nu }$ (provided ![]() $\nu > 2$), where
$\nu > 2$), where ![]() $\underline {e}_j$ is the
$\underline {e}_j$ is the ![]() $j$th vector in the standard basis. This implies that
$j$th vector in the standard basis. This implies that ![]() $m\underline {e}_j\in \mathrm {Sing}(Q_1',Q_2')$, and so
$m\underline {e}_j\in \mathrm {Sing}(Q_1',Q_2')$, and so ![]() $s_{\nu }(Q_1',Q_2')\geq 0$, giving us a contradiction.
$s_{\nu }(Q_1',Q_2')\geq 0$, giving us a contradiction.
If ![]() $s_{\nu }(Q_1,Q_2)\neq -1$, we invoke Lemma 2.1. As long as
$s_{\nu }(Q_1,Q_2)\neq -1$, we invoke Lemma 2.1. As long as ![]() $\nu \gg _n 1$, we obtain a basis
$\nu \gg _n 1$, we obtain a basis ![]() $\underline {e}_1,\ldots,\underline {e}_n$ of
$\underline {e}_1,\ldots,\underline {e}_n$ of ![]() $\mathbb {F}_\nu ^n$ such that the system of quadrics
$\mathbb {F}_\nu ^n$ such that the system of quadrics ![]() $\tilde {Q}_1,\tilde {Q}_2$ corresponding to the restriction of
$\tilde {Q}_1,\tilde {Q}_2$ corresponding to the restriction of ![]() $Q_1$ and
$Q_1$ and ![]() $Q_2$ onto the subspace
$Q_2$ onto the subspace ![]() $\Lambda _{n-s_{\nu }-1}$ obeys (2.2)–(2.3). This clearly defines a system of non-singular quadratic forms defined over
$\Lambda _{n-s_{\nu }-1}$ obeys (2.2)–(2.3). This clearly defines a system of non-singular quadratic forms defined over ![]() $n-s_{\nu }-1$, whose complete intersection is non-singular over
$n-s_{\nu }-1$, whose complete intersection is non-singular over ![]() $\overline {\mathbb {F}}_\nu$ as well. Now let
$\overline {\mathbb {F}}_\nu$ as well. Now let ![]() $\tilde {M}_1$ and
$\tilde {M}_1$ and ![]() $\tilde {M}_2$ denote the integer matrices defining the forms
$\tilde {M}_2$ denote the integer matrices defining the forms ![]() $\tilde {Q}_1$, and
$\tilde {Q}_1$, and ![]() $\tilde {Q}_2$ respectively. The lemma now follows from noticing that
$\tilde {Q}_2$ respectively. The lemma now follows from noticing that
for any pair ![]() $(a_1,a_2)\in \mathbb {F}_\nu ^2\setminus (0,0)$ and, further, using our analysis of the non-singular case above.
$(a_1,a_2)\in \mathbb {F}_\nu ^2\setminus (0,0)$ and, further, using our analysis of the non-singular case above.
One of the key bounds for exponential sums in this work will be provided by Weyl differencing. Typically, these bounds use a ‘Birch-type’ singular locus ![]() $\sigma _K'$ as defined in (2.12) instead of the singular locus (2.1) used here. A relation between the two has been studied in [Reference Browning and Heath-BrownBH17]. A minor modification of [Reference MyersonMye18, Lemma 1.1] readily provides us with the following result.
$\sigma _K'$ as defined in (2.12) instead of the singular locus (2.1) used here. A relation between the two has been studied in [Reference Browning and Heath-BrownBH17]. A minor modification of [Reference MyersonMye18, Lemma 1.1] readily provides us with the following result.
Lemma 2.3 Let ![]() $F,G$ be non-constant forms of any degree,
$F,G$ be non-constant forms of any degree, ![]() $K$ be a field, and let
$K$ be a field, and let
Then, we have
for any ![]() $(a_1,a_2)\in K\backslash \{(0,0)\}$.
$(a_1,a_2)\in K\backslash \{(0,0)\}$.
Our main exponential sum bound for square-full moduli ![]() $q$ will be in terms of the size of the null set
$q$ will be in terms of the size of the null set
for some matrix ![]() $M\in M_n(\mathbb {Z})$. The following three lemmas will be related to this set.
$M\in M_n(\mathbb {Z})$. The following three lemmas will be related to this set.
Lemma 2.4 For every ![]() $u,v\in \mathbb {N}$, and every
$u,v\in \mathbb {N}$, and every ![]() $M\in M_n(\mathbb {Z})$, we have
$M\in M_n(\mathbb {Z})$, we have
with equality if ![]() $(u,v)=1$.
$(u,v)=1$.
Proof. It is easy to prove that ![]() $\#\mathrm {Null}_{q}(M)$ is a multiplicative function, so we will not prove that
$\#\mathrm {Null}_{q}(M)$ is a multiplicative function, so we will not prove that
when ![]() $(u,v)=1$. We will be brief when showing the inequality, as this is a standard Hensel lemma type of argument. If
$(u,v)=1$. We will be brief when showing the inequality, as this is a standard Hensel lemma type of argument. If ![]() $\underline {x}\in \mathrm {Null}_{uv}(M)$, then we must have
$\underline {x}\in \mathrm {Null}_{uv}(M)$, then we must have ![]() $M\underline {x}\equiv \underline {0} \bmod u$. Hence, if we write
$M\underline {x}\equiv \underline {0} \bmod u$. Hence, if we write ![]() $\underline {x}:=\underline {y}+u\underline {z}$, where
$\underline {x}:=\underline {y}+u\underline {z}$, where ![]() $\underline {y}\in (\mathbb {Z}/u\mathbb {Z})^n$,
$\underline {y}\in (\mathbb {Z}/u\mathbb {Z})^n$, ![]() $\underline {z}\in (\mathbb {Z}/v\mathbb {Z})^n$, then
$\underline {z}\in (\mathbb {Z}/v\mathbb {Z})^n$, then ![]() $\underline {y}$ must be in
$\underline {y}$ must be in ![]() $\mathrm {Null}_u(M)$.
$\mathrm {Null}_u(M)$.
Now, fix ![]() $\underline {y}$ and assume that there is some
$\underline {y}$ and assume that there is some ![]() $\underline {z}_1,\underline {z}_2$ (not necessarily distinct) such that
$\underline {z}_1,\underline {z}_2$ (not necessarily distinct) such that ![]() $\underline {y}+u\underline {z}_i\in \mathrm {Null}_{uv}(M)$. Then
$\underline {y}+u\underline {z}_i\in \mathrm {Null}_{uv}(M)$. Then
and so
Therefore, upon letting ![]() $\underline {z}_2:=\underline {z}_1+\underline {z}'$ we must have
$\underline {z}_2:=\underline {z}_1+\underline {z}'$ we must have
Hence, there can only be at most ![]() $\#\mathrm {Null}_v(M)$ possible values for
$\#\mathrm {Null}_v(M)$ possible values for ![]() $\underline {z}'$ and so there can only be at most
$\underline {z}'$ and so there can only be at most ![]() $\#\mathrm {Null}_v(M)$ values for
$\#\mathrm {Null}_v(M)$ values for ![]() $\underline {z}$ such that
$\underline {z}$ such that ![]() $\underline {y}+u\underline {z}\in \mathrm {Null}_{uv}(M)$ for any given
$\underline {y}+u\underline {z}\in \mathrm {Null}_{uv}(M)$ for any given ![]() $\underline {y}$. We also have that
$\underline {y}$. We also have that ![]() $\underline {y}$ must be in
$\underline {y}$ must be in ![]() $\mathrm {Null}_{u}(M)$. This gives us
$\mathrm {Null}_{u}(M)$. This gives us
as required.
In both §§ 5 and 6, we will need to bound ![]() $\#\mathrm {Null}_{p}(M)$ for matrices of the form
$\#\mathrm {Null}_{p}(M)$ for matrices of the form ![]() $M({\underline {a}}):=a_1M_1+a_2M_2$, where
$M({\underline {a}}):=a_1M_1+a_2M_2$, where ![]() $M_1$ and
$M_1$ and ![]() $M_2$ are symmetric matrices associated to some quadratic forms
$M_2$ are symmetric matrices associated to some quadratic forms ![]() $Q_1(\underline {x})$,
$Q_1(\underline {x})$, ![]() $Q_2(\underline {x})$. In Proposition 2.2, we noted that for most values of
$Q_2(\underline {x})$. In Proposition 2.2, we noted that for most values of ![]() ${\underline {a}}$,
${\underline {a}}$, ![]() $\mathrm {Rank}_{p}(M({\underline {a}}))\geq n-s_{p}-1$, but there were potentially a few lines of
$\mathrm {Rank}_{p}(M({\underline {a}}))\geq n-s_{p}-1$, but there were potentially a few lines of ![]() ${\underline {a}}$ where
${\underline {a}}$ where ![]() $\mathrm {Rank}_{p}(M({\underline {a}}))= n-s_{p}-2$. Naturally, a lower bound on the size of the rank of a matrix leads to an upper bound on the dimension of the nullspace of a matrix (due to the rank-nullity theorem), and so using
$\mathrm {Rank}_{p}(M({\underline {a}}))= n-s_{p}-2$. Naturally, a lower bound on the size of the rank of a matrix leads to an upper bound on the dimension of the nullspace of a matrix (due to the rank-nullity theorem), and so using ![]() $\mathrm {Rank}_{p}(M({\underline {a}}))\geq n-s_{p}-2$ in order to bound
$\mathrm {Rank}_{p}(M({\underline {a}}))\geq n-s_{p}-2$ in order to bound ![]() $\#\mathrm {Null}_{p}(M({\underline {a}}))$ for every
$\#\mathrm {Null}_{p}(M({\underline {a}}))$ for every ![]() ${\underline {a}}$ would be wasteful. This will lead us to considering averages of
${\underline {a}}$ would be wasteful. This will lead us to considering averages of ![]() $\#\mathrm {Null}_{p}(M({\underline {a}}))$, where
$\#\mathrm {Null}_{p}(M({\underline {a}}))$, where ![]() ${\underline {a}}$ is allowed to vary (this is the topic of the next lemma).
${\underline {a}}$ is allowed to vary (this is the topic of the next lemma).
Lemma 2.5 Let ![]() $Q_1,Q_2$ be quadratic forms in
$Q_1,Q_2$ be quadratic forms in ![]() $n$ variables,
$n$ variables, ![]() $q\in \mathbb {N}$, and
$q\in \mathbb {N}$, and ![]() $d$ be a square-free divisor of
$d$ be a square-free divisor of ![]() $q$. Furthermore, let
$q$. Furthermore, let ![]() $M_1, M_2$ be integer matrices defining
$M_1, M_2$ be integer matrices defining ![]() $Q_1$ and
$Q_1$ and ![]() $Q_2$, respectively, and let
$Q_2$, respectively, and let ![]() $s_p=s_p(Q_1,Q_2)$ be as defined in (2.8) for
$s_p=s_p(Q_1,Q_2)$ be as defined in (2.8) for ![]() $K=\mathbb {F}_p$,
$K=\mathbb {F}_p$, ![]() $p$ a prime. If
$p$ a prime. If ![]() $d=\prod _{i=1}^r p_i$ for some primes
$d=\prod _{i=1}^r p_i$ for some primes ![]() $p_i$, then
$p_i$, then
 \[ \sideset{}{^*}\sum_{{\underline{a}} \bmod{q}} \#\mathrm{Null}_d(a_1M_1+a_2M_2)\ll_n q^2 \prod_{i=1}^r p_i^{s_{p_i}+1}. \]
\[ \sideset{}{^*}\sum_{{\underline{a}} \bmod{q}} \#\mathrm{Null}_d(a_1M_1+a_2M_2)\ll_n q^2 \prod_{i=1}^r p_i^{s_{p_i}+1}. \]
Proof. For the duration of this proof only, we will use the notation
We first note that upon setting ![]() ${\underline {a}}=\underline {b}+d\underline {c}$,
${\underline {a}}=\underline {b}+d\underline {c}$,
 \begin{align} \mathrm{D}(d,q)&\leq \sum_{\substack{{\underline{a}} \bmod{q}\\ (a_1,a_2,d)=1}} \#\mathrm{Null}_d(a_1M_1+a_2M_2)\nonumber\\ &= \sum_{\substack{\underline{b} \bmod{d}\\ (b_1,b_2,d)=1}} \#\mathrm{Null}_d(b_1M_1+b_2M_2) \sum_{\underline{c} \bmod{q/d}} 1\nonumber\\ &= \bigg(\frac{q}{d}\bigg)^2\sideset{}{^*}\sum_{\underline{b} \bmod{d}} \#\mathrm{Null}_d(b_1M_1+b_2M_2)\nonumber\\ &= \bigg(\frac{q}{d}\bigg)^2 \mathrm{D}(d,d). \end{align}
\begin{align} \mathrm{D}(d,q)&\leq \sum_{\substack{{\underline{a}} \bmod{q}\\ (a_1,a_2,d)=1}} \#\mathrm{Null}_d(a_1M_1+a_2M_2)\nonumber\\ &= \sum_{\substack{\underline{b} \bmod{d}\\ (b_1,b_2,d)=1}} \#\mathrm{Null}_d(b_1M_1+b_2M_2) \sum_{\underline{c} \bmod{q/d}} 1\nonumber\\ &= \bigg(\frac{q}{d}\bigg)^2\sideset{}{^*}\sum_{\underline{b} \bmod{d}} \#\mathrm{Null}_d(b_1M_1+b_2M_2)\nonumber\\ &= \bigg(\frac{q}{d}\bigg)^2 \mathrm{D}(d,d). \end{align}For convenience, define
Using the Chinese remainder theorem, it is easy to see that ![]() $T(d)$ is a multiplicative function. In particular, we have
$T(d)$ is a multiplicative function. In particular, we have
 \begin{equation} T(d)=\prod_{\substack{i=1\\ p_i\mid d \textrm{ where } p_i \textrm{ prime }}}^r T(p_i). \end{equation}
\begin{equation} T(d)=\prod_{\substack{i=1\\ p_i\mid d \textrm{ where } p_i \textrm{ prime }}}^r T(p_i). \end{equation}It is therefore sufficient to consider
where ![]() $p$ is a prime. When
$p$ is a prime. When ![]() $p\ll _n 1$, the right-hand side is trivially
$p\ll _n 1$, the right-hand side is trivially ![]() $O(p^{2})$. It is therefore enough to consider the case
$O(p^{2})$. It is therefore enough to consider the case ![]() $p\gg _n 1$, where the implied constant is chosen as in the statement in Proposition 2.2. Proposition 2.2 now implies that except for
$p\gg _n 1$, where the implied constant is chosen as in the statement in Proposition 2.2. Proposition 2.2 now implies that except for ![]() $O_n(p)$ different exceptional pairs
$O_n(p)$ different exceptional pairs ![]() $(a_1,a_2)$,
$(a_1,a_2)$, ![]() $\mathrm {Rank}(a_1M_1+a_2M_2)\geq n-s_p-1$. Moreover, for the exceptional pairs we still have
$\mathrm {Rank}(a_1M_1+a_2M_2)\geq n-s_p-1$. Moreover, for the exceptional pairs we still have ![]() $\mathrm {Rank}(a_1M_1+a_2M_2)= n-s_p-2$. Finally, we note that if
$\mathrm {Rank}(a_1M_1+a_2M_2)= n-s_p-2$. Finally, we note that if ![]() $M$ is an integer matrix rank
$M$ is an integer matrix rank ![]() $k$ over
$k$ over ![]() $\mathbb {F}_p$, it is easy to see that
$\mathbb {F}_p$, it is easy to see that
Applying these results to (2.19) gives us
 \begin{align*} T(p)&\ll \sideset{}{^*}\sum_{\substack{{\underline{a}} \bmod{p}\\ \mathrm{Rank}(a_1M_1+a_2M_2)\geq n-s_p-1}} p^{s_p+1} + \sideset{}{^*}\sum_{\substack{{\underline{a}} \bmod{p}\\ \mathrm{Rank}(a_1M_1+a_2M_2)= n-s_p-2}} p^{s_p+2}\\ &\ll p^2\times p^{s_p+1}+p\times p^{s_p+2}\\ &\ll p^{2+s_p+1}, \end{align*}
\begin{align*} T(p)&\ll \sideset{}{^*}\sum_{\substack{{\underline{a}} \bmod{p}\\ \mathrm{Rank}(a_1M_1+a_2M_2)\geq n-s_p-1}} p^{s_p+1} + \sideset{}{^*}\sum_{\substack{{\underline{a}} \bmod{p}\\ \mathrm{Rank}(a_1M_1+a_2M_2)= n-s_p-2}} p^{s_p+2}\\ &\ll p^2\times p^{s_p+1}+p\times p^{s_p+2}\\ &\ll p^{2+s_p+1}, \end{align*}
and so
 \[ T(d)\ll\prod_{i=1}^r p_i^{2+s_{p_i}+1} = d^2 \prod_{i=1}^r p_i^{s_{p_i}+1} \]
\[ T(d)\ll\prod_{i=1}^r p_i^{2+s_{p_i}+1} = d^2 \prod_{i=1}^r p_i^{s_{p_i}+1} \]
by (2.18). Hence, by (2.16)–(2.17), we have
 \[ D(d,q)\leq \bigg{(}\frac{q}{d}\bigg{)}^2 T(d)\ll q^2 \prod_{i=1}^r p_i^{s_{p_i}+1}, \]
\[ D(d,q)\leq \bigg{(}\frac{q}{d}\bigg{)}^2 T(d)\ll q^2 \prod_{i=1}^r p_i^{s_{p_i}+1}, \]
as required.
During the process of bounding quadratic exponential sums, we will need to bound the size of the set
The next lemma will help us to do this by letting us relate ![]() $N_{\underline {b},q}(M)$ to
$N_{\underline {b},q}(M)$ to ![]() $\mathrm {Null}_q(M)$.
$\mathrm {Null}_q(M)$.
Lemma 2.6 Let ![]() $q\in \mathbb {N}$ be even,
$q\in \mathbb {N}$ be even, ![]() $M\in M_n(\mathbb {Z}/q\mathbb {Z})$ and let
$M\in M_n(\mathbb {Z}/q\mathbb {Z})$ and let ![]() $N_{\underline {b},q}(M)$ be defined as in (2.20). Then for every
$N_{\underline {b},q}(M)$ be defined as in (2.20). Then for every ![]() $\underline {b}\in \{0,1\}^n$, either
$\underline {b}\in \{0,1\}^n$, either ![]() $N_{\underline {b},q}(M)=\emptyset$ or there exists some
$N_{\underline {b},q}(M)=\emptyset$ or there exists some ![]() $\underline {y}_{\underline {b}}\in (\mathbb {Z}/q\mathbb {Z})^n$ such that
$\underline {y}_{\underline {b}}\in (\mathbb {Z}/q\mathbb {Z})^n$ such that
We will not prove this here as the argument used in the classical proof of Hensel's lemma can be trivially adapted to prove this lemma.
3. Initial setup
In this section we will start with some initial considerations which will help us to properly set up the circle method and state our main results which will be used to prove Theorem 1.2. As stated previously, the Hardy Littlewood circle method transforms the task of answering Theorem 1.2 to proving an asymptotic formula:
Here ![]() $K(\underline {\alpha })$ is the exponential sum as defined in (1.5) and
$K(\underline {\alpha })$ is the exponential sum as defined in (1.5) and ![]() $C_X$ denotes a product of local densities.
$C_X$ denotes a product of local densities.
Remark 3.1 In order to make some of the arguments in § 5 easier to state, we will assume that ![]() $2\,|\, (\mathrm {Cont}(F), \mathrm {Cont}(G))$, where
$2\,|\, (\mathrm {Cont}(F), \mathrm {Cont}(G))$, where ![]() $\mathrm {Cont}(F)$ is the greatest common denominator (gcd) of all of its coefficients. We can assume this without loss of generality since
$\mathrm {Cont}(F)$ is the greatest common denominator (gcd) of all of its coefficients. We can assume this without loss of generality since ![]() $F(\underline {x})=G(\underline {x})=0$ if and only if
$F(\underline {x})=G(\underline {x})=0$ if and only if ![]() $2F(\underline {x})=2G(\underline {x})=0$, and so we can always opt to work with the latter forms instead if necessary.
$2F(\underline {x})=2G(\underline {x})=0$, and so we can always opt to work with the latter forms instead if necessary.
We will start by splitting the box ![]() $[0,1]^2$ into a set of major arcs and minor arcs as follows. For any pair
$[0,1]^2$ into a set of major arcs and minor arcs as follows. For any pair ![]() $(\alpha _1,\alpha _2)$, we can use a two-dimensional version of Dirichlet's approximation theorem to find a simultaneous approximation
$(\alpha _1,\alpha _2)$, we can use a two-dimensional version of Dirichlet's approximation theorem to find a simultaneous approximation ![]() $(a_1/q,a_2/q)$. In particular, upon taking
$(a_1/q,a_2/q)$. In particular, upon taking ![]() $Q=\lfloor P^{3/2} \rfloor$, there exists
$Q=\lfloor P^{3/2} \rfloor$, there exists ![]() $\underline {a}=(a_1,a_2)\in \mathbb {Z}^2$ and
$\underline {a}=(a_1,a_2)\in \mathbb {Z}^2$ and ![]() $q\in \mathbb {N}$ such that
$q\in \mathbb {N}$ such that ![]() $(a_1,a_2,q)=1$,
$(a_1,a_2,q)=1$, ![]() $q\leq Q$, and
$q\leq Q$, and
We can therefore write
for some ![]() $|\underline {z}|:=\max \{|z_1|,|z_2|\}\leq 1/qQ^{1/2}$. The choice
$|\underline {z}|:=\max \{|z_1|,|z_2|\}\leq 1/qQ^{1/2}$. The choice ![]() $Q=\lfloor P^{3/2} \rfloor$ arises from our final optimisation of various bounds. We explain this in detail in § 9.3.1.
$Q=\lfloor P^{3/2} \rfloor$ arises from our final optimisation of various bounds. We explain this in detail in § 9.3.1.
Now let ![]() $0<\Delta <1$ be some small parameter also to be chosen later, and define
$0<\Delta <1$ be some small parameter also to be chosen later, and define
We then define the set of major arcs to be
 \begin{equation} \mathfrak{M}=\mathfrak{M}(\Delta):=\bigcup_{q\leq P^\Delta}\bigcup_{\substack{\underline{a}\bmod{q}\\ (\underline{a},q)=1}} \mathfrak{M}_{q,\underline{a}}(\Delta). \end{equation}
\begin{equation} \mathfrak{M}=\mathfrak{M}(\Delta):=\bigcup_{q\leq P^\Delta}\bigcup_{\substack{\underline{a}\bmod{q}\\ (\underline{a},q)=1}} \mathfrak{M}_{q,\underline{a}}(\Delta). \end{equation}
This union of sets is disjoint if ![]() $P^{-2\Delta }\geq 2 P^{-3+\Delta }$, namely when
$P^{-2\Delta }\geq 2 P^{-3+\Delta }$, namely when ![]() $\Delta <1$ and when
$\Delta <1$ and when ![]() $P$ is sufficiently large. Moreover, it is easy to check that
$P$ is sufficiently large. Moreover, it is easy to check that ![]() $P^{-3+\Delta }<1/qQ^{1/2}$ for any
$P^{-3+\Delta }<1/qQ^{1/2}$ for any ![]() $q\leq Q$, provided that
$q\leq Q$, provided that ![]() $Q< P^{3-\Delta }$. This is certainly true for our final choice
$Q< P^{3-\Delta }$. This is certainly true for our final choice ![]() $Q=P^{3/2}$ since we assumed
$Q=P^{3/2}$ since we assumed ![]() $\Delta <1$, and so we have that each set
$\Delta <1$, and so we have that each set ![]() $\mathfrak {M}_{q,\underline {a}}$ is contained in the corresponding range from (3.2). Therefore, the major arcs give the following contribution to the integral in (3.1):
$\mathfrak {M}_{q,\underline {a}}$ is contained in the corresponding range from (3.2). Therefore, the major arcs give the following contribution to the integral in (3.1):
 \begin{equation} S_{\mathfrak{M}}:=\sum_{1\leq q\leq P^{\Delta}} \,\,\sideset{}{^*}\sum_{\underline{a}\bmod{q}}\int_{|\underline{z}|\leq P^{-3+\Delta}} K({\underline{a}}/q+\underline{z}) \,d\underline{z}. \end{equation}
\begin{equation} S_{\mathfrak{M}}:=\sum_{1\leq q\leq P^{\Delta}} \,\,\sideset{}{^*}\sum_{\underline{a}\bmod{q}}\int_{|\underline{z}|\leq P^{-3+\Delta}} K({\underline{a}}/q+\underline{z}) \,d\underline{z}. \end{equation}
We then define the minor arcs to be ![]() $\mathfrak {m}=[0,1]^2\backslash \mathfrak {M}$. By the construction of
$\mathfrak {m}=[0,1]^2\backslash \mathfrak {M}$. By the construction of ![]() $\mathfrak {M}$, the individual minor arcs must therefore either have
$\mathfrak {M}$, the individual minor arcs must therefore either have
Hence, we can bound the minor arcs contribution, upon further bringing the average over ![]() ${\underline {a}}$ inside the integral in (3.1), by
${\underline {a}}$ inside the integral in (3.1), by
 \begin{equation} S_{\mathfrak{m}}=\sum_{1\leq q\leq P^{\Delta}}\int_{P^{-3+\Delta} \leq |\underline{z}|\leq 1/qQ^{1/2}} K(q,\underline{z}) \,d\underline{z} + \sum_{P^{\Delta}\leq q\leq Q }\int_{|\underline{z}|\leq 1/qQ^{1/2}} K(q,\underline{z}) \,d\underline{z}. \end{equation}
\begin{equation} S_{\mathfrak{m}}=\sum_{1\leq q\leq P^{\Delta}}\int_{P^{-3+\Delta} \leq |\underline{z}|\leq 1/qQ^{1/2}} K(q,\underline{z}) \,d\underline{z} + \sum_{P^{\Delta}\leq q\leq Q }\int_{|\underline{z}|\leq 1/qQ^{1/2}} K(q,\underline{z}) \,d\underline{z}. \end{equation}Here
Our techniques for dealing with the major arcs contribution are standard. Let
 \begin{equation} \begin{aligned} \mathfrak{S}(R) & :=\sum_{q=1}^R q^{-n}\sideset{}{^*}\sum_{\underline{a}\bmod{q}} \sum_{\underline{x} \bmod{q}} e_q(a_1F(\underline{x})+a_2G(\underline{x})),\\ \mathfrak{J}(R) & :=\int_{|\underline{z}|< R}\int_{\mathbb{R}^n}\omega(\underline{x})e(z_1F(\underline{x})+z_2G(\underline{x}))\, d\underline{x}\,d\underline{z}, \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \mathfrak{S}(R) & :=\sum_{q=1}^R q^{-n}\sideset{}{^*}\sum_{\underline{a}\bmod{q}} \sum_{\underline{x} \bmod{q}} e_q(a_1F(\underline{x})+a_2G(\underline{x})),\\ \mathfrak{J}(R) & :=\int_{|\underline{z}|< R}\int_{\mathbb{R}^n}\omega(\underline{x})e(z_1F(\underline{x})+z_2G(\underline{x}))\, d\underline{x}\,d\underline{z}, \end{aligned} \end{equation}and let
denote the singular series and the corresponding singular integral, provided the limits exist. Our main major arcs estimate is the following lemma.
Lemma 3.2 Assume that ![]() $n-\sigma (F,G)\geq 34$, where
$n-\sigma (F,G)\geq 34$, where ![]() $\sigma (F,G):=\sigma (X_{F,G})$ as defined in (1.1), and assume that
$\sigma (F,G):=\sigma (X_{F,G})$ as defined in (1.1), and assume that ![]() $\mathfrak {S}$ is absolutely convergent, satisfying
$\mathfrak {S}$ is absolutely convergent, satisfying
for some ![]() $\phi >0$. Then provided that we have
$\phi >0$. Then provided that we have ![]() $\Delta \in (0,1/7)$,
$\Delta \in (0,1/7)$,
The proof of this lemma, along with the proof of convergence of the singular series will be established in § 10.
The majority of our effort will be spent in bounding the minor arcs contribution. In order to state the proposition we aim to prove for the minor arcs, we need to further specify our choice of weight function and the point which it will centred on. Let ![]() $\underline {x}_0$ be a fixed point satisfying
$\underline {x}_0$ be a fixed point satisfying ![]() $|\underline {x}_0|<1$ and
$|\underline {x}_0|<1$ and
Without loss of generality, we may assume that
for some ![]() $0< C'<1$, possibly depending on
$0< C'<1$, possibly depending on ![]() $\underline {x}_0$. Here and throughout, by
$\underline {x}_0$. Here and throughout, by ![]() $\|\underline {x}\|$ we denote the
$\|\underline {x}\|$ we denote the ![]() $\ell ^2$ norm of the vector
$\ell ^2$ norm of the vector ![]() $\underline {x}$. Note that this norm is equivalent to the sup-norm on
$\underline {x}$. Note that this norm is equivalent to the sup-norm on ![]() $\mathbb {R}^n$. We will also slightly expand our definition of the test function
$\mathbb {R}^n$. We will also slightly expand our definition of the test function ![]() $\omega$ to assume it to be supported in a box
$\omega$ to assume it to be supported in a box ![]() $\underline {x}_0+(-\rho,\rho )^n$, for a small parameter
$\underline {x}_0+(-\rho,\rho )^n$, for a small parameter ![]() $\rho >0$ to be chosen in due course. Moreover, we ask that
$\rho >0$ to be chosen in due course. Moreover, we ask that ![]() $\omega \in \mathcal {W}_n$, where
$\omega \in \mathcal {W}_n$, where ![]() $\mathcal {W}_n$ is defined to be the set of infinitely differentiable functions
$\mathcal {W}_n$ is defined to be the set of infinitely differentiable functions ![]() $\hat {\omega }: \mathbb {R}^n\rightarrow \mathbb {R}_{\geq 0}$ with compact support contained within
$\hat {\omega }: \mathbb {R}^n\rightarrow \mathbb {R}_{\geq 0}$ with compact support contained within ![]() $[-S_n,S_n]^n$ for some fixed
$[-S_n,S_n]^n$ for some fixed ![]() $S_n$, and with the following bound to be true on its derivatives:
$S_n$, and with the following bound to be true on its derivatives:
for every ![]() $j\geq 0$. A satisfactory bound for the minor arcs will be produced by the following proposition, which we aim to prove.
$j\geq 0$. A satisfactory bound for the minor arcs will be produced by the following proposition, which we aim to prove.
Proposition 3.3 Let ![]() $F,G$ be a system of two cubic forms with a smooth intersection satisfying
$F,G$ be a system of two cubic forms with a smooth intersection satisfying ![]() $n\geq 39$, and let
$n\geq 39$, and let ![]() $\omega \in \mathbb {C}^\infty _c(\underline {x}_0+(-\rho,\rho )^n)$ satisfy (3.13), where
$\omega \in \mathbb {C}^\infty _c(\underline {x}_0+(-\rho,\rho )^n)$ satisfy (3.13), where ![]() $\underline {x}_0$ satisfies (3.12). Then there exists some
$\underline {x}_0$ satisfies (3.12). Then there exists some ![]() $\delta =\delta (\Delta )>0$ and some
$\delta =\delta (\Delta )>0$ and some ![]() $\rho _0>0$, such that for any
$\rho _0>0$, such that for any ![]() $0<\Delta < 1/7$ and for any
$0<\Delta < 1/7$ and for any ![]() $0<\rho <\rho _0$, we have
$0<\rho <\rho _0$, we have
Here, given a polynomial ![]() $F$, let
$F$, let ![]() $\|F\|$ denote the maximum of all its coefficients.
$\|F\|$ denote the maximum of all its coefficients.
A major part of the rest of this work will be dedicated to proving Proposition 3.3, which will ultimately be achieved in § 9. Before we move on, it will be desirable to obtain a consequence of our choice of ![]() $\omega$ and
$\omega$ and ![]() $\underline {x}_0$, akin to the conditions [Reference Marmon and VisheMV19, (2.15) and (2.16)]. This will be our aim in Lemma 3.4 below, which will be useful in setting up a two-dimensional van der Corput differencing argument in § 4 and, in particular, in the proof of Lemma 4.3. In order to state Lemma 3.4, we will choose an orthonormal basis for the two-dimensional vector space spanned by
$\underline {x}_0$, akin to the conditions [Reference Marmon and VisheMV19, (2.15) and (2.16)]. This will be our aim in Lemma 3.4 below, which will be useful in setting up a two-dimensional van der Corput differencing argument in § 4 and, in particular, in the proof of Lemma 4.3. In order to state Lemma 3.4, we will choose an orthonormal basis for the two-dimensional vector space spanned by ![]() $\{\nabla F(\underline {x}_0),\nabla G(\underline {x}_0)\}$:
$\{\nabla F(\underline {x}_0),\nabla G(\underline {x}_0)\}$:
where ![]() $\gamma =\nabla G(\underline {x}_0)\cdot \underline {e}_1'$, and
$\gamma =\nabla G(\underline {x}_0)\cdot \underline {e}_1'$, and ![]() $\gamma _1=\|\nabla G(\underline {x}_0)-\gamma \underline {e}_1'\|$ is a non-zero constant by (3.12).
$\gamma _1=\|\nabla G(\underline {x}_0)-\gamma \underline {e}_1'\|$ is a non-zero constant by (3.12).
Lemma 3.4 Let ![]() $F$ and
$F$ and ![]() $G$ be cubic forms and
$G$ be cubic forms and ![]() $\omega$ be a compactly supported function supported in
$\omega$ be a compactly supported function supported in ![]() $\underline {x}_0+(-\rho,\rho )^n$ satisfying (3.13), where
$\underline {x}_0+(-\rho,\rho )^n$ satisfying (3.13), where ![]() $\underline {x}_0$ satisfies (3.12). Then there exist constants
$\underline {x}_0$ satisfies (3.12). Then there exist constants ![]() $M_1,M_2>0$ and there exists some
$M_1,M_2>0$ and there exists some ![]() $0<\rho _0\leq 1$ such that if
$0<\rho _0\leq 1$ such that if ![]() $\rho \leq \rho _0$, then
$\rho \leq \rho _0$, then
Furthermore, ![]() $M_1$ and
$M_1$ and ![]() $M_2$ depend only on
$M_2$ depend only on ![]() $F$,
$F$, ![]() $G$ and our choice of
$G$ and our choice of ![]() $\underline {x}_0$ (in particular,
$\underline {x}_0$ (in particular, ![]() $M_1$ and
$M_1$ and ![]() $M_2$ do not depend on
$M_2$ do not depend on ![]() $\rho$).
$\rho$).
Proof. A key in the proof here will be the following bound, which is an easy consequence of the mean value theorem: given any ![]() $\underline {x}\in \mathrm {Supp}(P\omega )$, we have
$\underline {x}\in \mathrm {Supp}(P\omega )$, we have
Let us first prove that the conditions for ![]() $\nabla F(\underline {x})$ in (3.15)–(3.16) are met. The key here is conditions (3.11) and (3.12). Clearly, using (3.17) we have
$\nabla F(\underline {x})$ in (3.15)–(3.16) are met. The key here is conditions (3.11) and (3.12). Clearly, using (3.17) we have
 \begin{align*} \nabla F(\underline{x})\cdot \underline{e}_1'&=(\nabla F(\underline{x})-\nabla F(P\underline{x}_0))\cdot \underline{e}_1'+\nabla F(P\underline{x}_0)\cdot \underline{e}_1'\\ &=(\nabla F(\underline{x})-\nabla F(P\underline{x}_0))\cdot \underline{e}_1'+P^2\nabla F(\underline{x}_0)\cdot \nabla F(\underline{x}_0)/\|\nabla F(\underline{x}_0)\|\\ &=(\nabla F(\underline{x})-\nabla F(P\underline{x}_0))\cdot \underline{e}_1'+P^2\|\nabla F(\underline{x}_0)\|\\ &\geq (1-O(\rho))P^2\|\nabla F(\underline{x}_0)\|\\ &\geq M_{F,1} P^2 \end{align*}
\begin{align*} \nabla F(\underline{x})\cdot \underline{e}_1'&=(\nabla F(\underline{x})-\nabla F(P\underline{x}_0))\cdot \underline{e}_1'+\nabla F(P\underline{x}_0)\cdot \underline{e}_1'\\ &=(\nabla F(\underline{x})-\nabla F(P\underline{x}_0))\cdot \underline{e}_1'+P^2\nabla F(\underline{x}_0)\cdot \nabla F(\underline{x}_0)/\|\nabla F(\underline{x}_0)\|\\ &=(\nabla F(\underline{x})-\nabla F(P\underline{x}_0))\cdot \underline{e}_1'+P^2\|\nabla F(\underline{x}_0)\|\\ &\geq (1-O(\rho))P^2\|\nabla F(\underline{x}_0)\|\\ &\geq M_{F,1} P^2 \end{align*}
for some ![]() $M_{F,1}>0$ which is independent of
$M_{F,1}>0$ which is independent of ![]() $\rho$, provided that
$\rho$, provided that ![]() $\rho$ is chosen to be small enough. Similarly, we may also assure that
$\rho$ is chosen to be small enough. Similarly, we may also assure that
In both of these equations, the implied constants only depend on ![]() $\| F\|$,
$\| F\|$, ![]() $\| G\|$ and
$\| G\|$ and ![]() $n$. This will be a feature of all implied constants appearing in this proof. On the other hand, since
$n$. This will be a feature of all implied constants appearing in this proof. On the other hand, since ![]() $\nabla F(\underline {x}_0)=\|\nabla F(\underline {x}_0)\|\,\underline {e}_1'$ is orthogonal to
$\nabla F(\underline {x}_0)=\|\nabla F(\underline {x}_0)\|\,\underline {e}_1'$ is orthogonal to ![]() $\underline {e}_2'$, we have
$\underline {e}_2'$, we have
by (3.17). In other words, there is some ![]() $M_{F,2}>0$ independent of
$M_{F,2}>0$ independent of ![]() $\rho$ such that
$\rho$ such that
To deal with the inequalities concerning ![]() $G$, we use (3.12), which hands us a constant
$G$, we use (3.12), which hands us a constant ![]() $0< C'<1$ satisfying
$0< C'<1$ satisfying
Therefore, for any ![]() $\underline {x}\in \mathrm {Supp}(P\omega )$, by (3.17) and (3.20), we have that
$\underline {x}\in \mathrm {Supp}(P\omega )$, by (3.17) and (3.20), we have that
 \begin{align*} |\nabla F(\underline{x}_0)\cdot \nabla G(\underline{x})|&\leq |\nabla F(\underline{x}_0)\cdot \nabla G(P\underline{x}_0)|+ |\nabla F(\underline{x}_0)\cdot (\nabla G(\underline{x})-\nabla G(P\underline{x}_0))|\\ &\leq C' P^2\|\nabla G(\underline{x}_0)\|\|\nabla F(\underline{x}_0)\|+O_{\|G\|}(\rho) P^2\|\nabla F(\underline{x}_0)\|. \end{align*}
\begin{align*} |\nabla F(\underline{x}_0)\cdot \nabla G(\underline{x})|&\leq |\nabla F(\underline{x}_0)\cdot \nabla G(P\underline{x}_0)|+ |\nabla F(\underline{x}_0)\cdot (\nabla G(\underline{x})-\nabla G(P\underline{x}_0))|\\ &\leq C' P^2\|\nabla G(\underline{x}_0)\|\|\nabla F(\underline{x}_0)\|+O_{\|G\|}(\rho) P^2\|\nabla F(\underline{x}_0)\|. \end{align*}
Hence (since ![]() $\|\nabla G(\underline {x}_0)\|>0$ is a constant), provided that the support
$\|\nabla G(\underline {x}_0)\|>0$ is a constant), provided that the support ![]() $\rho$ is sufficiently small, we may choose some
$\rho$ is sufficiently small, we may choose some ![]() $0< C''<1$ independent of
$0< C''<1$ independent of ![]() $\rho$ such that
$\rho$ such that
Thus, for any ![]() $\underline {x}\in \mathrm {Supp}(P\omega )$,
$\underline {x}\in \mathrm {Supp}(P\omega )$,
 \begin{align*} |\nabla G(\underline{x})\cdot(\nabla G(\underline{x}_0)-\gamma \underline{e}_1')|&=|\nabla G(\underline{x})\cdot \nabla G(\underline{x}_0)- \gamma\|\nabla F(\underline{x}_0)\|^{-1}\nabla G(\underline{x})\cdot \nabla F(\underline{x}_0)|\\ &\geq (1-O(\rho)-C'C'')P^2\|\nabla G(\underline{x}_0)\|^2, \end{align*}
\begin{align*} |\nabla G(\underline{x})\cdot(\nabla G(\underline{x}_0)-\gamma \underline{e}_1')|&=|\nabla G(\underline{x})\cdot \nabla G(\underline{x}_0)- \gamma\|\nabla F(\underline{x}_0)\|^{-1}\nabla G(\underline{x})\cdot \nabla F(\underline{x}_0)|\\ &\geq (1-O(\rho)-C'C'')P^2\|\nabla G(\underline{x}_0)\|^2, \end{align*}
where we have used (3.20) to bound ![]() $\gamma$ by
$\gamma$ by ![]() $C'\|\nabla G(\underline {x}_0)\|$, as well as (3.21) and (3.18). Hence, provided that the support
$C'\|\nabla G(\underline {x}_0)\|$, as well as (3.21) and (3.18). Hence, provided that the support ![]() $\rho$ is chosen to be sufficiently small, there is some
$\rho$ is chosen to be sufficiently small, there is some ![]() $M_{G,1}>0$ such that
$M_{G,1}>0$ such that
Hence, upon taking
we conclude that (3.15) is true. Finally, (3.21) also hands us
for any ![]() $\underline {x}\in \mathrm {Supp}(P\omega )$. Therefore, upon setting
$\underline {x}\in \mathrm {Supp}(P\omega )$. Therefore, upon setting ![]() $M_{2,G}:=C''\| G (\underline {x}_0)\|$, and taking
$M_{2,G}:=C''\| G (\underline {x}_0)\|$, and taking
we are now able to verify (3.16). Furthermore, there is some ![]() $\rho _0>1$, such that
$\rho _0>1$, such that ![]() $M_1$ and
$M_1$ and ![]() $M_2$ are independent of
$M_2$ are independent of ![]() $\rho$ provided that
$\rho$ provided that ![]() $\rho \leq \rho _0$. This concludes the proof of the lemma.
$\rho \leq \rho _0$. This concludes the proof of the lemma.
4. Van der Corput differencing
In this section, we will use van der Corput differencing to bound ![]() $K({\underline {a}}/q+\underline {z})$ by a quadratic exponential sum. We will introduce the topic by beginning with the simpler pointwise van der Corput differencing used in [Reference Browning and Heath-BrownBH09] before attempting to generalise the differencing arguments from [Reference HanselmannHan12] and [Reference VisheVis23] to attain a bound which also takes advantage of averaging over the both
$K({\underline {a}}/q+\underline {z})$ by a quadratic exponential sum. We will introduce the topic by beginning with the simpler pointwise van der Corput differencing used in [Reference Browning and Heath-BrownBH09] before attempting to generalise the differencing arguments from [Reference HanselmannHan12] and [Reference VisheVis23] to attain a bound which also takes advantage of averaging over the both ![]() $\underline {z}$ integrals. In both cases, we will innovate on the standard differencing approach in order to introduce a path to attaining Kloosterman refinement.
$\underline {z}$ integrals. In both cases, we will innovate on the standard differencing approach in order to introduce a path to attaining Kloosterman refinement.
4.1 Pointwise van der Corput
For convenience, we will set
where ![]() $F$ and
$F$ and ![]() $G$ are cubic forms. Since
$G$ are cubic forms. Since ![]() $\underline {x}$ is summed over all of
$\underline {x}$ is summed over all of ![]() $\mathbb {Z}^n$, we can replace
$\mathbb {Z}^n$, we can replace ![]() $\underline {x}$ with
$\underline {x}$ with ![]() $\underline {x}+\underline {h}$, for any
$\underline {x}+\underline {h}$, for any ![]() $\underline {h}\in \mathbb {Z}^n$, giving
$\underline {h}\in \mathbb {Z}^n$, giving
 \begin{equation} K(q,\underline{z})=\sideset{}{^*}\sum_{{\underline{a}}}\bigg{|}\sum_{\underline{x}\in\mathbb{Z}^n} \omega((\underline{x}+\underline{h})/P)e(\hat{F}_{\underline{a},q,\underline{z}}(\underline{x}+\underline{h}))\bigg{|}, \end{equation}
\begin{equation} K(q,\underline{z})=\sideset{}{^*}\sum_{{\underline{a}}}\bigg{|}\sum_{\underline{x}\in\mathbb{Z}^n} \omega((\underline{x}+\underline{h})/P)e(\hat{F}_{\underline{a},q,\underline{z}}(\underline{x}+\underline{h}))\bigg{|}, \end{equation}
where ![]() $K(q,\underline {z})$ is as defined in (3.8). Let
$K(q,\underline {z})$ is as defined in (3.8). Let ![]() $\mathcal {H}\subset \mathbb {Z}^n$ be a set of lattice points (which we may choose freely). In the case of pointwise van der Corput differencing, we can just take
$\mathcal {H}\subset \mathbb {Z}^n$ be a set of lattice points (which we may choose freely). In the case of pointwise van der Corput differencing, we can just take ![]() $\mathcal {H}$ to be the set of lattice points
$\mathcal {H}$ to be the set of lattice points ![]() ${\underline {h}}$ such that
${\underline {h}}$ such that ![]() $|{\underline {h}}|< H$, for some
$|{\underline {h}}|< H$, for some ![]() $1\leq H\ll P$ which we may choose freely. However, we will not specify this in the arguments that follow since we will need a different choice of
$1\leq H\ll P$ which we may choose freely. However, we will not specify this in the arguments that follow since we will need a different choice of ![]() $\mathcal {H}$ when we come to averaged van der Corput differencing later. Applying the Cauchy–Schwarz inequality to (4.2) gives the following
$\mathcal {H}$ when we come to averaged van der Corput differencing later. Applying the Cauchy–Schwarz inequality to (4.2) gives the following
 \begin{align*}
\#\mathcal{H}K(q,\underline{z})&=
\sideset{}{^*}\sum_{{\underline{a}}}\bigg{|}\sum_{\underline{h}\in\mathcal{H}}\sum_{\underline{x}\in\mathbb{Z}^n}
\omega((\underline{x}+\underline{h})/P)e(\hat{F}_{\underline{a},q,\underline{z}}(\underline{x}+\underline{h}))\bigg{|}\\
&\leq
\sideset{}{^*}\sum_{{\underline{a}}}\sum_{\underline{x}\in\mathbb{Z}^n}
\bigg{|}\sum_{\underline{h}\in\mathcal{H}}\omega((\underline{x}+\underline{h})/P)e(\hat{F}_{\underline{a},q,\underline{z}}(\underline{x}+\underline{h}))\bigg{|}\\
&\leq \bigg{(}
\sideset{}{^*}\sum_{{\underline{a}}}\sum_{|\underline{x}|<2P} 1
\bigg{)}^{1/2}
\bigg{(}\sideset{}{^*}\sum_{{\underline{a}}}\sum_{\underline{x}\in\mathbb{Z}^n}\bigg{|}\sum_{\underline{h}\in\mathcal{H}}
\omega((\underline{x}+\underline{h})/P)e(\hat{F}_{\underline{a},q,\underline{z}}(\underline{x}+\underline{h}))\bigg{|}^2\bigg{)}^{1/2}\\
&\ll q P^{n/2}
\bigg{(}\sideset{}{^*}\sum_{{\underline{a}}}\sum_{\underline{x}\in\mathbb{Z}^n}
\sum_{\underline{h}_1,\underline{h}_2\in\mathcal{H}}
\omega((\underline{x}+\underline{h}_1)/P)\overline{\omega((\underline{x}+\underline{h}_2)/P)}\\
&\quad \times
e(\hat{F}_{\underline{a},q,\underline{z}}(\underline{x}+\underline{h}_1))
\overline{e(\hat{F}_{\underline{a},q,\underline{z}}(\underline{x}+\underline{h}_2))}\bigg{)}^{1/2}.
\end{align*}
\begin{align*}
\#\mathcal{H}K(q,\underline{z})&=
\sideset{}{^*}\sum_{{\underline{a}}}\bigg{|}\sum_{\underline{h}\in\mathcal{H}}\sum_{\underline{x}\in\mathbb{Z}^n}
\omega((\underline{x}+\underline{h})/P)e(\hat{F}_{\underline{a},q,\underline{z}}(\underline{x}+\underline{h}))\bigg{|}\\
&\leq
\sideset{}{^*}\sum_{{\underline{a}}}\sum_{\underline{x}\in\mathbb{Z}^n}
\bigg{|}\sum_{\underline{h}\in\mathcal{H}}\omega((\underline{x}+\underline{h})/P)e(\hat{F}_{\underline{a},q,\underline{z}}(\underline{x}+\underline{h}))\bigg{|}\\
&\leq \bigg{(}
\sideset{}{^*}\sum_{{\underline{a}}}\sum_{|\underline{x}|<2P} 1
\bigg{)}^{1/2}
\bigg{(}\sideset{}{^*}\sum_{{\underline{a}}}\sum_{\underline{x}\in\mathbb{Z}^n}\bigg{|}\sum_{\underline{h}\in\mathcal{H}}
\omega((\underline{x}+\underline{h})/P)e(\hat{F}_{\underline{a},q,\underline{z}}(\underline{x}+\underline{h}))\bigg{|}^2\bigg{)}^{1/2}\\
&\ll q P^{n/2}
\bigg{(}\sideset{}{^*}\sum_{{\underline{a}}}\sum_{\underline{x}\in\mathbb{Z}^n}
\sum_{\underline{h}_1,\underline{h}_2\in\mathcal{H}}
\omega((\underline{x}+\underline{h}_1)/P)\overline{\omega((\underline{x}+\underline{h}_2)/P)}\\
&\quad \times
e(\hat{F}_{\underline{a},q,\underline{z}}(\underline{x}+\underline{h}_1))
\overline{e(\hat{F}_{\underline{a},q,\underline{z}}(\underline{x}+\underline{h}_2))}\bigg{)}^{1/2}.
\end{align*}
The key difference between this and the standard van der Corput differencing process is the introduction of the ![]() ${\underline {a}}$ sum in the Cauchy–Schwarz step. In particular, this enables us to bring the
${\underline {a}}$ sum in the Cauchy–Schwarz step. In particular, this enables us to bring the ![]() ${\underline {a}}$ sum inside of the bracket in the final step which, in turn, gives us a path to Kloosterman refinement. We still need to write
${\underline {a}}$ sum inside of the bracket in the final step which, in turn, gives us a path to Kloosterman refinement. We still need to write ![]() $K(q,\underline {z})$ in terms of a quadratic exponential sum however, so we will come back to Kloosterman refinement later.
$K(q,\underline {z})$ in terms of a quadratic exponential sum however, so we will come back to Kloosterman refinement later.
Set ![]() $\underline {y}:=\underline {x}+\underline {h}_2$,
$\underline {y}:=\underline {x}+\underline {h}_2$, ![]() $\underline {h}=\underline {h}_1-\underline {h}_2$ and recall that we defined
$\underline {h}=\underline {h}_1-\underline {h}_2$ and recall that we defined ![]() $\omega$ to be a real weight function. Therefore, after setting
$\omega$ to be a real weight function. Therefore, after setting
we get
Recall that ![]() $\hat {F}_{\underline {a},q,\underline {z}}(\underline {x})=(a_1/q+z_1)F(\underline {x})+(a_2/q+z_2)G(\underline {x})$. Therefore if we set
$\hat {F}_{\underline {a},q,\underline {z}}(\underline {x})=(a_1/q+z_1)F(\underline {x})+(a_2/q+z_2)G(\underline {x})$. Therefore if we set ![]() $F_{{\underline {h}}}$ and
$F_{{\underline {h}}}$ and ![]() $G_{{\underline {h}}}$ be the differenced polynomials
$G_{{\underline {h}}}$ be the differenced polynomials
we have
Hence,
where
denote the corresponding exponential sum for the system of quadratic polynomials ![]() $F_{{\underline {h}}}$ and
$F_{{\underline {h}}}$ and ![]() $G_{{\underline {h}}}$. Note that the top form of
$G_{{\underline {h}}}$. Note that the top form of ![]() $F_{{\underline {h}}}$,
$F_{{\underline {h}}}$, ![]() $F_{{\underline {h}}}^{(0)}$, is precisely (1.8). Finally, by noting that
$F_{{\underline {h}}}^{(0)}$, is precisely (1.8). Finally, by noting that ![]() $N({\underline {h}})\leq \#\mathcal {H}=H^n$, we arrive at the following.
$N({\underline {h}})\leq \#\mathcal {H}=H^n$, we arrive at the following.
Lemma 4.1 For any ![]() $1\leq H\ll P$, for any fixed choice of
$1\leq H\ll P$, for any fixed choice of ![]() $\underline {z}\in [0,1]^2$, we have
$\underline {z}\in [0,1]^2$, we have
 \[ |K(q,\underline{z})|\ll H^{-n/2}P^{n/2}q\bigg{(}\sum_{\underline{h}\ll H}|T_{\underline{h}}(q,\underline{z})|\bigg{)}^{1/2}. \]
\[ |K(q,\underline{z})|\ll H^{-n/2}P^{n/2}q\bigg{(}\sum_{\underline{h}\ll H}|T_{\underline{h}}(q,\underline{z})|\bigg{)}^{1/2}. \]
This bound will be useful to us when ![]() $t:=|\underline {z}|$ is small, say of size
$t:=|\underline {z}|$ is small, say of size ![]() $P^{-3-\Delta }$, since it is wasteful to use averaged van der Corput differencing in this case. We will now set up averaged van der Corput differencing, which will be a key in proving Proposition 3.3.
$P^{-3-\Delta }$, since it is wasteful to use averaged van der Corput differencing in this case. We will now set up averaged van der Corput differencing, which will be a key in proving Proposition 3.3.
4.2 Averaged van der Corput
Throughout this section, ![]() $\underline {x}_0$ will denote a fixed point satisfying
$\underline {x}_0$ will denote a fixed point satisfying ![]() $|\underline {x}_0|<1$ in
$|\underline {x}_0|<1$ in ![]() $\underline {x}_0\in \mathrm {Supp}(\omega )$, where
$\underline {x}_0\in \mathrm {Supp}(\omega )$, where ![]() $\mathrm {Supp}(\omega )$ is contained in the set
$\mathrm {Supp}(\omega )$ is contained in the set ![]() $\underline {x}_0+(-\rho,\rho )^n$. Likewise,
$\underline {x}_0+(-\rho,\rho )^n$. Likewise, ![]() $F$ and
$F$ and ![]() $G$ will be cubic polynomials whose leading forms satisfy (3.15) and (3.16) for a fixed orthonormal set of vectors
$G$ will be cubic polynomials whose leading forms satisfy (3.15) and (3.16) for a fixed orthonormal set of vectors ![]() $\underline {e}_1',\underline {e}_2'$ (see (3.14)). Let
$\underline {e}_1',\underline {e}_2'$ (see (3.14)). Let
denote an extended orthonormal basis of ![]() $\mathbb {R}^n$. We will begin our effort to bound the sum
$\mathbb {R}^n$. We will begin our effort to bound the sum
 \begin{equation} \sum_{P^{\Delta}\leq q\leq Q }\int_{P^{-3-\Delta}\leq|\underline{z}|\leq 1/qQ^{1/2}} K(q,\underline{z})\,d\underline{z}, \end{equation}
\begin{equation} \sum_{P^{\Delta}\leq q\leq Q }\int_{P^{-3-\Delta}\leq|\underline{z}|\leq 1/qQ^{1/2}} K(q,\underline{z})\,d\underline{z}, \end{equation}
where ![]() $K(q,\underline {z})=\sideset {}{^*}\sum _{{\underline {a}}\bmod {q}} |K({\underline {a}}/q+\underline {z})|$ is as defined in (3.8). As in the previous section, let
$K(q,\underline {z})=\sideset {}{^*}\sum _{{\underline {a}}\bmod {q}} |K({\underline {a}}/q+\underline {z})|$ is as defined in (3.8). As in the previous section, let ![]() $1\leq H\ll P$ be a parameter to be chosen later. Typically,
$1\leq H\ll P$ be a parameter to be chosen later. Typically, ![]() $H$ will be chosen as a small power of
$H$ will be chosen as a small power of ![]() $P$, so it is safe to further assume
$P$, so it is safe to further assume ![]() $H\log P\ll P$. In addition, let
$H\log P\ll P$. In addition, let ![]() $\varepsilon >0$ be an arbitrarily small absolute constant to be chosen at the end. Note that the implied constants will be allowed to depend on the choice of
$\varepsilon >0$ be an arbitrarily small absolute constant to be chosen at the end. Note that the implied constants will be allowed to depend on the choice of ![]() $\varepsilon$ after it is introduced into our bounds. As is standard (see, for example, [Reference VisheVis23]), we start by splitting the integral over
$\varepsilon$ after it is introduced into our bounds. As is standard (see, for example, [Reference VisheVis23]), we start by splitting the integral over ![]() $\underline {z}$ above as a sum over
$\underline {z}$ above as a sum over ![]() $O(P^\varepsilon )$ dyadic intervals of the form
$O(P^\varepsilon )$ dyadic intervals of the form ![]() $[t,2t]$ where
$[t,2t]$ where ![]() $P^{-3+\Delta }\leq t\leq 1/(qQ^{1/2})$. For convenience, given
$P^{-3+\Delta }\leq t\leq 1/(qQ^{1/2})$. For convenience, given ![]() $t\in \mathbb {R}_{>0}^2$, we will set
$t\in \mathbb {R}_{>0}^2$, we will set
Analogous to [Reference HanselmannHan12] and [Reference Marmon and VisheMV19, Section 3], for a fixed value of ![]() $P^{-3-\Delta }< t<1/qQ^{1/2}$ we choose two sets
$P^{-3-\Delta }< t<1/qQ^{1/2}$ we choose two sets ![]() $T_1$,
$T_1$, ![]() $T_2$, each of cardinality
$T_2$, each of cardinality ![]() $O(1+tHP^2)$ such that
$O(1+tHP^2)$ such that
 \begin{align} \{\underline{z}: t\leq |\underline{z}|\leq 2t\}&\subseteq \bigcup_{\underline{\tau} \in T_1\times T_2} {[}\tau_1-(HP^2)^{-1},\tau_1+(HP^2)^{-1}{]}\times {[}\tau_2-(HP^2)^{-1},\tau_2+(HP^2)^{-1}{]}\nonumber\\ &\subseteq \{\underline{z}: t\leq|\underline{z}|\leq 2(t+(HP^2)^{-1})\}. \end{align}
\begin{align} \{\underline{z}: t\leq |\underline{z}|\leq 2t\}&\subseteq \bigcup_{\underline{\tau} \in T_1\times T_2} {[}\tau_1-(HP^2)^{-1},\tau_1+(HP^2)^{-1}{]}\times {[}\tau_2-(HP^2)^{-1},\tau_2+(HP^2)^{-1}{]}\nonumber\\ &\subseteq \{\underline{z}: t\leq|\underline{z}|\leq 2(t+(HP^2)^{-1})\}. \end{align}Thus, an application of Cauchy–Schwarz further gives
 \begin{align} I(q,t)&\ll ((HP^2)^{-1}+t)\bigg(\int_{t\leq|\underline{z}|\leq 2(HP^2)^{-1}+t)}|K(q,\underline{z})|^2\,d\underline{z}\bigg)^{1/2}\nonumber\\ &\ll((HP^2)^{-1}+t) \bigg(\sum_{\underline{\tau}\in \underline{T}} \mathcal{M}_q(\underline{\tau},H)\bigg)^{1/2}, \end{align}
\begin{align} I(q,t)&\ll ((HP^2)^{-1}+t)\bigg(\int_{t\leq|\underline{z}|\leq 2(HP^2)^{-1}+t)}|K(q,\underline{z})|^2\,d\underline{z}\bigg)^{1/2}\nonumber\\ &\ll((HP^2)^{-1}+t) \bigg(\sum_{\underline{\tau}\in \underline{T}} \mathcal{M}_q(\underline{\tau},H)\bigg)^{1/2}, \end{align}where
 \begin{align} \mathcal{M}_q(\underline{\tau},H)&:=\int_{\underline{\tau}-(HP^2)^{-1}}^{\underline{\tau}+(HP^2)^{-1}} |K(q,\underline{z})|^2 \,d\underline{z}\nonumber\\ &\ll \int_{\mathbb{R}^2} \exp(-H^2P^4[(\tau_1-z_1)^2+(\tau_2-z_2)^2])|K(q,\underline{z})|^2 \,d\underline{z}. \end{align}
\begin{align} \mathcal{M}_q(\underline{\tau},H)&:=\int_{\underline{\tau}-(HP^2)^{-1}}^{\underline{\tau}+(HP^2)^{-1}} |K(q,\underline{z})|^2 \,d\underline{z}\nonumber\\ &\ll \int_{\mathbb{R}^2} \exp(-H^2P^4[(\tau_1-z_1)^2+(\tau_2-z_2)^2])|K(q,\underline{z})|^2 \,d\underline{z}. \end{align}
Here we have used ![]() $\underline {T}:=T_1\times T_2$, and
$\underline {T}:=T_1\times T_2$, and ![]() $\int _{\underline {\tau }-(HP^2)^{-1}}^{\underline {\tau }+(HP^2)^{-1}}$ to denote the integral
$\int _{\underline {\tau }-(HP^2)^{-1}}^{\underline {\tau }+(HP^2)^{-1}}$ to denote the integral
in order to simplify the notation. After an inspection of the right-hand side of (4.8), it is easy to see that
 \[ \int_{P^{-3-\Delta}\leq |\underline{z}|\leq 1/qQ^{1/2}} K(q,\underline{z})\, d\underline{z}\ll \sum_{t}((HP^2)^{-1}+t)\bigg(\sum_{\underline{\tau}\in \underline{T}} \mathcal{M}_q(\underline{\tau},H)\bigg)^{1/2}, \]
\[ \int_{P^{-3-\Delta}\leq |\underline{z}|\leq 1/qQ^{1/2}} K(q,\underline{z})\, d\underline{z}\ll \sum_{t}((HP^2)^{-1}+t)\bigg(\sum_{\underline{\tau}\in \underline{T}} \mathcal{M}_q(\underline{\tau},H)\bigg)^{1/2}, \]
where the sum over ![]() $t$ runs over
$t$ runs over ![]() $O_\varepsilon (P^\varepsilon )$ choices satisfying
$O_\varepsilon (P^\varepsilon )$ choices satisfying
Note that the choice of the parameter ![]() $H$ will ultimately depend on
$H$ will ultimately depend on ![]() $t$. For now, we will assume
$t$. For now, we will assume ![]() $t$ to be fixed.
$t$ to be fixed.
We are therefore first led to find a bound for ![]() $|K(q,\underline {z})|^2$ using van der Corput differencing. Recall that results (4.4) and (4.5) from § 4.1 hold for any subset of integer vectors
$|K(q,\underline {z})|^2$ using van der Corput differencing. Recall that results (4.4) and (4.5) from § 4.1 hold for any subset of integer vectors ![]() $\mathcal {H}$ satisfying
$\mathcal {H}$ satisfying ![]() $|{\underline {h}}|\ll P$ for every
$|{\underline {h}}|\ll P$ for every ![]() ${\underline {h}}\in \mathcal {H}$. Therefore, by (4.4), (4.9) and (4.10), we have shown the following.
${\underline {h}}\in \mathcal {H}$. Therefore, by (4.4), (4.9) and (4.10), we have shown the following.
Lemma 4.2 For any ![]() $1\leq H\leq P$,
$1\leq H\leq P$, ![]() $\mathcal {H}\subset \mathbb {Z}^n$ and
$\mathcal {H}\subset \mathbb {Z}^n$ and ![]() $t$ satisfying (4.11) we have
$t$ satisfying (4.11) we have
 \begin{align} I(q,t)&\ll ((HP^2)^{-1}+t)\#\mathcal{H}^{-1}P^{n/2}q\nonumber\\ &\quad \times\bigg{(} \sum_{\underline{\tau}\in \underline{T}}\sum_{\underline{h}\in \mathcal{H}} N(\underline{h})\int_{\mathbb{R}^2} \exp(-H^2P^4[(\tau_1-z_1)^2+(\tau_2-z_2)^2])T_{\underline{h}}(q,\underline{z})\, d\underline{z}\bigg{)}^{1/2}. \end{align}
\begin{align} I(q,t)&\ll ((HP^2)^{-1}+t)\#\mathcal{H}^{-1}P^{n/2}q\nonumber\\ &\quad \times\bigg{(} \sum_{\underline{\tau}\in \underline{T}}\sum_{\underline{h}\in \mathcal{H}} N(\underline{h})\int_{\mathbb{R}^2} \exp(-H^2P^4[(\tau_1-z_1)^2+(\tau_2-z_2)^2])T_{\underline{h}}(q,\underline{z})\, d\underline{z}\bigg{)}^{1/2}. \end{align} Since we intend to develop a two-dimensional version of averaged van der Corput differencing, we intend to choose ![]() $\mathcal {H}$ to be a set of size
$\mathcal {H}$ to be a set of size ![]() $O(P^2H^{n-2})$ and then use averaging over
$O(P^2H^{n-2})$ and then use averaging over ![]() $z_1$ and
$z_1$ and ![]() $z_2$ to show that for all but
$z_2$ to show that for all but ![]() $O((H\log (P))^n)$ of
$O((H\log (P))^n)$ of ![]() $\underline {h}\in \mathcal {H}$, the value of the averaged integral
$\underline {h}\in \mathcal {H}$, the value of the averaged integral ![]() $\mathcal {M}_q(\underline {\tau },H)$ defined in (4.10) is negligible. This will enable us to ‘win’ an extra factor of
$\mathcal {M}_q(\underline {\tau },H)$ defined in (4.10) is negligible. This will enable us to ‘win’ an extra factor of ![]() $P/H$ in our final estimate for (4.7) when compared with pointwise van der Corput differencing.
$P/H$ in our final estimate for (4.7) when compared with pointwise van der Corput differencing.
Our choice of ![]() $\mathcal {H}$ will be informed by the following lemma.
$\mathcal {H}$ will be informed by the following lemma.
Lemma 4.3 For any ![]() $\underline {h}\in \mathbb {R}^n$, any
$\underline {h}\in \mathbb {R}^n$, any ![]() $1\leq H\leq P$, any fixed
$1\leq H\leq P$, any fixed ![]() $\underline {\tau }$ and any
$\underline {\tau }$ and any ![]() $N>0$,
$N>0$,
provided that ![]() $\underline {h}=\sum _{i=1}^n h_i'\underline {e}_i'$ satisfies
$\underline {h}=\sum _{i=1}^n h_i'\underline {e}_i'$ satisfies
where ![]() $\mathcal {L}=\log (P)$,
$\mathcal {L}=\log (P)$, ![]() $\{\underline {e}_1',\ldots,\underline {e}_n'\}$ denote the basis chosen in (4.6) and the implied constants only depend on
$\{\underline {e}_1',\ldots,\underline {e}_n'\}$ denote the basis chosen in (4.6) and the implied constants only depend on ![]() $n,\|F\|$ and
$n,\|F\|$ and ![]() $\|G\|$.
$\|G\|$.
Proof. We start by rewriting
 \begin{align*} &\int_{\mathbb{R}^2}\exp(-H^2P^4[(\tau_1-z_1)^2+(\tau_2-z_2)^2])T_{\underline{h}}(q,\underline{z})\, d\underline{z}\\ &\quad =\sum_{\underline{y}\in\mathbb{Z}^n}\sum_{{\underline{a}}}{}^*\omega_{\underline{h}} (\underline{y}/P)e_q(a_1F_{{\underline{h}}}(\underline{y})+a_2G_{{\underline{h}}}(\underline{y}))J(\underline{h},\underline{y}), \end{align*}
\begin{align*} &\int_{\mathbb{R}^2}\exp(-H^2P^4[(\tau_1-z_1)^2+(\tau_2-z_2)^2])T_{\underline{h}}(q,\underline{z})\, d\underline{z}\\ &\quad =\sum_{\underline{y}\in\mathbb{Z}^n}\sum_{{\underline{a}}}{}^*\omega_{\underline{h}} (\underline{y}/P)e_q(a_1F_{{\underline{h}}}(\underline{y})+a_2G_{{\underline{h}}}(\underline{y}))J(\underline{h},\underline{y}), \end{align*}
where
and ![]() $e_q(x):=e^{2\pi i x/q}$. We may separate the two integrals over
$e_q(x):=e^{2\pi i x/q}$. We may separate the two integrals over ![]() $\underline {z}$ and integrate them to get
$\underline {z}$ and integrate them to get
We note that if either ![]() $|F_{\underline {h}}(\underline {y})|$ or
$|F_{\underline {h}}(\underline {y})|$ or ![]() $|G_{\underline {h}}(\underline {y})|$ are
$|G_{\underline {h}}(\underline {y})|$ are ![]() $\gg HP^2\mathcal {L}$, then trivially bounding everything in
$\gg HP^2\mathcal {L}$, then trivially bounding everything in ![]() $J$ from above gives
$J$ from above gives
 \begin{align*} \sum_{\underline{y}\in\mathbb{Z}^n}\sideset{}{^*}\sum_{{\underline{a}}\bmod{q}}\omega_{\underline{h}}(\underline{y}/P) e_q(a_1F_{{\underline{h}}}(\underline{y})+a_2G_{{\underline{h}}}(\underline{y}))J(\underline{h},\underline{y})&\ll P^nq^2\frac{1}{H^2P^4}\exp(-m\mathcal{L}^2)\\ &\ll_N P^{-N}, \end{align*}
\begin{align*} \sum_{\underline{y}\in\mathbb{Z}^n}\sideset{}{^*}\sum_{{\underline{a}}\bmod{q}}\omega_{\underline{h}}(\underline{y}/P) e_q(a_1F_{{\underline{h}}}(\underline{y})+a_2G_{{\underline{h}}}(\underline{y}))J(\underline{h},\underline{y})&\ll P^nq^2\frac{1}{H^2P^4}\exp(-m\mathcal{L}^2)\\ &\ll_N P^{-N}, \end{align*}
for some constant ![]() $m>0$. Therefore, it is sufficient to show that there exist constants
$m>0$. Therefore, it is sufficient to show that there exist constants ![]() $0< c_1, c_2<1$ such that for every
$0< c_1, c_2<1$ such that for every
 \begin{equation} \underline{h}=\sum_{i=1}^n h_i\underline{e}_i=\sum_{i=1}^n h_i'\underline{e}_i' \end{equation}
\begin{equation} \underline{h}=\sum_{i=1}^n h_i\underline{e}_i=\sum_{i=1}^n h_i'\underline{e}_i' \end{equation}
with ![]() ${\underline {h}}\in \mathbb {R}^n$,
${\underline {h}}\in \mathbb {R}^n$,
we have
We will rewrite ![]() $F_{\underline {h}}$ as follows:
$F_{\underline {h}}$ as follows:
where ![]() $F_{\underline {h}}^{(2)}$ is the constant part of
$F_{\underline {h}}^{(2)}$ is the constant part of ![]() $F_{\underline {h}}$ and
$F_{\underline {h}}$ and ![]() $\mathcal {H}_F(\underline {y})$ is the Hessian of
$\mathcal {H}_F(\underline {y})$ is the Hessian of ![]() $F$ evaluated at
$F$ evaluated at ![]() $\underline {y}$. Now for
$\underline {y}$. Now for ![]() $\underline {h}$ satisfying (4.16), we have
$\underline {h}$ satisfying (4.16), we have
 \begin{align} F_{\underline{h}}(\underline{y})&=\nabla F(\underline{y})\cdot \underline{h}+\bigg{(}\sum h_i'\underline{e}_i'\bigg{)}^t\mathcal{H}_F(\underline{y})\bigg{(}\sum h_i'\underline{e}_i'\bigg{)}+F_{\underline{h}}^{(2)}\nonumber\\ &=\nabla F(\underline{y})\cdot \underline{h}+F_{\underline{h}}^{(2)}+O(|h_1'|^2P)+O(|h_2'|^2P)+O(HP^2), \end{align}
\begin{align} F_{\underline{h}}(\underline{y})&=\nabla F(\underline{y})\cdot \underline{h}+\bigg{(}\sum h_i'\underline{e}_i'\bigg{)}^t\mathcal{H}_F(\underline{y})\bigg{(}\sum h_i'\underline{e}_i'\bigg{)}+F_{\underline{h}}^{(2)}\nonumber\\ &=\nabla F(\underline{y})\cdot \underline{h}+F_{\underline{h}}^{(2)}+O(|h_1'|^2P)+O(|h_2'|^2P)+O(HP^2), \end{align}
where ![]() $F_{{\underline {h}}}^{(2)}$ is a cubic polynomial in
$F_{{\underline {h}}}^{(2)}$ is a cubic polynomial in ![]() ${\underline {h}}$, and the implied constants depend only on
${\underline {h}}$, and the implied constants depend only on ![]() $\|F\|$,
$\|F\|$, ![]() $\|G\|$ and
$\|G\|$ and ![]() $n$. Note that
$n$. Note that
and so we may simplify (4.18) to
since ![]() $H, |h_1'|, |h_2'|< P$. We also write
$H, |h_1'|, |h_2'|< P$. We also write ![]() ${\underline {h}}=h_1'\underline {e}_1'+\cdots +h_n'\underline {e}_n'$ and invoke (3.15) and (3.16) to further get that for all
${\underline {h}}=h_1'\underline {e}_1'+\cdots +h_n'\underline {e}_n'$ and invoke (3.15) and (3.16) to further get that for all ![]() $\underline {y}\in \mathrm {Supp}(P\omega )$ we have
$\underline {y}\in \mathrm {Supp}(P\omega )$ we have
and so we get
by (4.19). For now, let us focus on the case ![]() $|h_2'|\ll \rho ^{-1/2}| h_1'|$. In this case, we must have that
$|h_2'|\ll \rho ^{-1/2}| h_1'|$. In this case, we must have that ![]() $h_1'$ satisfies
$h_1'$ satisfies ![]() $H\mathcal {L}\ll |h_1'|$. Furthermore, upon choosing
$H\mathcal {L}\ll |h_1'|$. Furthermore, upon choosing ![]() $c_1\leq \rho ^2$ and by (4.16), we have
$c_1\leq \rho ^2$ and by (4.16), we have
 \begin{gather*} \rho |h_2'| P^2\ll
\rho^{1/2} |h_1'|P^2,\quad |h_1'|^2P\leq c_1 |h_1'|P^2 \leq
\rho^2 |h_1'|P^2,\\ |h_2'|^2P\ll \rho^{-1}|h_1'|^2P\leq
\rho^{-1}c_1|h_1'| P^2 \leq \rho |h_1'|P^2.
\end{gather*}
\begin{gather*} \rho |h_2'| P^2\ll
\rho^{1/2} |h_1'|P^2,\quad |h_1'|^2P\leq c_1 |h_1'|P^2 \leq
\rho^2 |h_1'|P^2,\\ |h_2'|^2P\ll \rho^{-1}|h_1'|^2P\leq
\rho^{-1}c_1|h_1'| P^2 \leq \rho |h_1'|P^2.
\end{gather*}
Hence, we may simplify (4.20) to obtain
provided that ![]() $\rho$ is chosen to be sufficiently small with respect to
$\rho$ is chosen to be sufficiently small with respect to ![]() $M_1$.
$M_1$.
It now remains to study the case ![]() $|h_1'|\ll \rho ^{1/2}|h_2'|$. In this case, we instead have that
$|h_1'|\ll \rho ^{1/2}|h_2'|$. In this case, we instead have that ![]() $|h_2'|\gg H\mathcal {L}$. We now apply the same process used to obtain (4.19) to
$|h_2'|\gg H\mathcal {L}$. We now apply the same process used to obtain (4.19) to ![]() $G_{\underline {h}}(\underline {y})$ to obtain
$G_{\underline {h}}(\underline {y})$ to obtain
where the implied constants again depend only on ![]() $n$,
$n$, ![]() $\|F\|$ and
$\|F\|$ and ![]() $\|G\|$. Note again that
$\|G\|$. Note again that
Combining this with (4.21), and applying (3.15)–(3.16) gives
We now aim to simplify (4.22). Using the assumption that ![]() $|h_1'|\ll \rho ^{1/2}|h_2'|$, the fact that
$|h_1'|\ll \rho ^{1/2}|h_2'|$, the fact that ![]() $|h_2'|$ must obey (4.16) in this case, and setting
$|h_2'|$ must obey (4.16) in this case, and setting ![]() $c_2\leq \rho$ we have
$c_2\leq \rho$ we have
 \begin{gather*}|h_1'| P^2 \ll \rho^{1/2}
|h_2'|P^2,\quad |h_1'|^2P\ll \rho |h_2'|^2P\leq \rho
c_2|h_2'| P^2 \leq \rho^2 |h_2'|P^2,\\ |h_2'|^2P \leq c_2
|h_2'|P^2 \leq \rho |h_1'|P^2,\quad HP^2\ll |h_1'|P^2
\mathcal{L}^{-1}\ll \rho |h_1'|P^2.
\end{gather*}
\begin{gather*}|h_1'| P^2 \ll \rho^{1/2}
|h_2'|P^2,\quad |h_1'|^2P\ll \rho |h_2'|^2P\leq \rho
c_2|h_2'| P^2 \leq \rho^2 |h_2'|P^2,\\ |h_2'|^2P \leq c_2
|h_2'|P^2 \leq \rho |h_1'|P^2,\quad HP^2\ll |h_1'|P^2
\mathcal{L}^{-1}\ll \rho |h_1'|P^2.
\end{gather*}
Hence,
as long as ![]() $\rho$ is chosen small enough depending only on
$\rho$ is chosen small enough depending only on ![]() $M_1$ and
$M_1$ and ![]() $M_2$.
$M_2$.
The lemma above leads to the following natural choice for ![]() $\mathcal {H}$:
$\mathcal {H}$:
where ![]() $c_1$ and
$c_1$ and ![]() $c_2$ are the implied constants arising in (4.13). Essentially,
$c_2$ are the implied constants arising in (4.13). Essentially, ![]() $\mathcal {H}$ is chosen to be the collection of lattice points inside of a fixed
$\mathcal {H}$ is chosen to be the collection of lattice points inside of a fixed ![]() $n$-dimensional cuboid,
$n$-dimensional cuboid, ![]() $B_P$, centred at the origin, with volume
$B_P$, centred at the origin, with volume ![]() $\mathrm {Vol}(B_P)=c_1c_2P^2H^{n-2}$. The sides of the cuboid are in the direction of the basis vectors
$\mathrm {Vol}(B_P)=c_1c_2P^2H^{n-2}$. The sides of the cuboid are in the direction of the basis vectors ![]() $\{\underline {e}_1',\ldots,\underline {e}_n'\}$. We now claim that
$\{\underline {e}_1',\ldots,\underline {e}_n'\}$. We now claim that
This follows very easily from the following asymptotic formula for a general cuboid ![]() $B$ with side lengths
$B$ with side lengths ![]() $l_1,\ldots,l_n$. It is easy to see that
$l_1,\ldots,l_n$. It is easy to see that
 \[ \#\{\mathbb{Z}^n\cap B\}=\mathrm{Vol}(B)+\sum_{i=1}^n O\bigg(\prod_{j\neq i} l_j\bigg). \]
\[ \#\{\mathbb{Z}^n\cap B\}=\mathrm{Vol}(B)+\sum_{i=1}^n O\bigg(\prod_{j\neq i} l_j\bigg). \]
The error comes from estimating the ![]() $(n-1)$-dimensional boundary of
$(n-1)$-dimensional boundary of ![]() $B$. In our case
$B$. In our case ![]() $l_1=c_1P$,
$l_1=c_1P$,![]() $l_2=c_2P$,
$l_2=c_2P$, ![]() $l_i=H$ for
$l_i=H$ for ![]() $i\geq 3$, which leads to (4.24). Note that
$i\geq 3$, which leads to (4.24). Note that ![]() $\mathcal {H}$ is chosen as in (4.23) so that we can use the bound Lemma 4.3. In particular, we can now show the following.
$\mathcal {H}$ is chosen as in (4.23) so that we can use the bound Lemma 4.3. In particular, we can now show the following.
Lemma 4.4 Let ![]() $1\leq H\leq P$ and let
$1\leq H\leq P$ and let
Then for any ![]() $1\leq H\leq P$, any
$1\leq H\leq P$, any ![]() $1\leq N$, and any
$1\leq N$, and any ![]() $t>0$ such that (4.11) holds, we have
$t>0$ such that (4.11) holds, we have
 \[ I(q,t)\ll H^{-n/2+1}\log(P)P^{n/2-1}q((HP^2)^{-1}+t)^2\bigg{(}\sum_{\underline{h}\in \tilde{\mathcal{H}}}\max_{\underline{z}}|T_{\underline{h}}(q,\underline{z})|\bigg{)}^{1/2}+O_N(P^{-N}), \]
\[ I(q,t)\ll H^{-n/2+1}\log(P)P^{n/2-1}q((HP^2)^{-1}+t)^2\bigg{(}\sum_{\underline{h}\in \tilde{\mathcal{H}}}\max_{\underline{z}}|T_{\underline{h}}(q,\underline{z})|\bigg{)}^{1/2}+O_N(P^{-N}), \]
where the maximum over ![]() $\underline {z}$ is taken over the set
$\underline {z}$ is taken over the set
Proof. Let ![]() $\mathcal {H}$ be as in (4.23). Then we use the decomposition
$\mathcal {H}$ be as in (4.23). Then we use the decomposition ![]() $\mathcal {H}=(\tilde {\mathcal {H}}\cap \mathcal {H})\bigcup \mathcal {H}\backslash \tilde {\mathcal {H}}$. By construction,
$\mathcal {H}=(\tilde {\mathcal {H}}\cap \mathcal {H})\bigcup \mathcal {H}\backslash \tilde {\mathcal {H}}$. By construction,
Furthermore, note that for any fixed ![]() ${\underline {h}}$,
${\underline {h}}$, ![]() $N({\underline {h}})$ as defined in (4.3) satisfies the bound
$N({\underline {h}})$ as defined in (4.3) satisfies the bound
Therefore, by Lemma 4.3, and a bound ![]() $\#\underline {T}\ll (1+tHP^2)^2\ll P^6$, which arises from using crude bounds
$\#\underline {T}\ll (1+tHP^2)^2\ll P^6$, which arises from using crude bounds ![]() $t\leq 1$ and
$t\leq 1$ and ![]() $1\leq H\leq P$
$1\leq H\leq P$
 \[ \#\mathcal{H}^{-1}\bigg(\sum_{\underline{\tau}\in\underline{T}}\sum_{\underline{h}\in \mathcal{H}\setminus\tilde{\mathcal{H}}} N(\underline{h})\int_{\mathbb{R}^2} \exp(-H^2P^4[(\tau_1-z_1)^2+(\tau_2-z_2)^2])T_{\underline{h}}(q,\underline{z}) \,d\underline{z}\bigg)^{1/2} \ll P^{-N}. \]
\[ \#\mathcal{H}^{-1}\bigg(\sum_{\underline{\tau}\in\underline{T}}\sum_{\underline{h}\in \mathcal{H}\setminus\tilde{\mathcal{H}}} N(\underline{h})\int_{\mathbb{R}^2} \exp(-H^2P^4[(\tau_1-z_1)^2+(\tau_2-z_2)^2])T_{\underline{h}}(q,\underline{z}) \,d\underline{z}\bigg)^{1/2} \ll P^{-N}. \]
Further combining with the bounds ![]() $q\leq Q\leq P^{3/2}$, we may bound the contribution from the sum over
$q\leq Q\leq P^{3/2}$, we may bound the contribution from the sum over ![]() ${\underline {h}}\in \mathcal {H}\setminus \tilde {\mathcal {H}}$ in (4.12) as follows:
${\underline {h}}\in \mathcal {H}\setminus \tilde {\mathcal {H}}$ in (4.12) as follows:
 \begin{align*} &\ll((HP^2)^{-1}+t)P^{n/2}q\#\mathcal{H}^{-1}\\ &\quad\times\bigg{(}\sum_{\underline{\tau}\in \underline{T}}\sum_{\underline{h}\in \mathcal{H}\setminus \tilde{\mathcal{H}}} N(\underline{h})\int_{\mathbb{R}^2} \exp(-H^2P^4[(\tau_1-z_1)^2+(\tau_2-z_2)^2])T_{\underline{h}}(q,\underline{z})\,d\underline{z}\bigg{)}^{1/2}\\ &\ll_N P^{n/2+3/2-N}\ll_{n,N} P^{-N}, \end{align*}
\begin{align*} &\ll((HP^2)^{-1}+t)P^{n/2}q\#\mathcal{H}^{-1}\\ &\quad\times\bigg{(}\sum_{\underline{\tau}\in \underline{T}}\sum_{\underline{h}\in \mathcal{H}\setminus \tilde{\mathcal{H}}} N(\underline{h})\int_{\mathbb{R}^2} \exp(-H^2P^4[(\tau_1-z_1)^2+(\tau_2-z_2)^2])T_{\underline{h}}(q,\underline{z})\,d\underline{z}\bigg{)}^{1/2}\\ &\ll_N P^{n/2+3/2-N}\ll_{n,N} P^{-N}, \end{align*}
as ![]() $N$ is allowed to be arbitrarily large. Therefore, combining this with Lemma 4.2, we get
$N$ is allowed to be arbitrarily large. Therefore, combining this with Lemma 4.2, we get
 \begin{align} I(q,t)&\ll ((HP^2)^{-1}+t)\#\mathcal{H}^{-1/2}P^{n/2}q\nonumber\\ &\quad \times\bigg{(}\sum_{\underline{\tau}\in \underline{T}}\sum_{\underline{h}\in \tilde{\mathcal{H}}}\int_{\mathbb{R}^2} \exp(-H^2P^4[(\tau_1-z_1)^2+(\tau_2-z_2)^2])T_{\underline{h}}(q,\underline{z})\, d\underline{z}\bigg{)}^{1/2}\nonumber\\ &\quad +O_{n,N}(P^{-N}). \end{align}
\begin{align} I(q,t)&\ll ((HP^2)^{-1}+t)\#\mathcal{H}^{-1/2}P^{n/2}q\nonumber\\ &\quad \times\bigg{(}\sum_{\underline{\tau}\in \underline{T}}\sum_{\underline{h}\in \tilde{\mathcal{H}}}\int_{\mathbb{R}^2} \exp(-H^2P^4[(\tau_1-z_1)^2+(\tau_2-z_2)^2])T_{\underline{h}}(q,\underline{z})\, d\underline{z}\bigg{)}^{1/2}\nonumber\\ &\quad +O_{n,N}(P^{-N}). \end{align}
Further note that for a fixed ![]() $\tau$ and for any
$\tau$ and for any ![]() $z$ satisfying
$z$ satisfying ![]() $|z-\tau |\geq HP^2\mathcal {L}$ we have the following decay of the function in the integrand:
$|z-\tau |\geq HP^2\mathcal {L}$ we have the following decay of the function in the integrand:
Thus, in the same vein as before, using the bound (4.28) in (4.27) we may obtain
 \[ I(q,t)\ll ((HP^2)^{-1}+t)\#\mathcal{H}^{-1/2}P^{n/2}q\bigg{(}\sum_{\underline{\tau}\in \underline{T}}\sum_{\underline{h}\in \tilde{\mathcal{H}}}\int_{\underline{\tau}-(HP^2)^{-1}\mathcal{L}}^{\underline{\tau}+(HP^2)^{-1}\mathcal{L}}|T_{\underline{h}}(q,\underline{z})|\, d\underline{z}\bigg{)}^{1/2}+O_{n,N}(P^{-N}). \]
\[ I(q,t)\ll ((HP^2)^{-1}+t)\#\mathcal{H}^{-1/2}P^{n/2}q\bigg{(}\sum_{\underline{\tau}\in \underline{T}}\sum_{\underline{h}\in \tilde{\mathcal{H}}}\int_{\underline{\tau}-(HP^2)^{-1}\mathcal{L}}^{\underline{\tau}+(HP^2)^{-1}\mathcal{L}}|T_{\underline{h}}(q,\underline{z})|\, d\underline{z}\bigg{)}^{1/2}+O_{n,N}(P^{-N}). \]
The lemma now follows after using (4.24) to estimate ![]() $\#\mathcal {H}$, using the estimate
$\#\mathcal {H}$, using the estimate ![]() $\#\underline {T}=O((1+tHP^2)^2)$, and (4.8) which allows us to take the maximum over all possible
$\#\underline {T}=O((1+tHP^2)^2)$, and (4.8) which allows us to take the maximum over all possible ![]() $\underline {z}$ appearing in the expression.
$\underline {z}$ appearing in the expression.
Since ![]() $H$ is arbitrary, we may relabel
$H$ is arbitrary, we may relabel ![]() $H\mathcal {L}$ as
$H\mathcal {L}$ as ![]() $H$ at the expense of a factor of size at most
$H$ at the expense of a factor of size at most ![]() $O_\varepsilon (P^\varepsilon )$ we can now conclude as follows.
$O_\varepsilon (P^\varepsilon )$ we can now conclude as follows.
Lemma 4.5 For any ![]() $1\leq H\ll P$, any
$1\leq H\ll P$, any ![]() $0<\varepsilon <1$, any
$0<\varepsilon <1$, any ![]() $\underline {t}$ satisfying (4.11) and any
$\underline {t}$ satisfying (4.11) and any ![]() $N\geq 1$ we have
$N\geq 1$ we have
 \[ I(q,t)\ll_{\varepsilon,n,N} H^{-n/2+1}P^{n/2-1+\varepsilon}q((HP^2)^{-1}+t)^2\bigg{(}\max_{|\underline{z}|}\sum_{|{\underline{h}}|\ll H}|T_{\underline{h}}(q,\underline{z})|\bigg{)}^{1/2}+P^{-N}, \]
\[ I(q,t)\ll_{\varepsilon,n,N} H^{-n/2+1}P^{n/2-1+\varepsilon}q((HP^2)^{-1}+t)^2\bigg{(}\max_{|\underline{z}|}\sum_{|{\underline{h}}|\ll H}|T_{\underline{h}}(q,\underline{z})|\bigg{)}^{1/2}+P^{-N}, \]
where the maximum over ![]() $\underline {z}$ is taken over the set
$\underline {z}$ is taken over the set
5. Quadratic exponential sums: initial consideration
The differencing technique used in § 4 leads us to consider quadratic exponential sums ![]() $T_{\underline {h}}(q,\underline {z})$ (see (4.5)) for a family of differenced quadratic forms
$T_{\underline {h}}(q,\underline {z})$ (see (4.5)) for a family of differenced quadratic forms ![]() $F_{{\underline {h}}}$ and
$F_{{\underline {h}}}$ and ![]() $G_{\underline {h}}$. Throughout this section, let
$G_{\underline {h}}$. Throughout this section, let ![]() $q$ denote an arbitrary but fixed integer. Our main goal here is to estimate quadratic sums corresponding to a general system of quadratic polynomials
$q$ denote an arbitrary but fixed integer. Our main goal here is to estimate quadratic sums corresponding to a general system of quadratic polynomials ![]() $f,g$ defined as
$f,g$ defined as
 \begin{equation} T(q,\underline{z}):=\sideset{}{^*}\sum_{{\underline{a}}}^q\sum_{\underline{y}\in\mathbb{Z}^n} \omega(\underline{y}/P)e((a_1/q+z_1)f(\underline{y})+(a_2/q+z_2)g(\underline{y})). \end{equation}
\begin{equation} T(q,\underline{z}):=\sideset{}{^*}\sum_{{\underline{a}}}^q\sum_{\underline{y}\in\mathbb{Z}^n} \omega(\underline{y}/P)e((a_1/q+z_1)f(\underline{y})+(a_2/q+z_2)g(\underline{y})). \end{equation}
Here ![]() $f$ and
$f$ and ![]() $g$ denote a system of quadratic polynomials with integer coefficients and
$g$ denote a system of quadratic polynomials with integer coefficients and ![]() $\omega$ denotes a compactly supported function on
$\omega$ denotes a compactly supported function on ![]() $\mathbb {R}^n$. Let us denote leading quadratic parts of
$\mathbb {R}^n$. Let us denote leading quadratic parts of ![]() $f$ and
$f$ and ![]() $g$ by
$g$ by ![]() $f^{(0)}$ and
$f^{(0)}$ and ![]() $g^{(0)}$, respectively. We further assume that the quadratic forms
$g^{(0)}$, respectively. We further assume that the quadratic forms ![]() $f^{(0)}$ and
$f^{(0)}$ and ![]() $g^{(0)}$ are defined by integer matrices
$g^{(0)}$ are defined by integer matrices ![]() $M_1$ and
$M_1$ and ![]() $M_2$, respectively. We will later apply the estimates in this section by setting
$M_2$, respectively. We will later apply the estimates in this section by setting ![]() $f=F_{\underline {h}}$ and
$f=F_{\underline {h}}$ and ![]() $g=G_{\underline {h}}$.
$g=G_{\underline {h}}$.
Given a (finite or infinite) prime ![]() $p$, by
$p$, by ![]() $s_p$ we denote
$s_p$ we denote
where, further, given a set of forms ![]() $F_1,F_2$,
$F_1,F_2$, ![]() $s_p(F_1,F_2)$ denotes the dimension of singular locus of the projective complete intersection variety defined by the simultaneous zero locus of the forms
$s_p(F_1,F_2)$ denotes the dimension of singular locus of the projective complete intersection variety defined by the simultaneous zero locus of the forms ![]() $F_1,F_2$. That is,
$F_1,F_2$. That is,
When ![]() $n\geq 2$, given an integer
$n\geq 2$, given an integer ![]() $q$, we define
$q$, we define ![]() $D(q)$ by
$D(q)$ by
 \begin{equation} D_{f,g}(q)=D(q):=\prod_{\substack{p\mid q\\ p \textrm{ prime }}} p^{s_p(f^{(0)},g^{(0)})+1}. \end{equation}
\begin{equation} D_{f,g}(q)=D(q):=\prod_{\substack{p\mid q\\ p \textrm{ prime }}} p^{s_p(f^{(0)},g^{(0)})+1}. \end{equation}
On the other hand, when ![]() $n=1$, we define
$n=1$, we define ![]() $D(q)$ as
$D(q)$ as
where, given a polynomial ![]() $f$,
$f$, ![]() $\mathrm {Cont}(f)$ is the gcd of all its coefficients.
$\mathrm {Cont}(f)$ is the gcd of all its coefficients.
As is standard, we begin by applying Poisson summation to ![]() $T(q,\underline {z})$. This will allow us separate the sum over
$T(q,\underline {z})$. This will allow us separate the sum over ![]() ${\underline {a}}$ and the integral over
${\underline {a}}$ and the integral over ![]() $\underline {z}$, into an exponential sum and an exponential integral respectively. In particular, applying Poisson summation gives us the following.
$\underline {z}$, into an exponential sum and an exponential integral respectively. In particular, applying Poisson summation gives us the following.
Lemma 5.1 We have
where
 \begin{equation} S(q; \underline{m},f,g)=S(q; \underline{m}):=\sideset{}{^*}\sum_{{\underline{a}}}^q\sum_{\underline{u} \bmod{q}} e_q(a_1f(\underline{u})+a_2g(\underline{u})+\underline{m}\cdot\underline{u}), \end{equation}
\begin{equation} S(q; \underline{m},f,g)=S(q; \underline{m}):=\sideset{}{^*}\sum_{{\underline{a}}}^q\sum_{\underline{u} \bmod{q}} e_q(a_1f(\underline{u})+a_2g(\underline{u})+\underline{m}\cdot\underline{u}), \end{equation}and
Proof. The proof of Lemma 5.1 is standard and can be obtained by slightly modifying [Reference Browning and Heath-BrownBH09, Lemma 8]: let ![]() $\underline {x}=\underline {u}+q\underline {v}$. Then
$\underline {x}=\underline {u}+q\underline {v}$. Then
 \begin{align*} T(q,\underline{z})&=\sideset{}{^*}\sum_{{\underline{a}}}^q\sum_{\underline{u} \bmod{q}}\sum_{\underline{v}\in\mathbb{Z}^n} \omega((\underline{u}+q\underline{v})/P)e([a_1/q+z_1]f(\underline{u}+q\underline{v})+[a_2/q+z_2]g(\underline{u}+q\underline{v}))\\ &=\sideset{}{^*}\sum_{{\underline{a}}}^q\sum_{\underline{u} \bmod{q}} e_q(a_1f(\underline{u})+a_2g(\underline{u}))\sum_{\underline{v}\in\mathbb{Z}^n}\omega((\underline{u}+q\underline{v})/P)e(z_1f(\underline{u}+q\underline{v})+z_2g(\underline{u}+q\underline{v})). \end{align*}
\begin{align*} T(q,\underline{z})&=\sideset{}{^*}\sum_{{\underline{a}}}^q\sum_{\underline{u} \bmod{q}}\sum_{\underline{v}\in\mathbb{Z}^n} \omega((\underline{u}+q\underline{v})/P)e([a_1/q+z_1]f(\underline{u}+q\underline{v})+[a_2/q+z_2]g(\underline{u}+q\underline{v}))\\ &=\sideset{}{^*}\sum_{{\underline{a}}}^q\sum_{\underline{u} \bmod{q}} e_q(a_1f(\underline{u})+a_2g(\underline{u}))\sum_{\underline{v}\in\mathbb{Z}^n}\omega((\underline{u}+q\underline{v})/P)e(z_1f(\underline{u}+q\underline{v})+z_2g(\underline{u}+q\underline{v})). \end{align*}
We now apply Poisson summation on the second sum (and use the substitution ![]() $\underline {x}=\underline {u}+q\underline {v}$) to get
$\underline {x}=\underline {u}+q\underline {v}$) to get
 \begin{align*} T(q,\underline{z})&=\sideset{}{^*}\sum_{{\underline{a}}}^q\sum_{\underline{u} \bmod{q}} e_q(a_1f(\underline{u})+a_2g(\underline{u})) \\ &\quad\times\sum_{\underline{m}\in\mathbb{Z}^n}\int_{\mathbb{R}^n} \omega((\underline{u}+q\underline{v})/P)e(z_1f(\underline{u}+q\underline{v})+z_2g(\underline{u}+q\underline{v})-\underline{m}\cdot \underline{v})\, d\underline{v}\\ &=q^{-n}\sum_{\underline{m}\in\mathbb{Z}^n}\sideset{}{^*}\sum_{{\underline{a}}}^q\sum_{\underline{u} \bmod{q}} e_q(a_1f(\underline{u})+a_2g(\underline{u})+\underline{m}\cdot \underline{u})\\ &\quad \times\int_{\mathbb{R}^n} \omega(\underline{x}/P)e(z_1f(\underline{x})+z_2g(\underline{x})-q^{-1}\underline{m}\cdot \underline{x}),\, d\underline{x} \end{align*}
\begin{align*} T(q,\underline{z})&=\sideset{}{^*}\sum_{{\underline{a}}}^q\sum_{\underline{u} \bmod{q}} e_q(a_1f(\underline{u})+a_2g(\underline{u})) \\ &\quad\times\sum_{\underline{m}\in\mathbb{Z}^n}\int_{\mathbb{R}^n} \omega((\underline{u}+q\underline{v})/P)e(z_1f(\underline{u}+q\underline{v})+z_2g(\underline{u}+q\underline{v})-\underline{m}\cdot \underline{v})\, d\underline{v}\\ &=q^{-n}\sum_{\underline{m}\in\mathbb{Z}^n}\sideset{}{^*}\sum_{{\underline{a}}}^q\sum_{\underline{u} \bmod{q}} e_q(a_1f(\underline{u})+a_2g(\underline{u})+\underline{m}\cdot \underline{u})\\ &\quad \times\int_{\mathbb{R}^n} \omega(\underline{x}/P)e(z_1f(\underline{x})+z_2g(\underline{x})-q^{-1}\underline{m}\cdot \underline{x}),\, d\underline{x} \end{align*}
as required.
As a result, we trivially have the following pointwise bound
The treatment of the exponential integral is standard. In particular, upon letting ![]() $\|f\|$ denote the supremum of absolute values of its coefficients and defining
$\|f\|$ denote the supremum of absolute values of its coefficients and defining
we can use the following lemma to bound ![]() $I(\underline {z};q^{-1}\underline {m})$.
$I(\underline {z};q^{-1}\underline {m})$.
Lemma 5.2 Let ![]() $f,g$ be quadratic polynomials such that
$f,g$ be quadratic polynomials such that ![]() $\max \{\|f\|_P,\|g\|_P\}\ll H$. Furthermore, let
$\max \{\|f\|_P,\|g\|_P\}\ll H$. Furthermore, let ![]() $V:=1+q P^{\varepsilon -1}\max \{1,HP^2|\underline {z}|\}^{1/2}$,
$V:=1+q P^{\varepsilon -1}\max \{1,HP^2|\underline {z}|\}^{1/2}$, ![]() $\varepsilon >0$, and
$\varepsilon >0$, and ![]() $N\in \mathbb {N}$. Then
$N\in \mathbb {N}$. Then
where
Furthermore, if ![]() $|\underline {m}|\geq q P^{\epsilon -1}\max \{1,HP^2|\underline {z}|\}$, then we have
$|\underline {m}|\geq q P^{\epsilon -1}\max \{1,HP^2|\underline {z}|\}$, then we have
The proof of this is almost identical to the proofs of [Reference Browning, Dietmann and Heath-BrownBDH15, Lemmas 6.5 and 6.6], and so we will not provide details here. In particular, the only thing in the proofs that needs to be tweaked in order to verify Lemma 5.2 is that ![]() $\Theta$ in [Reference Browning, Dietmann and Heath-BrownBDH15, equation (6.11)] must be replaced with
$\Theta$ in [Reference Browning, Dietmann and Heath-BrownBDH15, equation (6.11)] must be replaced with
We also note that we use ![]() $|\nabla \hat {f}_{\underline {z}}(\underline {y})-\underline {m}|\leq V$ instead of
$|\nabla \hat {f}_{\underline {z}}(\underline {y})-\underline {m}|\leq V$ instead of ![]() $Pq^{-1}|\nabla \hat {f}_{\underline {z}}(\underline {y})-\underline {m}|\leq Pq^{-1}V$ since we are using slightly different notation.
$Pq^{-1}|\nabla \hat {f}_{\underline {z}}(\underline {y})-\underline {m}|\leq Pq^{-1}V$ since we are using slightly different notation.
The latter bound enables us to handle the tail of the sum over ![]() $\underline {m}$. Let
$\underline {m}$. Let ![]() $\hat {V}:=q P^{\epsilon -1}\max \{1,HP^2|\underline {z}|\}$. By trivially bounding
$\hat {V}:=q P^{\epsilon -1}\max \{1,HP^2|\underline {z}|\}$. By trivially bounding ![]() $|S(q;\underline {m})|$ by
$|S(q;\underline {m})|$ by ![]() $q^n$, and setting
$q^n$, and setting ![]() $N\geq n+2$, it is easy to show that
$N\geq n+2$, it is easy to show that
by the second half of Lemma 5.2. Hence,
Now by the first half of Lemma 5.2 (setting ![]() $N\geq n+4$), we have
$N\geq n+4$), we have
 \begin{align*} |T_{\underline{h}}(q,\underline{z})|&\ll 1+q^{-n}\sum_{|\underline{m}|\ll \hat{V}} |S(q;\underline{m})|\cdot \mathrm{meas}(\{\underline{y}\in P\,\mathrm{Supp}(\omega)\,:\, |\nabla \hat{f}_{\underline{z}}(\underline{y})-\underline{m}|\leq V\}\\ &= 1+q^{-n}\sum_{|\underline{m}|\ll \hat{V}} |S(q;\underline{m})|\int_{\underline{y}\in P\,\mathrm{Supp}(\omega)} \mathrm{Char}(\underline{m},\underline{y})\, d\underline{y}, \end{align*}
\begin{align*} |T_{\underline{h}}(q,\underline{z})|&\ll 1+q^{-n}\sum_{|\underline{m}|\ll \hat{V}} |S(q;\underline{m})|\cdot \mathrm{meas}(\{\underline{y}\in P\,\mathrm{Supp}(\omega)\,:\, |\nabla \hat{f}_{\underline{z}}(\underline{y})-\underline{m}|\leq V\}\\ &= 1+q^{-n}\sum_{|\underline{m}|\ll \hat{V}} |S(q;\underline{m})|\int_{\underline{y}\in P\,\mathrm{Supp}(\omega)} \mathrm{Char}(\underline{m},\underline{y})\, d\underline{y}, \end{align*}
where
 \[ \mathrm{Char}(\underline{m},\underline{y})=\begin{cases} 1 & \text{if }\; |\nabla \hat{f}_{\underline{z}}(\underline{y})-\underline{m}|\leq V,\\ 0 & \text{else,} \end{cases} \]
\[ \mathrm{Char}(\underline{m},\underline{y})=\begin{cases} 1 & \text{if }\; |\nabla \hat{f}_{\underline{z}}(\underline{y})-\underline{m}|\leq V,\\ 0 & \text{else,} \end{cases} \]
 \begin{align*} \implies |T_{\underline{h}}(q,\underline{z})|&\ll 1+q^{-n}\int_{\underline{y}\in P\,\mathrm{Supp}(\omega)}\sum_{\substack{|\underline{m}|\ll \hat{V}\\|\nabla \hat{f}_{\underline{z}}(\underline{y})-\underline{m}|\leq V}}|S(q;\underline{m})| \,d\underline{y}\\ &\ll 1+q^{-n}\int_{\underline{y}\in P\,\mathrm{Supp}(\omega)}\sum_{|\underline{m}-\underline{m}_0(\underline{y})|\leq V}|S(q;\underline{m})| \,d\underline{y}. \end{align*}
\begin{align*} \implies |T_{\underline{h}}(q,\underline{z})|&\ll 1+q^{-n}\int_{\underline{y}\in P\,\mathrm{Supp}(\omega)}\sum_{\substack{|\underline{m}|\ll \hat{V}\\|\nabla \hat{f}_{\underline{z}}(\underline{y})-\underline{m}|\leq V}}|S(q;\underline{m})| \,d\underline{y}\\ &\ll 1+q^{-n}\int_{\underline{y}\in P\,\mathrm{Supp}(\omega)}\sum_{|\underline{m}-\underline{m}_0(\underline{y})|\leq V}|S(q;\underline{m})| \,d\underline{y}. \end{align*}
where ![]() $\underline {m}_0(\underline {y}):=\nabla \hat {f}_{\underline {z}}(\underline {y})$. Hence, we have the following.
$\underline {m}_0(\underline {y}):=\nabla \hat {f}_{\underline {z}}(\underline {y})$. Hence, we have the following.
Proposition 5.3 Let ![]() $|\underline {z}|=\max \{|z_1|,|z_2|\}$. Then for any
$|\underline {z}|=\max \{|z_1|,|z_2|\}$. Then for any ![]() $q\in \mathbb {N}$,
$q\in \mathbb {N}$,
 \[ |T(q,\underline{z})|\ll 1+q^{-n}P^n\sup_{\underline{y}\in P\,\mathrm{Supp}(\omega)}\bigg{\{}\sum_{|\underline{m}-\underline{m}_0(\underline{y})|\leq V}|S(q;\underline{m})| \bigg{\}}, \]
\[ |T(q,\underline{z})|\ll 1+q^{-n}P^n\sup_{\underline{y}\in P\,\mathrm{Supp}(\omega)}\bigg{\{}\sum_{|\underline{m}-\underline{m}_0(\underline{y})|\leq V}|S(q;\underline{m})| \bigg{\}}, \]
for some ![]() $\underline {m}_0(\underline {y})$, where
$\underline {m}_0(\underline {y})$, where
Our attention now turns to finding a suitable bound for ![]() $|S(q;\underline {m})|$. As is standard when dealing with exponential sum bounds, we will take advantage of the multiplicative property of
$|S(q;\underline {m})|$. As is standard when dealing with exponential sum bounds, we will take advantage of the multiplicative property of ![]() $S(q;\underline {m})$ and decompose
$S(q;\underline {m})$ and decompose ![]() $q$ into its square-free, square and cube-full components so that we can use better bounds in the former two cases (in particular, we will make use of the
$q$ into its square-free, square and cube-full components so that we can use better bounds in the former two cases (in particular, we will make use of the ![]() ${\underline {a}}$ sum to improve our bounds in the former cases). Indeed, we may use a lemma of Hooley [Reference HooleyHoo78, Lemma 3.2] to get the following result.
${\underline {a}}$ sum to improve our bounds in the former cases). Indeed, we may use a lemma of Hooley [Reference HooleyHoo78, Lemma 3.2] to get the following result.
Lemma 5.4 Let ![]() $\underline {a}\in \mathbb {Z}^2$ such that
$\underline {a}\in \mathbb {Z}^2$ such that ![]() $(q,\underline {a})=1$,
$(q,\underline {a})=1$, ![]() $q=rs$ where
$q=rs$ where ![]() $(r,s)=1$ and
$(r,s)=1$ and ![]() $\underline {m}\in \mathbb {Z}^n$. Then
$\underline {m}\in \mathbb {Z}^n$. Then
where ![]() $r\bar {r}+s\bar {s}=1$.
$r\bar {r}+s\bar {s}=1$.
The above lemma is proved using a very standard argument akin to [Reference Browning and Heath-BrownBH09, Lemma 10] and [Reference Marmon and VisheMV19, Lemma 4.5], and therefore we will skip its proof here. Our treatment of bounds for the quadratic exponential sums will vary depending on whether ![]() $q$ is square-free, a square or cube-full. Since the exponential sums satisfy the mutliplicativity relation (5.10), it is natural to set
$q$ is square-free, a square or cube-full. Since the exponential sums satisfy the mutliplicativity relation (5.10), it is natural to set ![]() $q=b_1b_2q_3$ where
$q=b_1b_2q_3$ where
 \begin{equation} b_1:=\prod_{p||q}p,\quad b_2:=\prod_{p^2||q}p^2,\quad q_3:=\prod_{\substack{p^e||q\\ e>2}}p^e. \end{equation}
\begin{equation} b_1:=\prod_{p||q}p,\quad b_2:=\prod_{p^2||q}p^2,\quad q_3:=\prod_{\substack{p^e||q\\ e>2}}p^e. \end{equation}Then by Lemma 5.4, we have that
for some constants ![]() $c_1,c_2,c_3$ such that
$c_1,c_2,c_3$ such that ![]() $(b_1,c_1)=(b_2,c_2)=(q_3,c_3)=1$. Finding suitable bounds for the size of these three exponential sums will be the topic of the rest of this section.
$(b_1,c_1)=(b_2,c_2)=(q_3,c_3)=1$. Finding suitable bounds for the size of these three exponential sums will be the topic of the rest of this section.
5.1 Square-free exponential sums
In this section, we will briefly consider the quadratic exponential sums ![]() $S(b_1;\underline {m})$ when
$S(b_1;\underline {m})$ when ![]() $q=b_1$ is square-free. This case is extensively studied in [Reference Marmon and VisheMV19, Section 5], where bounds are obtained for exponential sums for a general system of polynomials
$q=b_1$ is square-free. This case is extensively studied in [Reference Marmon and VisheMV19, Section 5], where bounds are obtained for exponential sums for a general system of polynomials ![]() $f$ and
$f$ and ![]() $g$. Using the multiplicativity of the exponential sum in (5.10), it is enough to consider the sums
$g$. Using the multiplicativity of the exponential sum in (5.10), it is enough to consider the sums ![]() $S(p,\underline {m})$ where
$S(p,\underline {m})$ where ![]() $p$ is a prime. We may rewrite
$p$ is a prime. We may rewrite
where
 \begin{equation} \Sigma_1:=\sum_{a_1=1}^p\sum_{a_2=1}^p \sum_{\underline{u} \bmod{q}} e_p(a_1f(\underline{u})+a_2g(\underline{u})+\underline{m}\cdot\underline{u})\quad\textrm{ and }\quad\Sigma_4:=\sum_{\underline{u} \bmod{q}} e_p(\underline{m}\cdot\underline{u}). \end{equation}
\begin{equation} \Sigma_1:=\sum_{a_1=1}^p\sum_{a_2=1}^p \sum_{\underline{u} \bmod{q}} e_p(a_1f(\underline{u})+a_2g(\underline{u})+\underline{m}\cdot\underline{u})\quad\textrm{ and }\quad\Sigma_4:=\sum_{\underline{u} \bmod{q}} e_p(\underline{m}\cdot\underline{u}). \end{equation}
Here the notation ![]() $\Sigma _1$ and
$\Sigma _1$ and ![]() $\Sigma _4$ is used to correspond to the corresponding sums in [Reference Marmon and VisheMV19, Section 5]. Note that the argument in [Reference Marmon and VisheMV19, Section 5] does not depend on the degree of the forms
$\Sigma _4$ is used to correspond to the corresponding sums in [Reference Marmon and VisheMV19, Section 5]. Note that the argument in [Reference Marmon and VisheMV19, Section 5] does not depend on the degree of the forms ![]() $f$ and
$f$ and ![]() $g$. In fact, our exponential sums are more ‘natural’ than those which appear in [Reference Marmon and VisheMV19] and, as a result, only sums
$g$. In fact, our exponential sums are more ‘natural’ than those which appear in [Reference Marmon and VisheMV19] and, as a result, only sums ![]() $\Sigma _1$ and
$\Sigma _1$ and ![]() $\Sigma _4$ appear in our analysis. We may now use the results in [Reference Marmon and VisheMV19, Section 5] directly here as they do indeed bound the sums
$\Sigma _4$ appear in our analysis. We may now use the results in [Reference Marmon and VisheMV19, Section 5] directly here as they do indeed bound the sums ![]() $\Sigma _1$ and
$\Sigma _1$ and ![]() $\Sigma _4$ as well, but only in the case where
$\Sigma _4$ as well, but only in the case where ![]() $f^{(0)}$ and
$f^{(0)}$ and ![]() $g^{(0)}$ intersect properly over
$g^{(0)}$ intersect properly over ![]() $\overline {\mathbb {F}}_p$. When
$\overline {\mathbb {F}}_p$. When ![]() $n\geq 2$, we may use [Reference Marmon and VisheMV19, Prop. 5.2, Lemma 5.4] to get the following.
$n\geq 2$, we may use [Reference Marmon and VisheMV19, Prop. 5.2, Lemma 5.4] to get the following.
Proposition 5.5 Let ![]() $f,g\in \mathbb {Z}[x_1,\ldots,x_n]$ be quadratic polynomials such that
$f,g\in \mathbb {Z}[x_1,\ldots,x_n]$ be quadratic polynomials such that ![]() $s_{\infty }(f^{(0)},g^{(0)})=-1$. Let
$s_{\infty }(f^{(0)},g^{(0)})=-1$. Let ![]() $b_1$ be a square-free number. If
$b_1$ be a square-free number. If ![]() $n>1$, then there exists some
$n>1$, then there exists some ![]() $\Phi _{f,g}=\Phi \in \mathbb {Z}[x_1,\ldots,x_n]$ such that
$\Phi _{f,g}=\Phi \in \mathbb {Z}[x_1,\ldots,x_n]$ such that
for every ![]() $\underline {m}\in \mathbb {Z}^n$. Furthermore,
$\underline {m}\in \mathbb {Z}^n$. Furthermore, ![]() $\Phi$ has the following properties:
$\Phi$ has the following properties:
(1)
 $\Phi$ is homogeneous;
$\Phi$ is homogeneous;(2)
 $\deg (\Phi )\ll _n 1$;
$\deg (\Phi )\ll _n 1$;(3)
 $\log \|\Phi \|\ll _n \log \|f\| + \log \|g\|$;
$\log \|\Phi \|\ll _n \log \|f\| + \log \|g\|$;(4)
 $\mathrm {Cont}(\Phi )=1$.
$\mathrm {Cont}(\Phi )=1$.
Note that all the implied constants here only depend on ![]() $n$ and are independent of
$n$ and are independent of ![]() $\|f\|$ and
$\|f\|$ and ![]() $\|g\|$.
$\|g\|$.
Proof. To begin, since ![]() $s_p(f^{(0)},g^{(0)})=-1$, we may use a
$s_p(f^{(0)},g^{(0)})=-1$, we may use a ![]() $\mathbb {Q}$ version of the dual variety explicitly described in [Reference VisheVis23, Lemma 4.2] to see that the polynomial defining the dual variety of the intersection variety of
$\mathbb {Q}$ version of the dual variety explicitly described in [Reference VisheVis23, Lemma 4.2] to see that the polynomial defining the dual variety of the intersection variety of ![]() $f^{(0)},g^{(0)}$ satisfies the four conditions for
$f^{(0)},g^{(0)}$ satisfies the four conditions for ![]() $\Phi$ in the statement of this proposition. Hence, we may let
$\Phi$ in the statement of this proposition. Hence, we may let ![]() $\Phi$ be this polynomial. This allows us to improve the first assertion of [Reference Marmon and VisheMV19, Proposition 5.2]: indeed, if we let
$\Phi$ be this polynomial. This allows us to improve the first assertion of [Reference Marmon and VisheMV19, Proposition 5.2]: indeed, if we let ![]() $\delta _p(\underline {v}):=s_p(f^{(0)},g^{(0)},L_{\underline {v}})$, where
$\delta _p(\underline {v}):=s_p(f^{(0)},g^{(0)},L_{\underline {v}})$, where ![]() $L_{\underline {v}}$ is the hyperplane defined by
$L_{\underline {v}}$ is the hyperplane defined by ![]() $\underline {v}$, then
$\underline {v}$, then ![]() $\delta _p(\underline {v})\leq s_p(f^{(0)},g^{(0)})$ whenever
$\delta _p(\underline {v})\leq s_p(f^{(0)},g^{(0)})$ whenever ![]() $p\nmid \Phi (\underline {v})$. We automatically get this since
$p\nmid \Phi (\underline {v})$. We automatically get this since
for every ![]() $\underline {v}$ not on the dual variety of
$\underline {v}$ not on the dual variety of ![]() $f^{(0)},g^{(0)}$ (over
$f^{(0)},g^{(0)}$ (over ![]() $\overline {\mathbb {F}}_p$), and we must have
$\overline {\mathbb {F}}_p$), and we must have ![]() $p\mid \Phi (\underline {v})$ when
$p\mid \Phi (\underline {v})$ when ![]() $\underline {v}$ is on the dual variety by our choice of
$\underline {v}$ is on the dual variety by our choice of ![]() $\Phi$.
$\Phi$.
Note that if ![]() $f^{(0)},g^{(0)}$ intersect properly, then the bounds in [Reference Marmon and VisheMV19, Lemmas 5.1 and 5.4] hold for all polynomials
$f^{(0)},g^{(0)}$ intersect properly, then the bounds in [Reference Marmon and VisheMV19, Lemmas 5.1 and 5.4] hold for all polynomials ![]() $f,g$ regardless of any condition on their degrees. The key difference to the situation here is that, in the case when we have improper intersection, we define the singular locus differently to [Reference Marmon and VisheMV19]. This is due to both of our polynomials varying here, whilst one of the corresponding polynomials in [Reference Marmon and VisheMV19] is fixed. In particular, in this case our singular locus can either be
$f,g$ regardless of any condition on their degrees. The key difference to the situation here is that, in the case when we have improper intersection, we define the singular locus differently to [Reference Marmon and VisheMV19]. This is due to both of our polynomials varying here, whilst one of the corresponding polynomials in [Reference Marmon and VisheMV19] is fixed. In particular, in this case our singular locus can either be ![]() $n-2$ or
$n-2$ or ![]() $n-1$ as discussed in the proof of Lemma 2.1, while in [Reference Marmon and VisheMV19] in the case of improper intersection of top forms, the singular locus is defined to be
$n-1$ as discussed in the proof of Lemma 2.1, while in [Reference Marmon and VisheMV19] in the case of improper intersection of top forms, the singular locus is defined to be ![]() $n-1$ uniformly. Our proof here will follow that of [Reference Marmon and VisheMV19, Lemma 5.4].
$n-1$ uniformly. Our proof here will follow that of [Reference Marmon and VisheMV19, Lemma 5.4].
In the case when quadratic polynomials ![]() $f^{(0)},g^{(0)}$ intersect properly over
$f^{(0)},g^{(0)}$ intersect properly over ![]() $\overline {\mathbb {F}}_p$, [Reference Marmon and VisheMV19, Lemma 5.4] (and our improvement to [Reference Marmon and VisheMV19, Proposition 5.2]) goes through handing us
$\overline {\mathbb {F}}_p$, [Reference Marmon and VisheMV19, Lemma 5.4] (and our improvement to [Reference Marmon and VisheMV19, Proposition 5.2]) goes through handing us
It now remains to consider the case when ![]() $f^{(0)}$ and
$f^{(0)}$ and ![]() $g^{(0)}$ intersect improperly in greater detail. In each of the cases of improper intersection of
$g^{(0)}$ intersect improperly in greater detail. In each of the cases of improper intersection of ![]() $f^{(0)}$ and
$f^{(0)}$ and ![]() $g^{(0)}$, the singular locus
$g^{(0)}$, the singular locus ![]() $s_{p}(f^{(0)},g^{(0)})\geq n-2$. We therefore note that the trivial bound
$s_{p}(f^{(0)},g^{(0)})\geq n-2$. We therefore note that the trivial bound
suffices for every ![]() $n\geq 2$. We now turn our attention to
$n\geq 2$. We now turn our attention to ![]() $\Sigma _1$. We will first show that
$\Sigma _1$. We will first show that
in the case that ![]() $f^{(0)}$ and
$f^{(0)}$ and ![]() $g^{(0)}$ intersect improperly over
$g^{(0)}$ intersect improperly over ![]() $\overline {\mathbb {F}}_p$. In the case where
$\overline {\mathbb {F}}_p$. In the case where ![]() $n>1$, there are two cases to consider:
$n>1$, there are two cases to consider: ![]() $s_{p}(f^{(0)},g^{(0)})= n-1$ and
$s_{p}(f^{(0)},g^{(0)})= n-1$ and ![]() $s_{p}(f^{(0)},g^{(0)})= n-2$ (see the proof of Lemma 2.1). In the former case, we may again use the trivial bound:
$s_{p}(f^{(0)},g^{(0)})= n-2$ (see the proof of Lemma 2.1). In the former case, we may again use the trivial bound:
When ![]() $s_{p}(f^{(0)},g^{(0)})= n-2$, we instead note that
$s_{p}(f^{(0)},g^{(0)})= n-2$, we instead note that
 \begin{align*} |\Sigma_1|&=\bigg{|}p^2\sum_{\substack{\underline{x}\bmod{p}\\f(\underline{x})\equiv g(\underline{x})\equiv 0 \bmod{p}}} e_p(\underline{m}\cdot\underline{x})\bigg{|}\nonumber\\ &\leq p^2 \#\{\underline{x}\in \mathbb{F}_p^n \, : \, f(\underline{x})=g(\underline{x})=0\}\\ &\ll p^{2+n-1}=p^{2+s_{p}(f^{(0)},g^{(0)})}=p^2D(p). \end{align*}
\begin{align*} |\Sigma_1|&=\bigg{|}p^2\sum_{\substack{\underline{x}\bmod{p}\\f(\underline{x})\equiv g(\underline{x})\equiv 0 \bmod{p}}} e_p(\underline{m}\cdot\underline{x})\bigg{|}\nonumber\\ &\leq p^2 \#\{\underline{x}\in \mathbb{F}_p^n \, : \, f(\underline{x})=g(\underline{x})=0\}\\ &\ll p^{2+n-1}=p^{2+s_{p}(f^{(0)},g^{(0)})}=p^2D(p). \end{align*}
Here, we could bound ![]() $\#\{\underline {x}\in \mathbb {F}_p^n \, : \, f(\underline {x})=g(\underline {x})=0\}$ by
$\#\{\underline {x}\in \mathbb {F}_p^n \, : \, f(\underline {x})=g(\underline {x})=0\}$ by ![]() $O(p^{n-1})$ due to the fact that
$O(p^{n-1})$ due to the fact that
Hence, we have shown that when ![]() $f^{(0)}$,
$f^{(0)}$, ![]() $g^{(0)}$ intersect improperly, we have
$g^{(0)}$ intersect improperly, we have
provided that ![]() $n\geq 2$, as required. Therefore, we may conclude that for a general
$n\geq 2$, as required. Therefore, we may conclude that for a general ![]() $p$ (irrespective of whether or not the intersection is proper)
$p$ (irrespective of whether or not the intersection is proper)
where ![]() $C$ is some constant. Finally, by Lemma 5.4, we have
$C$ is some constant. Finally, by Lemma 5.4, we have
 \begin{align*} S(b_1,\underline{m})&=\prod_{p\mid b_1} S(p,c_p\underline{m})\\ &\leq C(n)^{d(b_1)} b_1^{1+n/2+\varepsilon}D(b_1)\prod_{p\mid b_1}(p,\Phi(c_p\underline{m}))^{1/2}\\ &=C(n)^{d(b_1)} b_1^{1+n/2+\varepsilon}D(b_1)(b_1,\Phi(\underline{m}))^{1/2}, \end{align*}
\begin{align*} S(b_1,\underline{m})&=\prod_{p\mid b_1} S(p,c_p\underline{m})\\ &\leq C(n)^{d(b_1)} b_1^{1+n/2+\varepsilon}D(b_1)\prod_{p\mid b_1}(p,\Phi(c_p\underline{m}))^{1/2}\\ &=C(n)^{d(b_1)} b_1^{1+n/2+\varepsilon}D(b_1)(b_1,\Phi(\underline{m}))^{1/2}, \end{align*}
where ![]() $d(b_1):=\#\{p\mid b_1\}$ is the divisor function of
$d(b_1):=\#\{p\mid b_1\}$ is the divisor function of ![]() $b_1$. We could replace
$b_1$. We could replace ![]() $(p,\Phi (c_p\underline {m}))$ with
$(p,\Phi (c_p\underline {m}))$ with ![]() $(b_1,\Phi (\underline {m}))$ because
$(b_1,\Phi (\underline {m}))$ because ![]() $\Phi$ is homogeneous and
$\Phi$ is homogeneous and ![]() $(p,c_p)=1$. All that is left to do is show that
$(p,c_p)=1$. All that is left to do is show that ![]() $C(n)^{d(b_1)}$ does not contribute more than
$C(n)^{d(b_1)}$ does not contribute more than ![]() $O(P^{\varepsilon })$. To see this, we note that
$O(P^{\varepsilon })$. To see this, we note that ![]() $d(b_1)\ll \log (b_1)/\log \log (b_1)$. Hence, there is some constant
$d(b_1)\ll \log (b_1)/\log \log (b_1)$. Hence, there is some constant ![]() $d$ such that
$d$ such that
provided that ![]() $b_1\gg _{\varepsilon } 1$. We automatically have
$b_1\gg _{\varepsilon } 1$. We automatically have ![]() $d(b_1)\ll 1$ if
$d(b_1)\ll 1$ if ![]() $b_1\not \gg 1$, so we get
$b_1\not \gg 1$, so we get ![]() $c^{d(b_1)}\ll 1\ll b_1^{\varepsilon }$ in that case. Hence, we may conclude that Proposition 5.5 is true. We will bound the
$c^{d(b_1)}\ll 1\ll b_1^{\varepsilon }$ in that case. Hence, we may conclude that Proposition 5.5 is true. We will bound the ![]() $C(n)$ term in future lemmas by
$C(n)$ term in future lemmas by ![]() $b_1^{\epsilon }$ without further comment.
$b_1^{\epsilon }$ without further comment.
We also must consider when ![]() $n=1$. In this case, it is sufficient for us to use a weaker bound than [Reference Marmon and VisheMV19, Lemma 5.5]. We will show the following.
$n=1$. In this case, it is sufficient for us to use a weaker bound than [Reference Marmon and VisheMV19, Lemma 5.5]. We will show the following.
Proposition 5.6 Let ![]() $f,g\in \mathbb {Z}[x]$ be quadratic polynomials and let
$f,g\in \mathbb {Z}[x]$ be quadratic polynomials and let ![]() $b_1$ be a square-free integer. Then
$b_1$ be a square-free integer. Then
Proof. The proof of Proposition 5.6 is almost trivial. We start by applying Lemma 5.4 so that we may consider ![]() $S(p; cm)$ for some
$S(p; cm)$ for some ![]() $p\nmid c$. We note that
$p\nmid c$. We note that
and we trivially have ![]() $|\Sigma _4|\leq p$. Hence, by (5.4) and noting that
$|\Sigma _4|\leq p$. Hence, by (5.4) and noting that ![]() $(p,\mathrm {Cont}(f),\mathrm {Cont}(g))\leq (p,\mathrm {Cont}(f^{(0)}),\mathrm {Cont}(g^{(0)}))$:
$(p,\mathrm {Cont}(f),\mathrm {Cont}(g))\leq (p,\mathrm {Cont}(f^{(0)}),\mathrm {Cont}(g^{(0)}))$:
and so
for any ![]() $m\in \mathbb {Z}$.
$m\in \mathbb {Z}$.
5.2 Square-full bound
In this section, we will derive the bound which will be used when ![]() $q$ is square-full. When
$q$ is square-full. When ![]() $q$ is square-full, we give up on saving
$q$ is square-full, we give up on saving ![]() $q$ over the
$q$ over the ![]() ${\underline {a}}$ sum, and instead start with the bound
${\underline {a}}$ sum, and instead start with the bound
 \begin{equation} |S(q;\underline{m})|\leq \sideset{}{^*}\sum_{{\underline{a}}}^q |S({\underline{a}},q;\underline{m})|, \end{equation}
\begin{equation} |S(q;\underline{m})|\leq \sideset{}{^*}\sum_{{\underline{a}}}^q |S({\underline{a}},q;\underline{m})|, \end{equation}
where ![]() $f,g$ are quadratic polynomials, and
$f,g$ are quadratic polynomials, and
For a fixed value of ![]() ${\underline {a}}$, the exponential sum
${\underline {a}}$, the exponential sum ![]() $S(\underline {a}, q; \underline {m})$ is a standard quadratic exponential sum with leading quadratic part defined by the matrix
$S(\underline {a}, q; \underline {m})$ is a standard quadratic exponential sum with leading quadratic part defined by the matrix
We will assume further that ![]() $2\,|\, (\mathrm {Cont}(f^{(0)}),\mathrm {Cont}(g^{(0)}))$ so that
$2\,|\, (\mathrm {Cont}(f^{(0)}),\mathrm {Cont}(g^{(0)}))$ so that ![]() $M({\underline {a}})\in M_n(\mathbb {Z})$ for every
$M({\underline {a}})\in M_n(\mathbb {Z})$ for every ![]() ${\underline {a}}$.
${\underline {a}}$.
Remark 5.7 In the broader context of the argument that we are building, the reason why we may assume that ![]() $2\,|\, (\mathrm {Cont}(f^{(0)}),\mathrm {Cont}(g^{(0)}))$ is due to Remark 3.1: if the coefficients of our original cubic forms in § 3 are divisible by
$2\,|\, (\mathrm {Cont}(f^{(0)}),\mathrm {Cont}(g^{(0)}))$ is due to Remark 3.1: if the coefficients of our original cubic forms in § 3 are divisible by ![]() $2$, then the coefficients of the differenced quadratic polynomials coming from § 4 must also be divisible by
$2$, then the coefficients of the differenced quadratic polynomials coming from § 4 must also be divisible by ![]() $2$.
$2$.
A standard squaring argument as obtained in [Reference VisheVis23, Lemma 2.5], for example, readily hands us a bound
where ![]() $\#\mathrm {Null}_q(M)$ denotes the number of solutions of the equation
$\#\mathrm {Null}_q(M)$ denotes the number of solutions of the equation ![]() $M\underline {x}\equiv \underline {\mathrm {0}}\bmod {q}$ as defined in (2.14). To estimate this, we will resort to using a Smith normal form of the matrix
$M\underline {x}\equiv \underline {\mathrm {0}}\bmod {q}$ as defined in (2.14). To estimate this, we will resort to using a Smith normal form of the matrix ![]() $M$. The Smith normal form of
$M$. The Smith normal form of ![]() $M$ hands us invertible integer matrices
$M$ hands us invertible integer matrices ![]() $S$ and
$S$ and ![]() $T$ be with determinant
$T$ be with determinant ![]() $\pm 1$ such that
$\pm 1$ such that
 \begin{equation} SMT=\mathrm{Smith}(M)=\begin{pmatrix} \lambda_1 & 0 & 0 & \cdots & 0\\ 0 & \lambda_2 & 0 & \cdots & 0 \\ 0 & 0 & \ddots & & \vdots\\ \vdots & \vdots & & \ddots\\ 0 & 0 & \cdots & & \lambda_n \end{pmatrix}\in M_n(\mathbb{Z}), \end{equation}
\begin{equation} SMT=\mathrm{Smith}(M)=\begin{pmatrix} \lambda_1 & 0 & 0 & \cdots & 0\\ 0 & \lambda_2 & 0 & \cdots & 0 \\ 0 & 0 & \ddots & & \vdots\\ \vdots & \vdots & & \ddots\\ 0 & 0 & \cdots & & \lambda_n \end{pmatrix}\in M_n(\mathbb{Z}), \end{equation}
where ![]() $\lambda _1\mid \lambda _2\mid \cdots \mid \lambda _n$. Since the forms
$\lambda _1\mid \lambda _2\mid \cdots \mid \lambda _n$. Since the forms ![]() $f^{(0)}$ and
$f^{(0)}$ and ![]() $g^{(0)}$ are assumed to be arbitrary for now, it is easy to conclude that
$g^{(0)}$ are assumed to be arbitrary for now, it is easy to conclude that
 \begin{equation} |S(\underline{a}, q; \underline{m})|\ll q^{n/2}\prod_{i=1}^n \lambda_{q,i}^{1/2}, \end{equation}
\begin{equation} |S(\underline{a}, q; \underline{m})|\ll q^{n/2}\prod_{i=1}^n \lambda_{q,i}^{1/2}, \end{equation}where
Remark 5.8 Recall that we aim to finally substitute ![]() $f=F_{\underline {h}}$ and
$f=F_{\underline {h}}$ and ![]() $g=G_{\underline {h}}$. Note that the extra factor appearing on the right-hand side of (5.20) is a generalisation of the factor
$g=G_{\underline {h}}$. Note that the extra factor appearing on the right-hand side of (5.20) is a generalisation of the factor ![]() $D(b_1)^{1/2}$ appearing in Proposition 5.5. This is a drawback of van der Corput differencing that although one starts with a nice pair of forms
$D(b_1)^{1/2}$ appearing in Proposition 5.5. This is a drawback of van der Corput differencing that although one starts with a nice pair of forms ![]() $F$ and
$F$ and ![]() $G$, one ends up with exponential sums of differenced polynomials
$G$, one ends up with exponential sums of differenced polynomials ![]() $F_{\underline {h}}$ and
$F_{\underline {h}}$ and ![]() $G_{\underline {h}}$, which can be highly singular modulo
$G_{\underline {h}}$, which can be highly singular modulo ![]() $q$. If
$q$. If ![]() $q=p^\ell$ for some prime
$q=p^\ell$ for some prime ![]() $p$, if the singular locus
$p$, if the singular locus ![]() $s_p$ as defined in (5.2) is large, then this gives restrictions on the vector
$s_p$ as defined in (5.2) is large, then this gives restrictions on the vector ![]() ${\underline {h}}\bmod {p}$. When
${\underline {h}}\bmod {p}$. When ![]() $\ell$ is small, the extra factors appearing can be compensated from the corresponding bounds on the
$\ell$ is small, the extra factors appearing can be compensated from the corresponding bounds on the ![]() ${\underline {h}}$ sum. However, in the case at hand, when
${\underline {h}}$ sum. However, in the case at hand, when ![]() $q=p^\ell$ for a large
$q=p^\ell$ for a large ![]() $\ell$, we cannot rule out the possibility that for many
$\ell$, we cannot rule out the possibility that for many ![]() ${\underline {h}}$, there may exist a large
${\underline {h}}$, there may exist a large ![]() $q$ such that the factor
$q$ such that the factor ![]() $\prod _{i=1}^n \lambda _{q,i}^{1/2}$ is as large as
$\prod _{i=1}^n \lambda _{q,i}^{1/2}$ is as large as ![]() $q^{n/2}$. This complication arises partly due to the simplicity of the quadratic exponential sums appearing. However, later we would need to average the sums over various
$q^{n/2}$. This complication arises partly due to the simplicity of the quadratic exponential sums appearing. However, later we would need to average the sums over various ![]() $|\underline {m}-\underline {m}_0|\leq V$. We will aim to salvage some of this loss by gaining a congruence condition on
$|\underline {m}-\underline {m}_0|\leq V$. We will aim to salvage some of this loss by gaining a congruence condition on ![]() $\underline {m}$ instead and saving from the sum over
$\underline {m}$ instead and saving from the sum over ![]() $\underline {m}$. This idea partly has already featured in Vishe's work [Reference VisheVis23, Lemma 6.4]. However, in [Reference VisheVis23], the authors are dealing with fixed
$\underline {m}$. This idea partly has already featured in Vishe's work [Reference VisheVis23, Lemma 6.4]. However, in [Reference VisheVis23], the authors are dealing with fixed ![]() $f$ and
$f$ and ![]() $g$, which is not the case here.
$g$, which is not the case here.
Our main goal here is to prove the following result.
Proposition 5.9 Let ![]() ${\underline {a}}\in \mathbb {Z}^2$ and
${\underline {a}}\in \mathbb {Z}^2$ and ![]() $q\in N$ be such that
$q\in N$ be such that ![]() $({\underline {a}},q)=1$, let
$({\underline {a}},q)=1$, let ![]() $\underline {m}\in \mathbb {Z}^n$ and let
$\underline {m}\in \mathbb {Z}^n$ and let ![]() $f,g$ be quadratic polynomials such that
$f,g$ be quadratic polynomials such that ![]() $2\,|\, (\mathrm {Cont}(f^{(0)}),\mathrm {Cont}(g^{(0)}))$. Furthermore, let
$2\,|\, (\mathrm {Cont}(f^{(0)}),\mathrm {Cont}(g^{(0)}))$. Furthermore, let
Then
where
 \begin{equation} \Delta_q(\underline{m}):=\Delta_{T,q}(\underline{m}):=\begin{cases} 1 & \text{if } \lambda_{q,i} \mid (T^t\underline{m})_i\textrm{ for } 1\leq i \leq n,\\ 0 & \text{else.} \end{cases} \end{equation}
\begin{equation} \Delta_q(\underline{m}):=\Delta_{T,q}(\underline{m}):=\begin{cases} 1 & \text{if } \lambda_{q,i} \mid (T^t\underline{m})_i\textrm{ for } 1\leq i \leq n,\\ 0 & \text{else.} \end{cases} \end{equation}
Here, ![]() $T$ is the matrix appearing in the Smith normal form of
$T$ is the matrix appearing in the Smith normal form of ![]() $M$ in (5.19), the
$M$ in (5.19), the ![]() $\lambda _{q,i}$ are defined in (5.21) and given a vector
$\lambda _{q,i}$ are defined in (5.21) and given a vector ![]() $\underline {v}$,
$\underline {v}$, ![]() $(\underline {v})_i$ denotes its
$(\underline {v})_i$ denotes its ![]() $i$th component.
$i$th component.
Proof. To estimate ![]() $|S({\underline {a}},q;\underline {m})|$, we begin by working with its square:
$|S({\underline {a}},q;\underline {m})|$, we begin by working with its square:
 \begin{align*} |S(\underline{a},q;\underline{m})|^2&= \sum_{\underline{x},\underline{y} \bmod{q}} e_{q}((a_1f+a_2g)(\underline{x})+\underline{m}\cdot\underline{x})\overline{e_{q}((a_1f+a_2g)(\underline{y})+\underline{m}\cdot\underline{y})}\\ &= \sum_{\underline{x},\underline{y} \bmod{q}} e_{q}(\underline{x}^t M\underline{x}-\underline{y}^t M\underline{y}+(\underline{m}+\underline{\mathfrak{b}})\cdot(\underline{x}-\underline{y})). \end{align*}
\begin{align*} |S(\underline{a},q;\underline{m})|^2&= \sum_{\underline{x},\underline{y} \bmod{q}} e_{q}((a_1f+a_2g)(\underline{x})+\underline{m}\cdot\underline{x})\overline{e_{q}((a_1f+a_2g)(\underline{y})+\underline{m}\cdot\underline{y})}\\ &= \sum_{\underline{x},\underline{y} \bmod{q}} e_{q}(\underline{x}^t M\underline{x}-\underline{y}^t M\underline{y}+(\underline{m}+\underline{\mathfrak{b}})\cdot(\underline{x}-\underline{y})). \end{align*}
We will now change order of summation by setting ![]() $\underline {x}=\underline {y}+\underline {z}$. Then
$\underline {x}=\underline {y}+\underline {z}$. Then
 \begin{align*} |S(\underline{a},q;\underline{m})|^2&= \sum_{\underline{y},\underline{z} \bmod{q}} e_{q}(\underline{z}^t M\underline{z}+(\underline{m}+\underline{\mathfrak{b}})\cdot\underline{z} +2\underline{y}^t M \underline{z})\\ &=\sum_{\underline{z} \bmod{q}} e_{q}(\underline{z}^t M\underline{z}+\underline{m}'\cdot\underline{z})\sum_{\underline{y} \bmod{q}} e_{q}(\underline{y}\cdot 2M\underline{z}), \end{align*}
\begin{align*} |S(\underline{a},q;\underline{m})|^2&= \sum_{\underline{y},\underline{z} \bmod{q}} e_{q}(\underline{z}^t M\underline{z}+(\underline{m}+\underline{\mathfrak{b}})\cdot\underline{z} +2\underline{y}^t M \underline{z})\\ &=\sum_{\underline{z} \bmod{q}} e_{q}(\underline{z}^t M\underline{z}+\underline{m}'\cdot\underline{z})\sum_{\underline{y} \bmod{q}} e_{q}(\underline{y}\cdot 2M\underline{z}), \end{align*}
where ![]() $\underline {m}'=\underline {m}+\underline {\mathfrak {b}}$. Therefore,
$\underline {m}'=\underline {m}+\underline {\mathfrak {b}}$. Therefore,
where
 \begin{equation} \delta_{M}(\underline{z}):=\begin{cases} 1 & \text{if } M\underline{z}\equiv 0\mod q,\\ 0 & \text{otherwise.} \end{cases} \end{equation}
\begin{equation} \delta_{M}(\underline{z}):=\begin{cases} 1 & \text{if } M\underline{z}\equiv 0\mod q,\\ 0 & \text{otherwise.} \end{cases} \end{equation}
The ‘2’ appearing in ![]() $\delta _{2M}(\underline {z})$ gives rise to some minor technical difficulties in the case when
$\delta _{2M}(\underline {z})$ gives rise to some minor technical difficulties in the case when ![]() $q$ is even. Therefore, we will start by first considering the case when
$q$ is even. Therefore, we will start by first considering the case when ![]() $q$ is odd.
$q$ is odd.
5.2.1 Case:  $q$ odd
$q$ odd
In this case, ![]() $\delta _{2M}(\underline {z})=1$ if and only if
$\delta _{2M}(\underline {z})=1$ if and only if ![]() $M\underline {z}\equiv \underline {0} \mod {q}$, and so we may replace
$M\underline {z}\equiv \underline {0} \mod {q}$, and so we may replace ![]() $\delta _{2M}(\underline {z})$ in (5.24) by
$\delta _{2M}(\underline {z})$ in (5.24) by ![]() $\delta _M(\underline {z})$. Furthermore, we note that
$\delta _M(\underline {z})$. Furthermore, we note that ![]() $M\underline {z}\equiv \underline {0} \mod {q}$ implies that
$M\underline {z}\equiv \underline {0} \mod {q}$ implies that ![]() $\underline {z}^t M\underline {z}\equiv \underline {0} \mod {q}$. Hence, (5.24) simplifies as
$\underline {z}^t M\underline {z}\equiv \underline {0} \mod {q}$. Hence, (5.24) simplifies as
Now, ![]() $M$ has a Smith normal form
$M$ has a Smith normal form ![]() $\mathrm {Smith}(M):=SMT$, for some matrices
$\mathrm {Smith}(M):=SMT$, for some matrices ![]() $S,T\in SL_n(\mathbb {Z})$. In particular, matrices
$S,T\in SL_n(\mathbb {Z})$. In particular, matrices ![]() $S$ and
$S$ and ![]() $T$ are invertible modulo
$T$ are invertible modulo ![]() $q$, for any
$q$, for any ![]() $q\in \mathbb {N}$.
$q\in \mathbb {N}$.
First, we note that
Therefore, on using the substitution ![]() $\underline {z}\mapsto T^{-1}\underline {z}$, (5.24) becomes
$\underline {z}\mapsto T^{-1}\underline {z}$, (5.24) becomes
since ![]() $\delta _{SM}(T\underline {z})=\delta _{SMT}(\underline {z})$ by (5.25). We will now work towards determining which
$\delta _{SM}(T\underline {z})=\delta _{SMT}(\underline {z})$ by (5.25). We will now work towards determining which ![]() $\underline {z}$ make
$\underline {z}$ make ![]() $\delta _{SMT}(\underline {z})$ non-zero. By definition,
$\delta _{SMT}(\underline {z})$ non-zero. By definition, ![]() $\delta _{SMT}(\underline {z})\neq 0$ if and only if
$\delta _{SMT}(\underline {z})\neq 0$ if and only if
or, equivalently,
Hence, we may simplify (5.27) as follows:
 \begin{align} |S(\underline{a},q;\underline{m})|^2&=q^{n}\sum_{\underline{z}\in \mathrm{Null}_q(SMT)} e_{q}(\underline{m}'\cdot T\underline{z})\nonumber\\ &=q^{n}\sum_{\underline{z}\in \mathrm{Null}_q(SMT)} e_{q}(\underline{z}\cdot T^t\underline{m}'), \end{align}
\begin{align} |S(\underline{a},q;\underline{m})|^2&=q^{n}\sum_{\underline{z}\in \mathrm{Null}_q(SMT)} e_{q}(\underline{m}'\cdot T\underline{z})\nonumber\\ &=q^{n}\sum_{\underline{z}\in \mathrm{Null}_q(SMT)} e_{q}(\underline{z}\cdot T^t\underline{m}'), \end{align}
where ![]() $T^t$ is the transpose of
$T^t$ is the transpose of ![]() $T$. This is true because
$T$. This is true because
We now turn our attention to the structure of the ![]() $\mathrm {Null}_q(SMT)$. Since
$\mathrm {Null}_q(SMT)$. Since ![]() $S$ and
$S$ and ![]() $T$ are defined to be the unique matrices (up to units) such that
$T$ are defined to be the unique matrices (up to units) such that ![]() $SMT=\mathrm {Smith}(M)$, it is quite easy to determine precisely when
$SMT=\mathrm {Smith}(M)$, it is quite easy to determine precisely when ![]() $\underline {z}\in \mathrm {Null}_q(SMT)$. Therefore,
$\underline {z}\in \mathrm {Null}_q(SMT)$. Therefore, ![]() $SMT\underline {z}\equiv \underline {0} \mod q$ if and only if
$SMT\underline {z}\equiv \underline {0} \mod q$ if and only if
for every ![]() $i\in \{1,\ldots, n\}$. Therefore,
$i\in \{1,\ldots, n\}$. Therefore,
 \begin{equation} \#\mathrm{Null}_q(SMT)=\prod_{i=1}^n \lambda_{q,i}. \end{equation}
\begin{equation} \#\mathrm{Null}_q(SMT)=\prod_{i=1}^n \lambda_{q,i}. \end{equation}Hence, by (5.21) and (5.28)–(5.29), we have the following:
 \begin{equation} |S(\underline{a},q;\underline{m})|^2=q^{n}\prod_{i=1}^n\sum_{({q}/{\lambda_{q,i}})\mid z_i}e_q(z_i(T^t\underline{m}')_i)=q^{n}\prod_{i=1}^n\sum_{x_i=1}^{\lambda_{q,i}}e_{\lambda_{q,i}}(x_i(T^t\underline{m}')_i) =q^{n}\prod_{i=1}^n \lambda_{q,i} \delta_{q,i}(\underline{m}'), \end{equation}
\begin{equation} |S(\underline{a},q;\underline{m})|^2=q^{n}\prod_{i=1}^n\sum_{({q}/{\lambda_{q,i}})\mid z_i}e_q(z_i(T^t\underline{m}')_i)=q^{n}\prod_{i=1}^n\sum_{x_i=1}^{\lambda_{q,i}}e_{\lambda_{q,i}}(x_i(T^t\underline{m}')_i) =q^{n}\prod_{i=1}^n \lambda_{q,i} \delta_{q,i}(\underline{m}'), \end{equation}where
 \begin{equation} \delta_{q,i}(\underline{u}):=\begin{cases} 1 & \text{if } \lambda_{q,i} \mid (T^t\underline{u})_i,\\ 0 & \text{otherwise,} \end{cases} \end{equation}
\begin{equation} \delta_{q,i}(\underline{u}):=\begin{cases} 1 & \text{if } \lambda_{q,i} \mid (T^t\underline{u})_i,\\ 0 & \text{otherwise,} \end{cases} \end{equation}
and ![]() $(\underline {v})_i$ is the
$(\underline {v})_i$ is the ![]() $i$th component of vector
$i$th component of vector ![]() $\underline {v}$. Therefore, by (5.30) and (5.31):
$\underline {v}$. Therefore, by (5.30) and (5.31):
 \[ |S(\underline{a},q;\underline{m})|^2=q^{n}\#\mathrm{Null}_q(SMT)\prod_{i=1}^n\delta_{q,i}(\underline{m}'). \]
\[ |S(\underline{a},q;\underline{m})|^2=q^{n}\#\mathrm{Null}_q(SMT)\prod_{i=1}^n\delta_{q,i}(\underline{m}'). \]
Finally, it is easy to check that
since ![]() $S$ and
$S$ and ![]() $T$ are both invertible over
$T$ are both invertible over ![]() $\mathbb {Z}/q\mathbb {Z}$ and, therefore, in this case we establish
$\mathbb {Z}/q\mathbb {Z}$ and, therefore, in this case we establish
which clearly suffices.
5.2.2 Case:  $q$ even
$q$ even
We now turn to the case where ![]() $q$ is even. In this case, the above argument needs to be modified due to not being able to directly replace the condition
$q$ is even. In this case, the above argument needs to be modified due to not being able to directly replace the condition ![]() $\delta _{2M}(\underline {z})$ with
$\delta _{2M}(\underline {z})$ with ![]() $\delta _M(\underline {z})$ in (5.24). Instead, we note that
$\delta _M(\underline {z})$ in (5.24). Instead, we note that ![]() $\delta _{2M}(\underline {z})\neq 0$ if and only if
$\delta _{2M}(\underline {z})\neq 0$ if and only if ![]() $M\underline {z}\equiv \underline {0} \mod q/2$. In particular, there must be some
$M\underline {z}\equiv \underline {0} \mod q/2$. In particular, there must be some ![]() $\underline {c}\in \{0,1\}^n$ such that
$\underline {c}\in \{0,1\}^n$ such that
Therefore, if we let
then ![]() $\delta _{2M(\underline {z})}\neq 0$ if and only if
$\delta _{2M(\underline {z})}\neq 0$ if and only if ![]() $\underline {z}\in N_{\underline {c},q}$ for some
$\underline {z}\in N_{\underline {c},q}$ for some ![]() $\underline {c}$. Hence, we may rewrite (5.24) as follows:
$\underline {c}$. Hence, we may rewrite (5.24) as follows:
We now wish to write ![]() $N_{\underline {c},q}$ in terms of
$N_{\underline {c},q}$ in terms of ![]() $\mathrm {Null}_q(M)$ as this will enable us to use the arguments discussed in the odd case. To do this, we invoke Lemma 2.6 to see that either
$\mathrm {Null}_q(M)$ as this will enable us to use the arguments discussed in the odd case. To do this, we invoke Lemma 2.6 to see that either ![]() $N_{\underline {c},q}=\emptyset$ or there exists some
$N_{\underline {c},q}=\emptyset$ or there exists some ![]() $\underline {y}_{\underline {c}}\in (\mathbb {Z}/q\mathbb {Z})^n$ such that
$\underline {y}_{\underline {c}}\in (\mathbb {Z}/q\mathbb {Z})^n$ such that
Hence,
 \begin{align} |S(\underline{a}, q; \underline{m})|^2&= q^n\sum_{\substack{\underline{c}\in \{0,1\}^n\\ N_{\underline{c},q}(M)\neq \emptyset}} \sum_{\underline{z}\in \underline{y}_{\underline{c}} + \mathrm{Null}_{q}(M)} e_q(\underline{z}^t M \underline{z} + \underline{m}'\cdot \underline{z})\nonumber\\ &=q^n\sum_{\substack{\underline{c}\in \{0,1\}^n\\ N_{\underline{c},q}(M)\neq \emptyset}} \sum_{\underline{z}\in \mathrm{Null}_{q}(M)} e_q([\underline{y}_{\underline{c}}+\underline{z}]^t M [\underline{y}_{\underline{c}}+\underline{z}] + \underline{m}'\cdot [\underline{y}_{\underline{c}}+\underline{z}])\nonumber\\ &= q^n\sum_{\substack{\underline{c}\in \{0,1\}^n\\ N_{\underline{c},q}(M)\neq \emptyset}} e_q(\underline{y}_{\underline{c}}^t M \underline{y}_{\underline{c}} + \underline{m}'\cdot \underline{y}_{\underline{c}}) \sum_{\underline{z}\in \mathrm{Null}_{q}(M)} e_q((\underline{z}+2\underline{y}_{\underline{c}})^t M \underline{z} + \underline{m}'\cdot \underline{z})\nonumber\\ &\leq q^n\sum_{\underline{c}\in \{0,1\}^n} \bigg{|} \sum_{\underline{z}\in \mathrm{Null}_{q}(M)} e_q((\underline{z}+2\underline{y}_{\underline{c}})^t M \underline{z} + \underline{m}'\cdot \underline{z})\bigg{|}. \end{align}
\begin{align} |S(\underline{a}, q; \underline{m})|^2&= q^n\sum_{\substack{\underline{c}\in \{0,1\}^n\\ N_{\underline{c},q}(M)\neq \emptyset}} \sum_{\underline{z}\in \underline{y}_{\underline{c}} + \mathrm{Null}_{q}(M)} e_q(\underline{z}^t M \underline{z} + \underline{m}'\cdot \underline{z})\nonumber\\ &=q^n\sum_{\substack{\underline{c}\in \{0,1\}^n\\ N_{\underline{c},q}(M)\neq \emptyset}} \sum_{\underline{z}\in \mathrm{Null}_{q}(M)} e_q([\underline{y}_{\underline{c}}+\underline{z}]^t M [\underline{y}_{\underline{c}}+\underline{z}] + \underline{m}'\cdot [\underline{y}_{\underline{c}}+\underline{z}])\nonumber\\ &= q^n\sum_{\substack{\underline{c}\in \{0,1\}^n\\ N_{\underline{c},q}(M)\neq \emptyset}} e_q(\underline{y}_{\underline{c}}^t M \underline{y}_{\underline{c}} + \underline{m}'\cdot \underline{y}_{\underline{c}}) \sum_{\underline{z}\in \mathrm{Null}_{q}(M)} e_q((\underline{z}+2\underline{y}_{\underline{c}})^t M \underline{z} + \underline{m}'\cdot \underline{z})\nonumber\\ &\leq q^n\sum_{\underline{c}\in \{0,1\}^n} \bigg{|} \sum_{\underline{z}\in \mathrm{Null}_{q}(M)} e_q((\underline{z}+2\underline{y}_{\underline{c}})^t M \underline{z} + \underline{m}'\cdot \underline{z})\bigg{|}. \end{align}
Finally, we note that ![]() $M\underline {z}\equiv \underline {0} \mod q$ since
$M\underline {z}\equiv \underline {0} \mod q$ since ![]() $\underline {z}\in \mathrm {Null}_q(M)$, and so by (5.34), we have the following:
$\underline {z}\in \mathrm {Null}_q(M)$, and so by (5.34), we have the following:
 \begin{align*} |S(\underline{a}, q; \underline{m})|^2 &\leq q^n\sum_{\underline{c}\in \{0,1\}^n} \bigg{|} \sum_{\underline{z}\in \mathrm{Null}_{q}(M)} e_q(\underline{m}'\cdot \underline{z})\bigg{|}\\ &=2^n q^n \bigg{|} \sum_{\underline{z} \bmod{q}} e_q(\underline{m}'\cdot \underline{z}) \delta_{M}(\underline{z})\bigg{|}. \end{align*}
\begin{align*} |S(\underline{a}, q; \underline{m})|^2 &\leq q^n\sum_{\underline{c}\in \{0,1\}^n} \bigg{|} \sum_{\underline{z}\in \mathrm{Null}_{q}(M)} e_q(\underline{m}'\cdot \underline{z})\bigg{|}\\ &=2^n q^n \bigg{|} \sum_{\underline{z} \bmod{q}} e_q(\underline{m}'\cdot \underline{z}) \delta_{M}(\underline{z})\bigg{|}. \end{align*}
This is precisely (5.26) with an extra factor of ![]() $2^n$ and some absolute value signs around the sum (which are irrelevant). We may therefore repeat the arguments in the
$2^n$ and some absolute value signs around the sum (which are irrelevant). We may therefore repeat the arguments in the ![]() $q$ odd case which follow from (5.26) to establish Proposition 5.9.
$q$ odd case which follow from (5.26) to establish Proposition 5.9.
5.2.3 Special case:  $n=1$
$n=1$
We will now briefly consider the case when ![]() $n=1$, as we will need to deal with this case separately later. The arguments used above are still valid in this case, but the bound that we get is simpler due to the matrix,
$n=1$, as we will need to deal with this case separately later. The arguments used above are still valid in this case, but the bound that we get is simpler due to the matrix, ![]() $M$, becoming an integer. In particular, Proposition 5.9 becomes the following.
$M$, becoming an integer. In particular, Proposition 5.9 becomes the following.
Proposition 5.10 Let ![]() ${\underline {a}}\in \mathbb {Z}^2$ and
${\underline {a}}\in \mathbb {Z}^2$ and ![]() $q\in N$ be such that
$q\in N$ be such that ![]() $({\underline {a}},q)=1$, let
$({\underline {a}},q)=1$, let ![]() $m\in \mathbb {Z}$ and let
$m\in \mathbb {Z}$ and let ![]() $f,g\in \mathbb {Z}[x]$ be quadratic polynomials such that
$f,g\in \mathbb {Z}[x]$ be quadratic polynomials such that ![]() $2\,|\, (\mathrm {Cont}(f^{(0)}),\mathrm {Cont}(g^{(0)}))$. Let
$2\,|\, (\mathrm {Cont}(f^{(0)}),\mathrm {Cont}(g^{(0)}))$. Let
Then
where
 \begin{equation} \Delta_{q}'(m):=\begin{cases} 1 & \text{if } (q,M) \mid m,\\ 0 & \text{otherwise.} \end{cases} \end{equation}
\begin{equation} \Delta_{q}'(m):=\begin{cases} 1 & \text{if } (q,M) \mid m,\\ 0 & \text{otherwise.} \end{cases} \end{equation} We will use Propositions 5.9 and 5.10 directly in our future treatment of the cube-full part of ![]() $S(q_3;\underline {m})$ (see (5.12)) in order to get additional saving over the
$S(q_3;\underline {m})$ (see (5.12)) in order to get additional saving over the ![]() $\underline {m}$ sum. For the perfect square part,
$\underline {m}$ sum. For the perfect square part, ![]() $b_2$, however, we will derive a slightly weaker bound from this which will be used to get saving over the
$b_2$, however, we will derive a slightly weaker bound from this which will be used to get saving over the ![]() ${\underline {h}}$ sum later on in the argument.
${\underline {h}}$ sum later on in the argument.
5.3 Cube-free square exponential sums
In this section, we will assume that ![]() $q=b_2$ or, equivalently, that
$q=b_2$ or, equivalently, that ![]() $q$ is a cube-free square. In this case, we will give up on the potential saving we could attain via the
$q$ is a cube-free square. In this case, we will give up on the potential saving we could attain via the ![]() $\underline {m}$ sum from the
$\underline {m}$ sum from the ![]() $\Delta _q(\underline {m}')$ term in Proposition 5.9, and bound
$\Delta _q(\underline {m}')$ term in Proposition 5.9, and bound ![]() $\#\mathrm {Null}_q(M({\underline {a}}))^{1/2}$ in terms of the singular locus of
$\#\mathrm {Null}_q(M({\underline {a}}))^{1/2}$ in terms of the singular locus of ![]() $f^{(0)},g^{(0)}$, where
$f^{(0)},g^{(0)}$, where ![]() $M({\underline {a}})$ is defined as in (5.22). In this special case, we will need to obtain a pointwise saving over the
$M({\underline {a}})$ is defined as in (5.22). In this special case, we will need to obtain a pointwise saving over the ![]() ${\underline {a}}$ sum in order for our bound to be useful. We will start with the case when
${\underline {a}}$ sum in order for our bound to be useful. We will start with the case when ![]() $n\geq 2$. Upon letting
$n\geq 2$. Upon letting ![]() $b_2=c^2$, by Proposition 5.9, Lemmas 2.4–2.5 and (5.16) we have
$b_2=c^2$, by Proposition 5.9, Lemmas 2.4–2.5 and (5.16) we have
 \begin{align} |S(b_2,\underline{m})|&\ll \sideset{}{^*}\sum_{{\underline{a}}}^{b_2}|S(\underline{a}, b_2; \underline{m})|\ll b_2^{n/2}\sideset{}{^*}\sum_{{\underline{a}}}^{b_2}\#\mathrm{Null}_{c^2}(M({\underline{a}}))^{1/2}\ll b_2^{n/2}\sideset{}{^*}\sum_{{\underline{a}}}^{b_2}\#\mathrm{Null}_{c}(M({\underline{a}}))\nonumber\\ &\ll b_2^{2+n/2}c^{s_p+1}=b_2^{2+n/2}\prod_{\substack{p^2\mid q\nonumber\\ p \textrm{ prime }}} p^{s_p+1} =b_2^{2+n/2}D(b_2). \end{align}
\begin{align} |S(b_2,\underline{m})|&\ll \sideset{}{^*}\sum_{{\underline{a}}}^{b_2}|S(\underline{a}, b_2; \underline{m})|\ll b_2^{n/2}\sideset{}{^*}\sum_{{\underline{a}}}^{b_2}\#\mathrm{Null}_{c^2}(M({\underline{a}}))^{1/2}\ll b_2^{n/2}\sideset{}{^*}\sum_{{\underline{a}}}^{b_2}\#\mathrm{Null}_{c}(M({\underline{a}}))\nonumber\\ &\ll b_2^{2+n/2}c^{s_p+1}=b_2^{2+n/2}\prod_{\substack{p^2\mid q\nonumber\\ p \textrm{ prime }}} p^{s_p+1} =b_2^{2+n/2}D(b_2). \end{align}
When ![]() $n=1$, we have
$n=1$, we have ![]() $M({\underline {a}})=a_1d_f+a_2d_g$ for some constants
$M({\underline {a}})=a_1d_f+a_2d_g$ for some constants ![]() $d_f,d_g$. By Proposition 5.10,
$d_f,d_g$. By Proposition 5.10,
 \begin{align}
|S(p^2,\underline{m})|&\ll p\sideset{}{^*}\sum_{{\underline{a}}\bmod{p^2}}(p^2,M({\underline{a}}))^{1/2}\ll
p\sideset{}{^*}\sum_{{\underline{a}}\bmod{p^2}}(p,a_1d_f+a_2d_g)\nonumber\\
&= p \bigg{(} \sideset{}{^*}\sum_{\substack{{\underline{a}}\bmod{p^2}\\ \underline{p} | a_1d_f+a_2d_g}} p +
\sideset{}{^*}\sum_{\substack{{\underline{a}}\bmod{p^2}\\ \underline{p} \nmid a_1d_f+a_2d_g}} 1 \bigg{)}\nonumber\\
&\leq \begin{cases} 2p^{5} & \text{if } (d_f, d_g,
p)=1, \\ p^6 &\text{otherwise.
}\end{cases} \end{align}
\begin{align}
|S(p^2,\underline{m})|&\ll p\sideset{}{^*}\sum_{{\underline{a}}\bmod{p^2}}(p^2,M({\underline{a}}))^{1/2}\ll
p\sideset{}{^*}\sum_{{\underline{a}}\bmod{p^2}}(p,a_1d_f+a_2d_g)\nonumber\\
&= p \bigg{(} \sideset{}{^*}\sum_{\substack{{\underline{a}}\bmod{p^2}\\ \underline{p} | a_1d_f+a_2d_g}} p +
\sideset{}{^*}\sum_{\substack{{\underline{a}}\bmod{p^2}\\ \underline{p} \nmid a_1d_f+a_2d_g}} 1 \bigg{)}\nonumber\\
&\leq \begin{cases} 2p^{5} & \text{if } (d_f, d_g,
p)=1, \\ p^6 &\text{otherwise.
}\end{cases} \end{align}
Hence, upon recalling (5.4), we may bound (5.38) by
We may then use the multiplicativity relation in Lemma 5.4 to get
Combining this with (5.37) gives us the following.
Proposition 5.11 Let ![]() $b_2\in \mathbb {N}$ be a cube-free square. Then
$b_2\in \mathbb {N}$ be a cube-free square. Then
6. Quadratic exponential sums: finalisation
In this section, we will combine all of the bounds we have found in § 5 to reach our final estimate for ![]() $T(q,\underline {z})$. Recall that Proposition 5.3 hands us
$T(q,\underline {z})$. Recall that Proposition 5.3 hands us
 \begin{equation} |T(q,\underline{z})|\ll 1+q^{-n}P^n\sup_{\underline{y}\in P\,\mathrm{Supp}(\omega)}\bigg{\{}\sum_{|\underline{m}-\underline{m}_0(\underline{y})|\leq V}|S(q;\underline{m})|\bigg{\}}. \end{equation}
\begin{equation} |T(q,\underline{z})|\ll 1+q^{-n}P^n\sup_{\underline{y}\in P\,\mathrm{Supp}(\omega)}\bigg{\{}\sum_{|\underline{m}-\underline{m}_0(\underline{y})|\leq V}|S(q;\underline{m})|\bigg{\}}. \end{equation}
In the last section, we focused on getting bounds for individual exponential sums ![]() $|S(q;\underline {m})|$. We begin by considering averages of exponential sums. Throughout, let
$|S(q;\underline {m})|$. We begin by considering averages of exponential sums. Throughout, let ![]() $\underline {m}_0$ be an arbitrary but fixed vector in
$\underline {m}_0$ be an arbitrary but fixed vector in ![]() $\mathbb {Z}^n$ and let
$\mathbb {Z}^n$ and let ![]() ${\underline {\mathfrak {b}}}({\underline {a}})={\underline {\mathfrak {b}}}$ be defined as in (5.22). For
${\underline {\mathfrak {b}}}({\underline {a}})={\underline {\mathfrak {b}}}$ be defined as in (5.22). For ![]() $n\geq 2$: by Lemma 5.4 and Propositions 5.5, 5.9, and 5.11, there are some constants
$n\geq 2$: by Lemma 5.4 and Propositions 5.5, 5.9, and 5.11, there are some constants ![]() $c_1,c_2,c_3$ such that
$c_1,c_2,c_3$ such that ![]() $(b_1,c_1)=(b_2,c_2)=(q_3,c_3)=1$, and
$(b_1,c_1)=(b_2,c_2)=(q_3,c_3)=1$, and
 \begin{align} \sum_{|\underline{m}-\underline{m}_0|\leq V}|S(q;\underline{m})|&\leq \sum_{|\underline{m}-\underline{m}_0|\leq V}|S(b_1;c_1\underline{m})|\cdot|S(b_2;c_2\underline{m})|\cdot|S(q_3;c_3\underline{m})|\nonumber\\ &\ll q^{n/2+\varepsilon} b_1b_2^2 D(b_1b_2)\sum_{|\underline{m}-\underline{m}_0(\underline{m}_0)|\leq V} (\Phi(c_1\underline{m}),b_1)^{1/2}\nonumber\\ &\quad \times\sideset{}{^*}\sum_{{\underline{a}}}^{q_3}\#\mathrm{Null}_{q_3}(a_1M_1+a_2M_2)^{1/2}\Delta_{T,q_3}(c_3\underline{m}+{\underline{\mathfrak{b}}}) \nonumber\\ &:= q^{n/2+\varepsilon} b_1b_2^2 D(b_1b_2)\sideset{}{^*}\sum_{{\underline{a}}}^{q_3}\#\mathrm{Null}_{q_3}(M({\underline{a}}))^{1/2}B(b_1,q_3, V; \underline{m}_0), \end{align}
\begin{align} \sum_{|\underline{m}-\underline{m}_0|\leq V}|S(q;\underline{m})|&\leq \sum_{|\underline{m}-\underline{m}_0|\leq V}|S(b_1;c_1\underline{m})|\cdot|S(b_2;c_2\underline{m})|\cdot|S(q_3;c_3\underline{m})|\nonumber\\ &\ll q^{n/2+\varepsilon} b_1b_2^2 D(b_1b_2)\sum_{|\underline{m}-\underline{m}_0(\underline{m}_0)|\leq V} (\Phi(c_1\underline{m}),b_1)^{1/2}\nonumber\\ &\quad \times\sideset{}{^*}\sum_{{\underline{a}}}^{q_3}\#\mathrm{Null}_{q_3}(a_1M_1+a_2M_2)^{1/2}\Delta_{T,q_3}(c_3\underline{m}+{\underline{\mathfrak{b}}}) \nonumber\\ &:= q^{n/2+\varepsilon} b_1b_2^2 D(b_1b_2)\sideset{}{^*}\sum_{{\underline{a}}}^{q_3}\#\mathrm{Null}_{q_3}(M({\underline{a}}))^{1/2}B(b_1,q_3, V; \underline{m}_0), \end{align}
where ![]() $M({\underline {a}})$ be as in (5.17) and
$M({\underline {a}})$ be as in (5.17) and
where ![]() ${\underline {\mathfrak {b}}}'\equiv c_3^{-1}{\underline {\mathfrak {b}}} \mod q_3$. We used
${\underline {\mathfrak {b}}}'\equiv c_3^{-1}{\underline {\mathfrak {b}}} \mod q_3$. We used ![]() $(\Phi (\underline {m}),b_1)$ instead of
$(\Phi (\underline {m}),b_1)$ instead of ![]() $(\Phi (c_1\underline {m}),b_1)$ in the definition of
$(\Phi (c_1\underline {m}),b_1)$ in the definition of ![]() $B(b_1,q_3,V;\underline {m}_0)$ because
$B(b_1,q_3,V;\underline {m}_0)$ because ![]() $\Phi$ is homogeneous and
$\Phi$ is homogeneous and ![]() $(b_1,c_1)=1$. Likewise, by inspecting the definition of
$(b_1,c_1)=1$. Likewise, by inspecting the definition of ![]() $\Delta$, we can use
$\Delta$, we can use ![]() $\Delta _{T,q_3}(\underline {m}+{\underline {\mathfrak {b}}}')$ in the definition of
$\Delta _{T,q_3}(\underline {m}+{\underline {\mathfrak {b}}}')$ in the definition of ![]() $B(b_1,q_3,V;\underline {m}_0)$ instead of
$B(b_1,q_3,V;\underline {m}_0)$ instead of ![]() $\Delta _{T,q_3}(c_3\underline {m}+{\underline {\mathfrak {b}}})$ since we can ‘divide through’ by
$\Delta _{T,q_3}(c_3\underline {m}+{\underline {\mathfrak {b}}})$ since we can ‘divide through’ by ![]() $c_3$, as
$c_3$, as ![]() $(c_3,q_3)=1$ (in particular,
$(c_3,q_3)=1$ (in particular, ![]() $(c_3,\lambda )=1$ for any divisor,
$(c_3,\lambda )=1$ for any divisor, ![]() $\lambda$, of
$\lambda$, of ![]() $q_3$).
$q_3$).
The first and most difficult task for this section is to bound ![]() $B(b_1,q_3, V; \underline {m}_0)$. This will be quite a delicate task since we need to save over the
$B(b_1,q_3, V; \underline {m}_0)$. This will be quite a delicate task since we need to save over the ![]() $\underline {m}$ sum in two different ways, simultaneously. The following lemma will provide our main estimate for this sum.
$\underline {m}$ sum in two different ways, simultaneously. The following lemma will provide our main estimate for this sum.
Lemma 6.1 Let ![]() $b_1,q_3, V\in \mathbb {N}$ and
$b_1,q_3, V\in \mathbb {N}$ and ![]() $\underline {m}_0\in \mathbb {Z}^n$. Furthermore, let
$\underline {m}_0\in \mathbb {Z}^n$. Furthermore, let ![]() $c$ and
$c$ and ![]() $q_3$ be defined as follows:
$q_3$ be defined as follows:
 \begin{equation} \hat{q}_3:=\prod_{\substack{p^e||q_3\\ 2\nmid e}} p, \quad q_3=c^2\hat{q}_3. \end{equation}
\begin{equation} \hat{q}_3:=\prod_{\substack{p^e||q_3\\ 2\nmid e}} p, \quad q_3=c^2\hat{q}_3. \end{equation}Then
Proof. We begin by noting that
and so by the definition of ![]() $\Delta _{T, q_3}$ (5.23) we clearly have that
$\Delta _{T, q_3}$ (5.23) we clearly have that
for any ![]() $\underline {x}\in \mathbb {Z}^n$. Therefore, since we are looking for an upper bound of
$\underline {x}\in \mathbb {Z}^n$. Therefore, since we are looking for an upper bound of ![]() $B(b_1,q_3, V; \underline {m}_0)$, we may replace
$B(b_1,q_3, V; \underline {m}_0)$, we may replace ![]() $\Delta _{T, q_3}(\underline {m}+{\underline {\mathfrak {b}}}')$ in (6.3) with
$\Delta _{T, q_3}(\underline {m}+{\underline {\mathfrak {b}}}')$ in (6.3) with ![]() $\Delta _{T, c}(\underline {m}+{\underline {\mathfrak {b}}}')$. Furthermore, since all elements of our sum are non-negative, we may extend the sum in (6.3) if we wish. In particular, the following bound must be true:
$\Delta _{T, c}(\underline {m}+{\underline {\mathfrak {b}}}')$. Furthermore, since all elements of our sum are non-negative, we may extend the sum in (6.3) if we wish. In particular, the following bound must be true:
where
We have extended the sum up to ![]() $\hat {V}$ so that we can consider complete sums modulo
$\hat {V}$ so that we can consider complete sums modulo ![]() $c$, as this will make it easier to acquire saving from
$c$, as this will make it easier to acquire saving from ![]() $\Delta _{T,c}$ later. To this end, let
$\Delta _{T,c}$ later. To this end, let ![]() $\underline {m}:=\underline {m}_0+\underline {m}_1+c\underline {m}_2$, where
$\underline {m}:=\underline {m}_0+\underline {m}_1+c\underline {m}_2$, where ![]() $\underline {m}_1\in (\mathbb {Z}/c\mathbb {Z})^n$ and
$\underline {m}_1\in (\mathbb {Z}/c\mathbb {Z})^n$ and ![]() $|\underline {m}_2|\leq \hat {V}/c$. Applying this decomposition on the right-hand side of (6.5) gives
$|\underline {m}_2|\leq \hat {V}/c$. Applying this decomposition on the right-hand side of (6.5) gives
 \begin{align} B(b_1,q_3, V; \underline{m}_0)&\leq \sum_{\underline{m}_1 \bmod{c}}\,\sum_{|\underline{m}_2|\leq \hat{V}/c} (\Phi(\underline{m}_0+\underline{m}_1+c\underline{m}_2),b_1)^{1/2}\Delta_{T,c}(\underline{m}_0+\underline{m}_1 +c\underline{m}_2+{\underline{\mathfrak{b}}}')\nonumber\\ &=\sum_{\underline{m}_1 \bmod{c}}\Delta_{T,c}(\underline{m}_0+\underline{m}_1+{\underline{\mathfrak{b}}}')\sum_{\underline{m}_2\in U(\underline{m}_1)} (\Phi(\underline{m}_0+\underline{m}_1+c\underline{m}_2),b_1)^{1/2}. \end{align}
\begin{align} B(b_1,q_3, V; \underline{m}_0)&\leq \sum_{\underline{m}_1 \bmod{c}}\,\sum_{|\underline{m}_2|\leq \hat{V}/c} (\Phi(\underline{m}_0+\underline{m}_1+c\underline{m}_2),b_1)^{1/2}\Delta_{T,c}(\underline{m}_0+\underline{m}_1 +c\underline{m}_2+{\underline{\mathfrak{b}}}')\nonumber\\ &=\sum_{\underline{m}_1 \bmod{c}}\Delta_{T,c}(\underline{m}_0+\underline{m}_1+{\underline{\mathfrak{b}}}')\sum_{\underline{m}_2\in U(\underline{m}_1)} (\Phi(\underline{m}_0+\underline{m}_1+c\underline{m}_2),b_1)^{1/2}. \end{align}
The upshot of reordering our sum in this way is that we have managed to separate ![]() $\Delta _{T,c}(\underline {m}_0+\underline {m}_1+{\underline {\mathfrak {b}}}')$ and
$\Delta _{T,c}(\underline {m}_0+\underline {m}_1+{\underline {\mathfrak {b}}}')$ and ![]() $(\Phi (\underline {m}_0+\underline {m}_1+c\underline {m}_2),b_1)^{1/2}$. In particular, we can treat
$(\Phi (\underline {m}_0+\underline {m}_1+c\underline {m}_2),b_1)^{1/2}$. In particular, we can treat ![]() $\underline {m}_1$ as fixed for now, and since
$\underline {m}_1$ as fixed for now, and since ![]() $\underline {m}_0$ and
$\underline {m}_0$ and ![]() $c$ are also fixed, we may focus on acquiring saving in the
$c$ are also fixed, we may focus on acquiring saving in the ![]() $\underline {m}_2$ sum via
$\underline {m}_2$ sum via ![]() $(\Phi _{c,\underline {m}_1}(\underline {m}_2),b_1)^{1/2}$, where
$(\Phi _{c,\underline {m}_1}(\underline {m}_2),b_1)^{1/2}$, where
We observe that ![]() $(\Phi _{c,\underline {m}_0,\underline {m}_1}(\underline {m}_2),b_1)$ must be equal to some divisor of
$(\Phi _{c,\underline {m}_0,\underline {m}_1}(\underline {m}_2),b_1)$ must be equal to some divisor of ![]() $b_1$, so we will decompose the
$b_1$, so we will decompose the ![]() $\underline {m}_2$ sum as follows:
$\underline {m}_2$ sum as follows:
We now aim to use [Reference Browning and Heath-BrownBH09, Lemma 4] to bound the right-hand side. Since ![]() $\Phi$ is homogeneous with
$\Phi$ is homogeneous with ![]() $\mathrm {Cont}(\Phi )=1$ by Proposition 5.5, and since
$\mathrm {Cont}(\Phi )=1$ by Proposition 5.5, and since ![]() $c$ and
$c$ and ![]() $d$ are co-prime, we have that
$d$ are co-prime, we have that
Hence, for every prime ![]() $p$ dividing
$p$ dividing ![]() $d$,
$d$, ![]() $\Phi (\underline {m}_0+\underline {m}_1+c\underline {x})$ is a non-trivial polynomial and therefore the corresponding variety is of dimension
$\Phi (\underline {m}_0+\underline {m}_1+c\underline {x})$ is a non-trivial polynomial and therefore the corresponding variety is of dimension ![]() $n-1$. Therefore, we may now use [Reference Browning and Heath-BrownBH09, Lemma 4] to conclude that
$n-1$. Therefore, we may now use [Reference Browning and Heath-BrownBH09, Lemma 4] to conclude that
Substituting this back into (6.8) gives the following:
 \begin{align} \sum_{|\underline{m}_2|\leq \hat{V}/c} (\Phi(\underline{m}_0+\underline{m}_1+c\underline{m}_2),b_1)^{1/2}&\ll \sum_{d\mid b_1} d^{1/2}+\bigg{(} \frac{V}{c}\bigg{)}^{n-1}d^{1/2}+ \bigg{(} \frac{V}{c}\bigg{)}^n d^{-1/2}\nonumber\\ &\ll b_1^{\varepsilon}\bigg{(} b_1^{1/2}+ \bigg{(} \frac{V}{c}\bigg{)}^{n-1}b_1^{1/2}+ \bigg{(} \frac{V}{c}\bigg{)}^n \bigg{)}. \end{align}
\begin{align} \sum_{|\underline{m}_2|\leq \hat{V}/c} (\Phi(\underline{m}_0+\underline{m}_1+c\underline{m}_2),b_1)^{1/2}&\ll \sum_{d\mid b_1} d^{1/2}+\bigg{(} \frac{V}{c}\bigg{)}^{n-1}d^{1/2}+ \bigg{(} \frac{V}{c}\bigg{)}^n d^{-1/2}\nonumber\\ &\ll b_1^{\varepsilon}\bigg{(} b_1^{1/2}+ \bigg{(} \frac{V}{c}\bigg{)}^{n-1}b_1^{1/2}+ \bigg{(} \frac{V}{c}\bigg{)}^n \bigg{)}. \end{align}
This, in turn, will enable us to find a suitable bound for ![]() $B(b_1,q_2,V;\underline {m}_0)$. By (6.7) and (6.9), we have
$B(b_1,q_2,V;\underline {m}_0)$. By (6.7) and (6.9), we have
 \begin{equation} B(b_1,q_3, V; \underline{m}_0)\ll b_1^{\varepsilon}\bigg{(} b_1^{1/2}+ \bigg{(} \frac{V}{c}\bigg{)}^{n-1}b_1^{1/2}+ \bigg{(} \frac{V}{c}\bigg{)}^n \bigg{)} \sum_{\underline{x}\bmod{c}}\Delta_{T,c}(\underline{x}+\underline{m}_0+{\underline{\mathfrak{b}}}'). \end{equation}
\begin{equation} B(b_1,q_3, V; \underline{m}_0)\ll b_1^{\varepsilon}\bigg{(} b_1^{1/2}+ \bigg{(} \frac{V}{c}\bigg{)}^{n-1}b_1^{1/2}+ \bigg{(} \frac{V}{c}\bigg{)}^n \bigg{)} \sum_{\underline{x}\bmod{c}}\Delta_{T,c}(\underline{x}+\underline{m}_0+{\underline{\mathfrak{b}}}'). \end{equation}
In order to find the bound we desire for ![]() $B(b_1,q_3, V; \underline {m}_0)$, we will need to turn our attention to the sum of type
$B(b_1,q_3, V; \underline {m}_0)$, we will need to turn our attention to the sum of type
for some fixed ![]() $\underline {l}\in \mathbb {Z}^n$. Our bound here will be independent of the choice of the vector
$\underline {l}\in \mathbb {Z}^n$. Our bound here will be independent of the choice of the vector ![]() $\underline {l}$. This sum is much easier to handle since we have a complete sum at hand. It is easy to check from the definition of
$\underline {l}$. This sum is much easier to handle since we have a complete sum at hand. It is easy to check from the definition of ![]() $\Delta _{T,c}(\underline {x}+\underline {l})$ (and the fact that
$\Delta _{T,c}(\underline {x}+\underline {l})$ (and the fact that ![]() $\det (T^t)=1$) that
$\det (T^t)=1$) that
 \begin{align*} \sum_{\underline{x}\bmod{c}}\Delta_{T,c}(\underline{x}+\underline{l})&=\#\{\underline{x} \bmod{c} \, : \, (T^t\underline{x})_i\equiv -(T^t\underline{l})_i \bmod{\lambda_{c,i}}, \; i\in\{1,\ldots, n\}\}\\ &\leq \#\{\underline{x} \bmod{c} \, : \, (T^t\underline{x})_i\equiv 0 \bmod{\lambda_{c,i}}, \; i\in\{1,\ldots, n\}\}\\ &= \#\{\underline{x} \bmod{c} \, : \, x_i\equiv 0 \bmod{\lambda_{c,i}}, \; i\in\{1,\ldots, n\}\}\\ &=\frac{c^n}{\prod_i \lambda_{c,i}}=c^n \#\mathrm{Null}_c(M({\underline{a}}))^{-1}. \end{align*}
\begin{align*} \sum_{\underline{x}\bmod{c}}\Delta_{T,c}(\underline{x}+\underline{l})&=\#\{\underline{x} \bmod{c} \, : \, (T^t\underline{x})_i\equiv -(T^t\underline{l})_i \bmod{\lambda_{c,i}}, \; i\in\{1,\ldots, n\}\}\\ &\leq \#\{\underline{x} \bmod{c} \, : \, (T^t\underline{x})_i\equiv 0 \bmod{\lambda_{c,i}}, \; i\in\{1,\ldots, n\}\}\\ &= \#\{\underline{x} \bmod{c} \, : \, x_i\equiv 0 \bmod{\lambda_{c,i}}, \; i\in\{1,\ldots, n\}\}\\ &=\frac{c^n}{\prod_i \lambda_{c,i}}=c^n \#\mathrm{Null}_c(M({\underline{a}}))^{-1}. \end{align*}
Therefore, by (6.10), we have
as required.
We are now ready to obtain a final bound for ![]() $\sum _{|\underline {m}-\underline {m}_0|\leq V} |S(q;\underline {m})|$. Before substituting (6.11) back into (6.2), we will perform some simplifications. First, we note that by (6.4) and Lemma 2.4, we have
$\sum _{|\underline {m}-\underline {m}_0|\leq V} |S(q;\underline {m})|$. Before substituting (6.11) back into (6.2), we will perform some simplifications. First, we note that by (6.4) and Lemma 2.4, we have
Furthermore, by Lemma 2.5, we have
 \begin{equation} \sideset{}{^*}\sum_{{\underline{a}}}^{q_3}\#\mathrm{Null}_{\hat{q}_3}(M({\underline{a}}))^{1/2}\leq \sideset{}{^*}\sum_{{\underline{a}}}^{q_3}\#\mathrm{Null}_{\hat{q}_3}(M({\underline{a}})) \ll q_3^{2+\varepsilon} \prod_{p_i | \hat{q}_3} p_i^{s_{p_i}(f^{(0)},g^{(0)})+1} =q_3^{2+\varepsilon} D(\hat{q}_3). \end{equation}
\begin{equation} \sideset{}{^*}\sum_{{\underline{a}}}^{q_3}\#\mathrm{Null}_{\hat{q}_3}(M({\underline{a}}))^{1/2}\leq \sideset{}{^*}\sum_{{\underline{a}}}^{q_3}\#\mathrm{Null}_{\hat{q}_3}(M({\underline{a}})) \ll q_3^{2+\varepsilon} \prod_{p_i | \hat{q}_3} p_i^{s_{p_i}(f^{(0)},g^{(0)})+1} =q_3^{2+\varepsilon} D(\hat{q}_3). \end{equation}Finally, by combining (6.11)–(6.13) with (6.2), we arrive at the following bound.
Lemma 6.2 For every ![]() $q\in \mathbb {N}$, if
$q\in \mathbb {N}$, if ![]() $n>1$, then
$n>1$, then
where ![]() $q_3=c^2\hat {q}_3$ as defined in the statement of Lemma 6.1.
$q_3=c^2\hat {q}_3$ as defined in the statement of Lemma 6.1.
Recall that our ultimate goal was to find a suitable bound for ![]() $|T(q,\underline {z})|$. Upon noting that the above treatment of
$|T(q,\underline {z})|$. Upon noting that the above treatment of ![]() $\sum _{|\underline {m}-\underline {m}_0|\leq V}|S(q;\underline {m})|$ works for any value of
$\sum _{|\underline {m}-\underline {m}_0|\leq V}|S(q;\underline {m})|$ works for any value of ![]() $\underline {y}\in P\,\mathrm {Supp}(\omega )$ we may now substitute the bound in Lemma 6.2 into (6.1) to get the following bound for
$\underline {y}\in P\,\mathrm {Supp}(\omega )$ we may now substitute the bound in Lemma 6.2 into (6.1) to get the following bound for ![]() $T(q,\underline {z})$:
$T(q,\underline {z})$:
If ![]() $q$ is sufficiently small (
$q$ is sufficiently small (![]() $q< P^2$ say), then the right-hand term dominates over
$q< P^2$ say), then the right-hand term dominates over ![]() $1$ for every
$1$ for every ![]() $n\geq 1$. Therefore, we finally reach the following bound for
$n\geq 1$. Therefore, we finally reach the following bound for ![]() $|T(q,\underline {z})|$:
$|T(q,\underline {z})|$:
where ![]() $q_3=c^2\hat {q}_3$ as defined in Lemma 6.1. Note that if we use a weaker bound
$q_3=c^2\hat {q}_3$ as defined in Lemma 6.1. Note that if we use a weaker bound ![]() $c\leq b_3^{1/3}q_4^{1/2}$ and
$c\leq b_3^{1/3}q_4^{1/2}$ and ![]() $D(\hat {q}_3)\leq D(q_3)$, and use the quality
$D(\hat {q}_3)\leq D(q_3)$, and use the quality ![]() $q_3=b_3q_4$, where
$q_3=b_3q_4$, where ![]() $b_3$ is the fourth power-free cube part of
$b_3$ is the fourth power-free cube part of ![]() $q$ and
$q$ and ![]() $q_i$ is the
$q_i$ is the ![]() $i$th power-full part of
$i$th power-full part of ![]() $q$, the above bound becomes the following.
$q$, the above bound becomes the following.
Proposition 6.3 For every ![]() $q=b_1b_2q_3< P^2$,
$q=b_1b_2q_3< P^2$, ![]() $\underline {z}$ and every
$\underline {z}$ and every ![]() $\varepsilon >0$, if
$\varepsilon >0$, if ![]() $n>1$, we have
$n>1$, we have
where ![]() $n$ is the number of variables of
$n$ is the number of variables of ![]() $f, g$.
$f, g$.
The bound for the ![]() $n=1$ case is much simpler to derive than in the
$n=1$ case is much simpler to derive than in the ![]() $n>1$ case. By Lemma 5.4 and Propositions 5.6, 5.10 and 5.11, we have
$n>1$ case. By Lemma 5.4 and Propositions 5.6, 5.10 and 5.11, we have
 \begin{align} \sum_{|m-m_0|\leq V}|S(q;m)| &\ll q^{1/2+\varepsilon}b_1^{3/2} b_2^2D(b_1b_2) \sideset{}{^*}\sum_{{\underline{a}}}^{q_3}(q_3,M({\underline{a}}))^{1/2}\sum_{|m-m_0|\leq V} \Delta'_{q_3}(c_3m+\mathfrak{b})\nonumber\\ &\leq q^{1/2+\varepsilon}b_1^{3/2} b_2^2D(b_1b_2)\sideset{}{^*}\sum_{{\underline{a}}}^{q_3}(q_3,M({\underline{a}}))^{1/2}\bigg{(} 1 + \frac{V}{(q_3,M({\underline{a}}))} \bigg{)}\nonumber\\ &\leq q^{1/2+\varepsilon}b_1^{3/2} b_2^2D(b_1b_2)\sideset{}{^*}\sum_{{\underline{a}}}^{q_3}{(}(q_3,M({\underline{a}}))^{1/2} + V {)}. \end{align}
\begin{align} \sum_{|m-m_0|\leq V}|S(q;m)| &\ll q^{1/2+\varepsilon}b_1^{3/2} b_2^2D(b_1b_2) \sideset{}{^*}\sum_{{\underline{a}}}^{q_3}(q_3,M({\underline{a}}))^{1/2}\sum_{|m-m_0|\leq V} \Delta'_{q_3}(c_3m+\mathfrak{b})\nonumber\\ &\leq q^{1/2+\varepsilon}b_1^{3/2} b_2^2D(b_1b_2)\sideset{}{^*}\sum_{{\underline{a}}}^{q_3}(q_3,M({\underline{a}}))^{1/2}\bigg{(} 1 + \frac{V}{(q_3,M({\underline{a}}))} \bigg{)}\nonumber\\ &\leq q^{1/2+\varepsilon}b_1^{3/2} b_2^2D(b_1b_2)\sideset{}{^*}\sum_{{\underline{a}}}^{q_3}{(}(q_3,M({\underline{a}}))^{1/2} + V {)}. \end{align}
We trivially have ![]() $\sum _{{\underline {a}}} V\leq q_3^2 V$. As for the other part of the sum, upon recalling that
$\sum _{{\underline {a}}} V\leq q_3^2 V$. As for the other part of the sum, upon recalling that ![]() $q_3=\hat {q}_3c^2$, we have
$q_3=\hat {q}_3c^2$, we have
 \[ \sideset{}{^*}\sum_{{\underline{a}}}^{q_3}(q_3,M({\underline{a}}))^{1/2}\leq c \sideset{}{^*}\sum_{{\underline{a}}}^{q_3}(\hat{q}_3,M({\underline{a}}))^{1/2}\leq c^5 \sideset{}{^*}\sum_{{\underline{a}}}^{\hat{q}_3}(\hat{q}_3,M({\underline{a}}))^{1/2}\ll q_3^2 c D(\hat{q}_3)\leq q_3^2 c D(q_3), \]
\[ \sideset{}{^*}\sum_{{\underline{a}}}^{q_3}(q_3,M({\underline{a}}))^{1/2}\leq c \sideset{}{^*}\sum_{{\underline{a}}}^{q_3}(\hat{q}_3,M({\underline{a}}))^{1/2}\leq c^5 \sideset{}{^*}\sum_{{\underline{a}}}^{\hat{q}_3}(\hat{q}_3,M({\underline{a}}))^{1/2}\ll q_3^2 c D(\hat{q}_3)\leq q_3^2 c D(q_3), \]
by the same argument as the proof of Proposition 5.11. Combining this with (6.14) gives the following result.
Lemma 6.4 Let ![]() $q=b_1b_2q_3\in \mathbb {N}$,
$q=b_1b_2q_3\in \mathbb {N}$, ![]() $m\in \mathbb {Z}$ and
$m\in \mathbb {Z}$ and ![]() $q_3:=c^2 \hat {q}_3$ be defined as in Lemma 6.1. Then for every
$q_3:=c^2 \hat {q}_3$ be defined as in Lemma 6.1. Then for every ![]() $\varepsilon >0$,
$\varepsilon >0$,
Finally, upon recalling that ![]() $q_3=b_3q_4$,
$q_3=b_3q_4$, ![]() $c\leq b_3^{1/3}q_4^{1/2}$, we may combine this lemma with (6.1) to get our final bound for
$c\leq b_3^{1/3}q_4^{1/2}$, we may combine this lemma with (6.1) to get our final bound for ![]() $|T(q,\underline {z})|$ in the
$|T(q,\underline {z})|$ in the ![]() $n=1$ case.
$n=1$ case.
Proposition 6.5 For every ![]() $q< P^2$,
$q< P^2$, ![]() $\underline {z}$ and every
$\underline {z}$ and every ![]() $\varepsilon >0$, if
$\varepsilon >0$, if ![]() $n=1$, we have
$n=1$, we have
where ![]() $n$ is the number of variables of
$n$ is the number of variables of ![]() $f, g$.
$f, g$.
7. Finalisation of the Poisson bound
In this section, we will adapt the arguments used in [Reference Browning and Heath-BrownBH09, Section 7] and [Reference Marmon and VisheMV19, Section 8] to our context in order to finalise our main bounds coming from Poisson summation. Throughout this section, we treat ![]() $\underline {z}$ as fixed. Lemmas 4.1 and 4.5 allow us to consider bounding the sum
$\underline {z}$ as fixed. Lemmas 4.1 and 4.5 allow us to consider bounding the sum
where
is the quadratic exponential sum as defined in (4.5). We may therefore apply our bounds for quadratic exponential sums in Propositions 6.3 and 6.5 to estimate these.
Now that ![]() $\underline {h}$ is allowed to vary, we will define
$\underline {h}$ is allowed to vary, we will define
where ![]() $F_{\underline {h}}^{(0)}$ and
$F_{\underline {h}}^{(0)}$ and ![]() $G_{\underline {h}}^{(0)}$ denote the leading quadratic parts of
$G_{\underline {h}}^{(0)}$ denote the leading quadratic parts of ![]() $F_{\underline {h}}$ and
$F_{\underline {h}}$ and ![]() $G_{\underline {h}}$, respectively. We recall that
$G_{\underline {h}}$, respectively. We recall that ![]() $q=b_1b_2q_3$, where
$q=b_1b_2q_3$, where ![]() $q_3$ is the cube-full part of
$q_3$ is the cube-full part of ![]() $q$, and
$q$, and ![]() $b_1,b_2$ are the square-free and cube-free square parts of
$b_1,b_2$ are the square-free and cube-free square parts of ![]() $q$. Since we are fixing
$q$. Since we are fixing ![]() $q$ for now,
$q$ for now, ![]() $b_1$,
$b_1$, ![]() $b_2$ and
$b_2$ and ![]() $q_3$ are also fixed. Recall that we may write
$q_3$ are also fixed. Recall that we may write ![]() $b_i=b_{i,0}b_{i,1}\cdots b_{i,n}$,
$b_i=b_{i,0}b_{i,1}\cdots b_{i,n}$, ![]() $q_3=q_{3,0}q_{3,1}\cdots q_{3,n}$ where
$q_3=q_{3,0}q_{3,1}\cdots q_{3,n}$ where ![]() $b_{i,j}$, and
$b_{i,j}$, and ![]() $q_{3,j}$ now depend on
$q_{3,j}$ now depend on ![]() $\underline {h}$ and are defined to be
$\underline {h}$ and are defined to be
 \[ b_{i,j}(\underline{h})=\prod_{\substack{p^i||b_i\\s_p(\underline{h})=j-1}} p^i,\quad q_{3,j}(\underline{h})=\prod_{\substack{p^e||q_3\\s_p(\underline{h})=j-1}} p^e. \]
\[ b_{i,j}(\underline{h})=\prod_{\substack{p^i||b_i\\s_p(\underline{h})=j-1}} p^i,\quad q_{3,j}(\underline{h})=\prod_{\substack{p^e||q_3\\s_p(\underline{h})=j-1}} p^e. \]
We see that for any ![]() $q$ fixed, there are at most
$q$ fixed, there are at most ![]() $O(q^{\varepsilon })=O(P^{\varepsilon })$ possible choices for
$O(q^{\varepsilon })=O(P^{\varepsilon })$ possible choices for
since there are only at most ![]() $O(q^{\varepsilon })$ partitions of
$O(q^{\varepsilon })$ partitions of ![]() $q$ into multiplicative factors. Therefore, using the triangle inequality, we have that
$q$ into multiplicative factors. Therefore, using the triangle inequality, we have that
 \[ \sum_{\underline{h}\ll H} |T_{\underline{h}}(q,z)|\leq P^{\varepsilon}\max_{\underline{c}}\bigg{\{}\sum_{\substack{\underline{h}\\ \underline{c}(\underline{h})=\underline{c}}} |T_{\underline{h}}(q,z)|\bigg{\}}=P^{\varepsilon}\sum_{\substack{\underline{h}\\ \underline{c}(\underline{h})=\underline{c}'}} |T_{\underline{h}}(q,z)| \]
\[ \sum_{\underline{h}\ll H} |T_{\underline{h}}(q,z)|\leq P^{\varepsilon}\max_{\underline{c}}\bigg{\{}\sum_{\substack{\underline{h}\\ \underline{c}(\underline{h})=\underline{c}}} |T_{\underline{h}}(q,z)|\bigg{\}}=P^{\varepsilon}\sum_{\substack{\underline{h}\\ \underline{c}(\underline{h})=\underline{c}'}} |T_{\underline{h}}(q,z)| \]
for some particular ![]() $\underline {c}'$, and
$\underline {c}'$, and ![]() $\underline {c}(\underline {h}):=(b_{1,0}(\underline {h}),\ldots, q_{3,n}(\underline {h}))$. We can then decompose this sum further by grouping the
$\underline {c}(\underline {h}):=(b_{1,0}(\underline {h}),\ldots, q_{3,n}(\underline {h}))$. We can then decompose this sum further by grouping the ![]() $\underline {h}$ with
$\underline {h}$ with ![]() $s_{\infty }(\underline {h})=s$:
$s_{\infty }(\underline {h})=s$:
 \begin{equation} \implies \sum_{\underline{h}\ll H} |T_{\underline{h}}(q,z)|\leq P^{\varepsilon}\sum_{s=-1}^{n-1}\sum_{\underline{h}\in\mathcal{H}_s} |T_{\underline{h}}(q,z)|, \end{equation}
\begin{equation} \implies \sum_{\underline{h}\ll H} |T_{\underline{h}}(q,z)|\leq P^{\varepsilon}\sum_{s=-1}^{n-1}\sum_{\underline{h}\in\mathcal{H}_s} |T_{\underline{h}}(q,z)|, \end{equation}where
Here, given ![]() $\nu$ either a prime or
$\nu$ either a prime or ![]() $\infty$, we define
$\infty$, we define
We now aim to estimate the size of ![]() $\mathcal {H}_s$. We start by noting that we must have that
$\mathcal {H}_s$. We start by noting that we must have that ![]() $\mathcal {H}_s=\emptyset$ unless
$\mathcal {H}_s=\emptyset$ unless ![]() $b_{1,i}=b_{2,i}=q_{3,i}=1$ for
$b_{1,i}=b_{2,i}=q_{3,i}=1$ for ![]() $i\leq s$. This is because
$i\leq s$. This is because ![]() $s_p(\underline {h})\geq s_{\infty }(\underline {h})$ for every
$s_p(\underline {h})\geq s_{\infty }(\underline {h})$ for every ![]() $p$. To get a bound on
$p$. To get a bound on ![]() $\#\mathcal {H}_s$ we will start by constructing a set which contains
$\#\mathcal {H}_s$ we will start by constructing a set which contains ![]() $\mathcal {H}_s$ that is easier to work with. Let
$\mathcal {H}_s$ that is easier to work with. Let
Then, upon defining ![]() $[{\underline {h}}]_p$ to be the reduction modulo
$[{\underline {h}}]_p$ to be the reduction modulo ![]() $p$ of a point
$p$ of a point ![]() ${\underline {h}}\in \mathbb {Z}^n$, we have (possibly up to multiplying
${\underline {h}}\in \mathbb {Z}^n$, we have (possibly up to multiplying ![]() $H$ by a constant)
$H$ by a constant)
In order to bound this larger set, we will need the following lemma, which is analogous to [Reference Marmon and VisheMV19, Lemma 8.2].
Lemma 7.1 Let ![]() $F$,
$F$, ![]() $G$ be a pair of forms of degree
$G$ be a pair of forms of degree ![]() $d_1$,
$d_1$, ![]() $d_2$, and define
$d_2$, and define ![]() $\sigma :=s_{\infty }(F,G)$. Then there is an absolute constant
$\sigma :=s_{\infty }(F,G)$. Then there is an absolute constant ![]() $C$ such that
$C$ such that
as long as ![]() $\nu =p>C$ or
$\nu =p>C$ or ![]() $\nu =\infty$.
$\nu =\infty$.
Proof. We prove this result for any pair of forms instead of two cubics as it does not change the argument. Since
 \begin{align*} & s_{\nu}(F^{(0)}_{\underline{h}},G^{(0)}_{\underline{h}})\\ &\quad =\dim\Bigg(\Bigg\{\underline{x}\in\mathbb{P}_{\overline{\mathbb{F}}_{\nu}}^{n-1}\,
|\,\underline{h}\cdot \nabla
F^{(0)}(\underline{x})=\underline{h}\cdot \nabla
G^{(0)}(\underline{x})=0, \,\mathrm{Rank}\begin{pmatrix}
\underline{h}\cdot \nabla^2 F^{(0)}(\underline{x})\\
\underline{h}\cdot \nabla^2 G^{(0)}(\underline{x})
\end{pmatrix}<2\Bigg\}\Bigg), \end{align*}
\begin{align*} & s_{\nu}(F^{(0)}_{\underline{h}},G^{(0)}_{\underline{h}})\\ &\quad =\dim\Bigg(\Bigg\{\underline{x}\in\mathbb{P}_{\overline{\mathbb{F}}_{\nu}}^{n-1}\,
|\,\underline{h}\cdot \nabla
F^{(0)}(\underline{x})=\underline{h}\cdot \nabla
G^{(0)}(\underline{x})=0, \,\mathrm{Rank}\begin{pmatrix}
\underline{h}\cdot \nabla^2 F^{(0)}(\underline{x})\\
\underline{h}\cdot \nabla^2 G^{(0)}(\underline{x})
\end{pmatrix}<2\Bigg\}\Bigg), \end{align*}
we can use [Reference MarmonMar08, Lemma 2.9(ii)] to conclude that ![]() $\dim (V_{\nu,i})\leq \min \{n,n+\sigma +1-i\}$, provided that
$\dim (V_{\nu,i})\leq \min \{n,n+\sigma +1-i\}$, provided that ![]() $\nu =p\gg _{d_1,d_2} 1$. Therefore, we only need to check
$\nu =p\gg _{d_1,d_2} 1$. Therefore, we only need to check ![]() $V_{\infty,i}$. We will use a slight modification to the argument used in [Reference Browning and Heath-BrownBH09, Lemma 1] in order to show that
$V_{\infty,i}$. We will use a slight modification to the argument used in [Reference Browning and Heath-BrownBH09, Lemma 1] in order to show that ![]() $\dim (V_{\infty,i})\leq \min \{n,n+\sigma +1-i\}$. Let
$\dim (V_{\infty,i})\leq \min \{n,n+\sigma +1-i\}$. Let
for ![]() $F,G$ homogeneous forms of degree 3, and let
$F,G$ homogeneous forms of degree 3, and let ![]() $D:=\{(\underline {x},\underline {y})\in \mathbb {A}_{\mathbb {Q}}^{2n} \: | \: \underline {x}=\underline {y}\}$. Then by the affine dimension theorem, we have that
$D:=\{(\underline {x},\underline {y})\in \mathbb {A}_{\mathbb {Q}}^{2n} \: | \: \underline {x}=\underline {y}\}$. Then by the affine dimension theorem, we have that
Next, we note that
 \begin{align*} U\cap D&=\bigg\{\underline{x}\in\mathbb{A}_{\mathbb{Q}}^{n} \, | \,\underline{x}\cdot \nabla F(\underline{x})=\underline{x}\cdot \nabla G(\underline{x})=0, \;\mathrm{Rank}\begin{pmatrix} \nabla(\underline{x}\cdot \nabla F(\underline{x}))\\ \nabla(\underline{x}\cdot \nabla G(\underline{x})) \end{pmatrix}<2\bigg\}\\ &=\bigg\{\underline{x}\in\mathbb{A}_{\mathbb{Q}}^{n} \, | \,F(\underline{x})=G(\underline{x})=0, \;\mathrm{Rank}\begin{pmatrix} \nabla F(\underline{x})\\ \nabla G(\underline{x}) \end{pmatrix}<2\bigg\}, \end{align*}
\begin{align*} U\cap D&=\bigg\{\underline{x}\in\mathbb{A}_{\mathbb{Q}}^{n} \, | \,\underline{x}\cdot \nabla F(\underline{x})=\underline{x}\cdot \nabla G(\underline{x})=0, \;\mathrm{Rank}\begin{pmatrix} \nabla(\underline{x}\cdot \nabla F(\underline{x}))\\ \nabla(\underline{x}\cdot \nabla G(\underline{x})) \end{pmatrix}<2\bigg\}\\ &=\bigg\{\underline{x}\in\mathbb{A}_{\mathbb{Q}}^{n} \, | \,F(\underline{x})=G(\underline{x})=0, \;\mathrm{Rank}\begin{pmatrix} \nabla F(\underline{x})\\ \nabla G(\underline{x}) \end{pmatrix}<2\bigg\}, \end{align*}
by Euler's identity. Hence, we have
and so by (7.6) we have
Finally, we let ![]() $F=F^{(0)}$,
$F=F^{(0)}$, ![]() $G=G^{(0)}$. If
$G=G^{(0)}$. If
then, by definition, we have that
 \begin{align*} \dim \big( \big\{(\underline{x},{\underline{h}})\in\mathbb{A}_{\mathbb{Q}}^{2n}\, |\, s_{\infty}\big(F_{{\underline{h}}}^{(0)}, G_{{\underline{h}}}^{(0)}\big)\geq i-1, \ \underline{x}\in s_{\infty}\big(F_{{\underline{h}}}^{(0)}, G_{{\underline{h}}}^{(0)}\big)\big\}\big)&> (n+\sigma+1-i) + i\\ &=n+\sigma+1. \end{align*}
\begin{align*} \dim \big( \big\{(\underline{x},{\underline{h}})\in\mathbb{A}_{\mathbb{Q}}^{2n}\, |\, s_{\infty}\big(F_{{\underline{h}}}^{(0)}, G_{{\underline{h}}}^{(0)}\big)\geq i-1, \ \underline{x}\in s_{\infty}\big(F_{{\underline{h}}}^{(0)}, G_{{\underline{h}}}^{(0)}\big)\big\}\big)&> (n+\sigma+1-i) + i\\ &=n+\sigma+1. \end{align*}
It is easy to check that
and so
This contradicts (7.7). Hence, ![]() $\dim (V_{\infty, i}) \leq n+\sigma +1-i$ as required.
$\dim (V_{\infty, i}) \leq n+\sigma +1-i$ as required.
We can now use (7.5) and the argument found in [Reference Browning and Heath-BrownBH09, Section 7] and upon further setting ![]() $\sigma =-1$ in the bounds in [Reference Browning and Heath-BrownBH09], we get the following upper bound for
$\sigma =-1$ in the bounds in [Reference Browning and Heath-BrownBH09], we get the following upper bound for ![]() $\#\mathcal {H}$:
$\#\mathcal {H}$:
 \begin{equation} \#\mathcal{H}_s\ll q^{\varepsilon} \max_{s+1\leq\eta\leq n}\frac{H^{n-\eta}}{\prod_{i=\eta+1}^n(b_{1,i}b_{2,i}^{1/2}\tilde{q}_{3,i})^{i-\eta}}, \end{equation}
\begin{equation} \#\mathcal{H}_s\ll q^{\varepsilon} \max_{s+1\leq\eta\leq n}\frac{H^{n-\eta}}{\prod_{i=\eta+1}^n(b_{1,i}b_{2,i}^{1/2}\tilde{q}_{3,i})^{i-\eta}}, \end{equation}where
 \[ \tilde{q}_{3,i}:=\prod_{\substack{p|q_3\\ s_p(\underline{h})=i-1}} p. \]
\[ \tilde{q}_{3,i}:=\prod_{\substack{p|q_3\\ s_p(\underline{h})=i-1}} p. \]
For convenience, set
(recall that ![]() $\sum _{{\underline {h}}\ll H}T_{{\underline {h}}}(q,\underline {z})\ll P^{\varepsilon } \sum _{s=-1}^{n-1} \mathcal {U}_s$ by (7.2)). We will use (7.8) to bound
$\sum _{{\underline {h}}\ll H}T_{{\underline {h}}}(q,\underline {z})\ll P^{\varepsilon } \sum _{s=-1}^{n-1} \mathcal {U}_s$ by (7.2)). We will use (7.8) to bound ![]() $\mathcal {U}_s$ later, but for now, we need to find a bound on
$\mathcal {U}_s$ later, but for now, we need to find a bound on ![]() $|T_{\underline {h}}(q,\underline {z})|$. To do this we will need to apply the hyperplane intersections lemma, namely Lemma 2.1 and then apply the bounds found in Propositions 6.3 and 6.5.
$|T_{\underline {h}}(q,\underline {z})|$. To do this we will need to apply the hyperplane intersections lemma, namely Lemma 2.1 and then apply the bounds found in Propositions 6.3 and 6.5.
Let ![]() $\eta$ be chosen so as to maximise the expression in (7.8). Let
$\eta$ be chosen so as to maximise the expression in (7.8). Let ![]() $\Pi$ be the set of primes
$\Pi$ be the set of primes ![]() $p|q$ so that
$p|q$ so that ![]() $r=\omega (q)$ where
$r=\omega (q)$ where ![]() $\omega (q)$ denotes the number of distinct prime factors of
$\omega (q)$ denotes the number of distinct prime factors of ![]() $q$, and
$q$, and ![]() $\{F_1,F_2\}=\{F_{\underline {h}}^{(0)},G_{\underline {h}}^{(0)}\}$. We may now invoke Lemma 2.1 to find a lattice
$\{F_1,F_2\}=\{F_{\underline {h}}^{(0)},G_{\underline {h}}^{(0)}\}$. We may now invoke Lemma 2.1 to find a lattice ![]() $\Lambda _{\eta }$ of rank
$\Lambda _{\eta }$ of rank ![]() $n-\eta$ and a basis
$n-\eta$ and a basis ![]() $\underline {e}_1,\ldots,\underline {e}_{n-\eta }$ for
$\underline {e}_1,\ldots,\underline {e}_{n-\eta }$ for ![]() $\Lambda _{\eta }$ such that for every
$\Lambda _{\eta }$ such that for every ![]() $\underline {t}\in \mathbb {Z}^n$, the polynomials
$\underline {t}\in \mathbb {Z}^n$, the polynomials
 \[ \tilde{F}_{{\underline{h}},\underline{t}}(\underline{y}):=F_{\underline{h}}^{(0)}\bigg(\underline{t}+\sum_{i=1}^{n-\eta} y_i\underline{e}_i\bigg),\quad \tilde{G}_{{\underline{h}},\underline{t}}(\underline{y}):=G_{\underline{h}}^{(0)}\bigg(\underline{t}+\sum_{i=1}^{n-\eta} y_i\underline{e}_i\bigg) \]
\[ \tilde{F}_{{\underline{h}},\underline{t}}(\underline{y}):=F_{\underline{h}}^{(0)}\bigg(\underline{t}+\sum_{i=1}^{n-\eta} y_i\underline{e}_i\bigg),\quad \tilde{G}_{{\underline{h}},\underline{t}}(\underline{y}):=G_{\underline{h}}^{(0)}\bigg(\underline{t}+\sum_{i=1}^{n-\eta} y_i\underline{e}_i\bigg) \]
satisfy
for every ![]() $\nu \in \{\infty \}\cup \Pi _{cr}$. We also note that
$\nu \in \{\infty \}\cup \Pi _{cr}$. We also note that ![]() $\deg (\tilde {F}_{{\underline {h}},\underline {t}})=\deg (\tilde {G}_{{\underline {h}},\underline {t}})=2$ (this is necessary in order to be able to use the bounds from the previous section). In order to apply the bounds found in the previous section, we must first fix our choice of basis
$\deg (\tilde {F}_{{\underline {h}},\underline {t}})=\deg (\tilde {G}_{{\underline {h}},\underline {t}})=2$ (this is necessary in order to be able to use the bounds from the previous section). In order to apply the bounds found in the previous section, we must first fix our choice of basis ![]() $\{\underline {e}_1,\ldots,\underline {e}_n\}$, and so we will use the same process as earlier when we fixed
$\{\underline {e}_1,\ldots,\underline {e}_n\}$, and so we will use the same process as earlier when we fixed ![]() $(b_{1,0},\ldots, q_{3,n})$: we recall that the
$(b_{1,0},\ldots, q_{3,n})$: we recall that the ![]() $L$ used in (2.4) is of size
$L$ used in (2.4) is of size ![]() $L=O(r+1)=O(\log (q))$. Therefore, there are at most
$L=O(r+1)=O(\log (q))$. Therefore, there are at most ![]() $O(\log (q)^n)$ choices of basis satisfying (2.4), and so by (7.9), and the triangle inequality, there is one such choice for which
$O(\log (q)^n)$ choices of basis satisfying (2.4), and so by (7.9), and the triangle inequality, there is one such choice for which
where ![]() $\sum '$ denotes that the sum is taken over the vectors
$\sum '$ denotes that the sum is taken over the vectors ![]() $\underline {h}$ in the original sum for which (7.10) holds for our chosen basis
$\underline {h}$ in the original sum for which (7.10) holds for our chosen basis ![]() $\{\underline {e}_1,\ldots,\underline {e}_n\}$. For such
$\{\underline {e}_1,\ldots,\underline {e}_n\}$. For such ![]() $\underline {h}$, we can now separate the
$\underline {h}$, we can now separate the ![]() $\underline {x}$ sum defining
$\underline {x}$ sum defining ![]() $T_{\underline {h}}(q,\underline {z})$ into cosets
$T_{\underline {h}}(q,\underline {z})$ into cosets ![]() $\underline {t}+\Lambda _\eta$ of
$\underline {t}+\Lambda _\eta$ of ![]() $\Lambda _\eta$, where
$\Lambda _\eta$, where ![]() $\underline {t}$ runs over some subset
$\underline {t}$ runs over some subset ![]() $T_\eta \subset \mathbb {Z}^n$. All that is left to do is use Proposition 6.3 (or Proposition 6.5 for
$T_\eta \subset \mathbb {Z}^n$. All that is left to do is use Proposition 6.3 (or Proposition 6.5 for ![]() $\eta =n-1$) on each coset, and determine the size of
$\eta =n-1$) on each coset, and determine the size of ![]() $T_\eta$, as this bounds the number of cosets that we have. We claim that if
$T_\eta$, as this bounds the number of cosets that we have. We claim that if ![]() $\Lambda _{\eta }$ is chosen according to Lemma 2.1, then
$\Lambda _{\eta }$ is chosen according to Lemma 2.1, then ![]() $\# T_\eta =O(P^\eta )$. Indeed, consider
$\# T_\eta =O(P^\eta )$. Indeed, consider ![]() $\underline {x}$ in terms of our basis
$\underline {x}$ in terms of our basis ![]() $\underline {e}_1,\ldots,\underline {e}_n$, i.e. writing
$\underline {e}_1,\ldots,\underline {e}_n$, i.e. writing
 \[ \underline{x}=\sum_{i=1}^n u_i\underline{e}_i. \]
\[ \underline{x}=\sum_{i=1}^n u_i\underline{e}_i. \]
Now, if ![]() $\pi _i$ denotes the orthogonal projection onto the subspace spanned by the vectors
$\pi _i$ denotes the orthogonal projection onto the subspace spanned by the vectors ![]() $\underline {e}_j$,
$\underline {e}_j$, ![]() $i\neq j$, we have
$i\neq j$, we have
where ![]() $\Lambda \subset \mathbb {Z}^n$ denotes the full-dimensional lattice spanned by
$\Lambda \subset \mathbb {Z}^n$ denotes the full-dimensional lattice spanned by ![]() $\underline {e}_1,\ldots,\underline {e}_n$ and
$\underline {e}_1,\ldots,\underline {e}_n$ and ![]() $\Lambda _i$ the lattice spanned by each
$\Lambda _i$ the lattice spanned by each ![]() $\underline {e}_j\neq \underline {e}_i$. Now by (2.4) and (2.5), we get that
$\underline {e}_j\neq \underline {e}_i$. Now by (2.4) and (2.5), we get that
Therefore, we must have ![]() $|u_i|\ll P$ since we need
$|u_i|\ll P$ since we need ![]() $\|\underline {x}\|\ll P$. Hence, since
$\|\underline {x}\|\ll P$. Hence, since ![]() $\Lambda _{\eta }=\langle \underline {e}_1,\ldots, \underline {e}_{n-\eta }\rangle$, we may conclude that
$\Lambda _{\eta }=\langle \underline {e}_1,\ldots, \underline {e}_{n-\eta }\rangle$, we may conclude that ![]() $\underline {t}$ is of the form
$\underline {t}$ is of the form ![]() $\underline {t}=\sum _{i=n-\eta +1}^{n} \lambda _i\underline {e}_i$ such that
$\underline {t}=\sum _{i=n-\eta +1}^{n} \lambda _i\underline {e}_i$ such that ![]() $|\lambda _i|\ll P$. We now choose
$|\lambda _i|\ll P$. We now choose ![]() $T_\eta$ to be the collection of such
$T_\eta$ to be the collection of such ![]() $\underline {t}$ leading us to conclude that
$\underline {t}$ leading us to conclude that ![]() $\#T_{\eta }=O(P^{\eta })$.
$\#T_{\eta }=O(P^{\eta })$.
In order to complete the hyperplane intersections step, we will now define new weight functions in ![]() $n-\eta$ variables. In particular, upon recalling (4.3), we set
$n-\eta$ variables. In particular, upon recalling (4.3), we set
 \[ \tilde{\omega}_{{\underline{h}},\underline{t}}(y_1,\ldots, y_{n-\eta}):=\omega_{{\underline{h}}}\bigg{(} P^{-1}\underline{t}+L^{-1}\sum_{i=1}^{n-\eta} y_i\underline{e}_i\bigg{)}. \]
\[ \tilde{\omega}_{{\underline{h}},\underline{t}}(y_1,\ldots, y_{n-\eta}):=\omega_{{\underline{h}}}\bigg{(} P^{-1}\underline{t}+L^{-1}\sum_{i=1}^{n-\eta} y_i\underline{e}_i\bigg{)}. \]
This gives us
where
 \begin{equation} T_{{\underline{h}},\underline{t}}(q,\underline{z}):=\sideset{}{^*}\sum_{{\underline{a}}\bmod{q}}\sum_{\underline{y}\in\mathbb{Z}^{n-\eta}} \tilde{\omega}_{{\underline{h}},\underline{t}}(L\underline{y}/P)e((a_1/q+z_1)\tilde{F}_{{\underline{h}},\underline{t}}(\underline{y})+(a_2/q+z_2)\tilde{G}_{{\underline{h}},\underline{t}}(\underline{y})). \end{equation}
\begin{equation} T_{{\underline{h}},\underline{t}}(q,\underline{z}):=\sideset{}{^*}\sum_{{\underline{a}}\bmod{q}}\sum_{\underline{y}\in\mathbb{Z}^{n-\eta}} \tilde{\omega}_{{\underline{h}},\underline{t}}(L\underline{y}/P)e((a_1/q+z_1)\tilde{F}_{{\underline{h}},\underline{t}}(\underline{y})+(a_2/q+z_2)\tilde{G}_{{\underline{h}},\underline{t}}(\underline{y})). \end{equation}
We now need to verify that ![]() $T_{{\underline {h}},\underline {t}}(q,\underline {z})$ and
$T_{{\underline {h}},\underline {t}}(q,\underline {z})$ and ![]() $\tilde {\omega }_{{\underline {h}},\underline {t}}$ satisfy the various properties that we assumed in order to acquire the results we have found in the previous sections. First, we refer to the proof Proposition 2 of [Reference Browning and Heath-BrownBH09] to see that
$\tilde {\omega }_{{\underline {h}},\underline {t}}$ satisfy the various properties that we assumed in order to acquire the results we have found in the previous sections. First, we refer to the proof Proposition 2 of [Reference Browning and Heath-BrownBH09] to see that ![]() $\tilde {\omega }_{{\underline {h}},\underline {t}}\in \mathcal {W}_{n-\eta }$ for
$\tilde {\omega }_{{\underline {h}},\underline {t}}\in \mathcal {W}_{n-\eta }$ for ![]() $\underline {t}\ll P$, where
$\underline {t}\ll P$, where ![]() $\mathcal {W}_{n-\eta }$ is as defined in and before (3.13). We also see that
$\mathcal {W}_{n-\eta }$ is as defined in and before (3.13). We also see that
and similarly ![]() $\|\tilde {G}_{{\underline {h}},\underline {t}}\|_{P/L}\ll P^{\varepsilon }H$. Next, we note that
$\|\tilde {G}_{{\underline {h}},\underline {t}}\|_{P/L}\ll P^{\varepsilon }H$. Next, we note that ![]() $\eta \geq s+1$, and so we automatically have
$\eta \geq s+1$, and so we automatically have ![]() $s_{\infty }(\tilde {F}_{{\underline {h}},\underline {t}},\tilde {G}_{{\underline {h}},\underline {t}})=-1$. This covers all conditions that we have needed in the previous sections on exponential sums.
$s_{\infty }(\tilde {F}_{{\underline {h}},\underline {t}},\tilde {G}_{{\underline {h}},\underline {t}})=-1$. This covers all conditions that we have needed in the previous sections on exponential sums.
Therefore, by (7.11), (7.13) and (7.8):
 \begin{align} \mathcal{U}_s&\ll P^{\varepsilon}\sum_{\underline{h}\in\mathcal{H}_s}{}^{\prime}\sum_{\underline{t}\in T_{\eta}} |T_{{\underline{h}},\underline{t}}(q,\underline{z})| \nonumber\\ &\ll P^{\varepsilon} \#\mathcal{H}_s \# T_{\eta} \max_{\underline{h}\in\mathcal{H}_s}{}^{\prime}\max_{\underline{t}\in T_{\eta}} |T_{{\underline{h}},\underline{t}}(q,\underline{z})| \nonumber\\ &\ll \max_{s+1\leq\eta\leq n}\frac{P^{\eta+\varepsilon}H^{n-\eta}}{\prod_{i=\eta+1}^n((b_{1,i}b_{2,i}^{1/2}\tilde{q}_{3,i}))^{i-\eta}}\cdot \max_{{\underline{h}}\in\mathcal{H}_s}{}'\max_{\underline{t}\in T_{\eta}} T_{{\underline{h}},\underline{t}}(q,\underline{z}). \end{align}
\begin{align} \mathcal{U}_s&\ll P^{\varepsilon}\sum_{\underline{h}\in\mathcal{H}_s}{}^{\prime}\sum_{\underline{t}\in T_{\eta}} |T_{{\underline{h}},\underline{t}}(q,\underline{z})| \nonumber\\ &\ll P^{\varepsilon} \#\mathcal{H}_s \# T_{\eta} \max_{\underline{h}\in\mathcal{H}_s}{}^{\prime}\max_{\underline{t}\in T_{\eta}} |T_{{\underline{h}},\underline{t}}(q,\underline{z})| \nonumber\\ &\ll \max_{s+1\leq\eta\leq n}\frac{P^{\eta+\varepsilon}H^{n-\eta}}{\prod_{i=\eta+1}^n((b_{1,i}b_{2,i}^{1/2}\tilde{q}_{3,i}))^{i-\eta}}\cdot \max_{{\underline{h}}\in\mathcal{H}_s}{}'\max_{\underline{t}\in T_{\eta}} T_{{\underline{h}},\underline{t}}(q,\underline{z}). \end{align}Recall that
 \begin{equation} \sum_{{\underline{h}}\ll H}T_{{\underline{h}}}(q,\underline{z})\ll P^{\varepsilon} \sum_{s=-1}^{n-1} \mathcal{U}_s\ll P^{\varepsilon} \max_{-1\leq s\leq n-1} \mathcal{U}_s. \end{equation}
\begin{equation} \sum_{{\underline{h}}\ll H}T_{{\underline{h}}}(q,\underline{z})\ll P^{\varepsilon} \sum_{s=-1}^{n-1} \mathcal{U}_s\ll P^{\varepsilon} \max_{-1\leq s\leq n-1} \mathcal{U}_s. \end{equation}
by (7.2) and (7.9). We will therefore be able to attain our final bound for ![]() $\sum _{{\underline {h}}\ll H}T_{{\underline {h}}}(q,\underline {z})$ if we can find a bound for
$\sum _{{\underline {h}}\ll H}T_{{\underline {h}}}(q,\underline {z})$ if we can find a bound for ![]() $T_{{\underline {h}},\underline {t}}(q,\underline {z})$ by (7.15).
$T_{{\underline {h}},\underline {t}}(q,\underline {z})$ by (7.15).
We may use Propositions 6.3 and 6.5 to bound ![]() $T_{{\underline {h}},\underline {t}}(q,\underline {z})$ from above when
$T_{{\underline {h}},\underline {t}}(q,\underline {z})$ from above when ![]() $\eta < n-1$ and
$\eta < n-1$ and ![]() $\eta =n-1$, respectively. When
$\eta =n-1$, respectively. When ![]() $\eta =n$, we may proceed by a much simpler argument to bound
$\eta =n$, we may proceed by a much simpler argument to bound ![]() $T_{{\underline {h}},\underline {t}}(q,\underline {z})$. We trivially have
$T_{{\underline {h}},\underline {t}}(q,\underline {z})$. We trivially have
and by Lemma 7.1 (![]() $v=\infty$,
$v=\infty$, ![]() $i=n$), we have that
$i=n$), we have that
Hence,
 \begin{equation} \sum_{\substack{{\underline{h}}\ll H \\ s_{\infty}({\underline{h}})=n-1}}|T_{{\underline{h}} (q,\underline{z})}|\ll q^2P^n. \end{equation}
\begin{equation} \sum_{\substack{{\underline{h}}\ll H \\ s_{\infty}({\underline{h}})=n-1}}|T_{{\underline{h}} (q,\underline{z})}|\ll q^2P^n. \end{equation}
Returning to ![]() $\eta \leq n-1$: By (7.10) (and recalling (5.3)), we may use the proof of Proposition 2 from [Reference Browning and Heath-BrownBH09] to conclude that for every
$\eta \leq n-1$: By (7.10) (and recalling (5.3)), we may use the proof of Proposition 2 from [Reference Browning and Heath-BrownBH09] to conclude that for every ![]() $\underline {t}\in T_{\eta }$, we have
$\underline {t}\in T_{\eta }$, we have
 \[ D_{\tilde{F}_{{\underline{h}},\underline{t}},\tilde{G}_{{\underline{h}},\underline{t}}}(b_{1,i}b_{2,i}\tilde{q}_{3,i})\ll q^{\varepsilon}\prod_{i=\eta+1}^n (b_{1,i}b_{2,i}^{1/2}\tilde{q}_{3,i})^{i-\eta}, \]
\[ D_{\tilde{F}_{{\underline{h}},\underline{t}},\tilde{G}_{{\underline{h}},\underline{t}}}(b_{1,i}b_{2,i}\tilde{q}_{3,i})\ll q^{\varepsilon}\prod_{i=\eta+1}^n (b_{1,i}b_{2,i}^{1/2}\tilde{q}_{3,i})^{i-\eta}, \]
when ![]() $\eta < n-1$. When
$\eta < n-1$. When ![]() $\eta =n-1$,
$\eta =n-1$, ![]() $(p,\mathrm {Cont}(\tilde {F}_{{\underline {h}},\underline {t}}),\mathrm {Cont}(\tilde {G}_{{\underline {h}},\underline {t}}))=p$ if and only if
$(p,\mathrm {Cont}(\tilde {F}_{{\underline {h}},\underline {t}}),\mathrm {Cont}(\tilde {G}_{{\underline {h}},\underline {t}}))=p$ if and only if ![]() $p|\tilde {F}_{{\underline {h}},\underline {t}},\tilde {G}_{{\underline {h}},\underline {t}}$ or
$p|\tilde {F}_{{\underline {h}},\underline {t}},\tilde {G}_{{\underline {h}},\underline {t}}$ or ![]() $p\ll P^{\varepsilon }$. In particular,
$p\ll P^{\varepsilon }$. In particular, ![]() $p| b_{1,n}b_{2,n}^{1/2}\tilde {q}_{3,n}$ or
$p| b_{1,n}b_{2,n}^{1/2}\tilde {q}_{3,n}$ or ![]() $p\ll P^{\epsilon }\asymp q^{\varepsilon }$, and so we again have
$p\ll P^{\epsilon }\asymp q^{\varepsilon }$, and so we again have
Therefore, by (7.15), (7.16) and Propositions 6.3 and 6.5 and (7.17), we may conclude as follows.
Proposition 7.2 Let ![]() $q< P^2$, and let
$q< P^2$, and let
for ![]() $\eta \in \{0,\ldots, n-2\}$ and let
$\eta \in \{0,\ldots, n-2\}$ and let
Then
 \[ \sum_{{\underline{h}}\in H_s}|T_{{\underline{h}}}(q,\underline{z})|\ll q^2P^{n+\varepsilon}\bigg{(} 1+\sum_{\eta=0}^{n-1} \mathcal{Y}_{\eta}\bigg{)}. \]
\[ \sum_{{\underline{h}}\in H_s}|T_{{\underline{h}}}(q,\underline{z})|\ll q^2P^{n+\varepsilon}\bigg{(} 1+\sum_{\eta=0}^{n-1} \mathcal{Y}_{\eta}\bigg{)}. \]
Here,
8. Weyl differencing
In this section, we will derive several auxiliary bounds using Weyl differencing which will serve as complementary bounds to the more powerful ones coming from van der Corput differencing and Poisson summation. We will need a bound which uses Weyl differencing twice, as well as two bounds which come from applying variations of van der Corput differencing once, followed by a single application of Weyl differencing on the resulting quadratic exponential sum. In the case of the former, the topic of performing Weyl differencing repeatedly on a system of forms has already been covered extensively by Lee in the context of function fields [Reference LeeLee11]. The Weyl differencing arguments that are used in his paper do not rely on being in a function fields setting, and so we may freely invoke the results in [Reference LeeLee11, Section 3]. In particular, upon setting ![]() $d=3$ and
$d=3$ and ![]() $R=2$, an application of [Reference LeeLee11, Lemma 3.7] gives us
$R=2$, an application of [Reference LeeLee11, Lemma 3.7] gives us
 \[ |K(\underline{a}/q+\underline{z})|\ll P^{n+\varepsilon}\bigg{(} P^{-4}+q^2|\underline{z}|^2+q^2P^{-6}+q^{-1}\min\bigg\{1,\frac{1}{|\underline{z}|P^3}\bigg\}\bigg{)}^{(n-\sigma'-1)/16}, \]
\[ |K(\underline{a}/q+\underline{z})|\ll P^{n+\varepsilon}\bigg{(} P^{-4}+q^2|\underline{z}|^2+q^2P^{-6}+q^{-1}\min\bigg\{1,\frac{1}{|\underline{z}|P^3}\bigg\}\bigg{)}^{(n-\sigma'-1)/16}, \]
where
and ![]() $f^{(0)}$ and
$f^{(0)}$ and ![]() $g^{(0)}$ are defined to be the top forms of
$g^{(0)}$ are defined to be the top forms of ![]() $F$ and
$F$ and ![]() $G$, respectively. However, we may use Lemma 2.3 to conclude that
$G$, respectively. However, we may use Lemma 2.3 to conclude that ![]() $\sigma '\leq \sigma (f^{(0)},g^{(0)})+1$. Hence, we arrive at the following.
$\sigma '\leq \sigma (f^{(0)},g^{(0)})+1$. Hence, we arrive at the following.
Proposition 8.1 (Weyl/Weyl)
Let ![]() $F$,
$F$, ![]() $G$ be cubic polynomials such that
$G$ be cubic polynomials such that
and ![]() $\sigma (F^{(0)},G^{(0)})=\sigma$. Then,
$\sigma (F^{(0)},G^{(0)})=\sigma$. Then,
 \[ |K(\underline{a}/q+\underline{z})|\ll P^{n+\varepsilon}\bigg{(} P^{-4}+q^2|\underline{z}|^2+q^2P^{-6}+q^{-1}\min\bigg\{1,\frac{1}{|\underline{z}|P^3}\bigg\}\bigg{)}^{(n-\sigma-2)/16}. \]
\[ |K(\underline{a}/q+\underline{z})|\ll P^{n+\varepsilon}\bigg{(} P^{-4}+q^2|\underline{z}|^2+q^2P^{-6}+q^{-1}\min\bigg\{1,\frac{1}{|\underline{z}|P^3}\bigg\}\bigg{)}^{(n-\sigma-2)/16}. \]
We now aim to bound the exponential sum,
that we get after performing van der Corput differencing once. In this case, ![]() $F$ and
$F$ and ![]() $G$ are quadratic polynomials such that
$G$ are quadratic polynomials such that ![]() $\|f^{(0)}\|,\|g^{(0)}\|\ll H$, for some
$\|f^{(0)}\|,\|g^{(0)}\|\ll H$, for some ![]() $1\leq H\leq P$. The aforementioned work of Lee has also kept an explicit dependence of the dependence on
$1\leq H\leq P$. The aforementioned work of Lee has also kept an explicit dependence of the dependence on ![]() $H$ throughout the Weyl differencing process. In particular, the following lemma is a direct consequence of [Reference LeeLee11, Equation (3.20)].
$H$ throughout the Weyl differencing process. In particular, the following lemma is a direct consequence of [Reference LeeLee11, Equation (3.20)].
Proposition 8.2 (van der Corput/Weyl)
Let ![]() $F$,
$F$, ![]() $G$ be quadratic polynomials such that
$G$ be quadratic polynomials such that
and let ![]() $\sigma :=\sigma (f^{(0)},g^{(0)})$. Then,
$\sigma :=\sigma (f^{(0)},g^{(0)})$. Then,
 \[ |T({\underline{a}},q,\underline{z})|\ll P^{n+\varepsilon}\bigg{(} P^{-2}+q^2H^2|\underline{z}|^2+q^2P^{-4}+q^{-1}H^2\min\bigg\{1,\frac{1}{H|\underline{z}|P^2}\bigg\}\bigg{)}^{(n-\sigma-2)/4}. \]
\[ |T({\underline{a}},q,\underline{z})|\ll P^{n+\varepsilon}\bigg{(} P^{-2}+q^2H^2|\underline{z}|^2+q^2P^{-4}+q^{-1}H^2\min\bigg\{1,\frac{1}{H|\underline{z}|P^2}\bigg\}\bigg{)}^{(n-\sigma-2)/4}. \]
We refer the readers not familiar with the function field version to the first author's PhD thesis [Reference NortheyNor00a, Section 6] for a detailed proof of this result.
9. Minor arcs estimate
In this Section, we will combine all of the approaches we have been developing throughout this paper to finally prove Proposition 3.3. In particular, we aim to show that, provided that ![]() $F,G$ intersect smoothly, and
$F,G$ intersect smoothly, and ![]() $n\geq 39$, we have
$n\geq 39$, we have
for some ![]() $\delta >0$. To achieve this, we will split the
$\delta >0$. To achieve this, we will split the ![]() $q$ sum of
$q$ sum of ![]() $S_{\mathfrak {m}}$ into square-free, cube-free square, fourth power-free cube and fourth power-full parts (
$S_{\mathfrak {m}}$ into square-free, cube-free square, fourth power-free cube and fourth power-full parts (![]() $b_1,b_2,b_3, q_4$, respectively), and further split these sums into
$b_1,b_2,b_3, q_4$, respectively), and further split these sums into ![]() $O(P^{\varepsilon }$) dyadic ranges. In particular, we will be focusing on the sum
$O(P^{\varepsilon }$) dyadic ranges. In particular, we will be focusing on the sum
 \[ D_P(R,t,\underline{R}):=\sum_{b_1=R_1}^{2R_1}\sum_{b_2=R_2}^{2R_2}\sum_{b_3=R_3}^{2R_3}\sum_{q_4=R_4}^{2R_4}\sideset{}{^*}\sum_{{\underline{a}}}\int_{t\ll|\underline{z}|\ll t} | K({\underline{a}}/q+\underline{z}) |\,d\underline{z}, \]
\[ D_P(R,t,\underline{R}):=\sum_{b_1=R_1}^{2R_1}\sum_{b_2=R_2}^{2R_2}\sum_{b_3=R_3}^{2R_3}\sum_{q_4=R_4}^{2R_4}\sideset{}{^*}\sum_{{\underline{a}}}\int_{t\ll|\underline{z}|\ll t} | K({\underline{a}}/q+\underline{z}) |\,d\underline{z}, \]
where ![]() $\underline {R}:=(R_1,R_2,R_3,R_4)$ and
$\underline {R}:=(R_1,R_2,R_3,R_4)$ and
(the latter is apparent from the definition of ![]() $D_P(R,t,\underline {R})$, but it will be helpful to be able to reference this later). From the definition of
$D_P(R,t,\underline {R})$, but it will be helpful to be able to reference this later). From the definition of ![]() $S_{\mathfrak {m}}$, we need only consider
$S_{\mathfrak {m}}$, we need only consider ![]() $D_P(R,t,\underline {R})$ when
$D_P(R,t,\underline {R})$ when
Likewise, we must also either have
Now, upon bounding ![]() $K({\underline {a}}/q+\underline {z})$ trivially for
$K({\underline {a}}/q+\underline {z})$ trivially for ![]() $t\leq P^{-5}$, we see that
$t\leq P^{-5}$, we see that
Our aim in this section is to show that ![]() $D_P(R,t,\underline {R})\ll P^{n-6-\delta }$ for some
$D_P(R,t,\underline {R})\ll P^{n-6-\delta }$ for some ![]() $\delta >0$, as this is sufficient to bound our minor arcs by
$\delta >0$, as this is sufficient to bound our minor arcs by ![]() $P^{n-6-\delta }$ by (9.4). Note that this is equivalent to proving that
$P^{n-6-\delta }$ by (9.4). Note that this is equivalent to proving that
for some ![]() $\delta >0$, and for
$\delta >0$, and for ![]() $P$ sufficiently large (so that the implied constant in (9.4) becomes negligible), where
$P$ sufficiently large (so that the implied constant in (9.4) becomes negligible), where
Finally, as mentioned in § 3 we will choose
from this point onwards (this choice will be explained in § 9.3.1). With this last bit of setup, we are now ready to start the process of bounding ![]() $S_{\mathfrak {m}}$. We will do this by applying a total of five different bounds based on different combinations of van der Corput differencing, Weyl differencing and Poisson summation to bound
$S_{\mathfrak {m}}$. We will do this by applying a total of five different bounds based on different combinations of van der Corput differencing, Weyl differencing and Poisson summation to bound ![]() $D_P(R,t,\underline {R})$ for different ranges of
$D_P(R,t,\underline {R})$ for different ranges of ![]() $R$ and
$R$ and ![]() $t$. In each range, we will take the minimum of all available bounds. To do so for all possible values of
$t$. In each range, we will take the minimum of all available bounds. To do so for all possible values of ![]() $R$ and
$R$ and ![]() $t$ is incredibly complicated. Therefore, instead of the tedious process of manually comparing and simplifying these bounds, a route which is traditionally taken, we take the idea of automating this process as in [Reference Marmon and VisheMV19] one step further. We will directly feed these bounds into the existing Min-Max algorithm in Mathematica and obtain an explicit value of the minimum value of our bounds on the Minor arcs. We have also verified this value using an open-source algorithm [Reference NortheyNor00b] designed by the first author. In its current form, this algorithm is significantly less efficient than the inbuilt one in Mathematica, but it allowed the authors to double check the bounds coming from this inbuilt function.
$t$ is incredibly complicated. Therefore, instead of the tedious process of manually comparing and simplifying these bounds, a route which is traditionally taken, we take the idea of automating this process as in [Reference Marmon and VisheMV19] one step further. We will directly feed these bounds into the existing Min-Max algorithm in Mathematica and obtain an explicit value of the minimum value of our bounds on the Minor arcs. We have also verified this value using an open-source algorithm [Reference NortheyNor00b] designed by the first author. In its current form, this algorithm is significantly less efficient than the inbuilt one in Mathematica, but it allowed the authors to double check the bounds coming from this inbuilt function.
Throughout this section, we will use the following lemma.
Lemma 9.1 Let ![]() $q=b_1b_2\cdots b_k q_{k+1}$, where
$q=b_1b_2\cdots b_k q_{k+1}$, where ![]() $b_i$ is the
$b_i$ is the ![]() $i$th power,
$i$th power, ![]() $(i+1)$th powerfree part of
$(i+1)$th powerfree part of ![]() $q$ and let
$q$ and let ![]() $q_{k+1}$ be the
$q_{k+1}$ be the ![]() $(k+1)$th power-full part of
$(k+1)$th power-full part of ![]() $q$. Then
$q$. Then
 \[ \sum_{\substack{b_i=R_i\\ i\in\{1,\ldots,\, k\}}}^{2R_i}\sum_{q_{k+1}=R_{k+1}}^{2R_{k+1}} b_1^{a_1} b_2^{a_2}\cdots b_k^{a_k} q_3^{a_{k+1}} \ll \prod_{i=1}^{k+1} R_i^{a_i+1/i}, \]
\[ \sum_{\substack{b_i=R_i\\ i\in\{1,\ldots,\, k\}}}^{2R_i}\sum_{q_{k+1}=R_{k+1}}^{2R_{k+1}} b_1^{a_1} b_2^{a_2}\cdots b_k^{a_k} q_3^{a_{k+1}} \ll \prod_{i=1}^{k+1} R_i^{a_i+1/i}, \]
for every ![]() $a_1,\ldots,a_{k+1}\geq 0$.
$a_1,\ldots,a_{k+1}\geq 0$.
The proof of this lemma is standard, and is similar to [Reference Browning and Heath-BrownBH09, Lemma 20] so we omit it here. This lemma enables us to get away with using slightly worse exponential sum bounds for the perfect square and cube-full parts of ![]() $q$ (a close inspection of the bounds found in § 5 will show that our bounds in these cases are indeed worse). We have stated Lemma 9.1 in this level of generality because it will be useful for us when considering the singular series of the major arcs. We will spend the remainder of this section finding our final bounds for the minor arcs in the case when
$q$ (a close inspection of the bounds found in § 5 will show that our bounds in these cases are indeed worse). We have stated Lemma 9.1 in this level of generality because it will be useful for us when considering the singular series of the major arcs. We will spend the remainder of this section finding our final bounds for the minor arcs in the case when ![]() $F$,
$F$,![]() $G$ are non-singular.
$G$ are non-singular.
9.1 Averaged van der Corput/Poisson
In this section, we will find a bound for ![]() $B_P(\phi, \tau, \underline {\phi }):=\log _P(D_P(R,t,\underline {R}))$ by combining the improved averaged van der Corput differencing process with Poisson summation. We will aim to show that
$B_P(\phi, \tau, \underline {\phi }):=\log _P(D_P(R,t,\underline {R}))$ by combining the improved averaged van der Corput differencing process with Poisson summation. We will aim to show that ![]() $B_P(\phi, \tau, \underline {\phi })\leq n-6-\delta$ for some
$B_P(\phi, \tau, \underline {\phi })\leq n-6-\delta$ for some ![]() $\delta >0$, provided that
$\delta >0$, provided that ![]() $n$ is sufficiently large. By Lemma 4.5, we have
$n$ is sufficiently large. By Lemma 4.5, we have
 \begin{align} D_P(R,t,\underline{R})&\ll_{\varepsilon,N} P^{-N}+\sum_{q,(9.1)}H^{-n/2+1}P^{n/2-1+\varepsilon}q((HP^2)^{-1}+t)^2\nonumber\\ &\quad \times \bigg{(}\max_{\underline{z}}\sum_{|{\underline{h}}|\ll H}|T_{\underline{h}}(q,\underline{z})|\bigg{)}^{1/2}, \end{align}
\begin{align} D_P(R,t,\underline{R})&\ll_{\varepsilon,N} P^{-N}+\sum_{q,(9.1)}H^{-n/2+1}P^{n/2-1+\varepsilon}q((HP^2)^{-1}+t)^2\nonumber\\ &\quad \times \bigg{(}\max_{\underline{z}}\sum_{|{\underline{h}}|\ll H}|T_{\underline{h}}(q,\underline{z})|\bigg{)}^{1/2}, \end{align}where
By Proposition 7.2 we have
 \begin{equation} \sum_{{\underline{h}}\ll H}|T_{{\underline{h}}}(q,\underline{z})|\ll q^2P^{n+\varepsilon}\bigg{\{} 1+\sum_{\eta=0}^{n-1} \mathcal{Y}_{\eta}\bigg{\}} , \end{equation}
\begin{equation} \sum_{{\underline{h}}\ll H}|T_{{\underline{h}}}(q,\underline{z})|\ll q^2P^{n+\varepsilon}\bigg{\{} 1+\sum_{\eta=0}^{n-1} \mathcal{Y}_{\eta}\bigg{\}} , \end{equation}where
for ![]() $\eta \in \{0,\ldots, n-2\}$,
$\eta \in \{0,\ldots, n-2\}$,
and by (5.9),
Up until now, we have assumed that ![]() $1\leq H\ll P$ was some arbitrary parameter (coming from the van der Corput differencing process) which we could choose freely. However, we did not explicitly make this choice due to our arguments in the previous sections being valid for any such
$1\leq H\ll P$ was some arbitrary parameter (coming from the van der Corput differencing process) which we could choose freely. However, we did not explicitly make this choice due to our arguments in the previous sections being valid for any such ![]() $H$. From this point onward, the choice of
$H$. From this point onward, the choice of ![]() $H$ becomes relevant for our bounds so we will define
$H$ becomes relevant for our bounds so we will define ![]() $H$ as follows:
$H$ as follows:
Our choice of ![]() $H$ is informed by the fact that we desire
$H$ is informed by the fact that we desire ![]() $H$ to be as small as possible in order to minimise the size of
$H$ to be as small as possible in order to minimise the size of ![]() $\mathcal {Y}_{0}$ in (9.9) whilst also making
$\mathcal {Y}_{0}$ in (9.9) whilst also making ![]() $H$ large enough to suppress the contribution coming from the ‘
$H$ large enough to suppress the contribution coming from the ‘![]() $1$’ term in (9.9) (note the large negative power of
$1$’ term in (9.9) (note the large negative power of ![]() $H$ in (9.7)). This is the ideal way to choose
$H$ in (9.7)). This is the ideal way to choose ![]() $H$ due to Lemma 9.2, which we will see later.
$H$ due to Lemma 9.2, which we will see later.
We will now continue the bounding process. We first recall that ![]() $|\underline {z}|\ll \max \{P^{\varepsilon }(HP^2)^{-1},t\}$ by (9.8) and note that
$|\underline {z}|\ll \max \{P^{\varepsilon }(HP^2)^{-1},t\}$ by (9.8) and note that ![]() $V(q,|\underline {z}|)\ll V(q,t)$ (up to a relabeling of
$V(q,|\underline {z}|)\ll V(q,t)$ (up to a relabeling of ![]() $\varepsilon$) in the range of
$\varepsilon$) in the range of ![]() $\underline {z}$ that we have. This is because by (9.12)
$\underline {z}$ that we have. This is because by (9.12)
 \begin{align} V(q,|\underline{z}|)=1+qP^{\varepsilon-1}\max\{1,\sqrt{HP^2|\underline{z}|}\}&\ll 1+qP^{\varepsilon-1}\max\{1,\sqrt{HP^2\cdot P^{\varepsilon}(HP^2)^{-1}},\sqrt{HP^2t}\}\nonumber\\ &\ll 1+qP^{2\varepsilon-1}\max\{1,\sqrt{HP^2t}\}\nonumber\\ &= V(q,t). \end{align}
\begin{align} V(q,|\underline{z}|)=1+qP^{\varepsilon-1}\max\{1,\sqrt{HP^2|\underline{z}|}\}&\ll 1+qP^{\varepsilon-1}\max\{1,\sqrt{HP^2\cdot P^{\varepsilon}(HP^2)^{-1}},\sqrt{HP^2t}\}\nonumber\\ &\ll 1+qP^{2\varepsilon-1}\max\{1,\sqrt{HP^2t}\}\nonumber\\ &= V(q,t). \end{align}
Hence, by (9.7) (assuming ![]() $N$ is chosen sufficiently large):
$N$ is chosen sufficiently large):
 \begin{align} D_P(R,t,\underline{R})&\ll \sum_{q,(9.1)}H^{-n/2+1}P^{n-1+\varepsilon}q^2((HP^2)^{-1}+t)^2 \bigg{(} 1+\sum_{\eta=0}^{n-1}\mathcal{Y}_{\eta}(q,b_1,b_3,q_4,t)\bigg{)}^{1/2}\nonumber\\ &\ll P^{n-1+\varepsilon}\sum_{\substack{b_i=R_i\nonumber\\ i\in\{1,2,3\}}}^{2R_i}\sum_{q_4=R_4}^{2R_4}R^2H^{-n/2+1}((HP^2)^{-1}+t)^2 (1+\mathcal{Y}_{0}+\cdots+\mathcal{Y}_{n-1})^{1/2} \end{align}
\begin{align} D_P(R,t,\underline{R})&\ll \sum_{q,(9.1)}H^{-n/2+1}P^{n-1+\varepsilon}q^2((HP^2)^{-1}+t)^2 \bigg{(} 1+\sum_{\eta=0}^{n-1}\mathcal{Y}_{\eta}(q,b_1,b_3,q_4,t)\bigg{)}^{1/2}\nonumber\\ &\ll P^{n-1+\varepsilon}\sum_{\substack{b_i=R_i\nonumber\\ i\in\{1,2,3\}}}^{2R_i}\sum_{q_4=R_4}^{2R_4}R^2H^{-n/2+1}((HP^2)^{-1}+t)^2 (1+\mathcal{Y}_{0}+\cdots+\mathcal{Y}_{n-1})^{1/2} \end{align}
where ![]() $\mathcal {R}:=R_1^{1/2}R_2^{1/2}R_3^{1/3}R_4^{1/4}$,
$\mathcal {R}:=R_1^{1/2}R_2^{1/2}R_3^{1/3}R_4^{1/4}$, ![]() $H=H(R)$,
$H=H(R)$, ![]() $V=V(R,t)$ and
$V=V(R,t)$ and ![]() $\mathcal {Y}_{i}=\mathcal {Y}_i(R,R_1,R_3,R_4,t)$ in (9.15)–(9.16). For the most part, we will continue to use
$\mathcal {Y}_{i}=\mathcal {Y}_i(R,R_1,R_3,R_4,t)$ in (9.15)–(9.16). For the most part, we will continue to use ![]() $H$,
$H$, ![]() $V$ and
$V$ and ![]() $\mathcal {Y}_{i}$ instead of
$\mathcal {Y}_{i}$ instead of ![]() $H(R)$,
$H(R)$, ![]() $V(R,t)$ and
$V(R,t)$ and ![]() $\mathcal {Y}_i(R,R_1,R_3,R_4,t)$ to avoid making the algebra more complicated than it already is. The final assertion is by Lemma 9.1.
$\mathcal {Y}_i(R,R_1,R_3,R_4,t)$ to avoid making the algebra more complicated than it already is. The final assertion is by Lemma 9.1.
We will start by simplifying the right-most bracket.
Lemma 9.2 For every ![]() $R,R_1,R_3,R_4,t$ satisfying (9.2), we have
$R,R_1,R_3,R_4,t$ satisfying (9.2), we have
Proof. For this proof, we will introduce the following sequence:
 \begin{align*} \mathcal{Y}_{\eta}'&:= \frac{H^{n-\eta}}{R^{(n-\eta)/2}}R_1^{-1}(R_1^{\eta/n}V^{n-\eta}+R_1^{1/2}R_3^{1/3-\eta/3n}R_4^{1/2-\eta/2n}V^{n-\eta-1+\eta/n}\\ &\quad+ R_1^{1/2}R_3^{(n-\eta)/3}R_4^{(n-\eta)/2}). \end{align*}
\begin{align*} \mathcal{Y}_{\eta}'&:= \frac{H^{n-\eta}}{R^{(n-\eta)/2}}R_1^{-1}(R_1^{\eta/n}V^{n-\eta}+R_1^{1/2}R_3^{1/3-\eta/3n}R_4^{1/2-\eta/2n}V^{n-\eta-1+\eta/n}\\ &\quad+ R_1^{1/2}R_3^{(n-\eta)/3}R_4^{(n-\eta)/2}). \end{align*}
We will prove that this sequence has the following three properties:
(1)
 $\mathcal {Y}_{\eta }\ll \mathcal {Y}_{\eta }'$ for every
$\mathcal {Y}_{\eta }\ll \mathcal {Y}_{\eta }'$ for every  $\eta \in \{0,\ldots, n-1\}$;
$\eta \in \{0,\ldots, n-1\}$;(2)
 $\mathcal {Y}_{0}'=\mathcal {Y}_{0}$, and
$\mathcal {Y}_{0}'=\mathcal {Y}_{0}$, and  $\mathcal {Y}_{n}'\asymp 1$;
$\mathcal {Y}_{n}'\asymp 1$;(3)
 $\sum _{\eta =0}^n\mathcal {Y}_{\eta }'$ is a sum of three geometric series.
$\sum _{\eta =0}^n\mathcal {Y}_{\eta }'$ is a sum of three geometric series.
Verifying these three facts is sufficient to complete the proof since properties (1) and (2) imply that ![]() $(1+\mathcal {Y}_{0}+\cdots +\mathcal {Y}_{n-1})\ll (\mathcal {Y}_{0}'+\cdots +\mathcal {Y}_{n-1}'+\mathcal {Y}_n')$, property (3) implies that
$(1+\mathcal {Y}_{0}+\cdots +\mathcal {Y}_{n-1})\ll (\mathcal {Y}_{0}'+\cdots +\mathcal {Y}_{n-1}'+\mathcal {Y}_n')$, property (3) implies that ![]() $(\mathcal {Y}_{0}'+\cdots +\mathcal {Y}_{n-1}'+\mathcal {Y}_n')\ll (\mathcal {Y}_{0}'+\mathcal {Y}_{n}')$, and property (2) implies that
$(\mathcal {Y}_{0}'+\cdots +\mathcal {Y}_{n-1}'+\mathcal {Y}_n')\ll (\mathcal {Y}_{0}'+\mathcal {Y}_{n}')$, and property (2) implies that ![]() $(\mathcal {Y}_{0}'+\mathcal {Y}_{n}')=(1+\mathcal {Y}_{0})$.
$(\mathcal {Y}_{0}'+\mathcal {Y}_{n}')=(1+\mathcal {Y}_{0})$.
For property (1), we note that the term outside of the bracket of ![]() $\mathcal {Y}_{\eta }'$ is equal to the analogous term in
$\mathcal {Y}_{\eta }'$ is equal to the analogous term in ![]() $\mathcal {Y}_{\eta }$. It therefore suffices to bound each term in the bracket of
$\mathcal {Y}_{\eta }$. It therefore suffices to bound each term in the bracket of ![]() $\mathcal {Y}_{\eta }$ from above by a term in
$\mathcal {Y}_{\eta }$ from above by a term in ![]() $\mathcal {Y}_{\eta }'$: we clearly have
$\mathcal {Y}_{\eta }'$: we clearly have ![]() $V^{n-\eta }\leq R_1^{\eta /n}V^{n-\eta }$ when
$V^{n-\eta }\leq R_1^{\eta /n}V^{n-\eta }$ when ![]() $\eta \in \{1,\ldots,n-2\}$ and
$\eta \in \{1,\ldots,n-2\}$ and ![]() $R_1^{1/2}V\leq R_1^{(n-1)/n}V$ for every
$R_1^{1/2}V\leq R_1^{(n-1)/n}V$ for every ![]() $n\geq 1$. The third term of
$n\geq 1$. The third term of ![]() $\mathcal {Y}_{\eta }$ and
$\mathcal {Y}_{\eta }$ and ![]() $\mathcal {Y}_{\eta }'$ coincide with each other for every
$\mathcal {Y}_{\eta }'$ coincide with each other for every ![]() $\eta \in \{1,\ldots,n-1\}$.
$\eta \in \{1,\ldots,n-1\}$.
As for the middle term,
if and only if ![]() $V\geq R_3^{1/3}R_4^{1/2}$. However, if
$V\geq R_3^{1/3}R_4^{1/2}$. However, if ![]() $V< R_3^{1/3}R_4^{1/2}$, then
$V< R_3^{1/3}R_4^{1/2}$, then
which is the third term of ![]() $\mathcal {Y}_{\eta }'$. Hence, we have
$\mathcal {Y}_{\eta }'$. Hence, we have ![]() $\mathcal {Y}_{\eta }\ll \mathcal {Y}_{\eta }'$.
$\mathcal {Y}_{\eta }\ll \mathcal {Y}_{\eta }'$.
Property (2) is trivial so we will move to verifying property (3). Again, we will go term by term: let
Then
If we similarly define ![]() $\mathcal {Y}_{\eta,2}'$ and
$\mathcal {Y}_{\eta,2}'$ and ![]() $\mathcal {Y}_{\eta,3}'$ in the obvious way, then we see that
$\mathcal {Y}_{\eta,3}'$ in the obvious way, then we see that
Hence, we may represent ![]() $\sum \mathcal {Y}_{\eta }'$ as a sum of three geometric series, as required. This completes the proof.
$\sum \mathcal {Y}_{\eta }'$ as a sum of three geometric series, as required. This completes the proof.
We may use Lemma 9.2 to conclude that
We now aim to simplify this expression further by showing that ![]() $V^{n}\leq R^{1/2}R_3^{1/3}R_4^{1/2}V^{n-1}$ or, equivalently, that
$V^{n}\leq R^{1/2}R_3^{1/3}R_4^{1/2}V^{n-1}$ or, equivalently, that ![]() $V\leq R^{1/2}R_3^{1/3}R_4^{1/2}$. Doing this, will let us show the following.
$V\leq R^{1/2}R_3^{1/3}R_4^{1/2}$. Doing this, will let us show the following.
Lemma 9.3 Let ![]() $Q=P^{3/2}$ and let
$Q=P^{3/2}$ and let ![]() $H$ and
$H$ and ![]() $V$ be defined as above. If
$V$ be defined as above. If ![]() $n\geq 23$, then
$n\geq 23$, then
In particular,
Proof. As mentioned we will first prove that ![]() $V\leq R^{1/2}$. Recall that
$V\leq R^{1/2}$. Recall that
We clearly have ![]() $1\leq R^{1/2}$.
$1\leq R^{1/2}$.
When ![]() $V=RP^{-1+\varepsilon }$, we note that
$V=RP^{-1+\varepsilon }$, we note that ![]() $R>P^{1-\varepsilon }$ otherwise
$R>P^{1-\varepsilon }$ otherwise ![]() $RP^{-1+\varepsilon }\leq 1$, and so
$RP^{-1+\varepsilon }\leq 1$, and so ![]() $V$ cannot be equal to
$V$ cannot be equal to ![]() $RP^{-1+\varepsilon }$. Furthermore, we see that
$RP^{-1+\varepsilon }$. Furthermore, we see that ![]() $R\leq Q=P^{3/2}$ or, equivalently,
$R\leq Q=P^{3/2}$ or, equivalently, ![]() $P^{-1}\leq R^{-2/3}$. Hence, provided that
$P^{-1}\leq R^{-2/3}$. Hence, provided that ![]() $\varepsilon$ is chosen small enough so that
$\varepsilon$ is chosen small enough so that ![]() $P^{\varepsilon }\leq R^{1/6}$, then we also have
$P^{\varepsilon }\leq R^{1/6}$, then we also have ![]() $P^{-1+\varepsilon }< R^{-1/2}$. Since
$P^{-1+\varepsilon }< R^{-1/2}$. Since ![]() $R>P^{1-\varepsilon }$,
$R>P^{1-\varepsilon }$, ![]() $\varepsilon <0.1$ would suffice for example.
$\varepsilon <0.1$ would suffice for example.
Finally, we consider when ![]() $V=RP^{-1+\varepsilon }(H(R)P^2t)^{1/2}$. In this case, since
$V=RP^{-1+\varepsilon }(H(R)P^2t)^{1/2}$. In this case, since ![]() $t\leq (RQ^{1/2})^{-1}$,
$t\leq (RQ^{1/2})^{-1}$,
But since ![]() $R\leq Q$,
$R\leq Q$, ![]() $P< Q$ (and
$P< Q$ (and ![]() $5/(n-2)>4/(n+2)$), we have
$5/(n-2)>4/(n+2)$), we have
provided ![]() $n\geq 23$.
$n\geq 23$.
This concludes the proof that ![]() $V\leq R^{1/2}$. For the second statement of the lemma, we start by noting that
$V\leq R^{1/2}$. For the second statement of the lemma, we start by noting that ![]() $V^{n}\leq R^{1/2}V^{n-1}$, and so by (9.10) and (9.2):
$V^{n}\leq R^{1/2}V^{n-1}$, and so by (9.10) and (9.2):
 \begin{align*} \mathcal{Y}_{0}(R,R_1,R_3,R_4,t)&:=\frac{H^{n}}{R^{n/2}}R_1^{-1}( V^{n}+R_1^{1/2}R_3^{1/3}R_4^{1/2}V^{n-1} +R_1^{1/2}R_3^{n/3}R_4^{n/2})\\ &\leq \frac{H^{n}}{R^{n/2}}R_1^{-1}( V^{n}+R^{1/2}V^{n-1} +R^{1/2}R_3^{n/3-1/2}R_4^{(n-1)/2})\\ &\ll \frac{H^{n}}{R^{n/2}}R_1^{-1}(R^{1/2}V^{n-1} +R^{1/2}R_3^{n/3-1/2}R_4^{(n-1)/2})\\ &=R^{(1-n)/2}R_1^{-1}H^n(V^{n-1} + R_3^{n/3-1/2}R_4^{(n-1)/2}). \end{align*}
\begin{align*} \mathcal{Y}_{0}(R,R_1,R_3,R_4,t)&:=\frac{H^{n}}{R^{n/2}}R_1^{-1}( V^{n}+R_1^{1/2}R_3^{1/3}R_4^{1/2}V^{n-1} +R_1^{1/2}R_3^{n/3}R_4^{n/2})\\ &\leq \frac{H^{n}}{R^{n/2}}R_1^{-1}( V^{n}+R^{1/2}V^{n-1} +R^{1/2}R_3^{n/3-1/2}R_4^{(n-1)/2})\\ &\ll \frac{H^{n}}{R^{n/2}}R_1^{-1}(R^{1/2}V^{n-1} +R^{1/2}R_3^{n/3-1/2}R_4^{(n-1)/2})\\ &=R^{(1-n)/2}R_1^{-1}H^n(V^{n-1} + R_3^{n/3-1/2}R_4^{(n-1)/2}). \end{align*}
Hence, if we let
then we now may Lemma 9.3 and (9.17) to bound ![]() $D_P(R,t,\underline {R})$ as follows:
$D_P(R,t,\underline {R})$ as follows:
 \begin{align} D_P(R,t,\underline{R})&\ll P^{n-1+\varepsilon}\mathcal{R}R^{2}H^{-n/2+1} ((HP^2)^{-1}+t)^2(R_1+\mathcal{X}_{1}+\mathcal{X}_{2})^{1/2})\nonumber\\ &\ll P^{n-1+\varepsilon}R^{5/2}H^{(2-n)/2} \max\{(HP^2)^{-1},t\}^2\max\{R,\mathcal{X}_{1},\mathcal{X}_{2}\}^{1/2}. \end{align}
\begin{align} D_P(R,t,\underline{R})&\ll P^{n-1+\varepsilon}\mathcal{R}R^{2}H^{-n/2+1} ((HP^2)^{-1}+t)^2(R_1+\mathcal{X}_{1}+\mathcal{X}_{2})^{1/2})\nonumber\\ &\ll P^{n-1+\varepsilon}R^{5/2}H^{(2-n)/2} \max\{(HP^2)^{-1},t\}^2\max\{R,\mathcal{X}_{1},\mathcal{X}_{2}\}^{1/2}. \end{align}
Finally, note that ![]() $D_P(R,t,\underline {R})\ll P^{n-6-\delta }$ for some
$D_P(R,t,\underline {R})\ll P^{n-6-\delta }$ for some ![]() $\delta >0$ if
$\delta >0$ if ![]() $\log _{P}(D_P(R,t,\underline {R}))\leq n-6-\delta$ (provided
$\log _{P}(D_P(R,t,\underline {R}))\leq n-6-\delta$ (provided ![]() $P$ is chosen large enough) and so it is sensible to consider bounding
$P$ is chosen large enough) and so it is sensible to consider bounding ![]() $B_P(\phi, \tau, \underline {\phi }):=\log _P(D_P(R,t,\underline {R}))$. By (9.20) and upon letting
$B_P(\phi, \tau, \underline {\phi }):=\log _P(D_P(R,t,\underline {R}))$. By (9.20) and upon letting ![]() $R:=P^{\phi }$,
$R:=P^{\phi }$, ![]() $R_i:=P^{\phi _i}$,
$R_i:=P^{\phi _i}$, ![]() $t:=P^{\tau }$, we have
$t:=P^{\tau }$, we have
 \begin{align} B_P(\phi, \tau, \underline{\phi}) &\leq \log_P(P^{n-1+\varepsilon}R^{5/2}H^{(2-n)/2} \max\{(HP^2)^{-1},t\}^2\max\{R,\mathcal{X}_{1},\mathcal{X}_{2}\}^{1/2})\nonumber\\ &= n-1 + \varepsilon + \frac{5\phi}{2}+ \frac{(2-n)}{2}\cdot \log_P(H) + 2\max\{-2-\log_P(H),\tau\} \nonumber\\ &\quad +\frac{1}{2}\max\{\phi, \log_P(\mathcal{X}_{1}),\log_P(\mathcal{X}_{2})\} +\log_P(C), \end{align}
\begin{align} B_P(\phi, \tau, \underline{\phi}) &\leq \log_P(P^{n-1+\varepsilon}R^{5/2}H^{(2-n)/2} \max\{(HP^2)^{-1},t\}^2\max\{R,\mathcal{X}_{1},\mathcal{X}_{2}\}^{1/2})\nonumber\\ &= n-1 + \varepsilon + \frac{5\phi}{2}+ \frac{(2-n)}{2}\cdot \log_P(H) + 2\max\{-2-\log_P(H),\tau\} \nonumber\\ &\quad +\frac{1}{2}\max\{\phi, \log_P(\mathcal{X}_{1}),\log_P(\mathcal{X}_{2})\} +\log_P(C), \end{align}
where ![]() $C$ is the implied constant in (9.20). If
$C$ is the implied constant in (9.20). If ![]() $P$ is made to be sufficiently large,
$P$ is made to be sufficiently large, ![]() $\log _P(C)$ can be absorbed into
$\log _P(C)$ can be absorbed into ![]() $\varepsilon$. Hence (recalling (9.13)–(9.12), (9.18)–(9.19)), if we set
$\varepsilon$. Hence (recalling (9.13)–(9.12), (9.18)–(9.19)), if we set
 \begin{align} \mathcal{X}\_\text{brac}(\phi,\tau,\phi_3,\phi_4)&:=\max\bigg\{\phi,\, \frac{(1-n)\phi}{2} + n\,\hat{H}(\phi)+ (n-1)\, \hat{V}(\phi,\tau), \nonumber\\ &\qquad \frac{(1-n)\phi}{2}+\bigg{(}\frac{n}{3}-\frac{1}{2}\bigg{)}\phi_3+\frac{(n-1)\phi_4}{2}+ n\,\hat{H}(\phi)\bigg\}, \end{align}
\begin{align} \mathcal{X}\_\text{brac}(\phi,\tau,\phi_3,\phi_4)&:=\max\bigg\{\phi,\, \frac{(1-n)\phi}{2} + n\,\hat{H}(\phi)+ (n-1)\, \hat{V}(\phi,\tau), \nonumber\\ &\qquad \frac{(1-n)\phi}{2}+\bigg{(}\frac{n}{3}-\frac{1}{2}\bigg{)}\phi_3+\frac{(n-1)\phi_4}{2}+ n\,\hat{H}(\phi)\bigg\}, \end{align}
(for some small ![]() $\varepsilon '>0$ that we may choose freely), then (9.21) gives us the following.
$\varepsilon '>0$ that we may choose freely), then (9.21) gives us the following.
Lemma 9.4 Let ![]() $n$ be fixed, and
$n$ be fixed, and
Then ![]() $B_{AV/P}(\phi,\tau,\phi _3,\phi _4)$ is a continuous, piecewise linear function, and for every
$B_{AV/P}(\phi,\tau,\phi _3,\phi _4)$ is a continuous, piecewise linear function, and for every ![]() $\varepsilon >0$, there is a sufficiently large
$\varepsilon >0$, there is a sufficiently large ![]() $P$ such that
$P$ such that
for every ![]() $\phi \in [0,3/2]$,
$\phi \in [0,3/2]$, ![]() $\phi _i\in [0,\phi ]$,
$\phi _i\in [0,\phi ]$, ![]() $\phi _1+\phi _2+\phi _3+\phi _4=\phi$ and
$\phi _1+\phi _2+\phi _3+\phi _4=\phi$ and ![]() $\tau \in [-5,-\phi -0.75]$.
$\tau \in [-5,-\phi -0.75]$.
The naming convention used is to make it easier to parse the algorithm's input. For example, ![]() $\tau \_\mathrm {brac}$ and
$\tau \_\mathrm {brac}$ and ![]() $\hat {H}$ correspond to Tau_bracket and H_Poisson, respectively, in the algorithm's code.
$\hat {H}$ correspond to Tau_bracket and H_Poisson, respectively, in the algorithm's code.
9.1.1 The limiting case
In this subsection, we will briefly illustrate why we should expect the condition ![]() $n\geq 39$ to appear in Proposition 3.3 (or, equivalently, why we should expect
$n\geq 39$ to appear in Proposition 3.3 (or, equivalently, why we should expect ![]() $D_P(R,t,\underline {R})\ll P^{n-6-\delta }$ to be true for
$D_P(R,t,\underline {R})\ll P^{n-6-\delta }$ to be true for ![]() $n\geq 39$). In general, we expect the limiting condition on
$n\geq 39$). In general, we expect the limiting condition on ![]() $n$ to be determined by the so-called ‘generic case’ for
$n$ to be determined by the so-called ‘generic case’ for ![]() $(R,t,\underline {R})$, which is
$(R,t,\underline {R})$, which is
This is the case where ![]() $R$ is as large as possible and is square-free, and
$R$ is as large as possible and is square-free, and ![]() $t$ is as large as possible. In this case, we expect the averaged van der Corput/Poisson bound to dominate over the other bounds since it is our main bound. We will therefore pinpoint which component of (9.20) dominates and then solve this part by hand. When we do this, we will see that the condition
$t$ is as large as possible. In this case, we expect the averaged van der Corput/Poisson bound to dominate over the other bounds since it is our main bound. We will therefore pinpoint which component of (9.20) dominates and then solve this part by hand. When we do this, we will see that the condition ![]() $n\geq 39$ arises naturally.
$n\geq 39$ arises naturally.
First, it is easy to check via the definitions of ![]() $H$ and
$H$ and ![]() $V$ (9.13)–(9.12) that when
$V$ (9.13)–(9.12) that when ![]() $R\asymp P^{3/2}$,
$R\asymp P^{3/2}$, ![]() $t\asymp P^{-9/4}$,
$t\asymp P^{-9/4}$, ![]() $R_1=R$,
$R_1=R$, ![]() $R_2=R_3=R_4=1$, we have
$R_2=R_3=R_4=1$, we have
 \begin{align} V&=P^{1/2}\max\{1,\: P^{10/(n-2)-1/4+\epsilon'},\: P^{11/(n+2)-1/4+\epsilon'}\}^{1/2}\nonumber\\ &=P^{3/8+\epsilon'/2}\max\{ P^{1/8},\: P^{5/(n-2)},P^{11/2(n+2)}\}. \end{align}
\begin{align} V&=P^{1/2}\max\{1,\: P^{10/(n-2)-1/4+\epsilon'},\: P^{11/(n+2)-1/4+\epsilon'}\}^{1/2}\nonumber\\ &=P^{3/8+\epsilon'/2}\max\{ P^{1/8},\: P^{5/(n-2)},P^{11/2(n+2)}\}. \end{align}
Note that when ![]() $n\leq 42$, it is easy to check that
$n\leq 42$, it is easy to check that ![]() $P^{10/(n-2)-1/4+\epsilon '}\geq P^{11/(n+2)-1/4+\epsilon '}>1$, and when
$P^{10/(n-2)-1/4+\epsilon '}\geq P^{11/(n+2)-1/4+\epsilon '}>1$, and when ![]() $n \geq 42$ we have
$n \geq 42$ we have ![]() $P^{10/(n-2)-1/4+\epsilon '}, P^{11/(n+2)-1/4+\epsilon '}<1$. It makes sense, therefore, to consider the cases
$P^{10/(n-2)-1/4+\epsilon '}, P^{11/(n+2)-1/4+\epsilon '}<1$. It makes sense, therefore, to consider the cases ![]() $n\leq 42$ and
$n\leq 42$ and ![]() $n>42$ separately so that we can simplify
$n>42$ separately so that we can simplify ![]() $H$ and
$H$ and ![]() $V$ further. We will just consider
$V$ further. We will just consider ![]() $n\leq 42$ here to avoid repetition, as the purpose here is to only illustrate the expected limit of our bounds.
$n\leq 42$ here to avoid repetition, as the purpose here is to only illustrate the expected limit of our bounds.
When ![]() $n\leq 42$, then by (9.26) and (9.27), we have
$n\leq 42$, then by (9.26) and (9.27), we have
We aim to insert these values into the right-hand side of (9.20), but we will first perform some simplifications. In particular, we note that
since ![]() $n\leq 42$. Similarly by (9.18)–(9.19), we see that
$n\leq 42$. Similarly by (9.18)–(9.19), we see that ![]() $\mathcal {X}_1>\mathcal {X}_2$ since
$\mathcal {X}_1>\mathcal {X}_2$ since ![]() $R_3=R_4=1$ and
$R_3=R_4=1$ and ![]() $V>1$. Hence,
$V>1$. Hence,
 \begin{align} \max\{R, \mathcal{X}_1, \mathcal{X}_2\}&= \max\{R, R^{(1-n)/2}\cdot P^{10n/(n-2)+n\epsilon'}\cdot P^{3(n-1)/8+5(n-1)/(n-2)+(n-1)\epsilon'/2}\}\nonumber\\ &=\max\{P^{3/2}, P^{3(1-n)/4+10n/(n-2)+3(n-1)/8+5(n-1)/(n-2)+\epsilon'}\}\nonumber\\ &=\max\{P^{3/2}, P^{3(1-n)/8+(15n-5)/(n-2)+\epsilon'}\}\nonumber\\ &=P^{3/2}, \end{align}
\begin{align} \max\{R, \mathcal{X}_1, \mathcal{X}_2\}&= \max\{R, R^{(1-n)/2}\cdot P^{10n/(n-2)+n\epsilon'}\cdot P^{3(n-1)/8+5(n-1)/(n-2)+(n-1)\epsilon'/2}\}\nonumber\\ &=\max\{P^{3/2}, P^{3(1-n)/4+10n/(n-2)+3(n-1)/8+5(n-1)/(n-2)+\epsilon'}\}\nonumber\\ &=\max\{P^{3/2}, P^{3(1-n)/8+(15n-5)/(n-2)+\epsilon'}\}\nonumber\\ &=P^{3/2}, \end{align}
provided that ![]() $n\geq 38.8111\cdots +\epsilon '$. In other words, as long as
$n\geq 38.8111\cdots +\epsilon '$. In other words, as long as ![]() $n\geq 39$ and
$n\geq 39$ and ![]() $\epsilon '$ is chosen small enough, we have
$\epsilon '$ is chosen small enough, we have ![]() $\max \{R, \mathcal {X}_1, \mathcal {X}_2\}=R=P^{3/2}$. Inserting (9.28)–(9.30) into (9.20) gives the following:
$\max \{R, \mathcal {X}_1, \mathcal {X}_2\}=R=P^{3/2}$. Inserting (9.28)–(9.30) into (9.20) gives the following:
 \begin{align*} D_P(R,t,\underline{R})&\ll P^{n-1+\varepsilon}R^{5/2}H^{(2-n)/2} \max\{(HP^2)^{-1},t\}^2\max\{R,\mathcal{X}_{1},\mathcal{X}_{2}\}^{1/2}\\ &= P^{n-1+\varepsilon}\cdot P^{15/4} \cdot P^{[(2-n)/2] \times [10/(n-2) + \epsilon']} \cdot P^{-9/2} \cdot P^{3/4}\\ &= P^{n-1+18/4-5-9/2+\epsilon-(n-2)\epsilon'/2}\\ &= P^{n-6-\delta(\epsilon,\epsilon')}, \end{align*}
\begin{align*} D_P(R,t,\underline{R})&\ll P^{n-1+\varepsilon}R^{5/2}H^{(2-n)/2} \max\{(HP^2)^{-1},t\}^2\max\{R,\mathcal{X}_{1},\mathcal{X}_{2}\}^{1/2}\\ &= P^{n-1+\varepsilon}\cdot P^{15/4} \cdot P^{[(2-n)/2] \times [10/(n-2) + \epsilon']} \cdot P^{-9/2} \cdot P^{3/4}\\ &= P^{n-1+18/4-5-9/2+\epsilon-(n-2)\epsilon'/2}\\ &= P^{n-6-\delta(\epsilon,\epsilon')}, \end{align*}
where ![]() $\delta >0$ provided that
$\delta >0$ provided that ![]() $\epsilon$ is chosen sufficiently small with respect to
$\epsilon$ is chosen sufficiently small with respect to ![]() $\epsilon '$ (and
$\epsilon '$ (and ![]() $n>2$).
$n>2$).
9.2 Pointwise van der Corput/Poisson
Next, we will find a bound for ![]() $B_P(\phi, \tau, \underline {\phi })$ by combining the improved Pointwise van der Corput differencing process with Poisson summation. This time, we may assume
$B_P(\phi, \tau, \underline {\phi })$ by combining the improved Pointwise van der Corput differencing process with Poisson summation. This time, we may assume ![]() $|\underline {z}|\asymp t$. By Lemma 4.1 and Proposition 7.2, the fact that the
$|\underline {z}|\asymp t$. By Lemma 4.1 and Proposition 7.2, the fact that the ![]() $\mathcal {Y}_i$s are a geometric series, and Lemmas 9.2–9.3 (using the same values for
$\mathcal {Y}_i$s are a geometric series, and Lemmas 9.2–9.3 (using the same values for ![]() $\mathcal {Y}, V, H$), we have
$\mathcal {Y}, V, H$), we have
 \begin{align} D_P(R,t,\underline{R})&\ll
\sum_{q,(9.1)} \int_{|\underline{z}|\asymp t}
H(q)^{-n/2}P^{n/2}q\bigg{(}\sum_{\underline{h}\ll
H}|T_{\underline{h}}(q,\underline{z})|\bigg{)}^{1/2}\,d\underline{z}\nonumber\\
&\ll P^{n+\varepsilon}\sum_{q,(9.1)}
\int_{|\underline{z}|\asymp t}
H(q)^{-n/2}q^2(1+\mathcal{Y}_{0}(q,b_1,q_3,|\underline{z}|))^{1/2}\,d\underline{z}\nonumber\\
&\ll P^{n+\varepsilon}\sum_{q,(9.1)} t^2
H(R)^{-n/2}R^2(1+\mathcal{Y}_{0}(R,R_1,R_3,t))^{1/2}\nonumber\\
&\ll P^{n+\varepsilon} \mathcal{R} t^2
H(R)^{-n/2}R^2(R_1+\mathcal{X}_{1}+\mathcal{X}_{2})^{1/2}\nonumber\\
&\ll P^{n+\varepsilon} R^{5/2} t^2
H(R)^{-n/2}(R+\mathcal{X}_{1}+\mathcal{X}_{2})^{1/2},
\end{align}
\begin{align} D_P(R,t,\underline{R})&\ll
\sum_{q,(9.1)} \int_{|\underline{z}|\asymp t}
H(q)^{-n/2}P^{n/2}q\bigg{(}\sum_{\underline{h}\ll
H}|T_{\underline{h}}(q,\underline{z})|\bigg{)}^{1/2}\,d\underline{z}\nonumber\\
&\ll P^{n+\varepsilon}\sum_{q,(9.1)}
\int_{|\underline{z}|\asymp t}
H(q)^{-n/2}q^2(1+\mathcal{Y}_{0}(q,b_1,q_3,|\underline{z}|))^{1/2}\,d\underline{z}\nonumber\\
&\ll P^{n+\varepsilon}\sum_{q,(9.1)} t^2
H(R)^{-n/2}R^2(1+\mathcal{Y}_{0}(R,R_1,R_3,t))^{1/2}\nonumber\\
&\ll P^{n+\varepsilon} \mathcal{R} t^2
H(R)^{-n/2}R^2(R_1+\mathcal{X}_{1}+\mathcal{X}_{2})^{1/2}\nonumber\\
&\ll P^{n+\varepsilon} R^{5/2} t^2
H(R)^{-n/2}(R+\mathcal{X}_{1}+\mathcal{X}_{2})^{1/2},
\end{align}
where the ![]() $\mathcal {X}_i$s are defined as in (9.18)–(9.19). Taking logs and recalling the definitions (9.22)–(9.25) gives us
$\mathcal {X}_i$s are defined as in (9.18)–(9.19). Taking logs and recalling the definitions (9.22)–(9.25) gives us
where ![]() $C$ is the implied constant in (9.31). Hence, we arrive at the following.
$C$ is the implied constant in (9.31). Hence, we arrive at the following.
Lemma 9.5 Let ![]() $n$ be fixed,
$n$ be fixed, ![]() $\log _P D_P(R,t,\underline {R}):= B_P(\phi, \tau, \underline {\phi })$, and
$\log _P D_P(R,t,\underline {R}):= B_P(\phi, \tau, \underline {\phi })$, and
Then ![]() $B_{PV/P}(\phi,\tau,\phi _3,\phi _4)$ is a continuous, piecewise linear function, and for every
$B_{PV/P}(\phi,\tau,\phi _3,\phi _4)$ is a continuous, piecewise linear function, and for every ![]() $\varepsilon >0$, there is a sufficiently large
$\varepsilon >0$, there is a sufficiently large ![]() $P$ such that
$P$ such that
for every ![]() $\phi \in [0,3/2]$,
$\phi \in [0,3/2]$, ![]() $\phi _i\in [0,\phi ]$,
$\phi _i\in [0,\phi ]$, ![]() $\phi _1+\phi _2+\phi _3+\phi _4=\phi$ and
$\phi _1+\phi _2+\phi _3+\phi _4=\phi$ and ![]() $\tau \in [-5,-\phi -0.75]$.
$\tau \in [-5,-\phi -0.75]$.
9.3 Averaged van der Corput/Weyl
We will now find a bound for ![]() $B_P(\phi, \tau, \underline {\phi })$ using the averaged van der Corput differencing process discussed in § 4, followed by one Weyl differencing step as in § 8. By Lemma 4.5 (upon choosing
$B_P(\phi, \tau, \underline {\phi })$ using the averaged van der Corput differencing process discussed in § 4, followed by one Weyl differencing step as in § 8. By Lemma 4.5 (upon choosing ![]() $N$ to be sufficiently large), we have
$N$ to be sufficiently large), we have
 \begin{align} D_P(R,t,\underline{R})&\ll_{\varepsilon,N} P^{-N}+ \sum_{q,(9.1)}H^{-n/2+1}P^{n/2-1+\varepsilon}q((HP^2)^{-1}+t)^2\nonumber\\ &\quad \times\bigg{(}\max_{t\leq|\underline{z}|\leq 2t+2(HP^{2-\varepsilon})^{-1}}\sum_{|{\underline{h}}|\ll H}|T_{\underline{h}}(q,\underline{z})| \bigg{)}^{1/2}. \end{align}
\begin{align} D_P(R,t,\underline{R})&\ll_{\varepsilon,N} P^{-N}+ \sum_{q,(9.1)}H^{-n/2+1}P^{n/2-1+\varepsilon}q((HP^2)^{-1}+t)^2\nonumber\\ &\quad \times\bigg{(}\max_{t\leq|\underline{z}|\leq 2t+2(HP^{2-\varepsilon})^{-1}}\sum_{|{\underline{h}}|\ll H}|T_{\underline{h}}(q,\underline{z})| \bigg{)}^{1/2}. \end{align}
We may now use Proposition 8.2 and (9.1)–(9.2) to bound ![]() $T_{\underline {h}}(q,\underline {z})$ as follows:
$T_{\underline {h}}(q,\underline {z})$ as follows:
 \begin{equation} |T_{\underline{h}}(q,\underline{z})|\ll R^2P^{n+\varepsilon} \bigg{(} P^{-2}+H^2R^2|\underline{z}|^2+R^2P^{-4}+R^{-1}H^2\min\bigg\{1,\frac{1}{H|\underline{z}|P^2}\bigg\}\bigg{)}^{(n-\sigma_{\infty}({\underline{h}})-2)/4}. \end{equation}
\begin{equation} |T_{\underline{h}}(q,\underline{z})|\ll R^2P^{n+\varepsilon} \bigg{(} P^{-2}+H^2R^2|\underline{z}|^2+R^2P^{-4}+R^{-1}H^2\min\bigg\{1,\frac{1}{H|\underline{z}|P^2}\bigg\}\bigg{)}^{(n-\sigma_{\infty}({\underline{h}})-2)/4}. \end{equation}
Next, we note that ![]() $t\leq |\underline {z}|\leq 2(t+(HP^{2-\varepsilon })^{-1})$ and so we wish apply a similar idea to (9.14) to replace
$t\leq |\underline {z}|\leq 2(t+(HP^{2-\varepsilon })^{-1})$ and so we wish apply a similar idea to (9.14) to replace ![]() $|\underline {z}|$ with
$|\underline {z}|$ with ![]() $t$ in (9.33): indeed, we see that
$t$ in (9.33): indeed, we see that
with ![]() $H^2P^{\varepsilon -4}$ equalling the third term of (9.33) (up to a relabelling
$H^2P^{\varepsilon -4}$ equalling the third term of (9.33) (up to a relabelling ![]() $\varepsilon$), and
$\varepsilon$), and
Hence, after relabelling ![]() $\varepsilon$, we see that
$\varepsilon$, we see that
 \begin{equation} |T_{\underline{h}}(q,\underline{z})|\ll R^2P^{n+\varepsilon} \bigg{(} P^{-2}+H^2R^2t^2+R^2P^{-4}+R^{-1}H^2\min\bigg\{1,\frac{1}{HtP^2}\bigg\}\bigg{)}^{(n-\sigma_{\infty}({\underline{h}})-2)/4}. \end{equation}
\begin{equation} |T_{\underline{h}}(q,\underline{z})|\ll R^2P^{n+\varepsilon} \bigg{(} P^{-2}+H^2R^2t^2+R^2P^{-4}+R^{-1}H^2\min\bigg\{1,\frac{1}{HtP^2}\bigg\}\bigg{)}^{(n-\sigma_{\infty}({\underline{h}})-2)/4}. \end{equation}In this subsection, we will choose
Here ![]() $H$ is chosen so as to simplify the bounds here, as will be evident from our subsequent results. Note
$H$ is chosen so as to simplify the bounds here, as will be evident from our subsequent results. Note ![]() $H=(RtP^2)^{1/5}$ when
$H=(RtP^2)^{1/5}$ when ![]() $t\geq (HP^2)^{-1}$, and
$t\geq (HP^2)^{-1}$, and ![]() $H=R^{1/6}$ when
$H=R^{1/6}$ when ![]() $t\leq (HP^2)^{-1}$. This is convenient for us since considering these two cases for
$t\leq (HP^2)^{-1}$. This is convenient for us since considering these two cases for ![]() $t$ separately is natural due to the min bracket in (9.34).
$t$ separately is natural due to the min bracket in (9.34).
Before we substitute (9.34) back into (9.32), we will simplify this expression significantly using the following lemma.
Lemma 9.6 Let ![]() $q\asymp R\leq Q$,
$q\asymp R\leq Q$, ![]() $Q=P^{3/2}$,
$Q=P^{3/2}$, ![]() $|\underline {z}|\asymp t\leq (qQ^{1/2})^{-1}$ and
$|\underline {z}|\asymp t\leq (qQ^{1/2})^{-1}$ and ![]() $|{\underline {h}}|\ll H$, where
$|{\underline {h}}|\ll H$, where ![]() $H$ is defined as in (9.35). Finally, let
$H$ is defined as in (9.35). Finally, let ![]() $\sigma _{\infty }({\underline {h}}):=s_{\infty }(F_{{\underline {h}}}^{(0)},G_{{\underline {h}}}^{(0)})$. Then
$\sigma _{\infty }({\underline {h}}):=s_{\infty }(F_{{\underline {h}}}^{(0)},G_{{\underline {h}}}^{(0)})$. Then
 \[ T_{\underline{h}}(q,\underline{z})\ll R^2P^{n+\varepsilon}\bigg{(}R^{-1}H^2\min\bigg\{1,\frac{1}{HtP^2}\bigg\}\bigg{)}^{(n-\sigma_{\infty}({\underline{h}})-2)/4}. \]
\[ T_{\underline{h}}(q,\underline{z})\ll R^2P^{n+\varepsilon}\bigg{(}R^{-1}H^2\min\bigg\{1,\frac{1}{HtP^2}\bigg\}\bigg{)}^{(n-\sigma_{\infty}({\underline{h}})-2)/4}. \]
Proof. First we will assume that ![]() $t>(HP^2)^{-1}$. In this case the right-most term simplifies to
$t>(HP^2)^{-1}$. In this case the right-most term simplifies to ![]() $H/(RtP^2)$. Before we get into the proof that
$H/(RtP^2)$. Before we get into the proof that ![]() $H/(RtP^2)$ dominates all other terms, we will show the for our choice of
$H/(RtP^2)$ dominates all other terms, we will show the for our choice of ![]() $H$ (see (9.35)), the following is true:
$H$ (see (9.35)), the following is true:
Indeed,
This will be useful to us as we attempt to show that ![]() $H/(RtP^2)$ dominates all other terms for every value of
$H/(RtP^2)$ dominates all other terms for every value of ![]() $t$ and
$t$ and ![]() $R$. We now turn to proving this. Going from left to right in the bracket of (9.34), we first see that
$R$. We now turn to proving this. Going from left to right in the bracket of (9.34), we first see that
But, we know that ![]() $t\leq (RQ^{1/2})^{-1}$, and so
$t\leq (RQ^{1/2})^{-1}$, and so ![]() $Rt\ll 1$. We certainly have that
$Rt\ll 1$. We certainly have that ![]() $H\gg 1$, and so
$H\gg 1$, and so ![]() $H\gg Rt$ must be true. Next,
$H\gg Rt$ must be true. Next,
Using the fact that ![]() $H\ll P^{1/4}$ by (9.36), and
$H\ll P^{1/4}$ by (9.36), and ![]() $Q\asymp P^{3/2}$ and
$Q\asymp P^{3/2}$ and ![]() $Rt\ll Q^{-1/2}$ by the assumptions in the lemma, we see that
$Rt\ll Q^{-1/2}$ by the assumptions in the lemma, we see that
as required. Finally,
This one has a few more steps. Recall that we are trying to show the dominance of the right term for every ![]() $\underline {t}$ and
$\underline {t}$ and ![]() $R$. By our choice of
$R$. By our choice of ![]() $H$ and the fact that
$H$ and the fact that ![]() $t\ll (RQ^{1/2})^{-1}$,
$t\ll (RQ^{1/2})^{-1}$, ![]() $R\leq Q$, we have
$R\leq Q$, we have
 \begin{align*} &R^3 tP^{-2}\ll H=(RtP^2)^{1/5} \quad \forall t, R \quad \Leftrightarrow \quad R^{14/5} t^{4/5}P^{-12/5}\ll 1 \quad \forall t, R\\ \Leftrightarrow \quad &\max\{R\}^{7} \max\{t\}^{2}P^{-6}\ll 1,\quad \Leftrightarrow \quad Q^{7}(RQ^{-1/2})^{-2}P^{-6}\ll 1\\ \Leftrightarrow \quad &Q^{4}P^{-6}\ll 1,\quad \Leftrightarrow \quad Q\ll P^{3/2}, \end{align*}
\begin{align*} &R^3 tP^{-2}\ll H=(RtP^2)^{1/5} \quad \forall t, R \quad \Leftrightarrow \quad R^{14/5} t^{4/5}P^{-12/5}\ll 1 \quad \forall t, R\\ \Leftrightarrow \quad &\max\{R\}^{7} \max\{t\}^{2}P^{-6}\ll 1,\quad \Leftrightarrow \quad Q^{7}(RQ^{-1/2})^{-2}P^{-6}\ll 1\\ \Leftrightarrow \quad &Q^{4}P^{-6}\ll 1,\quad \Leftrightarrow \quad Q\ll P^{3/2}, \end{align*}
which is true. Hence, for our choices of ![]() $H$ and
$H$ and ![]() $Q$, we have shown that
$Q$, we have shown that ![]() $H^2R^{-1}\min \{1, (HtP^2)^{-1})\}=H/(RtP^2)$ dominates over all other terms in the expression for every
$H^2R^{-1}\min \{1, (HtP^2)^{-1})\}=H/(RtP^2)$ dominates over all other terms in the expression for every ![]() $R\leq Q\asymp P^{3/2}$ and
$R\leq Q\asymp P^{3/2}$ and ![]() $(HP^2)^{-1}\leq t \leq (RQ^{1/2})^{-1}$.
$(HP^2)^{-1}\leq t \leq (RQ^{1/2})^{-1}$.
A similar set of arguments can be used in the case that ![]() $t<(HP^2)^{-1}$. In this case, we have
$t<(HP^2)^{-1}$. In this case, we have ![]() $H=R^{1/6}$, and
$H=R^{1/6}$, and
Again going from left to right in the bracket of (9.34):
which is true since ![]() $R\leq Q\asymp P^{3/2}$. Next,
$R\leq Q\asymp P^{3/2}$. Next,
which is again true by our assumptions from the lemma. We used the fact that ![]() $Rt\leq Q^{-1/2}$ since
$Rt\leq Q^{-1/2}$ since ![]() $t\leq (RQ^{1/2})^{-1}$. Finally,
$t\leq (RQ^{1/2})^{-1}$. Finally,
This is also true since ![]() $R\leq Q\asymp P^{3/2}$. Hence, we have shown that
$R\leq Q\asymp P^{3/2}$. Hence, we have shown that ![]() $H^2R^{-1}\min \{1, (HtP^2)^{-1})\}=H^2R^{-1}$ dominates over all other terms in the expression for every
$H^2R^{-1}\min \{1, (HtP^2)^{-1})\}=H^2R^{-1}$ dominates over all other terms in the expression for every ![]() $R\leq Q\asymp P^{3/2}$ and
$R\leq Q\asymp P^{3/2}$ and ![]() $t \leq (HP^2)^{-1}$. This completes the proof of the lemma.
$t \leq (HP^2)^{-1}$. This completes the proof of the lemma.
We could now substitute the results from Lemma 9.6 into (9.32) directly, but the expression is rather complicated so we will instead just focus on the ![]() ${\underline {h}}$ sum inside of the integral for now. Our treatment of it will be analogous to the proof of the
${\underline {h}}$ sum inside of the integral for now. Our treatment of it will be analogous to the proof of the ![]() ${\underline {h}}$ sum bound in § 7, but it will be a much simpler process this time around. The reason for our choice of
${\underline {h}}$ sum bound in § 7, but it will be a much simpler process this time around. The reason for our choice of ![]() $H$ will also become apparent as we deal with this sum. We aim to show the following.
$H$ will also become apparent as we deal with this sum. We aim to show the following.
Lemma 9.7 Let ![]() $q\asymp R\leq Q$,
$q\asymp R\leq Q$, ![]() $Q=P^{3/2}$,
$Q=P^{3/2}$, ![]() $|\underline {z}|\asymp t\leq (qQ^{1/2})^{-1}$ and
$|\underline {z}|\asymp t\leq (qQ^{1/2})^{-1}$ and ![]() $|{\underline {h}}|\ll H$, where
$|{\underline {h}}|\ll H$, where ![]() $H$ is defined as in (9.35). Then
$H$ is defined as in (9.35). Then
In particular, we save a factor of ![]() $H^n$ over the trivial bound.
$H^n$ over the trivial bound.
Proof. We will again consider the cases when ![]() $t\geq (HP^2)^{-1}$ and
$t\geq (HP^2)^{-1}$ and ![]() $t\leq (HP^2)^{-1}$ separately. Starting with
$t\leq (HP^2)^{-1}$ separately. Starting with ![]() $t\geq (HP^2)^{-1}$ first: by Lemma 9.6, we have
$t\geq (HP^2)^{-1}$ first: by Lemma 9.6, we have
 \begin{align} \sum_{|{\underline{h}}|\ll H} |T_{\underline{h}}(q,\underline{z})|&\ll R^2P^{n+\varepsilon}\sum_{i=-1}^{n-1}\sum_{\substack{|{\underline{h}}|\ll H \nonumber\\ \sigma_{\infty}({\underline{h}})=i}} \bigg{(} \frac{H}{RtP^2}\bigg{)}^{(n-i-2)/4}\nonumber\\ &\ll R^2P^{n+\varepsilon}\max_{-1\leq i\leq n-1} \#\{|{\underline{h}}|\ll H \,|\, \sigma_{\infty}({\underline{h}})=i\} \bigg{(} \frac{H}{RtP^2}\bigg{)}^{(n-i-2)/4}\nonumber\\ &\ll R^2P^{n+\varepsilon}\max_{-1\leq i\leq n-1} H^{n-i-1} \bigg{(} \frac{H}{RtP^2}\bigg{)}^{(n-i-2)/4}, \end{align}
\begin{align} \sum_{|{\underline{h}}|\ll H} |T_{\underline{h}}(q,\underline{z})|&\ll R^2P^{n+\varepsilon}\sum_{i=-1}^{n-1}\sum_{\substack{|{\underline{h}}|\ll H \nonumber\\ \sigma_{\infty}({\underline{h}})=i}} \bigg{(} \frac{H}{RtP^2}\bigg{)}^{(n-i-2)/4}\nonumber\\ &\ll R^2P^{n+\varepsilon}\max_{-1\leq i\leq n-1} \#\{|{\underline{h}}|\ll H \,|\, \sigma_{\infty}({\underline{h}})=i\} \bigg{(} \frac{H}{RtP^2}\bigg{)}^{(n-i-2)/4}\nonumber\\ &\ll R^2P^{n+\varepsilon}\max_{-1\leq i\leq n-1} H^{n-i-1} \bigg{(} \frac{H}{RtP^2}\bigg{)}^{(n-i-2)/4}, \end{align}
by Lemma 7.1. Recall that when ![]() $t\geq (HP^2)^{-1}$, we have
$t\geq (HP^2)^{-1}$, we have ![]() $H\asymp (R|t|P^2)^{1/5}$. This value for
$H\asymp (R|t|P^2)^{1/5}$. This value for ![]() $H$ has been chosen specifically so that
$H$ has been chosen specifically so that ![]() $H=(H/(RtP^2))^{-1/4}$ when
$H=(H/(RtP^2))^{-1/4}$ when ![]() $t>(HP^2)^{-1}$. The reason for doing this is so that the product within the max bracket in (9.37) will become
$t>(HP^2)^{-1}$. The reason for doing this is so that the product within the max bracket in (9.37) will become ![]() $H$. Indeed, substituting this value for
$H$. Indeed, substituting this value for ![]() $H$ into (9.37) gives
$H$ into (9.37) gives
 \begin{align*} \sum_{|{\underline{h}}|\ll H} |T_{\underline{h}}(q,\underline{z})|&\ll R^2P^{n+\varepsilon}\max_{-1\leq i\leq n-1} (RtP^2)^{(n-i-1)/5} \bigg{(} \frac{1}{(RtP^2)^{4/5}}\bigg{)}^{(n-i-2)/4}\\ &= R^2P^{n+\varepsilon}\max_{-1\leq i\leq n-1} (RtP^2)^{(n-i-1)/5} (RtP^2)^{-(n-i-2)/5}\\ &=R^2P^{n+\varepsilon}(RtP^2)^{1/5}\\ &=R^2P^{n+\varepsilon}H. \end{align*}
\begin{align*} \sum_{|{\underline{h}}|\ll H} |T_{\underline{h}}(q,\underline{z})|&\ll R^2P^{n+\varepsilon}\max_{-1\leq i\leq n-1} (RtP^2)^{(n-i-1)/5} \bigg{(} \frac{1}{(RtP^2)^{4/5}}\bigg{)}^{(n-i-2)/4}\\ &= R^2P^{n+\varepsilon}\max_{-1\leq i\leq n-1} (RtP^2)^{(n-i-1)/5} (RtP^2)^{-(n-i-2)/5}\\ &=R^2P^{n+\varepsilon}(RtP^2)^{1/5}\\ &=R^2P^{n+\varepsilon}H. \end{align*}
In theory, it would be nice if we could choose ![]() $H$ to be even larger, so that we get something smaller than
$H$ to be even larger, so that we get something smaller than ![]() $R^2P^{n+\varepsilon }H$. However, if one chooses
$R^2P^{n+\varepsilon }H$. However, if one chooses ![]() $H$ to be larger than this value, then Lemma 9.6 becomes false (in particular, the term
$H$ to be larger than this value, then Lemma 9.6 becomes false (in particular, the term ![]() $H^2R^2t^2$ dominates when
$H^2R^2t^2$ dominates when ![]() $H>P^{1/4}$). This is therefore the optimal choice for
$H>P^{1/4}$). This is therefore the optimal choice for ![]() $H$ when
$H$ when ![]() $t>(HP^2)^{-1}$.
$t>(HP^2)^{-1}$.
The argument in the case the ![]() $t\leq (HP^2)^{-1}$ is almost identical. Recall that when
$t\leq (HP^2)^{-1}$ is almost identical. Recall that when ![]() $t\leq (HP^2)^{-1}$, we have
$t\leq (HP^2)^{-1}$, we have ![]() $H\asymp R^{1/6}$. By Lemma 9.6, we have
$H\asymp R^{1/6}$. By Lemma 9.6, we have
 \begin{align*} \sum_{|{\underline{h}}|\ll H} |T_{\underline{h}}(q,\underline{z})|&\ll R^2P^{n+\varepsilon}\sum_{i=-1}^{n-1}\sum_{\substack{|{\underline{h}}|\ll H \\ \sigma_{\infty}({\underline{h}})=i}} \big{(} H^2R^{-1}\big{)}^{(n-i-2)/4}\nonumber\\ &\ll R^2P^{n+\varepsilon}\max_{-1\leq i\leq n-1} \#\{|{\underline{h}}|\ll H \,|\, \sigma_{\infty}({\underline{h}})=i\} \, R^{-(n-i-2)/6}\nonumber\\ &\ll R^2P^{n+\varepsilon}\max_{-1\leq i\leq n-1} H^{n-i-1}R^{-(n-i-2)/6}\nonumber\\ &\ll_n R^2P^{n+\varepsilon}R^{1/6}\ll R^2P^{n+\varepsilon}H, \end{align*}
\begin{align*} \sum_{|{\underline{h}}|\ll H} |T_{\underline{h}}(q,\underline{z})|&\ll R^2P^{n+\varepsilon}\sum_{i=-1}^{n-1}\sum_{\substack{|{\underline{h}}|\ll H \\ \sigma_{\infty}({\underline{h}})=i}} \big{(} H^2R^{-1}\big{)}^{(n-i-2)/4}\nonumber\\ &\ll R^2P^{n+\varepsilon}\max_{-1\leq i\leq n-1} \#\{|{\underline{h}}|\ll H \,|\, \sigma_{\infty}({\underline{h}})=i\} \, R^{-(n-i-2)/6}\nonumber\\ &\ll R^2P^{n+\varepsilon}\max_{-1\leq i\leq n-1} H^{n-i-1}R^{-(n-i-2)/6}\nonumber\\ &\ll_n R^2P^{n+\varepsilon}R^{1/6}\ll R^2P^{n+\varepsilon}H, \end{align*}
by Lemma 7.1, and by the fact that when ![]() $t\leq (HP^2)^{-1}$, we have
$t\leq (HP^2)^{-1}$, we have ![]() $H\asymp R^{1/6}$. This value for
$H\asymp R^{1/6}$. This value for ![]() $H$ has again been chosen specifically so that
$H$ has again been chosen specifically so that ![]() $H^{n-i-1}R^{-(n-i-1)/6}=1$ for every
$H^{n-i-1}R^{-(n-i-1)/6}=1$ for every ![]() $i$. when
$i$. when ![]() $t>(HP^2)^{-1}$. For the same reasons as before, we cannot choose
$t>(HP^2)^{-1}$. For the same reasons as before, we cannot choose ![]() $H$ to be larger than this without causing other issues, and so this makes our choice of
$H$ to be larger than this without causing other issues, and so this makes our choice of ![]() $H$ in (9.35) optimal for our situation.
$H$ in (9.35) optimal for our situation.
Substituting the result of Lemma 9.7 back into (9.32) gives
Finally, we split the ![]() $R$ sum into its cube-free and cube-full components, and use Lemma 9.1 as follows:
$R$ sum into its cube-free and cube-full components, and use Lemma 9.1 as follows:
 \begin{align} D_P(R,t,\underline{R})&\ll P^{n-1+\varepsilon} \sum_{b_1=R_1}^{2R_1}\sum_{b_2=R_2}^{2R_2}\sum_{b_3=R_3}^{2R_3}\sum_{q_4=R_4}^{2R_4} R^2 H(R, t)^{(3-n)/2}((H(R,t)P^{2})^{-1}+ t)^2\nonumber\\ &\ll P^{n-1+\varepsilon}R^3 R_2^{-1/2}R_3^{-2/3}R_4^{-3/4}H(R, t)^{(3-n)/2}((H(R,t)P^{2})^{-1}+ t)^2\nonumber\\ &\ll P^{n-1+\varepsilon}R^3 R_3^{-2/3}R_4^{-3/4}H(R, t)^{(3-n)/2}((H(R,t)P^{2})^{-1}+ t)^2. \end{align}
\begin{align} D_P(R,t,\underline{R})&\ll P^{n-1+\varepsilon} \sum_{b_1=R_1}^{2R_1}\sum_{b_2=R_2}^{2R_2}\sum_{b_3=R_3}^{2R_3}\sum_{q_4=R_4}^{2R_4} R^2 H(R, t)^{(3-n)/2}((H(R,t)P^{2})^{-1}+ t)^2\nonumber\\ &\ll P^{n-1+\varepsilon}R^3 R_2^{-1/2}R_3^{-2/3}R_4^{-3/4}H(R, t)^{(3-n)/2}((H(R,t)P^{2})^{-1}+ t)^2\nonumber\\ &\ll P^{n-1+\varepsilon}R^3 R_3^{-2/3}R_4^{-3/4}H(R, t)^{(3-n)/2}((H(R,t)P^{2})^{-1}+ t)^2. \end{align}
Therefore, upon setting ![]() $R:=P^{\phi }$,
$R:=P^{\phi }$, ![]() $R_i:=P^{\phi _i}$,
$R_i:=P^{\phi _i}$, ![]() $t:=P^{\tau }$ and (recall (9.35))
$t:=P^{\tau }$ and (recall (9.35))
we have
where ![]() $C$ is the implied constant in (9.38). Hence, if
$C$ is the implied constant in (9.38). Hence, if ![]() $P$ is chosen to be sufficiently large, we may absorb
$P$ is chosen to be sufficiently large, we may absorb ![]() $\log _P(C)$ into
$\log _P(C)$ into ![]() $\varepsilon$, giving us the following.
$\varepsilon$, giving us the following.
Lemma 9.8 Let ![]() $n$ be fixed, and
$n$ be fixed, and
Then ![]() $B_{AV/W}(\phi,\tau,\phi _3,\phi _4)$ is a continuous, piecewise linear function, and for every
$B_{AV/W}(\phi,\tau,\phi _3,\phi _4)$ is a continuous, piecewise linear function, and for every ![]() $\varepsilon >0$, there is a sufficiently large
$\varepsilon >0$, there is a sufficiently large ![]() $P$ such that
$P$ such that
for every ![]() $\phi \in [0,3/2]$,
$\phi \in [0,3/2]$, ![]() $\phi _i\in [0,\phi ]$,
$\phi _i\in [0,\phi ]$, ![]() $\phi _1+\phi _2+\phi _3+\phi _4=\phi$ and
$\phi _1+\phi _2+\phi _3+\phi _4=\phi$ and ![]() $\tau \in [-5,-\phi -0.75]$.
$\tau \in [-5,-\phi -0.75]$.
9.3.1 Explaining the choice of  $Q$
$Q$
As an aside, we will briefly explain our choice of ![]() $Q\asymp P^{3/2}$, as promised in § 3. We see in the proof of Lemma 9.6, that the optimal choice for
$Q\asymp P^{3/2}$, as promised in § 3. We see in the proof of Lemma 9.6, that the optimal choice for ![]() $Q$ is
$Q$ is ![]() $P^{3/2}$. In particular, if we choose any other value for
$P^{3/2}$. In particular, if we choose any other value for ![]() $Q$, then we cannot simplify the Weyl bound to such a large extent. We normally optimise our choice for
$Q$, then we cannot simplify the Weyl bound to such a large extent. We normally optimise our choice for ![]() $Q$ based on our main bound, which in this case is the averaged van der Corput/Poisson bound. This value for
$Q$ based on our main bound, which in this case is the averaged van der Corput/Poisson bound. This value for ![]() $Q$ turns out to be
$Q$ turns out to be
which is the choice of ![]() $Q$ that guarantees
$Q$ that guarantees ![]() $HP^2|\underline {z}|\ll 1$ for every
$HP^2|\underline {z}|\ll 1$ for every ![]() $\underline {z}$ (optimising our
$\underline {z}$ (optimising our ![]() $V$ term), where
$V$ term), where ![]() $H$ and
$H$ and ![]() $V$ are defined as in (9.13)–(9.12). In the range of
$V$ are defined as in (9.13)–(9.12). In the range of ![]() $n$ that we are considering, this value is largest when
$n$ that we are considering, this value is largest when ![]() $n=39$, giving us
$n=39$, giving us ![]() $Q\asymp P^{1.5135\ldots }$, which is very close to the optimal choice for the van der Corput/Weyl bounds. In the end, the authors chose
$Q\asymp P^{1.5135\ldots }$, which is very close to the optimal choice for the van der Corput/Weyl bounds. In the end, the authors chose ![]() $Q\asymp P^{3/2}$ because it is simpler and it makes the van der Corput/Weyl bounds significantly easier to work with. Most importantly, this choice does not cause any issues for our Poisson bounds, since it is ‘almost’ optimal.
$Q\asymp P^{3/2}$ because it is simpler and it makes the van der Corput/Weyl bounds significantly easier to work with. Most importantly, this choice does not cause any issues for our Poisson bounds, since it is ‘almost’ optimal.
9.4 Pointwise van der Corput/Weyl
In this subsection, we will find a bound for ![]() $B_P(\phi, \tau, \underline {\phi })$ by using Pointwise van der Corput differencing, followed by one Weyl step. We start by applying Lemma 4.1 to
$B_P(\phi, \tau, \underline {\phi })$ by using Pointwise van der Corput differencing, followed by one Weyl step. We start by applying Lemma 4.1 to ![]() $D_P(R,t,\underline {R})$:
$D_P(R,t,\underline {R})$:
 \[ D_P(R,t,\underline{R})\ll \sum_{q,(9.1)} \int_{|\underline{z}|\asymp t} H^{-n/2}P^{n/2}q\bigg{(}\sum_{\underline{h}\ll H}|T_{\underline{h}}(q,\underline{z})|\bigg{)}^{1/2}\,d\underline{z}. \]
\[ D_P(R,t,\underline{R})\ll \sum_{q,(9.1)} \int_{|\underline{z}|\asymp t} H^{-n/2}P^{n/2}q\bigg{(}\sum_{\underline{h}\ll H}|T_{\underline{h}}(q,\underline{z})|\bigg{)}^{1/2}\,d\underline{z}. \]
Upon setting ![]() $H:=\max \{q^{1/6}, (qtP^2)^{1/5}\}$ again, we may use Lemma 9.7 and Proposition 8.2 to conclude that
$H:=\max \{q^{1/6}, (qtP^2)^{1/5}\}$ again, we may use Lemma 9.7 and Proposition 8.2 to conclude that
 \begin{align} D_P(R,t,\underline{R})&\ll P^{n+\varepsilon}\sum_{q,(9.1)}\int_{|\underline{z}|\asymp t} H(q,t)^{(1-n)/2}q^2 \,d\underline{z} \nonumber\\ &\ll P^{n+\varepsilon}R^3 R_3^{-2/3}R_4^{-3/4} t^2 H(R,t)^{(1-n)/2}. \end{align}
\begin{align} D_P(R,t,\underline{R})&\ll P^{n+\varepsilon}\sum_{q,(9.1)}\int_{|\underline{z}|\asymp t} H(q,t)^{(1-n)/2}q^2 \,d\underline{z} \nonumber\\ &\ll P^{n+\varepsilon}R^3 R_3^{-2/3}R_4^{-3/4} t^2 H(R,t)^{(1-n)/2}. \end{align}Hence, upon recalling (9.39), we have
where ![]() $C$ is the implied constant in (9.41). Therefore, if
$C$ is the implied constant in (9.41). Therefore, if ![]() $P$ is chosen to be sufficiently large, we may absorb
$P$ is chosen to be sufficiently large, we may absorb ![]() $\log _P(C)$ into
$\log _P(C)$ into ![]() $\varepsilon$, giving us the following.
$\varepsilon$, giving us the following.
Lemma 9.9 Let ![]() $n$ be fixed, and
$n$ be fixed, and
Then ![]() $B_{PV/W}(\phi,\tau,\phi _3,\phi _4)$ is a continuous, piecewise linear function, and for every
$B_{PV/W}(\phi,\tau,\phi _3,\phi _4)$ is a continuous, piecewise linear function, and for every ![]() $\varepsilon >0$, there is a sufficiently large
$\varepsilon >0$, there is a sufficiently large ![]() $P$ such that
$P$ such that
for every ![]() $\phi \in [0,3/2]$,
$\phi \in [0,3/2]$, ![]() $\phi _i\in [0,\phi ]$,
$\phi _i\in [0,\phi ]$, ![]() $\phi _1+\phi _2+\phi _3+\phi _4=\phi$ and
$\phi _1+\phi _2+\phi _3+\phi _4=\phi$ and ![]() $\tau \in [-5,-\phi -0.75]$.
$\tau \in [-5,-\phi -0.75]$.
9.5 Weyl
In this subsection, we will find a bound for ![]() $B_P(\phi, \tau, \underline {\phi })$ by using Weyl differencing twice. We start by applying Proposition 8.1 to
$B_P(\phi, \tau, \underline {\phi })$ by using Weyl differencing twice. We start by applying Proposition 8.1 to ![]() $D_P(R,t,\underline {R})$:
$D_P(R,t,\underline {R})$:
 \[ D_P(R,t,\underline{R})\ll P^{n+\varepsilon}\sum_{q,(9.1)} \sideset{}{^*}\sum_{{\underline{a}}} \int_{|\underline{z}|\asymp t}\bigg{(} P^{-4}+q^2|\underline{z}|^2+q^2P^{-6}+q^{-1}\min\bigg\{1,\frac{1}{|\underline{z}|P^3}\bigg\}\bigg{)}^{(n-1)/16}\,d\underline{z}. \]
\[ D_P(R,t,\underline{R})\ll P^{n+\varepsilon}\sum_{q,(9.1)} \sideset{}{^*}\sum_{{\underline{a}}} \int_{|\underline{z}|\asymp t}\bigg{(} P^{-4}+q^2|\underline{z}|^2+q^2P^{-6}+q^{-1}\min\bigg\{1,\frac{1}{|\underline{z}|P^3}\bigg\}\bigg{)}^{(n-1)/16}\,d\underline{z}. \]
First, it is easy to use (9.1)–(9.3) to check that
Hence,
 \begin{align} D_P(R,t,\underline{R})&\ll P^{n+\varepsilon}\sum_{q,(9.1)} \sideset{}{^*}\sum_{{\underline{a}}} \int_{|\underline{z}|\asymp t} \bigg{(} q^2|\underline{z}|^2+q^{-1}\min\bigg\{1,\frac{1}{|\underline{z}|P^3}\bigg\}\bigg{)}^{(n-1)/16}\,d\underline{z}\nonumber\\ &\ll P^{n+\varepsilon}\sum_{q,(9.1)} q^2 t^2 \bigg{(} q^2t^2+q^{-1}\min\bigg\{1,\frac{1}{tP^3}\bigg\}\bigg{)}^{(n-1)/16}\nonumber\\ &\ll P^{n+\varepsilon}\sum_{q,(9.1)} q^2 t^2 \bigg{(} q^2t^2+q^{-1}\min\bigg\{1,\frac{1}{tP^3}\bigg\}\bigg{)}^{(n-1)/16}\nonumber\\ &\ll P^{n+\varepsilon}R^3 R_3^{-2/3} t^2 \bigg{(} R^2t^2+R^{-1}\min\bigg\{1,\frac{1}{tP^3}\bigg\}\bigg{)}^{(n-1)/16}. \end{align}
\begin{align} D_P(R,t,\underline{R})&\ll P^{n+\varepsilon}\sum_{q,(9.1)} \sideset{}{^*}\sum_{{\underline{a}}} \int_{|\underline{z}|\asymp t} \bigg{(} q^2|\underline{z}|^2+q^{-1}\min\bigg\{1,\frac{1}{|\underline{z}|P^3}\bigg\}\bigg{)}^{(n-1)/16}\,d\underline{z}\nonumber\\ &\ll P^{n+\varepsilon}\sum_{q,(9.1)} q^2 t^2 \bigg{(} q^2t^2+q^{-1}\min\bigg\{1,\frac{1}{tP^3}\bigg\}\bigg{)}^{(n-1)/16}\nonumber\\ &\ll P^{n+\varepsilon}\sum_{q,(9.1)} q^2 t^2 \bigg{(} q^2t^2+q^{-1}\min\bigg\{1,\frac{1}{tP^3}\bigg\}\bigg{)}^{(n-1)/16}\nonumber\\ &\ll P^{n+\varepsilon}R^3 R_3^{-2/3} t^2 \bigg{(} R^2t^2+R^{-1}\min\bigg\{1,\frac{1}{tP^3}\bigg\}\bigg{)}^{(n-1)/16}. \end{align}
As usual, we are interested in ![]() $\log _P(D_P(R,t,\underline {R}))$ since this will be piecewise linear. The bound above gives
$\log _P(D_P(R,t,\underline {R}))$ since this will be piecewise linear. The bound above gives
 \begin{align*} B_P(\phi, \tau, \underline{\phi})&\leq n+\varepsilon +3\phi + 2\tau-\frac{2\phi_3}{3} -\frac{3\phi_4}{4} + \log_P(C)\\ &\quad +\frac{n-1}{16}\max\{2\phi+2\tau, \, -\phi+\min \{0,-3-\tau\}\}, \end{align*}
\begin{align*} B_P(\phi, \tau, \underline{\phi})&\leq n+\varepsilon +3\phi + 2\tau-\frac{2\phi_3}{3} -\frac{3\phi_4}{4} + \log_P(C)\\ &\quad +\frac{n-1}{16}\max\{2\phi+2\tau, \, -\phi+\min \{0,-3-\tau\}\}, \end{align*}
where ![]() $\log _P(C)$ is the implied constant in (9.42). Therefore, upon setting
$\log _P(C)$ is the implied constant in (9.42). Therefore, upon setting
we arrive at the following bound for ![]() $B_P$:
$B_P$:
Lemma 9.10 Let ![]() $n$ be fixed,
$n$ be fixed, ![]() $\log _P D_P(R,t,\underline {R}):= B_P(\phi, \tau, \underline {\phi })$ and
$\log _P D_P(R,t,\underline {R}):= B_P(\phi, \tau, \underline {\phi })$ and
Then ![]() $B_{\rm Weyl}(\phi,\tau,\phi _3,\phi _4)$ is a continuous, piecewise linear function, and for every
$B_{\rm Weyl}(\phi,\tau,\phi _3,\phi _4)$ is a continuous, piecewise linear function, and for every ![]() $\varepsilon >0$, there is a sufficiently large
$\varepsilon >0$, there is a sufficiently large ![]() $P$ such that
$P$ such that
for every ![]() $\phi \in [0,3/2]$,
$\phi \in [0,3/2]$, ![]() $\phi _i\in [0,\phi ]$,
$\phi _i\in [0,\phi ]$, ![]() $\phi _1+\phi _2+\phi _3+\phi _4=\phi$ and
$\phi _1+\phi _2+\phi _3+\phi _4=\phi$ and ![]() $\tau \in [-5,-\phi -0.75]$.
$\tau \in [-5,-\phi -0.75]$.
9.6 Proof of Proposition 3.3
Recall that our ultimate goal is to show that
for some ![]() $\delta >0$, for every
$\delta >0$, for every ![]() $n\geq 39$. This is equivalent to having
$n\geq 39$. This is equivalent to having
We assume that ![]() $\rho$ is chosen sufficiently small to facilitate average van der Corput differencing bounds. We may now use all of the previous subsections to bound
$\rho$ is chosen sufficiently small to facilitate average van der Corput differencing bounds. We may now use all of the previous subsections to bound ![]() $\log _P(S_{\mathfrak {m}})$ by a continuous, piecewise linear function in three variables: by (9.4), we have
$\log _P(S_{\mathfrak {m}})$ by a continuous, piecewise linear function in three variables: by (9.4), we have
where ![]() $c_1$ is the implied constant. We clearly have that
$c_1$ is the implied constant. We clearly have that ![]() $\log _P(c_1) + \varepsilon +n-7\leq n-6-\varepsilon$ for sufficiently large
$\log _P(c_1) + \varepsilon +n-7\leq n-6-\varepsilon$ for sufficiently large ![]() $P$, so we will assume that this is the case. Hence, by Lemmas 9.8–9.5, we have
$P$, so we will assume that this is the case. Hence, by Lemmas 9.8–9.5, we have
 \begin{align} \log_P(S_{\mathfrak{m}})&\leq \varepsilon+\max\bigg{\{} \min_{(\phi,\tau,\phi_3,\phi_4) \in D_1\cup D_2} \{ B_{AV/P}(\phi,\tau,\phi_3,\phi_4), B_{PV/P}(\phi,\tau,\phi_3,\phi_4),\nonumber\\ &\qquad B_{AV/W}(\phi,\tau,\phi_3,\phi_4),\, B_{PV/W}(\phi,\tau,\phi_3,\phi_4), \nonumber\\ &\qquad B_{\rm Weyl}(\phi,\tau,\phi_3,\phi_4)\} , n-6-2\varepsilon\bigg\}, \end{align}
\begin{align} \log_P(S_{\mathfrak{m}})&\leq \varepsilon+\max\bigg{\{} \min_{(\phi,\tau,\phi_3,\phi_4) \in D_1\cup D_2} \{ B_{AV/P}(\phi,\tau,\phi_3,\phi_4), B_{PV/P}(\phi,\tau,\phi_3,\phi_4),\nonumber\\ &\qquad B_{AV/W}(\phi,\tau,\phi_3,\phi_4),\, B_{PV/W}(\phi,\tau,\phi_3,\phi_4), \nonumber\\ &\qquad B_{\rm Weyl}(\phi,\tau,\phi_3,\phi_4)\} , n-6-2\varepsilon\bigg\}, \end{align}where
 \begin{align*} D_1&:=\{(\phi,\tau,\phi_3,\phi_4)\in \mathbb{R}^3 \, : \, \Delta\leq \phi \leq 3/2, \ 0\leq \phi_3 \leq \phi, \ -5 \leq \tau \leq -\phi-3/4 \},\\ D_2&:=\{(\phi,\tau,\phi_3,\phi_4)\in \mathbb{R}^3 \, : \, 0\leq \phi \leq \Delta, \ 0\leq \phi_3 \leq \phi, \ -3+\Delta \leq \tau \leq -\phi-3/4 \}. \end{align*}
\begin{align*} D_1&:=\{(\phi,\tau,\phi_3,\phi_4)\in \mathbb{R}^3 \, : \, \Delta\leq \phi \leq 3/2, \ 0\leq \phi_3 \leq \phi, \ -5 \leq \tau \leq -\phi-3/4 \},\\ D_2&:=\{(\phi,\tau,\phi_3,\phi_4)\in \mathbb{R}^3 \, : \, 0\leq \phi \leq \Delta, \ 0\leq \phi_3 \leq \phi, \ -3+\Delta \leq \tau \leq -\phi-3/4 \}. \end{align*}
Since ![]() $D_1$ and
$D_1$ and ![]() $D_2$ are convex polytopes and the function which we have bounded
$D_2$ are convex polytopes and the function which we have bounded ![]() $\log _P(S_{\mathfrak {m}})$ is continuous and piecewise linear for every
$\log _P(S_{\mathfrak {m}})$ is continuous and piecewise linear for every ![]() $n\in \mathbb {N}$. Each region on which this function is linear is a convex polytope. It is well known that extremum value of such a function must be taken at a vertex of one of these polytopes. Therefore, one may numerically compute the exact maxima in (9.44). We compute this maxima two different ways and check that both values coincide.
$n\in \mathbb {N}$. Each region on which this function is linear is a convex polytope. It is well known that extremum value of such a function must be taken at a vertex of one of these polytopes. Therefore, one may numerically compute the exact maxima in (9.44). We compute this maxima two different ways and check that both values coincide.
The first way is to use an inbuilt Min-Max function in Mathematica that compares the two bounds. This algorithm can be found in Appendix 10.1. An executable version of code can also be found in the first author's Github page [Reference NortheyNor00b].
We have also verified this using an open-source Python-based algorithm (this can be found in [Reference NortheyNor00b]).
After taking ![]() $\varepsilon '=0.0001$ (see (9.22)),
$\varepsilon '=0.0001$ (see (9.22)), ![]() $\Delta =1/7-0.001$, both numerical verifications proves that
$\Delta =1/7-0.001$, both numerical verifications proves that
for every ![]() $(\phi,\tau,\phi _3,\phi _4)\in D_1\cup D_2$, provided that
$(\phi,\tau,\phi _3,\phi _4)\in D_1\cup D_2$, provided that ![]() $39\leq n \leq 48$. The limiting case is when
$39\leq n \leq 48$. The limiting case is when ![]() $n=39$,
$n=39$, ![]() $\phi =3/2$,
$\phi =3/2$, ![]() $\tau =-2.25$ and
$\tau =-2.25$ and ![]() $\phi _2=\phi _3=\phi _4=0$. When
$\phi _2=\phi _3=\phi _4=0$. When ![]() $n\geq 49$, we may instead refer to Birch [Reference BirchBir61].
$n\geq 49$, we may instead refer to Birch [Reference BirchBir61].
10. Major arcs
Finally, we will complete the proof of Theorems 1.1–1.2 by showing that
where
 \begin{equation} S_{\mathfrak{M}}=\sum_{q\leq P^{\Delta}}\sideset{}{^*}\sum_{{\underline{a}}}^q\int_{|\underline{z}|< P^{-3+\Delta}} K(\underline{a}/q+\underline{z}) \,d\underline{z}, \end{equation}
\begin{equation} S_{\mathfrak{M}}=\sum_{q\leq P^{\Delta}}\sideset{}{^*}\sum_{{\underline{a}}}^q\int_{|\underline{z}|< P^{-3+\Delta}} K(\underline{a}/q+\underline{z}) \,d\underline{z}, \end{equation}
and ![]() $C_X$ is a product of local densities. Let
$C_X$ is a product of local densities. Let
 \[ \mathfrak{S}(R):=\sum_{q=1}^R q^{-n}\sideset{}{^*}\sum_{{\underline{a}}}^q S_{\underline{a},q},\quad \mathfrak{J}(R):=\int_{|\underline{z}|< R}\int_{\mathbb{R}^n}\omega(\underline{x})e(z_1F(\underline{x})+z_2G(\underline{x}))\, d\underline{x}\,d\underline{z}, \]
\[ \mathfrak{S}(R):=\sum_{q=1}^R q^{-n}\sideset{}{^*}\sum_{{\underline{a}}}^q S_{\underline{a},q},\quad \mathfrak{J}(R):=\int_{|\underline{z}|< R}\int_{\mathbb{R}^n}\omega(\underline{x})e(z_1F(\underline{x})+z_2G(\underline{x}))\, d\underline{x}\,d\underline{z}, \]
where
and
if the limits exist. In the following, let ![]() $\sigma$ denote the dimension of the singular locus of the complete intersection
$\sigma$ denote the dimension of the singular locus of the complete intersection ![]() $X$. For our application here we only need to establish the
$X$. For our application here we only need to establish the ![]() $\sigma =-1$ case. However, a general version is equally straightforward. We will start by showing the following.
$\sigma =-1$ case. However, a general version is equally straightforward. We will start by showing the following.
Lemma 10.1 Assume that ![]() $n-\sigma \geq 34$ and that
$n-\sigma \geq 34$ and that ![]() $\mathfrak {S}$ is absolutely convergent, satisfying
$\mathfrak {S}$ is absolutely convergent, satisfying
Then provided that we have ![]() $\Delta \in (0,1/7)$,
$\Delta \in (0,1/7)$,
We note that under the assumption (1.3), it remains to check that ![]() $\mathfrak {S}\mathfrak {J}>0$. Checking that
$\mathfrak {S}\mathfrak {J}>0$. Checking that ![]() $\mathfrak {S}>0$ follows a standard line of reasoning, as in [Reference BirchBir61, Lemma 7.1], and makes use of the fact that
$\mathfrak {S}>0$ follows a standard line of reasoning, as in [Reference BirchBir61, Lemma 7.1], and makes use of the fact that ![]() $\mathfrak {S}$ is absolutely convergent. To show that
$\mathfrak {S}$ is absolutely convergent. To show that ![]() $\mathfrak {J}>0$, it will suffice to show that
$\mathfrak {J}>0$, it will suffice to show that ![]() $\mathfrak {J}(R)\gg 1$ for sufficiently large values of
$\mathfrak {J}(R)\gg 1$ for sufficiently large values of ![]() $R$. This is again a standard argument and can be easily derived from the argument outlined in numerous sources including [Reference Browning, Dietmann and Heath-BrownBDH15, Section 8]. A rigorous proof of
$R$. This is again a standard argument and can be easily derived from the argument outlined in numerous sources including [Reference Browning, Dietmann and Heath-BrownBDH15, Section 8]. A rigorous proof of ![]() $\mathfrak {S}\mathfrak {J}>0$ under the conditions of Lemma 10.1 is obtained in the first author's PhD thesis [Reference NortheyNor00a]. We refer the reader to [Reference NortheyNor00a, Section 13], should they wish to see a full proof.
$\mathfrak {S}\mathfrak {J}>0$ under the conditions of Lemma 10.1 is obtained in the first author's PhD thesis [Reference NortheyNor00a]. We refer the reader to [Reference NortheyNor00a, Section 13], should they wish to see a full proof.
Following the proof found in [Reference Browning and Heath-BrownBH09], the first step towards proving Lemma 10.1 is to show that
where
for ![]() $\underline {t}\in \mathbb {R}^2$. In order to achieve this, we need to be able to separate the dependence of
$\underline {t}\in \mathbb {R}^2$. In order to achieve this, we need to be able to separate the dependence of ![]() $K(\underline {\alpha })$ on
$K(\underline {\alpha })$ on ![]() $\underline {a}$ from its dependence on
$\underline {a}$ from its dependence on ![]() $\underline {z}$. Write
$\underline {z}$. Write ![]() $\underline {x}=\underline {u}+q\underline {v},$ where
$\underline {x}=\underline {u}+q\underline {v},$ where ![]() $\underline {u}$ runs over the complete set of residues modulo
$\underline {u}$ runs over the complete set of residues modulo ![]() $q$ and recall that
$q$ and recall that ![]() $\underline {\alpha }=\underline {a}/q+\underline {z}$. Then
$\underline {\alpha }=\underline {a}/q+\underline {z}$. Then
where
In order to have it so that ![]() $\underline {a}$ and
$\underline {a}$ and ![]() $\underline {z}$ are independent from each other, we will replace our
$\underline {z}$ are independent from each other, we will replace our ![]() $\underline {v}$ sum with a crude integral estimate which has no dependence on
$\underline {v}$ sum with a crude integral estimate which has no dependence on ![]() $\underline {u}$. In particular, upon defining
$\underline {u}$. In particular, upon defining
we can use the fact that ![]() $\Phi _{\underline {u}}(\underline {v}+\underline {x})=\Phi _{\underline {u}}(\underline {v})+O(\max _{y\in [0,1]^n}|\nabla \Phi _{\underline {u}}(\underline {v}+\underline {y})|)$ for any
$\Phi _{\underline {u}}(\underline {v}+\underline {x})=\Phi _{\underline {u}}(\underline {v})+O(\max _{y\in [0,1]^n}|\nabla \Phi _{\underline {u}}(\underline {v}+\underline {y})|)$ for any ![]() $\underline {x}\in [0,1]^n$, to conclude the following:
$\underline {x}\in [0,1]^n$, to conclude the following:
 \begin{align} \bigg{|}\int_{\mathbb{R}^n}\Phi_{\underline{u}}(\underline{v}) \,d\underline{v}-\sum_{\underline{v}\in\mathbb{Z}^n}\Phi_{\underline{u}}(\underline{v})\bigg{|}&\leq \#\mathcal{N}_{P,q,\underline{u}} \max_{\underline{\hat{v}}\in \mathcal{N}_{P,q,\underline{u}}}\bigg{|}\int_{ \underline{\hat{v}}+[0,1]^n}\Phi_{\underline{u}}(\underline{v}) \,d\underline{v}-\Phi_{\underline{u}}(\underline{\hat{v}})\bigg{|}\nonumber\\ &\ll \#\mathcal{N}_{P,q,\underline{u}} \max_{\underline{\hat{v}}\in\mathcal{N}_{P,q,\underline{u}}} \max_{\underline{y}\in[0,1]^n}|\nabla \Phi_{\underline{u}}(\underline{\hat{v}}+\underline{y})|. \end{align}
\begin{align} \bigg{|}\int_{\mathbb{R}^n}\Phi_{\underline{u}}(\underline{v}) \,d\underline{v}-\sum_{\underline{v}\in\mathbb{Z}^n}\Phi_{\underline{u}}(\underline{v})\bigg{|}&\leq \#\mathcal{N}_{P,q,\underline{u}} \max_{\underline{\hat{v}}\in \mathcal{N}_{P,q,\underline{u}}}\bigg{|}\int_{ \underline{\hat{v}}+[0,1]^n}\Phi_{\underline{u}}(\underline{v}) \,d\underline{v}-\Phi_{\underline{u}}(\underline{\hat{v}})\bigg{|}\nonumber\\ &\ll \#\mathcal{N}_{P,q,\underline{u}} \max_{\underline{\hat{v}}\in\mathcal{N}_{P,q,\underline{u}}} \max_{\underline{y}\in[0,1]^n}|\nabla \Phi_{\underline{u}}(\underline{\hat{v}}+\underline{y})|. \end{align}
In order to simplify (10.4), we note that if ![]() $\omega _{P,q,\underline {u}}(\underline {v}):=\omega ([\underline {u}+q\underline {v}]/P)$, then for any
$\omega _{P,q,\underline {u}}(\underline {v}):=\omega ([\underline {u}+q\underline {v}]/P)$, then for any ![]() $\underline {u}\in (\mathbb {Z}/q\mathbb {Z})^n$,
$\underline {u}\in (\mathbb {Z}/q\mathbb {Z})^n$, ![]() $\underline {v}\in \mathrm {Supp}(\omega _{P,q,\underline {u}})$, and
$\underline {v}\in \mathrm {Supp}(\omega _{P,q,\underline {u}})$, and ![]() $i\in \{1,\ldots, n\}$, we have
$i\in \{1,\ldots, n\}$, we have
 \begin{align} |\partial_i\Phi_{\underline{u}}(\underline{v})|&\leq |\partial_i\omega_{P,q,\underline{u}}(\underline{v})|+|\omega_{P,q,\underline{u}}(\underline{v})(z_1 \partial_iF(\underline{u}+q\underline{v})+z_2\partial_i G(\underline{u}+q\underline{v}))|\nonumber\\ &\ll q/P+|\underline{z}|qP^2, \end{align}
\begin{align} |\partial_i\Phi_{\underline{u}}(\underline{v})|&\leq |\partial_i\omega_{P,q,\underline{u}}(\underline{v})|+|\omega_{P,q,\underline{u}}(\underline{v})(z_1 \partial_iF(\underline{u}+q\underline{v})+z_2\partial_i G(\underline{u}+q\underline{v}))|\nonumber\\ &\ll q/P+|\underline{z}|qP^2, \end{align}
by the chain rule, since ![]() $\omega \in \mathcal {W}_n$ (see (3.13)),
$\omega \in \mathcal {W}_n$ (see (3.13)), ![]() $F$ and
$F$ and ![]() $G$ are cubic forms, and
$G$ are cubic forms, and ![]() $|\underline {v}|\ll P/q$ since
$|\underline {v}|\ll P/q$ since ![]() $\underline {v}\in \mathrm {Supp}(\omega _{P,q,\underline {u}})$. Furthermore, by the definition of
$\underline {v}\in \mathrm {Supp}(\omega _{P,q,\underline {u}})$. Furthermore, by the definition of ![]() $\omega$ (see (1.4)), we note that the points in
$\omega$ (see (1.4)), we note that the points in ![]() $\mathcal {N}_{P,q,\underline {u}}$ must lie within an
$\mathcal {N}_{P,q,\underline {u}}$ must lie within an ![]() $n$-dimensional cube with sides of order
$n$-dimensional cube with sides of order ![]() $1+P/q\leq 2P/q$. Hence, by (10.4)–(10.5), we have
$1+P/q\leq 2P/q$. Hence, by (10.4)–(10.5), we have
 \begin{align*} \bigg{|}\int_{\mathbb{R}^n}\Phi_{\underline{u}}(\underline{v}) \,d\underline{v}-\sum_{\underline{v}\in\mathbb{Z}^n}\Phi_{\underline{u}}(\underline{v})\bigg{|}&\ll P^n q^{-n}(q/P+q|\underline{z}|P^2)\\ &= P^{n-1}q^{1-n}+|\underline{z}|P^{n+2}q^{1-n}, \end{align*}
\begin{align*} \bigg{|}\int_{\mathbb{R}^n}\Phi_{\underline{u}}(\underline{v}) \,d\underline{v}-\sum_{\underline{v}\in\mathbb{Z}^n}\Phi_{\underline{u}}(\underline{v})\bigg{|}&\ll P^n q^{-n}(q/P+q|\underline{z}|P^2)\\ &= P^{n-1}q^{1-n}+|\underline{z}|P^{n+2}q^{1-n}, \end{align*}
since the points in ![]() $\mathcal {N}_{P,q,\underline {u}}$ lie within an
$\mathcal {N}_{P,q,\underline {u}}$ lie within an ![]() $n$-dimensional cube with sides of order
$n$-dimensional cube with sides of order ![]() $1+P/q\leq 2P/q$. Therefore, upon setting
$1+P/q\leq 2P/q$. Therefore, upon setting ![]() $P\underline {x}=\underline {u}+q\underline {v},$ we arrive at the following expression for
$P\underline {x}=\underline {u}+q\underline {v},$ we arrive at the following expression for ![]() $\sum _{\underline {v}} \Phi _{\underline {u}}(\underline {v})$:
$\sum _{\underline {v}} \Phi _{\underline {u}}(\underline {v})$:
 \[ \sum_{\underline{v}\in\mathbb{Z}^n} \Phi_{\underline{u}}(\underline{v})=\frac{P^n}{q^n}\int_{\mathbb{R}^n}\omega(\underline{x})e(z_1P^3F(\underline{x})+z_2P^3G(\underline{x})) \,d\underline{x}+O(P^{n-1}q^{1-n}+|\underline{z}|P^{n+2}q^{1-n}). \]
\[ \sum_{\underline{v}\in\mathbb{Z}^n} \Phi_{\underline{u}}(\underline{v})=\frac{P^n}{q^n}\int_{\mathbb{R}^n}\omega(\underline{x})e(z_1P^3F(\underline{x})+z_2P^3G(\underline{x})) \,d\underline{x}+O(P^{n-1}q^{1-n}+|\underline{z}|P^{n+2}q^{1-n}). \]
We can therefore conclude that
by (10.3). Since ![]() $|\underline {z}|\leq P^{-3+\Delta }$ and
$|\underline {z}|\leq P^{-3+\Delta }$ and ![]() $q\leq P^{\Delta }$, we can now conclude that (10.2) is indeed true. Furthermore, by substituting (10.2) into
$q\leq P^{\Delta }$, we can now conclude that (10.2) is indeed true. Furthermore, by substituting (10.2) into ![]() $S_\mathfrak {M}$ and, for the error term, noting that the major arcs have measure
$S_\mathfrak {M}$ and, for the error term, noting that the major arcs have measure ![]() $O(P^{-6+5\Delta })$ (
$O(P^{-6+5\Delta })$ (![]() $P^{-6+2\Delta }$ from the integrals,
$P^{-6+2\Delta }$ from the integrals, ![]() $P^{3\Delta }$ from the sums), we conclude that
$P^{3\Delta }$ from the sums), we conclude that
Since we have assumed ![]() $\mathfrak {S}(R)=\mathfrak {S}+O_\phi (R^{-\phi })$ for some
$\mathfrak {S}(R)=\mathfrak {S}+O_\phi (R^{-\phi })$ for some ![]() $\phi >0$, we can replace
$\phi >0$, we can replace ![]() $\mathfrak {S}(P^{\Delta })$ with
$\mathfrak {S}(P^{\Delta })$ with ![]() $\mathfrak {S}$ leading us to
$\mathfrak {S}$ leading us to
We will prove that this assumption is true in the next section. We now aim to show that we can replace ![]() $\mathfrak {J}(P^{\Delta })$ with
$\mathfrak {J}(P^{\Delta })$ with ![]() $\mathfrak {J}$. In order to do this, we need
$\mathfrak {J}$. In order to do this, we need ![]() $\mathfrak {J}$ to exist, and
$\mathfrak {J}$ to exist, and ![]() $|\mathfrak {J}-\mathfrak {J}(P^{\Delta })|$ to be sufficiently small. Now, it is easy to see that
$|\mathfrak {J}-\mathfrak {J}(P^{\Delta })|$ to be sufficiently small. Now, it is easy to see that
and so this motivates us to find a bound for the size of ![]() $I(\underline {t})$. We will show the following.
$I(\underline {t})$. We will show the following.
Lemma 10.2 Let
Then
Proof. We will again follow the same procedure as in [Reference Browning and Heath-BrownBH09]. Here ![]() $I(\underline {t})\ll 1$ is trivial since
$I(\underline {t})\ll 1$ is trivial since ![]() $|I(\underline {t})|\leq \mathrm {meas}(\mathrm {Supp}(\omega ))$ for every
$|I(\underline {t})|\leq \mathrm {meas}(\mathrm {Supp}(\omega ))$ for every ![]() $\underline {t}$. For the second estimate, we can assume
$\underline {t}$. For the second estimate, we can assume ![]() $|\underline {t}|>1$. Then on taking
$|\underline {t}|>1$. Then on taking ![]() $\underline {a}=0$,
$\underline {a}=0$, ![]() $q=1$ in (10.6) we get
$q=1$ in (10.6) we get
for any ![]() $P\geq 1$. Likewise, for
$P\geq 1$. Likewise, for ![]() $|\underline {\alpha }|< P^{-1}$, we can also use Proposition 8.1 with
$|\underline {\alpha }|< P^{-1}$, we can also use Proposition 8.1 with ![]() $\underline {a}=\underline {0}$,
$\underline {a}=\underline {0}$, ![]() $q=1$, to conclude that
$q=1$, to conclude that
Hence, for such ![]() $\alpha$, we may set
$\alpha$, we may set ![]() $\underline {t}=\underline {\alpha }P^3$ and combine these estimates to get
$\underline {t}=\underline {\alpha }P^3$ and combine these estimates to get
when ![]() $1<|\underline {t}|< P^{2}$. Finally, we note that this is true for every
$1<|\underline {t}|< P^{2}$. Finally, we note that this is true for every ![]() $P\geq 1$ and
$P\geq 1$ and ![]() $I(\underline {t})$ does not depend on
$I(\underline {t})$ does not depend on ![]() $P$ at all. Hence, we can choose
$P$ at all. Hence, we can choose ![]() $P=|\underline {t}|^{(16+n-\sigma -1)/16}$ to reach our second estimate of
$P=|\underline {t}|^{(16+n-\sigma -1)/16}$ to reach our second estimate of ![]() $I(\underline {t})$.
$I(\underline {t})$.
We can now use Lemma 10.2 to conclude that
For ![]() $n-\sigma \geq 34$, this shows that
$n-\sigma \geq 34$, this shows that ![]() $\mathfrak {J}$ is absolutely convergent. Finally, replacing
$\mathfrak {J}$ is absolutely convergent. Finally, replacing ![]() $\mathfrak {J}(P^{\Delta })$ by
$\mathfrak {J}(P^{\Delta })$ by ![]() $\mathfrak {J}$ in (10.8) gives us
$\mathfrak {J}$ in (10.8) gives us
which is permissible for Lemma 10.1 provided that ![]() $\Delta \in (0,1/7)$,
$\Delta \in (0,1/7)$, ![]() $\phi >0$ and
$\phi >0$ and ![]() $\varepsilon >0$ is taken to be sufficiently small.
$\varepsilon >0$ is taken to be sufficiently small.
10.1 Convergence of the singular series
Finally, we turn to the issue of showing that the singular series
 \[ \sum_{q=1}^{\infty} q^{-n} \sideset{}{^*}\sum_{{\underline{a}}} S_{\underline{a},q} \]
\[ \sum_{q=1}^{\infty} q^{-n} \sideset{}{^*}\sum_{{\underline{a}}} S_{\underline{a},q} \]
converges absolutely, and obeys the assumption made in Lemma 10.1. In particular, we will show the following.
Theorem 10.3 Assume ![]() $n-\sigma \geq 35$. Then
$n-\sigma \geq 35$. Then ![]() $\mathfrak {S}$ is absolutely convergent. Furthermore, there is some
$\mathfrak {S}$ is absolutely convergent. Furthermore, there is some ![]() $\phi >0$ such that
$\phi >0$ such that
To see that ![]() $\mathfrak {S}$ converges for
$\mathfrak {S}$ converges for ![]() $n-\sigma \geq 35$, we will again adopt the approach of Browning and Heath Brown in [Reference Browning and Heath-BrownBH09]. We start by noting that
$n-\sigma \geq 35$, we will again adopt the approach of Browning and Heath Brown in [Reference Browning and Heath-BrownBH09]. We start by noting that
 \[ \mathfrak{S}=q^{-n} \sideset{}{^*}\sum_{{\underline{a}}}^{q} S_{\underline{a},q} \]
\[ \mathfrak{S}=q^{-n} \sideset{}{^*}\sum_{{\underline{a}}}^{q} S_{\underline{a},q} \]
is a multiplicative function of ![]() $q$, and so it follows that
$q$, and so it follows that ![]() $\mathfrak {S}$ is absolutely convergent if and only if
$\mathfrak {S}$ is absolutely convergent if and only if ![]() $\prod _p (1+\sum _{k=1}^{\infty } a_p(k))$ is, where
$\prod _p (1+\sum _{k=1}^{\infty } a_p(k))$ is, where
 \[ a_p(k):=p^{-kn} \sideset{}{^*}\sum_{{\underline{a}}}^{p^k} |S_{\underline{a},p^k}|. \]
\[ a_p(k):=p^{-kn} \sideset{}{^*}\sum_{{\underline{a}}}^{p^k} |S_{\underline{a},p^k}|. \]
But by taking logs, this is equivalent to ![]() $\sum _p\sum _{k=1}^{\infty } a_p(k)$ converging. Now by Proposition 8.1 with
$\sum _p\sum _{k=1}^{\infty } a_p(k)$ converging. Now by Proposition 8.1 with ![]() $\underline {a}=\underline {0}$,
$\underline {a}=\underline {0}$, ![]() $q=p^k$,
$q=p^k$, ![]() $|\underline {z}|< P^{-3+\Delta }$,
$|\underline {z}|< P^{-3+\Delta }$, ![]() $\omega =\chi$, we have that
$\omega =\chi$, we have that
for any ![]() $k\geq 1$, and so this enables us to establish that
$k\geq 1$, and so this enables us to establish that ![]() $\mathfrak {S}$ converges absolutely provided that
$\mathfrak {S}$ converges absolutely provided that ![]() $n-\sigma \geq 50$. We can use (10.9) far more effectively than this if we are more careful: we will assume that
$n-\sigma \geq 50$. We can use (10.9) far more effectively than this if we are more careful: we will assume that ![]() $n-\sigma \geq 35$ from now on. Then by (10.9), we have
$n-\sigma \geq 35$ from now on. Then by (10.9), we have
 \[ \sum_p\sum_{k\geq 16} a_p(k)\ll \sum_{p} p^{33+\sigma-n+\varepsilon}< \sum_{m=1}^{\infty} m^{-2+\varepsilon}\ll 1, \]
\[ \sum_p\sum_{k\geq 16} a_p(k)\ll \sum_{p} p^{33+\sigma-n+\varepsilon}< \sum_{m=1}^{\infty} m^{-2+\varepsilon}\ll 1, \]
assuming ![]() $\varepsilon >0$ is sufficiently small. We now need to show that
$\varepsilon >0$ is sufficiently small. We now need to show that ![]() $\sum _p \sum _{1\leq k \leq 15}$ also converges. For
$\sum _p \sum _{1\leq k \leq 15}$ also converges. For ![]() $2\leq k \leq 15$, we will use [Reference Browning and Heath-BrownBH09, Lemma 25]. This shows that
$2\leq k \leq 15$, we will use [Reference Browning and Heath-BrownBH09, Lemma 25]. This shows that
Hence,
 \[ \sum_p\sum_{k=2}^{15} a_p(k)\ll \sum_{p}\sum_{k=2}^{15}p^{k(2-n)}p^{(k-1)n+s_p(a_1F+a_2G)+1}=\sum_{p}\sum_{k=2}^{15}p^{2k+1-n+s_p(a_1F+a_2G)}. \]
\[ \sum_p\sum_{k=2}^{15} a_p(k)\ll \sum_{p}\sum_{k=2}^{15}p^{k(2-n)}p^{(k-1)n+s_p(a_1F+a_2G)+1}=\sum_{p}\sum_{k=2}^{15}p^{2k+1-n+s_p(a_1F+a_2G)}. \]
But by Lemma 2.3, we have ![]() $s_p(a_1F+a_2G)\leq s_p(F,G)+1$. Furthermore, since
$s_p(a_1F+a_2G)\leq s_p(F,G)+1$. Furthermore, since ![]() $F$ and
$F$ and ![]() $G$ are fixed,
$G$ are fixed, ![]() $s_p(F,G)=\sigma$ for all but finitely many primes, and so by increasing the size of the implicit multiplicative constant if necessary, we have that
$s_p(F,G)=\sigma$ for all but finitely many primes, and so by increasing the size of the implicit multiplicative constant if necessary, we have that
 \[ \sum_{p}\sum_{k=2}^{15}p^{2k+2-n+\sigma}\ll \sum_p p^{32-n+\sigma}\ll 1, \]
\[ \sum_{p}\sum_{k=2}^{15}p^{2k+2-n+\sigma}\ll \sum_p p^{32-n+\sigma}\ll 1, \]
since we have assumed ![]() $n-\sigma \geq 35$.
$n-\sigma \geq 35$.
All that is left to check is ![]() $k=1$. By Lemma 7 in [Reference Browning and Heath-BrownBH09], we have
$k=1$. By Lemma 7 in [Reference Browning and Heath-BrownBH09], we have
This enables us to establish Theorem 10.3. Finally, we will follow the approach used in [Reference Marmon and VisheMV19] to prove that there exists some ![]() $\phi >0$ such that
$\phi >0$ such that
We will continue to work under the assumption that ![]() $n-\sigma \geq 35$. First, let
$n-\sigma \geq 35$. First, let
 \[ S_q:= \sideset{}{^*}\sum_{{\underline{a}}}^q\sum_{\underline{x}}^q e_q(a_1F(\underline{x})+a_2G(\underline{x})). \]
\[ S_q:= \sideset{}{^*}\sum_{{\underline{a}}}^q\sum_{\underline{x}}^q e_q(a_1F(\underline{x})+a_2G(\underline{x})). \]
Then, we have
We will split ![]() $q$ into several of its multiplicative components and bound each component separately. Let
$q$ into several of its multiplicative components and bound each component separately. Let
 \[ b_i:=\prod_{p^i || q} p^i, \quad q_i:=\prod_{\substack{p^e || q\\ e\geq i}} p^e. \]
\[ b_i:=\prod_{p^i || q} p^i, \quad q_i:=\prod_{\substack{p^e || q\\ e\geq i}} p^e. \]
Then ![]() $q=q_k\prod _{i=1}^{k-1} b_i$ for every
$q=q_k\prod _{i=1}^{k-1} b_i$ for every ![]() $k$ (e.g.
$k$ (e.g. ![]() $q=b_1b_2q_3$). Recall that by Lemma 9.1, we have the following for any
$q=b_1b_2q_3$). Recall that by Lemma 9.1, we have the following for any ![]() $R_1,\ldots,R_k>0$:
$R_1,\ldots,R_k>0$:
 \begin{equation} \sum_{\substack{b_1\sim R_1, \ldots, b_{k-1}\sim R_{k-1}\\ q_k\sim R_k }} 1 \ll \prod_{i=1}^k R_i^{1/i}. \end{equation}
\begin{equation} \sum_{\substack{b_1\sim R_1, \ldots, b_{k-1}\sim R_{k-1}\\ q_k\sim R_k }} 1 \ll \prod_{i=1}^k R_i^{1/i}. \end{equation}
We will use ![]() $k=16$. Now
$k=16$. Now
 \[ |S_q|\leq |S_{q_{16}}|\prod_{i=1}^{15} |S_{b_i}|. \]
\[ |S_q|\leq |S_{q_{16}}|\prod_{i=1}^{15} |S_{b_i}|. \]
We will bound each of these in turn:
by Proposition 8.1. For ![]() $b_3,\ldots, b_{15}$, we split
$b_3,\ldots, b_{15}$, we split ![]() $b_k$ into prime powers and use Lemma 25 from [Reference Browning and Heath-BrownBH09]:
$b_k$ into prime powers and use Lemma 25 from [Reference Browning and Heath-BrownBH09]:
 \[ |S_{p^k}|\ll \sideset{}{^*}\sum_{{\underline{a}}}^{p^k} p^{(k-1)n+s_p(a_1F+a_2G)+1}\ll p^{(k-1)n+\sigma+2+2k} \]
\[ |S_{p^k}|\ll \sideset{}{^*}\sum_{{\underline{a}}}^{p^k} p^{(k-1)n+s_p(a_1F+a_2G)+1}\ll p^{(k-1)n+\sigma+2+2k} \]
for ![]() $p\gg 1$. Hence, for
$p\gg 1$. Hence, for ![]() $k\in \{3,\ldots,15\}$,
$k\in \{3,\ldots,15\}$,
Finally, for ![]() $b_1,b_2$, we use Lemma 7 from [Reference Browning and Heath-BrownBH09]. By following the same argument as for
$b_1,b_2$, we use Lemma 7 from [Reference Browning and Heath-BrownBH09]. By following the same argument as for ![]() $S_{b_3},\ldots, S_{b_15}$, we get
$S_{b_3},\ldots, S_{b_15}$, we get
for ![]() $k\in \{1,2\}$. Hence,
$k\in \{1,2\}$. Hence,
or, equivalently,
 \[ |S_{q}|\ll \frac{q^{2+n+\varepsilon}}{(b_1b_2)^{(m-1)/2}b_3^{(m-1)/3}\cdots b_{15}^{(m-1)/15}q_{16}^{m/16}}, \]
\[ |S_{q}|\ll \frac{q^{2+n+\varepsilon}}{(b_1b_2)^{(m-1)/2}b_3^{(m-1)/3}\cdots b_{15}^{(m-1)/15}q_{16}^{m/16}}, \]
where ![]() $m=n-\sigma -1$. Therefore, by (10.10), we have
$m=n-\sigma -1$. Therefore, by (10.10), we have
 \begin{align*} |\mathfrak{S}-\mathfrak{S}(R)|&\ll \sum_{b_1\cdots b_{15}q_{16}\geq R} (b_1b_2)^{2+\varepsilon-(m-1)/2}b_3^{2+\varepsilon-(m-1)/3}\cdots b_{15}^{2+\varepsilon-(m-1)/15}q_{16}^{2+\varepsilon-m/16}\\ &\ll \sum_{b_1\cdots b_{15}q_{16}\geq R} (b_1b_2)^{(5+\varepsilon-m)/2}b_3^{(7+\varepsilon-m)/3}\cdots b_{15}^{(31+\varepsilon-m)/15}q_{16}^{(32+\varepsilon-m)/16}. \end{align*}
\begin{align*} |\mathfrak{S}-\mathfrak{S}(R)|&\ll \sum_{b_1\cdots b_{15}q_{16}\geq R} (b_1b_2)^{2+\varepsilon-(m-1)/2}b_3^{2+\varepsilon-(m-1)/3}\cdots b_{15}^{2+\varepsilon-(m-1)/15}q_{16}^{2+\varepsilon-m/16}\\ &\ll \sum_{b_1\cdots b_{15}q_{16}\geq R} (b_1b_2)^{(5+\varepsilon-m)/2}b_3^{(7+\varepsilon-m)/3}\cdots b_{15}^{(31+\varepsilon-m)/15}q_{16}^{(32+\varepsilon-m)/16}. \end{align*}
When ![]() $m\geq 34$, we clearly have
$m\geq 34$, we clearly have
 \begin{align*} |\mathfrak{S}-\mathfrak{S}(R)|&\ll \sum_{b_1\cdots b_{15}q_{16}\geq R} (b_1b_2)^{-29/2+\varepsilon}b_3^{-27/3+\varepsilon}\cdots b_{15}^{-3/15+\varepsilon}q_{16}^{-2/16+\varepsilon}\\ &\ll R^{-1/16+2\varepsilon} \sum_{b_1\cdots b_{15}q_{16}\geq R} (b_1b_2)^{-1-\varepsilon}b_3^{-1/3-\varepsilon}\cdots b_{15}^{-1/15-\varepsilon}q_{16}^{-1/16-\varepsilon}\\ & < R^{-1/16+2\varepsilon} \sum_{b_1,\ldots, b_{15},q_{16}= 1}^{\infty} (b_1b_2)^{-1-\varepsilon}b_3^{-1/3-\varepsilon}\cdots b_{15}^{-1/15-\varepsilon}q_{16}^{-1/16-\varepsilon}, \end{align*}
\begin{align*} |\mathfrak{S}-\mathfrak{S}(R)|&\ll \sum_{b_1\cdots b_{15}q_{16}\geq R} (b_1b_2)^{-29/2+\varepsilon}b_3^{-27/3+\varepsilon}\cdots b_{15}^{-3/15+\varepsilon}q_{16}^{-2/16+\varepsilon}\\ &\ll R^{-1/16+2\varepsilon} \sum_{b_1\cdots b_{15}q_{16}\geq R} (b_1b_2)^{-1-\varepsilon}b_3^{-1/3-\varepsilon}\cdots b_{15}^{-1/15-\varepsilon}q_{16}^{-1/16-\varepsilon}\\ & < R^{-1/16+2\varepsilon} \sum_{b_1,\ldots, b_{15},q_{16}= 1}^{\infty} (b_1b_2)^{-1-\varepsilon}b_3^{-1/3-\varepsilon}\cdots b_{15}^{-1/15-\varepsilon}q_{16}^{-1/16-\varepsilon}, \end{align*}
and this sum converges by (10.11). Hence, we conclude that
where ![]() $\phi =1/16-\varepsilon$, provided that
$\phi =1/16-\varepsilon$, provided that ![]() $n-\sigma \geq 35$.
$n-\sigma \geq 35$.
Acknowledgements
We would like to thank Tim Browning and Oscar Marmon for their help.
Conflicts of Interest
None.
Appendix A. Mathematica code
Here, we will include the Mathematica code that verifies our minor arcs bound. An executable version of this can be found at [Reference NortheyNor00b].