Hostname: page-component-89b8bd64d-j4x9h Total loading time: 0 Render date: 2026-05-06T23:43:29.421Z Has data issue: false hasContentIssue false
  • English
  • Français

Ordinary primes in Hilbert modular varieties

Part of: Arithmetic problems. Diophantine geometry Discontinuous groups and automorphic forms Arithmetic algebraic geometry

Published online by Cambridge University Press:  06 February 2020

Junecue Suh
Junecue Suh*
Affiliation:
Department of Mathematics, University of California, 1156 High St, Santa Cruz, CA 95064, USA email jusuh@ucsc.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

A well-known conjecture, often attributed to Serre, asserts that any motive over any number field has infinitely many ordinary reductions (in the sense that the Newton polygon coincides with the Hodge polygon). In the case of Hilbert modular cuspforms 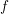$f$ of parallel weight $(2,\ldots ,2)$, we show how to produce more ordinary primes by using the Sato–Tate equidistribution and combining it with the Galois theory of the Hecke field. Under the assumption of stronger forms of Sato–Tate equidistribution, we get stronger (but conditional) results. In the case of higher weights, we formulate the ordinariness conjecture for submotives of the intersection cohomology of proper algebraic varieties with motivic coefficients, and verify it for the motives whose $\ell$-adic Galois realisations are abelian on a finite-index subgroup. We get some results for Hilbert cuspforms of weight $(3,\ldots ,3)$, weaker than those for $(2,\ldots ,2)$.

Keywords

Hilbert modular formordinary reductionSato–Tate equidistribution

MSC classification

Primary: 11F41: Automorphic forms on $(2)$; Hilbert and Hilbert-Siegel modular groups and their modular and automorphic forms; Hilbert modular surfaces
Secondary: 14G35: Modular and Shimura varieties 11F30: Fourier coefficients of automorphic forms 11G18: Arithmetic aspects of modular and Shimura varieties

Information

Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 4 , April 2020 , pp. 647 - 678
Copyright
© The Author 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

André, Y., Pour une théorie inconditionnelle des motifs, Publ. Math. Inst. Hautes Études Sci. 83 (1996), 5–49.CrossRefGoogle Scholar
Barnet-Lamb, T., Gee, T. and Geraghty, D., The Sato-Tate conjecture for Hilbert modular forms, J. Amer. Math. Soc. 24 (2011), 411–469.CrossRefGoogle Scholar
Barnet-Lamb, T., Geraghty, D., Harris, M. and Taylor, R., A family of Calabi-Yau varieties and potential automorphy II, Publ. Res. Inst. Math. Sci. 47 (2011), 29–98.CrossRefGoogle Scholar
Beĭlinson, A. A., Bernstein, J. and Deligne, P., Faisceaux pervers, in Analysis and topology on singular spaces, I (Luminy, 1981), Astérisque, vol. 100 (Société Mathématique de France, Paris, 1982), 5–171.Google Scholar
Blasius, D., Hilbert modular forms and the Ramanujan conjecture, in Noncommutative geometry and number theory, Aspects of Mathematics, vol. E37 (Friedr. Vieweg, Wiesbaden, 2006), 35–56.CrossRefGoogle Scholar
Blasius, D. and Rogawski, J., Motives for Hilbert modular forms, Invent. Math. 114 (1993), 55–87.CrossRefGoogle Scholar
Brylinski, J.-L. and Labesse, J.-P., Cohomologie d’intersection et fonctions L de certaines variétés de Shimura, Ann. Sci. Éc. Norm. Supér. (4) 17 (1984), 361–412.CrossRefGoogle Scholar
Carayol, H., Sur les représentations l-adiques associées aux formes modulaires de Hilbert, Ann. Sci. Éc. Norm. Supér. (4) 19 (1986), 409–468.CrossRefGoogle Scholar
Curtis, C. and Reiner, I., Methods of representation theory: with applications to finite groups and orders, Vol. II, Pure and Applied Mathematics (John Wiley & Sons, New York, 1987).Google Scholar
de Cataldo, M. A., The perverse filtration and the Lefschetz hyperplane theorem, II, J. Algebraic Geom. 21 (2012), 305–345.CrossRefGoogle Scholar
de Cataldo, M. A. and Migliorini, L., The projectors of the decomposition theorem are motivated, Math. Res. Lett. 22 (2015), 1061–1088.CrossRefGoogle Scholar
Deligne, P., Formes modulaires et représentations ℓ-adiques, in Séminaire Bourbaki. Vol. 1968/69: Exposés 347–363, Lecture Notes in Mathematics, vol. 175, Exp. No. 355 (Springer, Berlin, 1971), 139–172.CrossRefGoogle Scholar
Deligne, P., La conjecture de Weil. I, Publ. Math. Inst. Hautes Études Sci. 43 (1974), 273–307.CrossRefGoogle Scholar
Dimitrov, M., Automorphic symbols, p-adic L-functions and ordinary cohomology of Hilbert modular varieties, Amer. J. Math. 135 (2013), 1117–1155.CrossRefGoogle Scholar
Emerton, M., Pollack, R. and Weston, T., Variation of Iwasawa invariants in Hida families, Invent. Math. 163 (2006), 523–580.CrossRefGoogle Scholar
Faltings, G., p-adic Hodge theory, J. Amer. Math. Soc. 1 (1988), 255–299.Google Scholar
Faltings, G., Crystalline cohomology and p-adic Galois-representations, in Algebraic analysis, geometry, and number theory (Baltimore, MD, 1988) (Johns Hopkins University Press, Baltimore, MD, 1989), 25–80.Google Scholar
Fujiwara, K., Independence of ℓ for intersection cohomology (after Gabber), in Algebraic geometry 2000, Azumino (Hotaka), Advanced Studies in Pure Mathematics, vol. 36 (Mathematical Society of Japan, Tokyo, 2002), 145–151.CrossRefGoogle Scholar
Harris, M., Potential automorphy of odd-dimensional symmetric powers of elliptic curves and applications, in Algebra, arithmetic, and geometry: in honor of Yu. I. Manin. Vol. II, Progress in Mathematics, vol. 270 (Birkhäuser, Boston, 2009), 1–21.Google Scholar
Harris, M., Shepherd-Barron, N. and Taylor, R., A family of Calabi-Yau varieties and potential automorphy, Ann. of Math. (2) 171 (2010), 779–813.CrossRefGoogle Scholar
Henniart, G., Représentations ℓ-adiques abéliennes, in Seminar on Number Theory, Paris 1980–81, Progress in Mathematics, vol. 22 (Birkhäuser, Boston, 1982), 107–126.Google Scholar
Ivorra, F. and Morel, S., The four operations on perverse motives, Preprint (2019),arXiv:1901.02096v1.Google Scholar
Katz, N. M., On a theorem of Ax, Amer. J. Math. 93 (1971), 485–499.CrossRefGoogle Scholar
Katz, N. M. and Laumon, G., Transformation de Fourier et majoration de sommes exponentielles, Publ. Math. Inst. Hautes Études Sci. 62 (1985), 361–418.CrossRefGoogle Scholar
Katz, N. M. and Messing, W., Some consequences of the Riemann hypothesis for varieties over finite fields, Invent. Math. 23 (1974), 73–77.CrossRefGoogle Scholar
Mazur, B., Frobenius and the Hodge filtration (estimates), Ann. of Math. (2) 98 (1973), 58–95.CrossRefGoogle Scholar
Morel, S., Complexes pondérés sur les compactifications de Baily–Borel: le cas des variétés de Siegel, J. Amer. Math. Soc. 21 (2008), 23–61.CrossRefGoogle Scholar
Mumford, A., Rapoport, D., Ash, M. and Tai, Y., Smooth compactification of locally symmetric varieties, Lie Groups: History, Frontiers and Applications, vol. IV, first edition (Mathematical Science Press, Brookline, MA, 1975).Google Scholar
Nekovář, J., On the parity of ranks of Selmer groups. II, C. R. Acad. Sci. Paris Sér. I Math. 332 (2001), 99–104.CrossRefGoogle Scholar
Ochiai, T., On the two-variable Iwasawa main conjecture, Compos. Math. 142 (2006), 1157–1200.CrossRefGoogle Scholar
Ogus, A., Hodge cycles and crystalline cohomology, in Hodge cycles, Motives and Shimura varieties, Lecture Notes in Mathematics, vol. 900 (Springer, Berlin, 1982), 357–414.CrossRefGoogle Scholar
Ohta, M., On the zeta function of an abelian scheme over the Shimura curve, Jpn. J. Math. (N.S.) 9 (1983), 1–25.CrossRefGoogle Scholar
Patrikis, S., Generalized Kuga–Satake theory and rigid local systems, II: Rigid Hecke eigensheaves, Algebra Number Theory 10 (2016), 1477–1526.CrossRefGoogle Scholar
Pink, R., ℓ-adic algebraic monodromy groups, cocharacters, and the Mumford–Tate conjecture, J. Reine Angew. Math. 495 (1998), 187–237.CrossRefGoogle Scholar
Rapoport, M., Compactifications de l’espace de modules de Hilbert–Blumenthal, Compos. Math. 36 (1978), 255–335.Google Scholar
Ribet, K., Galois action on division points of Abelian varieties with real multiplications, Amer. J. Math. 98 (1976), 751–804.CrossRefGoogle Scholar
Serre, J.-P., Abelian ℓ-adic representations and elliptic curves, Research Notes in Mathematics, vol. 7 (A K Peters Ltd., Wellesley, MA, 1998), with the collaboration of Willem Kuyk and John Labute; revised reprint of the 1968 original.Google Scholar
Serre, J.-P., Lectures on N X(p), Chapman & Hall/CRC Research Notes in Mathematics, vol. 11 (CRC Press, Boca Raton, FL, 2012).Google Scholar
Serre, J.-P., Oeuvres/Collected papers. IV. 1985–1998, Springer Collected Works in Mathematics (Springer, Heidelberg, 2013), reprint of the 2000 edition; MR 1730973.Google Scholar
Skinner, C. and Urban, E., The Iwasawa main conjectures for GL2, Invent. Math. 195 (2014), 1–277.CrossRefGoogle Scholar
Taylor, R., On Galois representations associated to Hilbert modular forms, Invent. Math. 98 (1989), 265–280.CrossRefGoogle Scholar
Taylor, R., On Galois representations associated to Hilbert modular forms II, in Elliptic curves, modular forms, and Fermat’s last theorem (Hong Kong, 1993), Series on Number Theory. I (International Press, Cambridge, MA, 1995), 185–191.Google Scholar
Taylor, R., Representations of Galois groups associated to modular forms, in Proceedings of the International Congress of Mathematicians, Vol. 1, 2 (Zürich, 1994) (Birkhäuser, Basel, 1995), 435–442.CrossRefGoogle Scholar
Waldschmidt, M., Transcendance et exponentielles en plusieurs variables, Invent. Math. 63 (1981), 97–127.CrossRefGoogle Scholar
Wan, X., The Iwasawa main conjecture for Hilbert modular forms, Forum Math. Sigma 3 (2015), 95.CrossRefGoogle Scholar
Wiles, A., On ordinary 𝜆-adic representations associated to modular forms, Invent. Math. 94 (1988), 529–573.CrossRefGoogle Scholar