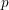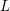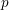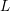Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dummit, Evan P.
Hablicsek, Márton
Harron, Robert
Jain, Lalit
Pollack, Robert
and
Ross, Daniel
2016.
Explicit computations of Hida families via overconvergent modular symbols.
Research in Number Theory,
Vol. 2,
Issue. 1,
Steele, G. Ander
2016.
The p-adic Shintani modular symbol and evil Eisenstein series.
Annales mathématiques du Québec,
Vol. 40,
Issue. 2,
p.
491.
Bellaïche, Joël
and
Pollack, Robert
2019.
Congruences with Eisenstein series and -invariants.
Compositio Mathematica,
Vol. 155,
Issue. 5,
p.
863.
Bellaïche, Joël
2021.
The Eigenbook.
p.
119.
Bellaïche, Joël
2021.
The Eigenbook.
p.
249.
Doyon, Anthony
and
Lei, Antonio
2024.
Lambda-invariants of Mazur–Tate elements attached to Ramanujan’s tau function and congruences with Eisenstein series.
Research in Number Theory,
Vol. 10,
Issue. 2,
Loeffler, David
and
Rivero Salgado, Oscar
2024.
Eisenstein degeneration of Euler systems.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2024,
Issue. 814,
p.
241.
Bergdall, John
Chenevier, Gaëtan
Clozel, Laurent
Darmon, Henri
Dasgupta, Samit
and
Medvedovsky, Anna
2025.
Joël Bellaïche (1974-2022).
Tunisian Journal of Mathematics,
Vol. 7,
Issue. 3-4,
p.
439.
Palacios, Luis Santiago
2025.
Non-cuspidal Bianchi modular forms and Katz p-adic L-functions.
Mathematische Zeitschrift,
Vol. 309,
Issue. 4,