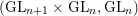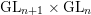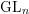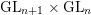Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sakellaridis, Yiannis
2016.
The Schwartz space of a smooth semi-algebraic stack.
Selecta Mathematica,
Vol. 22,
Issue. 4,
p.
2401.
Kaplan, Eyal
and
Yamana, Shunsuke
2017.
Twisted symmetric square L-functions for $$\mathrm {GL}_n$$ GL n and invariant trilinear forms.
Mathematische Zeitschrift,
Vol. 285,
Issue. 3-4,
p.
739.
Yamana, Shunsuke
2018.
PERIODS OF AUTOMORPHIC FORMS: THE TRILINEAR CASE.
Journal of the Institute of Mathematics of Jussieu,
Vol. 17,
Issue. 1,
p.
59.
Goldfeld, Dorian
and
Li, Xiaoqing
2018.
A Standard Zero Free Region for Rankin–Selberg L-Functions.
International Mathematics Research Notices,
Vol. 2018,
Issue. 22,
p.
7067.
Zydor, Michał
2018.
LA VARIANTE INFINITÉSIMALE DE LA FORMULE DES TRACES DE JACQUET-RALLIS POUR LES GROUPES LINÉAIRES.
Journal of the Institute of Mathematics of Jussieu,
Vol. 17,
Issue. 4,
p.
735.
Kobayashi, Toshiyuki
and
Speh, Birgit
2018.
Symmetry Breaking for Representations of Rank One Orthogonal Groups II.
Vol. 2234,
Issue. ,
p.
207.
Ichino, Atsushi
and
Yamana, Shunsuke
2019.
Periods of automorphic forms: The case of (U
n+1×U
n
,U
n
).
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2019,
Issue. 746,
p.
1.
Gan, Wee Teck
Gross, Benedict H.
and
Prasad, Dipendra
2020.
Branching laws for classical groups: the non-tempered case.
Compositio Mathematica,
Vol. 156,
Issue. 11,
p.
2298.
Zydor, Michał
2020.
Les formules des traces relatives de Jacquet–Rallis
grossières.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2020,
Issue. 762,
p.
195.
Beuzart-Plessis, Raphaël
Chaudouard, Pierre-Henri
and
Zydor, Michał
2022.
The global Gan-Gross-Prasad conjecture for unitary groups: the endoscopic case.
Publications mathématiques de l'IHÉS,
Vol. 135,
Issue. 1,
p.
183.
Chan, Kei Yuen
2023.
Ext-multiplicity theorem for standard representations of $$(\textrm{GL}_{n+1},\textrm{GL}_n)$$.
Mathematische Zeitschrift,
Vol. 303,
Issue. 2,
Haan, Jaeho
2024.
Regularized periods and the global Gan–Gross–Prasad conjecture: the case of $$U(n+2r) \times U(n)$$.
Mathematische Annalen,
Vol. 389,
Issue. 4,
p.
4149.
Beuzart-Plessis, Raphaël
and
Chaudouard, Pierre-Henri
2025.
The global Gan-Gross-Prasad conjecture for unitary groups. II. From Eisenstein series to Bessel periods.
Forum of Mathematics, Pi,
Vol. 13,
Issue. ,
Humphries, Peter
2025.
ARCHIMEDEAN NEWFORM THEORY FOR
$\operatorname {\mathrm {GL}}_n$
.
Journal of the Institute of Mathematics of Jussieu,
Vol. 24,
Issue. 1,
p.
41.