Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Choi, Jinwon
van Garrel, Michel
Katz, Sheldon
and
Takahashi, Nobuyoshi
2020.
Log BPS numbers of log Calabi-Yau surfaces.
Transactions of the American Mathematical Society,
Vol. 374,
Issue. 1,
p.
687.
Bousseau, Pierrick
2020.
The quantum tropical vertex.
Geometry & Topology,
Vol. 24,
Issue. 3,
p.
1297.
Bousseau, Pierrick
Brini, Andrea
and
Garrel, Michel van
2021.
Stable maps to Looijenga pairs: orbifold examples.
Letters in Mathematical Physics,
Vol. 111,
Issue. 4,
Davison, Ben
and
Mandel, Travis
2021.
Strong positivity for quantum theta bases of quantum cluster algebras.
Inventiones mathematicae,
Vol. 226,
Issue. 3,
p.
725.
Mandel, Travis
2021.
Scattering diagrams, theta functions, and refined tropical curve counts.
Journal of the London Mathematical Society,
Vol. 104,
Issue. 5,
p.
2299.
Gross, Mark
and
Siebert, Bernd
2022.
The canonical wall structure and intrinsic mirror symmetry.
Inventiones mathematicae,
Vol. 229,
Issue. 3,
p.
1101.
Argüz, Hülya
2022.
Lie Theory and Its Applications in Physics.
Vol. 396,
Issue. ,
p.
423.
Bousseau, Pierrick
2023.
Strong Positivity for the Skein Algebras of the 4-Punctured Sphere and of the 1-Punctured Torus.
Communications in Mathematical Physics,
Vol. 398,
Issue. 1,
p.
1.
Blomme, Thomas
2023.
Refined count of oriented real rational curves.
Journal of Algebraic Geometry,
Vol. 33,
Issue. 1,
p.
143.
Bousseau, Pierrick
Brini, Andrea
and
van Garrel, Michel
2024.
Stable maps to Looijenga pairs.
Geometry & Topology,
Vol. 28,
Issue. 1,
p.
393.
Fantini, Veronica
2024.
Scattering diagrams in mirror symmetry.
Bollettino dell'Unione Matematica Italiana,
Vol. 17,
Issue. 2,
p.
313.
Kennedy-Hunt, Patrick
Shafi, Qaasim
and
Urundolil Kumaran, Ajith
2024.
Tropical Refined Curve Counting with Descendants.
Communications in Mathematical Physics,
Vol. 405,
Issue. 10,
ONTANI, RICCARDO
and
STOPPA, JACOPO
2024.
Log Calabi–Yau surfaces and Jeffrey–Kirwan residues.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 176,
Issue. 3,
p.
547.
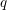 $q$-deformed scattering diagrams defined in terms of higher-genus log Gromov–Witten invariants, we construct deformation quantizations of these mirrors and we produce canonical bases of the corresponding non-commutative algebras of functions.
$q$-deformed scattering diagrams defined in terms of higher-genus log Gromov–Witten invariants, we construct deformation quantizations of these mirrors and we produce canonical bases of the corresponding non-commutative algebras of functions.
