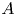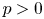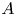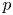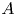1. Introduction
1.1 Main results
Let 
$p$ be an odd prime and let 
$\mathcal {A}_2$ denote the moduli stack of principally polarized abelian surfaces over 
$\mathbb {F}_p$. We view 
$\mathcal {A}_2$ as (the special fiber of the canonical integral model of) a GSpin Shimura variety and let 
$Z(m)$ denote the Heegner divisors in 
$\mathcal {A}_2$ for an integer 
$m\geq 1$; more precisely, 
$Z(m)$ parametrizes abelian surfaces with a special endomorphism 
$s$ such that 
$s\circ s$ is the endomorphism given by multiplication by 
$m$ (see § 2.2).
Theorem 1 Assume 
$p\geq 5$. Let 
$C$ be an irreducible smooth quasi-projective curve with a finite morphism 
$C\rightarrow \mathcal {A}_{2,\bar {\mathbb {F}}_p}$. Assume that the generic point of 
$C$ corresponds to an ordinary abelian surface.
(1) If the image of
$C$ is not contained in any Heegner divisor $Z(m)$, and if $C$ is projective, then there exist infinitely many $\bar {\mathbb {F}}_p$-points on $C$ which correspond to non-simple abelian surfaces.(2) If the image of
$C$ is contained in some $Z(m)$ such that $p\nmid m$, then there exist infinitely many $\bar {\mathbb {F}}_p$-points on $C$ which correspond to abelian surfaces isogenous to self-products of elliptic curves.
In Theorem 1(2), note that the elliptic curve may vary for these points. An equivalent statement is that there exist infinitely many 
$\bar {\mathbb {F}}_p$-points on 
$C$ which correspond to abelian surfaces whose Néron–Severi ranks are strictly larger than that of the generic point of 
$C$. Note that in case (2), any irreducible component of 
$Z(m)\subset \mathcal {A}_2$ is an irreducible component of a Hecke translate of some Hilbert modular surface associated to the real quadratic field 
$F=\mathbb {Q}(\sqrt {m})$ (if 
$m$ is a square number, then we obtain a Hecke translate of the self-product of the modular curve).
Remark 2 The assumption that the generic point is ordinary is necessary (especially if we formulate the theorem in terms of the Néron–Severi rank). For instance, in case (2), we may take 
$C$ to be an irreducible component of the non-ordinary locus. If 
$p$ is inert in 
$F$, then all the points on 
$C$ are supersingular and the Néron–Severi rank does not jump. If 
$p$ is split in 
$F$, then the only points where the Néron–Severi rank jumps are the finitely many supersingular points.
Remark 3 We make the (technical) assumption that 
$C$ is projective in case (1) because the Heegner divisors 
$Z(m)$ are all non-compact and we plan to remove this assumption in future work. On the other hand, the Hilbert modular surfaces considered in case (2) do contain compact special divisors (see the second half of § 2.2 for the definitions of special divisors in the Hilbert case, and § 4.3.3 for a criterion of when these special divisors are compact) the 
$\bar {\mathbb {F}}_p$-points of which parameterize abelian surfaces isogenous to a self-product of elliptic curves. By working exclusively with these compact special divisors, we no longer need assume that 
$C$ is projective.
Remark 4 A modification of our argument shows that with the same assumption as in case (1), for a fixed real quadratic number field 
$F$, there are infinitely many ordinary 
$\bar {\mathbb {F}}_p$-points on 
$C$ such that the corresponding abelian surfaces admit real multiplication by 
$F$.Footnote 1 Here we need to assume 
$p\geq 7$ if 
$p$ is ramified in 
$F$. Otherwise, 
$p\geq 5$ is enough.
The proof of Theorem 1(1) applies to the case when 
$p$ is split in 
$F/\mathbb {Q}$; and for the other cases, one needs to carry out a more general study of the local behavior at supersingular points (see the arXiv version [Reference Maulik, Shankar and TangMST18, § 9, Appendix A] for details).
To prove Theorem 1(1), we consider the intersection number of 
$C$ and 
$Z(\ell ^2)$, where 
$\ell$ is a varying prime number. If we consider 
$Z(\ell )$ with 
$\ell \equiv 3 \bmod 4$ instead, we prove the following theorem.
Theorem 5 Suppose we have the same assumptions as in Theorem 1(1). Then there are infinitely many ordinary 
$\bar {\mathbb {F}}_p$-points on 
$C$ such that, for each of these points, the corresponding abelian surface admits real multiplication by the ring of integers of some real quadratic field (note that the quadratic fields may vary for these points).
It would be interesting to find 
$\bar {\mathbb {F}}_p$-points of complex multiplication by maximal orders, but our current method only asserts real multiplication by maximal orders.
1.2 Previous work and heuristics
Theorem 1 is a generalization of [Reference Chai and OortCO06, Proposition 7.3], where Chai and Oort proved Theorem 1(2) with 
$\mathcal {A}_1 \times \mathcal {A}_1$ taking the place of a Hilbert modular surface. Their proof crucially uses the product structure of the Shimura variety, as well as the product structure of the Frobenius morphism. Following the discussion in § 7 of [Reference Chai and OortCO06], Theorem 1 is related to a bi-algebraicity conjecture. See § 1.4 for more details.
We offer the following heuristic for Theorem 1(1). Using Honda and Tate's classification of 
$\mathbb {F}_q^n$-isogeny classes of abelian varieties in terms of Weil-
$q^n$ numbers, the number of 
$\mathbb {F}_{q^n}$-isogeny classes of abelian varieties is seen to equal 
$q^{n(3/2 + o(1))}$. Similarly, the number of split 
$\mathbb {F}_{q^n}$-isogeny classes in 
$\mathcal {A}_2$ is seen to equal 
$q^{n(1 + o(1))}$. If we treat the map from 
$C(\mathbb {F}_{q^n})$ to the set of 
$\mathbb {F}_{q^n}$-isogeny classes as a random map, we expect that the number of 
$\mathbb {F}_{q^n}$ points of 
$C$ which are not simple is around 
$q^{n/2(1 + o(1))}$. Letting 
$n$ approach infinity, this heuristic suggests that infinitely many points of 
$C(\bar {\mathbb {F}}_q)$ that are split. There are analogous questions in other settings. For the case of equicharacteristic 
$0$, these results are well known (for instance, the density of Noether–Lefschetz loci is discussed in [Reference VoisinVoi02, Proposition 17.20]). In mixed characteristic, the analogue of Theorem 1(2) is treated in [Reference CharlesCha18, Reference Shankar and TangST20]. The major difference between Theorem 1 and these other cases is that the ordinary generic point assumption is crucial because the result is simply false otherwise (as remarked in § 1.1).
Indeed, this difference hints at the key difficulty in our setting, which is that the local intersection number at a supersingular point is of the same magnitude as the total intersection number, which makes the approach more complicated than that of [Reference Shankar and TangST20]; we discuss this in more detail in § 1.3.
1.3 Proof of the main results
We view both Hilbert modular surfaces and the Siegel three-fold as GSpin Shimura varieties attached to a quadratic space 
$(V,Q)$. In each setting, we have a notion of special endomorphisms and special divisors and, for simplicity, we use the same notation 
$Z(m)$.
The main idea of the proof is to compare the global and local intersection numbers ofFootnote 2 
$C. Z(m)$ for appropriate sequences of 
$m$ and show it is not possible for finitely many points to account for the total global intersection as 
$m$ increases.
More precisely:
(1) the global intersection number
$I(m) := C . Z(m)$ is controlled by Borcherds theory [Reference BorcherdsBor98] (see also [Reference MaulikMau14] and [Reference Howard and Madapusi PeraHMP20]);(2) we prove that as
$m\rightarrow \infty$, the total local contribution from supersingular points is at most $\frac {11}{12}I(m)$ by studying special endomorphisms;Footnote 3(3) we prove that the local contribution from a non-supersingular point is
$o(I(m))$ as $m\rightarrow \infty$.
This allows us to conclude that, as 
$m\rightarrow \infty$, more and more points of 
$C$ contribute to the intersection 
$C . Z(m)$. To prove Theorem 1(1), the sequence of 
$m$ will consist only of squares, and to prove Theorem 5, the sequence will consist only of primes. Note that in 
$\mathcal {A}_2$, the Heegner divisor 
$Z(m)$ for square 
$m$ parametrizes abelian surfaces which are not geometrically simple, thereby allowing us to deduce Theorem 1(1). Similar arguments allow us to deduce Theorem 1(2), and also Theorem 5.
Compared with the number field situation, the main difficulty of the positive characteristic function field case is that the local contributions at supersingular points are of the same magnitude as the global contribution. More precisely, taking the Hilbert case as an example, Borcherds theory implies that the generating series of 
$Z(m)$ is a non-cuspidal modular form of weight 
$2$; on the other hand, the theta series attached to the special endomorphism lattice at a supersingular point is also a non-cuspidal weight 
$2$ modular form because the lattice is of rank 
$4$. Therefore, even without considering higher intersection multiplicities, the local intersection number of 
$C.Z(m)$ at a supersingular point is also of the same magnitude as the growth rate of Fourier coefficients of an Eisenstein series of weight 
$2$.
Bounding the local contribution from a supersingular point
Let 
$A \rightarrow C$ denote the family of principally polarized abelian surfaces induced from a morphism 
$C\rightarrow \mathcal {A}_{2,\bar {\mathbb {F}}_p}$, and let 
$\operatorname {Spf} \bar {\mathbb {F}}_p[[t]] \rightarrow C$ denote the formal neighborhood of a supersingular point. For a special endomorphism 
$s$ such that 
$s\circ s=m$, we say that 
$s$ is of norm 
$m$.
The local contribution to 
$C . Z(m)$ from this supersingular point equals 
$\sum _{n=0}^{\infty } r_n(m)$, where 
$r_n(m)$ is the number of special endomorphisms of 
$A \mod t^{n+1}$ with norm 
$m$. Therefore, in order to bound the local contribution, it suffices to prove that, as 
$n\rightarrow \infty$, there are many special endomorphisms of 
$A \mod t^n$ which decay rapidly enough (see Definition 5.1.1 and Theorem 5.1.2 for precise statements).
A similar decay result appears in the mixed characteristic setting (see [Reference Shankar and TangST20]), by a straightforward application of Grothendieck–Messing theory. In the equicharacteristic case, however, proving our decay results is much more involved. In particular, we need to use Kisin's description [Reference KisinKis10, § 1.4, 1.5] of the 
$F$-crystal associated to a certain automorphic vector bundle 
$\mathbb {L}_\mathrm {cris}$, whose 
$F$-invariant part is the lattice of special endomorphisms, in order to prove the required decay. See § 3.1.5 and the proof of Theorem 5.1.2 for more details.
We focus on the Siegel case from now on. Let 
$L_0$ denote the lattice of special endomorphisms of 
$A \mod t$, and let 
$L_n \subset L_0$ be the lattice of special endomorphisms of 
$A \mod t^{n+1}$. These lattices are of rank 
$5$ and are equipped with natural quadratic forms such that 
$A \mod t^{n+1}$ admits a special endomorphism of norm 
$m$ if and only if 
$m$ is represented by 
$L_n$. Broadly speaking, we can bound the local contribution by using geometry-of-numbers techniques. To obtain the desired estimate, we choose the sequence 
$m$ as follows. We first prove the existence of a rank 
$2$ sublattice 
$P_n \subset L_n$ that has the following property: for all 
$m$ bounded by an appropriate function of 
$n$, the abelian surface 
$A \mod t^{n+1}$ has a special endomorphism of norm 
$m$ only if the quadratic form restricted to 
$P_n$ represents 
$m$. This fact follows from the existence of a rank 
$3$ submodule of special endomorphisms which decay rapidly (Theorem 5.1.2). Furthermore, the discriminant of 
$P_n$ goes to infinity as 
$n\rightarrow \infty$. Therefore, the density of numbers (or primes, or prime-squares) represented by the binary quadratic form 
$P_n$ approaches zero, as 
$n\rightarrow \infty$. We now pick a sequence of prime-squares 
$m$ none of which are represented by 
$P_n$ defined by the finitely many supersingular points on 
$C$.
The non-ordinary locus is singular at superspecial points. This allows us to prove the existence of a special endomorphism that decays ‘more rapidly than expected’ (see Definition 5.1.1(3)). Consequently, by the explicit formula of Eisenstein series in these cases by [Reference Bruinier and KussBK01], we prove that the sum of local contributions at supersingular points is at most 
$11/12$ of the global contribution.
We remark that our proof is more involved than the proof of [Reference Chai and OortCO06, Proposition 7.3] because the intersection theory on Hilbert modular surfaces and Siegel three-folds is more complicated than that on the product of 
$j$-lines.
1.4 Additional remarks
The key difference between the number field and function field situation is the following. Let 
$A$ be an abelian surface over 
$\mathcal {O}_K$, where 
$K$ is a local field. The 
$\mathbb {Z}_p$-module of special endomorphisms of 
$A[p^{\infty }]$ has rank at most 3. This rank equals 3 if and only if 
$A$ can be realized as the limit point (in the analytic topology) of a sequence of CM points. This can happen in the mixed characteristic case, but not in the equicharacteristic 
$p$ case unless 
$A$ is defined over a finite field.Footnote 4 Thus, we have a rank 
$3$ decay in the Decay Lemma (Theorem 5.1.2).
In the setting of higher-dimensional GSpin Shimura varieties, for the same reason, we expect that generalizations of the Decay Lemma will only yield a rank-
$3$ 
$\mathbb {Z}_p$-module that decays rapidly. This has the consequence of the existence of formal curves, such that the module of special endomorphisms of the 
$p$-divisible group over these formal curves have large rank. An interesting bi-algebraicity question is whether such formal curves can be algebraic without being special. In the ordinary case, Chai has the following conjecture.
Conjecture 6 [Reference ChaiChai03, Conjecture 7.2, Remark 7.2.1, Proposition 5.3, and Remark 5.3.1]
Let 
$X$ be a subvariety in a mod 
$p$ Shimura variety passing through an ordinary point 
$P$. Assume that the formal germ of 
$X$ at 
$P$ is a formal torus in the Serre–Tate coordinates. Then 
$X$ is a Shimura subvariety.
1.5 Organization of the paper
In § 2, we recall the notion of special endomorphisms, special divisors and crystalline realization 
$\mathbb {L}_\mathrm {cris}$ of the automorphic vector bundle of special endomorphisms. In § 3, we recall the lattices of special endomorphisms of a supersingular point and compute 
$\mathbb {L}_{\mathrm {cris}}$ on its deformation space. In § 4, we recall Borcherds theory and the explicit formula for the Fourier coefficients of vector-valued Eisenstein series due to Bruinier and Kuss; we use them to compare the global intersection number and the 
$\bmod \, t$ local intersection number at a supersingular point. Sections 5 and 6 are the key technical part of the paper. We prove the decay theorems for special endomorphisms, which we use to bound the higher local intersection multiplicities at supersingular points. Section 7 provides the outline of the main proofs and by geometry-of-numbers arguments, we prove Theorem 1(2) in § 8 and prove Theorems 1(1) and 5 in § 9.
To get the main idea of the proof, the reader may focus on Theorem 1(2) and start from §§ 7 and 8 and refer back to §§ 3–5 when necessary.
1.6 Notation
We write 
$f\asymp g$ if 
$f=O(g)$, 
$g=O(f)$. Throughout the paper, 
$p$ is an odd prime.
2. Special endomorphisms
In this section, we first introduce quadratic lattices 
$(L,Q)$ such that the associated GSpin Shimura varieties will be 
$\mathcal {A}_2$ and certain Hilbert modular surfaces related to the Heegner divisors 
$Z(m)$. The definition of special endomorphisms and Heegner divisors are given in § 2.2.
2.1 The global lattice $L$
For a quadratic 
$\mathbb {Z}$-lattice 
$(L,Q)$, let 
$C(L)$ (respectively, 
$C^+(L)$) denote the (respectively, even) Clifford algebra of 
$L$. Let 
$(-)'$ denote the standard involution on 
$C(L)$ fixing all elements in 
$L$ given by 
$(v_1\cdots v_n)'=v_n\cdots v_1$ for 
$v_i\in L$. Let 
$V$ denote 
$L\otimes \mathbb {Q}$ endowed with the quadratic form 
$Q$. There is a bilinear form 
$[-,-]$ on 
$V$ given by 
$[x,y]:=Q(x+y)-Q(x)-Q(y)$.
Let 
$L_{\rm S}$ be the rank-
$5$ 
$\mathbb {Z}$-lattice endowed with the quadratic form 
$Q(x)=x_0^2+x_1x_2-x_3x_4$ for 
$x=(x_0, \ldots, x_4)\in \mathbb {Z}^5$. This quadratic form has signature 
$(3,2)$ and 
$L_{\rm S}$ is an even lattice, maximal among 
$\mathbb {Z}$-valued sublattices in 
$L_{\rm S}\otimes \mathbb {Q}$. For 
$p>2$, 
$L_{\rm S}$ is self-dual at 
$p$. A direct computation shows that 
$C^+(L_{\rm S})\cong M_4(\mathbb {Z})$. Let
\begin{gather*} v_0=(1,0,0,0,0),\quad v_1=(0,1,1,0,0),\quad v_2=(0,1,-1,0,0),\\ \quad v_3=(0,0,0,1,1),\quad v_4=(0,0,0,1,-1). \end{gather*}
Then 
$\delta :=v_0\cdots v_4 \in C(L_{\rm S})$ lies in the center of 
$C(L_{\rm S})$ and 
$\delta '=\delta, \delta ^2=1$. Therefore, there is an isomorphism between quadratic spaces given by 
$L_{\rm S}\xrightarrow []{\simeq } \delta L_{\rm S} \subset C^+(L_{\rm S})$. (See, for instance, [Reference Kudla and RapoportKR00, App. A].)
Given a vector 
$x\in L_{\rm S}$ such that 
$Q(x)=m, m\in \mathbb {Z}_{>0}$, the orthogonal complement 
$x^\perp \subset L_{\rm S}$ endowed with the restriction of 
$Q$ on 
$x^\perp$ is a quadratic 
$\mathbb {Z}$-lattice of signature 
$(2,2)$ and let 
$L_{\rm H}\subset x^\perp \otimes \mathbb {Q}$ be a maximal lattice containing 
$x^\perp$. If 
$m$ is not a perfect square, let 
$F$ denote the real quadratic field 
$\mathbb {Q}(\sqrt {m})$. A direct computation shows that there is an isomorphism 
$L_{\rm H}\otimes \mathbb {Q}\cong \mathbb {Q}^2\oplus F$ such that 
$Q((a,b,\gamma ))=ab+\operatorname {Nm}_{F/\mathbb {Q}}\gamma$ (see, for instance, [Reference Howard and YangHY12, Proposition 2.2.2 (3)] and its proof).Footnote 5 The assumption 
$p\nmid m$ and 
$p>2$ implies that 
$x^\perp$ and, hence, 
$L_{\rm H}$ are self-dual at 
$p$.
Now let 
$(L,Q)$ have signature 
$(n,2)$, and let 
$p$ be a prime such 
$(L,Q)$ is self-dual at 
$p$. As in [Reference Andreatta, Goren, Howard and Madapusi PeraAGHMP18, §§ 4.1 and 4.2] and [Reference Kudla and RapoportKR00, § 1], there is a GSpin Shimura variety 
$M$ attached to 
$(L,Q)$ and this Shimura variety also admits a smooth integral model 
$\mathcal {M}$ over 
$\mathbb {Z}_{(p)}$ because 
$L$ is self-dual at 
$p$; the Shimura variety (and its integral model) recovers the moduli space of principally polarized abelian surfaces when 
$L=L_{\rm S}$ (see Remark 2.2.2 for details) and it is a Hilbert modular surface when 
$L=L_{\rm H}$ (see, for instance, [Reference Howard and YangHY12, §§ 2.2 and 3.1]). We may write 
$M_L$ and 
$\mathcal {M}_L$ to emphasis on the dependence on 
$L$.
To prove Theorems 1(1) and 5 we take 
$L=L_{\rm S}$ and to prove Theorem 1(2) we take 
$L=L_{\rm H}$.
2.2 Special endomorphisms and special divisors
We first introduce the notion of special endomorphisms when 
$L=L_{\rm S}$ and 
$\mathcal {M}$ is the moduli space of principally polarized abelian surfaces. Given an 
$\mathcal {M}$-scheme 
$S$, let 
$A_S$ denote the pull-back of the universal principally polarized abelian surface on 
$\mathcal {M}$ via 
$S\rightarrow \mathcal {M}$; let 
${\dagger}$ denote the Rosati involution on 
$A_S$.
Definition 2.2.1 A special endomorphism of 
$A_S$ is an element 
$s\in \operatorname {End}(A_S)$ such that 
$s^{\dagger} =s$ and 
$\operatorname {Tr} s=0$, where 
$\operatorname {Tr}$ is the reduced trace on the semisimple algebra 
$\operatorname {End}(A_S)\otimes \mathbb {Q}$.
Remark 2.2.2 Our definition of special endomorphisms is essentially the same as the one given by Kudla and Rapoport [Reference Kudla and RapoportKR00, Definition 2.1 and (2.21)]. Indeed, as in [Reference Kudla and RapoportKR00, §§ 1 and 2], the moduli problem indicates that every 
$\mathcal {M}$-scheme 
$S$ gives rise to a principally polarized abelian scheme 
$B_S$ over 
$S$ with 
$\iota : C^+(L)\hookrightarrow \operatorname {End}(B_S)$ and a polarization such that the induced Rosati involution 
${\dagger}$ satisfies 
$\iota (c)^{\dagger} =\iota (c^T)$, where 
$(-)^T$ is the transpose on 
$C^+(L)\simeq M_4(\mathbb {Z})$ (see condition (iii) and the first paragraph of [Reference Kudla and RapoportKR00, p. 701]); moreover, for each 
$\ell \neq p$, there is an isomorphism 
$C^+(L)\otimes \mathbb {Z}_\ell \simeq T_\ell (B_S)$, where 
$T_\ell$ denotes the 
$\ell$-adic Tate module, compatible with the 
$C^+(L)$-action (it acts on itself via left multiplication; see [Reference Kudla and RapoportKR00, p. 703]).Footnote 6 Therefore, via 
$\iota$, we have 
$B_S\cong A_S^4$, where 
$A_S$ is an abelian surface and by the compatibility of the polarization with 
$\iota$ (see also [Reference Kudla and RapoportKR00, Equations (1.9) and (1.10)]), and the polarization on 
$B_S$ is induced by the self-product of a principal polarization on 
$A_S$. Hence, 
$\mathcal {M}$ parameterizes principally polarized abelian surfaces. Moreover, an element 
$s_B$ in 
$\operatorname {End}(B_S)\cong M_4(\operatorname {End}(A_S))$ commuting with 
$\iota (C^+(L))$ is of form 
$\operatorname {diag}(s,s,s,s)$, where an endomorphism 
$s$ of 
$A_S$. In the sense of Kudla and Rapoport, such 
$s_B$ is special if and only if it is traceless and fixed by the Rosati involution on 
$B_S$; this is equivalent to that 
$s$ is traceless and fixed by the Rosati involution on 
$A_S$. Therefore, our definition is the same as that of Kudla and Rapoport.
Definition 2.2.3 Let 
$\mathbb {D}$ denote the Dieudonné crystal over 
$\mathcal {M}_{\mathbb {F}_p}$ (i.e. the first relative crystalline homology of the universal family of principally polarized abelian surface over 
$\mathcal {M}_{\mathbb {F}_p}$). Let 
$\mathbb {L}_\mathrm {cris}\subset \operatorname {End}(\mathbb {D})$ denote the sub-crystal of trace 
$0$ elements fixed by the Rosati involution.Footnote 7
By definition, when 
$S$ is a 
$\mathcal {M}_{\mathbb {F}_p}$-scheme, an element 
$s\in \operatorname {End}(A_S)$ is a special endomorphism if and only if the crystalline realization of 
$s\in \operatorname {End}(\mathbb {D}_S)$ lies in 
$\mathbb {L}_{\mathrm {cris},S}$.
Definition 2.2.4 For the 
$p$-divisible group 
$A_S[p^\infty ]$, we say 
$s\in \operatorname {End}(A_S[p^\infty ])$ is a special endomorphism if the image of 
$s$ in 
$\operatorname {End}(\mathbb {D}_S)$ lies in 
$\mathbb {L}_{\mathrm {cris},S}$.
Remark 2.2.5 In [Reference Madapusi PeraMP16, § 4.14], there is a definition of 
$\mathbb {L}_\mathrm {cris}$ as a direct summand of the endomorphism of the first relative crystalline cohomology of the Kuga–Satake abelian scheme over 
$\mathcal {M}_{\mathbb {F}_p}$. More precisely, the left multiplication of 
$\operatorname {GSpin}(V,Q)\subset C^+(V)^\times$ acting on 
$C(V)$ induces a variation of Hodge structures on 
$C(V)$ over 
$M$; this gives rise to the Kuga–Satake abelian scheme 
$A^{\mathrm {KS}}$ over 
$M$ and the Kuga–Satake abelian scheme extends over 
$\mathcal {M}$. The 
$8$-dimensional abelian scheme considered by Kudla and Rapoport is a sub abelian scheme of 
$A^{\mathrm {KS}}$ via the natural embedding 
$C^+(V)\subset C(V)$. (Note that in [Reference Kudla and RapoportKR00], 
$\gamma \in \operatorname {GSpin}(V,Q)$ acts on 
$C^+(V)$ by the right multiplication by 
$\gamma$ and 
$C^+(V)$ acts on 
$C^+(V)$ by left multiplication, which is opposite to the convention in [Reference Madapusi PeraMP16]. This difference is due to the different choices of the symplectic pairing on 
$C^+(V)$ and 
$C(V)$ in [Reference Kudla and RapoportKR00, (1.9)] and [Reference Madapusi PeraMP16, § 1.6]. If we use the symplectic pairing in [Reference Madapusi PeraMP16] for the discussion in [Reference Kudla and RapoportKR00], then we obtain similar results as in [Reference Kudla and RapoportKR00] but with the convention consistent with that in [Reference Madapusi PeraMP16].)
Let 
$\mathbb {D}^{\mathrm {KS}}$ denote the Dieudonné crystal of 
$A^{\mathrm {KS}}$ over 
$\mathcal {M}_{\mathbb {F}_p}$; Madapusi Pera defined 
$\mathbb {L}_\mathrm {cris} \subset \operatorname {End} (\mathbb {D}^{\mathrm {KS}})$ by the crystalline realization of the absolute Hodge cycle induced by the 
$\operatorname {GSpin}(V,Q)$-invariant idempotent which realizes 
$V\subset \operatorname {End}(C(V))$ as a direct summand. As the element 
$\delta$ given in § 2.1 lies in the center of 
$C(L)$, then it induces an isomorphism 
$\operatorname {End}(C(L))\supset L \cong \delta L \subset \operatorname {End}(C^+(L))$ compatible with 
$\operatorname {GSpin}(V,Q)$-action. Therefore, 
$\delta$ induces an isomorphism between the crystals 
$\mathbb {L}_\mathrm {cris}$ in our sense and that in the sense of Madapusi Pera; in particular, the notions of special endomorphisms coincide under the identification via 
$\delta$. In addition, for a special endomorphism 
$s$ in both cases, 
$s\circ s$ is a scalar multiple 
$Q(s)$ on the suitable abelian scheme; because 
$\delta ^2=1$, hence 
$Q(s)$ remains the same for images of 
$s$ under various identification of special endomorphisms. By [Reference Madapusi PeraMP16, Lemma 5.2], 
$Q(s)>0$ for all non-zero special endomorphism 
$s$.
Definition 2.2.6 For 
$m\in \mathbb {Z}_{>0}$, the special divisor 
$\mathcal {Z}(m)$ is the Deligne–Mumford stack over 
$\mathcal {M}$ with functor of points 
$\mathcal {Z}(m)(S) = \{s\in \operatorname {End}(A_S) \text { special } |\ Q(s) = m\}$ for any 
$\mathcal {M}$-scheme 
$S$. We use the same notation for the image of 
$\mathcal {Z}(m)$ in 
$\mathcal {M}$. By, for instance, [Reference Andreatta, Goren, Howard and Madapusi PeraAGHMP18, Proposition 4.5.8], 
$\mathcal {Z}(m)$ is flat over 
$\mathbb {Z}_{(p)}$ and hence 
$\mathcal {Z}(m)_{\mathbb {F}_p}$ is still a divisor of 
$\mathcal {M}_{\mathbb {F}_p}$; we denote 
$\mathcal {Z}(m)_{\mathbb {F}_p}$ by 
$Z(m)$.
Lemma 2.2.7 Every 
$\bar {\mathbb {F}}_p$-point of 
$Z(m^2)$ corresponds to a geometrically non-simple abelian surface.
Proof. Let 
$s$ be a special endomorphism of an abelian surface 
$A$ such that 
$s\circ s=[m^2]$. Then 
$(s-[m])\circ (s+[m])=0$. As 
$\operatorname {Tr} s=0$, then 
$s\pm [m]\neq 0$ and, hence, 
$s\pm [m]$ are not invertible. Then 
$\ker (s-[m])$ defines a non-trivial sub abelian scheme of 
$A$.
We now discuss the case when 
$L=L_{\rm H}$. We keep the same notation as in § 2.1. For simplicity, we first discuss the case when 
$L_{\rm H}=x^\perp$, where 
$x\in L_{\rm S}$ and 
$Q(x)=m$ with 
$p\nmid m$; for the general case, the following discussion still holds true when replacing endomorphisms with suitable elements in 
$\operatorname {End} \otimes \mathbb {Q}$ (see the end of this subsection). When 
$L_{\rm H}=x^\perp \subset L_{\rm S}$, the Shimura variety (and its integral model) 
$\mathcal {M}_{L_{\rm H}}$ defined by 
$L_{\rm H}$ is naturally a sub-Shimura variety of 
$\mathcal {M}_{L_{\rm S}}$, the moduli space of principally polarized abelian surfaces and, hence, a point on 
$\mathcal {M}_{L_{\rm H}}$ corresponds to a polarized abelian surface with real multiplication by 
$\mathcal {O}:=\mathbb {Z}[x]/(x^2-m)$. Let 
$\sigma$ denote the ring automorphism on 
$\mathcal {O}$ satisfying 
$x^{\sigma } = -x$. As before, let 
$S$ be a 
$\mathcal {M}_{L_{\rm H}}$-scheme, and let 
$A_S$ denote the abelian surface over 
$S$ with real multiplication by 
$\mathcal {O}$.
Definition 2.2.8 [Reference Howard and YangHY12, § 3.1, p. 26]
A special endomorphism (respectively, special quasi- endomorphism) of 
$A_S$ is an element 
$s\in \operatorname {End}(A_S)$ (respectively, 
$s\in \operatorname {End}(A_S)\otimes \mathbb {Q}$) such that 
$s^{\dagger} =s$ and 
$s\circ f =f^\sigma \circ s$ for all 
$f\in \mathcal {O}$.
We still use 
$\mathbb {D}$ to denote the pull-back to 
$\mathcal {M}_{L_{\rm H}, \mathbb {F}_p}$ the Dieudonné crystal over 
$\mathcal {M}_{L_{\rm S}, \mathbb {F}_p}$ in Definition 2.2.3; since the abelian surfaces over 
$\mathcal {M}_{L_{\rm H}}$ admit an 
$\mathcal {O}$-action, the Dieudonné crystal 
$\mathbb {D}$ is also endowed with an 
$\mathcal {O}$-action.
Definition 2.2.9 Let 
$\mathbb {L}_\mathrm {cris}\subset \operatorname {End}(\mathbb {D})$ denote the sub-crystal of elements 
$v$ fixed by Rosati involution and 
$s\circ f=f^\sigma \circ s$ for all 
$f\in \mathcal {O}$. For the 
$p$-divisible group 
$A_S[p^\infty ]$, we say 
$s\in \operatorname {End}(A_S[p^\infty ])$ is a special endomorphism if the image of 
$s$ in 
$\operatorname {End}(\mathbb {D}_S)$ lies in 
$\mathbb {L}_{\mathrm {cris},S}$.
Remark 2.2.10 By Remark 2.2.5 and [Reference Andreatta, Goren, Howard and Madapusi PeraAGHMP17, Proposition 2.5.1 and Prop. 2.6.4], to show that the above definitions of special endomorphisms and 
$\mathbb {L}_\mathrm {cris}$ can be identified with those by Madapusi Pera, we only need to show that for an endomorphism 
$s$ (of either the abelian surface or of its Dieudonné crystal 
$\mathbb {D}$) fixed by the Rosati involution is traceless and orthogonal to 
$x$ if and only if 
$s\circ x=-x\circ s$. To see this, note that if 
$\operatorname {Tr} s=0$, then 
$s\perp x$ if and only if 
$Q(s+x)-Q(s)-Q(x)=s\circ x+x\circ s=0$; on the other hand, if 
$s\circ x=-x\circ s$, then 
$x^{-1}\circ s \circ x =-s$ and, hence, 
$\operatorname {Tr} s=0$.
2.2.11
In general (i.e. when 
$x^\perp \subsetneq L_{\rm H}$), we may still use the same definition for 
$\mathbb {L}_\mathrm {cris}$ and special endomorphisms of 
$p$-divisible groups, as 
$x^\perp$ is self-dual at 
$p$ and, hence, 
$x^\perp \otimes \mathbb {Z}_p = L_{\rm H} \otimes \mathbb {Z}_p$. On the other hand, we consider special quasi-endomorphisms 
$s\in \operatorname {End}(A_S)\otimes \mathbb {Q}$ which satisfy the following integrality condition: the 
$\ell$-adic realizations of 
$s$ lie in 
$L_{\rm H}\otimes \mathbb {Z}_\ell \subset \operatorname {End}(T_\ell (A_S)\otimes \mathbb {Q}_\ell )$ for all 
$\ell \neq p$ and the crystalline realizations of 
$s$ lie in 
$\mathbb {L}_{\mathrm {cris}, S}$. As in Definition 2.2.6, the special divisor 
$\mathcal {Z}(m)$ is the Deligne–Mumford stack over 
$\mathcal {M}_{L_{\rm H}}$ with 
$\mathcal {Z}(m)(S)$ given by
\begin{align*} &\big\{s\in \operatorname{End}(A_S)\otimes\mathbb{Q} \text{ special quasi-endomorphism satisfying the integrality condition above }\\ &\quad \mid Q(s)=m\big\} \end{align*}
for any 
$\mathcal {M}$-scheme 
$S$. By the proof of [Reference Andreatta, Goren, Howard and Madapusi PeraAGHMP18, Proposition 4.5.8], where they used [Reference Madapusi PeraMP16, Proposition 5.21], 
$\mathcal {Z}(m)$ is flat over 
$\mathbb {Z}_p$. We use 
$Z(m)$ to denote the image of 
$\mathcal {Z}(m)_{\mathbb {F}_p}$ in 
$\mathcal {M}_{L_{\rm H},\mathbb {F}_p}$, which is a divisor in 
$\mathcal {M}_{L_{\rm H},\mathbb {F}_p}$.
2.3 Lattices of special endomorphisms of supersingular points
For a fixed supersingular point, let 
$A$ denote the abelian surface attached to this point.
Definition 2.3.1 Let 
$L''$ denote the 
$\mathbb {Z}$-lattice of special endomorphisms of 
$A$ (respectively, special quasi-endomorphisms when 
$L=L_{\rm H}$). Let 
$L''\subset L'\subset L''\otimes \mathbb {Q}$ be a 
$\mathbb {Z}$-lattice which is maximal at all 
$\ell \neq p$ and 
$L''\otimes \mathbb {Z}_p=L'\otimes \mathbb {Z}_p$. Let 
$Q'$ denote the natural quadratic form on 
$L'$ given by 
$s\circ s=[Q'(s)]\in \operatorname {End}(A)\otimes \mathbb {Q}$. By the positivity of the Rosati involution, 
$Q'$ is positive definite (see, for instance, [Reference Madapusi PeraMP16, Lemma 5.12]).
Even though there seem to be choices involved here, we see that for our computation, these choices do not matter and the result only depends on the Ekedahl–Oort stratum that the supersingular point lies in. The information of 
$L'\otimes \mathbb {Z}_p$ is provided in § 3.
Lemma 2.3.2 We have 
$(L'\otimes \mathbb {Z}_\ell, Q')\cong (L\otimes \mathbb {Z}_\ell, Q)$ for 
$\ell \neq p$.
Proof. Both lattices shall be maximal at 
$\ell$ and by [Reference Howard and PappasHP17, Remark 7.2.5], 
$(L'\otimes \mathbb {Q}_\ell, Q')\cong (L\otimes \mathbb {Q}_\ell, Q)$. Then we conclude by the fact that there is a unique isometry class of 
$\mathbb {Z}_\ell$-maximal sublattices of a given 
$\mathbb {Q}_\ell$-quadratic space (see, for instance, [Reference Howard and PappasHP17, Theorem A.1.2]).
Remark 2.3.3 Actually, for the case of Hilbert modular surfaces, the essential part of the above lemma is [Reference Howard and YangHY12, Proposition 3.1.3]. For the 
$\mathcal {A}_2$ case, we can explicitly compute 
$L''$ as follows and it is maximal. By [Reference EkedahlEke87, Proposition 5.2], for any 
$\ell \neq p$, there is a unique class (up to 
$\operatorname {GL}_4(\mathbb {Z}_\ell )$-conjugation) of principal polarizations on the Tate module 
$T_\ell (A)$. Therefore, to compute 
$L''\otimes \mathbb {Z}_\ell$, we may assume that 
$A=E^2$ and endowed with the product principal polarization, where 
$E$ is a supersingular elliptic curve. Hence, the quadratic form on the lattice 
$L''$, which is the trace 
$0$ part of 
$H^2(A)$, is given by 
$x_0^2+\operatorname {Nm}$, where 
$\operatorname {Nm}$ is the quadratic form given by the reduced norm on the quaternion algebra 
$\operatorname {End}(E)$.
3. The $F$-crystals $\mathbb {L}_{\mathrm {cris}}$ on local deformation spaces of supersingular points
Let 
$p$ be an odd prime. In this section, we compute the lattices (
$L''\otimes \mathbb {Z}_p$ in Definition 2.3.1) of special endomorphisms of supersingular points with the natural quadratic forms following Howard and Pappas [Reference Howard and PappasHP17, §§ 5 and 6].Footnote 8 In conjunction with [Reference KisinKis10, § 1], we then obtain 
$\mathbb {L}_{\mathrm {cris}}$ (see Definitions 2.2.3 and 2.2.9) on the formal neighborhoods of supersingular points in the Shimura variety 
$\mathcal {M}$. As a direct consequence, we obtain the local equation of the non-ordinary locus in § 3.4. These are the key inputs to §§ 5–6; in particular, we use the explicit descriptions of this section to prove our decay results.
3.1 A brief review of the work of Howard and Pappas and Kisin
As both [Reference Howard and PappasHP17] and [Reference KisinKis10] apply to GSpin Shimura varieties of any dimension, we first recall their results in the general setting.
Let 
$(V,Q)$ denote a quadratic 
$\mathbb {Q}$-vector space of signature 
$(n,2)$ and let 
$L\subset V$ be a maximal even lattice which is self-dual at 
$p$. Let 
$\mathcal {M}$ denote the smooth canonical integral model over 
$\mathbb {Z}_p$ of the GSpin Shimura variety attached to 
$(L,Q)$ in [Reference KisinKis10].
Set 
$k=\bar {\mathbb {F}}_p, W=W(k), K=W[1/p]$. In this section, we consider a fixed supersingular point 
$P\in \mathcal {M}(k)$. In the case of abelian surfaces considered in § 2 (with 
$L=L_{\rm S}$ or 
$L_{\rm H}$), 
$P$ supersingular means the corresponding abelian surface over 
$P$ is supersingular. This, in turn, is equivalent to the action of the crystalline Frobenius 
$\varphi$ on 
$\mathbb {L}_{\mathrm {cris},P}(W)$ being pure, with slope 
$0$. In the general setting, let 
$\mathbb {D}$ denote the Dieudonné crystal of the universal Kuga–Satake abelian variety over 
$\mathcal {M}_{\mathbb {F}_p}$ and let 
$\mathbb {L}_{\mathrm {cris}}\subset \operatorname {End}(\mathbb {D})$ denote the sub-crystal corresponding to 
$L\subset C(L)$ defined in [Reference Madapusi PeraMP16, § 4.14].Footnote 9 Let 
$\varphi$ denote the crystalline Frobenius on 
$\mathbb {D}_P(W)$ and 
$\mathbb {L}_{\mathrm {cris},P}(W)$. Then we say 
$P$ is supersingular if 
$\varphi$ acts on 
$\mathbb {L}_{\mathrm {cris},P}(W)$ with pure slope 
$0$ (see, for instance, [Reference Howard and PappasHP17, Lemma 4.2.4, § 7.2.1]).
By Dieudonné theory, we have 
$L''\otimes \mathbb {Z}_p=\mathbb {L}_{\mathrm {cris},P}(W)^{\varphi =1}$. To compute 
$L''\otimes \mathbb {Z}_p$ and the 
$\varphi$-action on 
$\mathbb {L}_{\mathrm {cris},P}(W)$, we introduce another free 
$W$-module 
$\mathbb {L}^\#_P(W)$ following [Reference Howard and PappasHP17, § 6.2.1].Footnote 10
Definition 3.1.1 The filtration on 
$\mathbb {D}_P(W)$ is given by 
$\operatorname {Fil}^1 \mathbb {D}_P(W):=\varphi ^{-1}(p\mathbb {D}_P(W))$. We define 
$\mathbb {L}^\#_P(W):=\{v\in \mathbb {L}_{\mathrm {cris},P}(W)\otimes _W K \mid v\operatorname {Fil}^1 \mathbb {D}_P(W)\subset \operatorname {Fil}^1 \mathbb {D}_P(W)\}$.
3.1.2
By [Reference Howard and PappasHP17, Theorem 7.2.4], studying supersingular points and their formal neighborhood in 
$\mathcal {M}$ reduces to study the points and their formal neighborhood in the associated Rapoport–Zink spaces and hence we use results in [Reference Howard and PappasHP17, §§ 5 and 6].
By [Reference Howard and PappasHP17, Proposition 5.2.2], 
$\varphi (\mathbb {L}^\#_P(W))=\mathbb {L}_{\mathrm {cris},P}(W)$. In particular,
\[ L''\otimes \mathbb{Z}_p=\mathbb{L}_{\mathrm{cris},P}(W)^{\varphi=1}=\mathbb{L}^\#_P(W)^{\varphi=1}. \]
Recall that in Definition 2.3.1, we endow 
$V':=L''\otimes \mathbb {Q}_p$ with a quadratic form 
$Q'$; let 
$[-,-]'$ denote the bilinear form on 
$V'$ given by 
$[x,y]'=Q'(x+y)-Q'(x)-Q'(y)$. Hence
\[ V'=(\mathbb{L}_{\mathrm{cris},P}(W)\otimes_W K)^{\varphi=1}. \]
Since 
$P$ is supersingular, we have 
$n=\operatorname {rk}_W \mathbb {L}_{\mathrm {cris},P}(W)=\operatorname {rk}_{\mathbb {Z}_p} L''=\dim _{\mathbb {Q}_p}V'$.
Let 
$\Lambda _P\subset V'$ denote the dual of 
$L''\otimes \mathbb {Z}_p$ with respect to 
$[-,-]'$. Then by [Reference Howard and PappasHP17, Propositions 5.2.2 and 6.2.2], 
$\Lambda _P$ is a vertex lattice, i.e. 
$\Lambda _P$ is a 
$\mathbb {Z}_p$-lattice in 
$V'$ such that 
$p\Lambda _P\subset \Lambda _P^\vee \subset \Lambda _P$. The type 
$t_P$ of 
$\Lambda _P$ is defined to be 
$\dim _{\mathbb {F}_p}(\Lambda _P/\Lambda _P^\vee )$. By [Reference Howard and PappasHP17, Proposition 5.1.2, (1.2.3.1)], there is 
$t_{\rm max}\in 2 \mathbb {Z}$ which only depends on 
$n$ and 
$\det (V')=\det (V_{\mathbb {Q}_p})$Footnote 11 such that 
$t_P\in 2\mathbb {Z}$ and 
$2\leq t_P \leq t_{\rm max}$. Moreover, there exists a vertex lattice 
$\Lambda \subset V'$ of type 
$t_{\rm max}$ such that 
$\Lambda _P\subset \Lambda$. Indeed, the proof of [Reference Howard and PappasHP17, Proposition 5.1.2] constructs all possible isometry classes of 
$\Lambda$ (with the quadratic form) for all 
$(V,Q)$ (note that in [Reference Howard and PappasHP17], they proved that for given 
$(V,Q)$, the isometry class of 
$\Lambda$ is unique).
Therefore, given 
$(V,Q)$, we first obtain the isometry class of 
$\Lambda$ of type 
$t_{\rm max}$ and then all isometry classes of the lattices of special endomorphisms 
$L''\otimes \mathbb {Z}_p$ attached to all supersingular points are given by the duals of the vertex lattices contained in 
$\Lambda$.
From 
$\Lambda$, we may compute all possible isomorphism classes of 
$\mathbb {L}_{\mathrm {cris},P}(W)$ and 
$\mathbb {L}_P^\#(W)$ as rank-
$n$ free 
$W$-modules endowed with a quadratic form/bilinear form and a 
$\sigma$-linear Frobenius 
$\varphi$ (here we use 
$\sigma$ to denote the Frobenius action on 
$W$) following [Reference Howard and PappasHP17, Proposition 6.2.2, § 5.3.1]. Indeed, 
$\mathbb {L}^\#_P(W)\subset \Lambda \otimes _{\mathbb {Z}_p}W=:\Lambda _W$ is the preimage of a Lagrangian 
$\overline {L}^\#_P\subset \Lambda _W/\Lambda _W^\vee$ with respect to the quadratic form 
$pQ'\bmod p$ such that
\begin{equation} \dim (\overline{L}^\#_P+\bar{\varphi}(\overline{L}^\#_P))=t_{{\rm max}}/2+1, \end{equation}
where we use 
$\varphi$ to denote the 
$\sigma$-linear map on 
$\Lambda _W$ given by 
$\operatorname {Id} \otimes \sigma$ and 
$\bar {\varphi }(\bar {v}):=\overline{\varphi (v)}$ is well-defined for 
$\bar {v}\in \Lambda _W/\Lambda _W^\vee$ with a lift 
$v\in \Lambda _W$. The quadratic form and 
$\varphi$-action on 
$\mathbb {L}^\#_P(W)$ are the restrictions of the quadratic forms and 
$\varphi$-action on 
$\Lambda _W$. We then obtain 
$\mathbb {L}_{\mathrm {cris},P}(W)=\varphi (\mathbb {L}^\#_P(W))$. Note that by [Reference Howard and PappasHP17, Proposition 5.1.2], the even-dimensional 
$\mathbb {F}_p$-quadratic space 
${(\Lambda /\Lambda ^\vee, pQ'\bmod p)}$ does not have a Lagrangian defined over 
$\mathbb {F}_p$ and, hence, is non-split; see [Reference Howard and PappasHP14, §§ 3.2-3.3] for a discussion on how to find all such 
$\overline {L}^\#_P$.
Definition 3.1.3 For a supersingular point 
$P$, we say 
$P$ is superspecial if 
$t_P=2$;Footnote 12 we say 
$P$ is supergeneric if 
$t_P=t_{\rm max}\neq 2$.
By [Reference Howard and PappasHP17, Proposition 5.2.2], 
$P$ is superspecial if and only if
\begin{equation} \varphi^2(\mathbb{L}_P^\#(W))\subset \mathbb{L}_P^\#(W) + \varphi (\mathbb{L}_P^\#(W)). \end{equation} By [Reference Howard and PappasHP17, (1.2.3.1)], in the setting of § 2, we have 
$t_{\rm max}\leq 4$ and, hence, the supersingular points in question are either superspecial or supergeneric.
Remark 3.1.4 By [Reference Madapusi PeraMP16, Proposition 4.7(iii) and (iv)], 
$\operatorname {GSpin}(L,Q)_W$ acts on 
$\mathbb {D}_P(W)$ and 
$\mathbb {L}_{\mathrm {cris},P}(W)$; moreover, as 
$W$-quadratic spaces, 
$\mathbb {L}_{\mathrm {cris},P}(W)\cong L\otimes W$ (we use 
$Q_W$ to denote the quadratic form on 
$L''\otimes \mathbb {Z}_p$) and for 
$x\in \mathbb {L}_{\mathrm {cris},P}(W), x\circ x = Q_W(x)\cdot \operatorname {Id} \in \operatorname {End}(\mathbb {D}_P(W))$. Therefore, 
$Q'$ on 
$L''\otimes \mathbb {Z}_p$ is the restriction of 
$Q$ on 
$\mathbb {L}_{\mathrm {cris},P}(W)$ to 
$L''\otimes \mathbb {Z}_p$. We introduce the notation 
$Q'$ to emphasize that 
$Q'$ and 
$Q$ (as 
$\mathbb {Z}_p$-quadratic forms) are restrictions of 
$Q_W$ to 
$\mathbb {Z}_p$-lattices in different 
$\mathbb {Q}_p$-subspaces. Hence, 
$\operatorname {GSpin}(L,Q)_W=\operatorname {GSpin} (\mathbb {L}_{\mathrm {cris},P}(W),Q')$.
3.1.5
We now describe the 
$F$-crystal 
$\mathbb {L}_{\mathrm {cris}}$ over the formal completion 
$\widehat {\mathcal {M}}_{P}$ along the supersingular point 
$P$ following [Reference KisinKis10, §§ 1.4 and 1.5] and [Reference MoonenMoo98, § 4.5]; see also [Reference Howard and PappasHP17, §§ 3.1.4 and 3.1.6].
The Hodge filtration 
$\operatorname {Fil}^1 \mathbb {D}_P(W) \bmod p \subset \mathbb {D}_P(k)$ corresponds to a cocharacter 
$\bar {\mu }: \mathbb {G}_{m,k}\rightarrow \operatorname {GSpin} (L,Q)_k$ and we pick a cocharacter 
$\mu : \mathbb {G}_{m,W}\rightarrow \operatorname {GSpin} (L,Q)_W$ which lifts 
$\bar {\mu }$. Let 
$U_P\subset \operatorname {GSpin}(L,Q)_W$ denote the opposite unipotent of the parabolic subgroup defined by 
$\mu$; and let 
$\widehat {U_P}$ denote the formal completion of 
$U_P$ along the identity. Pick coordinates and write 
$\widehat {U_P}=\operatorname {Spf} W[[x_1,\ldots, x_d]]$ such that 
$x_1=\cdots =x_d=0$ defines the identity element in 
$U_P$. Let 
$\sigma$ denote the Frobenius action on 
$W[[x_1,\ldots, x_d]]$ which lifts the 
$\sigma$-action on 
$W$ and for which 
$\sigma (x_i)=x_i^p$.
Let 
$R$ denote 
$\widehat {\mathcal {O}}_{\mathcal {M},P}$, the complete local ring of 
$\mathcal {M}$ at 
$P$. Then there exists an isomorphism from 
$\operatorname {Spf} R$ to 
$\widehat {U_P}$ (and we still use 
$\sigma$ to denote the Frobenius action on 
$R$ via the identification to 
$W[[x_1,\ldots, x_d]]$) such that:
(1)
$\mathbb {D}(R)=\mathbb {D}_P(W)\otimes _W R$ and $\mathbb {L}_{\mathrm {cris}}(R)=\mathbb {L}_{\mathrm {cris},P}(W)\otimes _W R$ as $R$-modules; and(2) under the above identifications, the
$\sigma$-linear Frobenius action, denoted by $\operatorname {Frob}$, on $\mathbb {D}(R)$ and $\mathbb {L}_{\mathrm {cris}}(R)$ is given by $u\cdot (\varphi \otimes \sigma )$, where $u$ denotes the universal $W[[x_1,\ldots, x_d]]$-point in $\widehat {U_P}$ and $\varphi$ is the crystalline Frobenius on $\mathbb {D}_P(W)$ or $\mathbb {L}_{\mathrm {cris},P}(W)$ given in § 3.1.2.
On 
$\mathbb {L}_{\mathrm {cris}}$, the 
$\operatorname {GSpin}(L,Q)_W$ action factors through the quotient 
$\operatorname {SO}(L,Q)_W$. Thus, from now on, because we only care about 
$\operatorname {Frob}$ on 
$\mathbb {L}_{\mathrm {cris}}$, then by Remark 3.1.4, we work with 
$\mu : \mathbb {G}_{m,W}\rightarrow \operatorname {SO}(\mathbb {L}_{\mathrm {cris},P}(W), Q')$ and 
$U_P$ the opposite unipotent of 
$\mu$ in 
$\operatorname {SO}(\mathbb {L}_{\mathrm {cris},P}(W), Q')$.
In the rest of this section, we apply §§ 3.1.2 and 3.1.5 to the setting in § 2 and we work with the coordinates on 
$\widehat {U_P}$. When 
$L=L_{\rm H}$, we write 
$\widehat {U_P}=\operatorname {Spf} W[[x,y]]$ and when 
$L=L_{\rm S}$, we write 
$\widehat {U_P}=\operatorname {Spf} W[[x,y,z]]$. We use 
$\epsilon \in \mathbb {Z}_p^\times$ to denote an element which is not a perfect square in 
$\mathbb {Z}_p$. Let 
$\mathbb {Z}_{p^2}$ (respectively, 
$\mathbb {Q}_{p^2}$) denote 
$W(\mathbb {F}_{p^2})$ (respectively, 
$W(\mathbb {F}_{p^2})[1/p]$) and let 
$\lambda \in \mathbb {Z}_{p^2}^\times$ be an element such that 
$\sigma (\lambda )=-\lambda$ (for instance, we can take 
$\lambda$ to be a root in 
$\mathbb {Z}_{p^2}$ of 
$x^2-\epsilon =0$). We use 
$\{v_i\}_{i=1}^{n+2}$ to denote a 
$W$-basis of 
$\mathbb {L}_{\mathrm {cris},P}(W)$ and 
$\{w_i\}_{i=1}^{n+2}$ to denote a 
$\mathbb {Z}_p$-basis of 
$\Lambda _P^\vee =\mathbb {L}_{\mathrm {cris},P}(W)^{\varphi =1}$; note that 
$\operatorname {Span}_W\{w_i\}$ is a 
$W$-sublattice of 
$\mathbb {L}_{\mathrm {cris},P}(W)$.
3.2 The Hilbert case $L=L_{\rm H}$
Recall that as in Theorem 1(2), we have 
$p\nmid m\in \mathbb {Z}_{>0}$.
3.2.1
Assume that 
$p$ is inert in 
$\mathbb {Q}(\sqrt {m})$;Footnote 13 then we have 
$t_{\rm max}=4$.
The vertex lattice with type 
$t_{\rm max}$ is 
$\Lambda =\operatorname {Span}_{\mathbb {Z}_p}\{e_1,f_1\}\oplus Z$, where
\[ [Z, e_1]'=[Z,f_1]'=[e_1,e_1]'=[f_1,f_1]'=0,\enspace [e_1,f_1]'=1/p,\enspace Z\cong \mathbb{Z}_{p^2},\enspace Q'(x)=x\sigma(x)/p,\ \forall x\in Z. \]
Hence, 
$\Lambda ^\vee =p\Lambda$. Set 
$e_2=(1\otimes 1+ (1/\lambda ) \otimes \lambda )/2, f_2=(1\otimes 1+ (-1/\lambda ) \otimes \lambda )/2 \in \mathbb {Z}_{p^2}\otimes _{\mathbb {Z}_p} Z$. Then, as elements in 
$\Lambda _W$,
\[ \varphi(e_1)=e_1,\quad \varphi(f_1)=f_1,\quad \varphi(e_2)=f_2,\quad \varphi(f_2)=e_2,\quad [e_2,e_2]'=[f_2,f_2]'=0,\quad [e_2,f_2]'=1/p. \] All possible 
$\overline {L}^\#_P$ are given by two families of Lagrangians in 
$k$-quadratic space spanned by 
$\bar {e}_1,\bar {e}_2,\bar {f}_1,\bar {f}_2\in \Lambda _W/\Lambda _W^\vee$ with quadratic form 
$pQ$ satisfying (3.1.1):
\[ \overline{L}^\#_P=\operatorname{Span}_k\{\bar{e}_1+\sigma^{-1}(\bar{c})\bar{f}_2,\bar{e}_2-\sigma^{-1}(\bar{c})\bar{f}_1\}, \text{ or } \overline{L}^\#_P=\operatorname{Span}_k\{\bar{e}_1+\sigma^{-1}(\bar{c})\bar{e}_2, \sigma^{-1}(\bar{c})\bar{f}_1-\bar{f}_2\}, \]
where 
$\bar {c}\in k$.Footnote 14 Therefore, we have that
\begin{align*} \mathbb{L}_{\mathrm{cris},P}(W)&=\operatorname{Span}_W\{e_1+ce_2, cf_1-f_2, pe_2, pf_1\},\end{align*}or
\begin{align*}\mathbb{L}_{\mathrm{cris},P}(W)&=\operatorname{Span}_W\{e_1+cf_2,e_2-cf_1, pf_1, pf_2\}, \end{align*}
where 
$c\in W$.Footnote 15 Moreover, by (3.1.2), 
$P$ is superspecial if and only if 
$\sigma ^{-1}(c)-\sigma (c)\in pW$, which is equivalent to the Teichmüller lift of 
$\bar {c}$ lying in 
$\mathbb {Z}_{p^2}$. Note that if 
$c-c'\in pW$, then 
$c,c'$ define the same 
$\mathbb {L}_{\mathrm {cris},P}(W)$. Therefore, without loss of generality, from now on, we only work with 
$c\in W$ which is the Teichmüller lifting of 
$\bar {c}\in k$. Hence, 
$P$ is superspecial if and only if there exists 
$c\in \mathbb {Z}_{p^2}$ such that 
$\mathbb {L}_{\mathrm {cris},P}(W)$ is given by the above form.
To compute the 
$F$-crystal 
$\mathbb {L}_{\mathrm {cris}}$, we pick the following 
$W$-basis 
$\{v_1,\ldots, v_4\}$ of 
$\mathbb {L}_{\mathrm {cris},P}(W)$ such that the Gram matrix of 
$[-,-]'$ with respect to this basis is 
$\big [\begin {smallmatrix}0 & I\\ I & 0\end {smallmatrix}\big ]$, where 
$I$ denotes the 
$2\times 2$ identity matrix. For the first family, take
\[ v_1=f_2-cf_1,\quad v_2=e_1+ce_2-\sigma^{-1}(c)cf_1+\sigma^{-1}(c)f_2,\quad v_3=pe_2-p\sigma^{-1}(c)f_1,\quad v_4=pf_1; \]for the second family, take
\[ v_1=e_2-cf_1,\quad v_2=\sigma^{-1}(c)e_2-\sigma^{-1}(c)cf_1+e_1+cf_2,\quad v_3=pf_2-p\sigma^{-1}(c)f_1,\quad v_4=pf_1. \]
Then on 
$\mathbb {L}_{\mathrm {cris},P}(W)$, with respect to 
$\{v_1,\ldots,v_4\}$, we have
\[ \varphi=b\sigma, \text{ with }b= \begin{bmatrix} 0 & \sigma(c)-\sigma^{-1}(c) & p & 0\\ 0 & 1 & 0 & 0\\ 1/p & 0 & 0 & 0\\ (\sigma^{-1}(c)-\sigma(c))/p & 0 & 0 & 1 \end{bmatrix}. \]
The filtration on 
$\mathbb {L}_{\mathrm {cris},P}(k)$ is given by
\[ \operatorname{Fil}^1\mathbb{L}_{\mathrm{cris},P}(k)=\operatorname{Span}_k\{\bar{v}_3\},\quad \operatorname{Fil}^0\mathbb{L}_{\mathrm{cris},P}(k)=\operatorname{Span}_k\{\bar{v}_2,\bar{v}_3, \bar{v}_4\},\quad \operatorname{Fil}^{-1}\mathbb{L}_{\mathrm{cris},P}(k)=\mathbb{L}_{\mathrm{cris},P}(k), \]
so we may choose 
$\mu : \mathbb {G}_{m,W}\rightarrow \operatorname {SO}(\mathbb {L}_{\mathrm {cris},P}(W),Q')$ to be 
$t\mapsto \operatorname {diag}(t^{-1}, 1, t, 1)$. Then 
$\widehat {U_P}=\operatorname {Spf} W[[x,y]]$ with the universal point
\[ u= \begin{bmatrix} 1 & x & -xy & y\\ 0 & 1 & -y & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & -x & 1 \end{bmatrix} \quad \text{and} \quad \operatorname{Frob}=ub\sigma, \quad \text{with }ub= \begin{bmatrix} -xy/p-ay/p & a+x & p & y\\ -y/p & 1 & 0 & 0\\ 1/p & 0 & 0 & 0\\ -x/p-a/p & 0 & 0 & 1 \end{bmatrix}, \]
where 
$a=\sigma (c)-\sigma ^{-1}(c)$; we have 
$a=0$ if 
$P$ is superspecial and 
$a\in W^\times$ if 
$P$ is supergeneric.
When 
$P$ is superspecial, 
$\{w_1=pv_1+v_3,w_2=\lambda (pv_1-v_3),w_3=v_2,w_4=v_4 \}$ is a 
$\mathbb {Z}_p$-basis of 
$L''\otimes \mathbb {Z}_p$. Using 
$\{w_1,\ldots, w_4\}$ as a 
$K$-basis of 
$\mathbb {L}_{\mathrm {cris},P}(W)[1/p]$, we have
\begin{equation} \operatorname{Frob}=\left(I+\begin{bmatrix} -\dfrac{xy}{2p} & \dfrac{\lambda xy}{2p} & \dfrac{x}{2p} & \dfrac{y}{2p}\\ -\dfrac{xy}{2\lambda p} & \dfrac{xy}{2p} & \dfrac{x}{2\lambda p} & \dfrac{y}{2\lambda p} \\ -y & \lambda y & 0 & 0 \\ -x & \lambda x & 0 & 0\end{bmatrix}\right) \circ \sigma. \end{equation} When 
$P$ is supergeneric, 
$\left\{ {w_1=v_4, w_2=pv_1+v_3+(c+\sigma ^{-1}(c))v_4, w_3} \right.$ 
$\left. {=\lambda (pv_1-v_3+(c-\sigma ^{-1}(c))v_4), w_4=pv_2-cv_3-p\sigma ^{-1}(c)v_1-c\sigma ^{-1}(c)v_4} \right\}$ is a 
$\mathbb {Z}_p$-basis of 
${L''\otimes \mathbb {Z}_p}$ and with respect to this basis, 
$\operatorname {Frob}=(I+({y}/{p})A+xB)\circ \sigma$, where
\[ A\!=\!\begin{bmatrix} -c & -c^2 & -\lambda c^2 & 0\\ 1/2 & 0 & \lambda c & c^2/2\\ 1/(2\lambda) & c/\lambda & 0 & -c^2/(2\lambda) \\ 0 & -1 & \lambda & c \end{bmatrix}, \quad B\!=\!\begin{bmatrix} 0 & -1\!+\!cy/p & \lambda cy/p \!+\!\lambda & -c^2y/p\\ 0 & -y/(2p) & \lambda y/(2p) & 1/2\!+\!cy/(2p)\\ 0 & -y/(2\lambda p) & y/(2p) & 1/(2\lambda) \!+\!cy/(2p\lambda)\\ 0 & 0 & 0 & 0 \end{bmatrix}. \]3.2.2
Assume that 
$p$ is split in 
$\mathbb {Q}(\sqrt {m})$; then we have 
$t_{\rm max}=2$ and, hence, every 
$P$ is superspecial.
The vertex lattice with type 
$t_{\rm max}$ is 
$\Lambda =\{(x_1,x_2,x_3,x_4)\in \mathbb {Z}_p^4\}$ with
\[ Q'((x_1,x_2,x_3,x_4))=x_1^2-\epsilon x_2^2-p^{-1} x_3^2 + \epsilon p^{-1} x_4^2; \]
we have 
$\Lambda ^\vee =\operatorname {Span}_{\mathbb {Z}_p}\{e_1,e_2, pe_3, pe_4\}$, where 
$e_i$ is the vector with 
$x_i=1$ and 
$x_j=0$ for 
$j\neq i$. Recall that we take 
$\epsilon =\lambda ^2$; we then haveFootnote 16 that
\begin{align*} \mathbb{L}_{\mathrm{cris},P}(W)&=\operatorname{Span}_W\bigl \{v_1= \tfrac{1}{2} (e_3+\lambda^{-1}e_4), v_2= \tfrac{1}{2} (e_1+\lambda^{-1}e_2), v_3=- \tfrac{1}{2} (pe_3-\lambda^{-1}pe_4),\\ &\quad v_4=\tfrac{1}{2}(e_1-\lambda^{-1}e_2) \bigr\}. \end{align*}
The Gram matrix is 
$\big [\begin {smallmatrix}0 & I\\ I & 0\end {smallmatrix}\big ]$ and on 
$\mathbb {L}_{\mathrm {cris},P}(W)$, the Frobenius 
$\varphi =b\sigma$ with
\[ b=\begin{bmatrix}0 & 0 & -p & 0\\ 0 & 0 & 0 & 1 \\ -1/p & 0 & 0 & 0\\ 0 & 1 & 0 & 0\end{bmatrix}. \]
The filtration on 
$\mathbb {L}_{\mathrm {cris},P}(k)$ given by 
$\varphi$ is the same as in § 3.2.1 and, hence, we may use the same 
$\mu$ and 
$u$ there. Therefore, on 
$\mathbb {L}_{\mathrm {cris}}(W[[x,y]])$, we have
\[ \operatorname{Frob}=ub\sigma, \text{ with } ub=\begin{bmatrix}xy/p & y & -p & x\\ y/p & 0 & 0 & 1 \\ -1/p & 0 & 0 & 0\\ x/p & 1 & 0 & 0\end{bmatrix}. \]
Moreover, 
$\{w_1=pv_1-v_3, w_2=\lambda (pv_1+v_3), w_3=v_2+v_4, w_4=\lambda (v_4-v_2)\}$ is a 
$\mathbb {Z}_p$-basis of 
${L''\otimes \mathbb {Z}_p}$ and with respect to this basis,
\begin{equation} \operatorname{Frob}=\left(I+\begin{bmatrix} \dfrac{xy}{2p} & -\dfrac{\lambda xy}{2p} & \dfrac{x+y}{2p} & \dfrac{-\lambda(x -y)}{2p}\\ \dfrac{xy}{2\lambda p} & - \dfrac{xy}{2p} & \dfrac{x+y}{2\lambda p} & \dfrac{-(x-y)}{2p}\\ \dfrac{x+y}{2} & \dfrac{-\lambda (x + y)}{2} & 0 & 0\\ \dfrac{x-y}{2\lambda} & \dfrac{-(x - y)}{2} & 0 & 0\\ \end{bmatrix}\right) \circ \sigma. \end{equation}3.3 The Siegel case $L=L_{\rm S}$
We now compute 
$\mathbb {L}_{\mathrm {cris}}$ for Theorems 1(1) and 5. In this case, we have 
$t_{\rm max}=4$.
The vertex lattice with type 
$t_{\rm max}$ is 
$\Lambda = \operatorname {Span}_{\mathbb {Z}_p}\{e_1,f_1 \} \oplus Z_S$, where 
$Z_S=\{(x_1,x_2,x_3)\in \mathbb {Z}_p^3\}$
\begin{gather*} [Z_S, e_1]'=[Z_S,f_1]'=[e_1,e_1]'=[f_1,f_1]'=0,\quad [e_1,f_1]'=1/p,\\ Q'((x_1,x_2,x_3))=c(-\epsilon x_1^2-p^{-1} x_2^2 +\epsilon p^{-1} x_3^2), \end{gather*}
for some 
$c\in \mathbb {Z}_p^\times$. As 
$\det \Lambda =\det L \in \mathbb {Q}_p^\times /(\mathbb {Q}_p^\times )^2$ and 
$\det L=2$, we have 
$c=-1$. Let 
$g=(1,0,0)\in Z_S$ and 
$Z=\operatorname {Span}_{\mathbb {Z}_p}\{(0,1,0), (0,0,1)\}\subset Z_S$. Then 
$\Lambda /\Lambda ^\vee =\operatorname {Span}_{\mathbb {F}_p}\{\overline {e}_1,\overline {f}_1\}\oplus Z/Z^\vee$. Note that 
$\operatorname {Span}_{\mathbb {Z}_p}\{e_1,f_1\}\oplus Z$ is exactly the same quadratic 
$\mathbb {Z}_p$-lattice which is denoted by 
$\Lambda$ in § 3.2.1; hence, the same computation there applies to find 
$\mathbb {L}_{\mathrm {cris},P}(W)\subset \Lambda \otimes W$. More precisely, there exist 
$v_1,\ldots, v_4\in \operatorname {Span}_W\{e_1,f_1\}\oplus Z\otimes W$ and 
$c\in W$ which is the Teichmüller lift of 
$\bar {c}\in k$ such that
(1)
$\mathbb {L}_{\mathrm {cris},P}(W)=\operatorname {Span}_W\{v_1,\ldots,v_4,v_5\}$, where $v_5=g$;(2) the Gram matrix of
$[-,-]'$ with respect to $\{v_1,\ldots,v_5\}$ is
where\[ \begin{bmatrix}0 & I & 0\\ I & 0 & 0\\ 0 & 0 & 2\epsilon\end{bmatrix}, \]$I$ is the $2\times 2$ identity matrix;(3) the Frobenius
$\varphi$ on $\mathbb {L}_{\mathrm {cris},P}(W)$ with respect to the basis $\{v_i\}$ is
\[ \varphi=b\sigma, \text{ with }b= \begin{bmatrix} 0 & \sigma(c)-\sigma^{-1}(c) & p & 0 & 0\\ 0 & 1 & 0 & 0 & 0\\ 1/p & 0 & 0 & 0 & 0\\ (\sigma^{-1}(c)-\sigma(c))/p & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}; \](4)
$P$ is superspecial if and only if $\sigma ^2(c)=c$.
We may choose 
$\mu : \mathbb {G}_{m,W}\rightarrow \operatorname {SO}(\mathbb {L}_{\mathrm {cris},P}(W),Q')$ to be 
$t\mapsto \operatorname {diag}(t^{-1}, 1, t, 1, 1)$. Then 
$\widehat {U_P}=\operatorname {Spf} W[[x,y,z]]$ with the universal point
\[ u= \begin{bmatrix} 1 & x & -xy-\dfrac{z^2}{4\epsilon} & y & z\\ 0 & 1 & -y & 0 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & -x & 1 & 0\\ 0 & 0 & -\dfrac{z}{2\epsilon} & 0 & 1 \end{bmatrix}\]and
\[ \operatorname{Frob}=ub\sigma, \quad \text{with }ub= \begin{bmatrix} -\dfrac{1}{p}\left(xy+\dfrac{z^2}{4\epsilon}\right)-\dfrac{ay}{p} & a+x & p & y & z\\ -\dfrac{y}{p} & 1 & 0 & 0 & 0\\ \dfrac{1}{p} & 0 & 0 & 0 & 0\\ -\dfrac{x+a}{p} & 0 & 0 & 1 & 0\\ -\dfrac{z}{2\epsilon p} & 0 & 0 & 0 & 1 \end{bmatrix} \]
acting on 
$\mathbb {L}_{\mathrm {cris}}(W[[x,y,z]])$, where 
$a=\sigma (c)-\sigma ^{-1}(c)$; note that 
$a=0$ if and only if 
$P$ is superspecial.
For the proofs of Theorems 1(1) and 5, we only need to study superspecial points so we only give the matrix of 
$\operatorname {Frob}$ with respect to a basis of 
$\mathbb {L}_{\mathrm {cris}} \otimes _W K$ consisting of elements in 
$L''\otimes \mathbb {Z}_p$ when 
$P$ is superspecial; we refer the reader to the appendix for the discussion when 
$P$ is supergeneric.
We now assume that 
$P$ is superspecial. Let 
$w_1=\lambda (pv_1-v_3), w_2=pv_1+v_3, w_3=v_2, w_4=v_4, w_5=v_5$. Then 
$L''\otimes \mathbb {Z}_p=\operatorname {Span}_{\mathbb {Z}_p}\{w_1,\ldots, w_5\}$. We view 
$\{w_i\}_{i=1}^5$ as a 
$K$-basis of 
$\mathbb {L}_{\mathrm {cris},P}(W)\otimes K$, then the Frobenius on 
$\mathbb {L}_{\mathrm {cris}}(W[[x,y,z]])$ is given by
\begin{equation} \operatorname{Frob}=\left(I+ \begin{bmatrix} \dfrac{1}{2p}\biggl(xy+\dfrac{z^2}{4\epsilon}\biggr) & -\dfrac{1}{2\lambda p}\biggl(xy+\dfrac{z^2}{4\epsilon}\biggr) & \dfrac{x}{2\lambda p} & \dfrac{y}{2\lambda p} & \dfrac{z}{2\lambda p}\\ \dfrac{\lambda}{2p}\biggl(xy+\dfrac{z^2}{4\epsilon}\biggr) & -\dfrac{1}{2p}\biggl(xy+\dfrac{z^2}{4\epsilon}\biggr) & \dfrac{x}{2p} & \dfrac{y}{2p} & \dfrac{z}{2p}\\ \lambda y & -y & 0 & 0 & 0\\ \lambda x & -x & 0 & 0 & 0\\ \dfrac{\lambda z}{2\epsilon} & -\dfrac{ z}{2\epsilon} & 0 & 0 & 0 \end{bmatrix}\right) \circ \sigma. \end{equation}3.4 Equation of non-ordinary locus
We now use the computation in §§ 3.2 and 3.3 to obtain the local equation of the non-ordinary locus in a formal neighborhood of a supersingular point 
$P$ using results in [Reference OgusOgu01]. Although [Reference OgusOgu01] only focuses on the case of K3 surfaces, the results that we recall here apply to any GSpin Shimura varieties. We follow the notation in § 3.1. For a perfect field 
$k'$ of characteristic 
$p$, for 
$P'\in \mathcal {M}(k')$, we say 
$P$ is ordinary if the slopes of the crystalline Frobenius 
$\varphi$ on 
$\mathbb {L}_{\mathrm {cris},P'}(W)$ are 
$-1,1$ with multiplicity 
$1$ and 
$0$ with multiplicity 
$n$.Footnote 17
The cocharacter 
$\bar {\mu }$ defines a filtration 
$\operatorname {Fil}^i, i=-1,0,1$ on 
$\mathbb {L}_{\mathrm {cris},P}(k)$, which is the Hodge filtration in [Reference OgusOgu01] and, in particular, 
$\dim \operatorname {Fil}^1 \mathbb {L}_{\mathrm {cris},P}(k)=1$, 
$\dim \operatorname {Fil}^0 \mathbb {L}_{\mathrm {cris},P}(k)=n+1$, 
$\dim \operatorname {Fil}^{-1} \mathbb {L}_{\mathrm {cris},P}(k)=n+2$ and the annihilator of 
$\operatorname {Fil}^1 \mathbb {L}_{\mathrm {cris},P}(k)$ in 
$\mathbb {L}_{\mathrm {cris},P}(k)$ with respect to 
$Q$ is 
$\operatorname {Fil}^0 \mathbb {L}_{\mathrm {cris},P}(k)$.Footnote 18 The Hodge filtration over the mod 
$p$ complete local ring 
$R\otimes _W k$ at 
$P$ is given by 
$\operatorname {Fil}^i \mathbb {L}_{\mathrm {cris}}(R\otimes _W k):=\operatorname {Fil}^i \mathbb {L}_{\mathrm {cris},P}(k)\otimes _k (R\otimes k)$. Note that 
$\operatorname {Frob} (\operatorname {Fil}^0 \mathbb {L}_{\mathrm {cris}}(R\otimes _W k) )\subset \operatorname {Fil}^0 \mathbb {L}_{\mathrm {cris}}(R\otimes _W k)$, so we have a well-defined map 
$p\operatorname {Frob}: \operatorname {gr}_{-1}\mathbb {L}_{\mathrm {cris}}(R\otimes _W k)\rightarrow \operatorname {gr}_{-1}{\mathbb{L}_{\mathrm {cris}}(R\otimes _W k)}$, where 
$\operatorname {gr}_{-1}\mathbb {L}_{\mathrm {cris}}(R\otimes _W k):=\operatorname {Fil}^{-1} \mathbb {L}_{\mathrm {cris}}(R\otimes _W k)/\operatorname {Fil}^0 \mathbb {L}_{\mathrm {cris}}(R\otimes _W k)$.
Lemma 3.4.1 (Ogus)
For a supersingular point 
$P$, The non-ordinary locus (over 
$k$) in the formal neighborhood of 
$P$ is given by the equation
\[ p\operatorname{Frob}|_{\operatorname{gr}_{-1}\mathbb{L}_{\mathrm{cris}}(R\otimes_W k)}=0. \]Proof. By [Reference OgusOgu01, Proposition 11], the discussion of the conjugate filtration on [Reference OgusOgu01, pp. 333–334], and the fact that the annihilator of 
$\operatorname {Fil}^1 \mathbb {L}_{\mathrm {cris}}(R\otimes k)$ in 
$\mathbb {L}_{\mathrm {cris}}(R\otimes k)$ with respect to 
$Q$ is 
$\operatorname {Fil}^0 \mathbb {L}_{\mathrm {cris}}(R\otimes k)$, we have that the equation defining the non-ordinary locus is the projection of the conjugate filtration (denoted by 
$F^2_{con}$ in [Reference OgusOgu01]) to 
$\operatorname {gr}_{-1}\mathbb {L}_{\mathrm {cris}}(R\otimes k)$. By definition, 
$F^2_{con}=p\operatorname {Frob} \mathbb {L}_{\mathrm {cris}}(R\otimes k)$ and then the lemma follows.
Corollary 3.4.2 When 
$L=L_{\rm H}$, the local equation of the non-ordinary locus in a formal neighborhood of a supersingular point 
$P$ is 
$xy=0$ if 
$P$ is superspecial and is 
$y=0$ if 
$P$ is supergeneric; when 
$L=L_{\rm S}$, the local equation is 
$xy+z^2/(4\epsilon )=0$ if 
$P$ is a superspecial point and 
$(x+a)y+z^2/(4\epsilon )=0$ if 
$P$ supergeneric, where 
$a\in W(k)^\times$ depends on 
$P$.
Proof. We prove this corollary in the case 
$L = L_{\rm S}$, because the other case is handled the same way. Recall we have the basis 
$v_1 \ldots v_5$ of 
$\mathbb {L}_{\mathrm {cris}}$, with 
$\operatorname {Fil}^-{1} = \mathbb {L}_{\mathrm {cris}}$ and 
$\operatorname {Fil}^0$ being spanned by 
$v_2,v_3,v_4$ and 
$v_5$. Therefore, using the explicit formulas from the previous section, we see the map 
$p\operatorname {Frob}: \operatorname {gr}_{-1}\mathbb {L}_{\mathrm {cris}}(R\otimes _W k) \rightarrow \operatorname {gr}_{-1}\mathbb {L}_{\mathrm {cris}}(R\otimes _W k)$ is given by 
$p\operatorname {Frob}(v_1) = -(xy + {z^2}/{4\epsilon } + ay)v_1$. Our result now follows from Ogus's description of the non-ordinary locus.
4. Arithmetic Borcherds theory, Siegel mass formula, and Eisenstein series
We use arithmetic Borcherds theory [Reference Howard and Madapusi PeraHMP20] to control the global intersection number of a curve 
$C$ with special divisors. More precisely, we use the work of Bruinier and Kuss in [Reference Bruinier and KühnBK03] to study the Fourier coefficients of the Eisenstein part of the (vector-valued) modular form arising from Borcherds theory. To compare the global intersection number with the local contribution later in the paper, we also apply the computations in [Reference Bruinier and KühnBK03] and the Siegel mass formula to the Eisenstein part of the theta series attached to a supersingular point and reduce the question to a computation of local densities and determinants of the lattices 
$L$ and 
$L'$ introduced in § 2.1 and Definition 2.3.1 (in § 4.2, we summarize the properties of 
$L'$). We use Hanke's method in [Reference HankeHan04] to compute the local densities. Throughout this section, 
$p$ is an odd prime such that 
$L$ is self-dual at 
$p$. For a prime 
$\ell$, we use 
$v_\ell : \mathbb {Z}_\ell \backslash \{0\}\rightarrow \mathbb {Z}_{\geq 0}$ to denote the 
$\ell$-adic valuation.
4.1 Arithmetic Borcherds theory and the explicit formula for the Eisenstein series
Recall the special divisors 
$Z(m)$ from Definition 2.2.6 and § 2.2.11. The following modularity result is the key input to the estimate of the intersection number 
$Z(m).C$.
To state the result using vector-valued modular forms, for 
$\mu \in L^\vee /L,\ m\in \mathbb {Q}_{>0}$, let 
$\mathcal {Z}(m,\mu )$ denote the special divisors over 
$\mathbb {Z}$ in 
$\mathcal {M}$ defined in [Reference Andreatta, Goren, Howard and Madapusi PeraAGHMP18, § 4.5, Definition 4.5.6]. By definition, 
$\mathcal {Z}(m,0)$ is the divisor 
$\mathcal {Z}(m)$ defined in § 2.2; and roughly speaking, 
$\mathcal {Z}(m,\mu )$ parametrizes abelian surfaces 
$A$ with a special quasi-endomorphism 
$s$ such that 
$Q(s)=m$ and the 
$\ell$-adic and crystalline realizations of 
$s$ lie in the image of 
$(\mu +L)\otimes \mathbb {Z}_\ell$ and 
$(\mu +L)\otimes \mathbb {Z}_p$ in 
$\operatorname {End}(T_\ell (A)\otimes \mathbb {Q}_\ell )$ and 
$\operatorname {End}(\mathbb {D}\otimes _W W[1/p])$, respectively, where 
$\mathbb {D}$ is the Dieudonné module of 
$A$. By the proof of [Reference Andreatta, Goren, Howard and Madapusi PeraAGHMP18, Proposition 4.5.8] and [Reference Madapusi PeraMP16, Proposition 5.21], the assumption that 
$L$ is self-dual at 
$p$ implies that 
$\mathcal {Z}(m,\mu )$ is flat over 
$\mathbb {Z}_p$. Let 
$Z(m,\mu )$ denote 
$\mathcal {Z}(m,\mu )_{\mathbb {F}_p}$. Let 
$(\mathfrak {e}_\mu )_{\mu \in L^\vee /L}$ denote the standard basis of 
$\mathbb {C}[L^\vee /L]$. Let 
$\omega \in \operatorname {Pic}(\mathcal {M}_{\mathbb {F}_p})_{\mathbb {Q}}$ denote the Hodge line bundle in the 
$\mathbb {Q}$-Picard group of 
$\mathcal {M}_{\mathbb {F}_p}$; in other words, 
$\omega$ is the line bundle of weight 
$1$ modular forms (see, for instance, [Reference Andreatta, Goren, Howard and Madapusi PeraAGHMP18, Theorem 4.4.6] for a definition of 
$\omega$).
Theorem 4.1.1 (Borcherds, Howard–Madapusi Pera)
Assume 
$(L,Q)$ is a maximal quadratic lattice of signature 
$(n,2)$ such that 
$L$ is self-dual at 
$p$. The generating series
\[ \omega^{-1}\mathfrak{e}_0+\sum_{m> 0,\, \mu\in L^\vee/L}Z(m,\mu) q^m \mathfrak{e}_\mu, \quad \text{where}\ q=e^{2\pi i \tau}, \]
lies in 
$M_{1+{n}/{2}}(\rho _L)\otimes \operatorname {Pic}(\mathcal {M}_{\mathbb {F}_p})_{\mathbb {Q}}$. Here, 
$\rho _L$ denotes the Weil representation on 
$\mathbb {C}[L^\vee /L]$ and 
$M_{1+{n}/{2}}(\rho _L)$ denotes the space of vector-valued modular forms of 
$\operatorname {Mp}_2(\mathbb {Z})$ with respect to 
$\rho _L$ of weight 
$1+{n}/{2}$.Footnote 19 In particular, for any 
$\mathbb {Q}$-linear functional 
$\alpha : \operatorname {Pic}(\mathcal {M}_{\mathbb {F}_p})_{\mathbb {Q}}\rightarrow \mathbb {C}$, the vector-valued power series
\[ \alpha(\omega^{-1})\mathfrak{e}_0+\sum_{m> 0,\, \mu\in L^\vee/L}\alpha(Z(m,\mu)) q^m \mathfrak{e}_\mu \]
is the Fourier expansion of an element of 
$M_{1+{n}/{2}}(\rho _L)$.
Proof. By abuse of notation, we also use 
$\omega$ to denote the Hodge line bundle over 
$\mathcal {M}$. By [Reference Howard and Madapusi PeraHMP20, Theorem B], the generating series 
$\omega ^{-1}\mathfrak {e}_0+\sum _{m> 0,\, \mu \in L^\vee /L}\mathcal {Z}(m,\mu ) q^m \mathfrak {e}_\mu \in M_{1+{n}/{2}}(\rho _L)\otimes \operatorname {Pic}(\mathcal {M})_{\mathbb {Q}}$. As 
$\mathcal {Z}(m,\mu )$ are flat over 
$\mathbb {Z}_p$, then the desired assertion follows from intersecting with 
$\mathcal {M}_{\mathbb {F}_p}$.
4.1.2
In the setting of Theorem 1(2) (i.e. the case when 
$L=L_{\rm H}$), we work with curves 
$C$ that are not necessarily proper. We therefore need a version of the above modularity result that holds for the special fiber a toroidal compactification of 
$\mathcal {M}$. To that end, let 
$\mathcal {M}^{\textrm {tor}}$ denote a toroidal compactification of 
$\mathcal {M}$, and let 
$D_1,\ldots, D_k$ denote irreducible components of the boundary 
$\mathcal {M}^{\textrm {tor}}_{\mathbb {F}_p}\setminus \mathcal {M}_{\mathbb {F}_p}$. In [Reference Bruinier, Burgos Gil and KühnBBGK07, Theorem 6.2], the authors prove the modularity result for 
$\mathcal {M}^{\textrm {tor}}$, which will directly imply the modularity result for 
$\mathcal {M}^{\textrm {tor}}_{\mathbb {F}_p}$. The constant term is still given by the Hodge line bundle, still denoted by 
$\omega$, on 
$\mathcal {M}^{\rm {tor}}_{\mathbb {F}_p}$ and the special divisors 
$Z(m,\mu )$ are replaced byFootnote 20 
$Z'(m,\mu ) + E(m,\mu )$, where 
$Z'(m,\mu )$ is the Zariski-closure of 
$Z(m,\mu )$ in 
$\mathcal {M}^{\textrm {tor}}_{\mathbb {F}_p}$, and 
$E(m,\mu )$ is a ‘correction term’, and has as its irreducible components the 
$D_i$ with appropriate multiplicity. Crucially, when 
$Z(m,\mu )$ is proper (see § 4.3.3 for when this happens), the multiplicities of the 
${D_i}$ in correction term 
$E(m,\mu )$ are all zero and, hence, 
$E(m,\mu )$ is trivial. Therefore, compact special divisors stay as they are in the modularity theorem for 
$\mathcal {M}^{\textrm {tor}}_{\mathbb {F}_p}$.Footnote 21
4.1.3
Recall that we have a finite morphism 
$\pi : C\rightarrow \mathcal {M}_{\bar {\mathbb {F}}_p}$. When 
$C$ is proper, for 
$Z\in \operatorname {Pic}(\mathcal {M}_{\mathbb {F}_p})_{\mathbb {Q}}$, we define 
$C.Z$ as the degree of 
$\pi ^* Z \in \operatorname {Pic}(C)_{\mathbb {Q}}$. For Theorem 1(2), we pick a toroidal compactification 
$\mathcal {M}^{\rm {tor}}$ of the Hilbert modular surface 
$\mathcal {M}$ and let 
$C'$ denote the smooth compactification of 
$C$ and the finite morphism 
$\pi$ extends to a finite morphism 
$\pi ': C'\rightarrow \mathcal {M}^{\rm {tor}}_{\bar {\mathbb {F}}_p}$. Then for a proper divisor 
$Z$ in 
$\mathcal {M}_{\mathbb {F}_p}$, we use 
$C.Z$ to denote 
$\deg _{C'}(\pi ^*Z)$; because 
$Z$ is proper, 
$C'\cap Z=C\cap Z$ so we only need to consider points in 
$\mathcal {M}_{\bar {\mathbb {F}}_p}$.
4.1.4
We apply Theorem 4.1.1 and § 4.1.2 to 
$\alpha (Z):=C.Z$ defined in § 4.1.3 for 
$Z\in \operatorname {Pic}(\mathcal {M}_{\mathbb {F}_p})_{\mathbb {Q}}$ (and we further assume that 
$Z$ is proper when 
$L=L_{\rm H}$). We decompose the modular form 
$-(\omega.C)\mathfrak {e}_0+\sum _{m> 0,\, \mu \in L^\vee /L}Z(m,\mu ).C q^m \mathfrak {e}_\mu$ as 
$E(q)+G(q)$, where 
$E(q)\in M_{1+{n}/{2}}(\rho _L)$ is an Eisenstein series and 
$G(q)\in M_{1+{n}/{2}}(\rho _L)$ is a cusp form. Note that the constant term of 
$E(q)$ is 
$-(\omega.C)\mathfrak {e}_0$.
We now recall the vector-valued Eisenstein series 
$E_0(\tau )\in M_{1+{n}/{2}}(\rho _L)$ which has constant term 
$\mathfrak {e}_0$. This Eisenstein series has been studied in [Reference BruinierBru02, § 1.2.3], [Reference Bruinier and KussBK01, § 4], and [Reference Bruinier and KühnBK03, § 3]. Here we follow [Reference BruinierBru17, § 2.1] as we use the same convention of quadratic forms. We denote an element in 
$\operatorname {Mp}_2(\mathbb {Z})$ by 
$(g,\sigma )$, where 
$g=\big [\begin {smallmatrix}a & b \\ c & d\end {smallmatrix}\big ]\in \operatorname {SL}_2(\mathbb {Z})$ and 
$\sigma$ is a choice of the square root of 
$\tau \mapsto c\tau +d$. Let 
$\Gamma '_\infty \subset \operatorname {Mp}_2(\mathbb {Z})$ denote the stabilizer of 
$\infty$. Then for 
$n\geq 3$, the following summation converges on the upper half plane and we define
\[ E_0(\tau)=\sum_{(g,\sigma)\in \Gamma'_\infty\backslash \operatorname{Mp}_2(\mathbb{Z})}\sigma(\tau)^{-(2+n)}(\rho_L(g,\sigma)^{-1}\mathfrak{e}_0). \]
When 
$n=2$, we define 
$E_0(\tau )$ use analytic continuation following [Reference Bruinier and KühnBK03, § 3]. Write 
$\tau =x+iy$ and define for 
$s\in \mathbb {C}$,
\[ E_0(\tau,s)=\sum_{(g,\sigma)\in \Gamma'_\infty\backslash \operatorname{Mp}_2(\mathbb{Z})}\sigma(\tau)^{-(2+n)}(\rho_L(g,\sigma)^{-1}(y^s\mathfrak{e}_0)), \]
which converges on the upper half plane for 
$s$ with 
$\Re s>0$ (
$n=2$ here). By [Reference Bruinier and KühnBK03, p. 1697], 
$E_0(\tau,s)$ has meromorphic continuation in 
$s$ to the entire 
$\mathbb {C}$ and it is holomorphic at 
$s=0$ and we define 
$E_0(\tau )$ to be the value at 
$s=0$ of the meromorphic continuation of 
$E_0(\tau,s)$. Moreover, by [Reference Bruinier and KühnBK03, p. 1697], 
$E_0(\tau )$ is holomorphic and, hence, lies in 
$M_{1+{n}/{2}}(\rho _L)$ if 
$\rho _L$ does not contain the trivial representation as a subquotient. In the proof of Theorem 1(2), we work with 
$L=L_{\rm H}$ and this condition for 
$\rho _L$ is always satisfied as far as the 
$m$ in the statement of Theorem 1(2) is not a perfect square, that is, 
$\mathcal {M}$ is not the product of modular curves.
We denote the 
$q$-expansion of 
$E_0(\tau )$ as 
$\sum _{m\geq 0,\, m\in \mathbb {Z}+Q(\mu )}q_L(m,\mu )q^m \mathfrak {e}_\mu$ and set 
$q_L(m):=q_L(m,0)$ for 
$m\in \mathbb {Z}_{>0}$.
4.1.5
We fix some notation before we state the explicit formula of 
$q_L(m)$ given by Bruinier and Kuss. Given a quadratic lattice 
$L$ (not necessarily the lattice 
$L_{\rm H},L_{\rm S}$), we write 
$\det (L)$ for the determinant of its Gram matrix. We have 
$|L^\vee /L|=|\!\det (L)|$.
For a rational prime 
$\ell$, we use 
$\delta (\ell, L,m)$ to denote the local density of 
$L$ representing 
$m$ over 
$\mathbb {Z}_\ell$. More precisely, 
$\delta (\ell, L,m)=\lim _{a\rightarrow \infty } \ell ^{a(1-\operatorname {rk} L)}\#\{v\in L/\ell ^a L \mid Q(v)\equiv m \bmod \ell ^a\}$. Here [Reference Bruinier and KussBK01, Lemma 5] asserts that the limit is stable once 
$a\geq 1+2v_\ell (2m)$. In particular, if 
$m$ is representable by 
$(L\otimes \mathbb {Z}_\ell, Q)$, then 
$\delta (\ell,L,m)>0$.
Given 
$0\neq D\in \mathbb {Z}$ such that 
$D\equiv 0,1 \bmod 4$, we use 
$\chi _D$ to denote the Dirichlet character 
$\chi _D(a)=(\frac {D}{a})$, where 
$(\frac {\cdot }{\cdot })$ is the Kronecker symbol. For a Dirichlet character 
$\chi$, we set 
$\sigma _s(m,\chi )=\sum _{d|m}\chi (d)d^s$.
Theorem 4.1.6 (Bruinier and Kuss; see also [Reference BruinierBru17, Theorems 2.3 and 2.4])
Consider 
$L\,{=}\,L_{\rm H},$ 
$L_{\rm S}$ defined in § 2.1 and 
$m\in \mathbb {Z}_{>0}$.
(1) For
$L=L_{\rm H}$, the Fourier coefficient $q_L(m)$ is
\[ -\frac{4\pi^2m\sigma_{-1}(m,\chi_{4\det L})}{\sqrt{|L^\vee/L|}L(2,\chi_{4\det L})}\prod_{\ell \mid 2\det(L)}\delta(\ell, L, m). \](2) For
$L=L_{\rm S}$, write $m=m_0f^2$, where ${\rm {gcd}}(f,2\det L)=1$ and $v_\ell (m_0)\in \{0,1\}$ for all ${\ell \nmid 2\det L}$. Then the Fourier coefficient $q_L(m)$ is
where\[ -\frac{16\sqrt{2}\pi^2m^{3/2}L(2,\chi_{\mathcal{D}})}{3\sqrt{|L^\vee/L|}\zeta(4)}\biggl(\sum_{d\mid f}\mu(d)\chi_{\mathcal{D}}(d)d^{-2}\sigma_{-3}(f/d)\biggr)\prod_{\ell\mid 2\det L}\big(\delta(\ell,L,m)/(1-\ell^{-4})\big), \]$\mu$ is the Mobius function and $\mathcal {D}=-2m_0\det L$.Footnote 22
Proof. When 
$L=L_{\rm S}$, this is [Reference Bruinier and KussBK01, Theorem 11]. When 
$L=L_{\rm H}$, one modifies the proof of [Reference Bruinier and KussBK01, Theorem 11] as follows. Using [Reference Bruinier and KühnBK03, Proposition 3.1] instead of [Reference Bruinier and KussBK01, Proposition 2], we obtain [Reference Bruinier and KussBK01, Proposition 3] because Shintani's formula works in general. To express the formula in [Reference Bruinier and KussBK01, Proposition 3] as a product of local terms, we use [Reference IwaniecIwa97, § 11.5, p. 196]. The rest of the proof, which computes the local terms at 
$\ell \nmid 2\det L$, works in the same way (see also [Reference IwaniecIwa97, Equations (11.71)–(11.74)]).
If 
$Z(m)\neq \emptyset$, then 
$m$ is representable by 
$(L,Q)$ and, in particular, for every 
$\ell$, 
$m$ is representable by 
$(L\otimes \mathbb {Z}_\ell,Q)$ and, hence, 
$\delta (\ell, L,m)>0$. By Theorem 4.1.6, we have 
$q_L(m)<0$ when 
$Z(m)\neq \emptyset$.
4.2 The lattice $L'$ and the Siegel mass formula
4.2.1
For a supersingular point 
$P\in \mathcal {M}(k)$, we defined 
$L''$, the lattice of special endomorphisms, in Definition 2.3.1 and picked 
$L'\supset L''$ which is maximal at all 
$\ell \neq p$ and 
$L'\otimes \mathbb {Z}_p=L''\otimes \mathbb {Z}_p$. Though there may be choices for 
$L'$, the local lattices 
$L'\otimes \mathbb {Z}_\ell$ are well-defined up to isometry. More precisely, for 
$\ell \neq p$, 
$L'\otimes \mathbb {Z}_\ell$ is given by Lemma 2.3.2; and for 
$\ell =p$, 
$L'\otimes \mathbb {Z}_p=L''\otimes \mathbb {Z}_p$ is computed in §§ 3.2–3.3. Note that given 
$L$, the isometry class of the quadratic lattice 
$L'\otimes \mathbb {Z}_p$ only depends on whether 
$P$ is superspecial or supergeneric; indeed, following the notation in § 3.1.2, if 
$t_P=t_{\rm max}$ (for instance, when 
$P$ is supergeneric), then 
$\Lambda _P$ is a maximal lattice with respect to 
$pQ'$ and, hence, its isometry class (and, thus, the isometry class of 
$L'\otimes \mathbb {Z}_p=\Lambda _P^\vee$) is unique; if 
$t_P=2$, that is, 
$P$ is superspecial, then 
$\Lambda _P^\vee$ is a maximal lattice with respect to 
$Q'$ and, hence, is unique up to isometry.
To compute the local intersection number of 
$Z(m).C$ at 
$P$, we also need to consider sublattices 
$L'''$ of 
$L'$ such that 
$L'''\otimes \mathbb {Z}_\ell =L'\otimes \mathbb {Z}_\ell$ for all 
$\ell \neq p$ (more precisely, we take 
$L'''$ to be the lattices defined in § 7.2.3). In particular, 
$\det L'''=p^{2a} \det L'$ for some 
$a\in \mathbb {Z}_{\geq 0}$.
Let 
$\theta _{L'''}(q)$ denote the theta series of the positive-definite lattice 
$L'''$, which is a modular form of weight 
$\operatorname {rk} L'/2$; we decompose 
$\theta _{L'''}(q)=E_{L'''}(q)+G_{L'''}(q)$, where 
$E_{L'''}$ is an Eisenstein series and 
$G_{L'''}$ is a cusp form. Let 
$q_{L'''}(m)$ denote the 
$m$th Fourier coefficients of 
$E_{L'''}$ (at the cusp 
$\infty$). The following theorem asserts that 
$q_{L'''}(m)$ only depends on the genus of 
$L'''$ and gives explicit formula for 
$q_{L'''}(m)$. In particular, when we consider the theta series for 
$L'$, we have that 
$q_{L'}(m)$ is independent of the choice of 
$L'$ above and it only depends on 
$L$ and whether 
$P$ is superspecial or supergeneric.
Theorem 4.2.2 (Siegel mass formula)
Notation as in § 4.2.1. The Eisenstein series 
$E_{L'''}$ only depends on the genus of 
$L'''$. Moreover, for 
$m\in \mathbb {Z}_{>0}$:
(1) when
$L=L_{\rm H}$,
\[ q_{L'''}(m)=\frac{4\pi^2m\sigma_{-1}(m,\chi_{4\det L'})}{\sqrt{|L'''^\vee/L'''|}L(2, \chi_{4\det L'})}\prod_{\ell \mid 2 det L'}\delta(\ell, L''',m); \](2) when
$L=L_{\rm S}$,
where we write\begin{align*} q_{L'''}(m)&=\frac{16\sqrt{2}\pi^2m^{3/2}L(2,\chi_{\mathcal{D}'})}{3\sqrt{|L'''^\vee/L'''|}\zeta(4)}\biggl(\sum_{d\mid f}\mu(d)\chi_{\mathcal{D}'}(d)d^{-2}\sigma_{-3}(f/d)\biggr)\\ &\quad \times\prod_{\ell\mid 2\det L'}\big(\delta(\ell,L''',m)/(1-\ell^{-4})\big), \end{align*}$m=m_0f^2$ with ${\rm {gcd}}(f,2\det L')=1$ and $v_\ell (m_0)\in \{0,1\}$ for all $\ell \nmid 2\det L'$ and $\mathcal {D}'=-2 m_0 \det L'$
Proof. The first assertion follows from the Siegel mass formula; see, for instance, [Reference Iwaniec and KowalskiIK04, Theorem 20.9, (20.121), and pp. 479-480]. To obtain the formula above, we note that the proof of [Reference Bruinier and KussBK01, Theorem 11] using [Reference Bruinier and KussBK01, Theorem 6] also applies to 
$L'''$ and, hence, we conclude that the formula in [Reference BruinierBru17, Theorems 2.3 and 2.4] also applies to 
$L'''$ and obtain the formulas in the theorem with all 
$L'$ replaced by 
$L'''$. Note that by the computations in §§ 3.2–3.3, we have 
$p\mid \det L'$ and, hence, 
$\ell \mid 2 \det L'''$ if and only if 
$\ell \mid 2 \det L'$; also 
$\chi _{4 \det L'''}=\chi _{4 \det L'}$ and 
$\chi _{D'}=\chi _{-2m_0 \det L'''}$. Hence, using 
$L'$ (instead of 
$L'''$) for 
$\chi, \mathcal {D}'$ and the product 
$\ell \mid 2 \det L'$ yields the same formulas.
4.3 The asymptotic of $q_L(m)$
The discussion of this subsection also applies to 
$q_{L'''}(m)$ when 
$m$ is representable by 
$(L''',Q')$, but we only focus on 
$q_L(m)$ here.
4.3.1
Assume that 
$m$ is representable by 
$(L\otimes \mathbb {Z}_\ell,Q)$ for every prime 
$\ell$. We also assume that, as 
$m$ varies within a specified set 
$T$, there exists an absolute constant 
$C>0$ such that for all 
$\ell \mid 2 \det L$, we have 
$v_\ell (m)\leq C$. As we shall see in § 4.3.3, we will always be in this situation.
For a given 
$\ell \mid 2 \det L$, as in [Reference BruinierBru17, proof of Proposition 2.5], by [Reference Bruinier and KussBK01, Lemma 5], we have 
$\delta (\ell,L,m)=\ell ^{a(1-\operatorname {rk} L)}\#\{v\in L/\ell ^a L \mid Q(v)\equiv m \bmod \ell ^a\}$ with 
$a=1+2C+2v_\ell (2)$ and, hence, 
$\ell ^{a(1-\operatorname {rk} L)}\leq \delta (\ell,L,m)\leq \ell ^a$.Footnote 23
Therefore, given 
$(L,Q)$, by Theorem 4.1.6, we have that 
$|q_L(m)|\asymp m \sigma _{-1}(m, \chi _{4\det L})$ and, hence, 
$m^{1-\epsilon }\ll _\epsilon |q_L(m)|\ll _\epsilon m^{1+\epsilon }$ for 
$L=L_{\rm H}$; and
\[ |q_L(m)|\asymp m^{3/2} L(2, \chi _{\mathcal {D}}) \sum _{d\mid f} \mu (d) \chi _{\mathcal {D}}(d) d^{-2} \sigma _{-3}{}(f/d) \]
for 
$L=L_{\rm S}$. As in the proof of [Reference BruinierBru17, Proposition 2.5], we have 
$\sum _{d\mid f}\mu (d)\chi _{\mathcal {D}}(d)d^{-2}\sigma _{-3}(f/d)\geq 1/5$ and
\[ \sum_{d\mid f}\mu(d)\chi_{\mathcal{D}}(d)d^{-2}\sigma_{-3}(f/d)\leq \sum_{d\mid f}d^{-2}\sigma_{-3}(f/d) <\sum_{d\mid f} d^{-2}\zeta(3)<\zeta(2)\zeta(3); \]
moreover, by [Reference BruinierBru17, Proposition 2.5], 
$L(2,\chi _D)\geq \zeta (4)/\zeta (2)$ and 
$L(2,\chi _D)\leq \prod _{p} (1-p^{-2})^{-1}=\zeta (2)$. Hence, 
$|q_L(m)|\asymp m^{3/2}$ when 
$L=L_{\rm S}$.
Lemma 4.3.2 We fix the same assumptions as in § 4.3.1. For 
$m\gg 1$, we have 
$Z(m)\neq \emptyset$ and the intersection number 
$Z(m).C = -q_L(m)(\omega. C)+o(|q_L(m)|)$. More precisely, when 
$L=L_{\rm H}$, the error term can be bounded by 
$O_\epsilon (m^{1/2+\epsilon })$ and when 
$L=L_{\rm S}$, the error term can be bounded by 
$O(m^{5/4})$.
Proof. We follow the discussion in § 4.1.4. Let 
$g(m), m\in \mathbb {Z}_{>0}$ denote the 
$m$th Fourier coefficients of 
$\mathfrak {e}_0$-component of 
$G(q)$, which is also a cusp form of weight 
$1+{n}/{2}$ with respect to a certain subgroup of 
$\operatorname {Mp}_2(\mathbb {Z})$ which is the preimage of a congruence subgroup of 
$\operatorname {SL}_2(\mathbb {Z})$ depending on 
$L$. When 
$L=L_{\rm H}$, by Deligne's bound [Reference DeligneDel73, Reference DeligneDel74], we have 
$|g(m)|\ll m^{1/2}\sigma _0(m)\ll _\epsilon m^{1/2+\epsilon }=o_\epsilon (m^{1-\epsilon })=o(|q_L(m)|)$ for any 
$0<\epsilon <1/4$. When 
$L=L_{\rm S}$, the trivial bound yields 
$|g(m)|\ll m^{5/4}=o(m^{3/2})$ (see [Reference SarnakSar90, Proposition 1.3.5]). Therefore, by Theorem 4.1.1, 
$Z(m).C=-q_L(m)(\omega.C)+o(|q_L(m)|)$; in particular, for 
$m\gg 1$, 
$Z(m).C>0$ and, hence, 
$Z(m)\neq \emptyset$.
4.3.3
When 
$L=L_{\rm S}$, recall from § 2.1 that the quadratic form is 
$Q(x)=x_0^2+x_1x_2-x_3x_4$ and hence every 
$m\in \mathbb {Z}_{>0}$ is representable by 
$(L,Q)$. In particular, 
$Z(m)\neq \emptyset$ and 
$\delta (\ell,L,m)>0$ for all 
$\ell$. Moreover, in order to prove Theorem 1(1) and Remark 4, we work with 
$m\in T:=\{Dq^2\mid q \text { prime and }q\neq p \}$, where we take 
$D=1$ for Theorem 1(1) and 
$D$ being the discriminant of the real quadratic field in Remark 4; and for Theorem 5, we work with 
$m\in T: = \{ q{\rm \mid }q{\rm prime and }q\ne p,q$ 
${\rm is a quadratic residue}\,\bmod \,p,{\rm and }q\equiv 3\,\bmod \,4\}$. In particular, for all such 
$m$, we have 
$v_\ell (m)\leq 2+v_\ell (D)$ and, hence, the assumptions in § 4.3.1 are satisfied.
When 
$L=L_{\rm H}$, because 
$L$ is maximal and isotropic, we have that the quadratic form on 
$L\otimes \mathbb {Z}_\ell$ is given by 
$xy+Q_1(z)$, where 
$x,y \in \mathbb {Z}_\ell$, 
$z\in \mathbb {Z}_\ell ^2$, and 
$Q_1$ is some quadratic form. Then 
$\delta (\ell, L,m)>0$ for all 
$\ell$; indeed, by [Reference HankeHan04, Definition 3.1 and Lemma 3.2], 
$\delta (\ell,L,m)>0$ if there exists 
$x,y \in \mathbb {Z}/\ell ^{1+2v_\ell (2)}$ such that 
$xy\equiv m \bmod \ell ^{1+2v_\ell (2)}$ and 
$x\not \equiv 0\bmod \ell$ (by the terminology in [Reference HankeHan04], this construct a good type solution (taking 
$z=0$) for 
$(L,Q)\bmod \ell ^{1+2v_\ell (2)}$, which can be lifted to 
$\mathbb {Z}/\ell ^k$ for any 
$k\geq 1+2v_\ell (2)$). Such 
$x,y$ always exists and, hence, every 
$m\in \mathbb {Z}_{>0}$ is representable by 
$(L\otimes \mathbb {Z}_\ell,Q)$ for all 
$\ell$ and, hence, by Lemma 4.3.2, there exists 
$N\in \mathbb {Z}_{>0}$ such that for all 
$m>N$, 
$m$ is representable by 
$(L,Q)$. For the proof of Theorem 1(2), we work with 
$m$ in
\[ T:=\{m\in \mathbb{Z}\mid m>N, p\nmid m, v_\ell(m)\leq C,\forall \ell \mid 2\det L, \text{ and }\exists\, q \| m \text{ such that } q \text{ inert in }F\}, \]
where 
$F$ is the real quadratic field attached to the Hilbert modular surface and the constant 
$C$ is chosen so that this set is non-empty. The existence of 
$q$ implies that 
$m\neq \operatorname {Nm}_{F/\mathbb {Q}}\gamma$ for any 
$\gamma \in F$ and, hence, for any 
$v\in L_{\rm H}\otimes \mathbb {Q}$ such that 
$Q(v)=m$, we have 
$v^\perp \subset L_{\rm H}\otimes \mathbb {Q}$ is anisotropic. Note that if 
$Z(m)$ is non-compact in 
$\mathcal {M}_{\mathbb {F}_p}$, then 
$Z(m)$ parametrizes abelian surfaces which are isogenous to the self-product of elliptic curves and then 
$v^\perp$ is isotropic. Therefore, for any 
$m\in T$, we have that 
$Z(m)$ is compact in 
$\mathcal {M}_{\mathbb {F}_p}$. Note that 
$T\subset \mathbb {Z}_{>0}$ is of positive density.
Lemma 4.3.4 For 
$L=L_{\rm H}$ and 
$M>0$, we have 
$\sum _{1\leq m \leq M,\, m\in T}|q_L(m)|\asymp M^2$.
Proof. By §§ 4.3.1 and 4.3.3, we have for 
$m\in T$, 
$|q_L(m)|\asymp m\sigma _{-1}(m,\chi )$, where 
$\chi =\chi _{4\det L}$. We write
\begin{align*} \sum_{1\leq m \leq M,\, m\in T} m\sigma_{-1}(m,\chi) & = \sum_{1\leq m\leq M,\, m\in T}\sum_{d\mid m}d\cdot \chi(m/d)= \sum_{1\leq d\leq M,\, 1\leq f\leq M,\, df\leq M, df\in T} d\cdot \chi(f)\\ &= \sum_{1\leq d\leq M^{1/2}}d \sum_{1\leq f\leq M/d,\, df\in T}\chi(f)+\sum_{1\leq f\leq M^{1/2}}\chi(f)\sum_{1\leq d\leq M/f,\, df\in T}d\\ &\quad -\biggl(\sum_{1\leq d\leq M^{1/2}}d\biggl(\sum_{1\leq f\leq M^{1/2},\, df\in T}\chi(f)\biggr)\biggr). \end{align*}Note that
\begin{gather*} \biggl|\sum_{1\leq d\leq M^{1/2}}d \sum_{1\leq f\leq M/d,\, df\in T}\chi(f)\biggr| \leq \sum_{1\leq d\leq M^{1/2}}d\cdot (M/d)=O(M^{3/2}),\\ \biggl|\biggl(\sum_{1\leq d\leq M^{1/2}}d\biggl(\sum_{1\leq f\leq M^{1/2},\, df\in T}\chi(f)\biggr)\biggr)\biggr|\leq \biggl(\sum_{1\leq d\leq M^{1/2}}d\biggr)\cdot \biggl(\sum_{1\leq f\leq M^{1/2}}1\biggr)=O( M^{3/2}). \end{gather*}
The second term is the main term. First, let 
$T':=\{m\in \mathbb {Z}\mid m>N, p\nmid m, v_\ell (m)\leq C,\forall \ell \mid 2\det L\}$, then
\[ \sum_{1\leq f\leq M^{1/2}}\chi(f)\sum_{1\leq d\leq M/f,\, df\in T'}d=\sum_{1\leq f\leq M^{1/2},\, p\nmid f}\chi(f)\sum_{1\leq d\leq M/f,\, p\nmid d,\, v_\ell(d)\leq C,\,\forall \ell \mid 2 \det L} d, \]
because 
$v_\ell (df)\leq C \iff v_\ell (d)\leq C, \forall \ell \mid 2 \det L$ when 
$v_\ell (f)=0, \forall \ell \mid 2 \det L$ and if 
$v_\ell (f)>0$ for some 
$\ell \mid 2 \det L$, then 
$\chi (f)=0$. As 
$\sum _{1\leq d\leq M/f,\, p\nmid d,\, v_\ell (d)\leq C,\,\forall \ell \mid 2 \det L}d=C_1 ({M^2}/{f^2})+O(M)$, where 
$C_1$ and the implicit constant only depend on 
$C,L,p$. Hence,
\[ \sum_{1\leq f\leq M^{1/2}}\chi(f)\sum_{1\leq d\leq M/f,\, df\in T'}d=C_1M^2\sum_{1\leq f\leq M^{1/2},\, p\nmid f}\chi(f)/f^2+O(M^{3/2})\asymp M^2. \]To finish the proof, we only need to show that
\[ \displaystyle\biggl|\sum_{1\leq f\leq M^{1/2}}\chi(f)\sum_{1\leq d\leq M/f,\, df\in T'\setminus T}d\biggr|=o(M^2). \] As 
$M/f\geq M^{1/2}$, by the definition of 
$T$, 
$\#\{d\mid 1\leq d \leq M/f, df\in T'\setminus T\}=o(M/f)$ with implicit constant independent of 
$f$ and, hence, we obtain the desired bound.Footnote 24
4.4 Local densities at $p$ and the ratios of Fourier coefficients
We set the same notation as in § 4.2.1. Theorems 4.1.6 and 4.2.2 reduce the comparison between 
$q_L(m)$ and 
$q_{L'''}(m)$ to the computation of the local density 
$\delta (p,L''',m)$, which we now compute following [Reference HankeHan04, § 3]. Recall that 
$p$ is an odd prime and 
$v_p(m)\leq 1$ for all 
$m\in T$ defined in § 4.3.3. For an arbitrary quadratic lattice 
$(L,Q)$, let 
$\alpha (p,L,m):=p^{1-\operatorname {rk} L}\#\{v\in L/pL \mid Q(v)\equiv m \bmod p\}$; if we diagonalize 
$L\otimes \mathbb {Z}_p$ such that 
$Q$ is given by 
$\sum _{i=1}^{\operatorname {rk} L} a_i x_i^2$ with 
$a_i\in \mathbb {Z}_p$, then we define
\begin{align*} \alpha^*(p,L,m)&:=p^{1-\operatorname{rk} L}\#\big\{v=(x_1,\ldots, x_{\operatorname{rk} L})\in L/pL \mid Q(v)\equiv m, \exists i \text{ such that }v_p(a_i)=0,\\ &\qquad\qquad\qquad x_i \not\equiv 0 \bmod p\big\}. \end{align*}Lemma 4.4.1 (Hanke)
If 
$p\nmid m$, we have
\[ \delta(p,L''',m)=\alpha(p,L''',m); \]
if 
$v_p(m)=1$, we have
\[ \delta(p,L''',m)=\alpha^*(p,L''',m)+ p^{1-s_0}\alpha(p, L'''_I, m/p), \]
where if we write 
$(L'''\otimes \mathbb {Z}_p, Q')$ into diagonal form 
$\sum _{i=1}^{\operatorname {rk} L'''}a_i x_i^2$ with 
$a_i\in \mathbb {Z}_p$, we define 
$s_0=\#\{a_i \mid v_p(a_i)=0\}$ and 
$L'''_I$ is the quadratic lattice with quadratic form 
$\sum _{i=1}^{\operatorname {rk} L'''}a'_i x_i^2$, where 
$a'_i =p a_i$ if 
$v_p(a_i)=0$ and 
$a'_i=p^{-1} a_i$ if 
$v_p(a_i)\geq 1$.
Proof. If 
$p\nmid m$, the assertion follows from [Reference HankeHan04, Remark 3.4.1(a) and Lemma 3.2]; if 
$v_p(m)=1$, then we only have good type and bad type I solutions in the sense of [Reference HankeHan04, Definition 3.1, p. 360] and the assertion follows from [Reference HankeHan04, Lemma 3.2, p. 360, and Remark 3.4.1(a)].
We first compute 
$\delta (p,L',m)$ by Lemma 4.4.1. We always pick 
$\epsilon \in \mathbb {Z}_p^\times \backslash (\mathbb {Z}_p^\times )^2$ as in § 3.1.2.
4.4.2
Consider 
$L=L_{\rm H}$ and recall that 
$p\nmid m, \ \forall m \in T$. Let 
$F$ denote the real quadratic field attached to the Hilbert modular surface defined by 
$L_{\rm H}$.
(1) Assume that
$p$ is inert in $F$ and $P$ is supergeneric. By § 3.2.1, $L'\otimes \mathbb {Z}_p=\Lambda ^\vee =p\Lambda$ and, hence, $p\mid Q'(v),\forall v\in L'$; in particular, $\delta (p,L',m)=0$.(2) Assume that
$p$ is inert in $F$ and $P$ is superspecial. By § 3.2.1, $Q'(v)=xy+p(z^2-\epsilon w^2)$, where $w_i$ are given right above (3.2.1) and $v=xw_3+yw_4+zw_1+ww_2$ with $x,y,z,w\in \mathbb {Z}_p$. Hence, $\delta (p,L',m)=\alpha (p,L',m)=1-1/p$.(3) Assume that
$p$ is split in $F$; hence, $P$ is superspecial. By § 3.2.2, $L'\otimes \mathbb {Z}_p=\Lambda ^\vee$ with $Q'(v)= x^2-\epsilon y^2-pz^2+\epsilon pw^2$, where $v=xe_1+ye_2+z(pe_3)+w(pe_4)$ with $x,y,z,w\in \mathbb {Z}_p$. Hence, $\delta (p,L',m)=\alpha (p,L',m)=1+1/p$.
4.4.3
Consider 
$L=L_{\rm S}$.
(1) Assume that
$P$ is superspecial. By § 3.3, we have $Q'(v)=xy+\epsilon z^2+pw^2-p\epsilon u^2$, where $v=xw_3+yw_4+zw_5+ww_2+uw_1$ with $x,y,z,w,u\in \mathbb {Z}_p$ and $w_i$ are given right above (3.3.1). Hence, if $p\nmid m$, then $\delta (p,L',m)=\alpha (p,L',m)\leq 1+1/p$ by [Reference HankeHan04, Table 1]. If $v_p(m)=1$, then the quadratic form of $L'_I$ is $p(xy+\epsilon z^2)+ w^2-\epsilon u^2$ and, hence, $\delta (p,{L}^{\prime},m) = \alpha ^*(p,{L}^{\prime},m) + p^{-2}\alpha (p,{{L}^{\prime}}_I,m/p)$ $= (1-p^{-2}) + p^{-2}(1 + p^{-1}) = 1 + p^{-3}$.(2) Assume that
$P$ is supergeneric. By § 3.3, $L'\otimes \mathbb {Z}_p=\Lambda ^\vee$ and, hence, the quadratic form is $pxy+\epsilon z^2+pw^2-p\epsilon u^2$. If $p\nmid m$, then $\delta (p,L',m)=\alpha (p,L',m)=0 \text { or } 2$; if $v_p(m)=1$, then the quadratic form of $L'_I$ is $p\epsilon z^2+xy+ w^2-\epsilon u^2$ and, hence, $\delta (p,L',m)=\alpha ^*(p,L',m)+\alpha (p,L'_I,m/p)=0+1+p^{-2}=1+p^{-2}$ by [Reference HankeHan04, Table 1].
We now estimate 
$\delta (p,L''',m)$ for sublattices lattices 
$L'''$ of 
$L'$ defined in § 4.2.1.
Lemma 4.4.4 If 
$p\nmid m$, then 
$\delta (p,L''',m)\leq 2$.
Proof. By Lemma 4.4.1, 
$\delta (p,L''',m)=\alpha (p,L''',m)$. Write the quadratic form 
$Q'$ on 
$L'''$ into the diagonal form 
$\sum _{i=1}^{\operatorname {rk} L'''} a_i x_i^2$ with 
$a_i\in \mathbb {Z}_p$ and we may assume that there exists 
$a_i$ such that 
$p\nmid a_i$; otherwise 
$\delta (p,L''',m)=0$, then we are done. Now let 
$\tilde {L}'''$ denote the quadratic form 
$\sum _{1\leq i\leq \operatorname {rk} L''',\, p\nmid a_i} a_i x_i^2$. Then by definition, 
$\alpha (p,L''',m)=\alpha (p, \tilde {L}''',m)$. Since 
$p\mid \operatorname {disc} L'$, then 
$p\mid \operatorname {disc} L'''$ and 
$\operatorname {rk} \widetilde {L'''}\leq \operatorname {rk} L'''-1\leq 4$. Then by [Reference HankeHan04, Table 1], 
$\alpha (p, \tilde {L}''',m)\leq 2$ and hence 
$\delta (p,L''',m)\leq 2$.
Lemma 4.4.5 Assume that 
$L=L_{\rm S}$ and 
$v_p(m)=1$. We have 
$\delta (p,L''',m)\leq 2+2p$. Moreover, if 
$P$ is superspecial and 
$[L':L''']=p$, then 
$\delta (p,L''',m)\leq 4$.
Proof. By Lemma 4.4.1, 
$\delta (p,L''',m)=\alpha ^*(p,L''',m)+p^{1-s_0}\alpha (p,L'''_I,m/p)\leq \alpha (p,L''',m)+p\alpha (p,L'''_I,m/p)$. By the proof of Lemma 4.4.4, we have 
$\alpha (p,L''',m)=\alpha (p,\tilde {L}''',m)\leq 2$. The same argument implies that 
$\alpha (p,L'''_I,m/p)\leq 2$ if 
$\operatorname {rk}(\tilde {L}''')\leq 4$. If 
$\operatorname {rk}(\tilde {L}''')=5$, then it is isotropic and we write the quadratic form as 
$xy+Q_1(z)$. The equation 
$xy+Q_1(z)\equiv (m/p) \bmod p$ has 
$(p-1)p^3$ solutions in 
$\mathbb {F}_p^5$ with 
$x\neq 0$ and has at most 
$p^4$ solutions with 
$x=0$. Hence 
$\alpha (p, L''',m/p)=\alpha (p, \tilde {L}''',m/p)<2$. Therefore, 
$\delta (p,L''',m)\leq 2+2p$.
If 
$P$ is superspecial and 
$[L':L''']=p$, then 
$s_0\geq 1$ and, hence, 
$\delta (p,L''',m)\leq \alpha ^*(p,L''',m)+\alpha (p,L'''_I,m/p)\leq 4$.
The following lemma, which is the main goal of this subsection, will be used to compare the local intersection number at a supersingular point 
$P$ with the global intersection number.
Lemma 4.4.6 Notation as in § 4.2.1 and consider 
$m\in T$ (defined in § 4.3.3).
(1) If
$P$ is superspecial or $L=L_{\rm H}$, then
\[ \frac{q(m)_{L'}}{-q(m)_L}\leq \frac{1}{p-1}. \](2) If
$L=L_{\rm S}$ and $P$ is supergeneric, then
\[ \frac{q(m)_{L'}}{-q(m)_L}\leq \frac{2}{p^2-1}. \](3) If
$p\nmid m$, then
\[ \frac{q(m)_{L'''}}{-q(m)_L}\leq \frac{2}{\sqrt{|(L'''\otimes \mathbb{Z}_p)^\vee/(L'''\otimes \mathbb{Z}_p)|}(1-p^{-2})}. \](4) Assumption as in Lemma 4.4.5, then
moreover, if\[ \frac{q(m)_{L'''}}{-q(m)_L}\leq \frac{2p}{\sqrt{|(L'''\otimes \mathbb{Z}_p)^\vee/(L'''\otimes \mathbb{Z}_p)|}(1-p^{-1})}; \]$P$ is superspecial and $[L':L''']=p$, then
\[ \frac{q(m)_{L'''}}{-q(m)_L}\leq \frac{4}{p^2-1}. \]
Proof. Recall from § 4.2.1 that 
$L'''\otimes \mathbb {Z}_\ell \cong L\otimes \mathbb {Z}_\ell, \forall \ell \neq p$; hence, for 
$\ell \neq p$, we have 
$\delta (\ell,L''',m)=\delta (\ell,L,m)$ and 
$\det L'''=p^k \det L$ for some 
$k\in \mathbb {Z}_{\geq 0}$. As 
$L$ is self-dual at 
$p$, then 
$p\nmid \det L$; by § 3.1.2, 
$\det L'=p^{2b} \det L$ for some 
$b\in \mathbb {Z}_{>0}$ (concretely, one may deduce this fact by the explicit formula of 
$Q'$ in §§ 4.4.2–4.4.3) and, hence, 
$k\in 2 \mathbb {Z}_{>0}$. Thus, 
$\chi _{4 \det L}(d)=\chi _{4 \det L'}(d)$ and 
$\chi _{-2 m_0 \det L}(d)=\chi _{-2 m_0 \det L'}(d)$ if 
$p\nmid d$.
Therefore, by Theorems 4.1.6 and 4.2.2, we have that for 
$L=L_{\rm H}$, 
$p\nmid m$,
\begin{align*} \frac{q(m)_{L'''}}{-q(m)_L}&=\frac{\delta(p,L''',m)}{\sqrt{|(L'''\otimes \mathbb{Z}_p)^\vee/(L'''\otimes \mathbb{Z}_p)|}(1-\chi_{4\det L}(p)p^{-2})}\\ &\leq \frac{\delta(p,L''',m)}{\sqrt{|(L'''\otimes \mathbb{Z}_p)^\vee/(L'''\otimes \mathbb{Z}_p)|}(1-p^{-2})}; \end{align*}
for 
$L=L_{\rm S}$, 
$v_p(m)\leq 1$, we observe that 
$m_0$ remains the same for 
$L$ and 
$L'''$ and 
$p\nmid f$ and, hence,
\[ \frac{q(m)_{L'''}}{-q(m)_L}=\frac{\delta(p,L''',m)(1-\chi_{\mathcal{D}}(p)p^{-2})}{\sqrt{|(L'''\otimes \mathbb{Z}_p)^\vee/(L'''\otimes \mathbb{Z}_p)|}(1-p^{-4})}\leq \frac{\delta(p,L''',m)}{\sqrt{|(L'''\otimes \mathbb{Z}_p)^\vee/(L'''\otimes \mathbb{Z}_p)|}(1-p^{-2})}. \]Therefore, parts (1) and (2) follow from §§ 4.4.2–4.4.3; part (3) follows from Lemma 4.4.4; part (4) follows from Lemma 4.4.5.
5. The decay lemma for supersingular points and its proof in the Hilbert case
The goal of this section is to prove that special endomorphisms ‘decay rapidly’. More precisely, consider a generically ordinary two-dimensional abelian scheme over 
$\bar {\mathbb {F}}_p[[t]]$ whose special fiber is supersingular. We consider the lattice of special endomorphisms of the abelian scheme mod 
$t^N$ as 
$N$ varies, and establish bounds for the covolume of these lattices. These bounds are exactly what we need to bound the local intersection multiplicity 
$\operatorname {Spf} \bar {\mathbb {F}}_p[[t]] \cdot Z(m)$: see Lemma 7.2.1. The precise definitions and results are in Definition 5.1.1 and Theorem 5.1.2.
Throughout this section, as in § 3, 
$k=\bar {\mathbb {F}}_p$, 
$W=W(k)$, and 
$K=W[1/p]$. We focus on the behavior of the curve 
$C$ in Theorems 1 and 5 in a formal neighborhood of a supersingular point 
$P$, so we may let 
$C = \operatorname {Spf} k[[t]]$ denote a generically ordinary formal curve in 
$\mathcal {M}_k$ which specializes to 
$P$. As in § 3.1.5, 
$\sigma$ denote both the Frobenius on 
$K$ and the Frobenius on the coordinate rings 
$W[[x,y], W[[x,y,z]]$ of 
$\widehat {\mathcal {M}}_{P}$, which is the unique extension of the Frobenius action on 
$W$ for which 
$\sigma (x)=x^p$, 
$\sigma (y)=y^p$, and 
$\sigma (z)=z^p$. For a matrix 
$M$ with entries in 
$K[[x,y]]$ or 
$K[[x,y,z]]$, we use 
$M^{(n)}$ to denote 
$\sigma ^n(M)$. Also recall we set 
$\lambda \in \mathbb {Z}_{p^2}^\times$ such that 
$\sigma (\lambda ) = - \lambda$. We use 
$\sigma _t$ to denote the Frobenius on 
$K[[t]]$ which extends 
$\sigma$ on 
$K$ and sends 
$t$ to 
$t^p$.
5.1 Statement of the decay lemma and the first reduction step
The map 
$C\rightarrow \mathcal {M}_k$ gives rise to a local ring homomorphism from 
$k[[x,y]] \rightarrow k[[t]]$ (in the Hilbert case) or 
$k[[x,y,z]]\rightarrow k[[t]]$ (in the Siegel case), and we denote by 
$x(t)$, 
$y(t)$, and 
$z(t)$ the images of 
$x$, 
$y$, and 
$z$, respectively. Let 
$v_t$ denote the 
$t$-adic valuation map on 
$k[[t]]$. Let 
$A$ denote the 
$t$-adic valuation of the local equation defining the non-ordinary locus in Corollary 3.4.2. More precisely, if 
$P$ superspecial, then 
$A=v_t(xy)$ in the Hilbert case and 
$A=v_t(xy+{z^2}/{4\epsilon })$ in the Siegel case.
Definition 5.1.1 Let 
$w$ denote a special endomorphism of the 
$p$-divisible group at 
$P$ (i.e. 
$w$ is an element in 
$L'\otimes \mathbb {Z}_p$; see Definitions 2.2.4 and 2.2.9).
(1) We say that
$w$ decays rapidly if $p^n w$ does not lift to an endomorphism modulo $t^{A_n+1}$ for all $n\in \mathbb {Z}_{\geq 0}$, where $A_n:=[A(p^n+p^{n-1}+\cdots +1+{1}/{p})]$; here $[x]$ denotes the maximal integer $y$ such that $y\leq x$.(2) We say that a
$\mathbb {Z}_p$-submodule of $L'\otimes \mathbb {Z}_p$ decays rapidly if every primitive vector in the submodule decays rapidly.(3) We say that
$w$ decays very rapidly if $p^n w$ does not lift to an endomorphism modulo $t^{A_{n-1} + ap^n+1}$ for some constant $a \leq A/2$ (independent of $n$), for all $n\in \mathbb {Z}_{\geq 0}$, where $A_n$ is defined in part (1) and we define $A_{-1}=[A/p]$.
We remark that the value 
$a$ will be one of the valuations of a local coordinate equation, used to prove Proposition 5.1.3.
Theorem 5.1.2 (Decay lemma)
Assume 
$P$ is superspecial. There exists a rank-
$3$ 
$\mathbb {Z}_p$-submodule of 
$L'\otimes \mathbb {Z}_p$ which decays rapidly and furthermore, there is a primitive vector in this submodule which decays very rapidly.
Here we only state the decay lemma for a superspecial point because we do not need to work with supergeneric points to prove Theorems 1 and 5. We refer the reader to the appendix of [Reference Maulik, Shankar and TangMST18] for a decay lemma when 
$P$ is supergeneric.
Proposition 5.1.3 Assume 
$P$ is superspecial. With respect to the 
$w_i$-basis in §§ 3.2–3.3, there exists a rank-
$3$ 
$\mathbb {Z}_p$-submodule of 
$L'\otimes \mathbb {Z}_p$ such that for every primitive 
$w$ in this submodule, the coefficients of 
$1=t^0, \ldots,t^{A(1+p+\cdots +p^n)}$ in the power series 
$p^n\tilde {w}\in (K[[t]])^4$ (or 
$(K[[t]])^5$) do not all lie in 
$W^4$ (or 
$W^5$) for all 
$n\in \mathbb {Z}_{\geq 0}$ (property DR); moreover, there exist 
$a\leq A/2$ (independent of 
$n$) and a primitive 
$w$ in the rank-
$3$ submodule such that the coefficients of 
$1,\ldots, t^{A(1+p+\cdots +p^{n-1})+ap^n}$ in 
$p^n\tilde {w}\in (K[[t]])^4$ (or 
$(K[[t]])^5$) do not all lie in 
$W^4$ (or 
$W^5$) for all 
$n\in \mathbb {Z}_{\geq 0}$ (property DvR).
We now prove the decay lemma assuming the above proposition holds.
Proof of Theorem 5.1.2 assuming Proposition 5.1.3 holds To ease exposition we focus on the Hilbert case and the proof holds verbatim for the Siegel case. For 
$m\in \mathbb {Z}_{\geq 0}$, let 
$S_m$ denote 
$\operatorname {Spec} k[t]/(t^m)$ and let 
$D_m$ denote the 
$p$-adic completion of the PD enveloping algebra of the ideal 
$(t^m,p)$ in 
$W[[t]]$. Let 
$\iota _m$ denote the composite map 
$S_m \rightarrow \operatorname {Spf} k[[t]] \rightarrow \operatorname {Spf} k[[x,y]]$. Then by [Reference de JongdJ95, § 2.3], there exists a functor from the category of 
$p$-divisible groups over 
$S_m$ to the category Dieudonné modules over 
$D_m$. More precisely, a special endomorphism 
$\tilde {w}_m$ of the 
$p$-divisible group over 
$S_m$ which specializes to 
$w\in L'\otimes \mathbb {Z}_p$ gives rise to an endomorphism of the Dieudonné module which specializes to 
$w$. By functoriality of Dieudonné modules, images of special endomorphisms are horizontal sections of 
$\iota _m^* \mathbb {L}_{\mathrm {cris}}(D_m)$ stable under the Frobenius action; here the connection on 
$\iota _m^* \mathbb {L}_{\mathrm {cris}}(D_m)$ is the pull-back of the connection on 
$\mathbb {L}_{\mathrm {cris}}(W[[x,y]])$ by a ring homomorphism 
$W[[x,y]]\rightarrow W[[t]]$ which liftsFootnote 25 
$k[[x,y]]\rightarrow k[[t]]$ given by 
$C$ and the 
$\sigma _t$-linear Frobenius is given in [Reference MoonenMoo98, § 4.3.3].Footnote 26
The connection on 
$\mathbb {L}_{\mathrm {cris}}(W[[x,y]])$ gives rise to a connection on 
$\mathbb {L}_{\mathrm {cris},P}(W)\otimes _W K[[x,y]]\supset \mathbb {L}_{\mathrm {cris}}(W[[x,y]])$. Let 
$\tilde {w}$ denote the horizontal section in 
$\mathbb {L}_{\mathrm {cris},P}(W)\otimes _W K[[x,y]]$ extending 
$w\in L'\otimes \mathbb {Z}_p\subset \mathbb {L}_{\mathrm {cris},P}(W)$. As the image of 
$\tilde {w}_m$ in 
$\iota _m^* \mathbb {L}_{\mathrm {cris}}(D_m)$ is horizontal and the connection on 
$\iota _m^* \mathbb {L}_{\mathrm {cris}}(D_m)$ is the pull-back connection, then 
$\tilde {w}_m=\iota _m^* \tilde {w}$. Therefore, if 
$w$ lifts to a special endomorphism in 
$S_m$, then 
$\iota _m^* \tilde {w} \in \iota _m^* \mathbb {L}_{\mathrm {cris}}(D_m)\subset \mathbb {L}_{\mathrm {cris},P}(W)\otimes _W K[[t]]$.
The section 
$\tilde {w}$ is constructed in [Reference KisinKis10, § 1.5.5] as follows. Recall from §§ 3.2–3.3, the Frobenius on 
$\mathbb {L}_{\mathrm {cris}}(W[[x,y]])$, with respect to a 
$\varphi$-invariant basis 
$\{w_i\}$, is given by 
$(I+F)\circ \sigma$ for some matrix 
$F$ with entries in 
$(x,y)K[x,y]$. We define 
$F_{\infty }$ to be the infinite product 
$\prod _{i = 0}^{\infty } (1 + F^{(i)})$, where 
$F^{(i)}$ is the 
$i$th 
$\sigma$-twist of 
$F$ (recall 
$\sigma (x)=x^p, \sigma (y)=y^p$). As 
$v_t(y), v_t(x)\geq 1$, the product is well-defined and the entries of 
$F_{\infty }$ are power series valued in 
$K[[t]]$. The 
$\mathbb {Q}_p$-span of the columns of 
$F_{\infty }$ are vectors of 
$\mathbb {L}_{\mathrm {cris},P}(W)\otimes K[[x,y]]$ which are Frobenius stable and horizontal. Then 
$\tilde {w}$ is the unique vector in the above 
$\mathbb {Q}_p$-span which specializes to 
$w$ modulo 
$(x,y)$; in other words, 
$\tilde {w}=F_{\infty } w$.
Now we are ready to reduce to the proof of the decay lemma to the following proposition. Indeed, by Proposition 5.1.3, with respect to 
$\{w_i\}$, there exists a rank-
$3$ 
$\mathbb {Z}_p$-submodule of 
$L'\otimes \mathbb {Z}_p$ such that for every primitive 
$w$ in this submodule, the coefficient of 
$t^{k_n}$ for some 
$k_n\leq A(1+p+\cdots +p^{n+1})$ in 
$p^n \tilde {w}$ does not lie in 
$(p^{-1}W)^4$; because 
$p\mathbb {L}_{\mathrm {cris},P}(W)\subset L'\otimes W$, with respect to a 
$W$-basis of 
$\mathbb {L}_{\mathrm {cris},P}(W)$, the coefficient of 
$t^{k_n}$ in 
$p^n \tilde {w}$ does not lie in 
$W^4$. On the other hand, for any 
$N< p(A_n+1)$, we have 
$p^{-1}t^N\notin D_{A_n+1}$. Note that 
$p(A_n+1)>p A(p^n+\cdots + 1/p)=A(p^{n+1}+\cdots +1)\geq k_n$. Hence, 
$p^n \tilde {w}$ does not extend to a special endomorphism over 
$S_{A_n+1}$. Thus, this rank-
$3$ submodule decays rapidly. Moreover, the existence of a vector decaying very rapidly follows by the second assertion of Proposition 5.1.3 via the same argument and the fact that 
$p(A_{n-1}+ap^n+1)>p( A(p^{n-1}+\cdots + 1/p)+ap^n)=A(p^{n}+\cdots +1)+ap^{n+1}$.
By a slight abuse of terminology, if a submodule of 
$L'\otimes \mathbb {Z}_p$ satisfies the property DR (with respect to basis 
$\{w_i\}$), we also say that this submodule decays rapidly; if a primitive vector satisfies property DvR, we also say that this vector decays very rapidly. By the proof of Theorem 5.1.2 above, property DR (respectively, DvR) implies decaying (respectively, very) rapidly in the sense of Definition 5.1.1.
The rest of this section is devoted to prove Proposition 5.1.3 for the Hilbert case and its proof for the Siegel case is given in § 6. In the following, the split/inert case means that 
$p$ is split/inert in the real quadratic field attached to the Hilbert modular surface.
In the Hilbert case, by Corollary 3.4.2, the non-ordinary locus is cut out by the equation 
$xy = 0$. As in the proof of reducing Theorem 5.1.2 to Proposition 5.1.3, we pick a lift 
$W[[x,y]]\rightarrow W[[t]]$ of the local ring homomorphism 
$k[[x,y]]\rightarrow k[[t]]$ defined by 
$C$. As 
$C$ is generically ordinary, we have that both 
$x$ and 
$y$ map to power series in 
$W[[t]]$ which are non-zero 
$\bmod \, p$. Without loss of generality, we assume that 
$v_t(x) \leq v_t(y)$, and that 
$x(t) = t^a + \cdots$ and 
$y(t) = \alpha t^b + \cdots$, where 
$\alpha \in W^\times$. We will see that the value 
$a = v_t(x)$ will be the one that is used in the statement of Proposition 5.1.3.
5.2 Decay in the split case
Notation as in the proof of Theorem 5.1.2. We first compute 
$F_\infty =\prod _{i = 0}^{\infty } (1 + F^{(i)})$, where by (3.2.2),
\begin{align*} F=\begin{bmatrix} \dfrac{xy}{2p} & -\dfrac{\lambda xy}{2p} & \dfrac{x+y}{2p} & \dfrac{-\lambda(x -y)}{2p}\\ \dfrac{xy}{2\lambda p} & - \dfrac{xy}{2p} & \dfrac{x+y}{2\lambda p} & \dfrac{-(x-y)}{2p}\\ \dfrac{x+y}{2} & \dfrac{-\lambda (x + y)}{2} & 0 & 0\\ \dfrac{x-y}{2\lambda} & \dfrac{-(x - y)}{2} & 0 & 0\\ \end{bmatrix}. \end{align*}
We remind the reader that 
$(I+F)\circ \sigma = \operatorname {Frob}$.
Let 
$F_{\infty }(1)$ and 
$F_{\infty }(2)$ denote the top-left and top-right 
$2 \times 2$ blocks of 
$F_{\infty }$ respectively. To simplify the notation, defineFootnote 27
\begin{align*} G = \begin{bmatrix} \dfrac{1}{2} & \dfrac{-\lambda}{2}\\ \dfrac{1}{2\lambda} & \dfrac{-1}{2} \end{bmatrix}, \quad H_u = \begin{bmatrix} \dfrac{1}{2} & \dfrac{-\lambda}{2}\\ \dfrac{1}{2\lambda} & \dfrac{-1}{2} \end{bmatrix}, \quad H_l = \begin{bmatrix} \dfrac{1}{2} & \dfrac{-\lambda}{2}\\ \dfrac{1}{2\lambda} & \dfrac{-1}{2} \end{bmatrix}, \end{align*}
and let 
$F_t$, 
$F_u$ and 
$F_l$ denote the top-left, top-right, and bottom-left 
$2 \times 2$ blocks of 
$F$. The product expansion of Frobenius 
$F_\infty =\prod _{i = 0}^{\infty } (1 + F^{(i)})$ allows for 
$F_{\infty }$ to be expressed as an infinite sum of finite products of 
$\sigma$-twists of 
$F_t$, 
$F_u$, and 
$F_l$. The following elementary lemma picks out the terms in 
$F_{\infty }(1), F_{\infty }(2)$ with the desired 
$p$-power on the denominators.
Lemma 5.2.1
(1) We have that
$F_{\infty }(1)$ is a sum of products of the form $\prod _{i=0}^{m_1 + 2m_2 } X_i^{(n_i)}$. Here $X_i$ is $F_t$, $F_u$, or $F_l$,Footnote 28 $m_1 + 1$ is the number of occurrences of $F_t$, and $m_2$ is the number of occurrences of the pair $F_u, F_l$ and $n_i$ is a strictly increasing sequence of non-negative integers. The $p$-adic valuation of $\prod _{i=0}^{m_1 + 2m_2 } X_i^{(n_i)}$ is $-(n+1)$, where $n = m_1 + m_2$. The analogous statement holds for $F_{\infty }(2)$.(2) Fix values of
$m_1,m_2$ as above. Among all the terms in the above sum, those with minimal $t$-adic valuation only occur when $n_i = i$, and either when $X_0 = X_1 = \cdots = X_{m_1} = F_t$ or $X_0 = X_2 = \cdots = X_{2m_2-2} = F_u$. The analogous statement holds for $F_{\infty }(2)$.(3) (For
$F_{\infty }(1)$) The product $\prod _{i =0}^{m_1}F_t^{(i)} \prod _{i = 0}^{m_2-1} F_u^{(m_1 + 2i + 1)}F_l^{(m_1 + 2i + 2)}$ (modulo terms with smaller $p$-power in denominatorsFootnote 29) equals
\[ \displaystyle \frac{1}{p^{n+1}}\prod_{i =0}^{m_1}G^{(i)}(xy)^{(i)} \prod_{i = 0}^{m_2 -1} H_u^{(m_1 + 2i + 1)}H_l^{(m_1 + 2i+2)}(x^{1+p} + y^{1+p})^{(m_1 + 2i + 1)}. \](4) (For
$F_{\infty }(2)$) The product $\prod _{i =0}^{m_1}F_t^{(i)} \prod _{i = 0}^{m_2-1} F_u^{(m_1 + 2i + 1)}F_l^{(m_1 + 2i + 2)} \cdot F_u^{(m_1 + 2m_2 + 1)}$ (modulo terms with smaller $p$-power in denominators) equals
\[ \displaystyle \frac{1}{p^{n+2}}\prod_{i =0}^{m_1}G^{(i)}(xy)^{(i)} \prod_{i = 0}^{m_2 - 1} H_u^{(m_1 + 2i + 1)}H_l^{(m_1 + 2i+2)}(x^{1+p} + y^{1+p} )^{(m_1 + 2i + 1)} \cdot F_u^{(m_1 + 2m_2 + 1)}. \]
5.2.2 Notation. We make the following definition to further lighten the notation.
Let 
$P(1)_{m_2,n}$ denote the product
\[ \displaystyle \prod_{i=0}^{m_1} G^{(i)}\prod_{i=0}^{m_2-1}H_u^{(m_1 + 2i + 1)}H_l^{(m_1 + 2i + 2)}. \]
Recall that 
$A = a + b$ denotes the 
$t$-adic valuation 
$v_t(xy)$ of 
$xy$ and let 
$B$ denote 
$v_t(x^{p+1} + y^{p+1})$. Note that 
$B \geq a(p+1)$ and the equality holds unless 
$a = b$.
To prove Proposition 5.1.3, we consider the following case-by-case analysis depending on the relation between 
$a$ and 
$b$. The following elementary lemmas will be used in the case-by-case analysis.
Lemma 5.2.3 Let 
$n, e, f$ be in 
$\mathbb {Z}_{\geq 0}$.
(1) The kernel of the
$2 \times 2$ matrix $P(1)_{e,n}$ modulo $p$ is defined over $\mathbb {F}_{p^2}$ but not over $\mathbb {F}_p$.(2) The reductions of
$P(1)_{e,n}$ and $P(1)_{f,n}$ modulo $p$ are not scalar multiples (over $k$) of each other if $e \not \equiv f \mod 2$. In particular, these reductions are not scalar multiples of each other if $f = e \pm 1$.
Proof. As the entries of 
$G$, 
$H_u$, and 
$H_l$ are all in 
$W(\mathbb {F}_{p^2})[1/p]$, it follows that 
$G^{(2m)} = G$ and 
$G^{(2m+1)} = G^{(1)}$ (and the analogous statements hold for 
$H_u$ and 
$H_l$). A direct computation shows that 
$GG^{(1)}G = G$, 
$H_uH_l^{(1)}H_uH_l^{(1)} = H_uH_l^{(1)}$, and 
$H_u^{(1)}H_lH_u^{(1)}H_l= H_u^{(1)}H_l$. Therefore, if 
$n-e$ is odd, then 
$P(1)_{e,n}$ simplifies to 
$GG^{(1)}H_uH_l^{(1)}$, 
$GG^{(1)}$, or 
$H_uH_l^{(1)}$; if 
$n-e$ is even, 
$P(1)_{e,n}$ simplifies to 
$G$ or 
$GH_u^{(1)}H_l$. A direct computation shows that the matrices 
$GG^{(1)}$, 
$H_uH_l^{(1)}$ and 
$GG^{(1)}H_uH_l^{(1)}$ (respectively, 
$G$ and 
$GH_u^{(1)}H_l$) are equal to
\[ \begin{bmatrix} \dfrac{1}{2} & \dfrac{\lambda}{2}\\ \dfrac{1}{2\lambda} & \dfrac{1}{2}\\ \end{bmatrix}\quad \left(\text{respectively, }\begin{bmatrix} \dfrac{1}{2} & \dfrac{-\lambda}{2}\\ \dfrac{1}{2\lambda} & \dfrac{-1}{2}\\ \end{bmatrix}\right). \] In either case, because 
$\lambda \in W(\mathbb {F}_{p^2})\backslash \mathbb {Z}_p$, there is no non-trivial 
$\mathbb {F}_p$-linear combination of the columns modulo 
$p$ which equals zero; this implies part (1). Furthermore, the above matrices are clearly not scalar multiples of each other, whence part (2) follows.
Lemma 5.2.4 Let 
$n, e, f$ be in 
$\mathbb {Z}_{\geq 0}$.
(1) The kernel of the
$2 \times 2$ matrix $P(1)_{e,n-1}\cdot H_u^{(n+e)}$ modulo $p$ is defined over $\mathbb {F}_{p^2}$ but not $\mathbb {F}_p$.(2) The reductions of
$P(1)_{e,n-1} \cdot H_u^{(n+e)}$ and $P(1)_{f,n-1}\cdot H_u^{(n+f)}$ modulo $p$ are not scalar multiples of each other if $e\not \equiv f \mod 2$. In particular, these reductions are not scalar multiples of each other if $f = e \pm 1$.
Proof. We argue along the lines of the proof of Lemma 5.2.3. Indeed, if 
$n-e$ is odd (respectively, even), we are reduced to the cases of 
$GG^{(1)}H_uH_l^{(1)}H_u$, 
$GG^{(1)}H_u$, 
$H_uH_l^{(1)}H_u$, and 
$H_u$ (respectively, 
$GH_u^{(1)}H_lH_u^{(1)}$ and 
$GH_u^{(1)}$). The rest of the argument is similar.
We now prove Proposition 5.1.3 when 
$p$ is split in the real quadratic field defining the Hilbert modular surface. The proof is a case-by-case study in the following four cases based on the relation of 
$a=v_t(x)$ and 
$b=v_t(y)$. The idea is to pick out the term(s) with minimal 
$t$-adic valuation among all the terms with the same 
$p$-power denominators given in Lemma 5.2.1. Case 4 is the generic case and it is easy to pick out such terms so we give the proof directly. In Cases 1–3, we first state the lemmas on the terms with minimal 
$t$-adic valuation and then prove the decay lemma. For the convenience of the reader, we summarize the desired vectors which decay rapidly enough at the beginning of each case.
Case 1: $a = b$
Recall that 
$A=v_t(xy)=a+b=2a$.
We prove that every vector in 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2,w_i\}$ decays rapidly, where 
$w_i = w_4$ if the 
$t$-adic valuation of 
$x - y$ is 
$> a$, and 
$w_i = w_3$ otherwise. Moreover, 
$w_i$, 
$i=3,4$ respectively, decays very rapidly.
Lemma 5.2.5
(1) Among the terms appearing in
$F_{\infty }(1)$ described in Lemma 5.2.1 with denominator $p^{n+1}$, the unique term with minimal $t$-adic valuation is
\[ P(1)_{0,n}(xy)^{1 + p + \cdots + p^{n}}. \](2) Among the terms appearing in
$F_{\infty }(2)$ described in Lemma 5.2.1 with denominator $p^{n+1}$, the unique term with minimal $t$-adic valuation is
\[ P(1)_{0,n-1}\cdot F_u^{(n )} (xy)^{1 + p + \cdots + p^{n-1}}. \]
This lemma follows directly from Lemma 5.2.1 and the assumption that 
$a = b$.
Proof of Proposition 5.1.3 in this case We first prove that every primitive vector 
$w\in \operatorname {Span}_{\mathbb {Z}_p} \{w_1,w_2\}$ decays rapidly. Indeed, write 
$w=cw_1+dw_2$, by Lemmas 5.2.3(1) and 5.2.5(1), there is a unique (non-vanishing) term in 
$F_{\infty }(1)w$ with denominator 
$1/p^{n+1}$ and minimal 
$t$-adic valuation 
$A(1+p+\cdots + p^n)$ given by 
$P(1)_{0,n}[c\quad d]^{\rm T} (xy)^{1+p+\cdots +p^n}$. Hence, modulo 
$t^{A(1+p+\cdots + p^n)+1}$, the horizontal section 
$p^n\tilde {w}=F_{\infty }(p^nw)$ does not lie in 
$W[[t]]$ and, hence, 
$w$ decays rapidly.
Second, let 
$i\in \{3,4\}$ be defined as above and we show that 
$w_i$ decays very rapidly. Note that our definition of 
$w_i$ implies that the first two entries of the 
$i$th row of 
$F$ have 
$t$-adic valuation equalling 
$a$. Furthermore, by Lemma 5.2.3(1), 
$P(1)_{0,n-1} \cdot v \neq 0$ mod 
$p$, where 
$v$ is the 
$n$th Frobenius twist of either column of 
$H_u$. Therefore, among the terms in the 
$i$th column of 
$F_{\infty }$ with denominator 
$p^{n+1}$, the term with minimal 
$t$-adic valuation has 
$t$-adic valuation 
$2a(1 + p + \cdots + p^{n-1}) + ap^n$. Hence, 
$w_i$ decays very rapidly since 
$a\leq (2a)/2=A/2$.
Finally, we show that every vector in 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2,w_i\}$ decays rapidly. Let 
$w_u$ denote a primitive vector in the span of 
$w_1,w_2$. It suffices to show that every vector which either has the form 
$p^m w_u + w_i$ or 
$w_u + p^m w_i$ decays rapidly, where 
$m \geq 0$. We first prove that every vector which has the form 
$p^m w_u + w_i$ decays rapidly where 
$m \geq 0$. Indeed, consider the two-dimensional vector whose entries are the first two entries of 
$F_{\infty } \cdot p^m w_u$. The 
$t$-adic valuation of the coefficient of 
$1/p^{n+1}$ equals 
$2a(1 + p + \cdots + p^{n+m})$. Similarly, consider the two-dimensional vector whose entries are the first two entries of 
$F_{\infty } \cdot w_i$. The 
$t$-adic valuation of the coefficient of 
$1/p^{n+1}$ equals 
$2a(1 + p + \cdots + p^{n-1}) + ap^n$. Regardless of the value of 
$m$, the latter quantity is always smaller than the former quantity, whence it follows that 
$p^mw_u + w$ decays rapidly. Now, consider a vector of the form 
$w_u + p^m w_i$, where 
$m > 0$. Analogous to the previous case, consider the two-dimensional vector whose entries are the first two entries of 
$F_{\infty } \cdot w_u$. The 
$t$-adic valuation of the sum of all terms with denominator 
$p^{n+1}$ equals 
$2a(1 + p + \cdots + p^n)$. Similarly, consider the two-dimensional vector whose entries are the first two entries of 
$F_{\infty } \cdot p^m w_i$. The 
$t$-adic valuation of the coefficient of 
$1/p^{n+1}$ equals 
$2a(1 + p + \cdots + p^{n+m-1}) + ap^{n+m}$. Regardless of the value of 
$m$ (recall that 
$m>0$), the latter quantity is always greater than the former quantity, whence it follows that 
$p^mw_u + w$ decays rapidly.
Case 2: $b = p^{2e}a$ for some $e\in \mathbb {Z}_{\geq 1}$
We prove that 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2,w\}$ decays rapidly where 
$w$ is some primitive vector in 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$. We further prove that 
$w$ decays very rapidly.
Lemma 5.2.6
(1) Among the terms appearing in
$F_{\infty }(1)$ described in Lemma 5.2.1 with denominator $p^{n+1}$, the unique term with minimal $t$-adic valuation is
\[ P(1)_{e,n}(xy)^{1 + p + \cdots + p^{n-e}}x^{p^{n - e + 1} + p^{n-e+2} + \cdots + p^{n + e}}. \](2) Among the terms appearing in
$F_{\infty }(2)$ described in Lemma 5.2.1 with denominator $p^{n+1}$, there are exactly two terms with minimal $t$-adic valuation, and they are
and\[ P(1)_{e,n-1}\cdot F_u^{(n + e -1)} (xy)^{1 + p + \cdots + p^{n-e-1}}x^{p^{n - e} + p^{n-e+1} + \cdots + p^{n + e-2}}, \]\[ P(1)_{e+1,n-1}\cdot F_u^{(n + e)} (xy)^{1 + p + \cdots + p^{n-e-2}}x^{p^{n - e-1} + p^{n-e} + \cdots + p^{n + e-1}}. \]
Proof. In the following, we prove part (1); part (2) follows by an identical argument.
Note that the 
$t$-adic valuation of all the entries of 
$F(1)$ is 
$a+b$, and the 
$t$-adic valuation of the entries of 
$F_u$ and 
$F_l$ is 
$a$. Let 
$k,l$ be in 
$\mathbb {Z}_{\geq 0}$ such that 
$k + l = n+1$. Consider the following terms of 
$F_{\infty }(1)$ with denominator exactly 
$p^{n+1}$:
\[ X_{k,l}:= F(1)\cdot F(1)^{(1)} \cdot \cdots \cdot F(1)^{(k-1)}\cdot F_u^{(k)}F_{l}^{(k+1)}\ldots F_u^{(k+2l-2)}F_l^{(k+2l-1)}. \] Similar to Lemma 5.2.1(2), we observe that among all the terms of 
$F_{\infty }(1)$ with denominator exactly 
$p^{n+1}$ given in Lemma 5.2.1(1), for each other term 
$X$ not listed above, there exists at least one 
$X_{k,l}$ (as 
$k$ and 
$l$ vary over all non-negative integers constrained by 
$k + l = n+1$) such that 
$v_t(X_{k,l})< v_t(X)$. Therefore, to prove part (1), it suffices to show that 
$v_t(X_{k,l})$ with 
$k = n - e + 1$ and 
$l = e$ is less than 
$v_t(X_{k,l})$ with any other choice of 
$k,l$.
As 
$b = ap^{2e}$ and 
$k + l = n+1$, then
\[ f(k) := v_t(X_{k,n}) = a \biggl ((1 + p^{2e})\frac{p^k-1}{p-1} + \frac{p^{2(n-k+1)}-1}{p-1}p^k \biggr), \]
and we need to prove that 
$k = n-e +1$ minimizes this expression as 
$k$ ranges over 
$\mathbb {Z} \cap [0,n+1]$. Note that if we allow 
$k$ to take all real values in the interval 
$[0,n+1]$, a direct computation shows that 
$f$ is convex (i.e. 
$f''(k)>0$). Therefore, it suffices to show that 
$f(n-e+1)< f(n-e)$ and 
$f(n-e+1) < f(n-e+2)$. These claims can be verified directly and, hence, we prove part (1).
Proof of Proposition 5.1.3 in this case We first prove that 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ decays rapidly. Indeed, let 
$w'$ be a primitive vector in 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$. Lemma 5.2.3(1) implies that 
$P(1)_{e,n} \cdot w'$ mod 
$p$ is non-zero. This fact taken in conjunction with Lemma 5.2.6(1) yields that 
$w'$ decays rapidly.
Second, we prove that there exists a primitive vector 
$w\in \operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$ (independent of 
$n$) which decays very rapidly. Set
\begin{align*} Y_{e,n}&:= P(1)_{e,n-1}\cdot F_u^{(n + e -1)} (xy)^{1 + p + \cdots + p^{n-e-1}}x^{p^{n - e} + p^{n-e+1} + \cdots +p^{n + e-2}}\\ &\quad + P(1)_{e+1,n-1}\cdot F_u^{(n + e)} (xy)^{1 + p + \cdots + p^{n-e-2}}x^{p^{n - e-1} + p^{n-e} + \cdots + p^{n + e-1}}, \end{align*}
which is the sum of the two terms with minimal 
$t$-adic valuation listed in Lemma 5.2.6(2). The sum 
$Y_{e,n}$ is non-zero modulo 
$p$ by Lemma 5.2.3(2). Furthermore, up to Frobenius twists and multiplication by scalars, the matrix 
$Y_{e,n}\, \bmod p$ is independent of 
$n$. Therefore, there exists a vector 
$w\in \operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$ which is independent of 
$n$ and does not lie in the kernel of 
$Y_{e,n}\,\bmod p$. The very rapid decay of 
$w$ follows from this observation and Lemma 5.2.6(2).
Finally, a valuation-theoretic argument analogous to Case 1 shows that every primitive vector in 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2,w\}$ decays rapidly, thereby establishing Proposition 5.1.3 in this case.
Case 3: $b = p^{2e + 1} a$ for some $e\in \mathbb {Z}_{\geq 0}$
We prove that 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4,w\}$ decays rapidly where 
$w$ is some primitive vector in 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ and that 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$ decays very rapidly.
Lemma 5.2.7
(1) Among the terms appearing in
$F_{\infty }(2)$ described in Lemma 5.2.1 with denominator $p^{n+1}$, the unique term with minimal $t$-adic valuation is
\[ P(1)_{e,n-1}\cdot H_u^{(n+e)}(xy)^{1 + p + \cdots + p^{n-e-1}}x^{p^{n - e} + p^{n-e+1} + \cdots + p^{n + e}}. \](2) Among the terms appearing in
$F_{\infty }(1)$ described in Lemma 5.2.1 with denominator $p^{n+1}$, there are exactly two terms with minimal $t$-adic valuation, and they are
\[ P(1)_{e,n} (xy)^{1 + p + \cdots + p^{n-e-1}}x^{p^{n - e} + p^{n-e+1} + \cdots + p^{n + e-1}}, \]\[ P(1)_{e+1,n} (xy)^{1 + p + \cdots + p^{n-e-2}}x^{p^{n - e-1} + p^{n-e} + \cdots + p^{n + e}}. \]
Proof. The proof of this lemma is identical to that of Lemma 5.2.6, so we omit the details.
Proof of Proposition 5.1.3 in this case Analogous to Case 2, Lemmas 5.2.4 and 5.2.7(2) imply the existence of a primitive 
$w\in \operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ that decays rapidly; and by Lemmas 5.2.4(1) and 5.2.7(1), 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$ decays very rapidly. Finally, a valuation-theoretic argument shows that every primitive vector in 
$\operatorname {Span}_{\mathbb {Z}_p}\{w,w_3,w_4\}$ decays rapidly.
Case 4: $b \neq a p^e$ for any value of $e$
Proof of Proposition 5.1.3 As this is the easiest case, we are content with merely sketching a proof. Analogous to Lemmas 5.2.6 and 5.2.7, it is easy to see that in this case there are unique terms with minimal 
$t$-adic valuations with denominator 
$p^{n+1}$ occurring in both 
$F_{\infty }(1)$ and 
$F_{\infty }(2)$. It follows that every primitive vector in 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ decays rapidly and every vector in 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$ decays very rapidly. Finally, a valuation theoretic argument similar to Case 1 shows that every vector in the span of 
$w_1,w_2,w_3,w_4$ does decay rapidly, finishing the proof of Proposition 5.1.3.
5.3 Decay in the inert case
Notation as in the proof of Theorem 5.1.2 and § 3.2.1. Recall that 
$P$ is superspecial and we show that the 
$\mathbb {Z}_p$-span of 
$w_1,w_2,w_3$ decays rapidly, and the vector 
$w_3$ decays very rapidly.
Proof of Proposition 5.1.3 The proof goes along the same lines as the proof of the decay lemma for split Hilbert modular varieties, so we are content with just outlining the salient points.
We first compute 
$F_\infty =\prod _{i = 0}^{\infty } (1 + F^{(i)})$, where by (3.2.1), with respect to the basis 
$\{w_1,w_2,w_3,w_4 \}$, 
$F=\big (\begin {smallmatrix} F_t & F_u\\ F_l & 0 \end {smallmatrix}\big )$, where
\[ F_t=\frac{xy}{2p}\begin{pmatrix} -1 & \lambda \\ -1/\lambda & 1 \end{pmatrix},\quad F_u=\frac 1{2p} \begin{pmatrix} x & y\\ x/\lambda & y/\lambda \end{pmatrix},\quad F_l=\begin{pmatrix} -y & \lambda y\\ -x & \lambda x \end{pmatrix}. \]
Recall that the non-ordinary locus is cut out by the equation 
$xy = 0$ and 
$a = v_t(x)$, 
$b = v_t(y)\in \mathbb {Z}_{>0}$.
Similar to Lemma 5.2.1, it is easy to see that the top-left 
$2\times 2$ block of 
$F_{\infty }$ with 
$p$-adic valuation 
$-(n+1)$ has a term of the form 
$F_t F_t^{(1)} \ldots F_t^{(n)}$, and this term is the unique term with minimal 
$t$-adic valuation (equalling 
$(a + b)(1 + p + \cdots +p^n)$). Similarly, the top-right 
$2\times 2$ block of 
$F_{\infty }$ with 
$p$-adic valuation 
$-(n+1)$ has a term of the form 
$F_t F_t^{(1)} \ldots F_t^{(n-1)} F_u^{(n)}$, and this term is the unique term with minimal 
$t$-adic valuation (equaling 
$(a + b)(1 + p + \cdots + p^{n-1}) + ap^n$).
Arguments identical to Lemmas 5.2.3 and 5.2.4 yield that every primitive vector in the 
$\mathbb {Z}_p$ span of 
$w_1,w_2$ (and in the span of 
$w_3$) decays rapidly (very rapidly, in the case of 
$w_3$). Further, as the 
$t$-adic valuation of 
$F_t F_t^{(1)} \ldots F_t^{(m)}$ is different from the 
$t$-adic valuation of 
$F_t F_t^{(1)} \ldots F_t^{(n-1)} F_u^{(n)}$ for every pair of integers 
$n,m$, it follows that 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2, w_3\}$ also decays rapidly. The argument is elaborated on in the last paragraph of the proof for Case 1 in § 5.2.
6. Proof of the decay lemma in the Siegel case
In this section, we prove Proposition 5.1.3 and, hence, Theorem 5.1.2 (for superspecial points) in the Siegel case. We refer the reader to the appendix for a decay lemma for supergeneric points. The main idea of the proof is similar to that of the Hilbert case in § 5.
6.1 Preparation of the proof
We follow the notation in § 5, 
$k=\bar {\mathbb {F}}_p$, 
$W=W(k)$, 
$K=W[1/p]$, 
$\lambda \in \mathbb {Z}_{p^2}^\times$ such that 
$\sigma (\lambda ) = - \lambda$, and 
$C = \operatorname {Spf} k[[t]]$ a generically ordinary formal curve in 
$\mathcal {M}_k$ which specializes to a superspecial point 
$P$. This gives rise to a local ring homomorphism 
$k[[x,y,z]]\rightarrow k[[t]]$ and we pick a lift 
$W[[x,y,z]]\rightarrow W[[t]]$ (still a ring homomorphism), and we denote by 
$x(t)$, 
$y(t)$, and 
$z(t)$ the images of 
$x$, 
$y$, and 
$z$, respectively.
Let 
$a$, 
$b$, and 
$c$ denote the 
$t$-adic valuations of 
$x(t)$, 
$y(t)$, and 
$z(t)$, respectively. We adopt the convention that 
$a,b,c$ may take on the value 
$\infty$ if the corresponding power series is 
$0$. As before, 
$v_t$ denotes the 
$t$-adic valuation map on 
$K[[t]]$ or 
$k[[t]]$.
Also recall that 
$\sigma$ denotes both the Frobenius on 
$K$ and the Frobenius on the coordinate rings 
$W[[x,y,z]]$ with 
$\sigma (x)=x^p, \sigma (y)=y^p$, 
$\sigma (z)=z^p$; and for a matrix 
$M$ with entries in 
$K[[x,y,z]]$, 
$M^{(n)}$ denotes 
$\sigma ^n(M)$.
The preparation lemmas of the Siegel case are very similar to that of the split Hilbert case in the beginning of § 5.2.
6.1.1
Notation. Recall that 
$F_{\infty }=\prod _{i = 0}^{\infty } (1 + F^{(i)})$, where by (3.3.1), with respect to the basis 
$\{w_1,\ldots, w_5\}$,
\[ F=\begin{bmatrix} \dfrac{1}{2p}\biggl(xy+\dfrac{z^2}{4\epsilon}\biggr) & -\dfrac{1}{2\lambda p}\biggl(xy+\dfrac{z^2}{4\epsilon}\biggr) & \dfrac{x}{2\lambda p} & \dfrac{y}{2\lambda p} & \dfrac{z}{2\lambda p}\\ \dfrac{\lambda}{2p}\biggl(xy+\dfrac{z^2}{4\epsilon}\biggr) & -\dfrac{1}{2p}\biggl(xy+\dfrac{z^2}{4\epsilon}\biggr) & \dfrac{x}{2p} & \dfrac{y}{2p} & \dfrac{z}{2p} \\ \lambda y & -y & 0 & 0 & 0\\ \lambda x & -x & 0 & 0 & 0\\ \dfrac{\lambda z}{2\epsilon} & -\dfrac{ z}{2\epsilon} & 0 & 0 & 0 \end{bmatrix}, \]
where 
$\epsilon =\lambda ^2\in \mathbb {Z}_p^\times$. We denote by 
$F_t$, 
$F_u$, and 
$F_l$ the top-left 
$2 \times 2$ block, the top-right 
$2 \times 3$ block, and the bottom-left 
$3 \times 2$ block of 
$F$, respectively. Define
\[ G = \begin{bmatrix} \dfrac{1}{2} & \dfrac{-1}{2 \lambda}\\ \dfrac{\lambda}{2} & \dfrac{-1}{2} \end{bmatrix},\quad H_u = \begin{bmatrix} \dfrac{1}{2\lambda} & \dfrac{1}{2\lambda} & \dfrac{1}{2\lambda}\\ \dfrac{1}{2} & \dfrac{1}{2} & \dfrac{1}{2} \end{bmatrix}, \quad \text{and} \quad H_l = \begin{bmatrix} \lambda & -1\\ \lambda & -1\\ \lambda & -1 \end{bmatrix}. \]
Let 
$F_{\infty }(1)$ and 
$F_{\infty }(2)$ denote the top-left 
$2 \times 2$ block and top-right 
$2 \times 3$ of 
$F_{\infty }$, respectively.
By Corollary 3.4.2, the non-ordinary locus is cut out by the equation 
$xy + z^2/(4\epsilon ) = 0$. Let 
$\eta t^A$ and 
$\mu t^B$ denote the leading terms of 
$xy + z^2 /(4\epsilon )$ and 
$xy^p + x^p y + z^{1 + p}/(2\epsilon )$, respectively. In particular, 
$A=v_t(xy + z^2/(4 \epsilon ))$ and 
$B=v_t(xy^p + x^p y + z^{1 + p}/(2\epsilon ))$.
As in the Hilbert case, the product expansion of Frobenius 
$F_{\infty } = \prod _{i=0}^\infty (1+F^{(i)})$ allows for 
$F_{\infty }$ to be expressed as an infinite sum of finite products of 
$\sigma$-twists of 
$F_t$, 
$F_u$, and 
$F_l$. The following lemma picks out the terms in 
$F_{\infty }(1),F_{\infty }(2)$ with the desired 
$p$-power denominators, analogous to Lemma 5.2.1 in the Hilbert case.
Lemma 6.1.2
(1) We have that
$F_{\infty }(1)$ is a sum of products of the form $\prod _{i=0}^{m_1 + 2m_2 } X_i^{(n_i)}$. Here, $X_i$ is $F_t$, $F_u$, or $F_l$,Footnote 30 $m_1 + 1$ is the number of occurrences of $F_t$, and $m_2$ is the number of occurrences of the pair $F_u,F_l$, and $\{n_i\}_{i=0}^{m_1+2m_2}$ is a strictly increasing sequence of non-negative integers. The $p$-adic valuation of $\prod _{i=0}^{m_1 + 2m_2 } X_i^{(n_i)}$ is $-(n+1)$, where $n = m_1+m_2$. The analogous statement holds for $F_{\infty }(2)$.(2) Fix values of
$m_1,m_2$ as above. Among all the terms in the above sum, those with minimal $t$-adic valuation only occur when $n_i = i$ for all $i$, and either when $X_0 = X_1 = \cdots = X_{m_1} = F_t$ or $X_0 = X_2 = \cdots = X_{2m_2-2} = F_u$. The analogous statement holds for $F_{\infty }(2)$.(3) (For
$F_{\infty }(1)$) The product $\prod _{i =0}^{m_1}F_t^{(i)} \prod _{i = 0}^{m_2-1} F_u^{(m_1 + 1 + 2i)}F_l^{(m_1 + 2i + 2)}$ equals
\[ \displaystyle \frac{1}{p^{n+1}}\prod_{i =0}^{m_1}G^{(i)}(xy + z^2/2)^{(i)} \prod_{i = 0}^{m_2 -1} \frac{1}{3}H_u^{(m_1 + 2i + 1)}H_l^{(m_1 + 2i+2)}(xy^p + x^py + z^{p+1})^{(m_1 + 2i + 1)}. \](4) (For
$F_{\infty }(2)$) The product $\prod _{i =0}^{m_1}F_t^{(i)} \prod _{i = 0}^{m_2-1} F_u^{(m_1 + 2i + 1)}F_l^{(m_1 + 2i + 2)} \cdot F_u^{(m_1 + 2m_2 + 1)}$ equals
\begin{align*} &\displaystyle \frac{1}{p^{n+2}}\prod_{i =0}^{m_1}G^{(i)}(xy + z^2/2)^{(i)} \prod_{i = 0}^{m_2-1} \frac{1}{3}H_u^{(m_1 + 2i + 1)}H_l^{(m_1 + 2i+2)}(xy^p + x^py + z^{p+1})^{(m_1 + 2i + 1)}\\ &\qquad \cdot F_u^{(m_1 + 2m_2 + 1)}. \end{align*}
6.1.3
Notation. Let 
$P(1)_{m_2,n}$ denote the product 
$\displaystyle \prod _{i =0}^{m_1}G^{(i)} \prod _{i = 0}^{m_2 -1} \frac {1}{3}H_u^{(m_1 + 2i + 1)}H_l^{(m_1 + 2i+2)}$.
The following will play a similar role as Lemma 5.2.3.
Lemma 6.1.4 The kernel of 
$P(1)_{g,f+g} \bmod p$ does not contain any non-zero vector defined over 
$\mathbb {F}_p.$ Moreover, if 
$f$ is odd (respectively, even), the kernel of 
$P(1)_{g,f+g} \bmod p$ does not contain the vector 
$\big [\begin {smallmatrix} \lambda ^{-1}\\ 1 \end {smallmatrix}\big ]$ (respectively, 
$\big [\begin {smallmatrix} -\lambda ^{-1}\\ 1 \end {smallmatrix}\big ]$).
Proof. We prove the assertions by explicit computation as in Lemmas 5.2.3 and 5.2.4. Note that
\[ \frac{1}{3}H_u^{(2m)}H_l^{(2m+1)}=\frac{-1}{2}\begin{bmatrix} 1 & \lambda^{-1}\\ \lambda & 1 \end{bmatrix},\quad \frac{1}{3} H_u^{(2m-1)}H_l^{(2m)}=\frac{1}{2}\begin{bmatrix} -1 & \lambda^{-1}\\ \lambda & -1 \end{bmatrix} \]
Both these matrices satisfy the relation 
$X^2 = -X$ and, hence, 
$\prod _{i=0}^{m_2-1}H_u^{(m_1+2i+1)}H_l^{(m_1+2i+2)}$ equals, up to a multiple of 
$\pm 1$, one of these matrices depending on the parity of 
$m_1$. Similarly, we have
\[ G\cdots G^{(2m)}=\frac{1}{2}\begin{bmatrix} 1 & -\lambda^{-1}\\ \lambda & -1 \end{bmatrix},\quad G \cdots G^{(2m+1)}=\frac{1}{2}\begin{bmatrix} 1 & \lambda^{-1}\\ \lambda & 1 \end{bmatrix}. \]
Therefore, 
$P(1)_{g,f+g}$ equals 
$\pm \frac {1}{2} \big [\begin {smallmatrix} 1 & \lambda ^{-1}\\ \lambda & 1 \end {smallmatrix}\big ]$ if 
$f$ is odd, and equals 
$\pm \frac {1}{2}\big [\begin {smallmatrix} 1 & -\lambda ^{-1}\\ \lambda & -1 \end {smallmatrix}\big ]$ if 
$f$ is even. The lemma then follows immediately.
For fixed 
$n$, among the terms listed in Lemma 6.1.2 with denominator 
$p^{n+1}$, the number of terms with equal minimal 
$t$-adic valuation depends on certain numerical relation between 
$A$ and 
$B$. We then perform the following case-by-case analysis in §§ 6.2–6.4 to prove the decay lemma. The first case, while technically the easiest, holds the main ideas in general.
6.2 Case 1: $A < B$
Note that if 
$a + b \neq 2c$ or, more generally, if the leading terms of 
$xy$ and 
$z^2/(4\epsilon )$ do not cancel, then 
$A< B$.
Proof of Proposition 5.1.3 in this case For the ease of exposition, we assume that 
$a \leq b \leq c$. Note that this forces 
$2a \leq A$. Even though the statement of Proposition 5.1.3 is not symmetric in 
$a,b,c$, an identical argument as that below suffices to deal with all the other cases.
We prove that 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2,w_3\}$ decays rapidly. For a primitive vector 
$w\in \operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2,w_3\}$, write 
$w = \alpha _u w_u + \alpha _l w_3$, where 
$w_u$ is a primitive vector in 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$, and 
$\alpha _u,\alpha _l \in \mathbb {Z}_p$. As 
$w$ is primitive, then either 
$\alpha _u$ or 
$\alpha _l$ is a 
$p$-adic unit. We may assume that 
$\alpha _u$ is a unit: the other case is entirely analogous to this one. Suppose that the 
$p$-adic valuation of 
$\alpha _l$ is 
$m \geq 0$.
Consider the terms appearing in 
$F_{\infty }(1)$ described in Lemma 6.1.2 with denominator 
$p^{n+1}$. As 
$A < B$, the one with minimal 
$t$-adic valuation is 
$P(1)_{0,n}(xy + z^2/(4\epsilon ))^{1 + p + \cdots + p^{n}}$, and this is the unique term with this property. Similarly, consider the terms appearing in 
$F_{\infty }(2)$ with denominator 
$p^{n+1 + m}$. As 
$A < B$, the unique term whose first column has minimal 
$t$-adic valuation is 
$P(1)_{0,n+m-1}\cdot F_u^{(n+m)}(xy + z^2/(4\epsilon ))^{1 + p + \cdots + p^{n+m-1}}$.
Let 
$P$ denote the 
$2 \times 3$ matrix whose first two columns equal 
$P(1)_{0,n}(xy + z^2/(4\epsilon ))^{1 + p + \cdots + p^{n}}$ (part of 
$F_{\infty }(1)$), and whose last column is the first column of 
$P(1)_{0,n+m-1}\cdot F_u^{(n+m)}(xy + z^2/(4\epsilon ))^{1 + p + \cdots + p^{n+m-1}}$ (part of 
$F_{\infty }(2)$). As 
$1\leq a < A$, then for any 
$m\in \mathbb {Z}_{\geq 0}$, we have 
$A(1 + \cdots + p^n)\neq A(1 + \cdots + p^{n+m-1}) + ap^{m+n}$. Therefore, regardless of the value of 
$m$, the 
$t$-adic valuation of entries of the first two columns of 
$P$ are different from the 
$t$-adic valuation of the last column of 
$P$.
To prove that 
$w$ decays rapidly, it suffices to prove that among the monomials in 
$P w$ with 
$p$-adic valuation equalling 
$-(n+1)$, there exists a monomial with 
$t$-adic valuation 
$\leq A(1 + \cdots + p^n)$. By the proof of Proposition 5.1.3 in Case 1 in § 5.2, this, in turn, reduces to proving the following statement: if 
$m \geq 1$, then 
$w_u \bmod p$ is not in the kernel of 
$P(1)_{0,n}\bmod p$; and if 
$m = 0$, the vector 
$\big [\begin {smallmatrix} (\lambda ^{-1})^{(n)}\\ 1 \end {smallmatrix}\big ] \bmod p$ is not in the kernel of 
$P(1)_{0,n-1}\bmod p$. Both statements follow from Lemma 6.1.4, establishing the decay of the rank-
$3$ submodule 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2,w_3\}$.
Proposition 5.1.3 in this case follows from the observation that because 
$2a\leq A$, then 
$w_3$ decays very rapidly.
6.3 Case 2: $A \geq B, a \neq b$
Note that if 
$A \geq B$, then 
$a + b = 2c$ (as the only way this can happen is if 
$xy$ has the same 
$t$-adic valuation as 
$z^2/(4\epsilon )$). We may, therefore, assume without loss of generality that 
$a < b$. It follows then that 
$a < c < b$. Within this case, we need to consider the following two subcases.
Subcase $(2.1)_e$: $B (1 + p^{2e-1}) < A(1+p) < B(1 + p^{2e + 1})$ for some $e\in \mathbb {Z}_{\geq 1}$
In this subcase, we prove that 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2, w_i\}$ decays rapidly, where 
$i\in \{3,4,5 \}$ will be chosen depending on the values of 
$a$, 
$b$, and 
$c$.
The following lemma, in conjunction with Lemma 6.1.4, implies (as in Case 1) that 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ decays rapidly. It can be proved by the same argument as in the proof of Lemma 5.2.6(1), so we omit its proof.
Lemma 6.3.1 Among the terms appearing in 
$F_{\infty }(1)$ described in Lemma 6.1.2 with denominator 
$p^{n+1}$, the unique term with minimal 
$t$-adic valuation is
\[ P(1)_{e,n}(xy + z^2/(4\epsilon))^{(1 + \cdots + p^{n-e})}(xy^p + x^py +z^{1+p}/(2\epsilon))^{p^{n-e+ 1} + p^{n-e +3} + \cdots + p^{n + e -1}} . \]
The 
$t$-adic valuation of this term is 
$A(1 + \cdots + p^{n-e}) + B(p^{n-e+1} + p^{n-e+3} + \cdots + p^{n+e-1})$.
The following lemmas will be used to show that one of 
$w_3,w_4,w_5$ also decays rapidly. These lemmas imply that among the terms appearing in 
$F_{\infty }(2)$ with denominator 
$p^{n+1}$, for at least one of the columns of this matrix, there exists a unique term with minimum 
$t$-adic valuation.
Lemma 6.3.2 Given 
$g\in \mathbb {Z}_{\geq 1}, n\in \mathbb {Z}_{\geq 0}$, consider the multiset consisting of numbers of the form 
$A(1 + \cdots + p^{n - f -1}) + B(p^{n - f} + p^{n-f + 2} + \cdots + p^{n+f -2}) + gp^{n+f}$, as 
$f$ varies over 
${\mathbb {Z}\cap [0, n]}$. If the minimal number in this multiset occurs more than once, then it must occur for consecutive values of 
$f$.
Proof. For any choice of 
$f$, let us denote the expression by 
$v(f)$. It suffices to prove the following statement: for 
$f_1 < f_2-1$, if 
$v(f_1) = v(f_2)$, then 
$v(f_2) > v(f_2 -1)$. To that end, suppose that 
$v(f_1) = v(f_2)$. Then 
$A(1 + p + \cdots + p^{f_2-f_1-1}) = B(p^{f_2-f_1}-1)(p^{f_2 + f_1} +1)/(p^2-1)+gp^{f_2}(p^{f_2}-p^{f_1})$.
To prove 
$v(f_2)>v(f_2-1)$, note that 
$p^{-(n-f_2)}(v(f_2) - v(f_2-1)) = B(p^{2f_2-1}+1)/(p+1) + gp^{2f_2-1}(p-1) - A$. Multiplying this by 
$(1 + p + \cdots + p^{f_2-f_1})$ and applying the relation of 
$A$ and 
$B$ above, we have
\begin{align*} \frac{1 + p + \cdots + p^{f_2-f_1-1}}{p^{n-f_2}}(v(f_2) - v(f_2-1))&=\frac{B(p^{f_2-f_1} - 1)(p^{2f_2 -1} - p^{f_1 + f_2})}{p^2-1}\\ &\quad + g(p^{f_2 -f_1} -1)(p^{2f_2 -1} - p^{f_1 + f_2}), \end{align*}
which is positive because 
$f_2 > f_1+1$. The lemma follows.
Lemma 6.3.3 There are at most two numbers 
$g$ in the set 
$\{a,b,c\}$ such that there exists an integer 
$f$ (
$f$ is allowed to depend on the choice of 
$g$) with 
$A(1 + \cdots + p^{n-f-1}) + B(p^{n-f} + p^{n-f + 2} + \cdots + p^{n + f-2}) + gp^{n + f}$ 
$= A(1 + \cdots + p^{n-f}) + B(p^{n-f + 1} + p^{n-f + 1} + \cdots + p^{n + f-3}) + gp^{n + f-1}$.Footnote 31
Proof. Suppose there existed choices of 
$f\in \mathbb {Z}_{\geq 0}$ for all three choices of 
$g$. Let 
$f_1,f_2,f_3$ be the choices for 
$f$. Then, by the proof of Lemma 6.3.2, we have that 
$ap^{2f_1-1}(p-1) = A - B(1 + p^{2f_1 -1})/(1+p)$, and similarly 
$bp^{2f_2-1}(p-1) = A-B(1 + p^{2f_2-1})/(1 + p),$ 
$cp^{2f_3-1}(p-1) = A-B(1 + p^{2f_3-1})/(1 + p)$. Substituting these expressions in the equality 
$a + b = 2c$ yields the equation
\[ (p^{1-2f_1}+p^{1-2f_2}-2p^{1-2f_3})A=\frac{B}{p+1}(p^{1-2f_1}+p^{1-2f_2}-2p^{1-2f_3}). \]
As 
$A\geq B\geq p+1$, we have 
$A\neq B/(p+1)$ and hence 
$p^{1-2f_1}+p^{1-2f_2}-2p^{1-2f_3}=0$. As 
$f_1,f_2,f_3\in \mathbb {Z}_{\geq 1}$, we must have 
$f_1=f_2=f_3$ and, hence, 
$a=b=c$, which is a contradiction.
Proof of Proposition 5.1.3 in this case Let 
$h \in \{a,b,c\}$ be such that there is no 
$f$ which satisfies the hypothesis of Lemma 6.3.3 (indeed, the lemma guarantees the existence of such an 
$h$).
We first show the existence of a rank-
$3$ submodule which decays rapidly. Without loss of generality, we may assume that 
$h =a$ and we prove that 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2,w_3\}$ decays rapidly (if 
$h = b$ or 
$c$, the identical proof will show sufficient decay, with 
$w_4$ or 
$w_5$ taking the place of 
$w_3$).
As in Case 1, Lemmas 6.3.1 and 6.1.4–6.3.3 imply that 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ and 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3\}$ both decay rapidly. Therefore, it suffices to show that 
$\alpha _u w_u + \alpha _3 w_3$ decays rapidly, where 
$w_u$ is a primitive vector in the span of 
$w_1,w_2$, and either 
$\alpha _u$ or 
$\alpha _3$ in 
$\mathbb {Z}_p$ is a 
$p$-adic unit.
By Lemma 6.3.1, the 
$t$-adic valuation of the coefficient of 
$1/p^{n+1}$ of 
$F_{\infty } w_u$ is 
$d(n) = A(1 + \cdots + p^{n-e}) + B(p^{n-e + 1}+ p^{n-e+3} + \cdots + p^{n+e-1})$. Similarly, the 
$t$-adic valuation of the coefficient of 
$1/p^{m+1}$ of 
$F_{\infty } \cdot w_3$ is 
$c(m) = A(1 + \cdots + p^{m-f-1}) + B(p^{m-f }+ p^{m-f+2} + \cdots + p^{m+f-2}) + ap^{m + f}$ for some 
$f\in \mathbb {Z}\cap [0,n]$. As in Case 1, it suffices to prove that 
$d(n)$ is never equal to 
$c(m)$, regardless of the values of 
$n$ and 
$m$.
Let 
$c(f',m) = A(1 + \cdots + p^{m-f-1}) + B(p^{m-f' }+ p^{m-f'+2} + \cdots + p^{m+f'-2}) + ap^{m + f'}$, for any value of 
$f' \leq m$. By the definition of 
$f$, 
$c(m) = c(f,m)$, and 
$f' = f$ minimizes the value of 
$c(f',m)$.
If 
$n \geq m$, because 
$a< A$, then 
$d(n) > c(e,m) \geq c(f,m) = c(m)$, as required. On the other hand, if 
$m > n$, we have 
$c(m) > A(1 + \cdots + p^{m-f-1}) + B(p^{m-f }+ p^{m-f+2} + \cdots + p^{m+f-2})\geq d(n)$, where the last inequality follows from Lemma 6.3.1.
Finally, we treat the question of very rapid decay. If we may take 
$h = a$ or 
$h = c$, the very rapid decay of 
$w_3$ or 
$w_5$ is established by the inequality 
$2 a < 2c \leq A$. Otherwise, 
$h$ must be 
$b$ and for both 
$a,c$, there exist 
$f_1,f_3$ satisfying the equation in Lemma 6.3.3. As 
$a\neq c$, then 
$f_1\neq f_3$ and at least one 
$f_i\geq 2$. By the proof of Lemma 6.3.3, we have 
$A-B(1+p^{2f_i-1})/(p+1)>0$ and, hence, 
$A\geq 7B >2b$. Thus, 
$w_4$ decays very rapidly.
Subcase $(2.2)_e$: $A(1+p) = B(1 + p^{2e - 1})$ for some $e\in \mathbb {Z}_{\geq 1}$
In this subcase, we prove that 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4,w_5\}$ decays rapidly. We first need the following lemma.
Lemma 6.3.4 Among the terms appearing in 
$F_{\infty }(2)$ described in Lemma 6.1.2 with denominator 
$p^{n+1}$, the unique term with minimal 
$t$-adic valuation is
\[ P(1)_{e -1,n-1}F_u^{(n+e -1)}(xy + z^2/(4\epsilon))^{(1 + \cdots + p^{n-e})}(xy^p + x^py +z^{1+p}/(2\epsilon))^{p^{n-e+ 1} + p^{n-e +3} + \cdots + p^{n + e -3}} . \]
The 
$t$-adic valuation of the 
$i$th column term is 
$A(1 + \cdots + p^{n-e}) + B(p^{n-e+1} + p^{n-e+3} + \cdots + p^{n+e-3}) + gp^{n+e-1},$ where 
$g$ is 
$a$, 
$b$, or 
$c$ depending on whether 
$i$ is 
$1$, 
$2$, or 
$3$.
Proof. It suffices to prove that choice of 
$f = e$ minimizes the expression 
$A(1 + p + \cdots + p^{n-f}) + B(p^{n-f+1} + p^{n-f + 3} + \cdots + p^{n+f-3}) + gp^{n+f-1}$, where 
$f$ is allowed to range between 
$0$ and 
$n$. This can be verified by direct calculation.
Proof of Proposition 5.1.3 in this case It follows from Lemmas 6.3.4 and 6.1.4 that 
$w_3$, 
$w_4$, and 
$w_5$ individually decay rapidly, and that 
$w_3$ decays very rapidly. In order to show that 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4,w_5\}$ decays rapidly, it suffices to show that the 
$t$-adic valuations of the coefficients 
$1/p^{l+1},1/p^{m+1}, 1/p^{n+1}$ of 
$F_{\infty }(w_3),F_{\infty }(w_4),F_{\infty }(w_5)$ are always distinct, regardless of the values of 
$l,m,n$. By Lemma 6.3.4, these quantities equal 
$A(1 + p + \cdots + p^{l-e}) + B(p^{l-e+1} + p^{l-e + 3} + \cdots + p^{l+e-3}) + ap^{l+e-1}$, 
$A(1 + p + \cdots + p^{m-e}) + B(p^{m-e+1} + p^{m-e + 3} + \cdots + p^{m+e-3}) + bp^{m+e-1}$ and 
$A(1 + p + \cdots + p^{n-e}) + B(p^{n-e+1} + p^{n-e + 3} + \cdots + p^{n+e-3}) + cp^{n+e-1}$.
As 
$a,b,c$ are all strictly less than 
$B$, these quantities will all be different unless two of 
$l,m,n$ are equal. In this case, the quantities still differ, because 
$a,b,c$ are all distinct integers by assumption. Therefore, 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4,w_5\}$ decays rapidly.
6.4 Case 3: $A \geq B$ and $a = b$
In this case, 
$a = b = c$. We may assume that 
$x(t) = t^a$, 
$y(t) = \beta t^a + \sum _{i=a+1}^\infty \beta _i t^i$, and 
$z(t) = \gamma t^a + \sum _{i=a+1}^\infty \gamma _i t^i$. As 
$A\geq B$, we have 
$\beta + \gamma ^2 /(4\epsilon ) =0$. We break the proof of the decay lemma into two subcases and the following lemma is used in both cases.
Lemma 6.4.1 Suppose that 
$\gamma \in \mathbb {F}_p$. Let 
$a' > a$ denote the smallest integer such that either 
$\beta _{a'}\neq 0$ or 
$\gamma _{a'}\neq 0$. Then both 
$\beta _{a'}$ and 
$\gamma _{a'}$ are non-zero and, moreover, 
$B \geq (p-1)a + 2 a'$.
Proof. As 
$\gamma \in \mathbb {F}_p$ and 
$\beta +\gamma ^2/(4\epsilon )=0$, then 
$\beta \in \mathbb {F}_p$. Therefore, in 
$k[[t]]$,
\begin{align*} xy + z^2/(4\epsilon) &= \sum_{i \geq a'} (\beta_i + \gamma \gamma_i/(2\epsilon))t^{i+a} + (4\epsilon)^{-1}\sum_{i,j \geq a'}\gamma_i\gamma_j t^{i+j},\\ xy^p + x^p y + z^{1+p}/(2\epsilon)& = \sum_{i \geq a'}(\beta_i + \gamma \gamma_i/(2\epsilon))t^{i + pa}\\ &\quad + \sum_{i\geq a'}(\beta_i^p + \gamma \gamma_i^p/(2\epsilon)) t^{pi + a} + (2\epsilon)^{-1}\sum_{i,j \geq a'}\gamma_i\gamma_j^p t^{i + jp}. \end{align*} If one of 
$\beta _{a'}$ and 
$\gamma _{a'}$ were zero, then 
$A = a' + a$, whereas 
$B\geq a'+pa$; this contradicts with the assumption that 
$A\geq B$. Hence, we obtain the first assertion of the lemma.
Let 
$a'' \geq a'$ denote the smallest integer such that 
$\beta _i + \gamma \gamma _i/(2\epsilon ) \neq 0$. Then by applying the Frobenius action, we have 
$\beta _{a''}^p+\gamma \gamma _{a''}^p/(2\epsilon )\neq 0$ and 
$B \geq \min \{(p+1)a',a'' + pa \}$. If 
$B \geq (p+1)a'$, then the second assertion of the lemma follows.
Therefore, we assume that 
$B = a'' + pa < (p+1)a'$. The expansion of 
$xy + z^2/(4\epsilon )$ above has a non-zero term of the form 
$(\beta _{a''} + \gamma \gamma _{a''}/(2\epsilon ))t^{a + a''}$. As 
$A\geq B$, the term 
$(\beta _{a''} + \gamma \gamma _{a''}/(2\epsilon ))t^{a + a''}$ has to be cancelled out by a term of the form 
$(4\epsilon )^{-1}\sum _{i + j = a + a'',\, i,j \geq a'}\gamma _i\gamma _j t^{i+j}$. Therefore, it follows that 
$2a' \leq a + a''$ and, hence, 
$B = a'' + pa\geq (p-1)a+2a'$.
Case $(3.1)_e$: $B(1 + p^{2e-1}) < (p+1)A < B(1 + p^{2e + 1})$ for some $e\in \mathbb {Z}_{\geq 1}$
The same argument as in Case 2.1 suffices to prove Proposition 5.1.3, unless 
$A = B(({1 + p^{2e-1}})/({1+p})) + a(p^{2e} - p^{2e-1})$. Therefore, we assume that this is the case.
Lemma 6.4.2 Among the terms appearing in 
$F_{\infty }(2)$ described in Lemma 6.1.2 with denominator 
$p^{n+1}$, there are exactly two with minimal 
$t$-adic valuation. They are
\begin{align*} &P(1)_{e-1,n-1}F_u^{(n+e-1)} (xy + z^2/(4\epsilon))^{(1 + \cdots + p^{n-e})}(xy^p + x^py + z^{1+p}/(2\epsilon))^{p^{n-e + 1} + p^{n - e + 3 } + \cdots + p^{n + e -3}},\\ &P(1)_{e,n-1}F_u^{(n+e)} (xy + z^2/(4\epsilon))^{(1 + \cdots + p^{n-e -1})}(xy^p + x^py + z^{1+p}/(2\epsilon))^{p^{n-e } + p^{n - e + 2 } + \cdots + p^{n + e -2}}. \end{align*}
Both the terms have 
$t$-adic valuation 
$A(1 + \cdots + p^{n-e}) + B(p^{n-e + 1} + p^{n - e + 3} + \cdots + p^{n + e -3}) + ap^{n + e -1}$.
Proof. This lemma follows from a similar argument as Lemma 5.2.6(2) and the proofs of Lemmas 6.3.2 and 6.3.3, so we omit the details.
Proof of Proposition 5.1.3 in this case We show that either 
$w_3$ or 
$w_5$ decays very rapidly. There are two terms with minimal 
$t$-adic valuation as in Lemma 6.4.2, appearing in the coefficient of 
$1/p^{n+1}$ of 
$F_{\infty }(w_3)$ and 
$F_{\infty }(w_5)$. A direct computation yields that the sum of these two terms equals by
\[ \frac{1}{2p^{n+1}}P(1)_{0,n-e-1}(xy + z^2/(4\epsilon))^{1 + p + \cdots + p^{n-e -1}}(X(t)u(t)^{p^{2e}} + Y(t)u(t)^{p^{2e-1}})^{(n-e)}, \]where
(i)
$u(t)$ denotes either $x(t)$ or $z(t)$, according to whether we work with $w_3$ or $w_5$;(ii)
$X(t) = pF_u\cdot F_l^{(1)}\cdot pF_u^{(2)} \cdots F_l^{(2e-1)} \cdot [(\lambda ^{-1})^{(2e)},1]^{\textrm {T}}$; and(iii)
$Y(t) = pF_t \cdot pF_u^{(1)} \cdot F_l^{(2)} \cdots pF_u^{(2e-3)} \cdot F_l^{(2e -2)} \cdot [(\lambda ^{-1})^{(2e-1)},1]^{\textrm {T}}$; the superscript T denotes transpose.
The decay of 
$w_3$ and 
$w_5$ is determined by the 
$t$-adic valuation of the entries of 
$X(t) u(t)^{p^{2e}} + Y(t)u(t)^{p^{2e-1}}$. For the rest of the proof, it suffices to focus on the second row of 
$X(t), Y(t)$ and, hence, we view them as functions. We prove the very rapid decay of 
$w_3$ or 
$w_5$ in two cases. (1) Both 
$\beta,\gamma \in \mathbb {F}_p$. In this case, we claim that the 
$t$-adic valuation of 
$X(t) u(t)^{p^{2e}} + Y(t)u(t)^{p^{2e-1}}$ is at most 
$A + B(p + p^3 + \cdots + p^{2e-3}) + a'p^{2e-1}$ for at least one choice of 
$u(t)$ between 
$x(t)$ and 
$z(t)$, where 
$a'$ is defined in Lemma 6.4.1. This claim implies that the 
$t$-adic valuation of the coefficient of 
$1/p^{n+1}$ of 
$F_{\infty }(w_3)$ or 
$F_{\infty }(w_5)$ is at most 
$A(1 + \cdots + p^{n-e}) + B(p^{n-e+1} + p^{n-e + 3} + \cdots + p^{n + e -3}) + a'p^{n+e-1}$. This is sufficient to prove the rapid decay of 
$w_3$ or 
$w_5$. Indeed, this quantity is strictly less than 
$A(1 + \cdots + p^{n-f}) + B(p^{n-f+1} + p^{n-f + 3} + \cdots + p^{n + f -3}) + ap^{n+f-1}$ for all values of 
$f \neq e,e+1$ by Lemma 6.4.1 and, hence, the sum of the two terms in Lemma 6.4.2 gives the minimal 
$t$-adic valuation term of the coefficient of 
$1/p^{n+1}$ in 
$F_{\infty }(w_3)$ or 
$F_{\infty }(w_5)$. Moreover, the bounds on 
$a'$ in Lemma 6.4.1 proves that 
$w_3$ or 
$w_5$ decays very rapidly.
We now prove the claim by contradiction. Suppose that 
$X(t)x(t)^{p^{2e}} + Y(t)x(t)^{p^{2e-1}}$ has 
$t$-adic valuation greater than 
$A + B(p + p^3 + \cdots + p^{2e-3}) + a'p^{2e-1}$. As 
$z(t) = \gamma x(t) + \gamma _{a'}t^{a'} + \cdots$ with 
$\gamma \in \mathbb {F}_p$, 
$\gamma _{a'}\neq 0$ and we have assumed that 
$A = B(({1 + p^{2e-1}})/({1+p})) + a(p^{2e} - p^{2e-1})$, it follows that there is a unique monomial in 
$X(t)z(t)^{p^{2e}} + Y(t)z(t)^{p^{2e-1}}$ with 
$t$-adic valuation 
$A + B(p + p^3 + \cdots + p^{2e-3}) + a'p^{2e-1}$, thereby establishing the claim for 
$u(t)=z(t)$. (2) Either 
$\beta$ or 
$\gamma$ is not in 
$\mathbb {F}_p$. In this case, as 
$\beta + \gamma ^2/(4\epsilon ) = 0$, we may assume that 
$\gamma \notin \mathbb {F}_p$. We again consider the function 
$X(t)u(t)^{p^{2e}} + Y(t)u(t)^{p^{2e-1}}$. Suppose that the leading coefficient of 
$X(t)$ is 
$\mu _X$ and that of 
$Y(t)$ is 
$\mu _Y$. Then, the terms of minimal equal 
$t$-adic valuations cancel out in the case when 
$u(t) = x(t)$ only if 
$\mu _X + \mu _Y = 0$, otherwise, by the same idea as in part (1), 
$w_3$ decays very rapidly. Therefore, we may assume that 
$\mu _X + \mu _Y = 0$. However, in this case, if we pick 
$u(t) = z(t)$, then the terms with minimal equal 
$t$-adic valuations cancel out only if 
$\mu _X \gamma ^{p^{2e}} + \mu _Y \gamma ^{p^{2e-1}} = 0$, which is not possible as 
$\gamma ^{p^{2e}} \neq \gamma ^{p^{2e-1}}$. In other words, we show that in this case, 
$w_5$ decays very rapidly.
As in Case 2.1, 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ decays rapidly, and also every vector that can be written as 
$\alpha _u w_u + \alpha _iw_i$ with 
$\alpha _i\in \mathbb {Z}_p^\times$ (
$i = 3,5$ depending on whether 
$w_3$ or 
$w_5$ decays) decays very rapidly. The latter statement follows by the same valuation-theoretic argument as in the proof of Case 2.1, which also proves that 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2, w_i\}$ decays rapidly.
Case $(3.2)_e: A(1+p)=B(1+p^{2e-1})$ for some $e\in \mathbb {Z}_{\geq 1}$
Lemma 6.4.3 Among the terms appearing in 
$F_{\infty }(1)$ described in Lemma 6.1.2 with denominator 
$p^{n+1}$, there are exactly two with minimal 
$t$-adic valuation. They are
\begin{align*} & P(1)_{e,n}(xy + z^2/(4\epsilon))^{1 + \cdots + p^{n-e}}(xy^p+ x^py + z^{1+p}/(2\epsilon))^{p^{n-e+1} + p^{n-e+3} + \cdots +p^{n+e-1}},\\ & P(1)_{e-1,n}(xy + z^2/(4\epsilon))^{1 + \cdots + p^{n-e+1}}(xy^p+ x^py + z^{1+p}/(2\epsilon))^{p^{n-e+2} + p^{n-e+4} + \cdots +p^{n+e-2}}. \end{align*}
Both these terms have 
$t$-adic valuation 
$A(1 + \cdots + p^{n-e}) + B(p^{n-e+1} + p^{n-e+3} + \cdots + p^{n+e-1})$.
As we have seen many lemmas of this flavor, we omit the proof.
This lemma shows that there are two terms with the same 
$t$-adic valuation, which could, therefore, lead to cancellation, and such phenomenon prevents us from proving that 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ decays rapidly. Nevertheless, the following lemma shows that there is at least a saturated rank-1 submodule of 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ which decays rapidly.
Lemma 6.4.4 There is a vector 
$w_0$ in 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ which decays rapidly.
Proof. By Lemma 6.4.3 and the proof of Lemma 6.1.4, the coefficient (viewed as a power series in 
$t$) of the sum of the two terms with minimal 
$t$-adic valuation among the terms with denominator 
$p^{n+1}$ is of the form 
$\mu _1 M_1 + \mu _2 M_2$, for some 
$p$-adic units 
$\mu _i$, where 
$\{M_1,M_2\}=\big \{\big [\begin {smallmatrix} 1 & \lambda ^{-1}\\ \lambda & 1 \end {smallmatrix}\big ], \big [\begin {smallmatrix}1 & -\lambda ^{-1}\\ \lambda & -1 \end {smallmatrix}\big ]\big \}$.
As 
$M_1 \bmod p$ and 
$M_2 \bmod p$ are not scalar multiples of each other, the linear combination 
$\mu _1 M_1 + \mu _2 M_2 \bmod p$ is non-zero. Therefore, there exists a vector 
$\bar {w}_0$ defined over 
$\mathbb {F}_p$ which does not lie in 
$\ker (\mu _1 M_1 + \mu _2 M_2 \bmod p)$. Choosing 
$w_0\in \operatorname {Span}_{\mathbb {Z}_p}\{w_1,w_2\}$ which lifts 
$\bar {w}_0$ finishes the proof of this lemma.
We are now ready to prove the last remaining case of Proposition 5.1.3 (and also the decay lemma Theorem 5.1.2).
Proof of Proposition 5.1.3 We first prove that there is a rank-
$2$ submodule of 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4,w_5\}$ which decays rapidly. For ease of notation, let 
$\bar {F_u}$ denote the matrix 
$({1}/{t^a})F_u$ evaluated at 
$t=0$.
Let 
$K$ denote 
$\ker (P(1)_{n-1,e-1}\bar {F_u}^{(n+e-1)} \bmod p)\cap \operatorname {Span}_{\mathbb {F}_p}\{w_3,w_4,w_5\}$. If 
$\dim _{\mathbb {F}_p}K\leq 1$, then lifting two linearly independent 
$\mathbb {F}_p$-vectors 
$\notin K$ gives the desired rank 
$2$ submodule. Therefore, we assume that 
$\dim _{\mathbb {F}_p}K=2$ (note that because 
$P(1)_{n-1,e-1}\bar {F_u}^{(n+e-1)} \bmod p$ is not the zero matrix, so 
$\dim _{\mathbb {F}_p}K\neq 3$). It follows that 
$\beta,\gamma \in \mathbb {F}_p$.
We prove that 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$ decays rapidly. First, because 
$K\cap \operatorname {Span}_{\mathbb {F}_p}\{w_3,w_4\}=\operatorname {Span}_{\mathbb {F}_p}\{\beta w_3-w_4\}$, then any primitive vector in 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$ which modulo 
$p$ is not a multiple of 
$\beta w_3 - w_4$ must decay rapidly. Now we consider 
$\beta w_3 - w_4$. Up to constants, the coefficient of the 
$1/p^{n+1}$ part of the first entry of 
$F_{\infty }(\beta w_3 - w_4)$ equals 
$\beta _{a'} t^{A(1 + \cdots +p^{n-e}) + B(p^{n-e+1} + p^{n-e+2} + \cdots + p^{n+e-3}) + a' p^{n+e -1}}$. Lemma 6.4.1 establishes the required decay as follows: first, as 
$a' \leq B \leq A$, we have that the vector 
$\beta w_3 - w_4$ decays rapidly; second, the exact bound for 
$a'$ in Lemma 6.4.1 implies (as in the proof in Case 2.1) that 
$\operatorname {Span}_{\mathbb {Z}_p}\{w_3,w_4\}$ decays rapidly; finally, the very rapid decay of 
$w_3$,
$w_4$ follows from the bound 
$2a' \leq B \leq A$.
Then, Proposition 5.1.3 follows by an argument analogous to that in Case 2.1 with Lemma 6.4.4.
7. The setup of the main proofs
In this section, we provide the general setup of the proofs of Theorems 1 and 5. As mentioned in § 1.3, the proofs consist of the following parts:
(1) the sum of the local contributions at supersingular points is at most
$11/12$ of the global contribution; and(2) the local contribution from non-supersingular points is of smaller magnitude.
Proposition 7.2.5 makes part (1) precise, and is stated in § 7.2. We prove Proposition 7.2.5 and part (2) in § 8 for the Hilbert case and in § 9 for the Siegel case. The idea involved in the statement of Proposition 7.2.5 is that we break the global intersection number 
$C . Z(m)$ into pieces, one for each non-ordinary point on 
$C$, by using the relation between the Hasse invariant and the Hodge line bundle in § 7.1. We also relate the local intersection multiplicity at a point to a lattice-point count.
7.1 The global contribution and its decomposition
Recall that in § 4.3.3, we list the set 
$T$ of 
$m\in \mathbb {Z}_{>0}$ for which we will study 
$C.Z(m)$ to prove our main theorems. To study the asymptotic behavior, we define 
$T_M=\{m\in T\mid m\leq M\}$ for 
$M\in \mathbb {Z}_{>0}$. Moreover, in §§ 8–9, we construct a subset 
$S_M\subset T_M$ which consists of bad values of 
$m$ that we want to rule out. The total global intersection number that we consider is 
$\sum _{m\in T_M-S_M} C.Z(m)$. We sum over 
$m$ instead of working with individual 
$m$ because geometry-of-numbers techniques which we use to bound the local intersection multiplicity (for cumulative 
$m$) do not work for individual 
$m$. The following lemma gives the asymptotics of the global term using results in § 4.
Lemma 7.1.1 Assume that 
$\#S_M=O(M^{1-\epsilon })=O(\# T_M^{1-\epsilon })$ for some 
$\epsilon >0$ if 
$L=L_{\rm H}$ and that 
$\#S_M=o(\# T_M)$ if 
$L=L_{\rm S}$. Then
\[ \sum_{m\in T_M-S_M} C.Z(m)=(\omega.C)\sum_{m\in T_M-S_M} |q_L(m)|+o\biggl(\sum_{m\in T_M-S_M} |q_L(m)|\biggr). \]
Moreover, we have, for Theorem 1(2), 
$\sum _{m\in T_M-S_M} C.Z(m)\asymp M^2$; for Theorem 1(1) and Remark 4, 
$\sum _{m\in T_M-S_M} C.Z(m)\asymp M^2/\log M$; for Theorem 5, 
$\sum _{m\in T_M-S_M} C.Z(m)\asymp M^{5/2}/\log M$.
Proof. By § 4.3.1 and the assumption on 
$S_M$, we have 
$\sum _{m\in S_M}|q_L(m)|=o(\sum _{m\in T_M}|q_L(m)|)$. Then the assertions follow from § 4.3.1, Lemmas 4.3.2 and 4.3.4, and the prime number theorem.
For each non-ordinary point 
$P$ on 
$C\cap Z(m)$, we introduce the notion of global intersection number 
$g_P(m)$ at 
$P$ using the following (well-known) relation between the non-ordinary locus and the divisor class of the Hodge bundle. Note that in the proof we only use the notion 
$g_P(m)$ for a supersingular point.
Lemma 7.1.2 The non-ordinary locus in 
$\mathcal {M}_k$ and 
$\mathcal {M}^{\rm {tor}}_k$ is cut out by a Hasse-invariant 
$H$, which is a section of 
$\omega ^{p-1}$ and, hence, the number of non-ordinary points (counted with multiplicity) on 
$C$ is given by 
$(p-1)(C.\omega )$.
See, for instance, [Reference BoxerBox15, §§ 1.4 and 1.5, Theorem 6.2.3] for an explanation of this fact (and we use the fact that the ordinary Newton stratum coincides with the ordinary Ekedahl–Oort stratum). For the last assertion in the lemma, we remark that when 
$L=L_{\rm H}$, the boundary 
$\mathcal {M}^{\rm {tor}}_k\setminus \mathcal {M}_k$ is ordinary and, hence, the intersection of 
$C'$ (in § 4.1.3) with the non-ordinary locus is the same as the intersection of 
$C$ with the non-ordinary locus.
Definition 7.1.3 Let 
$t$ be the local coordinate at 
$P$ (i.e. 
$\hat {C}_{P}=\operatorname {Spf} k[[t]]$) and let 
$A=v_t(H)$. We define 
$g_P(m)=({A}/({p-1}))|q_L(m)|$.
Note that by the above lemmas, we have the following decomposition
\begin{align*} \sum_{P\in C \text{ non-ord}}\sum_{m\in T_M-S_M}g_P(m)&=\sum_{m\in T_M-S_M}|q_L(m)|(\omega. C)\\ &=\sum_{m\in T_M-S_M} C.Z(m) + o\biggl(\sum_{m\in T_M-S_M}|q_L(m)|(\omega. C)\biggr). \end{align*}7.2 The lattices and the outline of the proof
Let 
$B \rightarrow \operatorname {Spf} k[[t]]$ denote the generically ordinary abelian surface given by pulling back the universal family over 
$\mathcal {M}_k$ to 
$\hat {C}_{P}=\operatorname {Spf} k[[t]]$ for some point 
$P\in C$. Recall the notion of special endomorphisms from § 2.2 and by a slight abuse of terminology, when 
$L=L_{\rm H}$, we also refer to a special quasi-endomorphism with certain integrality condition in § 2.2.11 as a special endomorphism. For any 
$n\in \mathbb {Z}_{>0}$, the lattice is special endomorphisms of 
$B \bmod t^n$ is a sublattice of 
$B\bmod t$, which is equipped with a positive definite quadratic form 
$Q'$ (see Definition 2.3.1).
Lemma 7.2.1 The local intersection multiplicity of 
$C.Z(m)$ at 
$P$, denoted by 
$l_P(m)$, equals
\[ \sum_{n = 1} ^ {\infty} \#\{ \textrm{Special endomorphisms } s \textrm{ of }B \bmod t^n \textrm{ with } Q'(s)=m\}. \] The lemma follows directly from the moduli interpretation of 
$Z(m)$. Note that as 
$B$ generically has no special endomorphisms, this infinite sum can actually be truncated at some finite stage (which will depend on 
$m$).
Remark 7.2.2 Given 
$B$, the lattices of special endomorphisms of 
$B\bmod t^n$ have the same rank for all 
$n\in \mathbb {Z}_{>0}$. Indeed, the work of de Jong, Moonen, and Kisin cited in the proof of Theorem 5.1.2 applies to any 
$P$ and for any special endomorphism 
$w$ of 
$B\bmod t$, we have the parallel extension 
$\tilde {w}\in (K[[t]])^4$ (or 
$(K[[t]])^5$), which is invariant under the Frobenius on 
$\mathbb {L}_{\mathrm {cris}}(W[[t]])$. By de Jong's theory (here we need the fully faithfulness of the Dieudonné functor, see [Reference de JongdJ95, Corollary 2.4.9]), whether 
$w$ extends over 
$\bmod t^n$ depends on the 
$p$-powers in the denominators of the coefficients of 
$\tilde {w}$. Therefore, given 
$n$, there exists 
$N$ such that 
$p^Nw$ extends over 
$\bmod t^n$ and, hence, these lattices tensor 
$\mathbb {Z}_\ell, \ell \neq p$ are all isomorphic and, in particular, the rank of the lattices is independent of 
$n$.
Motivated by the decay lemma Theorem 5.1.2, we define the following lattices for supersingular points (note that the notation is slightly different from that in the introduction and we use the notation in this section for the rest of the paper).
7.2.3
Assume 
$P$ is superspecial and recall that 
$A=v_t(H)$, where 
$H$ is the Hasse invariant and we use the constants 
$a$ and 
$A_n=[A(p^n+p^{n-1}+\cdots +1+{1}/{p})]$ as in Definition 5.1.1.
Define 
$L_{0,1}$, 
$L_{n,1}, n\in \mathbb {Z}_{>0}$, and 
$L_{n,2}, n\in \mathbb {Z}_{\geq 0}$ to be the lattices of special endomorphisms of 
$B$ mod 
$t$, mod 
$t^{A_{n-1}+1}$, and mod 
$t^{A_{n-1}+ap^n+1}$, respectively. As in Definition 2.3.1, we pick a lattice 
$L'_{n,i}\subset L'$ such that 
$L_{n,i}\subset L'_{n,i}$ and for 
$\ell \neq p$, 
$L'_{n,i}\otimes \mathbb {Z}_\ell =L'\otimes \mathbb {Z}_\ell$, and 
$L'_{n,i}\otimes \mathbb {Z}_p=L_{n,i}\otimes \mathbb {Z}_p$. In particular, 
$L'_{0,1}=L'$ and by Theorem 5.1.2, we have 
$[L'_{n,1}: L'_{n,2}]\geq p$ and 
$[L':L'_{n,1}]\geq p^{3n}$.
As we assume that 
$C$ does not admit any global special endomorphisms, we have 
${\bigcap _{n=0}^\infty L_{n,i}=\{0\}}$. By Remark 7.2.2, the difference between 
$L'_{n,i}$ and 
$L_{n,i}$ is the same as that between 
$L_{0,i}$ and 
$L'$, we also have 
$\bigcap _{n=0}^\infty L'_{n,i}=\{0\}$.
Corollary 7.2.4 If 
$P$ is superspecial, then
\[ l_P(m)\leq \frac{A(p+2)}{2p}r_{0,1}(m)+ \frac{A}{2}r_{0,2}(m)+ \sum_{n=1}^\infty \frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m)), \]
where 
$r_{n,i}(m)=\#\{s\in L'_{n,i}\mid Q'(s)=m\}$.
Proof. By Lemma 7.2.1 and § 7.2.3, we have that for 
$P$ superspecial,
\begin{align*} l_P(m) & \leq (A_{-1}+a)r_{0,1}(m)+(A_0-A_{-1}-a) r_{0,2}(m)\\ &\quad + \sum_{n=1}^\infty (ap^n r_{n,1}(m) + (A_n-A_{n-1}-ap^n) r_{n,2}(m))\\ & =A_{-1}(r_{0,1}(m)-r_{0,2}(m)) + a\sum_{n=0}^\infty p^n(r_{n,1}(m)-r_{n,2}(m))+\sum_{n=0}^\infty A_n (r_{n,2}(m)-r_{n+1,2}(m))\\ & \leq \frac{A}{p}(r_{0,1}(m)-r_{0,2}(m)) + \frac{A}{2}\sum_{n=0}^\infty p^n(r_{n,1}(m)-r_{n,2}(m))\\ &\quad +\sum_{n=0}^\infty (A(p^n+\cdots +1+ p^{-1}) (r_{n,2}(m)-r_{n+1,2}(m)), \end{align*}
where the last equality follows from the facts that 
$r_{n,1}(m)\geq r_{n,2}(m)$, 
$r_{n,2}(m)\geq r_{n+1,2}(m)$ and 
$a\leq A/2$, 
$A_n\leq A(p^n+\cdots + p^{-1})$. We then obtain the assertion in part (1) by rearranging the summations.
The main task of the next two sections is to prove the following proposition.
Proposition 7.2.5 Given 
$C$, there exists 
$S_M$ satisfying the assumption in Lemma 7.1.1 such that for every supersingular point 
$P$ on 
$C$, we have
\[ \sum_{m\in T_M-S_M}l_P(m)\leq \frac{11}{12}\sum_{m\in T_M-S_M}g_P(m)+o\biggl(\sum_{m\in T_M-S_M}g_P(m)\biggr). \] Once we have this proposition, we prove that the local contribution from non-supersingular points have smaller order of magnitude, whence we conclude that there are infinitely many non-supersingular points on 
$C$ which lie in the desired special divisors.
7.3 Ordinary points
To bound 
$l_P(m)$, we need the following decay lemma for ordinary points, which follows directly from Serre–Tate theory. We thank Keerthi Madapusi Pera for pointing this out to us. Let 
$B \rightarrow \operatorname {Spf} k[[t]]$ denote the abelian surface with ordinary reduction given by pulling back the universal family over 
$\mathcal {M}_k$ to 
$\hat {C}_{P}=\operatorname {Spf} k[[t]]$ for an ordinary point 
$P$.
Lemma 7.3.1 Let 
$A$ be an integer such that 
$w$ is not a special endomorphism for the 
$p$-divisible group 
$B[p^\infty ] \bmod t^{A+1}$. Then, 
$pw$ is not a special endomorphism for 
$B[p^\infty ]\bmod t^{pA+1}$.
Proof. Note that an endomorphism of 
$B[p^\infty ] \bmod t^n$ is special if and only if its reduction on 
$B[p^\infty ]\bmod t$ is special. Hence, we only need to consider the deformation of endomorphisms. The statement now follows directly from [Reference KatzKat81, Theorem 2.1]
Lemma 7.3.2 Let 
$L_0, L_n, n\in \mathbb {Z}_{>0}$ be the lattices of special endomorphisms of 
$B\bmod t$ and 
$B\bmod t^{Ap^{n-1}+1}$, respectively, where 
$A\in \mathbb {Z}_{>0}$. Then:
(1) for any
$A$, we have $\operatorname {rk}_{\mathbb {Z}}L_n\leq 2$ if $L=L_{\rm H}$ and $\operatorname {rk}_{\mathbb {Z}}L_n\leq 3$ if $L=L_{\rm S}$;(2) there exist a constant
$A$ and a $\mathbb {Z}_p$-lattice $\Lambda$ (depending on $P$) with $\operatorname {rk}_{\mathbb {Z}_p}\Lambda \leq 1$ when $L=L_{\rm H}$ and $\operatorname {rk}_{\mathbb {Z}_p}\Lambda \leq 2$ when $L=L_{\rm S}$ such that $L_n\subset (\Lambda +p^{n-1} L_1\otimes \mathbb {Z}_p)\cap L_0$.
In particular, if 
$\operatorname {rk}_{\mathbb {Z}}L_n=3$ when 
$L=L_{\rm S}$ or 
$\operatorname {rk}_{\mathbb {Z}}L_n=2$ when 
$L=L_{\rm H}$, then 
$(\operatorname {disc} L_n)^{1/2}\geq p^{n-1}$.
Proof. Note that 
$L_n\subset L_n\otimes \mathbb {Z}_p\subset L_0\otimes \mathbb {Z}_p=\mathbb {L}_{\mathrm {cris},P}(W)^{\varphi =1}$, where 
$\mathbb {L}_{\mathrm {cris},P}$ is the fiber of the 
$F$-crystal 
$\mathbb {L}_{\mathrm {cris}}$ defined in Definitions 2.2.3 and 2.2.9 and 
$\varphi$ is the Frobenius action. As 
$P$ is ordinary, then 
$\varphi$ acts on 
$\mathbb {L}_{\mathrm {cris},P}(W)$ with slope 
$-1,1,0,0$ (Hilbert case) or 
$-1,1,0,0,0$ (Siegel case) and hence part (1) follows.
Let 
$\Lambda '$ be the 
$\mathbb {Z}_p$-lattice of special endomorphisms of 
$B[p^\infty ]$. As 
$\hat {C}_{P}$ is not contained in any special divisor,Footnote 32 
$B[p^\infty ]$ admits at most a rank-
$2$ (respectively, rank-
$1$) module of special endomorphisms when 
$L=L_{\rm S}$ (respectively, 
$L=L_{\rm H}$); indeed, if 
$\operatorname {rk}_{\mathbb {Z}_p}\Lambda '=3$ (respectively, 
$2$), then 
$\Lambda '\otimes \mathbb {Q}_p=L_0\otimes \mathbb {Q}_p$ and, thus, 
$B$ admits special endomorphisms.
We now mimic the proof of [Reference Shankar and TangST20, Theorem 4.1.1] using Lemma 7.3.1 instead of [Reference Shankar and TangST20, Lemma 4.1.2(2)]. Let 
$\Lambda \subset L_0\otimes \mathbb {Z}_p$ be the saturation of 
$\Lambda '$ in 
$L_0\otimes \mathbb {Z}_p$; then there exists 
$\Lambda _0\subset L_0\otimes \mathbb {Z}_p$ such that 
$L_0\otimes \mathbb {Z}_p=\Lambda \oplus \Lambda _0$. Let 
$\Lambda _n$ denote 
$(L_n\otimes \mathbb {Z}_p+\Lambda )\cap \Lambda _0$; then 
$L_n\otimes \mathbb {Z}_p+\Lambda =\Lambda \oplus \Lambda _n$. It suffices to show that there exists 
$A$ such that 
$\Lambda _n\subset p\Lambda _{n-1}$ (and this implies that 
$\Lambda _n\subset p^{n-1}\Lambda _1$).
By definition, none of the elements in 
$\Lambda _0$ extend to 
$\operatorname {Spf} k[[t]]$, then there exists 
$A$ such that 
$\Lambda _1\subset p\Lambda _0$. For 
$n\geq 2$, assume for contradiction that there exists 
$\alpha \in \Lambda _n\backslash p\Lambda _{n-1}$. If 
$\alpha \in p\Lambda _{n-2}$, then write 
$\alpha =p\beta$ with 
$\beta \in \Lambda _{n-2}$. As 
$p\beta =\alpha \in \Lambda _n$, then by Lemma 7.3.1, 
$\beta \in \Lambda _{n-1}$, which contradicts with the assumption that 
$\alpha \notin p\Lambda _{n-1}$. Thus we have 
$\alpha \notin p\Lambda _{n-2}$; by iterating the argument, we have 
$\alpha \notin p\Lambda _0$. This is a contradiction because 
$\alpha \in \Lambda _n\subset \Lambda _1\subset p\Lambda _0$.
8. Proof of Theorem 1(2)
In this section, we use the results proved in §§ 4 and 5 to prove Proposition 7.2.5 in the case of Hilbert modular surfaces. This, in conjunction with Lemma 8.1.2, yields Theorem 1(2).
8.1 The bad set $S_M$ and the local intersection multiplicities at non-supersingular points
We first construct the set 
$S_M$; the following lemma only concerns ordinary and superspecial points because we only need to consider such 
$P$ for the proof of Theorem 1(2). Indeed, if 
$P\in Z(m)$, then 
$P$ is either ordinary or supersingular and if 
$P\in Z(m), p\nmid m$, then by § 4.4.2(1), 
$P$ is not supergeneric. Therefore for 
$P\in Z(m), m\in T$, 
$P$ is either superspecial or ordinary.
Lemma 8.1.1 Notation is as in §§ 7.1 and 7.2.3 and Lemma 7.3.2. Given a finite set 
$\{P_i\}\subset (C\cap (\bigcup _{m\in \mathbb {Z}_{>0}} Z(m)))(k)$, there exists 
$S_M\subset T_M$ with 
$\#S_M=O(M^{1-\epsilon })$ for some 
$0<\epsilon <1/6$ such that for all 
$i$:
(1) if
$P_i$ is superspecial, then $\{s\in L'_{N,1} \mid 0\neq Q'(s)\leq M, Q'(s)\notin S_M\}=\emptyset$ where $N=(({1+\epsilon })/{3})\log _p M$;(2) if
$P_i$ is ordinary, then $\{s\in L_{N} \mid 0\neq Q'(s)\leq M, Q'(s)\notin S_M\}=\emptyset$ where $N=\epsilon \log _p M$.
Proof. As the union of finitely many sets with cardinality 
$O(M^{1-\epsilon })$ still has cardinality to be 
$O(M^{1-\epsilon })$, it suffices to prove the assertion for each 
$P_i$ separately. We follow the idea of the proof of [Reference Shankar and TangST20, Theorem 4.3.3].
If 
$P_i$ is superspecial, we take 
$S_M=\{m\in T_M\mid \exists s\in L'_{N,1} \text { with } Q'(s)=m\}$ and then it satisfies part (1) by definition. Note that 
$\#S_M\leq \#\{s\in L'_{N,1}\mid Q'(s)\leq M\}$. Then by a geometry-of-numbers argument (see, for instance, [Reference Shankar and TangST20, Lemma 4.2.1]) and Theorem 5.1.2, we have
\[ \#\{s\in L'_{N,1}\mid Q'(s)\leq M\}=O(M^2/p^{3N}+M^{3/2}/p^{2N}+M/p^N+ M^{1/2}/d_N), \]
where 
$d_N$ is the first successive minimum of 
$L'_{N,1}$ and 
$d_N\rightarrow \infty$ as 
$N\rightarrow \infty$ because 
$\cap L'_{N,1}=\{0\}$. Then 
$\#S_M=O(M^{1-\epsilon })$ by the definition of 
$N$.
If 
$P_i$ is ordinary, then 
$\operatorname {rk} L_N=2$ by Lemma 7.3.2 and the fact that 
$\operatorname {rk} L_N=\operatorname {rk} L_0$ is even by the Tate conjecture. Similar to the superspecial case, we take 
$S_M=\{m\in T_M \mid \exists s\in L_{N} \text { with } Q'(s)=m\}$ and then by Lemma 7.3.2, 
$\#S_M=O(M/p^N+M^{1/2}/d_N)=O(M^{1-\epsilon })$.
Lemma 8.1.2 Notation as in Lemma 8.1.1. For an ordinary point 
$P=P_i\in C(k)$, we have
\[ \sum_{m\in T_M-S_M} l_P(m)=O(M^{1+\epsilon})=o(M^2). \]Proof. By Lemmas 7.2.1, 7.3.2, and 8.1.1,
\[ \sum_{m\in T_M-S_M}l_P(m)=\sum_{m\in T_M-S_M}A(r_0(m)+\sum_{n=1}^N(p^n-p^{n-1})r_n(m))\leq A\sum_{n=0}^N p^n\sum_{m=1}^M r_n(m), \]
where 
$r_n(m)=\#\{s\in L_n\mid Q'(s)=m\}$. By a geometry-of-numbers argument and Lemma 7.3.2, we have 
$\sum _{m=1}^M r_n(m)=O(M/p^n+M^{1/2}/d_n)$, where 
$d_n$ is the first successive minimum of 
$L_n$ and the implicit constant here only depends on 
$p$. Thus, 
$\sum _{m\in T_M-S_M}l_P(m)=O(NM+p^N M^{1/2})=O(M^{1+\epsilon })$.
8.2 Proof of Proposition 7.2.5 in the Hilbert case
We follow the notation in Lemma 8.1.1 and 
$P=P_i$ superspecial. We break 
$\sum _{m\in T_M-S_M}l_P(m)$ into two parts and are treated in the following lemmas.
Lemma 8.2.1 Notation as in Corollary 7.2.4. For any 
$\epsilon >0$, there exists 
$c\in \mathbb {Z}_{>0}$ which only depends on 
$P$ and 
$\epsilon$ such that
\[ \sum_{m\in T_M-S_M}\sum_{n=c}^\infty \frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))\leq \epsilon M^2 + o(M^2). \]Proof. By Lemma 8.1.1, 
$r_{n,i}(m)=0$ for 
$n>N=(({1+\epsilon })/{3})\log _p M$ and, hence,
\begin{align*} \sum_{m\in T_M-S_M}\sum_{n=c}^\infty \frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))&=\sum_{m\in T_M-S_M}\sum_{n=c}^N \frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))\\ &\leq \sum_{n=c}^N\sum_{m=1}^M Ap^n r_{n,1}(m) \end{align*}
because 
$r_{n,1}(m)\geq r_{n,2}(m)$.
By a geometry-of-numbers argument, 
$\sum _{m=1}^M r_{n,1}(m)\leq c_2(M^2/p^{3n}+M^{3/2}/p^{2n}+M/p^n+M^{1/2}/d_n)$, where 
$c_2$ is an absolute constant and 
$d_n$ is the first successive minimum of 
$L'_{n,1}$. Hence,
\[ \sum_{n=c}^N Ap^n \sum_{m=1}^M r_{n,1}(m)\leq Ac_2M^2\sum_{n=c}^N 1/p^{2n}+\sum_{n=c}^N Ap^nc_2(M^{3/2}/p^{2n}+M/p^n+M^{1/2}/d_n). \]
Note that 
$Ac_2\sum _{n=c}^N\leq Ac_2 (p^{2c}(1-p^{-2}))^{-1}$, which goes to zero as 
$c\rightarrow \infty$ and the second term is
\[ O( M^{3/2})+O((\log M)M)+O(M^{1/2})\sum_{n=c}^N p^n=O(M^{3/2}). \]Thus, we obtain the desired estimate.
Lemma 8.2.2 Notation as in Corollary 7.2.4. For any 
$c\in \mathbb {Z}_{>0}$, we have
\begin{align*} &\sum_{m\in T_M-S_M}\biggl(\frac{A(p+2)}{2p}r_{0,1}(m)+ \frac{A}{2}r_{0,2}(m)+ \sum_{n=1}^c \frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))\biggr)\\ &\qquad \leq \alpha \sum_{m\in T_M-S_M} g_P(m)+o(M^2), \end{align*}
where 
$\alpha <11/12$ is an absolute constant.
Proof. Let 
$\theta _{n,i}$ denote the theta series attached to the lattice 
$L'_{n,i}$. We decompose 
$\theta _{n,i}=E_{n,i}+G_{n,i}$, where 
$G_{n,i}$ is a cusp form and 
$E_{n,i}$ is an Eisenstein series as in § 4.2 and follow the proof of Lemma 4.3.2.
Let
\begin{align*} E&=\frac{A(p+2)}{2p}E_{0,1}+ \frac{A}{2}E_{0,2}+\sum_{n=1}^c \frac{Ap^n}{2}( E_{n,1}+ E_{n,2}),\\ G&=\frac{A(p+2)}{2p}G_{0,1}+ \frac{A}{2}G_{0,2}+\sum_{n=1}^c \frac{Ap^n}{2}( G_{n,1}+ G_{n,2}). \end{align*} Note that 
$G$ is a weight-
$2$ cusp form and by Deligne's Weil bound, we have that its 
$m$th Fourier coefficient 
$q_G(m)=O(m^{1/2+\epsilon })$. Hence, the total contribution from the cusp form 
$G$ is 
$\sum _{m\in T_M-S_M}q_G(m)=O(M^{3/2+\epsilon })$.
Let 
$q_{n,i}(m)$ and 
$q(m)$ denote the 
$m$th Fourier coefficient of 
$E_{n,i}$ and 
$E$ respectively. Recall that for 
$p\nmid m$ for 
$m\in T_M$, by Lemma 4.4.6 and the fact that 
$|L'^\vee /L'|=p^2$, we have for any 
$n,i$ that
\[ \frac{q_{n,i}(m)}{|q(m)_L|}\leq \frac{2p}{(p^2- 1)[L':L'_{n,i}]}\quad \text{and}\quad \frac{q_{0,1}(m)}{|q(m)_L|}\leq \frac{1}{p-1}. \]
Recall from § 7.2.3 that 
$[L':L'_{n,1}]\geq p^{3n}$ and 
$[L':L'_{n,1}]\geq p^{3n+1}$; therefore,
\begin{align*} \frac{q(m)}{|q_L(m)|}&\leq \frac{A(p+2)}{2p}\cdot \frac{1}{p-1}+\frac{A}{2}\frac{2p}{(p^2-1)p}+\sum_{n=1}^c\frac{Ap^n}{2}\cdot \frac{2p}{p^2-1}(p^{-3n}+p^{-3n-1})\\ &\leq \frac{A}{p-1}\biggl(\frac{p+2}{2p}+\frac{p}{p^2-1}\biggr). \end{align*}
Take 
$\alpha =({p+2})/{2p}+{p}/({p^2-1})$, which is 
$<11/12$ when 
$p\geq 5$. We have the left-hand side equals
\[ \sum_{m\in T_M-S_M}(q(m)+q_G(m))\leq \sum_{m\in T_M-S_M}\frac{\alpha A}{p-1}|q_L(m)|+O(M^{3/2+\epsilon}), \]
which gives the desired estimate by the definition of 
$g_P(m)$.
Proof Proof of Proposition 7.2.5 when $L=L_{\rm H}$
The set 
$S_M$ is constructed by Lemma 8.1.1 and taking 
$\{P_i\}$ to contain all of (the finitely many) supersingular points in 
$C\cap (\bigcup _{p\nmid m}Z(m))$. Then the desired estimate follows from Lemmas 8.2.1 and 8.2.2 by taking 
$c$ such that 
$\epsilon <\frac {11}{12}-\alpha$.
Proof of Theorem 1(2) If 
$C$ is contained in 
$Z(m)$ with 
$m$ being a perfect square, then by applying suitable Hecke translates, we may assume that 
$C$ is contained in the product of modular curves and then the assertion is a special case of [Reference Chai and OortCO06, Proposition 7.3]. Now for the rest of the proof, we may assume that 
$C$ is contained in some Hilbert modular surface and we use 
$Z(m)$ to denote special divisors on the Hilbert modular surface. Note that any point on 
$Z(m)$ corresponds to an abelian surface isogenous to the self-product of an elliptic curve. Thus, we assume for contradiction that there are only finitely many points on 
$C\cap (\bigcup _{m\in T}Z(m))$ and take 
$\{P_i\}$ to be this finite set and apply Lemma 8.1.1 to construct 
$S_M$. As all 
$Z(m)$ are compact, it makes sense to consider 
$C.Z(m)$. We deduce a contradiction by Lemma 7.1.1, Proposition 7.2.5, and Lemma 8.1.2.
9. Proofs of Theorems 1(1) and 5
In this section, we prove all of Theorems 1 and 5. Section 9.1 consists of results pertaining to squares represented by positive-definite quadratic forms.Footnote 33 In § 9.2, we prove Proposition 7.2.5 by combining results proved in §§ 4, 6, and 9.1. Finally, we deal with the intersection multiplicities at non-supersingular points in § 9.3 to finish the proof of the main theorem.
We now set up notation that we use for § 9. For superspecial points 
$P$, recall that we defined 
$L'_{n,i}$ in § 7.2.3. Let 
$l(n)_i,\ i=1,\ldots, 5$, denote the 
$i$th successive minimum of the quadratic form 
$Q'$ restricted to 
$L'_{n,1}$. Let 
$P_n$ denote a rank two sublattice of 
$L'_{n,1}$ with minimal discriminant. Note that 
$l(n)_1l(n)_2\asymp d_n$, where 
$d_n$ denotes the root discriminant of 
$P_n$. Moreover, because 
$\bigcap _{n=0}^\infty L'_{n,i}=\{0\}$, we have 
$l(n)_1\rightarrow \infty$ as 
$n\rightarrow \infty$.
9.1 Preparation
We need the following results to prove Proposition 7.2.5. Although Lemma 9.1.2 is stated for the rank-
$5$ lattices 
$L'_{n,1}$, the proof does not use the assumption on rank and, hence, it holds for the lattices 
$L_n$ for ordinary points (notation as in Lemma 7.3.2) when 
$\operatorname {rk}_{\mathbb {Z}}L_0=3$; see § 9.3 for details.
Lemma 9.1.1 We have 
$l(n)_1l(n)_2\cdots l(n)_i\gg p^{(i-2)n}$ for 
$i\geq 3$.
Proof. Note that if we have two lattices 
$L_1\supset L_2$, then the successive minima of 
$L_2$ give upper bounds of that of 
$L_1$. Thus, we may enlarge 
$L'_{n,i}$ and prove the assertion for the enlarged lattices.
We enlarge 
$L'_{n,i}$ as follows. For 
$\ell \neq p$, we still require 
$L'_{n,i}\otimes \mathbb {Z}_\ell =L'\otimes \mathbb {Z}_\ell$; at 
$p$, let 
$\Lambda _0$ denote the rank-
$3$ submodule of 
$L'\otimes \mathbb {Z}_p$ which decays rapidly in the decay lemma (Theorem 5.1.2), then we enlarge 
$L'_{n,1}$ such that 
$L'_{n,1}\otimes \mathbb {Z}_p=p^n \Lambda _0+L'\otimes \mathbb {Z}_p$.
For the enlarged 
$L'_{n,1}$, we have
\[ l(n)_j \ll p^n, j=1,\ldots,5, \quad l(n)_1l(n)_2 \cdots l(n)_5 \asymp p^{3n}, \]
where the implied constants only depend on the lattice 
$L'$. Thus, the assertion follows.
Lemma 9.1.2 Suppose that 
$d_n^2M=o(p^{2n})$ as 
$n\rightarrow \infty$. Then, for any vector 
$v \in L'_{n,1}$ such that 
$Q(v) \leq M$, we have that 
$v \in P_n$ for 
$n\gg 1$. In particular, if 
$d_n \leq p^{n / 2}$, then for any vector 
$v\in L'_{n,1}$ such that 
$Q'(v) < p^{n - \epsilon }$ for some absolute constant 
$\epsilon >0$, we have that 
$v \in P_n$ for 
$n\gg 1$. (All the implicit constants here are independent of 
$n,M$.)
Proof. Recall that 
$l(n)_1 \cdot l(n)_2 \asymp d_n$. Thus, by Lemma 9.1.1, we have
\[ {}l(n)_1l(n)_2l(n)_3 \gg p^n, \quad l(n)_3 \gg p^{n}/d_n. \]
In other words, for any vector 
$v$ linearly independent to 
$P_n$, we have 
$Q'(v)\geq l(n)_3^2\gg p^{2n}/d_n^2$. Then the first assertion follows. The second assertion follows directly from the first assertion by taking 
$M=p^{n-\epsilon }$.
Proposition 9.1.3 Fix 
$D\in \mathbb {Z}_{>0}$. Recall 
$r_{n,i}(m)$ from Corollary 7.2.4. Then we have the following two bounds:
(1)
$\displaystyle \sum _{m=D\ell ^2,\, m\leq M,\, \ell \text { prime }} r_{n,1}(m) = O_\epsilon \biggl (\frac {M^{2+\epsilon }}{p^{2n}} + \frac {M^{3/2 +\epsilon }}{p^{n}} + M^{1 + \epsilon } \biggr )$;(2)
$\displaystyle \sum _{m=D\ell ^2,\, m\leq M, \ell \text { prime }} r_{n,1}(m)$ and $\displaystyle \sum _{\ell \leq M,\, \ell \text { prime }} r_{n,1}(\ell )$ are both
\begin{equation*} O \biggl (\frac{M^{5/2}}{p^{3n}} + \frac{M^{2}}{p^{2n}} + \frac{M^{3/2}}{p^{n}} + \frac{M}{d_n} + \frac{M^{1/2}}{l(n)_1} \biggr). \end{equation*}
Proof. In the proof, for the simplicity of notation, we write 
$L'_n, r_n(m)$ for 
$L'_{n,1}, r_{n,1}(m)$.
We note that bound (2) is a trivial upper bound from a geometry-of-numbers argument. Indeed, both 
$\sum _{m=D\ell ^2,\, m\leq M,\, \ell \text { prime }} r_n(m)$ and 
$\sum _{\ell \leq M,\, \ell \text { prime }} r_n(\ell )$ are no greater than 
$\sum _{m=1}^M r_n(m)$; we then obtain the desired bound by [Reference Shankar and TangST20, Lemma 4.2.1] and Lemma 9.1.1.
Now we prove part (1). We may assume that there exists a vector 
$v_0\in L'_0$ such that 
$Q'(v_0)=D\ell _0^2$ for some prime 
$\ell _0$. Otherwise 
$r_n(m)=0$ for all 
$m=D\ell ^2$ for any prime 
$\ell$. Let 
$e_1$ denote a primitive vector in 
$L'_n$ such that 
$e_1=p^k v_0$ for some 
$k\in \mathbb {Z}_{\geq 0}$. By definition, 
$p^nL'_0\subset L'_n$ and, thus, 
$p^nv_0\in L'_n$. Therefore, 
$k\leq n$. As 
$e_1$ is primitive in 
$L'_n$, we extend it into a basis 
$\{e_1,e_2,\ldots, e_5\}$ of 
$L'_n$. Let 
$\widetilde {L'}_n$ denote the sublattice of 
$L'_0$ spanned by 
$f'_1:=v_0 = e_1/p^k,e_2,\ldots, e_5$; since 
$\widetilde {L'}_n$ is a sublattice of 
$L'_0$, then 
$Q'|_{\widetilde {L'}_n}$ is still 
$\mathbb {Z}$-valued. We have 
$Q'(f'_1)=D\ell _0^2=:N$. Let 
$f_1 = {f'_1}/{2N}$, and let 
$f_i = e_i - f_1\cdot [f'_1,e_i]'$ for 
$i>1$. As 
$[f'_1, e_i]\in \mathbb {Z}$ for 
$i\geq 2$, we then have 
$f_1,f_2, \ldots, f_5 \in (2N)^{-1}\widetilde {L'}_n$ with 
$[f_i,f_1]'=0$ for 
$i\geq 2$, and 
$\operatorname {Span}_{\mathbb {Z}}\{f_1,f_2,f_3,f_4,f_5\}\supset \widetilde {L'}_n$.
Let 
$\widetilde {Q'}$ denote the restriction of 
$Q'\otimes \mathbb {Q}$ to 
$\operatorname {Span}_{\mathbb {Z}}\{f_2,f_3,f_4,f_5\}\subset L'_0\otimes \mathbb {Q}$. By the definition of 
$f_i$, we have 
$\widetilde {Q'}$ is a 
$(2N)^{-1}\mathbb {Z}$-valued quadratic form. Let 
$\widetilde {l(n)}_1,\ldots, \widetilde {l(n)}_4$ denote the successive minima of 
$\operatorname {Span}_{\mathbb {Z}}\{f_2,f_3,f_4,f_5\}$. As 
$(2N)^{-1}\widetilde {L'}_n=(2N)^{-1}L'_n+(2N)^{-1}p^{-k}\mathbb {Z} e_1$, then 
$\widetilde {l(n)}_1\cdots \widetilde {l(n)}_i\gg p^{(i-1)n-k}\geq p^{(i-2)n}$ for 
$i\geq 2$ (note that 
$k\leq n$ and 
$N$ is absorbed in the implicit constant as 
$N$ is independent of 
$n,k$). Then the standard geometry-of-numbers argument gives
\[ Y_n:=\#\{y\in \operatorname{Span}_{\mathbb{Z}}\{f_2,f_3,f_4,f_5\} \mid \widetilde{Q'}(y)\leq M\}=O\biggl(\frac{M^2}{p^{2n}} + \frac{M^{3/2}}{p^n} + M \biggr). \] On the other hand, on 
$\operatorname {Span}_{\mathbb {Z}}\{f_1,f_2,f_3,f_4,f_5\}$, for 
$v=xf_1+y_2f_2+\cdots + y_5f_5$, we have 
$Q'(v)=({1}/{4D\ell _0^2}) x^2 +\widetilde {Q'}(v_y)$, where 
$v_y=y_2f_2+\cdots + y_5f_5$. If 
$Q'(v)=D\ell ^2\leq M$, then 
$\widetilde {Q'}(v_y)\leq Q'(v)\leq M$ and 
$4D\ell _0^2\widetilde {Q'}(v_y)=(2D\ell _0\ell -x)(2D\ell _0\ell + x)$. For a given 
$v_y$ with 
$\widetilde {Q'}(v_y)\leq M$, there are at most 
$O_\epsilon (M^\epsilon )$ ways to factor 
$4 D\ell _0^2\widetilde {Q'}(v_y)$ into two factors (recall that 
$N=D\ell _0^2$ is independent of 
$n,M$ and, hence, gets absorbed in the implicit constant) and, thus, there are at most 
$O_\epsilon (M^\epsilon )$ possible 
$x$ such that for 
$v=xf_1+v_y$, we have 
$Q'(v)=D\ell ^2\leq M$ for some prime 
$\ell$. As 
$L'_n\subset \operatorname {Span}_{\mathbb {Z}}\{f_1,f_2,f_3,f_4,f_5\}$, then 
$\sum _{m=D\ell ^2,\, m\leq M,\, \ell \text { prime }} r_n(m)=O_\epsilon (M^\epsilon Y_n)$, which gives bound (1) by the above bound for 
$Y_n$.
Proposition 9.1.4 Fix 
$D\in \mathbb {Z}_{>0}$. The proportion of primes 
$\ell \leq (M/D)^{1/2}$ such that 
$D\ell ^2$ is represented by the quadratic form restricted to 
$P_n$ goes to zero as 
$n\rightarrow \infty$.
Proof. Let 
$R_n$ denote the imaginary quadratic ring with discriminant 
$-d_n^2$. The class group of 
$R_n$ is in bijection with equivalence classes of binary quadratic forms of discriminant 
$-d_n^2$. Let 
$\mathfrak {a}$ denote the ideal corresponding to 
$Q'$ restricted to 
$P_n$. Recall that 
$l(n)_1\rightarrow \infty$ as 
$n\rightarrow \infty$. Thus, for 
$n\gg 1$, we have that 
$\mathfrak {a}$ is not equivalent to any ideal whose norm is 
$D$, that is, 
$(P_n,Q')$ does not represent 
$D$. Note that it suffices to deal with primes 
$\ell$ which are relatively prime to 
$Dd_n^2$.
The correspondence between ideal classes and binary quadratic forms yields that the integer 
$D\ell ^2$ is represented by 
$(P_n,Q')$ if and only if there exists an invertible ideal 
$\mathfrak {b}$ equivalent to 
$\mathfrak {a}$ with 
$\operatorname {Nm} \mathfrak {b} = D\ell ^2$. This implies that 
$\ell = \mathfrak {c}_1 \mathfrak {c}_2$ (i.e. the prime 
$\ell$ splits in 
$R_n$), and that 
$\mathfrak {b} = \mathfrak {d}\mathfrak {c}_1^2$ or 
$\mathfrak {b} = \mathfrak {d}\mathfrak {c}_2^2$, where 
$\mathfrak {d}$ is some ideal such that 
$\operatorname {Nm} \mathfrak {d}=D$ (the case 
$\mathfrak {b} = \mathfrak {c}_1 \mathfrak {c}_2$ is ruled out by the above discussion that 
$\mathfrak {a}$ and, therefore, 
$\mathfrak {b}$ is not equivalent to any ideal whose norm is 
$D$). In other words, 
$Q'$ restricted to 
$P_n$ represents 
$D\ell ^2$ if and only if there exist some ideals 
$\mathfrak {c},\mathfrak {d}$ such that 
$\operatorname {Nm} \mathfrak {c}=\ell$, 
$\operatorname {Nm} \mathfrak {d}=D$, and 
$\mathfrak {c}^2\mathfrak {d}$ is equivalent to 
$\mathfrak {a}$.
Let 
$C$ denote the equivalence classes of ideals 
$\mathfrak {c}$ such that 
$\mathfrak {c}^2$ is equivalent to 
$\mathfrak {a}\mathfrak {d}^{-1}$ for some 
$\mathfrak {d}$ with 
$\operatorname {Nm} \mathfrak {d}=D$. As 
$D$ is fixed, then 
$C$ is a finite (independent of 
$n$) union of torsors for the 
$2$-torsion of the class group of 
$R_n$, when 
$C$ is non-empty. By genus theory, the cardinality of the two-torsion of the class group of 
$R_n$ is bounded above by the number of divisors of 
$d_n^2$; this is classical and dates back to Gauss in the case when 
$R_n$ is the maximal order in its field of fractions, and can be deduced for non-maximal orders from [Reference NeukirchNeu99, Proposition 12.9]. Thus, 
$\# C=O_\epsilon (d_n^{\epsilon })$.
We finish the proof in two cases.
(1) If 
$d_n \leq (\log M)^2$, it follows by [Reference Thorner and ZamanTZ18, Corollary 1.3] that the proportion of primes represented by the quadratic form associated to any ideal class 
$\mathfrak {c}$ is 
$1/d_n$ because 
$d_n\asymp$ the class number of 
$R_n$. Thus, the total proportion of 
$\ell$ such that 
$D\ell ^2$ is representable is 
$\#C/d_n=O_\epsilon (d_n^{\epsilon -1})$, which goes to zero as 
$d_n\rightarrow \infty$.
(2) If 
$d_n \geq (\log M)^2$, let 
$f_{\mathfrak {c}}$ denote the binary quadratic form associated to 
$\mathfrak {c}$. Then as in the proof of [Reference Shankar and TangST20, Claim 3.1.9], we have
\begin{align*} \#\{\ell \mid \ell & <(M/D)^{1/2} \text{ representable by }f_{\mathfrak{c}}\}\leq \#\{m \mid m<(M/D)^{1/2} \text{ representable by }f_{\mathfrak{c}}\}\\ & =O(M^{1/2}/d_n+M^{1/4}). \end{align*}Thus, by the above discussion,
\[ \#\{\ell \mid \exists v\in P_n, Q'(v)=D\ell^2\leq M\}=(\#C)O(M^{1/2}/d_n+M^{1/4})=o(M^{1/2}/\log M),\]which finishes the proof.
The following result gives a bound of Fourier coefficients of the cuspidal part of our theta series in terms of the discriminant of the quadratic lattice.
Proposition 9.1.5 (Duke and Waibel)
Let 
$S$ be a fixed finite set of primes. Let 
$\theta$ be the theta series attached to a positive definite quadratic lattice of rank-
$5$ with discriminant 
$D_\theta$ such that all prime factors of 
$D_\theta$ lie in 
$S$. Write 
$\theta =E+G$, where 
$E$ is an Eisenstein series and 
$G$ is a cusp form. Then, there exist absolutely bounded positive constants 
$N_0$ and 
$C$ such that for all 
$m\in T$ (the set 
$T$ defined in § 4.3.3), the 
$m$th Fourier coefficient 
$q_G(m)$ of 
$G$ satisfies that 
$q_G(m) \leq CD_\theta ^{N_0} m^{1 + 1/4}$.
By Remark 7.2.2, we have that 
$\operatorname {disc} L'_{n,i}$ are independent of 
$n,i$ away from 
$p$ and hence all the theta series attached to these lattices satisfy the assumption on 
$D_\theta$.
An analogous result of Proposition 9.1.5 was proved by Duke in the case of ternary quadratic forms. The main steps of his proof carry through in this case too, so we will be content with just sketching his proof.
Proof. The proof of [Reference DukeDuk05, Lemma 1] and the discussion on [Reference DukeDuk05, p.40] apply to rank-
$5$ quadratic forms (with suitable modification of the power of 
$D_\theta$) and we have that the Petersson norm of 
$G$ satisfies 
$\|G\|=O(D_\theta ^{N_1})$ for some absolute constant 
$N_1$ (here we use the fact that the level 
$N_\theta$ of 
$G$ is 
$O(D_\theta )$.
Thus, to obtain a bound for 
$q_G(m)$, we only need to bound the Fourier coefficients 
$a_j(m)$ for an orthonormal basis of the space of cusp forms of weight 
$5/2$ and level 
$N_\theta$ (with respect to certain quadratic character determined by 
$\theta$). Now we apply [Reference WaibelWai18, Theorem 1]. Using the notation there, we have that if 
$m=\ell$, then 
$t=\ell$, 
$v=1$, 
$w=1$, 
$(m,N_\theta )=O(1)$; if 
$m=D\ell ^2$, then 
$t=D, v\asymp 1, w\asymp \ell, (m,N_\theta )=O(1)$. Thus, 
$|a_j(m)|\ll _\epsilon m^{{27}/{28}+\epsilon }D_\theta ^\epsilon$ for 
$m=\ell$ and 
$|a_j(m)|\ll _\epsilon m^{{3}/{4}+\epsilon }D_\theta ^\epsilon$, which gives the desired bound once we combine with the above estimate of 
$\|G\|$.
9.2 Proof of Proposition 7.2.5 in the Siegel case
Notation as in § 7.2.3 and Corollary 7.2.4. For a supersingular point 
$P$ with non-zero local intersection number, we first prove that it must be superspecial in the settings of Theorems 1 and 5 and Remark 4 when 
$p$ splits in 
$F$ and then estimate 
$\sum _{m\in T_M-S_M}r_{n,i}(m)$ with respect to different ranges of 
$n$.
Definition 9.2.1 Given absolute constants 
$\epsilon _0,\epsilon _1>0$ (we choose 
$\epsilon _0,\epsilon _1$ in the proof of Proposition 7.2.5), the ranges of 
$n$ are defined as follows:
(i)
$n$ is small if $n \leq \epsilon _0 \log _p M$;(ii)
$n$ is in the lower medium range if $\epsilon _0 \log _p M < n \leq \frac {3}{4} \log _p M$;(iii)
$n$ is in the upper medium range if $\frac {3}{4} \log _p M < n \leq (1 + \epsilon _1)\log _p M$;(iv)
$n$ is large if $n > (1 + \epsilon _1)\log _p M$.
Proof Proof of Proposition 7.2.5 for Theorem 1(1) and Remark 4 with $p$ split in $F$
For 
$m\in T_M$, we have 
$m=D\ell ^2$, where 
$D$ is a non-zero quadratic residue mod 
$p$. Then by § 4.4.3(2), any supergeneric point does not lie on 
$Z(m)$. Hence, we only consider 
$P$ superspecial.
Recall from Lemma 7.1.1 that for any 
$S_M$ such that 
$\#S_M=o(\# T_M)$, we have
\[ \sum_{m\in T_M-S_M}C.Z(m)\asymp \sum_{m\in T_M-S_M}g_P(m)\asymp M^2(\log M)^{-1}. \]
We first prove that there exists 
$S_M$ such that 
$\#S_M=o(\# T_M)$ and the contribution from 
$n\geq \epsilon _0 \log _p M$ is 
$o(M^2/\log M)$.
The lower medium range. By Proposition 9.1.3(1),
\begin{align*} & \sum_{m\in T_M-S_M}\sum_{n=\lceil\epsilon_0 \log_p M\rceil}^{[({3}/{4})\log_p M]}\frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))\\ &\quad \leq \sum_{m=D\ell^2,\, m\leq M}\sum_{n=\lceil\epsilon_0 \log_p M\rceil}^{[({3}/{4})\log_p M]} Ap^n r_{n,1}(m)\\ &\quad = A\sum_{n=\lceil\epsilon_0 \log_p M\rceil}^{[({3}/{4})\log_p M]} p^n O_\epsilon (M^{2+\epsilon}/p^{2n} + M^{3/2+\epsilon}/p^n + M^{1+\epsilon})\\ &\quad=O_\epsilon(M^{2+\epsilon-\epsilon_0} + M^{3/2 + \epsilon} \log M + M^{7/4 + \epsilon}), \end{align*}
which is 
$o(M^2/\log M)$ once we take 
$\epsilon <\min \{\epsilon _0,1/4\}$.
The upper medium range. We treat this part in two ways according to whether 
$d_{n_0} \leq M^{1/8}$, where 
$n_0 = \lceil \frac {3}{4}\log _p M\rceil$.
(1) If 
$d_{n_0} \geq M^{1/8}$, then we bound this part using geometry-of-numbers. As 
$L'_{n,1}\subset L'_{n_0,1}$ for all 
$n\geq n_0$, then, by definition, 
$d_n\geq d_{n_0}\geq M^{1/8}$. By Proposition 9.1.3(2), we have that
\begin{align*} &\sum_{m\in T_M-S_M}\sum_{n=\lceil({3}/{4})\log_p M\rceil}^{[(1 + \epsilon_1)\log_p M]}\frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))\\ &\quad \leq \sum_{n=\lceil({3}/{4})\log_p M\rceil}^{[(1 + \epsilon_1)\log_p M]}\sum_{m=D\ell^2,\, m\leq M} Ap^n r_{n,1}(m)\\ &\quad = O((M + M^{5/4} + M^{3/2} + M^{15/8 + \epsilon_1} + M^{3/2 + \epsilon_1})\log M), \end{align*}
which is 
$o(M^2/\log M)$ once we take 
$\epsilon _1<1/8$.
(2) If 
$d_{n_0} < M^{1/8}$, we control this part by putting 
$m$ in this range into 
$S_M$. More precisely, consider 
$R_M:=\{m\in T_M \mid \exists v\in L'_{n_0,1}, Q'(v)=m\}$. By our assumption, 
$d_{n_0}^2M< M^{5/4}=o(p^{2n_0})$ and by Lemma 9.1.2, for 
$M\gg 1$, if 
$m\in R_M$, then 
$m$ is represented by 
$Q'\!\mid _{P_{n_0}}$, which is a binary quadratic form. Then by Proposition 9.1.4 (note that 
$n_0\rightarrow \infty$ as 
$M\rightarrow \infty$), 
$\#R_M=o(M^{1/2}/\log M)=o(\# T_M)$. Thus, we may choose 
$S_M$ such that 
$S_M\supset R_M$ and then
\[ \sum_{m\in T_M-S_M}\sum_{n=\lceil\frac{3}{4}\log_p M\rceil}^{[(1 + \epsilon_1)\log_p M]}\frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))=0. \]
The large 
$n$. Let 
$n_0=\lceil (1+\epsilon _1)\log _p M\rceil$ and let 
$R_M':=\{m\in T_M \mid \exists v\in L'_{n_0,1}, Q'(v)=m\}$. We show that 
$\#R'_M=o(M^{1/2}/\log M)$ and, thus, we may choose 
$S_M$ such that 
$S_M\supset R'_M$ and then
\[ \sum_{m\in T_M-S_M}\sum_{n=\lceil(1 + \epsilon_1)\log_p M\rceil}^{\infty}\frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))=0. \]
We bound the size of 
$R'_M$ case by case depending on the size of 
$d_{n_0}, l(n_0)_1$.
Case (1): 
$d_{n_0} \leq M^{1/2+\epsilon _2}$ for some absolute constant 
$\epsilon _2<\epsilon _1/2$. Then 
$d_{n_0}\leq M^{1/2+\epsilon _2}< p^{n_0/2}$ and 
$M< p^{n_0-\epsilon _1}$. By Lemma 9.1.2, for 
$M\gg 1$, if 
$m\in R'_M$, then 
$m$ is represented by 
$Q'\!\mid _{P_{n_0}}$. By Proposition 9.1.4, 
$\#R'_M=o(M^{1/2}/\log M)$.
Case (2): 
$d_{n_0} > M^{1/2+\epsilon _2}$ for all 
$\epsilon _2<\epsilon _1/2$ and 
$l(n_0)_1>M^{\epsilon _3}$ for some absolute constant 
$\epsilon _3>0$. We have 
$\#R'_M\leq \#\{v\in L'_{n_0,1}\mid Q'(v)\in T_M\}$, which is 
$O(M^{1/2-\epsilon _1}+M^{1/2-\epsilon _2}+M^{1/2}/l(n_0)_1)=o(M^{1/2}/\log M)$ by Proposition 9.1.3(2).
Case (3): 
$d_{n_0} > M^{1/2+\epsilon _2}$ for some 
$\epsilon _2<\epsilon _1/2$ and 
$l(n_0)_1\leq M^{\epsilon _3}$ for some 
$\epsilon _3<\epsilon _2$. Then 
$l(n_0)_2=d_{n_0}/l(n_0)_1>M^{1/2}$. In other words, any vector 
$v\in L'_{n_0,1}$ which is not a scalar multiple of the chosen vector 
$v_0$ of the minimum length has 
$Q'_{n_0}(v)\leq l(n_0)_2^2>M$. Therefore, any 
$m\in R'_M$ has to be represented by the rank-
$1$ quadratic form spanned by 
$v_0$. As 
$M\rightarrow \infty$, we have 
$l(n_0)_1\rightarrow \infty$. Thus, once 
$M$ is large enough such that 
$l(n_0)_1^2>D$, then this rank-
$1$ quadratic form would represent at most one element in 
$T_M$ and, hence, 
$\#R'_M=o(\# T_M)$.
In conclusion, taking 
$S_M=R_M\cup R'_M$, we have 
$\#S_M=o(\# T_M)$ and
\[ \sum_{m\in T_M-S_M}\sum_{n=\lceil\epsilon_0 \log_p M\rceil}^{\infty}\!\!\frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))=o(M^2/\log M). \]
The small 
$n$. We follow the notation and the idea of the proof in Lemma 8.2.2.
We enlarge 
$L'_{n,1}$ as in the proof of Lemma 9.1.1; also let 
$w$ be the vector which decays very rapidly in the decay lemma for superspecial points, then we enlarge 
$L'_{n,2}$ such that 
$L'_{n,2}\otimes \mathbb {Z}_p=L'_{n,1}\otimes \mathbb {Z}_p+p^{n+1}\mathbb {Z}_pw$. Then 
$\operatorname {disc} L'_{n,i}\asymp p^{6n}$ with the implicit constant only depending on 
$P$. Note that Corollary 7.2.4 still holds with the new definitions of 
$L'_{n,i}$.
Let
\begin{gather*} E=\frac{A(p+2)}{2p}E_{0,1}+ \frac{A}{2}E_{0,2}+\sum_{n=1}^{[\epsilon_0 \log_p M]} \frac{Ap^n}{2}( E_{n,1}+ E_{n,2}),\\ G=\frac{A(p+2)}{2p}G_{0,1}+ \frac{A}{2}G_{0,2}+\sum_{n=1}^{[\epsilon_0 \log_p M]} \frac{Ap^n}{2}( G_{n,1}+ G_{n,2}). \end{gather*}
Note that here the Eisenstein series 
$E$ and the cusp form 
$G$ depend on 
$M$.
As 
$\operatorname {disc} L'_{n,i}=O(p^{6\epsilon _0 \log _p M})=O(M^{6\epsilon _0})$ for 
$n\leq \epsilon _0 \log _p M$, then by Proposition 9.1.5, the 
$m$th Fourier coefficient
\[ q_G(m)\ll (M^{6\epsilon_0})^{N_0}m^{5/4}\sum_{n=0}^{[\epsilon_0 \log M]}p^n\ll M^{(6N_0+1)\epsilon_0} m^{5/4} \]
and 
$\sum _{m\in T_M-S_M} q_G(m)=O(M^{(6N_0+1)\epsilon _0+7/4})=o(M^2/\log M)$ once we take 
$\epsilon _0<(24N_0+4)^{-1}$.
The computation for the Eisenstein part is the same as in the proof of Lemma 8.2.2. More precisely, because 
$p\nmid m$, by Lemma 4.4.6(1) and (3), we have
\[ \frac{q(m)}{|q_L(m)|}\leq \frac{A(p+2)}{2p}\cdot \frac{1}{p-1}+\frac{A}{2}\frac{2p}{(p^2-1)p}+\sum_{n=1}^{[\epsilon_0 \log M]}\frac{Ap^n}{2}\cdot \frac{2p}{p^2-1}(p^{-3n}+p^{-3n-1})\leq \frac{11}{12}\cdot\frac{A}{p-1}. \]Thus, we finish the proof by putting all parts together and using Corollary 7.2.4.
Proof of Proposition 7.2.5 for Theorem 5 As every 
$m\in T_M$ in this case is a non-zero quadratic residue 
$\bmod p$, hence by § 4.4.3(2), all supersingular points on 
$Z(m)$ are superspecial. The idea of the proof is similar to the case of Theorem 1(1).
By Lemma 7.1.1, we have 
$\sum _{m\in T_M-S_M}g_P(m)\asymp M^{5/2}(\log M)^{-1}$. We construct 
$S_M$ by large 
$n$. More precisely, we set 
$S_M=\{m\in T_M \mid \exists v\in L'_{n_0,1}, Q'(v)=m\}$, where 
$n_0=\lceil (1+\epsilon _1)\log _p M\rceil$. Then
\begin{align*} \#S_M \leq \#\{v\in L'_{n_0,1}\mid Q'(v)\leq M\}&=O(M^{5/2}/p^{3n_0}+M^2/p^{2n_0}+M^{3/2}/p^{n_0}+M/d_{n_0}+M^{1/2})\\ &=O(M^{1/2}+M/d_{n_0}), \end{align*}
which is 
$o(M/\log M)=o(\# T_M)$ if there exists an absolute constant 
$\epsilon >0$ such that 
${d_{n_0}\gg M^\epsilon}$. If not, then by Lemma 9.1.2, we have that for 
$M\gg 1$, all 
$m\in S_M$ representable by the binary quadratic form 
$Q'|_{P_{n_0}}$. As 
$d_{n_0}\rightarrow \infty$, the density of primes representable by 
$Q'|_{P_{n_0}}$ goes to zero, that is, we still have 
$\#S_M=o(\# T_M)$. With this choice of 
$S_M$, we have
\[ \sum_{m\in T_M-S_M}\sum_{n=\lceil(1 + \epsilon_1)\log_p M\rceil}^{\infty}\frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))=0. \]
For 
$n$ in the medium range,
\[ \sum_{m\in T_M-S_M}\sum_{n=\lceil \epsilon_0 \log_p M\rceil}^{\lceil(1 + \epsilon_1)\log_p M\rceil}\frac{Ap^n}{2}(r_{n,1}(m)+r_{n,2}(m))\ll \sum_{n=\lceil \epsilon_0 \log_p M\rceil}^{\lceil(1 + \epsilon_1)\log_p M\rceil}\!\! p^n \sum_{m\leq M} r_{n,1}(m)=o(M^{5/2}/\log M) \]
because 
$\sum _{m\leq M} r_{n,1}(m)=O(M^{5/2}/p^{3n}+M^2/p^{2n}+M^{3/2}/p^n+M)$. The estimate for small 
$n$ is exactly as in the case for Theorem 1(1) above and, thus, we finish the proof.
9.3 Contribution from non-supersingular points and conclusions
To finish the proof, we only need to show that 
$\sum _{m\in T_M-S_M} l_P(m)$ for non-supersingular points 
$P$ are 
$o(\sum _{m\in T_M-S_M}C.Z(m))$, which is 
$o(M^2/\log M)$ for Theorem 1(1) and Remark 4 and is 
$o(M^{5/2}/\log M)$ for Theorem 5. We use the notation in Lemma 7.3.2 for ordinary points.
Recall that an abelian surface is ordinary, almost ordinary (i.e. its Newton polygon has slopes 
$0,1/2,1$), or supersingular.
Lemma 9.3.1 If 
$P$ is almost ordinary or if 
$P$ is ordinary with 
$\operatorname {rk}_{\mathbb {Z}} L_0\neq 3$, then
\[ \sum_{m\in T_M-S_M} l_P(m)=o\biggl(\sum_{m\in T_M-S_M}C.Z(m)\biggr). \]Proof. By the classification of endomorphism rings of char 
$p$ abelian surfaces (see, for instance, [Reference TateTat71, Theorem 1]), we see that if the abelian surface corresponding to 
$P$ has almost ordinary reduction, then its lattice of special endomorphisms has rank at most 
$1$. On the other hand, if 
$P$ is ordinary, then 
$\operatorname {rk}_{\mathbb {Z}} L_0$ is odd and, hence, 
$\operatorname {rk}_{\mathbb {Z}} L_0=1$. In both cases, let 
$a_n x^2$ denote the quadratic form with one variable given by 
$Q'$ restricted to the lattice of special endomorphisms of the abelian surface mod 
$t^n$. As the lattice mod 
$t^{n+1}$ is a sublattice of that mod 
$t^n$, we have 
$a_n\mid a_{n+1}$.
As 
$C$ does not have any global special endomorphisms, we have 
$a_n\rightarrow \infty$ and, hence, 
$a_nx^2$ does not represent any element in 
$T_M\subset \{D\ell ^2\mid \ell \text { prime}\}$ or 
$T_M\subset \{\ell \mid \ell \text { prime}\}$ once 
$n\gg 1$ (with then implicit constant only depending on 
$P$).
Thus, 
$\sum _{m\in T_M-S_M} l_P(m)=\sum _{m\in T_M-S_M} O(M^{1/2})=o(\sum _{m\in T_M-S_M}C.Z(m))$.
Now it only remains to treat the case when 
$P$ is ordinary and 
$\operatorname {rk}_{\mathbb {Z}}L_0=3$. We first construct 
$S_M$ for such 
$P$.
Lemma 9.3.2 Given 
$M$, set 
$n_0=\lceil (1+\epsilon _0)\log _p M\rceil$ and 
$S_M=\{m\in T_M\mid \exists v\in L_{n_0} \text { with} Q'(v)=m\}$. Then 
$\#S_M=o(\# T_M)$.
Proof. By a geometry-of-numbers argument and Lemma 7.3.2, we have
\[ \#S_M\leq \{v\in L_{n_0}\mid Q'(v)\leq M\}=O(M^{3/2}/p^{n_0}+M/b_{n_0}+M^{1/2}/a_{n_0}), \]
where 
$a_{n_0}$ is the minimal length of a non-zero vector in 
$L_{n_0}$ and 
$b_{n_0}$ is the minimal root discriminant of a rank 
$2$ sublattice in 
$L_{n_0}$. Since 
$C$ does not have any global special endomorphisms, we have 
$a_{n_0},b_{n_0}\rightarrow \infty$ as 
$M\rightarrow \infty$. Fix 
$0<\epsilon _1<\epsilon _0/4$. We prove the desired estimate by a case-by-case discussion based on the size of 
$a_{n_0},b_{n_0}$.
Case (1): 
$a_{n_0}< M^{\epsilon _1}$ and 
$b_{n_0}>M^{1/2+2\epsilon _1}$. Then we conclude as in the proof Proposition 7.2.5 for Theorem 1(1) for large 
$n$ case (3). More precisely, all 
$v\in L_{n_0}$ with 
$Q'(v)\leq M$ lie in a rank-
$1$ sublattice of 
$L_{n_0}$ and, thus, the total number of such 
$v$ is 
$o(\# T_M)$.
Case (2): 
$a_{n_0}\geq M^{\epsilon _1}$ and 
$b_{n_0}>M^{1/2+2\epsilon _1}$. Then
\[ \#S_M=O(M^{3/2}/p^{n_0}+M/b_{n_0}+M^{1/2}/a_{n_0})=O(M^{1/2-\epsilon_1})=o(M^{1/2}/\log M). \] Case (3): 
$b_{n_0}\leq M^{1/2+2\epsilon _1}$. Then 
$p^{n_0/2}=M^{1/2+\epsilon _0/2}\geq b_{n_0}$ and by Lemma 9.1.2 (note the proof of this lemma applies to this case), for 
$M\gg 1$, if 
$m\in S_M$, then 
$m$ is represented by the binary quadratic form given by restricting 
$Q'$ to the rank-
$2$ sublattice in 
$L_{n_0}$ with minimal discriminant(=
$b_{n_0}^2$). As 
$b_{n_0}\rightarrow \infty$, then we conclude by Proposition 9.1.4 for Theorem 1(1) and Remark 4 and by the fact that the density of primes represented by such quadratic forms goes to zero for Theorem 5.
Now we estimate the total local contribution at an ordinary point with 
$\operatorname {rk}_{\mathbb {Z}}L_0=3$.
Proposition 9.3.3 Assume 
$P$ is ordinary with 
$\operatorname {rk}_{\mathbb {Z}}L_0=3$. After possible enlarging 
$S_M$ in Lemma 9.3.2 (still with 
$\#S_M=o(\#T_M)$), we have
\[ \sum_{m\in T_M-S_M} l_P(m)=o \biggl (\sum_{m\in T_M-S_M}C.Z(m) \biggr ). \]Proof. Notation as in Lemma 7.3.2. By Lemmas 7.2.1, 7.3.2, and 9.3.2, we have
\begin{align*} \sum_{m\in T_M-S_M} l_P(m)&=\sum_{m\in T_M-S_M}A(r_0(m)+\sum_{n=1}^{[(1+\epsilon_0)\log_p M]}(p^n-p^{n-1})r_n(m))\\ &\ll \sum_{n=0}^{[(1+\epsilon_0)\log_p M]} p^n \sum_{m\in T_M-S_M} r_n(m). \end{align*}
Notation is as in Lemma 9.3.2. We have 
$\sum _{m=1}^M r_n(m)=O(M^{3/2}/p^n+M/b_n+M^{1/2}/a_n)$.
For Theorem 5, we have
\[ \sum_{m\in T_M-S_M} l_P(m)\ll \sum_{n=0}^{[(1+\epsilon_0)\log_p M]} p^n(M^{3/2}/p^n+M)=O(M^{2+\epsilon_0})=o(M^{5/2}/\log M), \]
when we take 
$\epsilon _0<1/2$.
For Theorem 1(1) and Remark 4, set 
$n_1=\lceil ({3}/{4})\log _p M\rceil$. First,
\[ \sum_{n=0}^{n_1} p^n \sum_{m\in T_M-S_M} r_n(m)\ll \sum_{n=0}^{n_1}p^n(M^{3/2}/p^n+M)=O(M^{7/4})=o(M^2/\log M). \]
Second, for 
$\sum _{n=n_1}^{[(1+\epsilon _0)\log _p M]} p^n \sum _{m\in T_M-S_M}r_n(m)$, we bound it by studying the following two cases separately.
Case (1): 
$b_{n_1}\geq M^{1/8}$. As in the first part, we have
\[ \sum_{n=n_1}^{[(1+\epsilon_0)\log_p M]}p^n \sum_{m\in T_M-S_M}r_n(m)\ll \sum_{n=n_1}^{[(1+\epsilon_0)\log_p M]} p^n(M^{3/2}/p^n+M/b_n+M^{1/2}), \]
which is 
$O(M^{3/2}\log M + M^{2+\epsilon _0-1/8}+M^{3/2+\epsilon _0})=o(M^2/\log M)$ once we take 
$\epsilon _0<1/8$.
Case (2): 
$b_{n_1} < M^{1/8}$. We are going to enlarge 
$S_M$ to be 
$\{m\in T_M\mid \exists v\in L_{n_1} \text { with } Q'(v)=m\}$. As 
$b_{n_1}^2 M < M^{5/4}=o(p^{2n_1})$, then we conclude, as in the upper medium range Case (2) in the proof of Proposition 7.2.5 for Theorem 1(1), by Lemma 9.1.2 and Proposition 9.1.4 that 
$\#S_M=o(\#T_M)$ and 
$\sum _{n=n_1}^{[(1+\epsilon _0)\log _p M]}p^n \sum _{m\in T_M-S_M}r_n(m)=0$.
Proof Proof of Theorem 1(1), Remark 4 with $p$ split in $F$, and Theorem 5
Assume for contradiction that there are only finitely many points on 
$C\cap (\bigcup _{m\in T}Z(m))$. Then we construct 
$S_M$ by taking the union of the 
$S_M$ in Proposition 7.2.5 for supersingular points and that in Lemma 9.3.2 and Proposition 9.3.3 for ordinary points with 
$\operatorname {rk}_{\mathbb {Z}}L_0=3$. As it is a finite union, we still have 
$\#S_M=o(\#T_M)$. We deduce a contradiction by Lemma 7.1.1, Proposition 7.2.5, Lemma 9.3.1, and Proposition 9.3.3.
Acknowledgements
We thank Johan de Jong, Keerthi Madapusi Pera, Arul Shankar, Salim Tayou, and Jacob Tsimerman for helpful discussions. D.M. is partially supported by NSF FRG grant DMS-1159265. A.N.S. is partially supported by the NSF grant DMS-2100436. Y.T. is partially supported by the NSF grant DMS-1801237. We would like to thank the anonymous referees for thorough readings and valuable suggestions which have greatly helped improve this paper.
Open access
