Hostname: page-component-77c78cf97d-d2fvj Total loading time: 0 Render date: 2026-04-25T00:47:57.771Z Has data issue: false hasContentIssue false
  • English
  • Français

Relations in the Sarkisov program

Part of: Birational geometry

Published online by Cambridge University Press:  28 August 2013

Anne-Sophie Kaloghiros
Anne-Sophie Kaloghiros*
Affiliation:
Department of Mathematics, Imperial College London, 180 Queen’s Gate, London SW7 2AZ, UK email a.kaloghiros@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

The Sarkisov program studies birational maps between varieties that are end products of the Minimal Model Program (MMP) on nonsingular uniruled varieties. If 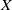$X$ and 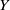$Y$ are terminal 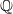$ \mathbb{Q} $-factorial projective varieties endowed with a structure of Mori fibre space, a birational map 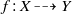$f: X\dashrightarrow Y$ is the composition of a finite number of elementary Sarkisov links. This decomposition is in general not unique: two such define a relation in the Sarkisov program. I define elementary relations, and show they generate relations in the Sarkisov program. Roughly speaking, elementary relations are the relations among the end products of suitable relative MMPs of 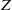$Z$ over 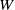$W$ with 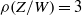$\rho (Z/ W)= 3$.

Keywords

Sarkisov programMinimal Model Program

MSC classification

Secondary: 14E30: Minimal model program (Mori theory, extremal rays) 14E05: Rational and birational maps

Information

Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 10 , October 2013 , pp. 1685 - 1709
Copyright
© The Author(s) 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Birkar, C., Cascini, P., Hacon, C. D. and McKernan, J., Existence of minimal models for varieties of log general type, J. Amer. Math. Soc. 23 (2010), 405–468.Google Scholar
Cascini, P. and Lazić, V., New outlook on the minimal model program, I, Duke Math. J. 161 (2012), 2415–2467; math.AG/1009.3188.Google Scholar
Corti, A., Factoring birational maps of threefolds after Sarkisov, J. Algebraic Geom. 4 (1995), 223–254; MR 1311348 (96c:14013).Google Scholar
Ein, L., Lazarsfeld, R., Mustaţă, M., Nakamaye, M. and Popa, M., Asymptotic invariants of base loci, Ann. Inst. Fourier (Grenoble) 56 (2006), 1701–1734.CrossRefGoogle Scholar
Grünbaum, B., Convex polytopes, Pure and Applied Mathematics, vol. 16 (John Wiley & Sons, New York, NY, 1967).Google Scholar
Hacon, C. D. and McKernan, J., The Sarkisov program, J. Algebraic Geom. 22 (2013), 389–405.Google Scholar
Kaloghiros, A.-S., Küronya, A. and Lazić, V., Minimal models and extremal rays, Advanced Studies in Pure Mathematics (Mathematical Society of Japan, Tokyo, 2013).Google Scholar
Kapovich, M. and Kollár, J., Fundamental groups and links of isolated singularities, Preprint (2011), math.AG/1109:4047.Google Scholar
Kawamata, Y., Flops connect minimal models, Publ. Res. Inst. Math. Sci. 44 (2008), 419–423.CrossRefGoogle Scholar
Kollár, J., Flips and abundance for algebraic threefolds, Astérisque 211 (Société Mathématique de France, Paris, 1992).Google Scholar
Lazarsfeld, R., Positivity in algebraic geometry. II, Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 49 (Springer, Berlin, 2004).Google Scholar
Mori, S. and Mukai, S., Classification of Fano 3-folds with ${B}_{2} \geq 2$, Manuscripta Math. 36 (1981), 147–162.Google Scholar
Mori, S. and Mukai, S., Classification of Fano 3-folds with ${B}_{2} \geq 2$. I, in Algebraic and topological theories, Kinosaki, 1984 (Kinokuniya, Tokyo, 1986), 496–545.Google Scholar
Shokurov, V. and Choi, S. R., Geography of log models: theory and applications, Cent. Eur. J. Math. 9 (2011), 489–534.Google Scholar