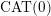Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Groves, Daniel
and
Manning, Jason Fox
2022.
Specializing cubulated relatively hyperbolic groups.
Journal of Topology,
Vol. 15,
Issue. 2,
p.
398.
Einstein, Eduard
and
Groves, Daniel
2022.
Relatively geometric actions on CAT$\operatorname{CAT}$(0) cube complexes.
Journal of the London Mathematical Society,
Vol. 105,
Issue. 1,
p.
691.
Reyes, Eduardo
2023.
On cubulated relatively hyperbolic groups.
Geometry & Topology,
Vol. 27,
Issue. 2,
p.
575.
Groves, Daniel
and
Manning, Jason Fox
2023.
Hyperbolic groups acting improperly.
Geometry & Topology,
Vol. 27,
Issue. 9,
p.
3387.
Bregman, Corey
Groves, Daniel
and
Zhu, Kejia
2024.
Relatively geometric actions of Kähler groups
on CAT(0) cube complexes.
Algebraic & Geometric Topology,
Vol. 24,
Issue. 7,
p.
4127.
Dahmani, François
Meda Satish, Suraj Krishna
and
Mutanguha, Jean Pierre
2025.
Hyperbolic hyperbolic-by-cyclic groups are cubulable.
Geometry & Topology,
Vol. 29,
Issue. 1,
p.
259.
Lafont, Jean‐François
and
Ruffoni, Lorenzo
2025.
Relative cubulation of relative strict hyperbolization.
Journal of the London Mathematical Society,
Vol. 111,
Issue. 4,
Einstein, Eduard
M S, Suraj Krishna
and
Ng, Thomas
2025.
On the boundary criterion for relative cubulation: Multiended parabolics.
Bulletin of the London Mathematical Society,
Vol. 57,
Issue. 7,
p.
2177.
Einstein, Eduard
and
Groves, Daniel
2025.
Corrigendum to “Relatively geometric actions on CAT(0) cube complexes”.
Journal of the London Mathematical Society,
Vol. 111,
Issue. 6,
Dahmani, François
and
Meda Satish, Suraj Krishna
2025.
Cubulating a free-product-by-cyclic group.
Algebraic & Geometric Topology,
Vol. 25,
Issue. 3,
p.
1561.
Zhu, Kejia
2025.
A note on complex hyperbolic lattices and strict hyperbolization.
Journal of Group Theory,